Numerical treatment of the space fractional advection–dispersion model arising in groundwater hydrology

Abstract

This paper studies a new computational method for the approximate solution of the space fractional advection–dispersion equation in sense of Caputo derivatives. In the first method, a time discretization is accomplished via the compact finite difference, while the fourth kind shifted Chebyshev polynomials are used to discretize the spatial derivative. The unconditional stability and convergence order of the method are studied via the energy method. Three examples are given for illustrating the effectiveness and accuracy of the new scheme when compared with existing numerical methods reported in the literature.

1 Introduction

Fractional calculus (FC) can be viewed as the generalization of classical calculus to non-integer orders (Podlubny 1998; Oldham and Spanier 1974; Milici et al. 2018). In recent years, FC has gained considerable popularity and importance in various fields of science and engineering including economics, optimal control, materials, chemistry, physics, and social science (Ortigueira and Machado 2020; Tenreiro Machado and Lopes 2019; Rigi and Tajadodi 2019; Mahmoudi et al. 2019). In fact, due to the adequacy of fractional derivatives for capturing memory effects, many physical systems can be well described by means of fractional differential equations (Toubaei et al. 2019; Golbabai et al. 2019b, a; Nikan et al. 2020).

We consider the general advection–dispersion equation that is naturally utilized to explain the transient transport of solutes as

$$\begin{aligned} R \frac{\partial C(\xi ,\tau )}{\partial \tau }=\left[ D_{L}\frac{\partial ^{2} }{\partial \xi ^{2}}-\nu \frac{\partial }{\partial \xi }\right] C(\xi ,\tau ), \end{aligned}$$

(1)

where $D_{L}=D_{e}+\alpha _{L}\nu$, $D_{L}>0,$ and $\nu > 0$. Table 1 lists the required parameters and variables for the equation (1).

Table 1 The parameters for advection–dispersion equation

Fractional space derivatives are applied for modeling anomalous diffusion or dispersion, where a particle spreads at a rate inconsistent with the classical Brownian motion model. The model (1) is based on the Fick’s law, which describes the transport of passive tracers carried through a fluid flow in a porous medium (Liu et al. 2004). The FADE is a fundamental equation of motion that is used for modeling water flow movement (Hu et al. 2016), material transport and diffusion (Hernandez et al. 1995). For convenience and without losing the generality, let us introduce dimensionless space, time, and concentration variables by

$$\begin{aligned} x=\frac{\xi }{L},\qquad t= \frac{\tau }{L/ \nu },\qquad u=\frac{C}{C_{0}}, \end{aligned}$$

respectively. Then the dimensionless advection–dispersion equation (ADE) can be rewritten as

$$\begin{aligned} \frac{\partial u({{x}},t)}{\partial t}=\gamma \frac{{\partial }^{2 }u({{x}},t)}{{\partial x}^{2} }- \mu \frac{{\partial } u({{x}},t)}{\partial x}\cdot , \end{aligned}$$

(2)

where the constants $\gamma$ and $\mu$ are the dispersion coefficient and the average fluid velocity, respectively. In virtue of the non-local importance of fractional derivatives, we suggest fractional order in Eq. (2) is used in the groundwater hydrology for modeling transport phenomena. The space fractional advection–dispersion equation (SFADE) is obtained from the classical equation by replacing the first-order and the second-order spatial derivatives by fractional derivatives termed in Caputo sense of order $\alpha \in (1, 2]$ and $\beta \in (0, 1]$, respectively. The SFADE is presented as

$$\begin{aligned} \frac{\partial u(x, t)}{\partial t}=\gamma {{\mathcal {D}}}_{x}^{\alpha }u(x, t)-\mu {{\mathcal {D}}}_{x}^{\beta }u(x, t)+q(x, t). \end{aligned}$$

(3)

In addition, the advection–dispersion equation (ADE) of integer or fractional orders is widely utilized in environmental engineering and aviation (Liu et al. 2016), as well as in the marine (Farahani et al. 2015), chemical (Colla et al. 2015) and metallurgy (Zaib and Shafie 2014) areas. Therefore, the development of efficient numerical schemes for solving ADE is important both from the theoretical and practical point of views.

Hereafter we outline some preliminary concepts of fractional derivatives that are useful in the subsequent discussion (Podlubny 1998; Oldham and Spanier 1974; Milici et al. 2018).

Definition 1

The fractional derivative of Caputo type can be defined as

$$\begin{aligned} {{\mathcal {D}}}_{x}^{\beta }u(x, t)= {\left\{ \begin{array}{ll} \frac{1}{\varGamma (n-\beta )}\int _{0}^{x}{(x-\tau )^{n-\beta -1}}\frac{{\partial }^{n} u(\tau , t) }{\partial {\tau }^{n}}\mathrm{d}\tau , &{} n-1<\beta \le n \in {\mathbb {N}}, \\ \\ \frac{{\partial }^{n} u(x, t) }{\partial {x}^{n}}, &{} \beta =n. \end{array}\right. } \end{aligned}$$

Remark 1

Some important properties of the Caputo derivative ${{\mathcal {D}}}_{x}^{\beta }$ are as listed:

• 1. ${{\mathcal {D}}}_{x}^{\beta }x^{\alpha }= \frac{\varGamma (1+\alpha )}{\varGamma (1+\alpha -\beta )}x^{\alpha -\beta }, \quad 0< \beta <\alpha +1, \beta >-1,$

• 2. ${{\mathcal {D}}}_{x}^{\beta }(\gamma f(x, t)+ \eta u(x, t))=\gamma {{\mathcal {D}}}_{x}^{\beta }f(x, t)+\eta {{\mathcal {D}}}_{x}^{\beta }u(x, t),$

• 3. ${{\mathcal {D}}}_{x}^{\beta }{{\mathcal {D}}}_{x}^{n}u(x, t)={{\mathcal {D}}}_{x}^{\beta +n}u(x, t)\ne {{\mathcal {D}}}_{x}^{n}{{\mathcal {D}}}_{x}^{\beta }u(x, t).$

In this article, we propose an numerical approach for computing the approximate solution of the SFADE as follows:

$$\begin{aligned} \frac{\partial u(x, t)}{\partial t}=\gamma {{\mathcal {D}}}_{x}^{\alpha }u(x, t)-\mu {{\mathcal {D}}}_{x}^{\beta }u(x, t)+q(x, t), \end{aligned}$$

(4)

with the initial condition

$$\begin{aligned}&u(x, 0)=f(x),\quad 0<x<L \end{aligned}$$

(5)

and boundary conditions

$$\begin{aligned}&u(0, t)={\upsilon }_{0}(t),\quad u(L, t)={\upsilon }_{1}(t), \quad 0<t\le T, \end{aligned}$$

(6)

in which $0< \beta \le 1,\quad 1 < \alpha \le 2$.

Several numerical algorithms have been proposed for solving the SFADE. Ervin and Roop (2007) investigated an approach for FADE using the variational iteration method on bounded domain. Su et al. (2010) used the weighted average finite difference method. Khader and Sweilam (2014) adopted the Legendre collocation method. Saw and Kumar (2018, 2019) applied the Chebyshev collocation methods to obtain the approximation solution of the SFADE. Safdari et al. (2020a, 2020b) adopted the spectral collocation method for solving SFADE. Aghdam et al. (2020) formulated a spectral collocation method to approximate SFADE.

The rest of this paper has the following organization. Section 2 presents the operational matrices of the fourth kind Chebyshev polynomials (FKCP) for fractional derivative. Section 3 describes the approximation of the fractional operator ${{\mathcal {D}}}_{x}^{\alpha }u(x, t)$ and implements the Chebyshev collocation approach to solve (4). The fourth kind shifted Chebyshev polynomials (FKSCP) and the compact finite difference are implemented to discretize the SFADE in the spatial and temporal variable, respectively. Section 4 discusses error analysis and upper bounds of time-discrete approach. Section 5 presents two numerical examples illustrating effectiveness and accuracy of the new scheme. Finally, Sect. 6 includes the main conclusions.

2 Some properties of the FKSCP

The FKCP ${\mathcal {W}}_{i}(x)$ defined in the domain $[-1, 1]$ are orthogonal polynomials of degree i as follows:

$$\begin{aligned} {\mathcal {W}}_{i}(x)=\frac{2^{2i}}{\left( {\begin{array}{c}2i\\ i\end{array}}\right) }P_{i}^{\Big (\frac{1}{2},\frac{-1}{2}\Big )}(x), \end{aligned}$$

where $P_{i}^{(r , s)}(x)$ is a Jacobi polynomial orthogonal corresponding to the weight function $\omega ^{(r , s)}(x)=(1-x)^{r}(1+x)^{s}$ over $[-1, 1]$, such that

$$\begin{aligned} P^{(r , s)}_{i}=\frac{\varGamma (r +i +1)}{i! \varGamma (r +s +i+1)}\sum _{m=0}^{i}\left( {\begin{array}{c}i\\ m\end{array}}\right) \frac{\varGamma (r +s +i+m+1)}{\varGamma (r +m+1)}\times \left( \frac{x-1}{2}\right) ^{m}. \end{aligned}$$

${\mathcal {W}}_{i}(x)$ can be organized

$$\begin{aligned} {\mathcal {W}}_{i}(x) ={\mathfrak {I}}_{i}\sum _{k=0}^{i-1}\sum _{\xi =0}^{k}{\mathfrak {K}}_{i, k, \xi }\times x^{k-\xi },\quad x\in [-1, 1], \quad i=1, 2, \ldots , \end{aligned}$$

where

$$\begin{aligned} {\mathfrak {I}}_{i}=\frac{(2^{2i-2})\varGamma (i +0.5)(i-1)!}{(2i-2)!},~~ {\mathfrak {K}}_{i, k, \xi }=\frac{(-1)^{\xi } \varGamma (i+k)}{2^{k}k!\times (i-k-1) \varGamma (k+1.5) }\times \left( {\begin{array}{c}k\\ \xi \end{array}}\right) . \end{aligned}$$

The polynomials ${\mathcal {W}}_{i}(x)$ on $[-1, 1]$ corresponding to the weight function are orthogonal with the inner product as

$$\begin{aligned} \langle {\mathcal {W}}_{m}(x), {\mathcal {W}}_{n}(x)\rangle =\int _{-1}^{1}\sqrt{\frac{1-x}{1+x}}{\mathcal {W}}_{m}(x){\mathcal {W}}_{n}(x)dx= {\left\{ \begin{array}{ll} 0, &{} m\ne n, \\ \pi , &{} m =n. \end{array}\right. } \end{aligned}$$

In the domain [0, 1], the SPCFK ${\mathcal {W}}_{i}^{*}(x)={\mathcal {W}}_{i}(2x-1)$ can be defined as follows:

$$\begin{aligned} {\mathcal {W}}_{i}^{*}(x)={\mathfrak {I}}_{i}\sum _{k=0}^{i-1}\sum _{\xi =0}^{k}{\mathfrak {K}}_{i, k, \xi }\times {2}^{k}\times x^{k-\xi },\quad x\in [0, 1], \quad i=1, 2, \ldots \cdot \end{aligned}$$

These polynomials are orthogonal in the domain [0, 1] with respect to $\sqrt{\frac{1-x}{x}}$:

$$\begin{aligned} \langle {\mathcal {W}}_{m}^{*}(x), {\mathcal {W}}_{n}^{*}(x)\rangle = \int _{0}^{1}\sqrt{\frac{1-x}{x}}{\mathcal {W}}^{*}_{m}(x){\mathcal {W}}^{*}_{n}(x)dx= {\left\{ \begin{array}{ll} 0, &{} m\ne n, \\ \frac{\pi }{2} , &{} m =n. \end{array}\right. } \end{aligned}$$

Let g(x) be a square-integrable function in [0, 1]. Then g(x) may be extended in terms of ${\mathcal {W}}^{*}_{i}(x)$ as

$$\begin{aligned} g(x)=\sum _{i=0}^{N}c_{i}{\mathcal {W}}^{*}_{i}(x), \quad x\in [0, 1], \end{aligned}$$

(7)

where the coefficients $c_{i}, i=0, 1, \ldots , N$ are defied by

$$\begin{aligned} c_{i}=\frac{2}{\pi }\int _{0}^{1}\sqrt{\frac{1-x}{x}}g(x){\mathcal {W}}^{*}_{{\mathfrak {i}}}(x)\mathrm{d}x. \end{aligned}$$

(8)

The fractional derivative of ${\mathcal {W}}_{i}^{*}(x)$ is formulated based on the linearity of the Caputo definition

$$\begin{aligned} {\mathcal {D}}^{\omega }({\mathcal {W}}_{i}^{*}(x))=0, \quad i=0, 1, \ldots , \lceil \omega \rceil -1,\quad \omega >0, \end{aligned}$$

(9)

where $\lceil \omega \rceil$ denotes the ceiling part of $\omega$. The closed formulation of ${\mathcal {D}}^{\omega }({\mathcal {W}}_{i}^{*}(x))$ can be written as

$$\begin{aligned} {\mathcal {D}}^{\omega }({\mathcal {W}}^{*}_{i}(x))=\sum _{k=0}^{i-\lceil \omega \rceil }\sum _{\xi =0}^{k}N_{i, k, \xi }^{\omega ,\lceil \omega \rceil } \times x^{k-\xi -\omega +\lceil \omega \rceil },\quad x\in [0, 1],\quad i=0, 1, \ldots , \end{aligned}$$

(10)

and $N_{i, k, \xi }^{\omega ,\lceil \omega \rceil }$ is defined by

$$\begin{aligned} \begin{aligned} N_{i, k, \xi }^{\omega ,\lceil \omega \rceil }&=\frac{2^{2i}\times (i)!\times \varGamma (i +0.5)}{(2i)!\times (i-k-\lceil \omega \rceil )!\times (k+\lceil \omega \rceil )! } \times \frac{\varGamma (i+k+\lceil \omega \rceil +1)}{\varGamma (k+\lceil \omega \rceil +1.5)}\\&\times (-1)^{\xi }\times \left( {\begin{array}{c}k+\lceil \omega \rceil \\ \xi \end{array}}\right) \times \frac{\varGamma (k-\xi +\lceil \omega \rceil +1)}{\varGamma (k-\xi -\omega +\lceil \omega \rceil +1)}\cdot \end{aligned} \end{aligned}$$

Using the properties listed in Remark 1 and combining Eqs. (7), (9) and (10), we have

$$\begin{aligned} {\mathcal {D}}^{\omega }(g(x))=\sum _{i=\lceil \omega \rceil }^{N}\sum _{k=0}^{i-\lceil \omega \rceil }\sum _{\xi =0}^{k}c_{i}\times N_{i, k, \xi }^{\omega , \lceil \omega \rceil } \times x^{k-\xi -\omega +\lceil \omega \rceil },\quad x\in [0, 1]. \end{aligned}$$

(11)

3 Numerical scheme

For discretizing (4), we consider the nodes $t_j = j \delta t~ (j = 0, 1,\ldots , M)$ in the time domain [0, T], where $t_n$ satisfies $0 = t_0< t_1<\cdots < t_{M} = T$ with mesh length $\delta t=T/M$ for some positive integer M and define the collocation points $\lbrace x_{r-1}\rbrace _{r=1}^{N+1-\lceil \upsilon \rceil }$ using the roots of the SCPSK $U^{*}_{N+1-\lceil \upsilon \rceil }(x)$. Based on the Taylor formula of $u(x, t)\in {\mathbb {C}}^{3}(0, 1)$, we have

$$\begin{aligned} \frac{\partial u(x_{r}, t_{j})}{\partial t}=P_{\delta \tau } u(x_{r}, t_{j})+\frac{\delta \tau }{2}\frac{\partial ^{2} u(x_{r}, t_{j})}{\partial t^{2}}+{\mathcal {O}}({\delta \tau }^{2}), \end{aligned}$$

(12)

where $P_{\delta \tau }u(x_{r}, t_{j})=\frac{u_{r}^{j}-u_{r}^{j-1}}{\delta \tau }$. Now, discretizing (4) in the grid points $(x_{r}, t_{j})$ and by substituting (12), it yields

$$\begin{aligned} P_{\delta \tau } u(x_{r}, t_{j})+T_{j}= \gamma \frac{{\partial }^{\alpha } u(x_{r}, t_{j})}{\partial x^{\alpha }}-\mu \frac{{\partial }^{\beta } u(x_{r}, t_{j})}{\partial x^{\beta }}+ q(x_{r}, t_{j}), \end{aligned}$$

(13)

with

$$\begin{aligned} T_{j}=\frac{\delta \tau }{2}\frac{\partial ^{2} u(x_{r}, t_{j})}{\partial t^{2}}+{\mathcal {O}}({\delta \tau }^{2}) \end{aligned}$$

and notice that

$$\begin{aligned} \frac{\partial ^{2} u(x_{r}, t_{j})}{\partial t^{2}}=\gamma {P}_{ \delta \tau }\frac{{\partial }^{\alpha } u(x_{r}, t_{j})}{\partial x^{\alpha }}-\mu {P}_{ \delta \tau }\frac{{\partial }^{\beta } u(x_{r}, t_{j})}{\partial x^{\beta }}+{P}_{ \delta \tau }q(x_{r}, t_{j}). \end{aligned}$$

(14)

Substituting Eq. (14) in $T_{j}$ and as well as in Eq. (13), one obtains

$$\begin{aligned} \begin{aligned} P_{\delta \tau } u(x_{r}, t_{j})&=\gamma \frac{{\partial }^{\alpha } u(x_{r}, t_{j})}{\partial x^{\alpha }}-\mu \frac{{\partial }^{\beta } u(x_{r}, t_{j})}{\partial x^{\beta }}+q(x_{r}, t_{j})\\&\quad -\frac{\delta \tau }{2}\big (\gamma {P}_{ \delta \tau }\frac{{\partial }^{\alpha } u(x_{r}, t_{j})}{\partial x^{\alpha }}-\mu {P}_{ \delta \tau }\frac{{\partial }^{\beta } u(x_{r}, t_{j})}{\partial x^{\beta }}+{P}_{ \delta \tau }q(x_{r}, t_{j})\big )+\cdots . \end{aligned} \end{aligned}$$

(15)

Let us define $u(x_{r}, t_{j})=U_{r}^{j}$, $q(x_{r}, t_{j})=q_{r}^{j}$. Then we get the semi-discrete scheme as

$$\begin{aligned} U_{r}^{j}- \frac{\delta \tau }{2} \gamma \frac{{\partial }^{\alpha } U_{r}^{j}}{\partial x^{\alpha }}+\frac{\delta \tau }{2} \mu \frac{{\partial }^{\beta } U_{r}^{j}}{\partial x^{\beta }} = U_{r}^{j-1}- \frac{\delta \tau }{2} \gamma \frac{{\partial }^{\alpha } U_{r}^{j-1}}{\partial x^{\alpha }}+\frac{\delta \tau }{2} \mu \frac{{\partial }^{\beta } U_{r}^{j-1}}{\partial x^{\beta }} +\frac{\delta \tau }{2}(q_{r}^{j}+q_{r}^{j-1})+{\mathcal {R}}^{j}(x){\delta \tau }^{3}, \end{aligned}$$

(16)

where ${\mathcal {R}}^{j}(x)$ stands for a truncation term. It follows that, for fully discretizing (4), we need to approximate the Caputo derivative in $\frac{{\partial }^{\alpha } U_{r}^{j}}{\partial x^{\alpha }}$ and $\frac{{\partial }^{\beta } U_{r}^{j}}{\partial x^{\beta }}$ using the result of Eq. (11). In the Chebyshev collocation scheme, the approximate solution u(x, t) can be represented as

$$\begin{aligned} u_{N}(x, t_{j})=\sum _{i=0}^{N}{\mathfrak {u}}_{i}(t_{j}){\mathcal {W}}^{*}_{i}(x). \end{aligned}$$

(17)

In view of relations (11), (16) and (17), we have

$$\begin{aligned} \begin{aligned}&\sum _{i=0}^{N}{\mathfrak {u}}_{i}^{j}{\mathcal {W}}^{*}_{i}(x) - \frac{\delta \tau }{2} \sum _{i=\lceil \alpha \rceil }^{N}{\mathfrak {u}}_{i}^{j}\times \Bigg ( \gamma \sum _{k=0}^{i-\lceil \alpha \rceil }\sum _{\xi =0}^{k} N_{i, k, \xi }^{\alpha , \lceil \alpha \rceil } \times x^{k-\xi -\alpha +\lceil \alpha \rceil }\\&\qquad + \mu \sum _{k=0}^{i-\lceil \beta \rceil }\sum _{\xi =0}^{k} N_{i, k, \xi }^{\beta , \lceil \beta \rceil } \times x^{k-\xi -\beta +\lceil \beta \rceil }\Bigg )\\&\quad = \sum _{i=0}^{N}{\mathfrak {u}}_{i}^{j-1}{\mathcal {W}}^{*}_{i}(x) - \frac{\delta \tau }{2} \sum _{i=\lceil \alpha \rceil }^{N}{\mathfrak {u}}_{i}^{j-1}\times \Bigg ( \gamma \sum _{k=0}^{i-\lceil \alpha \rceil }\sum _{\xi =0}^{k} N_{i, k, \xi }^{\alpha , \lceil \alpha \rceil } \times x^{k-\xi -\alpha +\lceil \alpha \rceil }\\&\qquad + \mu \sum _{k=0}^{i-\lceil \beta \rceil }\sum _{\xi =0}^{k} N_{i, k, \xi }^{\beta , \lceil \beta \rceil } \times x^{k-\xi -\beta +\lceil \beta \rceil }\Bigg )\\&\qquad +\frac{\delta \tau }{2}(q(x, t_{j})+q(x, t_{j-1})), \end{aligned} \end{aligned}$$

(18)

where ${\mathfrak {u}}_{i}^{j}$ represents the coefficients at the point $t_{j}$. With the roots of the FKSCP, $\{x_{r}\}_{r=1}^{N+1-\lceil \upsilon \rceil }$, we collocate Eq. (18) as follows:

$$\begin{aligned} \begin{aligned}&\sum _{i=0}^{N}{\mathfrak {u}}_{i}^{j}{\mathcal {W}}^{*}_{i}(x_{r}) - \frac{\delta \tau }{2} \sum _{i=\lceil \alpha \rceil }^{N}{\mathfrak {u}}_{i}^{j}\times \Bigg ( \gamma \sum _{k=0}^{i-\lceil \alpha \rceil }\sum _{\xi =0}^{k} N_{i, k, \xi }^{\alpha , \lceil \alpha \rceil } \times x_{r}^{k-\xi -\alpha +\lceil \alpha \rceil }\\&\qquad + \mu \sum _{k=0}^{i-\lceil \beta \rceil }\sum _{\xi =0}^{k} N_{i, k, \xi }^{\beta , \lceil \beta \rceil } \times x_{r}^{k-\xi -\beta +\lceil \beta \rceil }\Bigg )\\&\quad = \sum _{i=0}^{N}{\mathfrak {u}}_{i}^{j-1}{\mathcal {W}}^{*}_{i}(x_{r}) - \frac{\delta \tau }{2} \sum _{i=\lceil \alpha \rceil }^{N}{\mathfrak {u}}_{i}^{j-1}\times \Bigg ( \gamma \sum _{k=0}^{i-\lceil \alpha \rceil }\sum _{\xi =0}^{k} N_{i, k, \xi }^{\alpha , \lceil \alpha \rceil } \times x_{r}^{k-\xi -\alpha +\lceil \alpha \rceil }\\&\qquad + \mu \sum _{k=0}^{i-\lceil \beta \rceil }\sum _{\xi =0}^{k} N_{i, k, \xi }^{\beta , \lceil \beta \rceil } \times x_{r}^{k-\xi -\beta +\lceil \beta \rceil }\Bigg )\\&\qquad +\frac{\delta \tau }{2}(q(x_{r}, t_{j})+q(x_{r}, t_{j-1})). \end{aligned} \end{aligned}$$

(19)

Substituting the boundary conditions given in Eq. (6) into (17), we obtain the $\lceil \upsilon \rceil$ equations

$$\begin{aligned} \sum _{i=0}^{N}(-1)^{i}{\mathfrak {u}}_{i}(t)={\upsilon }_{0}(t),~~~\sum _{i=0}^{N}(2i+1){\mathfrak {u}}_{i}(t)={\upsilon }_{1}(t). \end{aligned}$$

(20)

Equation (19), together with $\lceil \nu \rceil$ equations of the boundary conditions (20) lead $N + 1$ of algebraic equations that can be obtained the unknowns $u_i,i = 0, 1,\ldots , N.$

4 Error analysis

This section examines the time-discrete scheme in terms of unconditional stability and convergence issues. Assume that $\varOmega$ represents an a bounded and open domain in ${\mathbb {R}}^{2}$. First, let us introduce the functional spaces endowed with standard norms and inner product

$$\begin{aligned} \langle u(x), v(x)\rangle =\int _{\varOmega }u(x)v(x)\mathrm{d}x, \qquad u, v\in L_{2}(\varOmega ), \end{aligned}$$

which induces the norm $\Vert u(x)\Vert _{2}=\big \langle u(x), u(x)\big \rangle ^{\frac{1}{2}}$ and let us define

$$\begin{aligned} H^{s}(\varOmega )=\lbrace u\in L_{2}(\varOmega ), \frac{\mathrm{d}^{s}u}{\mathrm{d}x^{s}}\in L_{2}(\varOmega ) \rbrace . \end{aligned}$$

Now, relation (16) can be rearranged according to the expression

$$\begin{aligned}&U^{k}-\frac{\delta \tau }{2}\Big ( \gamma {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{k} -\mu {}_{a}{\mathcal {D}}^{\beta }_{x}U^{k} \Big ) \nonumber \\&\quad =U^{k-1}+\frac{\delta \tau }{2}\Big ( \gamma {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{k-1} -\mu {}_{a}{\mathcal {D}}^{\beta }_{x}U^{k-1} \Big )+\frac{\delta \tau }{2}(q^{k}+q^{k-1}),\qquad k=1, 2, \ldots , M.\nonumber \\ \end{aligned}$$

(21)

We some lemmas that are introduced in the following (Ervin et al. 2007).

Lemma 1

Assume that $1< \alpha <2$. Then for any $u, \nu \in H^{\frac{\alpha }{2}}(\varOmega )$ it holds that

$$\begin{aligned} \langle {}_{a}{\mathcal {D}}^{\alpha }_{x}u, \nu \rangle =\langle {}_{a}{\mathcal {D}}^{\frac{\alpha }{2}}_{x}u, {}_{x}{\mathcal {D}}^{\frac{\alpha }{2}}_{b}\nu \rangle , \quad \langle {}_{x}{\mathcal {D}}^{\alpha }_{b}u, \nu \rangle =\langle {}_{x}{\mathcal {D}}^{\frac{\alpha }{2}}_{b}u, {}_{a}{\mathcal {D}}^{\frac{\alpha }{2}}_{x}\nu \rangle . \end{aligned}$$

Lemma 2

Let $\alpha > 0$ be given. Then it follows that

$$\begin{aligned} \langle {}_{a}{\mathcal {D}}^{\alpha }_{x}u, {}_{x}{{\mathcal {D}}}^{\alpha }_{b}u\rangle =\cos (\alpha \pi )\Vert {}_{a}{\mathcal {D}}^{\alpha }_{x}u\Vert ^{2}_{L_{2}(\varOmega )}=\cos (\alpha \pi )\Vert {}_{x}{\mathcal {D}}^{\alpha }_{b}u\Vert ^{2}_{L_{2}(\varOmega )}. \end{aligned}$$

Now, we need to prove the following lemma:

Lemma 3

For $1<\alpha \le 2$ and the functions $g(x), {}_{a}{{\mathcal {D}}}_{x}^{\alpha }g(x)\in H^{\alpha }(\varOmega )$, there exists a sufficiently small $\delta \tau$ such that

$$\begin{aligned} \Vert g(x)+\frac{\delta \tau }{2} {}_{a}{{\mathcal {D}}}_{x}^{\alpha }g(x) \Vert \le \Vert g(x) \Vert . \end{aligned}$$

Proof

By virtue of the nature of the inner product, one can arrive at

$$\begin{aligned} \begin{aligned} \Vert g(x)+\frac{\delta \tau }{2} {}_{a}{{\mathcal {D}}}_{x}^{\alpha }g(x) \Vert ^{2}&\le \left\langle g(x)+\frac{\delta \tau }{2} {}_{a}{{\mathcal {D}}}_{x}^{\alpha }g(x), g(x)+\frac{\delta \tau }{2} {}_{a}{{\mathcal {D}}}_{x}^{\alpha }g(x) \right\rangle \\&=\Vert g(x) \Vert ^{2}+ \delta \tau \langle {}_{a}{{\mathcal {D}}}_{x}^{\frac{\alpha }{2}}g(x), {}_{x}{{\mathcal {D}}}_{b}^{\frac{\alpha }{2}}g(x)\rangle + \frac{\delta \tau ^{2}}{4} \Vert {}_{a}{{\mathcal {D}}}_{x}^{\alpha }g(x)\Vert ^{2}. \end{aligned} \end{aligned}$$

From Lemma 2 and knowing that $1<\alpha \le 2$, we obtain

$$\begin{aligned} \langle {}_{a}{{\mathcal {D}}}_{x}^{\frac{\alpha }{2}}g(x), {}_{x}{{\mathcal {D}}}_{b}^{\frac{\alpha }{2}}g(x)\rangle =\cos \left( \frac{\alpha }{2}\pi \right) \Vert {}_{a}{{\mathcal {D}}}_{x}^{\frac{\alpha }{2}}g(x)\Vert ^{2}<0, \end{aligned}$$

thus, by choosing a small enough $\delta \tau$ that guarantees

$$\begin{aligned} \langle {}_{a}{{\mathcal {D}}}_{x}^{\frac{\alpha }{2}}g(x), {}_{x}{{\mathcal {D}}}_{a}^{\frac{\alpha }{2}}g(x)\rangle +\frac{\delta \tau }{4}\Vert {}_{a}{{\mathcal {D}}}_{x}^{\alpha }g(x)\Vert ^{2}<0. \end{aligned}$$

Finally, we obtain

$$\begin{aligned} \begin{aligned} \Vert g(x)+\frac{\delta \tau }{2} {}_{a}{{\mathcal {D}}}_{x}^{\alpha }g(x) \Vert ^{2}&\le \Vert g(x) \Vert ^{2}, \end{aligned} \end{aligned}$$

which proves the theorem. $\square$

Lemma 4

If $U^{k}\in H^{1}(\varOmega ), k=1, 2, \ldots , M,$ and $U^{0}$ be the solution of the time-discretized scheme (21) and the initial condition, respectively, then

$$\begin{aligned} \Vert U^{k}\Vert \le \Vert U^{0}\Vert +\max _{ 0\le r \le N} \frac{\delta \tau }{2}(\Vert q_{r}^{k}\Vert +\Vert q_{r}^{k-1}\Vert ). \end{aligned}$$

(22)

Proof

We will prove above result by principle of mathematical induction. First, when $k=1$, we have

$$\begin{aligned} U^{1}-\frac{\delta \tau }{2}\Big ( \gamma {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{1} -\mu {}_{a}{\mathcal {D}}^{\beta }_{x}U^{1} \Big ) =U^{0}+\frac{\delta \tau }{2}\Big ( \gamma {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{0} -\mu {}_{a}{\mathcal {D}}^{\beta }_{x}U^{0} \Big )+\frac{\delta \tau }{2}(q^{1}+q^{0}). \end{aligned}$$

(23)

Taking the inner product of Eq. (23) by $U^{1}$, one can obtain

$$\begin{aligned} \begin{aligned}&\Vert U^{1}\Vert ^{2}-\frac{\delta \tau }{2} \Big ( \gamma \langle {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{1},U^{1}\rangle -\mu \langle {}_{a}{\mathcal {D}}^{\beta }_{x}U^{1},U^{1}\rangle \Big ) \\&\quad =\langle U^{0},U^{1}\rangle +\frac{\delta \tau }{2} \Big ( \gamma \langle {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{0},U^{1}\rangle -\mu \langle {}_{a}{\mathcal {D}}^{\beta }_{x}U^{0},U^{1}\rangle \Big )\\&\quad \quad +\frac{\delta \tau }{2}(\langle q^{1},U^{1}\rangle +\langle q^{0},U^{1}\rangle ). \end{aligned} \end{aligned}$$

(24)

From Lemmas 1 and 2, it is clear that

$$\begin{aligned} \begin{aligned}&\langle {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{1},U^{1}\rangle =\langle {}_{a}{\mathcal {D}}^{\frac{\alpha }{2}}_{x}U^{1},{}_{x}{\mathcal {D}}^{\frac{\alpha }{2}}_{b}U^{1}\rangle =\cos \left( \frac{\alpha }{2}\pi \right) \Vert {}_{a}{\mathcal {D}}^{\frac{\alpha }{2}}_{x}U^{1}\Vert ^{2}\le 0,~~\forall ~1<\alpha \le 2,\\&\langle {}_{a}{\mathcal {D}}^{\beta }_{x}U^{1},U^{1}\rangle =\langle {}_{a}{\mathcal {D}}^{\frac{\beta }{2}}_{x}U^{1},{}_{x}{\mathcal {D}}^{\frac{\beta }{2}}_{b}U^{1}\rangle =\cos \left( \frac{\beta }{2}\pi \right) \Vert {}_{a}{\mathcal {D}}^{\frac{\beta }{2}}_{x}U^{1}\Vert ^{2}\ge 0,~~\forall ~ 0<\beta \le 1. \end{aligned} \end{aligned}$$

Regarding Lemma 3 and the Schwarz inequality, we have

$$\begin{aligned} \big \langle U^{0},U^{1}\rangle +\frac{\delta \tau }{2}\langle {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{0},U^{1}\rangle =\big \langle U^{0}+\frac{\delta \tau }{2} {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{0},U^{1}\big \rangle \le \big \Vert U^{0}+\frac{\delta \tau }{2} {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{0}\big \Vert \big \Vert U^{1}\big \Vert \le \big \Vert U^{0}\big \Vert \big \Vert U^{1}\big \Vert . \end{aligned}$$

The aforesaid relation can be rewritten as

$$\begin{aligned} \Vert U^{1}\Vert \le \Vert U^{0}\Vert +\max _{ 0\le r \le N} \frac{\delta \tau }{2}(\Vert q_{r}^{1}\Vert +\Vert q_{r}^{0}\Vert ). \end{aligned}$$

Suppose that the theorem is true for all j

$$\begin{aligned} \Vert U^{j}\Vert \le \Vert U^{0}\Vert +\max _{ 0\le r \le N} \frac{\delta \tau }{2}(\Vert q_{r}^{j}\Vert +\Vert q_{r}^{j-1}\Vert ), \quad j=1, 2, \ldots , k-1. \end{aligned}$$

Taking the inner product of Eq. (23) by $U^{k}$, we have

$$\begin{aligned} \begin{aligned}&\Vert U^{k}\Vert ^{2}-\frac{\delta \tau }{2} \Big ( \gamma \langle {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{k},U^{k}\rangle -\mu \langle {}_{a}{\mathcal {D}}^{\beta }_{x}U^{k},U^{k}\rangle \Big ) \\&\quad =\langle U^{k-1},U^{k}\rangle +\frac{\delta \tau }{2} \Big ( \gamma \langle {}_{a}{\mathcal {D}}^{\alpha }_{x}U^{k-1},U^{k}\rangle -\mu \langle {}_{a}{\mathcal {D}}^{\beta }_{x}U^{k-1},U^{k}\rangle \Big )\\&\quad \quad +\frac{\delta \tau }{2}(\langle q^{k},U^{k}\rangle +\langle q^{k-1},U^{k}\rangle ). \end{aligned} \end{aligned}$$

From the Schwarz inequality and $U^{k}\in H^{1}(\varOmega )$, we have the following inequality:

$$\begin{aligned} \Vert U^{k}\Vert \le \Vert U^{k-1}\Vert +\max _{ 0\le r \le N} \frac{\delta \tau }{2}(\Vert q_{r}^{k}\Vert +\Vert q_{r}^{k-1}\Vert ). \end{aligned}$$

Therefore, Lemma 4 is proven by induction on k. $\square$

Next theorem proves the stability of relation (16).

Theorem 1

The time semi-discretization (16) is unconditionally stable.

Proof

Let us consider that ${\widehat{U}}_{r}^{j}, j=1, 2, \ldots , M,$ is an approximate solution of (16), with the initial condition ${\widehat{U}}_{r}^{0}=u(x, 0)$. Then the error $\varepsilon ^{j}=U_{r}^{j}-{\widehat{U}}_{r}^{j}$ satisfies

$$\begin{aligned} \varepsilon ^{j}-\frac{\delta \tau }{2}\big ( \gamma {}_{a}{\mathcal {D}}^{\alpha }_{x}\varepsilon ^{j} -\mu {}_{a}{\mathcal {D}}^{\beta }_{x}\varepsilon ^{j} \big ) =\varepsilon ^{j-1}+\frac{\delta \tau }{2}\big ( \gamma {}_{a}{\mathcal {D}}^{\alpha }_{x}\varepsilon ^{j-1} -\mu {}_{a}{\mathcal {D}}^{\beta }_{x}\varepsilon ^{j-1} \big ). \end{aligned}$$

Using the aforesaid equation and Lemma 4, it follows that

$$\begin{aligned} \Vert \varepsilon ^{j}\Vert \le \Vert \varepsilon ^{0}\Vert , \quad j=1, 2, \ldots , M. \end{aligned}$$

This shows that the scheme (16) is unconditionally stable. $\square$

Theorem 2

Let $\varepsilon ^{j}=u(x, t_{j})-U^{j}, ~j=1, 2, \ldots , M,$ be the errors associated with Eq. (16). Then we obtain that

$$\begin{aligned} \Vert \varepsilon ^{j}\Vert \le C_{x}{\delta \tau }^{2}, \end{aligned}$$

where $C_{x} >0$ is depends on x.

Proof

First, we obtain the following weak form using Eq. (16) as

$$\begin{aligned} \Vert \varepsilon ^{j}\Vert ^{2}-\frac{\delta \tau }{2} \big ( \gamma \langle {}_{a}{\mathcal {D}}^{\alpha }_{x}\varepsilon ^{j},\varepsilon ^{j}\rangle -\mu \langle {}_{a}{\mathcal {D}}^{\beta }_{x}\varepsilon ^{j},\varepsilon ^{j}\rangle \big )= & {} \langle \varepsilon ^{j-1},\varepsilon ^{j}\rangle +\frac{\delta \tau }{2} \big ( \gamma \langle {}_{a}{\mathcal {D}}^{\alpha }_{x}\varepsilon ^{j-1},\varepsilon ^{j}\rangle \\&-\mu \langle {}_{a}{\mathcal {D}}^{\beta }_{x}\varepsilon ^{j-1},\varepsilon ^{j}\rangle \big )+\delta \tau ^{3}\langle {\mathcal {R}}^{j}(x), \varepsilon ^{j}\rangle . \end{aligned}$$

for $j=1, 2, \ldots , M$.

Based on the Lemmas 1, 2 ,3 and Cauchy–Schwarz inequality, we conclude that

$$\begin{aligned} \Vert \varepsilon ^{j}\Vert ^{2}\le \Vert \varepsilon ^{j-1}\Vert \Vert \varepsilon ^{j}\Vert +{(\delta \tau )}^{3}\Vert {\mathcal {R}}^{j}(x)\Vert \Vert \varepsilon ^{j}\Vert . \end{aligned}$$

So, one can get

$$\begin{aligned} \Vert \varepsilon ^{j}\Vert -\Vert \varepsilon ^{j-1}\Vert \le {(\delta \tau )}^{3}\Vert {\mathcal {R}}^{j}(x)\Vert ,~~\Longrightarrow \Vert \varepsilon ^{j}\Vert -\Vert \varepsilon ^{j-1}\Vert \le C{(\delta \tau )}^{3}. \end{aligned}$$

(25)

Summing for j from 1 to M, we obtain

$$\begin{aligned} \sum _{j=1}^{M}\left( \Vert \varepsilon ^{j}\Vert -\Vert \varepsilon ^{j-1}\Vert \right) \le \sum _{j=1}^{M} C{(\delta \tau )}^{3}. \end{aligned}$$

From the above relation, we can conclude

$$\begin{aligned} \Vert \varepsilon ^{M}\Vert -\Vert \varepsilon ^{0}\Vert \le C M {(\delta \tau )}^{3}, \end{aligned}$$

since $\Vert \varepsilon ^{0}\Vert =0$ and $\delta \tau =\frac{T}{M}$, we have

$$\begin{aligned} \Vert \varepsilon ^{M}\Vert \le C_{x}{\delta \tau }^{2}, \end{aligned}$$

where $C_{x}=CT$. The proof of Theorem 2 is completed. $\square$

Table 2 The maximum norm error $L_{\infty }$ obtained with the proposed method and those in Khader and Sweilam (2014); Saw and Kumar (2018, 2019) with $\alpha =2, \beta =1,$ $N=3$ and $M=400$ at $T=1$ for Example 1

5 Numerical examples

In this section, we present the numerical results of the proposed method on three test problems. Moreover, we will test the accuracy of proposed method for different values of N, M at final times T. In addition, the computational order (denoted by $C_{\delta \tau }$) is computed by the formula

$$\begin{aligned} C_{\delta \tau }=\frac{\log \left( \frac{E_{1}}{E_{2}}\right) }{\log \left( \frac{{\delta \tau }_{1}}{{\delta \tau }_{2}}\right) }, \end{aligned}$$

where $E_{1}$ and $E_{2}$ are the errors corresponding to grids with time steps ${\delta \tau }_{1}$ and ${\delta \tau }_{2}$, respectively.

Example 1

Consider the following SFADE

$$\begin{aligned} \begin{aligned}&\frac{\partial u(x, t)}{\partial t}=\frac{{\partial }^{\alpha } u(x, t)}{\partial x^{\alpha }}- \frac{{\partial }^{\beta } u(x, t)}{\partial x^{\beta }}+e^{-2t}\bigg ( 2(x^{\beta }-x^{\alpha })-\alpha !+\frac{\varGamma (\alpha +1)}{\varGamma (\alpha - \beta +1)}x^{\alpha -\beta }-\beta !\bigg ) \end{aligned} \end{aligned}$$

with boundary and initial conditions

$$\begin{aligned}&u(x,0)=x^{\alpha }-x^{\beta },\\&u(0, t)=u(1, t)=0. \end{aligned}$$

The analytical solution of this problem is $u(x, t)=e^{-2t}(x^{\alpha }-x^{\beta })$.

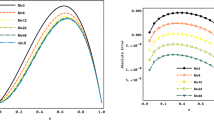
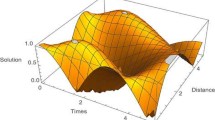
Tables 2–6 list the results for Example 1, with various values of M and N at different values of T. Tables 2 and 3 make a comparison between the obtained results with the techniques described in (Khader and Sweilam 2014; Saw and Kumar 2018, 2019) at $T=1$ and $T=2.$ We verify that the proposed method achieves superior accuracy than the techniques described in (Khader and Sweilam 2014; Saw and Kumar 2019, 2018). Table 4 includes the maximum norm error $L_{\infty }$ yielded by the proposed method for $N=5$ and various values of M,  at $T=1$. Table 5 reports that the computational order of the method in the time variable is approximately ${\mathcal {O}}( \delta \tau ^{2})$ which is in accordance with the theoretical results. Table 6 demonstrates the computational order at the final times $T \in \{2, 10\}$. Figure 1 illustrates the numerical solution and the maximum norm error $L_{\infty }$ with $N=7$ and $M=400$ at $T=1$. Figure 2 draws the behaviour of the maximum norm errors $L_{\infty }$ when adopting $N=3$ and $N=7$ for various values of M at $T=2$. Figure 3a includes the behaviour of the maximum norm error $L_{\infty }$ and $L_{2}$-norm when choosing $M=400,$ and various values N at $T=1$. Figure 3b plots the maximum norm error $L_{\infty }$ for $N=5$ and various values M at $T=1$. Figure 4 represents the behaviour of the maximum norm errors $L_{\infty }$ for different values of $\{\alpha ,\beta \},$ at $T=1$.

Table 3 The maximum norm error $L_{\infty }$ with the proposed method and those in Khader and Sweilam (2014); Saw and Kumar (2018, 2019) with $\alpha =2, \beta =1,$ $M=400$ and $N=5$ at $T=2$ for Example 1

Table 4 The maximum norm error $L_{\infty }$ obtained with the proposed method with $N=5$ at $T=1$ of Example 1

Table 5 The maximum norm error $L_{\infty }$, computational orders and CPU time with $N=7$ at $T=1$ for Example 1

Table 6 The maximum norm error $L_{\infty }$ and computational orders with $N=3$ at the final times $T \in \{2,10\}$ for Example 1

Fig. 1

The approximate solution (left panel) and the maximum norm error $L_\infty$ (right panel) with $M=400$ and $N=7$ at $T=1$ for Example 1

Fig. 2

The maximum error norms $L_\infty$ with $\{\alpha =1.9, \beta =1 \}$ and different values of N and M at $T=2$ for Example 1

Fig. 3

a The maximum norm errors $L_{\infty }$ with $\{\alpha =1.9, \beta =0.9 \}$ and $N=3$ at $T=1$ for Example 1. b The maximum norm error $L_{\infty }$ with $\{\alpha =1.9, \beta =0.9 \},$ and $M=400$ and $N\in \{3, 5, 7, 9\}$ at $T=1$ for Example 1

Fig. 4

The behavior of the approximate solutions for $\alpha \in \{1.5,1.6,1.7,1.8,1.9\}$, $\beta =1$ (left panel) and $\beta \in \{0.5,0.6,0.7,0.8,0.9\}$, $\alpha =1.5$ (right panel) for Example 1

Example 2

Consider the following SFADE

$$\begin{aligned} \begin{aligned}&\frac{\partial u(x, t)}{\partial t}=\frac{{\partial }^{1.5} u(x, t)}{\partial x^{1.5}}-2\frac{{\partial } u(x, t)}{\partial x}+x(x-1)(2t-1)+2t(t-1)(2x-1)-\frac{4\sqrt{x}t(t-1)}{\sqrt{\pi }}, \end{aligned} \end{aligned}$$

(26)

with boundary and initial conditions

$$\begin{aligned} u(x, 0)=0,~~~ u(0, t)=u(1, t)=0,~~ t>0, \end{aligned}$$

(27)

such that the analytical solution is $u(x, t)=xt(x-1)(t-1)$.

Table 7 makes the comparison between the numerical and the analytical solutions for various values of $T \in \{0.3,06,0.9\}$, showing that the method rapidly converges to the analytical solution. Figure 5 plots the behaviour of the maximum norm error for different values of $\{\alpha ,\beta \}$ at $T=10$.

Table 7 The analytical and approximate solutions with $\alpha =1.5$ and $\beta =1$ at various values of $T \in \{0.3, 0.6, 0.9\}$ of Example 2

Fig. 5

The approximate solutions of Example 2 for $\beta \in \{0.5,0.6,0.7,.8,0.9\}$, $\alpha =1$ (left panel) and $\alpha \in \{1.1,1.2,1.3,1.4\}$, $\beta =1$ (right panel) at final time $T=10$

Example 3

Consider the following SFADE

$$\begin{aligned} \begin{aligned} \frac{\partial u(x, t)}{\partial t}&=\varGamma (1.8)x^{1.2}\times \frac{{\partial }^{1.2} u(x, t)}{\partial x^{1.2}}-\varGamma (2.8)x^{0.2}\times \frac{{\partial }^{0.2} u(x, t)}{\partial x^{0.2}}-(x^{2}-x^{3})\sin (t)\\&\quad -6x^{3}\cos (t)(\frac{\varGamma (2.8)}{\varGamma (3.8)}-\frac{\varGamma (1.8)}{\varGamma (2.8)}),\\ \end{aligned} \end{aligned}$$

(28)

with boundary and initial conditions

$$\begin{aligned} u(x, 0)=x^{2}-x^{3},~~~ u(0, t)=u(1, t)=0,~~ t>0, \end{aligned}$$

(29)

which the analytical solution is $u(x, t)=(x^{2}-x^{3})\cos (t)$.

Table 8 demonstrates the computational order at the final times $T \in \{1,2\}$ which is in accordance with the theoretical results.

Table 8 The maximum norm error $L_{\infty }$ and computational orders with $N=5$ the final times $T \in \{1,2\}$ for Example 3

6 Conclusion

This paper proposed a new method for solving the SFADE. The numerical algorithm involves two steps. First, the compact finite difference is applied to discretize the time derivative. Second, the FKSCP is implemented to approximate the space fractional derivatives. The error analysis of the proposed method was investigated in $L^{2}$ space. To illustrate the applicability and validity of the new scheme, illustrative examples were provided. The numerical results verify well the theoretical analysis.