An iterative method for solving proximal split feasibility problems and fixed point problems

Abstract

The purpose of this research is to introduce a regularized algorithm based on the viscosity method for solving the proximal split feasibility problem and the fixed point problem in Hilbert spaces. A strong convergence result of our proposed algorithm for finding a common solution of the proximal split feasibility problem and the fixed point problem for nonexpansive mappings is established. We also apply our main result to the split feasibility problem, and the fixed point problem of nonexpansive semigroups, respectively. Finally, we give numerical examples for supporting our main result.

1 Introduction

Throughout this article, let $H_{1}$ and $H_{2}$ be two real Hilbert spaces. Let $f :H_{1}\rightarrow {\mathbb {R}} \cup \{+\infty \}$ and $g:H_{2} \rightarrow {\mathbb {R}} \cup \{+\infty \}$ be two proper and lower semicontinuous convex functions and $A : H_{1}\rightarrow H_{2}$ be a bounded linear operator.

In this paper, we focus our attention on the following proximal split feasibility problem (PSFP): find a minimizer $x^{*}$ of f, such that $Ax^{*}$ minimizes g, namely

$$\begin{aligned} x^{*}\in \mathop {\mathrm {argmin}}f \text { such that } Ax^{*}\in \mathop {\mathrm {argmin}}g, \end{aligned}$$

(1.1)

where $\mathop {\mathrm {argmin}}f:= \{{\bar{x}} \in H_{1}: f({\bar{x}}) \le f(x) \text { for all } x\in H_{1}\}$ and $\mathop {\mathrm {argmin}}g := \{{\bar{y}} \in H_{2}: g({\bar{y}}) \le g(y) \text { for all } y\in H_{2}\}$. We assume that the problem (1.1) has a nonempty solution set $\Gamma := \mathop {\mathrm {argmin}}f \cap A^{-1}(\mathop {\mathrm {argmin}}g)$.

Censor and Elfving (1994) introduced the split feasibility problem (in short, SFP). The split feasibility problem (SFP) has been used for many applications in various fields of science and technology, such as in signal processing and image reconstruction, and especially applied in medical fields such as intensity-modulated radiation therapy (IMRT) (for details, see Censor et al. (2006) and the references therein). Let C and Q be nonempty, closed, and convex subsets of $H_{1}$ and $H_{2}$, respectively, and then, the SFP is to find a point:

$$\begin{aligned} x\in C \text { such that } Ax\in Q, \end{aligned}$$

(1.2)

where $A : H_{1}\rightarrow H_{2}$ is a bounded linear operator. For solving the problem (1.2), Byrne (2002) introduced a popular algorithm which is called the CQ algorithm as follows:

$$\begin{aligned} x_{n+1}=P_{C}(x_{n}-\mu _{n} A^{*}(I-P_{Q})Ax_{n}), \quad \forall n \ge 1, \end{aligned}$$

where $P_{C}$ and $P_{Q}$ denote the metric projection onto the closed convex subsets C and Q, respectively, and $A^{*}$ is the adjoint operator of A and $\mu _{n}\in (0,2/\Vert A\Vert ^{2})$. Many research papers have increasingly investigated split feasibility problem [see, for instance (Lopez et al. 2012; Chang et al. 2014; Qu and Xiu 2005), and the references therein]. If $f=i_{C}$ [defined as $i_{C}(x)=0$ if $x\in C$ and $i_{C}(x) = +\infty$ if $x\notin C$] and $g=i_{Q}$ are indicator functions of nonempty, closed, and convex sets C and Q of $H_{1}$ and $H_2$, respectively. Then, the proximal split feasibility problem (1.1) becomes the split feasibility problem (1.2).

Moudafi and Thakur (2014) introduced the split proximal algorithm with a way of selecting the step-sizes, such that its implementation does not need any prior information about the operator norm. Given an initial point $x_{1}\in H_{1}$, assume that $x_n$ has been constructed and $\Vert A^{*}(I-{\text {prox}}_{\lambda g })Ax_{n}\Vert ^{2}+\Vert (I-{\text {prox}}_{\lambda f})x_{n}\Vert ^{2} \ne 0$, and then compute $x_{n+1}$ by the following iterative scheme:

$$\begin{aligned} x_{n+1}={\text {prox}}_{\lambda \mu _{n} f}(x_{n}-\mu _{n}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n}), \quad \forall n\ge 1, \end{aligned}$$

(1.3)

where the stepsize $\mu _{n}:=\rho _{n}\dfrac{h(x_{n})+l(x_{n})}{\theta ^{2}(x_{n})}$ with $0<\rho _{n}<4$, $h(x):=\frac{1}{2}\Vert (I-{\text {prox}}_{\lambda g}) Ax\Vert ^{2}$, $l(x):=\frac{1}{2}\Vert (I-{\text {prox}}_{\lambda \mu _{n} f}) x\Vert ^{2}$ and $\theta ^{2}(x):=\Vert A^{*}(I- {\text {prox}}_{\lambda g})Ax \Vert ^{2}+\Vert (I-{\text {prox}}_{\lambda \mu _{n} f}) x\Vert ^{2}.$ If $\theta ^{2}(x_{n})=0$, then $x_{n}$ is a solution of (1.1) and the iterative process stops; otherwise, we set $n:=n+1$ and compute $x_{n+1}$ using (1.3). They also proved the weak convergence of the sequence generated by Algorithm (1.3) to a solution of (1.1) under suitable conditions of parameter $\rho _{n}$ where $\varepsilon \le \rho _{n}\le \dfrac{4h(x_{n})}{h(x_{n})+l(x_{n})}-\varepsilon$ for some $\varepsilon >0.$

Yao et al. (2014) gave the regularized algorithm for solving the proximal split feasibility problem (1.1) and proposed a strong convergence theorem under suitable conditions:

$$\begin{aligned} x_{n+1}={\text {prox}}_{\lambda \mu _{n} f}(\alpha _{n}u+(1-\alpha _{n})x_{n}-\mu _{n}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n}),\quad \forall n\ge 1, \end{aligned}$$

(1.4)

where the stepsize $\mu _{n}:=\rho _{n}\dfrac{h(x_{n})+l(x_{n})}{\theta ^{2}(x_{n})}$ with $0<\rho _{n}<4$.

Shehu et al. (2015) introduced a viscosity-type algorithm for solving proximal split feasibility problems as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} &{}y_{n}=x_{n}-\mu _{n}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n},\\ &{}x_{n+1}=\alpha _{n}\psi (x_{n})+(1-\alpha _{n}){\text {prox}}_{\lambda \mu _{n} f}y_{n},\quad \forall n\ge 1, \end{array} \end{array}\right. } \end{aligned}$$

(1.5)

where $\psi :H_{1}\rightarrow H_{1}$ is a contraction mapping. They also proved a strong convergence of the sequences generated by iterative schemes (1.5) in Hilbert spaces.

Recently, Shehu and Iyiola (2015) introduced the following algorithm for solving split proximal algorithms and fixed point problems for k-strictly pseudocontractive mappings in Hilbert spaces:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{lll} u_{n}=(1-\alpha _{n})x_{n},\\ y_{n}={\text {prox}}_{\lambda \gamma _{n} f}(u_{n}-\gamma _{n}A^{*}(I- {\text {prox}}_{\lambda g})Au_{n}),\\ x_{n+1} =(1-\beta _{n})y_{n}+\beta _{n}Ty_{n},\quad \forall n\in {\mathbb {N}}, \end{array} \end{array}\right. } \end{aligned}$$

(1.6)

where the stepsize $\gamma _{n}:=\rho _{n}\dfrac{h(x_{n})+l(x_{n})}{\theta ^{2}(x_{n})}$ with $0<\rho _{n}<4$. They also showed that, under certain assumptions imposed on the parameters, the sequence $\{x_n\}$ generated by (1.6) converges strongly to $x^{*}\in F(S)\cap \Gamma .$ Many researchers have proposed some methods to solve the proximal split feasibility problem [see, for instance (Shehu et al. 2015; Shehu and Iyiola 2017a, b, 2018; Abbas et al. 2018; Witthayarat et al. 2018), and the references therein].

We note that Algorithm (1.6) is the Halpern-type algorithm with $u \equiv 0$ fixed. However, a viscosity-type algorithm is more general and desirable than a Halpern-type algorithm, because a contraction which is used in the viscosity-type algorithm influences the convergence behavior of the algorithm.

In this paper, inspired and motivated by these studies, we are interested to study the proximal split feasibility problem and the fixed point problem in Hilbert spaces. In Sect. 3, we introduce a regularized algorithm based on the viscosity method for finding a common solution of the proximal split feasibility problem and the fixed point problem of nonexpansive mappings, and prove a strong convergence theorem under some suitable conditions. In Sects. 4 and 5, we apply our main result to the split feasibility problem, and the fixed point problem of nonexpansive semigroups, respectively. In the last section, we first give a numerical result in Euclidean spaces to demonstrate the convergence of our algorithm. We also show the number of iterations of our algorithm by choosing different contractions $\psi$. In this case, if we take $\psi = 0$ in our algorithm, then we obtain Algorithm (1.6) (Shehu and Iyiola 2015, Algorithm 1). Moreover, we give an example in the infinite-dimensional spaces for supporting our main theorem.

2 Preliminaries

Throughout this article, let H be a real Hilbert space with inner product $\langle \cdot , \cdot \rangle$ and norm $\Vert \cdot \Vert$. Let C be a nonempty closed convex subset of H. Let $T:C\rightarrow C$ be a nonlinear mapping. A point $x\in C$ is called a fixed point of T if $Tx=x$. The set of fixed points of T is the set $F(T):= \{x\in C: Tx=x\}$.

Recall that A mapping T of C into itself is said to be

• (i) nonexpansive if

  $$\begin{aligned} \left\| Tx-Ty\right\| \le \left\| x-y\right\| , \quad \forall x,y \in C. \end{aligned}$$

• (ii) contraction if there exists a constant $\delta \in [0,1)$, such that

  $$\begin{aligned} \Vert Tx-Ty\Vert \le \delta \Vert x-y\Vert , \quad \forall x,y\in C. \end{aligned}$$

Recall that the proximal operator ${\text {prox}}_{\lambda g}:H \rightarrow H$ is defined by:

$$\begin{aligned} {\text {prox}}_{\lambda g}x:=\mathop {\mathrm {argmin}}_{u\in H}\left\{ g(u)+\dfrac{1}{2\lambda }\Vert u-x \Vert ^{2}\right\} . \end{aligned}$$

(2.1)

Moreover, the proximity operator of f is firmly nonexpansive, namely:

$$\begin{aligned} \left\langle {\text {prox}}_{\lambda g}(x)-{\text {prox}}_{\lambda g}(y),x-y \right\rangle \ge \Vert {\text {prox}}_{\lambda g}(x)-{\text {prox}}_{\lambda g}(y) \Vert ^{2}; \end{aligned}$$

(2.2)

for all $x,y\in H$, which is equivalent to

$$\begin{aligned} \Vert {\text {prox}}_{\lambda g}(x)-{\text {prox}}_{\lambda g}(y) \Vert ^{2}\le \Vert x-y \Vert ^{2}-\Vert (I-{\text {prox}}_{\lambda g})(x)- (I-{\text {prox}}_{\lambda g})(y)\Vert ^{2}.\nonumber \\ \end{aligned}$$

(2.3)

for all $x,y\in H$. For general information on proximal operator, see Combettes and Pesquet (2011a).

In a real Hilbert space H, it is well known that:

• (i) $\left\| \alpha x + (1-\alpha )y\right\| ^{2} = \alpha \left\| x \right\| ^{2} + (1-\alpha ) \left\| y \right\| ^{2} -\alpha (1-\alpha ) \left\| x-y \right\| ^{2},$ for all $x,y \in H$ and $\alpha \in [0,1]$;

• (ii) $\Vert x-y \Vert ^{2}=\Vert x \Vert ^{2}-2\langle x,y \rangle +\Vert y \Vert ^{2}$ for all $x,y \in H$;

• (iii) $\Vert x+y \Vert ^{2} \le \Vert x \Vert ^{2}+2\langle y,x+y \rangle$ for all $x,y \in H$.

Recall that the (nearest-point) projection $P_{C}$ from H onto C assigns to each $x \in H$ the unique point $P_{C}x \in C$ satisfying the property:

$$\begin{aligned} \displaystyle \Vert x- P_{C}x\Vert = \min _{y \in C} \Vert x- y\Vert . \end{aligned}$$

Lemma 2.1

(Takahashi 2000) Given $x \in H$ and $y \in C$. Then, $P_{C}x=y$ if and only if there holds the inequality:

$$\begin{aligned} \langle x-y, y-z \rangle \ge 0,\quad \forall z \in C. \end{aligned}$$

Lemma 2.2

(Xu 2003) Let $\{s_{n}\}$ be a sequence of nonnegative real numbers satisfying:

$$\begin{aligned} s_{n+1} = (1- \alpha _{n})s_{n} + \delta _{n}, \quad \forall n \ge 0, \end{aligned}$$

where $\{\alpha _{n}\}$ is a sequence in (0, 1) and $\{\delta _{n}\}$ is a sequence, such that

• 1. $\displaystyle \sum _{n=1}^{\infty } \alpha _{n} = \infty$;

• 2. $\displaystyle \limsup _{n \rightarrow \infty } \frac{\delta _{n}}{\alpha _{n}} \le 0$ or $\displaystyle \sum _{n=1}^{\infty } |\delta _{n} |< \infty$.

Then, $\lim _{n \rightarrow \infty } s_{n} = 0$.

Definition 2.3

Let C be a nonempty closed convex subset of a real Hilbert space H. A mapping $S: C \rightarrow C$ is called demi-closed at zero if for any sequence $\{x_{n}\}$ which converges weakly to x, and if the sequence $\{Tx_{n}\}$ converges strongly to 0, then $Tx = 0$.

Lemma 2.4

(Browder 1976) Let C be a nonempty closed convex subset of a real Hilbert space H. If $S : C \rightarrow C$ is a nonexpansive mapping, then $I-$S is demi-closed at zero.

Lemma 2.5

(Mainge 2008) Let $\{\Gamma _n\}$ be a sequence of real numbers that does not decrease at infinity in the sense that there exists a subsequence $\{\Gamma _{n_i}\}$ of $\{\Gamma _n\}$ which satisfies $\Gamma _{n_i}<\Gamma _{n_{i}+1}$ for all $i\in {\mathbb {N}}$. Define the sequence $\{\tau (n)\}_{n\ge n_0}$ of integers as follows:

$$\begin{aligned} \tau (n)=\max \left\{ k\le n:\Gamma _k<\Gamma _{k+1}\right\} , \end{aligned}$$

where $n_0\in {\mathbb {N}}$, such that $\{k\le n_0:\Gamma _k<\Gamma _{k+1}\}\ne \emptyset$. Then, the following hold:

• (i) $\tau ({n_0})\le \tau ({n_0+1})\le \cdots$ and $\tau (n)\longrightarrow \infty$;

• (ii) $\Gamma _{\tau _n}\le \Gamma _{\tau (n)+1}$ and $\Gamma _n\le \Gamma _{\tau (n)+1}$, $\forall n\ge n_0$.

3 Main results

In this section, we introduce an algorithm and prove a strong convergence for solving a common element of the set of fixed points of a nonexpansive mapping and the set of solutions of proximal split feasibility problems (1.1). Let $H_{1}$ and $H_{2}$ be two real Hilbert spaces. Let $f :H_{1}\rightarrow {\mathbb {R}} \cup \{+\infty \}$ and $g:H_{2} \rightarrow {\mathbb {R}} \cup \{+\infty \}$ be two proper and lower semicontinuous convex functions and $A : H_{1}\rightarrow H_{2}$ be a bounded linear operator. Let $S : H_{1}\rightarrow H_{1}$ be a nonexpansive mapping and Let $\psi :H_{1}\rightarrow H_{1}$ be a contraction mapping with $\delta \in (0,1)$.

We introduce the modified split proximal algorithm as follows:

Algorithm 3.1

Given an initial point $x_{1}\in H_{1}$. Assume that $x_n$ has been constructed and $\Vert A^{*}(I-{\text {prox}}_{\lambda g })Ax_{n}\Vert ^{2}+\Vert (I-{\text {prox}}_{\lambda f})x_{n}\Vert ^{2}\ne 0$, then compute $x_{n+1}$ by the following iterative scheme:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} &{}y_{n}={\text {prox}}_{\lambda \mu _{n} f}(\alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}-\mu _{n}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n})\\ &{}x_{n+1} =\beta _{n}y_{n}+(1-\beta _{n})Sy_{n},\quad \forall n\in {\mathbb {N}}, \end{array} \end{array}\right. } \end{aligned}$$

(3.1)

where the stepsize $\mu _{n}:=\rho _{n}\dfrac{\left( \frac{1}{2}\Vert (I-{\text {prox}}_{\lambda g}) Ax_{n}\Vert ^{2} \right) +\left( \frac{1}{2}\Vert (I-{\text {prox}}_{\lambda f}) x_{n}\Vert ^{2} \right) }{\Vert A^{*}(I-{\text {prox}}_{\lambda g })Ax_{n}\Vert ^{2}+\Vert (I-{\text {prox}}_{\lambda f})x_{n}\Vert ^{2}}$ with $0<\rho _{n}<4$ and $\{\alpha _{n}\}$, $\{\beta _{n}\} \subset (0,1)$.

We now prove our main theorem.

Theorem 3.2

Let $H_{1}$ and $H_{2}$ be two real Hilbert spaces. Let $f :H_{1}\rightarrow {\mathbb {R}} \cup \{+\infty \}$ and $g:H_{2} \rightarrow {\mathbb {R}} \cup \{+\infty \}$be two proper and lower semicontinuous convex functions, and $A : H_{1}\rightarrow H_{2}$ be a bounded linear operator. Let $\psi :H_{1}\rightarrow H_{1}$ be a contraction mapping with $\delta \in [0,1)$ and let $S : H_{1}\rightarrow H_{1}$ be a nonexpansive mapping, such that $\Omega := F(S)\cap \Gamma \ne 0$. If the control sequences $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\rho _{n}\}$ satisfy the following conditions:

• (C1) $\displaystyle \lim _{n \rightarrow \infty } \alpha _{n}= 0$ and $\displaystyle \sum _{n=1}^{\infty }\alpha _{n}=\infty$;

• (C2) $\displaystyle 0< \liminf _{n\rightarrow \infty }\beta _{n}\le \limsup _{n\rightarrow \infty }\beta _{n}< 1$;

• (C3) $\varepsilon \le \rho _{n}\le \dfrac{4(1-\alpha _{n})\left( \Vert (I-{\text {prox}}_{\lambda g}) Ax_{n}\Vert ^{2}\right) }{\left( \Vert (I-{\text {prox}}_{\lambda g}) Ax_{n}\Vert ^{2} \right) +\left( \Vert (I-{\text {prox}}_{\lambda f}) x_{n}\Vert ^{2} \right) }-\varepsilon$ for some $\varepsilon >0.$

Then, the sequence $\{x_{n}\}$ defined by Algorithm 3.1 converges strongly to a point $x^{*}\in \Omega$ which also solves the variational inequality:

$$\begin{aligned} \langle (\psi -I)x^{*}, x - x^{*} \rangle \le 0,\quad \forall x \in \Omega . \end{aligned}$$

Proof

Given any $\lambda > 0$ and $x \in H_{1}$, we define $h(x):=\frac{1}{2}\Vert (I-{\text {prox}}_{\lambda g}) Ax\Vert ^{2}$, $l(x):=\frac{1}{2}\Vert (I-{\text {prox}}_{\lambda f}) x\Vert ^{2}$, $\theta ^{2}(x):=\Vert A^{*}(I-{\text {prox}}_{\lambda g })Ax\Vert ^{2}+\Vert (I-{\text {prox}}_{\lambda f})x\Vert ^{2}$, and hence, $\mu _{n}=\rho _{n}\dfrac{h(x_{n})+l(x_{n})}{\theta ^{2}(x_{n})}$ where $0<\rho _{n}<4$.

By Banach fixed point theorem, there exists $x^{*} \in \Omega$ such that $x^{*} = P_{\Omega }\psi (x^{*})$. Then, $x^{*}={\text {prox}}_{\lambda \mu _{n} f}x^{*}$ and $Ax^{*}={\text {prox}}_{\lambda g}Ax^{*}$. Since ${\text {prox}}_{\lambda g }$ is firmly nonexpansive, we have $I-{\text {prox}}_{\lambda g }$ is also firmly nonexpansive. Hence

$$\begin{aligned} \langle A^{*}(I-{\text {prox}}_{\lambda g })Ax_{n},x_{n}-x^{*}\rangle =&~ \langle (I-{\text {prox}}_{\lambda g })Ax_{n},Ax_{n}-Ax^{*}\rangle \nonumber \\ =&~ \left\langle (I-{\text {prox}}_{\lambda g })Ax_{n}-(I-{\text {prox}}_{\lambda g })Ax^{*},Ax_{n}-Ax^{*}\right\rangle \nonumber \\ \ge&~ \Vert (I-{\text {prox}}_{\lambda g })Ax_{n}\Vert ^{2}=2h(x_{n}). \end{aligned}$$

(3.2)

From the definition of $y_{n}$ and the nonexpansivity of ${\text {prox}}_{\lambda \mu _{n} f}$, we have:

$$\begin{aligned} \Vert y_{n}-x^{*}\Vert =&~\Vert {\text {prox}}_{\lambda \mu _{n} f}(\alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}-\mu _{n}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n})-x^{*}\Vert \nonumber \\ \le&~\Vert \alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}-\mu _{n}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n}-x^{*}\Vert \nonumber \\ \le&~\alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert +(1-\alpha _{n})\left\| x_{n} -\dfrac{\mu _{n}}{(1-\alpha _{n})}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n}-x^{*}\right\| . \end{aligned}$$

(3.3)

From (3.2), we have:

$$\begin{aligned}&\left\| x_{n}-\dfrac{\mu _{n}}{(1-\alpha _{n})}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n}-x^{*}\right\| ^{2}\nonumber \\&\quad =~\Vert x_{n}-x^{*}\Vert ^{2}+\dfrac{\mu _{n}^{2}}{(1-\alpha _{n})^{2}}\Vert A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n} \Vert ^{2}\nonumber \\&\qquad -2\dfrac{\mu _{n}}{(1-\alpha _{n})}\langle A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n} , x_{n}-x^{*} \rangle \nonumber \\&\quad \le ~\Vert x_{n}-x^{*}\Vert ^{2}+\dfrac{\mu _{n}^{2}}{(1-\alpha _{n})^{2}}\Vert A^{*}(I-{\text {prox}}_{\lambda g})Ax_{n} \Vert ^{2} -4\dfrac{\mu _{n}}{(1-\alpha _{n})} h(x_{n})\nonumber \\&\quad =~\Vert x_{n}-x^{*}\Vert ^{2}+\rho _{n}^{2}\dfrac{(h(x_{n}) +l(x_{n}))^{2}}{(1-\alpha _{n})^{2}\theta ^{4}(x_{n})}\Vert A^{*}(I-{\text {prox}}_{\lambda g})Ax_{n} \Vert ^{2} -4\rho _{n}\dfrac{(h(x_{n})+l(x_{n}))}{(1-\alpha _{n}) \theta ^{2}(x_{n})}h(x_{n})\nonumber \\&\quad \le ~\Vert x_{n}-x^{*}\Vert ^{2}+\rho _{n}^{2}\dfrac{(h(x_{n}) +l(x_{n}))^{2}}{(1-\alpha _{n})^{2}\theta ^{2}(x_{n})}-4\rho _{n} \dfrac{(h(x_{n})+l(x_{n}))^{2}}{(1-\alpha _{n}) \theta ^{2}(x_{n})} \dfrac{h(x_{n})}{(h(x_{n})+l(x_{n}))}\nonumber \\&\quad =~\Vert x_{n}-x^{*}\Vert ^{2}-\rho _{n}\left( \dfrac{4h(x_{n})}{(h(x_{n}) +l(x_{n}))}-\dfrac{\rho _{n}}{1-\alpha _{n}}\right) \left( \dfrac{(h(x_{n})+l(x_{n}))^{2}}{(1-\alpha _{n})\theta ^{2}(x_{n})} \right) . \end{aligned}$$

(3.4)

By the condition (C3), we have $\dfrac{4h(x_{n})}{(h(x_{n})+l(x_{n}))}-\dfrac{\rho _{n}}{1-\alpha _{n}}\ge 0$ for all $n\ge 1.$ From (3.3) and (3.4), we have:

$$\begin{aligned} \Vert y_{n}-x^{*}\Vert \le&~\alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert +(1-\alpha _{n})\left\| x_{n}-\dfrac{\mu _{n}}{(1-\alpha _{n})}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n}-x^{*}\right\| \nonumber \\ \le&~\alpha _{n}\Vert \psi (x_{n})-\psi (x^{*})\Vert +\alpha _{n}\Vert \psi (x^{*})-x^{*}\Vert +(1-\alpha _{n})\left\| x_{n}-x^{*}\right\| \nonumber \\ \le&~\alpha _{n}\delta \Vert x_{n}-x^{*}\Vert +\alpha _{n} \Vert \psi (x^{*})-x^{*}\Vert +(1-\alpha _{n})\left\| x_{n}-x^{*}\right\| \nonumber \\ =&~(1-\alpha _{n}(1-\delta ))\Vert x_{n}-x^{*}\Vert +\alpha _{n} \Vert \psi (x^{*})-x^{*}\Vert . \end{aligned}$$

(3.5)

Since S is nonexpansive, by (3.1) and (3.5), we obtain:

$$\begin{aligned} \Vert x_{n+1}-x^{*}\Vert =&~\Vert \beta _{n}y_{n}+(1-\beta _{n})Sy_{n}-x^{*}\Vert \\ \le&~\beta _{n}\Vert y_{n}-x{*}\Vert +(1-\beta _{n})\Vert Sy_{n}-x^{*}\Vert \\ \le&~\beta _{n}\Vert y_{n}-x{*}\Vert +(1-\beta _{n})\Vert y_{n}-x^{*}\Vert \\ =&~\Vert y_{n}-x{*}\Vert \\ \le&~(1-\alpha _{n}(1-\delta ))\Vert x_{n}-x^{*}\Vert +\alpha _{n}\Vert \psi (x^{*})-x^{*}\Vert \\ \le&~\max \left\{ \Vert x_{n}-x^{*}\Vert , \dfrac{\Vert \psi (x^{*})-x^{*}\Vert }{1-\delta }\right\} . \end{aligned}$$

By mathematical induction, we have:

$$\begin{aligned} \Vert x_{n}-x^{*}\Vert \le \max \left\{ \Vert x_{1}-x^{*}\Vert , \dfrac{\Vert \psi (x^{*})-x^{*}\Vert }{1-\delta }\right\} ,\quad \forall n \in {\mathbb {N}}. \end{aligned}$$

Hence, $\{x_{n}\}$ is bounded and so are $\{\psi (x_{n})\}$, $\{Sy_{n}\}$.

From the definition of $y_{n}$ and (3.4), we have:

$$\begin{aligned} \Vert y_{n}-x^{*}\Vert ^{2}&=\Vert {\text {prox}}_{\lambda \mu _{n} f}(\alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}-\mu _{n}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n})-x^{*}\Vert ^{2}\nonumber \\&\le \Vert \alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}-\mu _{n}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n}-x^{*}\Vert ^{2},\nonumber \\&\le \alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert ^{2}+(1-\alpha _{n})\left\| x_{n} -\dfrac{\mu _{n}}{(1-\alpha _{n})}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n}-x^{*} \right\| ^{2}\nonumber \\&\le \alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert ^{2} +(1-\alpha _{n})\nonumber \\&\quad \times \left( \Vert x_{n}-x^{*}\Vert ^{2}-\rho _{n}\left( \dfrac{4h(x_{n})}{(h(x_{n}) +l(x_{n}))}-\dfrac{\rho _{n}}{1-\alpha _{n}}\right) \left( \dfrac{(h(x_{n})+l(x_{n}))^{2}}{(1-\alpha _{n})\theta ^{2}(x_{n})} \right) \right) \nonumber \\&\quad = \alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert ^{2} +(1-\alpha _{n})\Vert x_{n}-x^{*}\Vert ^{2}\nonumber \\&\qquad -\rho _{n}\left( \dfrac{4h(x_{n})}{(h(x_{n})+l(x_{n}))}-\dfrac{\rho _{n}}{1-\alpha _{n}}\right) \left( \dfrac{(h(x_{n})+l(x_{n}))^{2}}{\theta ^{2}(x_{n})} \right) . \end{aligned}$$

(3.6)

From the definition of $x_{n}$ and (3.6), we obtain:

$$\begin{aligned} \Vert x_{n+1}-x^{*}\Vert ^{2}=&~\Vert \beta _{n}y_{n}+(1-\beta _{n})Sy_{n}-x^{*}\Vert ^{2}\\ \le&~\beta _{n}\Vert y_{n}-x{*}\Vert ^{2}+(1-\beta _{n})\Vert Sy_{n}-x^{*}\Vert ^{2}\\ \le&~\Vert y_{n}-x{*}\Vert ^{2}\\ \le&~\alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert ^{2} +(1-\alpha _{n})\Vert x_{n}-x^{*}\Vert ^{2}\nonumber \\&-\rho _{n}\left( \dfrac{4h(x_{n})}{(h(x_{n})+l(x_{n}))}-\dfrac{\rho _{n}}{1-\alpha _{n}}\right) \left( \dfrac{(h(x_{n})+l(x_{n}))^{2}}{\theta ^{2}(x_{n})} \right) \\ \le&~\alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert ^{2} +\Vert x_{n}-x^{*}\Vert ^{2}\nonumber \\&-\rho _{n}\left( \dfrac{4h(x_{n})}{(h(x_{n}) +l(x_{n}))}-\dfrac{\rho _{n}}{1-\alpha _{n}}\right) \left( \dfrac{(h(x_{n})+l(x_{n}))^{2}}{\theta ^{2}(x_{n})} \right) . \end{aligned}$$

It implies that

$$\begin{aligned} \rho _{n}\left( \dfrac{4h(x_{n})}{(h(x_{n})+l(x_{n}))}-\dfrac{\rho _{n}}{1 -\alpha _{n}}\right) \left( \dfrac{(h(x_{n})+l(x_{n}))^{2}}{\theta ^{2}(x_{n})} \right)&\le \alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert ^{2}+\Vert x_{n}\nonumber \\&\quad -x^{*}\Vert ^{2}-\Vert x_{n+1}-x^{*}\Vert ^{2}. \end{aligned}$$

(3.7)

It follows from (3.6) that

$$\begin{aligned} \Vert x_{n+1}-x^{*}\Vert ^{2}=&~\Vert \beta _{n}y_{n}+(1-\beta _{n})Sy_{n}-x^{*}\Vert ^{2}\\ \le&~\beta _{n}\Vert y_{n}-x{*}\Vert ^{2}+(1-\beta _{n})\Vert Sy_{n}-x^{*} \Vert ^{2}-\beta _{n}(1-\beta _{n})\Vert y_{n}-Sy_{n}\Vert ^{2}\\ \le&~\Vert y_{n}-x{*}\Vert ^{2}-\beta _{n}(1-\beta _{n})\Vert y_{n}-Sy_{n}\Vert ^{2}\\ \le&~\alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert ^{2} +(1-\alpha _{n})\Vert x_{n}-x^{*}\Vert ^{2}-\beta _{n}(1-\beta _{n})\Vert y_{n}-Sy_{n}\Vert ^{2}\\ \le&~\alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert ^{2} +\Vert x_{n}-x^{*}\Vert ^{2}-\beta _{n}(1-\beta _{n})\Vert y_{n}-Sy_{n}\Vert ^{2}, \end{aligned}$$

which implies that

$$\begin{aligned} \beta _{n}(1-\beta _{n})\Vert y_{n}-Sy_{n}\Vert ^{2} \le&~\alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert ^{2} +\Vert x_{n}-x^{*}\Vert ^{2}-\Vert x_{n+1}-x^{*}\Vert ^{2}. \end{aligned}$$

(3.8)

Now, we divide our proof into two cases.

Case 1 Suppose that there exists $n_{0}\in {\mathbb {N}}$, such that $\{\Vert x_{n}-x^{*}\Vert \}^{\infty }_{n=1}$ is nonincreasing. Then, $\{\Vert x_{n}-x^{*}\Vert \}^{\infty }_{n=1}$ converges and $\Vert x_{n}-x^{*}\Vert ^{2}-\Vert x_{n+1}-x^{*}\Vert ^{2} \rightarrow 0$ as $n \rightarrow \infty$. From (3.7) and the condition (C1) and (C3), we obtain:

$$\begin{aligned} \rho _{n}\left( \dfrac{4h(x_{n})}{(h(x_{n})+l(x_{n}))} -\dfrac{\rho _{n}}{1-\alpha _{n}}\right) \left( \dfrac{(h(x_{n})+l(x_{n}))^{2}}{\theta ^{2}(x_{n})} \right) \rightarrow 0 \text { as } n \rightarrow \infty . \end{aligned}$$

Hence, we have:

$$\begin{aligned} \dfrac{(h(x_{n})+l(x_{n}))^{2}}{\theta ^{2}(x_{n})} \rightarrow 0 \text { as } n \rightarrow \infty . \end{aligned}$$

(3.9)

By the linearity and boundedness of A and the nonexpansivity of ${\text {prox}}_{\lambda g}$, we obtain that $\{\theta ^{2}(x_{n})\}$ is bounded.

It follows that

$$\begin{aligned} \lim _{n \rightarrow \infty }\left( (h(x_{n})+l(x_{n}))^{2}\right) =0, \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{n \rightarrow \infty }h(x_{n})= \lim _{n \rightarrow \infty }l(x_{n})=0. \end{aligned}$$

Next, we show that $\limsup _{n \rightarrow \infty } \left\langle \psi (x^{*})-x^{*}, x_{n} - x^{*} \right\rangle \le 0$, where $x^{*}=P_{\Omega }{\psi }(x^{*})$. Since $\{x_{n}\}$ is bounded, there exists a subsequence $\left\{ x_{n_j} \right\}$ of $\left\{ x_{n}\right\}$ satisfying $x_{n_{j}} \rightharpoonup \omega$ and

$$\begin{aligned} \displaystyle \limsup _{n \rightarrow \infty } \left\langle \psi (x^{*})-x^{*}, x_{n} - x^{*} \right\rangle = \lim _{j \rightarrow \infty }\left\langle \psi (x^{*})-x^{*}, x_{n_j} - x^{*}\right\rangle . \end{aligned}$$

(3.10)

By the lower semicontinuity of h, we have:

$$\begin{aligned} 0\le h(\omega )\le \liminf _{j\rightarrow \infty }h(x_{n_j }) = \lim _{n \rightarrow \infty }h(x_{n})=0. \end{aligned}$$

Therefore, $h(\omega )=\frac{1}{2}\Vert (I-{\text {prox}}_{\lambda g}) A\omega \Vert ^{2}=0$. Therefore, $A\omega$ is a fixed point of the proximal mapping of g or equivalently, $A\omega$ is a minimizer of g. Similarly, from the lower semicontinuity of l, we obtain:

$$\begin{aligned} 0\le l(\omega )\le \liminf _{j \rightarrow \infty }l(x_{n_j }) = \lim _{n \rightarrow \infty }l(x_{n})=0. \end{aligned}$$

Therefore, $l(\omega )=\frac{1}{2}\Vert (I-{\text {prox}}_{\lambda \mu _{n} f}) \omega \Vert ^{2}=0$. That is $\omega \in F({\text {prox}}_{\lambda \mu _{n} f})$. Then $\omega$ is a minimizer of f. Thus, $\omega \in \Gamma .$ We observe that

$$\begin{aligned} 0<\mu _{n}<4\dfrac{h(x_{n})+l(x_{n})}{\theta ^{2}(x_{n})}\rightarrow 0 \text { as } n\rightarrow \infty , \end{aligned}$$

and hence, $\mu _{n} \rightarrow 0 \text { as } n\rightarrow \infty$.

Next, we show that $\omega \in F(S)$. From (3.8) and the condition (C1), (C2), we have:

$$\begin{aligned} \Vert y_{n}-Sy_{n}\Vert \rightarrow 0 \text { as } n \rightarrow \infty . \end{aligned}$$

(3.11)

For each $n\ge 1$, let $u_{n}:=\alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}$. Then

$$\begin{aligned} \Vert u_{n}-x_{n}\Vert =&~\Vert \alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}-x_{n}\Vert \\ =&~ \alpha _{n}\Vert \psi (x_{n})-x_{n}\Vert . \end{aligned}$$

From the condition (C1), we have:

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert u_{n}-x_{n}\Vert =0. \end{aligned}$$

(3.12)

Observe that

$$\begin{aligned} \Vert u_{n}-{\text {prox}}_{\lambda \mu _{n} f}x_{n}\Vert \le \Vert u_{n}-x_{n}\Vert +\Vert (I-{\text {prox}}_{\lambda \mu _{n} f})x_{n}\Vert . \end{aligned}$$

From $\lim _{n \rightarrow \infty }l(x_{n})=\lim _{n \rightarrow \infty }\frac{1}{2}\Vert (I-{\text {prox}}_{\lambda \mu _{n} f}) x_{n}\Vert ^{2}=0$ and (3.12), we have:

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert u_{n}-{\text {prox}}_{\lambda \mu _{n} f}x_{n}\Vert =0. \end{aligned}$$

(3.13)

By the nonexpansiveness of ${\text {prox}}_{\lambda \mu _{n} f}$, we have:

$$\begin{aligned} \Vert y_{n}-{\text {prox}}_{\lambda \mu _{n} f}x_{n}\Vert =&\left\| {\text {prox}}_{\lambda \mu _{n} f}\left( u_{n}-\mu _{n}A^{*}\left( I- {\text {prox}}_{\lambda g}\right) Ax_{n}\right) - {\text {prox}}_{\lambda \mu _{n} f}x_{n}\right\| \\ \le&~\Vert u_{n}-\mu _{n}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n}- x_{n}\Vert \\ \le&~\Vert u_{n}- x_{n}\Vert +\mu _{n}\Vert A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n}\Vert . \end{aligned}$$

From (3.13) and $\mu _{n}\rightarrow 0$ as $n \rightarrow \infty$, we have:

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert y_{n}-{\text {prox}}_{\lambda \mu _{n} f}x_{n}\Vert =0. \end{aligned}$$

(3.14)

Since

$$\begin{aligned} \Vert y_{n}-u_{n}\Vert \le&~\Vert y_{n}-{\text {prox}}_{\lambda \mu _{n} f}x_{n}\Vert + \Vert u_{n}-{\text {prox}}_{\lambda \mu _{n} f}x_{n}\Vert , \end{aligned}$$

from (3.13) and (3.14), we obtain:

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert y_{n}-u_{n}\Vert =0. \end{aligned}$$

(3.15)

From (3.12) and (3.15), we obtain

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert y_{n}-x_{n}\Vert =0. \end{aligned}$$

(3.16)

From

$$\begin{aligned} \Vert Sy_{n}-x_{n}\Vert \le \Vert Sy_{n}-y_{n}\Vert + \Vert y_{n}-x_{n} \Vert , \end{aligned}$$

by (3.11), (3.16), we get:

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert Sy_{n}-x_{n}\Vert =0. \end{aligned}$$

(3.17)

From the definition of $x_{n}$, we have:

$$\begin{aligned} \Vert x_{n+1}-x_{n}\Vert \le \beta _{n} \Vert y_{n}-x_{n}\Vert + (1-\beta _{n})\Vert Sy_{n}-x_{n} \Vert . \end{aligned}$$

This implies from (3.16), and (3.17) that

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert x_{n+1}-x_{n}\Vert =0. \end{aligned}$$

(3.18)

Using $x_{n_j}\rightharpoonup \omega \in H_{1}$ and (3.16), we obtain $y_{n_j}\rightharpoonup \omega \in H_{1}$. Since $y_{n_j}\rightharpoonup \omega \in H_{1}$, $\Vert y_{n}-Sy_{n}\Vert \rightarrow 0$ as $n\rightarrow \infty$, by Lemma 2.4, we have $\omega \in F(S)$. Hence, $\omega \in {\mathcal {F}}= F(S)\cap \Gamma .$ Since $x_{n_j} \rightharpoonup \omega$ as $j\rightarrow \infty$ and $\omega \in {\mathcal {F}}$, by Lemma 2.1, we have:

$$\begin{aligned} \displaystyle \limsup _{n \rightarrow \infty } \left\langle \psi (x^{*})-x^{*}, x_{n} - x^{*} \right\rangle&= \lim _{j \rightarrow \infty }\left\langle \psi (x^{*})-x^{*}, x_{n_j} - x^{*} \right\rangle \nonumber \\&= \left\langle (\psi -I)x^{*}, \omega - x^{*}\right\rangle \nonumber \\&\le 0. \end{aligned}$$

(3.19)

Now, by the nonexpansiveness of S and ${\text {prox}}_{\lambda \mu _{n} f}$, and from (3.1) and (3.4), we have:

$$\begin{aligned} \Vert x_{n+1}-x^{*} \Vert ^{2}&\le \beta _{n}\Vert y_{n}-x^{*}\Vert ^{2}+(1-\beta _{n}) \Vert Sy_{n}-x^{*}\Vert ^{2}\le \Vert y_{n}-x^{*}\Vert ^{2}\nonumber \\&\le \Vert \alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}-\mu _{n}A^{*} (I- {\text {prox}}_{\lambda g})Ax_{n}-x^{*}\Vert ^{2}\nonumber \\&=(1-\alpha _{n})^{2}\Vert x_{n}-\dfrac{\mu _{n}}{(1-\alpha _{n})}A^{*} (I- {\text {prox}}_{\lambda g})Ax_{n}-x^{*}\Vert ^{2}+\alpha _{n}^{2}\Vert \psi (x_{n})-x^{*} \Vert ^{2}\nonumber \\&\quad +2\alpha _{n}(1-\alpha _{n})\left\langle \psi (x_{n})-x^{*}, x_{n} -\dfrac{\mu _{n}}{(1-\alpha _{n})}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n}-x^{*} \right\rangle \nonumber \\&\le (1-\alpha _{n})^{2}\Vert x_{n}-x^{*}\Vert ^{2}+\alpha _{n}^{2}\Vert \psi (x_{n}) -x^{*}\Vert ^{2}\nonumber \\&\quad +2\alpha _{n}(1-\alpha _{n})\langle \psi (x_{n})-x^{*}, x_{n}-x^{*}\rangle \nonumber \\&\quad -2\alpha _{n}\mu _{n}\langle \psi (x_{n})-x^{*},A^{*}(I-{\text {prox}}_{\lambda g}) Ax_{n} \rangle \nonumber \\&=(1-\alpha _{n})^{2}\Vert x_{n}-x^{*}\Vert ^{2}+\alpha _{n}^{2}\Vert \psi (x_{n})-x^{*}\Vert ^{2}\nonumber \\&\quad +2\alpha _{n}(1-\alpha _{n})\langle \psi (x_{n})-\psi (x^{*}), x_{n}-x^{*} \rangle \nonumber \\&\quad +2\alpha _{n}(1-\alpha _{n})\langle \psi (x^{*})-x^{*}, x_{n}-x^{*}\rangle \nonumber \\&\quad +2\alpha _{n}\mu _{n}\left\langle x^{*}- \psi (x_{n}),A^{*}(I -{\text {prox}}_{\lambda g})Ax_{n}\right\rangle \nonumber \\&\le (1-2\alpha _{n}+\alpha _{n}^{2})\Vert x_{n}-x^{*}\Vert ^{2}+\alpha _{n}^{2}\Vert \psi (x_{n})-x^{*}\Vert ^{2}\nonumber \\&\quad +2\alpha _{n}(1-\alpha _{n})\delta \Vert x_{n}-x^{*}\Vert ^{2} \nonumber \\&\quad +2\alpha _{n}(1-\alpha _{n})\langle \psi (x^{*})-x^{*}, x_{n}-x^{*}\rangle \nonumber \\&\quad +2\alpha _{n}\mu _{n}\Vert \psi (x_{n})-x^{*}\Vert \Vert A^{*}(I-{\text {prox}}_{\lambda g}) Ax_{n} \Vert \nonumber \\&=(1-2\alpha _{n}+\alpha _{n}^{2}+2\alpha _{n}(1-\alpha _{n})\delta )\Vert x_{n} -x^{*}\Vert ^{2}+\alpha _{n}^{2}\Vert \psi (x_{n})-x^{*}\Vert ^{2}\nonumber \\&\quad +2\alpha _{n}(1-\alpha _{n})\langle \psi (x^{*})-x^{*}, x_{n}-x^{*}\rangle \nonumber \\ {}&\quad +2\alpha _{n}\mu _{n}\Vert \psi (x_{n})-x^{*}\Vert \Vert A^{*}(I-{\text {prox}}_{\lambda g})Ax_{n}\Vert \nonumber \\&=(1-\epsilon _{n})\Vert x_{n}-x^{*}\Vert ^{2}+\epsilon _{n}\xi _{n}, \end{aligned}$$

(3.20)

where $\epsilon _{n}=\alpha _{n}(2-\alpha _{n}-2(1-\alpha _{n})\delta )$ and

$$\begin{aligned} \xi _{n}=\left[ \dfrac{\alpha _{n}\Vert \psi (x_{n})-x^{*}\Vert ^{2}+2(1-\alpha _{n})\langle \psi (x^{*})-x^{*}, x_{n}-x^{*}\rangle +2\mu _{n}\Vert A^{*}(I-{\text {prox}}_{\lambda g})Ax_{n}\Vert \Vert \psi (x_{n})-x^{*}\Vert }{2-\alpha _{n}-2(1-\alpha _{n})\delta } \right] . \end{aligned}$$

Note that $\mu _{n}\Vert A^{*}(I-{\text {prox}}_{\lambda g})Ax_{n} \Vert =\rho _{n}\dfrac{h(x_{n})+l(x_{n})}{\theta ^{2}(x_{n})}\Vert A^{*}(I-{\text {prox}}_{\lambda g})Ax_{n}\Vert$. Thus, $\mu _{n}\Vert A^{*}(I-{\text {prox}}_{\lambda g})Ax_{n} \Vert \rightarrow 0$ as $n\rightarrow \infty$. From the condition (C1), (3.19), (3.20) and Lemma 2.2, we can conclude that the sequence $\{x_{n}\}$ converges strongly to $x^{*}$.

Case 2 Assume that $\{\Vert x_{n}-x^{*}\Vert \}$ is not monotonically decreasing sequence. Then, there exists a subsequence ${n_l}$ of n, such that $\Vert x_{n_{l}}-x^{*}\Vert <\Vert x_{n_{l}+1}-x^{*}\Vert$ for all $l\in {\mathbb {N}}.$ Now, we define a positive integer sequence $\tau (n)$ by:

$$\begin{aligned} \tau (n):=\max \left\{ k\in {\mathbb {N}}: k\le n, \Vert x_{n_{l}}-x^{*}\Vert <\Vert x_{n_{l}+1}-x^{*}\Vert \right\} . \end{aligned}$$

for all $n \ge n_{0}$ (for some $n_{0}$ large enough). By Lemma 2.5, we have $\tau$ which is a non-decreasing sequence, such that $\tau (n)\rightarrow \infty$ as $n\rightarrow \infty$ and

$$\begin{aligned} \Vert x_{\tau (n)}-x^{*}\Vert ^{2}-\Vert x_{{\tau (n)}+1}-x^{*}\Vert ^{2}\le 0,\quad \forall n \ge n_{0} . \end{aligned}$$

By a similar argument as that of case 1, we can show that

$$\begin{aligned} \rho _{\tau (n)}\left( \dfrac{4h(x_{\tau (n)})}{(h(x_{\tau (n)}) +l(x_{\tau (n)}))}-\dfrac{\rho _{\tau (n)}}{1-\alpha _{\tau (n)}}\right) \left( \dfrac{(h(x_{\tau (n)})+l(x_{\tau (n)}))^{2}}{\theta ^{2}(x_{\tau (n)})} \right) \rightarrow 0 \text { as } n \rightarrow \infty . \end{aligned}$$

Then, we have:

$$\begin{aligned} \dfrac{(h(x_{\tau (n)})+l(x_{\tau (n)}))^{2}}{\theta ^{2}(x_{\tau (n)})} \rightarrow 0 \text { as } n \rightarrow \infty . \end{aligned}$$

(3.21)

It follows that

$$\begin{aligned} \lim _{n \rightarrow \infty }\left( (h(x_{\tau (n)})+l(x_{\tau (n)}))^{2}\right) =0, \end{aligned}$$

which implies that

$$\begin{aligned} \lim _{n \rightarrow \infty }h(x_{\tau (n)})= \lim _{n \rightarrow \infty }l(x_{\tau (n)})=0. \end{aligned}$$

Moreover, we have

$$\begin{aligned} \displaystyle \limsup _{n \rightarrow \infty } \left\langle \psi (x^{*})-x^{*}, x_{\tau (n)} - x^{*} \right\rangle \le 0. \end{aligned}$$

By the same computation as in Case 1, we have:

$$\begin{aligned} \Vert x_{\tau (n)+1}-x^{*} \Vert ^{2}&\le (1-\epsilon _{\tau (n)})\Vert x_{\tau (n)}-x^{*}\Vert ^{2}+\epsilon _{\tau (n)}\xi _{\tau (n)}, \end{aligned}$$

(3.22)

where $\epsilon _{\tau (n)}=\alpha _{\tau (n)}(2-\alpha _{\tau (n)}-2(1-\alpha _{\tau (n)})\delta )$ and

$$\begin{aligned}&\xi _{\tau (n)}\\&\quad =\left[ \dfrac{\alpha _{\tau (n)}\Vert \psi (x_{\tau (n)})-x^{*}\Vert ^{2}+2(1-\alpha _{\tau (n)})\langle \psi (x^{*})-x^{*}, x_{\tau (n)}-x^{*}\rangle +2\mu _{\tau (n)}\Vert A^{*}(I-{\text {prox}}_{\lambda g})Ax_{\tau (n)}\Vert \Vert \psi (x_{\tau (n)})-x^{*}\Vert }{2-\alpha _{\tau (n)}-2(1-\alpha _{\tau (n)})\delta } \right] . \end{aligned}$$

Since $\Vert x_{\tau (n)}-x^{*}\Vert ^{2} \le \Vert x_{{\tau (n)}+1}-x^{*}\Vert ^{2}$, then by (3.22), we have:

$$\begin{aligned} \Vert x_{\tau (n)}-x^{*}\Vert ^{2} \le \xi _{\tau (n)}. \end{aligned}$$

We note that $\limsup _{n \rightarrow \infty } \xi _{\tau (n)}\le 0.$ Thus, it follows from above inequality that

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert x_{\tau (n)}-x^{*} \Vert =0. \end{aligned}$$

From (3.22), we also have:

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert x_{\tau (n)+1}-x^{*} \Vert =0. \end{aligned}$$

It follows from Lemma 2.5 that

$$\begin{aligned} 0\le \Vert x_{n}-x^{*}\Vert \le \Vert x_{{\tau (n)}+1}-x^{*}\Vert \rightarrow 0 \end{aligned}$$

as $n \rightarrow \infty$. Therefore, $\{x_{n}\}$ converges strongly to $x^{*}$. This completes the proof.

$\square$

Taking $\psi (x)$ = u in Algorithm 3.1, we have the following Halpern-type algorithm.

Algorithm 3.3

Given an initial point $x_{1}\in H_{1}$. Assume that $x_n$ has been constructed and $\Vert A^{*}(I-{\text {prox}}_{\lambda g })Ax_{n}\Vert ^{2}+\Vert (I-{\text {prox}}_{\lambda f})x_{n}\Vert ^{2}\ne 0$, and then compute $x_{n+1}$ by the following iterative scheme:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} &{}y_{n}={\text {prox}}_{\lambda \mu _{n} f}(\alpha _{n}u+(1-\alpha _{n})x_{n}-\mu _{n}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n})\\ &{}x_{n+1} =\beta _{n}y_{n}+(1-\beta _{n})Sy_{n},\quad \forall n\in {\mathbb {N}}, \end{array} \end{array}\right. } \end{aligned}$$

(3.23)

where the stepsize $\mu _{n}:=\rho _{n}\dfrac{\left( \frac{1}{2}\Vert (I-{\text {prox}}_{\lambda g}) Ax_{n}\Vert ^{2} \right) +\left( \frac{1}{2}\Vert (I-{\text {prox}}_{\lambda f}) x_{n}\Vert ^{2} \right) }{\Vert A^{*}(I-{\text {prox}}_{\lambda g })Ax_{n}\Vert ^{2}+\Vert (I-{\text {prox}}_{\lambda f})x_{n}\Vert ^{2}}$ with $0<\rho _{n}<4$ and $\{\alpha _{n}\}$, $\{\beta _{n}\} \subset [0,1]$.

The following result is obtained directly by Theorem 3.2.

Corollary 3.4

Let $H_{1}$ and $H_{2}$ be two real Hilbert spaces. Let $f :H_{1}\rightarrow {\mathbb {R}} \cup \{+\infty \}$ and $g:H_{2} \rightarrow {\mathbb {R}} \cup \{+\infty \}$be two proper and lower semicontinuous convex functions and $A : H_{1}\rightarrow H_{2}$ be a bounded linear operator. Let $S : H_{1}\rightarrow H_{1}$ be a nonexpansive mapping, such that $\Omega := F(S)\cap \Gamma \ne 0$. If the control sequences $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\rho _{n}\}$ satisfy the following conditions:

• (C1) $\displaystyle \lim _{n \rightarrow \infty } \alpha _{n}= 0$ and $\displaystyle \sum _{n=1}^{\infty }\alpha _{n}=\infty$;

• (C2) $\displaystyle 0< \liminf _{n\rightarrow \infty }\beta _{n}\le \limsup _{n\rightarrow \infty }\beta _{n}< 1$;

• (C3) $\varepsilon \le \rho _{n}\le \dfrac{4(1-\alpha _{n})\left( \Vert (I-{\text {prox}}_{\lambda g}) Ax_{n}\Vert ^{2}\right) }{\left( \Vert (I-{\text {prox}}_{\lambda g}) Ax_{n}\Vert ^{2} \right) +\left( \Vert (I-{\text {prox}}_{\lambda f}) x_{n}\Vert ^{2} \right) }-\varepsilon$ for some $\varepsilon >0.$

Then, the sequence $\{x_{n}\}$ defined by Algorithm 3.3 converges strongly to $z=P_{\Omega }u$.

4 Convergence theorem for split feasibility problems

In this section, we give an application of Theorem 3.2 to the split feasibility problem.

Algorithm 4.1

Given an initial point $x_{1}\in H_{1}$. Assume that $x_n$ has been constructed and $\Vert A^{*}(I-P_{Q})Ax_{n}\Vert ^{2}+\Vert (I-P_{C})x_{n}\Vert ^{2}\ne 0$, and then compute $x_{n+1}$ by the following iterative scheme:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} &{}y_{n}=P_{C}(\alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}-\mu _{n}A^{*}(I- P_{Q})Ax_{n})\\ &{}x_{n+1} =\beta _{n}y_{n}+(1-\beta _{n})Sy_{n},\quad \forall n\in {\mathbb {N}}, \end{array} \end{array}\right. } \end{aligned}$$

(4.1)

where the stepsize $\mu _{n}:=\rho _{n}\dfrac{\left( \frac{1}{2}\Vert (I-P_{Q}) Ax_{n}\Vert ^{2} \right) +\left( \frac{1}{2}\Vert (I-P_{C}) x_{n}\Vert ^{2} \right) }{\Vert A^{*}(I-P_{Q})Ax_{n}\Vert ^{2}+\Vert (I-P_{C})x_{n}\Vert ^{2}}$ with $0<\rho _{n}<4$ and $\{\alpha _{n}\}$, $\{\beta _{n}\} \subset (0,1)$.

We now obtain a strong convergence theorem of Algorithm 4.1 for solving the split feasibility problem and the fixed point problem of nonexpansive mappings as follows:

Theorem 4.2

Let $H_{1}$ and $H_{2}$ be two real Hilbert spaces, and let C and Q be nonempty, closed and convex subsets of $H_{1}$ and $H_{2}$, respectively. Let $A : H_{1}\rightarrow H_{2}$ be a bounded linear operator. Let $\psi :H_{1}\rightarrow H_{1}$ be a contraction mapping with $\delta \in [0,1)$ and let $S : H_{1}\rightarrow H_{1}$ be a nonexpansive mapping. Assume that $\Omega := F(S) \cap C \cap A^{-1}(Q) \ne \emptyset$. If the control sequences $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\rho _{n}\}$ satisfy the following conditions:

• (C1) $\displaystyle \lim _{n \rightarrow \infty } \alpha _{n}= 0$ and $\displaystyle \sum _{n=1}^{\infty }\alpha _{n}=\infty$,

• (C2) $\displaystyle 0< \liminf _{n\rightarrow \infty }\beta _{n}\le \limsup _{n\rightarrow \infty }\beta _{n}< 1$;

• (C3) $\varepsilon \le \rho _{n}\le \dfrac{4(1-\alpha _{n})\left( \Vert (I-P_{Q}) Ax_{n}\Vert ^{2}\right) }{\left( \Vert (I-P_{Q}) Ax_{n}\Vert ^{2} \right) +\left( \Vert (I-P_{C}) x_{n}\Vert ^{2} \right) }-\varepsilon$ for some $\varepsilon >0.$

Then, the sequence $\{x_{n}\}$ generated by Algorithm 4.1 converges strongly to $z=P_{\Omega }{\psi }(z)$.

Proof

Taking $f=i_{C}$ and $g=i_{Q}$ in Theorem 3.2 ($i_{C}$ and $i_{Q}$ are indicator functions of C and Q, respectively), we have ${\text {prox}}_{\lambda f}=P_{C}$ and ${\text {prox}}_{\lambda g}=P_{Q}$ for all $\lambda$. We also have $\mathop {\mathrm {argmin}}f = C$ and $\mathop {\mathrm {argmin}}g = Q$. Therefore, from Theorem 3.2, we obtain the desired result. $\square$

5 Convergence theorem for nonexpansive semigroups

In this section, we prove a strong convergence theorem for finding a common solution of the proximal split feasibility problem and the fixed point problem of nonexpansive semigroups in Hilbert spaces.

Let C be a nonempty, closed, and convex subset of a real Banach space X. A one-parameter family $S = {S(t) : t \ge 0} : C\rightarrow C$ is said to be a nonexpansive semigroup on C if it satisfies the following conditions:

• (i) $S(0)x=x$ for all $x\in C$;

• (ii) $S(s+t)x=S(s)S(t)x$ for all $t,s>0$ and $x\in C$;

• (iii) for each $x\in C$ the mapping $t\longmapsto S(t)x$ is continuous;

• (iv) $\Vert S(t)x-S(t)y \Vert \le \Vert x -y\Vert$ for all $x,y \in C$ and $t>0.$

We use F(S) to denote the common fixed point set of the semigroup S, i.e., $F(S) = \bigcap _{t>0} F(S(t))=\{x\in C: x=S(t)x\}$. It is well known that F(S) is closed and convex (see Browder 1956).

Definition 5.1

(Aleyner and Censor 2005) Let C be a nonempty, closed, and convex subset of a real Hilbert space H, $S = {S(t) : t > 0}$ be a continuous operator semigroup on C. Then, S is said to be uniformly asymptotically regular (in short, u.a.r.) on C if for all $h \ge 0$ and any bounded subset K of C, such that

$$\begin{aligned} \lim _{t \rightarrow \infty }\sup _{x\in K}\Vert S(h)(S(t)x)-S(t)x \Vert =0. \end{aligned}$$

Lemma 5.2

(Shimizu and Takahashi 1997) Let C be a nonempty, closed, and convex subset of a real Hilbert space H, and let K be a bounded, closed, and convex subset of C. If we denote $S = {S(t) : t > 0}$ is a nonexpansive semigroup on C, such that $F(S) = \bigcap _{t>0} F(S(t))\ne \emptyset$. For all $h>0$, the set $\sigma _{t}(x)=\frac{1}{t}\int _{0}^{t}S(s)x\mathrm{d}s$, then

$$\begin{aligned} \lim _{t \rightarrow \infty }\sup _{x\in K}\Vert \sigma _{t}(x)-S(h)\sigma _{t}(x)\Vert =0. \end{aligned}$$

Let $H_{1}$ and $H_{2}$ be two real Hilbert spaces. Let $f :H_{1}\rightarrow {\mathbb {R}} \cup \{+\infty \}$ and $g:H_{2} \rightarrow {\mathbb {R}} \cup \{+\infty \}$ be two proper and lower semicontinuous convex functions and $A : H_{1}\rightarrow H_{2}$ be a bounded linear operator and let $\psi :H_{1}\rightarrow H_{1}$ be a contraction mapping with $\delta \in [0,1)$. Let $S:=\{S(t):t>0\}$ be a u.a.r nonexpansive semigroup on $H_{1}$.

Algorithm 5.3

Given an initial point $x_{1}\in H_{1}$. Assume that $x_n$ has been constructed and $\Vert A^{*}(I-{\text {prox}}_{\lambda g })Ax_{n}\Vert ^{2}+\Vert (I-{\text {prox}}_{\lambda f})x_{n}\Vert ^{2}\ne 0$, and then compute $x_{n+1}$ by the following iterative scheme:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} &{}y_{n}={\text {prox}}_{\lambda \mu _{n} f}(\alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}-\mu _{n}A^{*}(I- {\text {prox}}_{\lambda g})Ax_{n})\\ &{}x_{n+1} =\beta _{n}y_{n}+(1-\beta _{n})S(t_{n})y_{n},\quad \forall n\in {\mathbb {N}}, \end{array} \end{array}\right. } \end{aligned}$$

(5.1)

where the stepsize $\mu _{n}:=\rho _{n}\dfrac{\left( \frac{1}{2}\Vert (I-{\text {prox}}_{\lambda g}) Ax_{n}\Vert ^{2} \right) +\left( \frac{1}{2}\Vert (I-{\text {prox}}_{\lambda f}) x_{n}\Vert ^{2} \right) }{\Vert A^{*}(I-{\text {prox}}_{\lambda g })Ax_{n}\Vert ^{2}+\Vert (I-{\text {prox}}_{\lambda f})x_{n}\Vert ^{2}}$ with $0<\rho _{n}<4$, $\{\alpha _{n}\}$, $\{\beta _{n}\} \subset (0,1)$ and $\{t_{n}\}$ is a positive real divergent sequence.

We now prove a strong convergence result for the problem (1.1) and the fixed point problem of nonexpansive semigroups as follows:

Theorem 5.4

Suppose that $\bigcap _{t>0} F(S(t))\cap \Gamma \ne 0$. If the control sequences $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\rho _{n}\}$ satisfy the following conditions:

• (C1) $\displaystyle \lim _{n \rightarrow \infty } \alpha _{n}= 0$ and $\displaystyle \sum _{n=1}^{\infty }\alpha _{n}=\infty$;

• (C2) $\displaystyle 0< \liminf _{n\rightarrow \infty }\beta _{n}\le \limsup _{n\rightarrow \infty }\beta _{n}< 1$;

• (C3) $\varepsilon \le \rho _{n}\le \dfrac{4(1-\alpha _{n})\left( \Vert (I-{\text {prox}}_{\lambda g}) Ax_{n}\Vert ^{2}\right) }{\left( \Vert (I-{\text {prox}}_{\lambda g}) Ax_{n}\Vert ^{2} \right) +\left( \Vert (I-{\text {prox}}_{\lambda f}) x_{n}\Vert ^{2} \right) }-\varepsilon$ for some $\varepsilon >0.$

Then, the sequence $\{x_{n}\}$ generated by Algorithm 5.3 converges strongly to a point $x^{*}\in \bigcap _{t>0} F(S(t))\cap \Gamma$.

Proof

By continuing in the same direction as in Theorem 3.2, we have that $\lim _{n \rightarrow \infty }\Vert y_{n}-S(t_{n})y_{n}\Vert =0.$ Now, we only show that $\lim _{n \rightarrow \infty }\Vert y_{n}-S(h)y_{n}\Vert =0$ for all $h\ge 0.$ We observe that

$$\begin{aligned} \Vert y_{n}-S(h)y_{n}\Vert&\le \Vert y_{n}-S(t_{n})y_{n}\Vert +\Vert S(t_{n})y_{n}-S(h)S(t_{n})y_{n}\Vert +\Vert S(h)S(t_{n})y_{n}-S(h)y_{n}\Vert \\&\le 2\Vert y_{n}-S(t_{n})y_{n}\Vert +\sup _{x\in y_{n}}\Vert S(t_{n})x-S(h)S(t_{n})x\Vert . \end{aligned}$$

Since $\{S(t) : t \ge 0\}$ is a u.a.r. nonexpansive semigroup and $t_{n}\rightarrow \infty$ for all $h\ge 0$, we have:

$$\begin{aligned} \lim _{n \rightarrow \infty } \Vert y_{n}-S(h)y_{n}\Vert =0, \end{aligned}$$

for all $h\ge 0$. This completes the proof. $\square$

6 Numerical examples

We first give a numerical example in Euclidean spaces to demonstrate the convergence of Algorithm (3.1).

Example 6.1

Let $H_1 = {\mathbb {R}}^{2}$ and $H_2 = {\mathbb {R}}^{3}$ with the usual norms. Define a mapping $S : {\mathbb {R}}^{2} \rightarrow {\mathbb {R}}^{2}$ by:

$$\begin{aligned} S(a, b) := \frac{\sqrt{2}}{2}(a - b, a + b). \end{aligned}$$

One can show that S is nonexpansive. Define two functions $f{:}\, {\mathbb {R}}^{2} \rightarrow (-\infty , \infty ]$ and $g : {\mathbb {R}}^{3} \rightarrow (-\infty , \infty ]$ by $f:= 0$, where 0 is a zero operator and

$$\begin{aligned} g(a, b, c) := \frac{|-3a + 7b - 2c |^{2}}{2}. \end{aligned}$$

Then, the explicit forms of the proximity operators of f and g can be written by ${\text {prox}}_{\lambda f} = I$ and ${\text {prox}}_{1 g} = B^{-1}$, where $B = \begin{pmatrix} 10 &{} -21 &{} 6 \\ -21 &{} 50 &{} -14 \\ 6 &{} -14 &{} 5 \\ \end{pmatrix}$ (see Combettes and Pesquet 2011b). Let $A: {\mathbb {R}}^{2} \rightarrow {\mathbb {R}}^{3}$ be defined by:

$$\begin{aligned} A := \begin{pmatrix} 2 &{} 1 \\ 7 &{} -3\\ -5 &{} 4 \\ \end{pmatrix}, \end{aligned}$$

and let $\Omega := F(S) \cap \mathop {\mathrm {argmin}}f \cap A^{-1}(\mathop {\mathrm {argmin}}g)$. Now, we rewrite Algorithm (3.1) in the form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} &{}y_{n}= \alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}-\mu _{n}A^{T}(I- B^{-1})Ax_{n}\\ &{}x_{n+1} =\beta _{n}y_{n}+(1-\beta _{n})Sy_{n},\quad \forall n\in {\mathbb {N}}, \end{array} \end{array}\right. } \end{aligned}$$

(6.1)

where

$$\begin{aligned} \mu _{n} = \frac{\rho _{n}}{2}\frac{\Vert (I - B^{-1})Ax_{n}\Vert ^{2}}{\Vert A^{T}(I - B^{-1})Ax_{n}\Vert ^{2}}. \end{aligned}$$

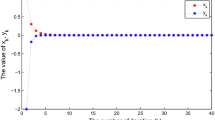
Take $\alpha _{n} = \frac{1}{n+1}$, $\beta _{n} = \frac{1}{2}$, $\rho _{n} = \frac{2n}{n+1}$. Consider a contraction $\psi : {\mathbb {R}}^{2} \rightarrow {\mathbb {R}}^{2}$ defined by $\psi (x) = \delta x$ for $0 \le \delta < 1$. We first start with the initial point $x_{1} = (3, -2)$ and the stopping criterion for our testing process is set as: $E_{n} := \Vert x_{n} - x_{n-1} \Vert < 10^{-6}$, where $x_{n} = (a_{n}, b_{n}).$ In Table 1, we show the convergence behavior of Algorithm (6.1) by choosing $\delta = 0.1$. In Table 2, we also show the number of iterations of Algorithm (6.1) by choosing different constants $\delta$. –

Table 1 The numerical experiment of Algorithm (6.1) by choosing $\delta = 0.1$

Table 2 The number of iterations of Algorithm (6.1) by choosing different constants $\delta$

Remark 6.2

In Example 6.1, by testing the convergence behavior of Algorithm (6.1), we observe that

• (i) It converges to a solution, i.e., $x_{n} \rightarrow (0, 0) \in \Omega$.

• (ii) The selection of a contraction $\psi$ in our algorithm influences the number of iterations of the algorithm. We also note that if $\psi \equiv 0$ is zero, then our algorithm becomes Algorithm (1.6) (Shehu and Iyiola 2015, Algorithm 1).

Next, we give an example in the infinite-dimensional space $L^{2}$ as follows.

Example 6.3

Let $H_1 = L^{2}([0, 1]) = H_{2}$. Let $x \in L^{2}([0, 1])$. Define a bounded linear operator $A : L^{2}([0, 1]) \rightarrow L^{2}([0, 1])$ by:

$$\begin{aligned} (Ax)(t) := 3tx(t). \end{aligned}$$

Define a mapping $S : L^{2}([0, 1]) \rightarrow L^{2}([0, 1])$ by:

$$\begin{aligned} (Sx)(t) := \sin (x(t)). \end{aligned}$$

Then, S is nonexpansive. Let

$$\begin{aligned} C = \left\{ x \in L^{2}([0, 1]) : \langle w, x \rangle \le 0 \right\} , \end{aligned}$$

where $w \in L^{2}([0, 1])$, such that $w(t) = 2t^{3}$, and let

$$\begin{aligned} Q = \left\{ x \in L^{2}([0, 1]) : x \ge 0 \right\} . \end{aligned}$$

Define two functions $f, g :L^{2}([0, 1]) \rightarrow (-\infty , \infty ]$ by $f := i_{C}$ and $g := i_{Q}$, where $i_{C}$ and $i_{Q}$ are indicator functions of C and Q, respectively. We can write the explicit forms of the proximity operators of f and g in the following forms:

$$\begin{aligned} {\text {prox}}_{\lambda f}x = P_{C}x = {\left\{ \begin{array}{ll} x - \frac{\langle w, x \rangle }{\Vert w\Vert ^{2}}w, ~ &{}\text {if}~x \notin C,\\ x, &{}\text {if}~x \in C, \end{array}\right. } \end{aligned}$$

and ${\text {prox}}_{\lambda g}x = P_{Q}x = x_{+}$, where $x_{+}(t) = \max \{x(t), 0\}$ (see Cegielski 2012). Therefore, Algorithm (3.1) can be rewritten in the form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \begin{array}{ll} &{}y_{n}=P_{C}(\alpha _{n}\psi (x_{n})+(1-\alpha _{n})x_{n}-\mu _{n}A^{*}(I- P_{Q})Ax_{n})\\ &{}x_{n+1} =\beta _{n}y_{n}+(1-\beta _{n})Sy_{n},\quad \forall n\in {\mathbb {N}}; \end{array} \end{array}\right. } \end{aligned}$$

(6.2)

$\mu _{n}=\rho _{n}\dfrac{\left( \frac{1}{2}\Vert (I-P_{Q}) Ax_{n}\Vert ^{2} \right) +\left( \frac{1}{2}\Vert (I-P_{C}) x_{n}\Vert ^{2} \right) }{\Vert A^{*}(I-P_{Q})Ax_{n}\Vert ^{2}+\Vert (I-P_{C})x_{n}\Vert ^{2}}$, for finding a common element in the set $\Omega := F(S) \cap C \cap A^{-1}(Q)$. By choosing the control sequences $\{\alpha _{n}\}$, $\{\beta _{n}\}$ and $\{\rho _{n}\}$ satisfying the conditions (C1)–(C3) in Theorem 3.2, it can guarantee that the sequence $\{x_{n}\}$ generated by (6.2) converges strongly to $x^{*} = 0 \in \Omega$.