1 Introduction

Historically, more than two hundred years many problems in mathematical biology, plasma physics, analytical chemistry, finance, quantum mechanics, and many other applications in science and engineering were formulated using the fractional calculus (Losada and Nieto 2015; Caputo and Fabrizio 2015; Atangana and Baleanu 2016; Atangana and Koca 2016; Algahtani 2016; Raja et al. 2015, 2016; Atangana 2016; Mandelbrot and Van Ness 1968; Atangana and Gómez-Aguilar 2017; Jumarie 2001, 2005a, b, 2009; Baleanu et al. 2010) The origin of fractional calculus was dated back to the work of the German mathematician Gottfried Wilhelm Leibniz in 1695 (see Oldham and Spanier 1974). The theory of fractional calculus can easily be used to study the memory effects of dynamic systems, and have the embedded efficiency to described these systems in the best way. Unfortunately, the concept of classical fractional calculus cannot be used to study some continuous dynamical systems with highly irregular surfaces and curves (Kolwankar and Gangal 1998). These dynamics systems are continuous but nowhere differentiable and arise naturally in many fields of physical science and engineering (Kolwankar and Gangal 1997). To overcome the limitations of classical fractional calculus, the concept of local fractional calculus was introduced by Kolwankar and Gangal (1996). The local fractional calculus is a modification of classical calculus and is suitable to study the behavior of these dynamics systems with highly irregular curves and surfaces (non-differentiable).

In recent years, there is a rapid development on the concept of local fractional calculus (see Yang 2011a, 2012; Yang et al. 2010, 2013a, b, 2014a, b, 2016a, b, c, 2017a, b, c, d, 2018; Hemeda et al. 2018; Ming-Sheng et al. 2012; Zhao et al. 2017; Wang et al. 2014; Chen et al. 2010; Golmankhaneh et al. 2015; Singh et al. 2016; Liu et al. 2014; Srivastava et al. 2014; Jafari et al. 2015a; Kumar et al. 2017a, b). Based on the current development, many numerical and analytical techniques such as local fractional Adomian decomposition method (Yan et al. 2014), the local fractional variational iteration method (Yang et al. 2013c, 2014c; Jafari and Kamil 2015; Jafari et al. 2015b), the local fractional homotopy perturbation method (Yang et al. 2015a; Zhang et al. 2015), the local fractional homotopy perturbation Sumudu transform method (Ziane et al. 2017), and the local fractional Laplace decomposition method (Jassim 2015) have been proposed and successfully applied to various applications.

The main aim of this present paper is to introduce an efficient numerical method which is a combination of homotopy analysis method (Liao 1995, 2003, 2005, 2010) and the local fractional Laplace transform (Yang 2011b; Yang et al. 2015b) for solving wave equations involving local fractional derivatives arising in physical sciences and engineering. The efficiency and the high accuracy of the method are demonstrated. The most significant novel features of the proposed scheme are as follows:

  • The proposed scheme can be applied directly without any linearization, transformations, discretizations of variables, or taking some restrictive assumptions.

  • The LFLHAM reduces the computational size and errors.

  • It is a semi-analytical method which provides an exact or approximate solution.

  • The LFLHAM avoids the cumbersome steps of some computational methods.

  • The proposed technique can easily be applied to nonlinear local fractional partial differential equations.

  • The cornerstone of the LFLHAM is the nonzero convergence-control parameter which provides us with a convenient way to guarantee the convergence of the series solutions.

The paper is organized as follows. In Sect. 2, some preliminaries of local fractional calculus and local fractional Laplace transform are presented. The basic idea of the homotopy analysis is presented in Sect. 3. Section 4 described the analysis and convergence of the local fractional Laplace homotopy analysis method. In Sect. 5 some applications of the LFLHAM are presented, and finally, in Sect. 6 conclusions of this paper are discussed. In Table 1, we presented some useful identities of the local fractional calculus.

Table 1 .
Full size table

2 Preliminaries of local fractional calculus

Definition 1

Let \(\phi : \mathfrak {I}\rightarrow \aleph \) be a function defined on fractal set \(\mathfrak {I}\) of fractal dimension \(\alpha \) say \((0<\alpha <1)\). Then a real-valued function on a fractal set \(\mathfrak {I}\) is defined as (Yang 2011a, 2012)

$$\begin{aligned} \phi (t)=t^\theta , \end{aligned}$$
(1)

where \(t^\theta \in \mathfrak {I}\) and \(0<\theta <1\).

Definition 2

The function \(\xi (t)\) is local fractional continuous at \(t=t_0\) if it is valid for (Yang 2011a, 2012)

$$\begin{aligned} |\xi (t)-\xi (t_0)|<\varepsilon ^\theta ,\,\,0<\theta \le 1, \end{aligned}$$
(2)

with \(|t-t_0|<\delta \),   for \(\varepsilon >0\) and \(\varepsilon \in \mathbb {R}\) For \(t\in (a,b)\), the function \(\xi (t)\in C_\theta (a,b)\) is called local fractional continuous on the interval (a, b).

Definition 3

(Local fractional derivative) The local fractional derivative of the function \(\xi (t)\) of order \(\theta \) at \(t=t_0\) is defined as (Yang 2011a, 2012)

$$\begin{aligned} \xi ^{(\theta )}(t)=\frac{{\text {d}}^\theta \xi }{({\text {d}}t)^\theta }|_{t=t_0}=\lim _{t\rightarrow t_0}\frac{\varDelta ^\theta (\xi (t)-\xi (t_0))}{(t-t_0)^\theta }, \end{aligned}$$
(3)

where

$$\begin{aligned} \varDelta ^\theta (\xi (t)-\xi (t_0)) \cong \varGamma (1+\theta )\left[ \xi (t)-\xi (t_0)\right] . \end{aligned}$$
(4)

Similarly, for any \(t\in (a,b)\), there exists,

$$\begin{aligned} \xi ^{(\theta )}(t)=D_t^{(\theta )}\xi (t), \end{aligned}$$
(5)

which is denoted by

$$\begin{aligned} \xi (t)\in D_t^{(\theta )}(a,b). \end{aligned}$$
(6)

The local fractional derivatives of higher order is written as (Yang 2011a, 2012)

$$\begin{aligned} D^{(n\theta )}_t(t)=\xi ^{(n\theta )}(t)=\overbrace{D^{(\theta )}_t\cdots D_t^{(\theta )}\xi (t)}^{n\,\,{\text {times}} }. \end{aligned}$$
(7)

The local fractional partial derivative of higher order is written as (Yang 2011a, 2012)

$$\begin{aligned} \frac{\partial ^{n\theta }\xi (t,x)}{\partial t^{n\theta }}= \overbrace{\frac{\partial ^\theta }{\partial t^\theta }\cdots \frac{\partial ^\theta }{\partial t^\theta }\xi (t,x)}^{n\,\,{\text {times}} }. \end{aligned}$$
(8)

Definition 4

(Local fractional integral) The local fractional integral of the function \(\xi (t)\) of order \(\theta \) in the interval \([\alpha , \beta ]\) is defined as (Yang 2011a, 2012)

$$\begin{aligned} {}_\beta I^{(\theta )}_\alpha =\frac{1}{\varGamma (1+\theta )}\int _{\alpha }^{\beta }\xi (\tau )({\text {d}}\tau )^\theta =\frac{1}{\varGamma (1+\theta )}\lim _{\varDelta \rightarrow 0}\sum _{i=0}^{N-1}\xi (\tau _i)(\varDelta _{\tau i})^\theta , \end{aligned}$$
(9)

where \(\varDelta _{\tau i}=\tau _{i+1}-\tau _i,\,\,\varDelta _\tau =\max \{\varDelta _{\tau 0},\varDelta _{\tau 1},\varDelta _{\tau 2},\ldots \}\), \(\tau _0=\alpha ,\,\,\tau _N=\beta \), and \(\{\tau _0,\tau _1,\dots ,\tau _N\}\) is a partition of the interval \([\alpha , \beta ].\)

Definition 5

(Local fractional Laplace transform) The local fractional Laplace transform of the function \(\xi (t)\) of local fractional order \(\theta \) is defined as (Yang 2011b; Yang et al. 2015b)

$$\begin{aligned} \pounds _\theta \left[ \xi (t)\right] =\varPhi _\theta (s)=\frac{1}{\varGamma (1+\theta )}\int _{0}^{\infty }E_\theta \left( -s^\theta t^\theta \right) \xi (t)({\text {d}}t)^\theta ,\quad 0<\theta \le 1, \end{aligned}$$
(10)

where \(\pounds _\theta \) is called the local fractional Laplace transform operator.

The sufficient condition for the convergence of Eq. (10) is given by

$$\begin{aligned} \frac{1}{\varGamma (1+\theta )}\int _{0}^{\infty }|\xi (t)|({\text {d}}t)^\theta<\gamma <\infty . \end{aligned}$$

Definition 6

The inverse local fractional Laplace transform is defined as

$$\begin{aligned} \pounds ^{-1}_\theta \left[ \varPhi (s)\right] =\xi (t)=\frac{1}{(2\pi )^\theta }\int _{0}^{\infty }E_\theta \left( s^\theta t^\theta \right) \varPhi (s)({\text {d}}s)^\theta . \end{aligned}$$
(11)

Definition 7

The nth derivative of local fractional Laplace transform is defined as (Yang 2011b; Yang et al. 2015b)

$$\begin{aligned} \pounds _\theta [\xi ^{(n\theta )}(t)]=s^{n\theta }\pounds _\theta \left[ \xi (t)\right] -\sum _{k=0}^{n}s^{(n-k)\theta }\xi ^{(k-1)\theta }. \end{aligned}$$
(12)

Definition 8

The Riemann–Liouville fractional integral operator of order \(\alpha >0\), of a function \(f(t)\in C^m_\tau ,\) and \(\tau \ge -1\) is defined as (Oldham and Spanier 1974).

$$\begin{aligned} I^{\theta }f(t)={\left\{ \begin{array}{ll} \frac{1}{\varGamma (\theta )}\int _{0}^{t}(t-\eta )^{\theta -1}f(\eta ){\text {d}}\eta , &{} \theta>0,\quad t>0,\\ f(t), &{} \theta =0. \end{array}\right. } \end{aligned}$$
(13)

Below we list some important properties of \(I^{\alpha }\) (see Oldham and Spanier 1974):

  1. (i)

    If \(f\in C_\tau ,\,\,\tau \ge -1,\,\alpha ,\,\beta \,\ge 0\),   and \(\gamma >-1\), then

    $$\begin{aligned} I^{\theta }t^x= & {} \frac{\varGamma (x+1)}{\varGamma (x+\theta +1)}t^{\theta +x}, \end{aligned}$$
    (14)
    $$\begin{aligned} I^{\theta }I^{\beta }f(t)= & {} I^{\theta +\beta },\quad I^{\theta }I^{\beta }f(t)=I^{\beta }I^{\theta }f(t). \end{aligned}$$
    (15)
  2. (ii)

    For \(m-1<\alpha \le m,\,\,m\in \mathbb {N}\)   and \(f\in C^{m}_\tau ,\,\,\tau \ge -1\), then

    $$\begin{aligned} D^\theta I^{\theta }f(t)=f(t),\quad I^\theta D^{\theta }f(t)=f(t)-\sum _{i=0}^{m-1}f^k(0^+)\frac{t^k}{k!},\quad t>0. \end{aligned}$$
    (16)

Definition 9

The function f(t) in Caputo fractional derivative is defined as (Oldham and Spanier 1974).

$$\begin{aligned} D^{\theta }f(t)= {\left\{ \begin{array}{ll} \frac{1}{\varGamma (m-\theta )}\int _{0}^{t}(t-\eta )^{m-\theta -1}f^{(m)}(\eta ){\text {d}}\eta ,&{}\\ I^{m-\theta }D^{m}f(t), &{} \end{array}\right. } \end{aligned}$$
(17)

where \(m-1<\theta <m,\,m\in \mathbb N, t>0.\)

Definition 10

(Some useful results in fractal space) In Table 1 below we defined some important identities on fractal space.

In the next section, we illustrate the fundamental idea of the standard HAM.

3 Basic idea of homotopy analysis method

In this section, we illustrate the basic idea of homotopy analysis method. Consider the following nonlinear local fractional partial differential equation

$$\begin{aligned} N\left[ u(x,t)\right] =0, \end{aligned}$$
(18)

where N is the nonlinear operator, x and t denotes the independent variables, and u(x, t) denotes the local fractional unknown function. For clarity, in this paper we ignore all initial and boundary conditions, which can be computed in the same way. Based on the fundamental of the traditional homotopy analysis method proposed by Liao (1995), we construct a convex non-differentiable homotopy called the zero-order deformation equation

$$\begin{aligned} (1-p)\pounds \left[ \varphi (x,t;p)-u_0(x,t)\right] =p\hslash H(x,t)N\left[ \varphi (x,t;p)\right] , \end{aligned}$$
(19)

where \(p\in [0,1]\) is an embedding parameter, \(\hslash \ne 0\) is the nonzero convergence-control parameter, and \(H(x,t)\ne 0\) is the local fractional nonzero auxiliary function, \(\varphi (x,t;p)\) is the local fractional unknown function, \(u_0(x,t)\) is an initial guess of u(x, t), and \(\pounds =\frac{\partial ^\theta \varphi }{\partial t^\theta }\) is the linear local fractional operator with the property that

$$\begin{aligned} \pounds [C]=0, \end{aligned}$$
(20)

where C is an integral constant. Based on the concept of homotopy analysis method, one has great freedom to choose the auxiliary linear operator and the initial guess. Obviously, when \(p=1\), and \(p=0\), it holds

$$\begin{aligned} \varphi (x,t;0)=u_0(x,t),\quad {\text {and}} \quad \varphi (x,t;1)=u(x,t), \end{aligned}$$
(21)

respectively. Thus, as p increases from 0 to 1, the solution \(\varphi (x,t;p)\) varies from the initial guess \(u_0(x,t)\) to the solution u(x, t). Expanding \(\varphi (x,t;p)\) using Taylor series with respect to p, we deduce

$$\begin{aligned} \varphi (x,t;p)=u_0(x,t)+\sum _{m=1}^{+\infty }u_m(x,t)p^{m}, \end{aligned}$$
(22)

where

$$\begin{aligned} u_m(x,t)=\left[ \frac{1}{m!}\frac{\partial ^ {m}\varphi (x,t;p)}{\partial p^{m}}\right] _{p=0}. \end{aligned}$$
(23)

If the auxiliary linear operator, the initial guess, the auxiliary function, and the convergence-control parameter are chosen properly, then Eq. (22) converges at \(p=1\), and

$$\begin{aligned} u(x,t)=u_0(x,t)+\sum _{m=1}^{+\infty }u_m(x,t), \end{aligned}$$
(24)

is the solution of the original problem Eq. (22). According to Eq. (22), the governing equation can be deduced from the zero deformation Eq. (19).

Define a local fractional vector

$$\begin{aligned} \vec {u}_{m}=\left\{ u_0(x,t),\, u_1(x,t),\, u_2(x,t),\ldots ,\, u_m(x,t)\right\} . \end{aligned}$$
(25)

Differentiating Eq. (19) m-times with respect to the embedding parameter p and then setting \(p=0\) and finally dividing by m!, we obtain the so-called Mth-order deformation equation

$$\begin{aligned} \pounds [u_m(x,t)-\chi _mu_{m-1}(x,t) ]=p H(x,t)R_m(\mathbf {u}_{m-1},x,t), \end{aligned}$$
(26)

where

$$\begin{aligned} R_m(\mathbf {u}_{m-1},x,t)=\left[ \frac{1}{(m-1)!}\frac{\partial ^ {(m-1)!}N\left[ \varphi (x,t;p)\right] }{\partial p^{(m-1)}}\right] _{p=0}, \end{aligned}$$
(27)

and

$$\begin{aligned} \chi _m= \left\{ \begin{array}{ll} 0 &{} \quad m \le 1 \\ 1 &{} \quad m > 1. \end{array}\right. \end{aligned}$$
(28)

Using symbolic computational software such as Mathematica or Maple, we can easily solve the Mth-order deformation equation.

In the next section, we demonstrate the idea of the LFLHAM.

4 Local fractional Laplace homotopy analysis method

Consider the following nonlinear local fractional partial differential equation

$$\begin{aligned} \varPi _\theta (\xi (x,t))+R_\theta (\xi (x,t))=\psi (x,t);\quad \theta >0,\quad m-1<\theta \le m,\quad m\in \mathbb {R}, \end{aligned}$$
(29)

where \(\varPi _\theta \xi (x,t)=\frac{\partial ^{m\theta }\xi (x,t)}{\partial t^{m\theta }}\) denotes the linear local fractional differential, \(R_\theta \xi (x,t)\) denotes the remaining linear operator, and \(\psi (x,t)\) states the non-homogeneous function of x and t which is the source term.

Computing the local fractional Laplace transform on both sides of Eq. (29), we get

$$\begin{aligned} \pounds _\theta \left[ \varPi _\theta (\xi (x,t))\right] +\pounds _\theta \left[ R_\theta ( \xi (x,t))\right] =\pounds _\theta \left[ \psi (x,t)\right] . \end{aligned}$$
(30)

Applying Eq. (12) on Eq. (30), we obtain

$$\begin{aligned} \pounds _\theta \left[ \xi (x,t)\right] -\sum _{k=0}^{m}\frac{1}{s^{k\theta }}\frac{\partial ^{k\theta } \xi (x,0)}{\partial t^{k\theta }}+\frac{1}{s^{m\theta }}\pounds _\theta \left[ R_\theta \xi (x,t)\right] =\frac{1}{s^{m\theta }}\pounds _\theta \left[ \psi (x,t)\right] . \end{aligned}$$
(31)

Equivalently

$$\begin{aligned}&\pounds _\theta \left[ \xi (x,t)\right] -\sum _{k=0}^{m} \frac{1}{s^{k\theta }}\frac{\partial ^{k\theta } \xi (x,0)}{\partial t^{k\theta }}\nonumber \\&\quad +\frac{1}{s^{m\theta }}\left( \pounds _\theta \left[ R_\theta \xi (x,t)\right] -\pounds _\theta \left[ \psi (x,t)\right] \right) =0. \end{aligned}$$
(32)

We define the nonlinear operator as

$$\begin{aligned} N[\eta (x,t;p)]= & {} \pounds _\theta \left[ \eta (x,t;p)\right] -\sum _{k=0}^{m}\frac{1}{s^{k\theta }}\frac{\partial ^{k\theta } \eta (x,0)}{\partial t^{k\theta }}\nonumber \\&+\frac{1}{s^{m\theta }}\left( \pounds _\theta \left[ R_\theta \eta (x,t)\right] -\pounds _\theta \left[ \psi (x,t)\right] \right) , \end{aligned}$$
(33)

where \(p \in [0,1]\) is a nonzero auxiliary parameter, and \(\vartheta (x,t;p)\) is a real-valued function of \(x,\,t,\,p\). We construct a homotopy as follows:

$$\begin{aligned} (1-p)\pounds _\theta \left[ \eta (x,t;p)-\xi _0(x,t)\right] =\hslash pH(x,t)N[\eta (x,t)], \end{aligned}$$
(34)

where \(\pounds _\theta \) denotes the local fractional Laplace transform, \(p \in [0,1]\) is the embedding parameter, H(x, t) denotes a nonzero auxiliary function, \(\hslash \ne 0\) is an auxiliary parameter, \(\xi _0(x,t)\) is the initial guess of \(\xi (x,t)\), and \(\eta (x,t;p)\) is the unknown function.

The greatest advantage of the LFLHAM is the great freedom to choose auxiliary parameter, and the initial guess. Obviously, when \(p=1\), and \(p=0\) in Eq. (34), the following results holds

$$\begin{aligned} \eta (x,t;0)=\xi _0(x,t),\quad {\text {and}} \quad \eta (x,t;1)=\xi (x,t), \end{aligned}$$
(35)

respectively. Thus, as p increases from 0 to 1, the solution \(\eta (x,t;p)\) varies from the initial guess \(\xi _0(x,t)\) to the solution \(\xi (x,t)\). Expanding \(\eta (x,t;p)\) as a local fractional Taylor series (Yang 2011a, 2012) with respect to p, we deduce

$$\begin{aligned} \eta (x,t;p)=\xi _0(x,t)+\sum _{m=1}^{+\infty }\xi _m(x,t)p^{m}, \end{aligned}$$
(36)

where

$$\begin{aligned} \xi _m(x,t)=\left[ \frac{1}{\varGamma (m+1)}\frac{\partial ^ {m}\eta (x,t;p)}{\partial p^{m}}\right] _{p=0}. \end{aligned}$$
(37)

The convergence of the series solutions of Eq. (36) is control by the convergence-control parameter \(\hslash \). If the auxiliary linear operator, the initial guess, the auxiliary parameter \(\hslash \), auxiliary function are chosen properly, then Eq. (36) converges at \(p=1\), and

$$\begin{aligned} \xi (x,t)=\xi _0(x,t)+\sum _{m=1}^{+\infty }\xi _m(x,t), \end{aligned}$$
(38)

is the solution of the original problem Eq. (29). According to Eq. (37), the governing equation can be deduced from the zero deformation Eq. (34).

Define the vectors

$$\begin{aligned} {{\vec {\xi _m}}}=\left\{ \xi _0(x,t), \xi _1(x,t), \xi _2(x,t),\ldots , \xi _m(x,t)\right\} . \end{aligned}$$
(39)

Differentiating Eq. (34) m-times with respect to the embedding parameter p and then setting \(p=0\) and finally dividing by \(\varGamma (m+1)\), we have the so-called Mth-order deformation equation

$$\begin{aligned} \pounds _\theta [\xi _m(x,t)-\chi _m\xi _{m-1}(x,t) ]=\hslash H(x,t)R_m({\varvec{\xi }}_{m-1},x,t), \end{aligned}$$
(40)

where

$$\begin{aligned} R_m({\varvec{\xi }}_{m-1},x,t)=\left[ \frac{1}{\varGamma (m)}\frac{\partial ^ {{(m-1)}}N\left[ \eta (x,t;p)\right] }{\partial p^{{(m-1)}}}\right] _{p=0}, \end{aligned}$$
(41)

and

$$\begin{aligned} \chi _m= \left\{ \begin{array}{ll} 0 &{} \quad m \le 1 \\ 1 &{} \quad m > 1. \end{array}\right. \end{aligned}$$
(42)

Taking the inverse local fractional Laplace transform on both sides of Eq. (40), we get

$$\begin{aligned} \xi _m(x,t)=\chi _m\xi _{m-1}(x,t)+\pounds _\theta ^{-1} [\hslash H(x,t)R_m({\varvec{\xi }}_{m-1},x,t) ]. \end{aligned}$$
(43)

And based on Eq. (29), our \(R_m({\varvec{\xi }}_{m-1})\) is define as

$$\begin{aligned} R_m({\varvec{\xi }}_{m-1},x,t)=\varPi _\theta \xi _{m-1}(x,t)+R_\theta \xi _{m-1}(x,t)-(1-\chi _m)\psi (x,t). \end{aligned}$$
(44)

Thus, using Eq. (40), we can easily compute \(v_m(x,t)\) for \(m\ge 1,\) and at Mth-order we deduce

$$\begin{aligned} \xi (x,t)=\sum _{m=0}^{+\infty }\xi _m(x,t). \end{aligned}$$
(45)

In the next theorem, we study the convergence analysis of the original problem Eq. (29).

Theorem 1

(Convergence of analysis of the LFLHAM) Suppose the series

$$\begin{aligned} \sum _{m=0}^{\infty }\xi _m(x,t)=\xi _0(x,t)+\sum _{m=1}^{+\infty }\xi _m(x,t), \end{aligned}$$
(46)

is converging to \(\zeta (x,t)\), where \(\xi _m(x,t)\) is obtained through Eq. (40). Then \(\xi (x,t)\) must be the exact solution of Eq. (29).

Proof

Since

$$\begin{aligned} \lim _{M\rightarrow \infty }\sum _{m=1}^{M}\xi _m(x,t)=\xi _0(x,t)+\lim _{M\rightarrow \infty }\sum _{m=1}^{M}\xi _m(x,t)=\zeta (x,t). \end{aligned}$$
(47)

Then we deduce that \(\lim _{M\rightarrow \infty }\sum _{m=1}^{M}\xi _m(x,t)=0\). Thus, using Eq. (40), yields

$$\begin{aligned}&\lim _{M\rightarrow \infty }\left[ \hslash H(x,t)\sum _{m=1}^{M}R_m({\varvec{\xi }}_{m-1},x,t)\right] =\lim _{M\rightarrow \infty }\left[ \sum _{m=1}^{M}\pounds _\theta \left[ \xi _m(x,t)-\chi _m\xi _{m-1}(x,t)\right] \right] \\&\quad =\pounds _\theta \left[ \lim _{M\rightarrow \infty }\sum _{m=1}^{M}\xi _m(x,t)-\lim _{M\rightarrow \infty }\sum _{m=1}^{M}\chi _m\xi _{m-1}(x,t)\right] \\&\quad =\pounds _\theta \left[ \lim _{M\rightarrow \infty }\sum _{m=1}^{M}\xi _m(x,t)\right] =0. \end{aligned}$$

On the other hand, since \(H(x,t)\ne 0\), \(\hslash \ne 0\) and the linearity property of Eq. (34), we deduce

$$\begin{aligned} \lim _{M\rightarrow \infty }\sum _{m=1}^{M}R_m({\varvec{\xi }}_{m-1},x,t)=0. \end{aligned}$$
(48)

Thus, based on Eq. (44), we get

$$\begin{aligned}&\lim _{M\rightarrow \infty }\sum _{m=1}^{M}R_m({\varvec{\xi }}_{m-1},x,t)\nonumber \\&\quad =\lim _{M\rightarrow \infty }\sum _{m=1}^{M}[\varPi _\theta v_{m-1}(x,t)+R_\theta v_{m-1}(x,t)-(1-\chi _m)\psi (x,t) ]\nonumber \\&\quad =\lim _{M\rightarrow \infty }\sum _{m=1}^{M}\varPi _\theta \lim _{M\rightarrow \infty }\sum _{m=1}^{M}\xi _{m-1}(x,t)+\lim _{M\rightarrow \infty }\sum _{m=1}^{M}R_\theta ( \xi _{m-1}(x,t))\nonumber \\&\qquad -\lim _{M\rightarrow \infty }\sum _{m=1}^{M}(1-\chi _m)\psi (x,t)\nonumber \\&\quad =\varPi _\theta (\xi (x,t))+R_\theta (\xi (x,t))-\psi (x,t)=0. \end{aligned}$$
(49)

Hence, Eq. (49) proved that \(\zeta (x,t)\) satisfies the solution of the original problem Eq. (29). \(\square \)

5 Applications of the LFLHAM

In this section, we illustrate the applications of the local fractional Laplace homotopy analysis method to show its efficiency and the high accuracy.

Example 1

Consider the following local fractional wave equation

$$\begin{aligned} \frac{\partial ^{2\theta } \xi (x,t)}{\partial t^{2\theta }}+\frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}=0, \end{aligned}$$
(50)

subject to the initial conditions

$$\begin{aligned} \xi (x,0)=\sin _\theta (x^\theta ),\quad \frac{\partial ^\theta \xi (x,0)}{\partial t^\theta }=\sin _\theta (x^\theta ),\quad 0\le x\le 1. \end{aligned}$$
(51)

Applying Eqs. (10) and (12) on both sides of Eq. (50), we deduce

$$\begin{aligned} \pounds _\theta \left[ \xi (x,t)\right] -\sum _{k=0}^{n}\frac{1}{s^{k\theta }}\frac{\partial ^{k\theta } \xi (x,0)}{\partial t^{k\theta }}+\frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}\right] =0,\quad t>0. \end{aligned}$$
(52)

The nonlinear operator is defined as

$$\begin{aligned}&N\left[ \eta (x,t;p)\right] =\pounds _\theta \left[ \eta (x,t)\right] -\sum _{k=0}^{n}\frac{1}{s^{k\theta }}\frac{\partial ^{k\theta } \eta (x,0)}{\partial t^{k\theta }}+ \ \frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{\partial ^{2\theta } \eta (x,t)}{\partial x^{2\theta }}\right] ,\nonumber \\&\quad 0\le p\le 1,\quad t>0. \end{aligned}$$
(53)

Thus

$$\begin{aligned} R_m({\varvec{\xi }}_{m-1},x,t)= & {} \pounds _\theta [\xi _{m-1}(x,t)]-(1-\chi _m) \left( \frac{1}{s^{\theta }}+\frac{1}{s^{2\theta }}\right) \sin _\theta (x^\theta )\nonumber \\&-\frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{\partial ^{2\theta } \xi _{m-1}(x,t)}{\partial x^{2\theta }}\right] ,\quad t>0. \end{aligned}$$
(54)

The Mth-order deformation equation is defined as

$$\begin{aligned} \pounds _\theta [\xi _m(x,t)-\chi _m\xi _{m-1}(x,t)]=\hslash H(x,t)R_m({\varvec{\xi }}_{m-1},x,t). \end{aligned}$$
(55)

Computing the inverse local fractional Laplace transform of Eq. (55), we obtain

$$\begin{aligned} \xi _m(x,t)=\chi _m\xi _{m-1}(x,t)+\pounds _\theta ^{-1}[\hslash H(x,t)R_m({\varvec{\xi }}_{m-1},x,t)]. \end{aligned}$$
(56)

Choosing \(H(x,t)=1\), we solve Eq. (56) recursively for \(m\ge 1\) and obtain the following results:

$$\begin{aligned} \xi _0(x,t)= & {} \sin _\theta (x^\theta )\left( 1+\frac{t^{\theta }}{\varGamma (\theta +1)}\right) \\ \xi _1(x,t)= & {} -\hslash \sin _\theta (x^\theta )\left( \frac{t^{2\theta }}{\varGamma (2\theta +1)}+\frac{t^{3\theta }}{\varGamma (3\theta +1)}\right) \\ \xi _2(x,t)= & {} \hslash ^2\sin _\theta (x^\theta )\left( \frac{t^{4\theta }}{\varGamma (4\theta +1)}+\frac{t^{5\theta }}{\varGamma (5\theta +1)}\right) \\&-\ \hslash (\hslash +1)\sin _\theta (x^\theta )\left( \frac{t^{2\theta }}{\varGamma (2\theta +1)}+\frac{t^{3\theta }}{\varGamma (3\theta +1)}\right) \\ \vdots , \end{aligned}$$

and so on.

Thus, the series solutions of Eq. (50) are given by

$$\begin{aligned} \xi (x,t)=\xi _0(x,t)+\xi _1(x,t)+\xi _2(x,t)+\xi _3(x,t)+\cdots \end{aligned}$$
(57)

In particular, choosing the convergence-control parameter \(\hslash =- \ 1\), we obtain

$$\begin{aligned} \xi (x,t)= & {} \sin _\theta (x^\theta )\left( 1+\frac{t^\theta }{\varGamma (\theta +1)}+\frac{t^{2\theta }}{\varGamma (2\theta +1)}+\frac{t^{3\theta }}{\varGamma (3\theta +1)}+\cdots \right) \nonumber \\= & {} \sin _\theta (x^\theta )E_\theta (t^\theta ). \end{aligned}$$
(58)

The result obtained in Eq. (58) is in complete agreement with the local fractional integral iterative method and the local fractional new iterative method (Hemeda et al. 2018), local fractional functional decomposition method (Wang et al. 2014) and (Yang 2011a, 2012).

Using the standard HAM spproach Equation (50) can be written as

$$\begin{aligned} \frac{\partial ^{2\theta }\xi (x,t)}{\partial t^{2\theta }}=-\frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}. \end{aligned}$$
(59)

For simplicity, one has

$$\begin{aligned} _\beta I^{(\theta )}_\eta \left[ \frac{\partial ^{2\theta } \xi (x,t)}{\partial t^{2\theta }}\right] =_\beta I^{(\theta )}_\eta \left[ -\frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}\right] , \end{aligned}$$
(60)

which yields according to Eq. (16)

$$\begin{aligned} \xi (x,t) =\sum _{k=0}^{m-1}\xi ^{(k)}(x,0^+)\frac{t^{k}}{k!}+_\beta I^{(\theta )}_\eta \left[ -\frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}\right] . \end{aligned}$$
(61)

We obtain the initial guess by neglecting the unknown term in the R.H.S. of Eq. (61) as

$$\begin{aligned} \xi _0(x,t)= & {} \sin _\theta (x^\theta )\left( 1+\frac{t^{\theta }}{\varGamma (\theta +1)}\right) . \end{aligned}$$
(62)

Let the linear operator be \(\pounds (\varphi )=\frac{\partial ^{2\theta } \xi (x,t)}{\partial t^{2\theta }}\).

We define the nonlinear operator as

$$\begin{aligned} N\left[ \varphi (x,t;p)\right]= & {} \frac{\partial ^{2\theta } \varphi (x,t)}{\partial t^{2\theta }}+\frac{\partial ^{2\theta } \varphi (x,t)}{\partial x^{2\theta }}. \end{aligned}$$
(63)

According to Eqs. (19) and (20), we deduce

$$\begin{aligned} _\beta I^{(\theta )}_\eta \left[ \frac{\partial ^{2\theta } \xi (x,t)}{\partial t^{2\theta }}\right] \left[ \xi _m(x,t)-\chi _m\xi _{m-1}(x,t)\right] =\hslash _\beta I^{(\theta )}_\eta H(x,t)R_m({\varvec{\xi }}_{m-1},x,t), \end{aligned}$$
(64)

where

$$\begin{aligned} R_m({\varvec{\xi }}_{m-1},x,t)= & {} \frac{\partial ^{2\theta } \xi _{m-1}(x,t)}{\partial t^{2\theta }}+\frac{\partial ^{2\theta }\xi _{m-1}(x,t)}{\partial x^{2\theta }}. \end{aligned}$$
(65)

Then using the property of Eqs. (16) and (51), and setting \(H(x,t)=1\), we obtain

$$\begin{aligned} {\xi }_m(x,t)= & {} (\chi _m+\hslash )\xi _{m-1}(x,t)+\hslash _\beta I^{(\theta )}_\eta \left[ -\frac{\partial ^{2\theta }\xi _{m-1}(x,t)}{\partial x^{2\theta }}\right] ,\quad m>1. \end{aligned}$$
(66)

Finally, using Eqs. (51) and (66), we easily obtain the remaining components as

$$\begin{aligned} \xi (x,t)=\xi _0(x,t)+\xi _1(x,t)+\xi _2(x,t)+\xi _3(x,t)+\cdots \end{aligned}$$
(67)
Fig. 1
figure 1

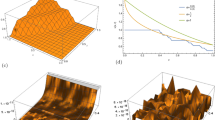
a Numerical simulation of Eq. (50) for \(\theta =\frac{1}{2}\), b 3D surface solution for \(\theta =1\), c 3D non-differentiable surface solution for \(\theta =\frac{\ln (2)}{\ln (3)}\), d 2D approximate solutions for \(\theta =1,\frac{1}{2}\) and \(\frac{\ln (2)}{\ln (3)}\), e absolute error \(E_{10}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\), f absolute error \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\), g absolute error of LFLHAM \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\) when \(\theta =\frac{\ln (2)}{\ln (3)}\), h absolute error of HAM \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\) when \(\theta =\frac{\ln (2)}{\ln (3)}\)

Full size image

Figure 1: The 3D surface solution of Eq.  (50) for \(\theta =\frac{1}{2}\) is presented in Fig. 1a. The surface solution of Eq.  (34) for \((\theta =1)\) is depicted in Fig. 1b. The non-differentiable surface solution is depicted in Fig. 1c. The surface solution behavior of \(\xi (x,t)\) for different values of \(\theta =1,\frac{1}{2},\frac{\ln (2)}{\ln (3)}\) is presented in Fig. 1d. The absolute error analysis for 20th-order approximations of the LFLHAM and HAM is presented in Fig. 1e, f. In Fig. 1g, h, the absolute error analyses of 20th-order approximations of the non-differentiable problem for \(\theta =\frac{\ln (2)}{\ln (3)}\) are clearly illustrated. The results of the absolute errors are in excellent agreement.

Example 2

Consider the following local fractional wave equation

$$\begin{aligned} \frac{\partial ^{2\theta } \xi (x,t)}{\partial t^{2\theta }}+\frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}=\sin _\theta (x^\theta ), \end{aligned}$$
(68)

subject to the initial conditions

$$\begin{aligned} \xi (x,0)=\sin _\theta (x^\theta ),\quad \frac{\partial ^\theta \xi (x,0)}{\partial t^\theta }=0,\quad 0\le x\le 1. \end{aligned}$$
(69)

Employing Eqs. (10) and (12) on both sides of Eq. (68), we get

$$\begin{aligned} \pounds _\theta \left[ \xi (x,t)\right]- & {} \sum _{k=0}^{n}\frac{1}{s^{k\theta }}\frac{\partial ^{k\theta } \xi (x,0)}{\partial t^{k\theta }}-\frac{1}{s^\theta }\sin _\theta (x^\theta )\nonumber \\&+ \ \frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}\right] =0,\quad t>0. \end{aligned}$$
(70)

The nonlinear operator is defined as

$$\begin{aligned} N\left[ \eta (x,t;p)\right]= & {} \pounds _\theta \left[ \eta (x,t)\right] -\sum _{k=0}^{n}\frac{1}{s^{k\theta }}\frac{\partial ^{k\theta } \eta (x,0)}{\partial t^{k\theta }}-\frac{1}{s^\theta }\sin _\theta (x^\theta )\nonumber \\&+\frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{\partial ^{2\theta } \eta (x,t)}{\partial x^{2\theta }}\right] ,\quad 0\le p\le 1,\quad t>0. \end{aligned}$$
(71)

Thus

$$\begin{aligned} R_m({\varvec{\xi }}_{m-1},x,t)= & {} \pounds _\theta \left[ \xi _{m-1}(x,t)\right] -(1-\chi _m)(\frac{1}{s^{\theta }}+\frac{1}{s^{2\theta }})\sin (x^\theta )\nonumber \\&-\frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{\partial ^{2\theta } \xi _{m-1}(x,t)}{\partial x^{2\theta }}\right] ,\quad t>0. \end{aligned}$$
(72)

The Mth-order deformation equation is defined as

$$\begin{aligned} \pounds _\theta [\xi _m(x,t)-\chi _m\xi _{m-1}(x,t)]=\hslash H(x,t)R_m({\varvec{\xi }}_{m-1},x,t). \end{aligned}$$
(73)

Computing the inverse local fractional Laplace transform of Eq. (73), we deduce

$$\begin{aligned} \xi _m(x,t)=\chi _m\xi _{m-1}(x,t)+\pounds _\theta ^{-1}\left[ \hslash H(x,t)R_m({\varvec{\xi }}_{m-1})\right] . \end{aligned}$$
(74)

Choosing \(H(x,t)=1\), we solved Eq. (74) for \(m\ge 1\) and obtained the following results:

$$\begin{aligned} \xi _0(x,t)= & {} \sin _\theta (x^\theta ) \left( 1+\frac{t^{2\theta }}{\varGamma (2\theta +1)}\right) \\ \xi _1(x,t)= & {} - \ \hslash \sin _\theta (x^\theta ) \left( \frac{t^{2\theta }}{\varGamma (2\theta +1)} +\frac{t^{4\theta }}{\varGamma (4\theta +1)}\right) \\ \xi _2(x,t)= & {} \hslash ^2\sin _\theta (x^\theta ) \left( \frac{t^{6\theta }}{\varGamma (6\theta +1)} -\frac{t^{2\theta }}{\varGamma (2\theta +1)}\right) \\&- \ \hslash \sin _\theta (x^\theta ) \left( \frac{t^{2\theta }}{\varGamma (2\theta +1)} +\frac{t^{4\theta }}{\varGamma (4\theta +1)}\right) \\ \vdots , \end{aligned}$$

and so on.

Thus, the series solutions of Eq. (68) is given by

$$\begin{aligned} \xi (x,t)=\xi _0(x,t)+\xi _1(x,t)+\xi _2(x,t)+\xi _3(x,t)+\cdots \end{aligned}$$
(75)

Setting the convergence-control parameter \(\hslash =-1\), we obtain

$$\begin{aligned} \xi (x,t)= & {} \sin _\theta (x^\theta )\left( 1+\frac{2t^{2\theta }}{\varGamma (2\theta +1)}+\frac{2t^{4\theta }}{\varGamma (4\theta +1)}+\frac{2t^{6\theta }}{\varGamma (6\theta +1)}+\cdots \right) \nonumber \\= & {} \sin _\theta (x^\theta ) (E_\theta (t^\theta )+E_\theta (-t^\theta )-1 ). \end{aligned}$$
(76)

The result obtained in Eq. (76) is in complete agreement with the local fractional integral iterative method and the local fractional new iterative method (Hemeda et al. 2018), local fractional functional decomposition method (Wang et al. 2014), and (Yang 2011a, 2012).

Fig. 2
figure 2

a Numerical simulation of Eq. (68) for \(\theta =\frac{1}{2}\), b 3D surface solution for \(\theta =1\), c 3D non-differentiable surface solution behavior for \(\theta =\frac{\ln (2)}{\ln (3)}\), d 2D approximate solutions for \(\theta =1,\frac{1}{2}\) and \(\frac{\ln (2)}{\ln (3)}\), e absolute error \(E_{10}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\), f absolute error \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\), g absolute error of the LFLHAM \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\) for \(\theta =\frac{\ln (2)}{\ln (3)}\), h absolute error of the HAM \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\) for \(\theta =\frac{\ln (2)}{\ln (3)}\)

Full size image

Figure 2: Surface solution of Eq.  (68) for \(\theta =\frac{1}{2}\) is given in Fig. 2a. Surface solution behavior of Eq.  (68) for \((\theta =1)\) is presented in Fig. 2b. The non-differentiable surface solution behavior is depicted in Fig. 2c. The 2D surface solution behavior for different values of \(\theta =1,\frac{1}{2},\frac{\ln (2)}{\ln (3)}\) is presented in Fig. 2d. The absolute error analysis for 20th-order approximations of the LFLHAM and HAM is given in Fig. 2e, f. The 20th-order absolute of the non-differentiable problem for \(\theta =\frac{\ln (2)}{\ln (3)}\) is presented in Fig. 2g, h, respectively. The absolute error analyses of the LFLHAM and HAM were in complete agreement.

Example 3

Consider the following local fractional wave equation:

$$\begin{aligned} \frac{\partial ^{2\theta } \xi (x,t)}{\partial t^{2\theta }}-\frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}+\frac{\partial ^{\theta } \xi (x,t)}{\partial x^{\theta }}=-\sin _\theta (x^\theta )\sin _\theta (t^\theta ), \end{aligned}$$
(77)

subject to the initial conditions

$$\begin{aligned} \xi (x,0)=0,\quad \frac{\partial ^\theta \xi (x,0)}{\partial t^\theta }=\cos _\theta (x^\theta ),\quad 0\le x\le 1. \end{aligned}$$
(78)

Applying Eqs. (10) and (12) on both sides of Eq. (77) yields

$$\begin{aligned}&\pounds _\theta \left[ \xi (x,t)\right] -\sum _{k=0}^{n}\frac{1}{s^{k\theta }}\frac{\partial ^{k\theta } \xi (x,0)}{\partial t^{k\theta }}-\frac{1}{s^{2\theta }+1}\sin _\theta (x^\theta )\nonumber \\&\quad + \ \frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{\partial ^{\theta } \xi (x,t)}{\partial x^{\theta }}-\frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}\right] =0,\quad t>0. \end{aligned}$$
(79)

The nonlinear operator is defined as

$$\begin{aligned} N\left[ \eta (x,t;p)\right]= & {} \pounds _\theta \left[ \eta (x,t)\right] -\sum _{k=0}^{n}\frac{1}{s^{k\theta }}\frac{\partial ^{k\theta } \eta (x,0)}{\partial t^{k\theta }}-\frac{\sin (x^\theta )}{s^{2\theta }+1}\nonumber \\&+\frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{\partial ^{\theta } \eta (x,t)}{\partial x^{\theta }}-\frac{\partial ^{2\theta } \eta (x,t)}{\partial x^{2\theta }}\right] ,\nonumber \\&0\le p\le 1,\quad t>0. \end{aligned}$$
(80)

Thus

$$\begin{aligned}&R_m({\varvec{\xi }}_{m-1},x,t)\nonumber \\&\quad =\pounds _\theta [\xi _{m-1}(x,t) ]-(1-\chi _m) \left( \frac{1}{s^{2\theta }}\cos _\theta (x^\theta ) +\sin _\theta (x^\theta )\left( \frac{1}{s^{2\theta }+1} -\frac{1}{s^{2\theta }}\right) \right) \nonumber \\&\qquad + \ \frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{\partial ^{\theta } \xi _{m-1}(x,t)}{\partial x^{\theta }}-\frac{\partial ^{2\theta } \xi _{m-1}(x,t)}{\partial x^{2\theta }}\right] ,\quad t>0. \end{aligned}$$
(81)

The Mth-order deformation equation is defined as

$$\begin{aligned} \pounds _\theta \left[ \xi _m(x,t)-\chi _m\xi _{m-1}(x,t)\right] =\hslash H(x,t)R_m({\varvec{\xi }}_{m-1},x,t). \end{aligned}$$
(82)

Computing the inverse local fractional Laplace transform of Eq. (82), we deduce

$$\begin{aligned} \xi _m(x,t)=\chi _m\xi _{m-1}(x,t)+\pounds _\theta ^{-1} [\hslash H(x,t)R_m({\varvec{\xi }}_{m-1}) ]. \end{aligned}$$
(83)

Choosing \(H(x,t)=1\), we solved Eq. (83) for \(m\ge 1\) and obtained the following approximations:

$$\begin{aligned}&\xi _0(x,t)=\cos _\theta (x^\theta )\frac{t^{\theta }}{\varGamma (\theta +1)} +\sin _\theta (x^\theta )\left( \sin _\theta (t^\theta ) -\frac{t^{\theta }}{\varGamma (\theta +1)}\right) \\&\xi _1(x,t)=\hslash \sin _\theta (x^\theta ) \left( \frac{t^{\theta }}{\varGamma (\theta +1)} +\frac{2t^{3\theta }}{\varGamma (3\theta +1)} -\sin _\theta (t^\theta )\right) \\&\quad + \ \hslash \cos _\theta (x^\theta )\left( \frac{t^{\theta }}{\varGamma (\theta +1)}-\sin _\theta (t^\theta )\right) \\&\xi _2(x,t)=-\hslash (\hslash +1) (\cos _\theta (x^\theta )+\sin _\theta (x^\theta ))\sin _\theta (t^\theta )\\&\quad + \ \hslash ^2\cos _\theta (x^\theta ) \left( \frac{2t^{3\theta }}{\varGamma (3\theta +1)} -\frac{2t^{5\theta }}{\varGamma (5\theta +1)} +\frac{t^{\theta }}{\varGamma (\theta +1)}-2\left( \frac{t^{\theta }}{\varGamma (\theta +1)} -\sin _\theta (t^\theta )\right) \right) \\&\quad + \ \hslash ^2\sin _\theta (x^\theta ) \left( \frac{2t^{5\theta }}{\varGamma (5\theta +1)} -\frac{2t^{3\theta }}{\varGamma (3\theta +1)}+\frac{t^{\theta }}{\varGamma (\theta +1)}\right) \\&\quad + \ \hslash \sin _\theta (x^\theta )\left( \frac{t^{\theta }}{\varGamma (\theta +1)} -\frac{2t^{3\theta }}{\varGamma (3\theta +1)}\right) \\&\quad + \ \hslash \cos _\theta (x^\theta )\frac{t^{\theta }}{\varGamma (\theta +1)}\\&\vdots , \end{aligned}$$

and so on. Thus, the series solutions of Eq. (77) is given by

$$\begin{aligned} \xi (x,t)=\xi _0(x,t)+\xi _1(x,t)+\xi _2(x,t)+\xi _3(x,t)+\cdots \end{aligned}$$
(84)

Choosing the convergence-control parameter \(\hslash =-1\), we obtain

$$\begin{aligned} \xi (x,t)= & {} \xi _0(x,t)+\xi _1(x,t)+\xi _2(x,t)+\xi _3(x,t)+\cdots \nonumber \\= & {} \sin _\theta (t^\theta )\cos _\theta (x^\theta ). \end{aligned}$$
(85)

The result obtained in Eq. (85) is in complete agreement with the local fractional integral iterative method and the local fractional new iterative method (Hemeda et al. 2018), local fractional functional decomposition method (Wang et al. 2014; Yang 2011a, 2012).

Fig. 3
figure 3

a Numerical solution of Eq. (85) for \(\theta =\frac{1}{2}\), b the 3D surface solution for \(\theta =1\), c the non-differentiable surface solution behavior for \(\theta =\frac{\ln (2)}{\ln (3)}\), d the approximate solutions for \(\theta =1,\frac{1}{2}\) and \(\frac{\ln (2)}{\ln (3)}\), e absolute error \(E_{10}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\), f absolute error \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\), g absolute error of the LFLHAM \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\) for \(\theta =\frac{\ln (2)}{\ln (3)}\), h absolute error of the HAM \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\) for \(\theta =\frac{\ln (2)}{\ln (3)}\)

Full size image

Figure 3: The surface solution behavior of Eq.  (68) for \(\theta =\frac{1}{2}\) is presented in Fig. 3a. Surface solution behavior of Eq.  (68) for \((\theta =1)\) is illustrated in Fig. 3b. The non-differentiable surface solution behavior for \(\theta =\frac{\ln (2)}{\ln (3)}\) is depicted in Fig. 3c. 2D surface solutions for different values of \(\theta =1,\frac{1}{2},\frac{\ln (2)}{\ln (3)}\) are presented in Fig. 3d. The absolute error analysis for 20th-order approximations of the LFLHAM and HAM are given in Fig. 3e, f, respectively. The 20th-order absolute error analysis of the non-differentiable problem for \(\theta =\frac{\ln (2)}{\ln (3)}\) are depicted in Fig. 3g, h, respectively. The obtained results were in complete agreement.

Example 4

Consider the following nonlinear local fractional heat equation:

$$\begin{aligned} \frac{\partial ^{2\theta } \xi (x,t)}{\partial t^{2\theta }}= & {} \frac{x^{2\theta }}{\varGamma (2\theta +1)}\frac{\partial ^\theta }{\partial x^\theta }\left( \frac{\partial ^{\theta } \xi (x,t)}{\partial x^{\theta }}\frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}\right) \nonumber \\&-\frac{x^{2\theta }}{\varGamma (2\theta +1)}\left( \frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}\right) ^2-\xi (x,t), \end{aligned}$$
(86)

subject to the initial conditions

$$\begin{aligned} \xi (x,0)=0,\quad \frac{\partial ^\theta \xi (x,0)}{\partial t^\theta }=\frac{x^{2\theta }}{\varGamma (2\theta +1)},\quad 0\le x\le 1. \end{aligned}$$
(87)

Employing Eqs. (10) and (12) on both sides of Eq. (86) yields

$$\begin{aligned}&\pounds _\theta \left[ \xi (x,t)\right] -\sum _{k=0}^{n} \frac{1}{s^{k\theta }}\frac{\partial ^{k\theta } \xi (x,0)}{\partial t^{k\theta }}\nonumber \\&\!\!\quad +\frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{x^{2\theta }}{\varGamma (2\theta +1)}\left[ \left( \frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}\right) ^2-\frac{\partial ^\theta }{\partial x^\theta }\left( \frac{\partial ^{\theta } \xi (x,t)}{\partial x^{\theta }}\frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}\right) \right] +\xi (x,t)\right] \!=0,\nonumber \\&\quad t>0. \end{aligned}$$
(88)

The nonlinear operator is defined as

$$\begin{aligned}&N\left[ \eta (x,t;p)\right] =\pounds _\theta \left[ \eta (x,t)\right] -\sum _{k=0}^{n}\frac{1}{s^{k\theta }}\frac{\partial ^{k\theta } \eta (x,0)}{\partial t^{k\theta }}\nonumber \\&\quad +\frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{x^{2\theta }}{\varGamma (2\theta +1)}\left[ \left( \frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}\right) ^2-\frac{\partial ^\theta }{\partial x^\theta }\left( \frac{\partial ^{\theta } \xi (x,t)}{\partial x^{\theta }}\frac{\partial ^{2\theta } \xi (x,t)}{\partial x^{2\theta }}\right) \right] +\xi (x,t)\right] ,\nonumber \\&\quad 0\le p\le 1,\quad t>0. \end{aligned}$$
(89)

Thus

$$\begin{aligned}&R_m({\varvec{\xi }}_{m-1},x,t)\nonumber \\&\quad =\pounds _\theta \left[ \xi _{m-1}(x,t)\right] -(1-\chi _m) \left( \frac{1}{s^{2\theta }}\frac{x^{2\theta }}{\varGamma (2\theta +1)}\right) \nonumber \\&\qquad +\frac{1}{s^{2\theta }}\pounds _\theta \left[ \frac{x^{2\theta }}{\varGamma (2\theta +1)} \left[ \sum _{i=0}^{m-1}\frac{\partial ^{2\theta } \xi _i(x,t)}{\partial x^{2\theta }}\frac{\partial ^{2\theta } \xi _{m-1-i}(x,t)}{\partial x^{2\theta }} \right. \right. \nonumber \\&\qquad \left. \left. -\sum _{i=0}^{m-1}\frac{\partial ^\theta }{\partial x^\theta }\left( \frac{\partial ^{\theta } \xi _i(x,t)}{\partial x^{\theta }}\frac{\partial ^{2\theta } \xi _{m-1-i}(x,t)}{\partial x^{2\theta }}\right) \right] -\xi (x,t)\right] ,\quad t>0. \end{aligned}$$
(90)

The Mth-order deformation equation is defined as

$$\begin{aligned} \pounds _\theta [\xi _m(x,t)-\chi _m\xi _{m-1}(x,t)]=\hslash H(x,t)R_m({\varvec{\xi }}_{m-1},x,t). \end{aligned}$$
(91)

Computing the inverse local fractional Laplace transform of Eq. (91), we obtain

$$\begin{aligned} \xi _m(x,t)=\chi _m\xi _{m-1}(x,t)+\pounds _\theta ^{-1} [\hslash H(x,t)R_m({\varvec{\xi }}_{m-1}) ]. \end{aligned}$$
(92)

Setting \(H(x,t)=1\), we solved Eq. (92) for \(m\ge 1\) and obtained the following results:

$$\begin{aligned} \xi _0(x,t)= & {} \frac{x^{2\theta }}{\varGamma (2\theta +1)} \frac{t^{\theta }}{\varGamma (\theta +1)}\\ \xi _1(x,t)= & {} \hslash \frac{x^{2\theta }}{\varGamma (2\theta +1)} \frac{t^{3\theta }}{\varGamma (3\theta +1)}\\ \xi _2(x,t)= & {} \hslash (\hslash +1)\frac{x^{2\theta }}{\varGamma (2\theta +1)} \frac{t^{3\theta }}{\varGamma (3\theta +1)}+\hslash ^2 \frac{x^{2\theta }}{\varGamma (2\theta +1)}\frac{t^{5\theta }}{\varGamma (5\theta +1)}\\&\vdots \end{aligned}$$

and so on. Thus, the series solutions of Eq. (86) is given by

$$\begin{aligned} \xi (x,t)=\xi _0(x,t)+\xi _1(x,t)+\xi _2(x,t)+\xi _3(x,t)+\cdots \end{aligned}$$
(93)

Choosing the convergence-control parameter \(\hslash =-1\), we obtained the following result:

$$\begin{aligned} \xi (x,t)= & {} \xi _0(x,t)+\xi _1(x,t)+\xi _2(x,t)+\xi _3(x,t)+\cdots \nonumber \\= & {} \frac{x^{2\theta }}{\varGamma (2\theta +1)} \left( \frac{t^{\theta }}{\varGamma (\theta +1)} -\frac{t^{3\theta }}{\varGamma (3\theta +1)}+\frac{t^{5\theta }}{\varGamma (5\theta +1)} -\cdots \right) \nonumber \\= & {} \frac{x^{2\theta }}{\varGamma (2\theta +1)}\sin _\theta (t^\theta ). \end{aligned}$$
(94)
Fig. 4
figure 4

a Surface solution of Eq. (86) for \(\theta =\frac{1}{2}\), b 3D surface solution for \(\theta =1\), c non-differentiable surface solution behavior for \(\theta =\frac{\ln (2)}{\ln (3)}\), d the approximate solutions for \(\theta =1,\frac{1}{2}\) and \(\frac{\ln (2)}{\ln (3)}\), e absolute error \(E_{10}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\), f absolute error \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\), g absolute error of the LFLHAM \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\) for \(\theta =\frac{\ln (2)}{\ln (3)}\), h absolute error of the HAM \(E_{20}(\xi (x,t))=|\xi _{\text {ext.}}(x,t)-\xi _{\text {appr.}}(x,t)|\) for \(\theta =\frac{\ln (2)}{\ln (3)}\)

Full size image

Figure 4: The surface solution behavior of Eq.  (86) for \(\theta =\frac{1}{2}\) is presented in Fig. 4a. Solution behavior of Eq.  (86) for \((\theta =1)\) is presented in Fig. 4b. The non-differentiable surface solution behavior is illustrated in Fig. 4c. The 2D surface solutions behavior for different values of \(\theta =1,\frac{1}{2},\frac{\ln (2)}{\ln (3)}\) are depicted in Fig. 4d. The absolute error analysis of 20th-order approximations of the LFLHAM and HAM are given in Fig. 4e, f, respectively. Absolute of the LFLHAM and HAM of 20th-order approximations of the non-differentiable problem for \(\theta =\frac{\ln (2)}{\ln (3)}\) are presented in Fig. 4g, h, respectively. The absolute errors obtained were in excellent agreement.

6 Conclusion

In this letter, we proposed an efficient computational technique called the local fractional Laplace homotopy analysis method (LFLHAM) for solving local fractional wave equations on Cantor set. The proposed technique reduces the computational size, and the series solutions converge rapidly. The greatest advantage of the LFLHAM over the existing techniques is the freedom of choosing the initial guess and the existence of the nonzero convergence-control parameter used to adjust and control the convergence of the method. We discussed the detailed convergence analysis of the method. Finally, based on the mathematical formulations and findings of LFLHAM in this paper, we conclude that it is highly efficient and user-friendly. In further research, one may intend to look for computational heuristic paradigms based on artificial intelligence algorithms to solve non-differentiable wave equations on Cantor sets. Besides, the proposed algorithm can also be treated as sequence of small intervals (i.e., step size) in the future.