1 Introduction

The developments of the numerical methods for the solution of multi-point boundary value problems are important since such problems arise in many branches of science as mathematical models of various real-world processes. Multi-point boundary value problems arise in several branches of engineering, applied mathematical sciences and physics, for instance modeling large-size bridges (Geng and Cui 2010), problems in the theory of elastic stability (Timoshenko 1961) and the flow of fluid such as water, oil and gas through ground layers and fluid flow through multi-layer porous medium (Hajji 2009). Bitsadze and Samarskii (1969) have studied a new problem in which the multi-point boundary conditions depend on the values of the solution in the interior and boundary of the domain. The Bitsadze–Samarskii multi-point boundary value problems (Bitsadze and Samarskii 1969) arise in mathematical modeling of plasma physics processes. The well-posedness, existence, uniqueness and multiplicity of solutions of Bitsadze–Samarskii-type multi-point boundary value problems have been investigated by many authors, see Hajji (2009), Kapanadze (1987), Ma (2004), Ashyralyev and Ozturk (2014) and the references given there. However, research for numerical solutions of the Bitsadze–Samarskii-type boundary value problems, has proceeded slowly. In recent years, the approximate solutions to multi-point boundary value problems were given by shooting method (Zou et al. 2007), the Sinc-collocation method (Saadatmandi and Dehghan 2012), shooting reproducing kernel Hilbert space method (Abbasbandy et al. 2015), difference scheme (Ashyralyev and Ozturk 2014) and method of successive iteration (Yao 2005). Methods of solution of the Bitsadze–Samarskii multi-point boundary value problems have been considered by some researchers (Geng and Cui 2010; Zou et al. 2007; Saadatmandi and Dehghan 2012; Ali et al. 2010; Tatari and Dehghan 2006; Reutskiy 2014; Azarnavid and Parand 2018; Ascher et al. 1994). Here, we use an iterative reproducing kernel Hilbert space pseudospectral (RKHS–PS) method for the solution of nonlinear Bitsadze–Samarskii boundary value problems with multi-point boundary conditions. In this article, we consider the nonlinear boundary value problems in the following form

$$\begin{aligned} u''=g(x,u,u'), x\in [a,b] \end{aligned}$$
(1.1)

with the nonhomogeneous Bitsadze–Samarskii-type multi-point boundary conditions

$$\begin{aligned} u(a)=\sum _{j=1}^{J}\alpha _{j}u(\xi _{j})+\psi _{1}, u(b)=\sum _{j=1}^{J}\beta _{j}u(\xi _{j})+\psi _{2}, \end{aligned}$$
(1.2)

where \(\psi _{1},\psi _{2}\) are some constant and \(\xi _{1},\xi _{2},\ldots ,\xi _{J}\) are some points in the interior of the domain and also

$$\begin{aligned} a<\xi _{1}<\xi _{2}<\cdots<\xi _{J}<b. \end{aligned}$$
(1.3)

Recently, several techniques based on the reproducing kernel Hilbert spaces have attracted great attention and are extensively used for the numerical solving of the various types of ordinary and partial differential equations (Abbasbandy and Azarnavid 2016; Azarnavid et al. 2015, 2018a, b; Emamjome et al. 2017; Arqub 2016a, b, 2017a, b; Arqub et al. 2013, 2016, 2017; Al-Smadi et al. 2016; Niu et al. 2012a, b, 2018; Lin et al. 2012; Akgül and Baleanu 2017; Akgül and Karatas 2015; Akgül et al. 2015, 2017; Inc et al. 2012, 2013a, b; Sakar et al. 2017; Inc and Akgül 2014; Akgül 2015). This paper presents an iterative approach based on reproducing kernel Hilbert space pseudospectral method to find the numerical solution of nonlinear boundary value problems with multi-point boundary conditions. There are two main techniques to deal with the boundary conditions for pseudospectral methods, restrict attention to the basis functions that satisfy the boundary conditions exactly or do not restrict the basis functions, but the boundary conditions are enforced by adding some additional equations. Using the basis functions that satisfy exactly the boundary conditions, is great if one can manage it, but it is often very difficult to achieve. Here, the reproducing kernels are constructed in such way that they satisfy the multi-point boundary conditions exactly, so the approximate solution also satisfies the boundary conditions exactly. Then, the operational matrices are constructed using the reproducing kernel Hilbert spaces and an iterative technique is used to overcome the nonlinearity of the problem. The convergence of the iterated technique for the nonlinear boundary problems with multi-point boundary conditions is proved and some test examples are presented to demonstrate the accuracy and versatility of the proposed method.

The advantages of the proposed reproducing kernel pseudospectral method lie in the following; first, the method eliminates the treatment of boundary conditions using the reproducing kernels which satisfies the boundary conditions exactly; second, the method can produce good globally smooth numerical solutions, and with the ability to solve many problems with complex conditions, such as multi-point boundary conditions; third, the numerical solutions and their derivatives are converging uniformly to the exact solutions and their derivatives, respectively; fourth, the numerical solutions and all their derivatives are calculable for each arbitrary point in the given domain.

2 Reproducing kernel Hilbert space pseudospectral method

In this section, we give a brief review of reproducing kernel Hilbert space pseudospectral (RKHS–PS) method. Here, the operational matrices are constructed using the reproducing kernel Hilbert spaces. In pseudospectral methods, we usually seek an approximate solution of the differential equation in the form

$$\begin{aligned} u_{N}(x)=\sum _{j=1}^{N}\lambda _{j}\phi _{j}(x), \end{aligned}$$
(2.1)

where \(\{\lambda _{j}\}_{j=1}^N\) are unknown coefficients and \(\{\phi _{i}\}_{j=1}^N\) are the basis functions. An important feature of pseudospectral methods is the fact that we want to obtain an approximation of the solution on a discrete set of grid points. Here, for the grid points \(x_{i},i=1,\ldots ,N,\) we use the basis functions \(\phi _{i}(x)= K(x,x_{i}),\) where K(., .) is the reproducing kernel of a Hilbert space. If we evaluate the unknown function \(u_{N}(x)\) at grid points \(x_{i},i=1,\ldots ,N,\) then we have,

$$\begin{aligned} u_{N}(x_{i})=\sum _{j=1}^{N}\lambda _{j}\phi _{j}(x_{i}), i=1,\ldots ,N, \end{aligned}$$
(2.2)

or in matrix notation,

$$\begin{aligned} \varvec{u}=A\varvec{\lambda }, \end{aligned}$$
(2.3)

where \(\varvec{\lambda }=[\lambda _{1},\ldots ,\lambda _{N}]^\mathrm{T}\) is the coefficient vector, the evaluation matrix A has the entries \(A_{i,j}=\phi _{j}(x_{i})\) and \(\varvec{u}=[u_{N}(x_{1}),\ldots ,u_{N}(x_{N})]^\mathrm{T}\). Let L be a linear operator, we can use the expansion (2.1) to compute the \(Lu_{N}\) by operating L on the basis functions,

$$\begin{aligned} Lu_{N}(x)=\sum _{j=1}^{N}\lambda _{j}L\phi _{j}(x), x\in \mathbb {R}. \end{aligned}$$
(2.4)

If we again evaluate at the grid points \(x_{i},i=1,\ldots ,N,\) then we get in matrix notation,

$$\begin{aligned} \varvec{L}\varvec{u}=A_{L}\varvec{\lambda }, \end{aligned}$$
(2.5)

where \(\varvec{u}\) and \(\varvec{\lambda }\) are as above and the matrix \(A_{L}\) has entries \(L\phi _{j}(x_{i})\). Then, we can use (2.3) to solve the coefficient vector \(\varvec{\lambda }=A^{-1}\varvec{u},\) and then (2.5) yields,

$$\begin{aligned} \varvec{L}\varvec{u}=A_{L}A^{-1}\varvec{u}, \end{aligned}$$
(2.6)

so that the operational matrix \(\varvec{L}\) corresponding to linear operator L is given by,

$$\begin{aligned} \varvec{L}=A_{L}A^{-1}. \end{aligned}$$
(2.7)

To obtain the differentiation matrix \(\varvec{L}\) we need to ensure invertibility of the evaluation matrix A. This generally depends both on the basis functions and the locations of the grid points \(x_{i},i=0,\ldots ,N\). The reproducing kernel of a Hilbert space is positive definite and then the evaluation matrix A is invertible for any set of distinct grid points. Suppose we have a linear differential equation of the form

$$\begin{aligned} Lu=f, \end{aligned}$$
(2.8)

by ignoring boundary conditions. An approximate solution at the grid points can be obtained by solving the discrete linear system

$$\begin{aligned} \varvec{L}\varvec{u}=\varvec{f}, \end{aligned}$$
(2.9)

where \(\varvec{u}=[u_{N}(x_{1}),\ldots ,u_{N}(x_{N})]^\mathrm{T}\) and \(\varvec{f}=[f(x_{1}),\ldots ,f(x_{N})]^\mathrm{T}\) contain the value of u and f at grid points and \(\varvec{L}\) is the mentioned operational matrix that corresponds to linear differential operator L.

3 Multi-point boundary condition

Multi-point boundary value problems have received considerable interest in the mathematical applications in different areas of science and engineering. In this chapter, we consider nonlinear boundary value problem (1.1) with multi-point boundary conditions (1.2). Let

$$\begin{aligned} h_{1}(x)=\psi _{1}\frac{x-b}{a-b}\Pi _{i=1}^{J}\frac{x-\xi _{i}}{a-\xi _{i}}, h_{2}(x)=\psi _{2}\frac{x-a}{b-a}\Pi _{i=1}^{J}\frac{x-\xi _{i}}{b-\xi _{i}}, \end{aligned}$$
(3.1)

then the boundary conditions (1.2) can be homogenized using

$$\begin{aligned} u(x)=v(x)+h_{1}(x)+h_{2}(x), \end{aligned}$$
(3.2)

and if

$$\begin{aligned} v(a)-\sum _{j=1}^{J}\alpha _{j}v(\xi _{j})=0, v(b)-\sum _{j=1}^{J}\beta _{j}v(\xi _{j})=0, \end{aligned}$$
(3.3)

then u satisfies the multi-point boundary conditions (1.2). After homogenization of the boundary conditions, the problem (1.1) and (1.2) can be converted in the following form

$$\begin{aligned} \left\{ \begin{array}{ll} v''=G(x,v,v'), x\in [a,b], \\ v(a)-\sum _{j=1}^{J}\alpha _{j}v(\xi _{j})=0, v(b)-\sum _{j=1}^{J}\beta _{j}v(\xi _{j})=0.\\ \end{array} \right. \end{aligned}$$
(3.4)

where \(G(x,v)=g(x,v+h_{1}+h_{2},v'+h'_{1}+h'_{2})-h''_{1}(x)-h''_{2}(x)\). To solve the problem (3.4), reproducing kernel spaces \(W_{2}^{s}[a,b]\) with \(s=1,2,3,\ldots \) are defined in the following, for more details and proofs we refer to Cui and Lin (2009).

Definition 3.1

The inner product space \(W_{2}^{s}[a,b]\) is defined as \(W_{2}^{s}[a,b]=\{ u(x)|u^{(s-1)}\) is absolutely continuous real-valued function, \(u^{(s)}\in L^{2}[a,b]\}\). The inner product in \(W_{2}^{s}[a,b]\) is given by

$$\begin{aligned} (u(.),v(.))_{W_{2}^{s}}=\sum _{i=0}^{s-1}u^{(i)}(a)v^{(i)}(a)+\int _{a}^{b}u^{(s)}(x)v^{(s)}(x)\mathrm{d}x, \end{aligned}$$
(3.5)

and the norm \(\Vert u\Vert _{W_{2}^{s}}\) is denoted by \(\Vert u\Vert _{W_{2}^{s}}=\sqrt{(u,u)_{W_{2}^{s}}}\),where \(u,v\in W_{2}^{s}[a,b]\).

Theorem 3.1

(Cui and Lin 2009) The space \(W_{2}^{s}[a,b]\) is a reproducing kernel space. That is, for any \(u(.)\in W_{2}^{s}[a,b]\) and each fixed \(x\in [a,b]\), there exists \(K(x,.)\in W_{2}^{s}[a,b]\), such that \((u(.),K(x,.))_{W_{2}^{s}}=u(x)\). The reproducing kernel K(x, .) can be denoted by

$$\begin{aligned} K(x,y)= \left\{ \begin{array}{ll} \sum _{i=1}^{2s}c_{i}(y)x^{i-1} , &{} x\le y, \\ \sum _{i=1}^{2s}d_{i}(y)x^{i-1}, &{} x>y,\\ \end{array} \right. \end{aligned}$$
(3.6)

where \(c_{i}\) and \(d_{i}\) are the coefficients of reproducing kernel and can be determined by solving a uniquely solvable linear system of algebraic equations, which is completely explained in Cui and Lin (2009). For more details about the method of obtaining kernel K(x, y), refer to Cui and Lin (2009), Geng and Cui (2007), and Li and Cui (2003). \(W_{2,0}^{s}[a,b]\) is defined as \(W_{2,0}^{s}[a,b]=\{u\in W_{2}^{s}[a,b]:u(a)-\sum _{j=1}^{J}\alpha _{j}u(\xi _{j})=0, u(b)-\sum _{j=1}^{J}\beta _{j}u(\xi _{j})=0\}\). Clearly, \(W_{2,0}^{s}[a,b]\) is a closed subspace of \(W_{2}^{s}[a,b]\) and, therefore, it is also a reproducing kernel space. In the following theorem (Geng and Cui 2012), the reproducing kernel of \(W_{2,0}^{s}[a,b]\) is introduced.

Theorem 3.2

Let \(L_{a}u(x)=u(a)-\sum _{j=1}^{J}\alpha _{j}u(\xi _{j}),\) \(L_{b}u(x)=u(b)-\sum _{j=1}^{J}\beta _{j}u(\xi _{j}),\)

$$\begin{aligned} K_{1}(x,y)=K(x,y)-\frac{L_{a,x}K(x,y)L_{a,y}K(x,y)}{L_{a,x}L_{a,y} K(x,y)}, \end{aligned}$$
(3.7)

and

$$\begin{aligned} K_{2}(x,y)=K_{1}(x,y)-\frac{L_{b,x}K_{1}(x,y)L_{b,y}K_{1}(x,y)}{L_{b,x}L_{b,y} K_{1}(x,y)}. \end{aligned}$$
(3.8)

where the subscript x, y on the operators indicates that the operators are applied to the function of x, y, respectively. If \(L_{a,x}L_{a,y} K(x,y)\ne 0\) and \(L_{b,x}L_{b,y} K_{1}(x,y)\ne 0\), then \(K_{2}(x,y)\) is the reproducing kernel of \(W_{2,0}^{s}[a,b]\).

In Azarnavid and Parand (2016), the authors show that the new constructed kernel satisfies required conditions and if the reference kernel is positive definite then new constructed kernel is positive definite, also. In the proposed method, first, the nonhomogeneous problem is reduced to a homogeneous one, after that we determine the reproducing kernel of \(W_{2}^{s}[a,b]\) for some \(s>2\). Then, \(K_2(x,.)\) the reproducing kernel of \(W_{2,0}^{s}[a,b]\) is constructed using (3.7) and (3.8) and then the functions \(\phi _{j}(x)=K_{2}(x,x_{j}),j=1,\ldots ,N\) are used as the basis functions in (2.1) to approximate the solution of the homogenized problem, hence the approximate solution satisfies the boundary conditions (3.3) exactly.

Theorem 3.3

Suppose that the boundary value problem (3.4) has a unique solution and \(G(x,v,v')\) satisfies Lipschitz condition, i.e., there exists constants \(\mathfrak {l}_{1}\) and \(\mathfrak {l}_{2}\) such that

$$\begin{aligned} |G(x,u,u')-G(x,v,v')|\le \mathfrak {l}_{1} |u-v|+\mathfrak {l}_{2} |u'-v'| , u,v \in C^{1}[a,b], \end{aligned}$$
(3.9)

If \((\frac{(b-a)^{2}}{8}\mathfrak {l}_{1}+\frac{b-a}{2}\mathfrak {l}_{2})<1\) then the sequence \(v_{n}\) is the solution of the following iterative scheme

$$\begin{aligned} \left\{ \begin{array}{ll} v''_{n+1}=G(x,v_{n},v'_{n}), x\in [a,b], \\ v_{n+1}(a)-\sum _{j=1}^{J}\alpha _{j}v_{n+1}(\xi _{j})=0, v_{n+1}(b)-\sum _{j=1}^{J}\beta _{j}v_{n+1}(\xi _{j})=0.\\ \end{array} \right. \end{aligned}$$
(3.10)

converges to the unique solution of (3.4).

Proof

Let \(C^{1}[a,b]\) be a Banach space with norm defined by

$$\begin{aligned} \Vert v\Vert =\max _{a\le x \le b}(\mathfrak {l}_{1} |v(x)|+\mathfrak {l}_{2} |v'(x)|), v\in C^{1}[a,b]. \end{aligned}$$
(3.11)

Suppose that v be the unique solution of problem (3.4) and let \(v(\xi _{j})=\mathfrak {v}_{j},j=0,\ldots ,J+1\) where \(\xi _{0}=a\) and \(\xi _{J+1}=b\). Now, we divide problem (3.4) into \(J+1\) subproblems as follows:

$$\begin{aligned} P_{j}: \left\{ \begin{array}{ll} v''=G(x,v,v'), x\in [\xi _{j-1},\xi _{j}], \\ v(\xi _{j-1})=\mathfrak {v}_{j-1}, v(\xi _{j})=\mathfrak {v}_{j},\\ \end{array} \right. \end{aligned}$$
(3.12)

for \(j=1,\ldots ,J+1\). Let \(\mathfrak {h}_{j}(x)=\frac{\xi _{j-1}\mathfrak {v}_{j}-\xi _{j}\mathfrak {v}_{j-1}+(\mathfrak {v}_{j-1}-\mathfrak {v}_{j})x}{\xi _{j-1}-\xi _{j}}\), the solution of the two-point boundary value problem \(P_{j}\) for \(j=1,\ldots ,J+1\) has the following form

$$\begin{aligned} v(x)=\mathfrak {h}_{j}(x)+\int _{\xi _{j-1}}^{\xi _{j}}H_{j}(x,s)G(s,v(s),v'(s))\mathrm{d}s, \end{aligned}$$
(3.13)

where

$$\begin{aligned} H_{j}(x,s)=\left\{ \begin{array}{ll} \frac{(\xi _{j}-x)(s-\xi _{j-1})}{\xi _{j-1}-\xi _{j}} , \xi _{j-1}\le s\le x \le \xi _{j},\\ \frac{(\xi _{j}-s)(x-\xi _{j-1})}{\xi _{j-1}-\xi _{j}} , \xi _{j-1}\le x\le s \le \xi _{j},\\ \end{array} \right. \end{aligned}$$
(3.14)

is the Green’s function of problem \(P_{j}\). For \(j=1,\ldots ,J+1\), we define \(\mathcal {T}_{j}:C^{1}[a,b]\rightarrow C^{1}[a,b]\) as

$$\begin{aligned} \mathcal {T}_{j}v=\mathfrak {h}_{j}(x)+\int _{\xi _{j-1}}^{\xi _{j}}H_{j}(x,s)G(s,v(s),v'(s))\mathrm{d}s. \end{aligned}$$
(3.15)

For any \(u,v \in C^{1}[a,b]\) we have

$$\begin{aligned} \begin{array}{ll} |\mathcal {T}_{j}u-\mathcal {T}_{j}v|&{}=\left| \displaystyle \int _{\xi _{j-1}}^{\xi _{j}}H_{j}(x,s)(G(s,u(s),u'(s))-G(s,v(s),v'(s)))\mathrm{d}s\right| \\ &{}\le \displaystyle \int _{\xi _{j-1}}^{\xi _{j}}|H_{j}(x,s)|\times |(G(s,u(s),u'(s))-G(s,v(s),v'(s)))|\mathrm{d}s\\ &{}\le \left( \displaystyle \int _{\xi _{j-1}}^{\xi _{j}}|H_{j}(x,s)|\mathrm{d}s\right) \left( \max _{a\le x \le b}(\mathfrak {l}_{1} |u(x)-v(x)|+\mathfrak {l}_{2}|u'(x)-v'(x)|)\right) \\ &{}\le \frac{(b-a)^{2}}{8}\Vert u-v\Vert ,\\ \end{array} \end{aligned}$$
(3.16)

and also

$$\begin{aligned} \begin{array}{ll} |\frac{\mathrm{d}}{\mathrm{d}x}(\mathcal {T}_{j}u-\mathcal {T}_{j}v)|&{}=\left| \displaystyle \int _{\xi _{j-1}}^{\xi _{j}}\frac{\mathrm{d}}{\mathrm{d}x}(H_{j}(x,s))(G(s,u(s),u'(s))-G(s,v(s),v'(s)))\mathrm{d}s\right| \\ &{}\le \displaystyle \int _{\xi _{j-1}}^{\xi _{j}}|\frac{\mathrm{d}}{\mathrm{d}x}(H_{j}(x,s))|\times |(G(s,u(s),u'(s))-G(s,v(s),v'(s)))|\mathrm{d}s\\ &{}\le \left( \displaystyle \int _{\xi _{j-1}}^{\xi _{j}}|\frac{\mathrm{d}}{\mathrm{d}x}(H_{j}(x,s))|\mathrm{d}s\right) \left( \max _{a\le x \le b}(\mathfrak {l}_{1} |u(x)-v(x)|+\mathfrak {l}_{2}|u'(x)-v'(x)|)\right) \\ &{}\le \frac{b-a}{2}\Vert u-v\Vert ,\\ \end{array} \end{aligned}$$
(3.17)

it is easy to see that

$$\begin{aligned} \int _{\xi _{j-1}}^{\xi _{j}}|H_{j}(x,s)|\mathrm{d}s\le \frac{(\xi _{j}-\xi _{j-1})^{2}}{8}\le \frac{(b-a)^{2}}{8} \end{aligned}$$
(3.18)

and

$$\begin{aligned} \int _{\xi _{j-1}}^{\xi _{j}}\left| \frac{\mathrm{d}}{\mathrm{d}x}(H_{j}(x,s))\right| \mathrm{d}s\le \frac{\xi _{j}-\xi _{j-1}}{2} \le \frac{b-a}{2}. \end{aligned}$$
(3.19)

Combining (3.16) and (3.17), we have

$$\begin{aligned} \Vert \mathcal {T}_{j}u-\mathcal {T}_{j}v\Vert \le \left( \frac{(b-a)^{2}}{8}\mathfrak {l}_{1}+\frac{b-a}{2}\mathfrak {l}_{2}\right) \Vert u-v\Vert . \end{aligned}$$
(3.20)

If \((\frac{(b-a)^{2}}{8}\mathfrak {l}_{1}+\frac{b-a}{2}\mathfrak {l}_{2})< 1\), then \(\mathcal {T}_{j}:C^{1}[a,b]\rightarrow C^{1}[a,b]\) is a contraction mapping and Banach fixed-point theorem implies that operator has a unique fixed point \(v_{j}=\mathcal {T}_{j}v_{j}\). If we let \(v(x)=v_{j}(x)\) for \(x\in [\xi _{j-1},\xi _{j}]\) the v is the unique solution of problem (3.4) and if we let \(v_{n}(x)=v_{j,n}(x)\) for \(x\in [\xi _{j-1},\xi _{j}]\) then it is easy to see that \(v_{n}\) satisfies the boundary condition (3.3) for each n and is the solution of problem (3.10). Hence, the sequence \(v_{n}\), the solution of the iterative scheme (3.10) converges to the unique solution of (3.4). \(\square \)

4 Iterative RKHS-PS method

In this section, we consider the general form of the differential equation

$$\begin{aligned} \mathcal {L}u_{n+1}=\mathcal {N}(u_{n})+f(x), x\in [a,b] \end{aligned}$$
(4.1)

where \(\mathcal {L}\) is a linear differential operator, \(\mathcal {N}\) is a nonlinear operator involving spatial derivatives and f is the nonhomogeneous term. An approximate solution at the grid points can be obtained by solving the discrete linear system

$$\begin{aligned} \varvec{L}\varvec{u}_{n+1}=\mathcal {N}\varvec{u}_{n}+\varvec{f}, \end{aligned}$$
(4.2)

where \(\varvec{u}_{n}\) and \(\varvec{f}\) contains the value of the nth approximate solution \(u_{n}\) and f at grid points and \(\varvec{L}\) is the operational matrix corresponds to the linear differential operator \(\mathcal {L}\) as defined in Sect. 2. Then, the \((n+1) th\) approximate solution at the grid points is given by

$$\begin{aligned} \varvec{u}_{n+1}=\varvec{L}^{-1}\left( \mathcal {N}\varvec{u}_{n}+\varvec{f}\right) . \end{aligned}$$
(4.3)

The condition number and the spectral radius of the matrix L are dependent on the basis functions and the number of collocation points.

Theorem 4.1

Suppose that \(\mathcal {N}(u)\) satisfies the Lipschitz condition with respect to u

$$\begin{aligned} |\mathcal {N}(u)-\mathcal {N}(v)|\le \mathfrak {L} |u-v|, \forall u,v \end{aligned}$$
(4.4)

where \(\mathfrak {L}\) is the Lipschitz constant. The proposed scheme (4.3) for the operator problem (4.1) is convergent, if \(\rho (L^{-1})<\frac{1}{\mathfrak {L}}\), where \(\rho (L^{-1})\) is the spectral radius of iteration matrix.

Fig. 1
figure 1

Comparison of approximate solutions obtained by the presented method with \(N=50\) data points and \(n=15\) iteration and successive iteration method (Yao 2005) with 5 and 10 iterations, for Example 5.1

Full size image

Proof

Let \(\Vert \varvec{u}\Vert _{\infty }=\max _{1\le i\le N}|u(x_{i})|\) for any \(\varvec{u}\in \mathbb {R}^{N}\). Using the Lipschitz condition, it is easy to see that

$$\begin{aligned} \Vert \mathcal {N}(\varvec{u})-\mathcal {N}(\varvec{v})\Vert _{\infty }\le \mathfrak {L} \Vert \varvec{u}-\varvec{v}\Vert _{\infty }. \end{aligned}$$
(4.5)

Then, from (4.3) we have

$$\begin{aligned} \varvec{u}_{n+1}-\varvec{u}_{n}=\varvec{L}^{-1}\left( \mathcal {N}\varvec{u}_{n}-\mathcal {N}\varvec{u}_{n-1}\right) . \end{aligned}$$
(4.6)

Let \(n\in \mathbb {N}\) and \(q:=\mathfrak {L}\times \rho (L^{-1})\) then we have

$$\begin{aligned} \Vert \varvec{u}_{n+1}-\varvec{u}_{n}\Vert _{\infty }< q \Vert \varvec{u}_{n}-\varvec{u}_{n-1}\Vert _{\infty }< q^{2} \Vert \varvec{u}_{n-1}-\varvec{u}_{n-2}\Vert _{\infty }<\cdots < q^{n} \Vert \varvec{u}_{1}-\varvec{u}_{0}\Vert _{\infty }. \end{aligned}$$
(4.7)

Let \(m,n\in \mathbb {N}\) such that \(m>n\) then

$$\begin{aligned} \Vert \varvec{u}_{m}-\varvec{u}_{n}\Vert _{\infty }&\le \Vert \varvec{u}_{m}-\varvec{u}_{m-1}\Vert _{\infty }+\Vert \varvec{u}_{m-1}-\varvec{u}_{m-2}\Vert _{\infty }+\cdots +\Vert \varvec{u}_{n+1}-\varvec{u}_{n}\Vert _{\infty }\nonumber \\&<q^{m-1}\Vert \varvec{u}_{1}-\varvec{u}_{0}\Vert _{\infty }+q^{m-2}\Vert \varvec{u}_{1}-\varvec{u}_{0}\Vert _{\infty }+\cdots +q^{n}\Vert \varvec{u}_{1}-\varvec{u}_{0}\Vert _{\infty } \nonumber \\&=q^{n}\left( \sum _{i=0}^{m-n-1}q^{i}\right) \Vert \varvec{u}_{1}-\varvec{u}_{0}\Vert _{\infty } \nonumber \\&\le q^{n}\left( \sum _{i=0}^{\infty }q^{i}\right) \Vert \varvec{u}_{1}-\varvec{u}_{0}\Vert _{\infty } \nonumber \\&=q^{n}\left( \frac{1}{1-q}\right) \Vert \varvec{u}_{1}-\varvec{u}_{0}\Vert _{\infty }. \end{aligned}$$
(4.8)

Let \(\epsilon >0\) be arbitrary, since \(q\in [0,1)\), there exists an enough large \(p\in \mathbb {N}\) such that

$$\begin{aligned} q^{p}<\frac{\epsilon (1-q)}{\Vert \varvec{u}_{1}-\varvec{u}_{0}\Vert _{\infty }}; \end{aligned}$$
(4.9)

therefore, for \(m>n>p\) we have

$$\begin{aligned} \Vert \varvec{u}_{m}-\varvec{u}_{n}\Vert _{\infty }\le \epsilon , \end{aligned}$$
(4.10)

this proves that \({\varvec{u}_{n}}\) is a cauchy sequence in \(\mathbb {R}^{N}\) and it is convergent. \(\square \)

From the previous section it is easy to see that the approximate solution satisfies the boundary conditions exactly.

Table 1 Comparison of the values of approximate solutions obtained by different methods (Ali et al. 2010; Saadatmandi and Dehghan 2012; Azarnavid and Parand 2018 and \(u^{*}_{10}\) in Yao (2005) and presented method using \(N=50\) data points and \(n=15\) iteration, for Example 5.1
Full size table

5 Numerical experiments

In this section, we show the efficiency of the proposed method with the numerical results of two examples. To access both the applicability and the accuracy of the method, we apply the algorithm to the multi-point boundary value problem as follows. The reproducing kernel of \(W^{10}_{2,0}[a,b]\) is used for all examples, except those that are specified. To show the efficiency of the proposed method in comparison with the other methods in the literature and the exact solution, we report maximum absolute errors of the approximate solutions, defined by

$$\begin{aligned} L_{\infty }= {\text {max}}_{1<i<N} |u_{i}-\hat{u}_{i}|, \end{aligned}$$
(5.1)

where N is the number of the collocation points and \(u_{i}\) and \(\hat{u}_{i}\) are the exact and computed values of solution u at point i. We report results of a very high accuracy even when we have used the proposed method with a relatively small number of data points and iterations.

Example 5.1

Here, we consider the following three-point second-order nonlinear differential equation

$$\begin{aligned} y''(x)+\frac{3}{8}y(x)+\frac{2}{1089}y'^{2}(x)+1=0, 0\le x\le 1 \end{aligned}$$
(5.2)

with the boundary conditions

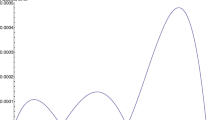
$$\begin{aligned} \left\{ \begin{array}{ll} y(0)=0,\\ y\left( \frac{1}{3}\right) =y(1).\\ \end{array} \right. \end{aligned}$$
(5.3)

Since the exact solution of this problem is unknown, the approximated solutions are compared with the approximated solutions given by Yao (2005). The comparison of approximate solutions obtained by presented method and successive iteration method (Yao 2005) are given in Fig. 1. The comparison of the values of approximate solutions obtained by different methods given in the literature are reported in Table 1. In the absence of the exact solution, we compare the obtained approximate solution using the proposed method with the reported approximate solutions in the literature. The results reported in Fig. 1 and Table 1 show the good agreements between the approximate solutions obtained by the proposed method and other approved methods.

Fig. 2
figure 2

Graph of absolute error for Example 5.2 with \(N=50\) data points and \(n=5,10,15\) iterations, respectively

Full size image
Table 2 Maximum absolute errors of the approximate solution using \(N=30,40,50\) data points and \(n=15\) iteration for Example 5.2 and comparison with the best result reported in Geng and Cui (2010), Saadatmandi and Dehghan (2012), Reutskiy (2014), and Azarnavid and Parand (2018)
Full size table

Example 5.2

In this example, we consider the four-point second-order nonlinear differential equation

$$\begin{aligned} y''(x)+(x^{3}+x+1)y^{2}(x)=f(x), 0\le x\le 1 \end{aligned}$$
(5.4)

with the boundary conditions

$$\begin{aligned} \left\{ \begin{array}{ll} y(0)=\frac{1}{6}y\left( \frac{2}{9}\right) +\frac{1}{3}y\left( \frac{7}{9}\right) -0.0286634,\\ y(1)=\frac{1}{5}y\left( \frac{2}{9}\right) +\frac{1}{2}y\left( \frac{7}{9}\right) -0.0401287,\\ \end{array} \right. \end{aligned}$$
(5.5)

where

$$\begin{aligned} f(x)=\frac{1}{9}(-6 \cos (x-x^{2})+\sin (x-x^{2})(-3(1-2x)^{2}+(1+x+x^{3})\sin (x-x^{2}))). \end{aligned}$$
(5.6)

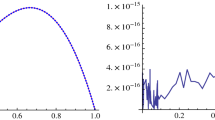
The exact solution is given by \(y(x)=\frac{1}{3}\sin (x-x^{2})\). The proposed method is applied on Example 5.2 using various n and N and the results are as follows. The absolute error of approximate solutions with \(N=50\) data points and \(n=5,10,15\) iterations are given in Fig. 2.

Fig. 3
figure 3

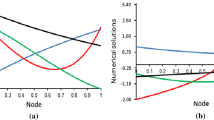
Graph of absolute error for Example 5.2 with \(N=20\) data points and \(n=15\) iterations in \(W^{8}_{2,0},W^{10}_{2,0},W^{12}_{2,0}\) reproducing kernel Hilbert spaces, respectively

Full size image

The absolute errors for Example 5.2 with \(N=20\) data points and \(n=15\) iterations in \(W^{8}_{2,0},W^{10}_{2,0},W^{12}_{2,0}\) reproducing kernel Hilbert spaces are presented in Fig. 3. The maximal absolute errors and comparison with the best results reported in Geng and Cui (2010), Saadatmandi and Dehghan (2012), Reutskiy (2014), and Azarnavid and Parand (2018) for Example 5.2 are shown in Table 2 with different numbers of data points \(N=20,30,40\) and \(n=15\) iteration. Table 2 shows the good accuracy of presented method even using a relatively small number of data points and iterations. Results show that more accurate approximations can be obtained using more data points, more iterations, and smoother reproducing kernel spaces.

6 Conclusions

In this paper, an iterative technique based on the reproducing kernel Hilbert spaces operational matrices and pseudospectral method is used to solve the nonlinear Bitsadze–Samarskii boundary value problems with multi-point boundary conditions. Furthermore, the convergence of the presented method is proved and some numerical tests reveal the high efficiency and versatility of the proposed method. To show how good and accurate the presented method is, the results of numerical experiments are compared with analytical solutions and the best results reported in the literature. The results confirm the good accuracy of the proposed technique.