Modeling and analysis of mixed convection stagnation point flow of nanofluid towards a stretching surface: OHAM and FEM approach

Abstract

A theoretical study of mixed convection stagnation point flow towards a stretching surface is presented. The governing boundary layer equations are transformed into a set of highly nonlinear ordinary differential equations using suitable similarity transforms. The semi-analytical solution is obtained using optimal homotopy analysis method (OHAM) and the numerical solution is obtained via finite element method (FEM). Solutions obtained via two different approaches are in excellent agreement, which validates the accuracy of present analysis. In a special case, the present OHAM solution is also validated with the earlier available results. Effect of pertinent flow parameters on the skin friction coefficient and Nusselt number is presented in tabular form, whereas the velocity, temperature and nanoparticle distribution are presented in graphical forms. Further, a quadratic multiple regression analysis on numeric data of skin friction coefficient and Nusselt number is performed. The findings suggest that velocity slip assists the fluid motion in presence of buoyancy forces, whereas it exhibits a retarding nature on fluid motion when no buoyancy forces exist.

1 Introduction

The demand for efficient and high-performance coolants in various industries ranging from automobile to electronics, medical to metallurgical and polymer to power production, encouraged the researchers to look at alternate options for high-performance coolants rather than traditional coolants, viz. water, ethylene glycol, etc. To enhance the thermal conductivity of these conventional liquids, researchers moved towards artificial liquids by suspending micron-sized metallic particles into traditional heat transfer liquids. Although these artificial liquids possess higher thermal conductivity, they had limited use in industries due to their clogging and stability issues. The modern nanotechnology allowed the researchers to look for colloidal suspension of nanometer-sized metallic or even non-metallic particles in traditional heat transfer liquids (base liquid). Due to homogeneity of nanoparticles with the base liquids molecules these artificially made liquids are assumed to have immense potential for application in various industries. Masuda and his colleagues Masuda et al. (1993) adopted the above said idea and demonstrated an enhanced thermal conductivity in colloidal suspension of water $\gamma$-$\mathrm{Al}_2\mathrm{O}_3$. Choi (1995) in his article coined the name nanofluid for the above-mentioned artificial liquid. Buongiorno (2006) pointed out that the increase in heat transfer in nanofluid is not just due to the enhanced thermal conductivity, but due to the thermal dispersion and intensified turbulence caused by motion of nanoparticles. He assumed seven slip mechanisms (Brownian diffusion, inertia, thermophoresis, diffusiophoresis, fluid drainage, Magnus effect and gravity) which are responsible for relative motion between nanoparticle and base fluid molecules. Out of these seven slip mechanisms, he proposed that only Brownian and thermophoretic diffusions play an important role in enhancing heat transfer rate of nanofluids. Based on the above assumption he modeled the transport equations for conservation of mass, momentum and energy for nanofluids. To explore the various aspects of enhanced thermal conductivity of these fluids, many researchers devoted their time and efforts to find possible reason behind this abnormal behavior of nanofluids. A useful collection of previous research studies on nanofluids can be found in the book by Das et al. (2007) and review articles (Kakaç and Pramuanjaroenkij 2009). Recently, some innovative and valuable studies on nanofluid flow and heat transfer were carried out by several researchers and published in forms of research articles (Rashidi et al. 2017; Esfahani et al. 2017; Shirvan et al. 2017; Rashidi et al. 2018). Kuznetsov and Nield (2013) noted that physically it is impossible to keep the nanoparticle volume fraction constant at the surface. They came out with an idea of zero mass flux of the nanoparticles at the surface which they incorporated in their article. In their article they revisited their problem Nield and Kuznetsov (2009) with zero nanoparticle mass flux condition and noticed that, contrary to the results reported in earlier studies the new approach dilutes the impact of Brownian diffusion on heat transfer drastically. They also presented a linear regression estimate for the Nusselt number corresponding to Brownian diffusion, thermophoresis and buoyancy effects. The revised model is acknowledged widely in the scientific community and utilized to study nanofluid flow problems by many researchers (Kuznetsov and Nield 2014; Halim et al. 2017; Tripathi et al. 2017).

Flow past an extruded surface was theoretically first studied by Crane (1970). He presented solution for skin friction coefficient and heat transfer coefficient of a viscous fluid considering the stretching rate of the sheet linearly proportional to distance of the sheet. However, it was observed that velocity of extruded surface in many industrial application does not possess the Crane’s (1970) proposed stretching velocity model. This limitation was addressed by many authors (see Refs. Pop and Na 1996; Seth et al. 2016). In all above studies it was assumed that the free stream velocity is zero, which is not the case in many practical applications. Due to this reason several researchers carried out investigations where it was assumed that the free stream is not zero and also moving with certain velocity (Ibrahim and Makinde 2016; Seini and Makinde 2014; Olanrewaju and Makinde 2013). Potential application of nanofluids attracted the researchers to study the flow of nanofluid over an extruded sheet. Khan and Pop (2010) became the first to study the heat transfer mechanism of nanofluids on stretching surface. In their study, they used Buongiorno’s model and demonstrated that the Nusselt number and Sherwood number both as a decreasing function of Brownian and thermophoretic diffusion parameters. Makinde and Aziz (2011) extended the pioneering work of Khan and Pop (2010) for convectively heated stretching surface. Boundary layer formed in nanofluid due to a nonlinearly stretching sheet was introduced by Rana and Bhargava (2012). They obtained the similarity solution using finite element method as well as finite difference method and concluded that increasing power law velocity of stretching sheet reduces the rate of heat and mass transfer at the sheet. Nanofluid flow induced by exponentially stretching surface was modeled and investigated by Nadeem and Lee (2012). They solved the transport equations proposed by Buongiorno (2006) using a semi-analytic homotopy analysis method (HAM). Ellahi et al. (2017) studied the $\mathrm{Fe}_3\mathrm{O}_4$ and water-based nanofluid flow induced by a rotating stretchable disk. Rehman et al. (2017) presented a thermophysical analysis of stagnation point flow of a non-Newtonian nanofluid past an inclined stretching cylindrical surface. Ishfaq et al. (2016) presented a linear as well as quadratic correlation model for the Nusselt number of nanofluid past a stretching sheet following passively controlled wall nanoparticle nanofluid model.

Magnetic field is used in various industries to control the boundary layer of the electrically conducting fluid flow, viz. polymer industry, metallurgy and nuclear fission. The magnetic field and temperature-dependent viscosity effect on the fluid flow and heat transfer is investigated by Makinde et al. (2016). They solved their problem numerically using the Nachtsheim and Swigert shooting technique along with a 6th order R-K integration algorithm. Study of MHD boundary layer flow of nanofluid near a stagnation point is carried out by Kandasamy et al. (2011). Bhatti et al. (2017) carried out an analysis to explore the effect of variable magnetic field and coagulation within a Jeffrey nanofluid containing gyrotactic micro-organism. Hassan et al. (2017) published a paper which deals with behavior of nanoparticle shapes on mass and heat flow of ferro-fluid past a rotating stretchable disk in the presence of a low oscillating magnetic field. Magnetic field effect on a non-aligned stagnation point flow of a nanofluid with variable viscosity was studied by Khan et al. (2016). Seth et al. (2017) modeled the transient magnetohydrodynamic flow of nanofluid past a sheet with power law stretching velocity and reported that unsteadiness causes an enhancement in the shear stress, Nusselt number and Sherwood number. Hayat with his colleagues (Hayat et al. 2017) reported the magnetohydrodynamic flow of a non-Newtonian (Powell–Eyring) nanofluid induced by a nonlinearly stretching surface by employing the newly proposed Buongiorno’s revised nanofluid model. A critical review of literature dealing with MHD convective flows of nanofluid is presented by Chamkha and his colleagues in their review article (Chamkha et al. 2015).

The density difference present within the fluid due to the temperature or concentration or due to both is also a reason for the convective flow. The flow induced by above means is known as “free” or “buoyant” or “natural”convective flow. When forced convection and free convection phenomenon are of comparable magnitude in a process, then it is termed as mixed convection. The free convection heat-removal mechanism is desired in many thermal engineering processes as it requires small power consumption and produces negligible operating noise. However, the inherently poor energy efficiency of natural convection, in comparison to the forced convection, and also the intrinsic small thermal conductivity of conventional coolants, limit the heat cooling rate via free convection. As it is confirmed that nanofluids possess a higher thermal conductivity, free convective heat transfer mechanism in nanofluids can play a phenomenal role. Khanafer et al. (2003) developed the single-phase nanofluid model to investigate the buoyancy-driven flow of Cu–water nanofluid filled in a cavity heated differentially at their sides and presented a correlation for Nusselt number. Kuznetsov and Nield (2013) utilized the Buongiorno’s (2006) model to describe buoyancy-driven flow past a vertical plate. Makinde et al. (2013) analyzed the MHD mixed convection stagnation point flow of nanofluid on stretching/shrinking sheet. Their numerical results indicate that a dual solution exist in case of shrinking sheet. They also reported that both the skin friction coefficient and the Sherwood number decrease, while the Nusselt number increases with increasing strength of buoyancy forces. Shirvan et al. (2017) studied the natural convection heat transfer within a copper water-based nanofluid enclosed in a corrugated square cavity. A detailed analysis of natural convective flows of MHD nanofluids under different geometrical situations using single-phase as well as double-phase nanofluids models is presented by Sheikholeslami and Ganji (2016).

Viscous dissipation within the fluid due to the work done by relative fluid layers plays an important role in various energy-efficient systems and also in case of electrically conducting fluid in a magnetically influenced region heat generated due to the movement of electrically conducting fluid known as “Joule heating” have potential to affect on the performance of the system and ignorance of these effects may lead to a faulty model. Makinde (2013) studied the combined effect of these two energy dissipative process within the boundary layer flow formed by nanofluid past a flat plate. Again Pal and Mandal (2015) investigated these phenomenon within a mixed convection nanofluid flow past a deforming surface. Makinde et al. (2013) investigated the effect of viscous and Joule dissipation on mixed convection stagnation point flow of nanofluid on a stretching surface. Apart from these assumptions, the classical non-adherence assumption between the solid fluid interface does not give the realistic results in many processes, viz. in the designing of various microfluidic systems, red blood flow through capillaries and in many technological processes such as lubrication and permeability of micro-porous media. Keeping in view these practical processes, many investigators employed the partial velocity slip condition to model nanofluid flow with heat and mass transfer problems (see Refs. Seth and Mishra 2017; Makinde et al. 2017; Ibrahim and Makinde 2016).

In view of the above studies, in the present investigation we have explored the slip mechanism and energy dissipation on mixed convection stagnation point flow of nanofluid. Apart from presenting the values of skin friction and Nusselt number corresponding to active flow parameters in a tabular form, we have also carried out a statistical analysis for estimating skin friction coefficient and Nusselt number with the help of quadratic multiple regression model. The present problem has the potential to serve as a model for many industrial processes, viz. manufacturing of polymeric sheets, glass sheets, crystalline materials, etc.

Fig. 1

Schematic diagram and coordinate system of the flow problem

2 Mathematical modeling of the problem

2.1 Equations governing the flow system

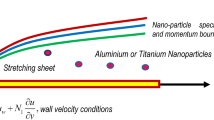
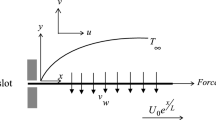
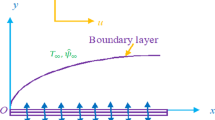
The physical situation is that of a nanofluid impinging normally on a surface which is being stretched in such a way that the speed at any point on the surface is proportional to a power law index of its distance from the origin, i.e., $u_\mathrm{s}=ax^n$. The free stream is also moving with same proportional velocity $u_{\infty }=bx^n$ as the surface ($a,\, b$ and n are the constants). A physical sketch depicting the flow configuration and coordinate system of the problem is presented in Fig. 1. The origin O of the Cartesian coordinate system is considered as the stagnation point from which the sheet is stretched due to application of equal and opposite forces. The flow is confined within the region $y\ge 0$. The surface is kept at a constant temperature $T=T_\mathrm{s}$, whereas the nanoparticle volume fraction C at the surface is governed passively as suggested in Kuznetsov and Nield (2014). A transverse magnetic field of intensity B is applied in a direction parallel to y-axis. The key assumptions which are made while deriving the governing equations are: no chemical reaction between base fluid and nanoparticles, base fluid and nanoparticles are in thermal equilibrium, the nanofluid is viscous, incompressible and electrically conducting, the magnetic Reynolds number is small enough to discard the induced magnetic filed (Davidson 2001), there is no external electric field and the induced electric field due to polarization of charges is negligible, the effect of density variation due to temperature or concentration differences is negligible except in case of buoyancy forces (Boussinesq approximation).

Under the above described constraints, the boundary layer equations are given as follows (Makinde et al. 2013; Olanrewaju and Makinde 2013):

$$\begin{aligned} \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}}&= 0, \end{aligned}$$

(1)

$$\begin{aligned} u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}}&= \upsilon \left( \frac{{{\partial ^2}u}}{{\partial {y^2}}}\right) + \frac{g}{\rho _{nf}}\left[ \left( 1-C_{\infty }\right) \rho _{nf\infty } {\beta }\left( T - {T_{\infty }} \right) \right. \nonumber \\&\quad \left. -\left( C-C_{\infty }\right) \left( {\rho _{np}} - {\rho _{nf\infty }} \right) \right] \nonumber \\&\quad +u_{\infty }\left( \frac{{{\partial }u_{\infty }}}{{\partial {x}}}\right) + \frac{\sigma }{\rho _{nf}} B^2\left( u_{\infty }-u\right) , \end{aligned}$$

(2)

$$\begin{aligned} {\left( \rho c_p\right) _{nf}} \left( u\frac{{\partial T}}{{\partial x}} + v\frac{{\partial T}}{{\partial y}}\right)&= {k}\left( \frac{{{\partial ^2}T}}{{\partial {y^2}}}\right) + {\left( \rho c_p\right) _{np}} \left[ {{D_B}\left( \frac{{\partial C }}{{\partial y}}\frac{{\partial T}}{{\partial y}} \right) + \frac{{{D_T}}}{{{T_{\infty }}}}\left( \frac{{\partial T}}{{\partial y}}\right) ^2}\right] \nonumber \\&+{{\sigma }{B^2}}{\left( u_{\infty }-u\right) ^2} + {\mu }\left( \frac{{\partial u}}{{\partial y}}\right) ^2, \end{aligned}$$

(3)

$$\begin{aligned} u\frac{{\partial C }}{{\partial x}} + v\frac{{\partial C }}{{\partial y}} =&{D_B}\left( \frac{{{\partial ^2}C }}{{\partial {y^2}}}\right) + \frac{{{D_T}}}{{{T_\infty }}}\left( \frac{{{\partial ^2}T}}{{\partial {y^2}}}\right) . \end{aligned}$$

(4)

The boundary conditions of the above described model are

$$\begin{aligned} \left. \begin{array}{l} u = {u_\mathrm{s}} + {u_{\mathrm{{slip}}}},\,\,v = 0,\,\,{T} = {T_\mathrm{s}},\,\,\,\,\frac{\partial C}{\partial y}=-\left( \frac{D_T}{D_B T_{\infty }}\right) \frac{\partial T}{\partial y}\,\,\,\mathrm{{at}} \,\, y = 0, \\ u \rightarrow {u_\infty },\,\,T \rightarrow {T_\infty },\,\,\,\,C \rightarrow C_{\infty }\,\,\,\,\,\mathrm{{as}}\,\,y \rightarrow \infty , \\ \end{array} \right\} \end{aligned}$$

(5)

where (u, v), $\ u_\mathrm{s}=ax^n, \ u_\mathrm{slip}=L \frac{{\partial u}}{{\partial y}}, \,u_{\infty }=bx^n, \, n,\,\,\rho _{np}, \, \rho _{nf}, \, \rho _{nf \infty },\,\beta ,\,\upsilon , \, k,\, {\left( \rho c_p\right) _{np}}, {\left( \rho c_p\right) _{nf}},\,\mu ,\, D_B, \, D_T$ and L are the velocity vector, stretching sheet velocity, slip velocity, free stream velocity, stretching index, density of nanoparticles, density of nanofluid, reference density of nanofluid, volumetric expansion coefficient of nanofluid, kinematic viscosity, thermal conductivity, specific heat capacity of nanoparticles, specific heat capacity of nanofluid, dynamic viscosity of nanofluid, Brownian diffusion coefficient, thermophoretic diffusion coefficient and slip coefficient, respectively.

2.2 Similarity variables and similarity transformation

To obtain similarity solution of Eqs. (2), (3) and (4) subjected to the boundary conditions (5), following similarity transforms are introduced

$$\begin{aligned} \eta = y\sqrt{\frac{{\left( {n + 1} \right) {u_\mathrm{s}}}}{{2 \nu x}}} ,\,\,\psi = \sqrt{\frac{{2{u_\mathrm{s}}\nu x}}{{n + 1}}} f\left( \eta \right) ,\,\,\theta \left( \eta \right) = \frac{{T - {T_\infty }}}{{{T_\mathrm{s}} - {T_\infty }}}\,\,\,\phi \left( \eta \right) = \frac{{C - {C_\infty }}}{{{C_\infty }}}, \end{aligned}$$

(6)

where $\eta , \,\,\psi$, $\theta$ and $\phi$ are, the similarity variable, stream function, non-dimensional temperature and non-dimensional nanoparticle volume fraction, respectively. With these assumptions, continuity Eq. (1) is automatically satisfied.

Using (6) in Eqs. (2), (3) and (4), we obtain

$$\begin{aligned} f''' + ff'' - \frac{{2n}}{{n + 1}}{f'^2} + \lambda \left( \theta -Nr\phi \right) - M\left( {f' - \gamma } \right) + \frac{{2n}}{{n + 1}}{\gamma ^2} = 0, \end{aligned}$$

(7)

$$\begin{aligned} \frac{1}{Pr}\theta '' + \mathrm{{ }}f\theta '+Nb\theta ' \phi '+Nt\left( \theta '\right) ^2 + {Ec}\left( { {f''}^2} + {M}{\left( {\gamma -f'} \right) ^2} \right) = 0, \end{aligned}$$

(8)

$$\begin{aligned} \phi '' + {Sc}f\phi ' + \frac{Nt}{Nb}{\theta ''} = 0. \end{aligned}$$

(9)

The boundary conditions (5) assumes the following form

$$\begin{aligned} \left. \begin{array}{ll} f\left( \eta \right) = 0,\,\,\,f'\left( \eta \right) = 1 + {s} f''\left( \eta \right) ,\,\,\,\theta \left( \eta \right) = 1,\,\,Nb\phi '\left( \eta \right) +Nt\theta '\left( \eta \right) =0\,\,\,\,\,\,&{}\mathrm{{at}}\,\,\eta = 0, \\ f'\left( \eta \right) \rightarrow \gamma ,\,\,\theta \left( \eta \right) \rightarrow 0,\,\,\phi \left( \eta \right) \rightarrow 0 \,\,&{} \mathrm{{as}}\,\,\eta \rightarrow \infty , \\ \end{array}\right\} \nonumber \\ \end{aligned}$$

(10)

where

$$\begin{aligned} \lambda= & {} \frac{2}{n+1}(1 - {C _\infty }){\rho _{{f_\infty }}}\frac{{G{r_x}}}{{Re}_{x}^{2}},\,\,\,\,\,\, G{r_x} = \frac{{g\beta \left( {{T_\mathrm{s}} - {T_\infty }} \right) {x^3}}}{{{\upsilon ^2}}},\,\,\,\,\,\, \\ {Nr}= & {} \frac{{\left( {{\rho _p} - {\rho _{{f_\infty }}}} \right) {{C _\infty }}}}{{{\rho _{{f_\infty }}}\beta {{\left( 1-C_\infty \right) }{\left( T_\mathrm{s}-T_\infty \right) }}}},\,\,\,\,\,\,{Re}_{x} = \frac{{{u_\mathrm{s}}x}}{\upsilon },\\ \gamma= & {} \frac{b}{a},\,\,\,\,\,\, M = \frac{{2\sigma {B^2}x}}{{(n+1)\rho _{nf} u_\mathrm{s}}},\,\,\,\, {Pr} = \frac{{\upsilon }}{{\alpha }},\,\,\,\,Sc ={Pr}{Ln}= \frac{\upsilon }{{{D_B}}},\,\,\,\,Ln=\frac{\alpha }{{{D_B}}},\,\,\,\,\,\\ Nt= & {} \frac{{{{\left( {\rho c_p} \right) }_{np}}{D_T}\left( {{T_w} - {T_\infty }} \right) }}{{{{\left( {\rho c_p} \right) _{nf}}}{T_\infty }\upsilon }},\\ Nb= & {} \frac{{{{\left( {\rho c_p} \right) _{np}}}{D_B}\left( {{C _\infty }} \right) }}{{{{\left( {\rho c_p}\right) _{nf} }}\upsilon }},\,\,\,\,\,\, Ec= \frac{u_\mathrm{s}^2}{\left( {c_p}\right) _{nf}\left( T_\mathrm{s}-T_{\infty }\right) },\,\,\,\,\,\, s = L\sqrt{\frac{a}{\upsilon }} \end{aligned}$$

are the mixed convection parameter, local Grashof number, buoyancy ratio parameter, local Reynolds number, stagnation parameter, local magnetic parameter, Prandtl number, Schmidt number, Lewis number, thermophoresis parameter, Brownian diffusion parameter, local Eckert number and slip parameter, respectively.

2.3 Physical quantities of engineering interests

The local skin friction or frictional drag coefficient $Cf_x$ and local Nusselt number $Nu_x$ which stimulate the stress at the surface and heat transfer rate from surface to fluid, respectively, are defined by

$$\begin{aligned} Cf_x = \frac{{{\tau _\mathrm{s}}}}{{{\rho }\,u_\mathrm{s}^2}}\mathrm{{ \quad and \quad }}\,N{u_x} = \frac{{x{q_\mathrm{s}}}}{{{k}({T_\mathrm{s}} - {T_\infty })}}, \end{aligned}$$

(11)

where $\tau _\mathrm{s}$ and $q_\mathrm{s}$ are the surface shear stress and surface heat flux, respectively, and are given by

$$\begin{aligned} {\tau _\mathrm{s}} = {\mu }\left( \frac{\partial u}{\partial y}\right) _{y = 0}\,\,\,\mathrm{{ and}}\,\,\,{q_\mathrm{s}} = -\, k\left( \frac{\partial T}{\partial y}\right) _{y = 0}. \end{aligned}$$

(12)

The dimensionless form of expressions in Eq. (11) is given as

$$\begin{aligned} C{f_x}{Re}_{x}^{1/2} = \sqrt{\frac{\left( n+1\right) }{2}} f''(0) \,\,\,\,\,\,\hbox {and}\,\,\,\,\, N{u_x}{Re}_{x}^{- 1/2} = - \sqrt{\frac{\left( n+1\right) }{2}}\theta '(0), \end{aligned}$$

(13)

where $f''(0)$ and $\theta '(0)$ are, respectively, dimensionless wall velocity gradient and wall temperature gradient. It is important to note that with the new boundary condition the Sherwood number, which represents the dimensionless mass flux, is identically zero (Kuznetsov and Nield 2014).

3 Solution methodology

Nonlinearity present in the system of Eqs. (7)–(9) restricts us to find a closed-form solution of this system of ordinary differential equations. But one can aim for an approximate solution of desired accuracy. The approximate solution can be obtained either numerically or analytically. There are various analytical methods which provide an approximate solution of nonlinear ordinary differential equations in terms of a series, viz. perturbation method, variational iteration method, differential transform method, Adomian decomposition method, homotopy analysis method, homotopy perturbation method, optimal homotopy analysis method, etc. In the same way there is a long list of numerical methods which provides sufficiently good approximate solution, viz. shooting method, finite difference method, finite element method, finite volume method, control volume finite element method, collocation method, etc. However, the choice of an efficient numerical scheme for individual problem depends upon various merits of the problem. The present problem has been solved analytically as well as numerically. For analytical solution we have employed optimal homotopy analysis method, whereas for numerical solution, we have used finite element method.

3.1 Analytical approach: optimal homotopy analysis method (OHAM)

Liao (2010) proposed a method to solve nonlinear problems that is known as the optimal homotopy analysis method (OHAM), which is simply an improved version of HAM (Liao 1992). The OHAM is preferred among all other analytical approaches because of the following reasons:

• 1. OHAM does not necessitate any large/small parameter in the problem.

• 2. The convergence region can be controlled easily.

• 3. The rate of approximation of series solution is modifiable.

• 4. It delivers freedom to choose altered sets of base functions.

It is well known that in the frame of HAM the solutions of the problem are presented in terms of series, in reference of our problem, the unknown terms $f(\eta ), \theta (\eta )$ and $\phi (\eta )$ are obtained in terms of series solution as follows:

$$\begin{aligned} f(\eta )=f_0(\eta )+\displaystyle \sum _{k=1}^{\infty } f_\mathrm{k}(\eta ),\theta (\eta )=\theta _0(\eta )+\displaystyle \sum _{k=1}^{\infty } \theta _\mathrm{k}(\eta ),\phi (\eta )=\phi _0(\eta )+\displaystyle \sum _{k=1}^{\infty } \phi _\mathrm{k}(\eta ), \end{aligned}$$

(14)

where $f_0(\eta ), \theta _0(\eta )$ and $\phi _0(\eta )$ are the initial guesses chosen in a way such that it satisfies the given boundary conditions (10). Thus,

$$\begin{aligned} f_0(\eta )=\gamma \eta +\frac{\left( 1-{s}\right) }{\left( 1+\gamma \right) }\left( 1-e^{-{s} \eta }\right) ,\,\,\,\,\, \theta _0(\eta )=e^{-\eta },\,\,\,\,\,\phi _0(\eta )=-\frac{Nt}{Nb}e^{-\eta }. \end{aligned}$$

(15)

And the functions $f_\mathrm{k}(\eta ),\, \theta _\mathrm{k}(\eta )$ and $\phi _\mathrm{k}(\eta )$ are obtained from higher order HAM deformation equations given by

$$\begin{aligned} L_\mathrm{f}\left[ f_\mathrm{k}(\eta )-\chi _\mathrm{k}(\eta )f_{k-1}(\eta )\right]= & {} h_\mathrm{f}R_\mathrm{k}^f(\eta ), \end{aligned}$$

(16)

$$\begin{aligned} L_\mathrm{f}\left[ \theta _\mathrm{k}(\eta )-\chi _\mathrm{k}(\eta )\theta _{k-1}(\eta )\right]= & {} h_{\theta }R_\mathrm{k}^{\theta }(\eta ), \end{aligned}$$

(17)

$$\begin{aligned} L_\mathrm{f}\left[ \phi _\mathrm{k}(\eta )-\chi _\mathrm{k}(\eta )\phi _{k-1}(\eta )\right]= & {} h_{\phi }R_\mathrm{k}^{\phi }(\eta ), \end{aligned}$$

(18)

which are bound to the following boundary conditions:

$$\begin{aligned} \left. \begin{array}{l} f_\mathrm{k}(0)=0,\,\,f_\mathrm{k}'(0)=0,\,\,\, \theta _\mathrm{k}(0)=0,\,\,\,\,\,Nb\phi _\mathrm{k}'(0)+Nt\theta _\mathrm{k}'(0)=0,\\ f_\mathrm{k}(\infty )=0,\,\,f_\mathrm{k}'(\infty )=0,\,\,\, \theta _\mathrm{k}(\infty )=0,\,\,\,\,\,\phi _\mathrm{k}(\infty )=0, \end{array} \right\} \end{aligned}$$

(19)

where $h_\mathrm{f},\, h_{\theta }$ and $h_{\phi }$ and $L_\mathrm{f},\, L_{\theta }$ and $L_{\phi }$ are the convergence control parameters to be determined later and auxiliary linear operators are defined by:

$$\begin{aligned} L_\mathrm{f}=\frac{\partial ^3}{\partial \eta ^3}-\frac{\partial }{\partial \eta },\,\,\,\,L_{\theta }=\frac{\partial ^2}{\partial \eta ^2}-\frac{\partial }{\partial \eta },\,\,\,L_{\phi }=\frac{\partial ^2}{\partial \eta ^2}-\frac{\partial }{\partial \eta } \end{aligned}$$

(20)

and

$$\begin{aligned} R_\mathrm{k}^f&=f_{k-1}''' + \displaystyle \sum _{j=1}^{k-1} {\left( f_j(\eta )f_{k-1-j}''(\eta )-\frac{{2n}}{{n + 1}}{f_j'f_{k-1-j}(\eta )}\right) } + \lambda \theta _{k-1}(\eta ) \nonumber \\&- M\left( {f_{k-1}'(\eta ) - \gamma } \right) + \frac{{2n}}{{n + 1}}{\gamma ^2}, \end{aligned}$$

(21)

$$\begin{aligned} R_\mathrm{k}^{\theta }&= \frac{1}{Pr}\theta _{k-1} ''(\eta ) + \displaystyle \sum _{j=1}^{k-1}\bigg ( \mathrm{{ }}f_j(\eta )\theta _{k-1-j}'(\eta )+Nb\theta _j '(\eta ) \phi _{k-1-j} '(\eta )+Nt\left( \theta _j '(\eta )\theta _{k-1-j}'(\eta )\right) \nonumber \\&+ {Ec}{\left( {f_j''(\eta )}{f_{k-1-j}''(\eta )} \right) } + {M\,Ec}{\left( {f_j'(\eta ) - \gamma } \right) \left( {f_{k-1-j}'(\eta ) - \gamma } \right) }\bigg ), \end{aligned}$$

(22)

$$\begin{aligned} R_\mathrm{k}^{\phi }&= \phi _{k-1} '' + \displaystyle \sum _{j=1}^{k-1}\left( {Sc}f_j(\eta )\phi _{k-1-j}(\eta ) '\right) + \frac{Nt}{Nb}{\left( \theta _{k-1}''(\eta )\right) }, \end{aligned}$$

(23)

where

$$\begin{aligned} {\chi _\mathrm{k}} = \left\{ \begin{array}{l} 0\,\,\,\,\,\,k \le 1\\ 1\,\,\,\,\,\,\,k > \,1. \end{array} \right. \end{aligned}$$

(24)

It may be noted that the series solution of $f,\,\theta$ and $\phi$ contains convergence control parameters $h_\mathrm{f},\, h_{\theta }$ and $h_{\phi }$ (Hayat et al. 2017), which controls the convergence region as well as convergence rate of these homotopy series solutions. Unlike HAM where the values of $h_\mathrm{f},\, h_{\theta }$ and $h_{\phi }$ were used to chosen from the so called h-curves, in OHAM, the kth order optimum values of these parameters are obtained by minimizing the kth order total discrete averaged squared residual error (Liao 2010) defined as:

$$\begin{aligned} E_\mathrm{k}^f&=\frac{1}{l+1}\displaystyle \sum _{j=1}^{l}\left[ N_\mathrm{f}\left( \displaystyle \sum _{i=1}^{k}f_i\left( \eta _j\right) \displaystyle \sum _{i=1}^{k}\theta _i\left( \eta _j\right) \displaystyle \sum _{i=1}^{k}\phi _i\left( \eta _j\right) \right) \right] ^2, \end{aligned}$$

(25)

$$\begin{aligned} E_\mathrm{k}^\theta&=\frac{1}{l+1}\displaystyle \sum _{j=1}^{l}\left[ N_{\theta }\left( \displaystyle \sum _{i=1}^{k}f_i\left( \eta _j\right) \displaystyle \sum _{i=1}^{k}\theta _i\left( \eta _j\right) \displaystyle \sum _{i=1}^{k}\phi _i\left( \eta _j\right) \right) \right] ^2, \end{aligned}$$

(26)

$$\begin{aligned} E_\mathrm{k}^\phi&=\frac{1}{l+1}\displaystyle \sum _{j=1}^{l}\left[ N_{\phi }\left( \displaystyle \sum _{i=1}^{k}f_i\left( \eta _j\right) \displaystyle \sum _{i=1}^{k}\theta _i\left( \eta _j\right) \displaystyle \sum _{i=1}^{k}\phi _i\left( \eta _j\right) \right) \right] ^2, \end{aligned}$$

(27)

where $N_\mathrm{f}, \, N_\theta$ and $N_\phi$ are the nonlinear differential operators used to represent Eqs. (7)–(9), l is number of discrete points of non-dimensional coordinate axis $\eta$, $\eta _j=j\delta \eta$ and $\delta \eta = \frac{\eta _{\text {max}}}{l+1}$. As far as our problem is concerned, the value of $\eta _{\text {max}}$ is chosen $\eta _{\text {max}} =6$. And the total discrete residual error

$$\begin{aligned} E_\mathrm{k}^t&=E_\mathrm{k}^f+E_\mathrm{k}^\theta +E_\mathrm{k}^\phi . \end{aligned}$$

(28)

All the calculations are carried out using BVPh2.0 Mathematica software package (BVPh2.0 software package 2017).

The total discrete residual error $E_\mathrm{k}^t$ defined by Eq. (28) and the optimal convergence control parameters $h_\mathrm{f}, \, h_\theta$ and $h_\phi$ along with the total computing time at different order of approximation are given in Table 1. As it can be seen that the $E_\mathrm{k}^t$ decreases very rapidly as order of approximation is increased.

Table 1 Optimal convergence control parameters and total discrete residual error with total CPU time at different approximation label

3.2 Numerical approach: finite element method (FEM)

Apart from the analytic solution, numerical solution is also obtained using a well-known Galerkin finite element method (Reddy and Gartling 2010). The essential steps involved in a typical finite element analysis are summarized below:

• 1. Generation of finite element mesh: like any other numerical technique this method also involves the process of discretization of entire physical domain into a finite set of sub-domains in such a non-overlapping manner that they entirely cover the whole flow domain of the problem. Each such sub-domain is termed as an element.

• 2. Derivation of the element equations: over a typical element from the discretized domain (i.e., finite element mesh) the variational (weak) formulation of the differential equation is constructed. An approximate solution of the unknowns, i.e., dependent variables assumed in the form of $U = \sum \nolimits _{i = 1}^n {{U_i}} {\varphi _i}$ is selected, where $\varphi _i$ are the element interpolating function or basis function and $U_i$ are the unknowns to be computed at the nodal points of the element. Substituting these approximate solutions into the variational formulation of the differential equation, the element equations over the typical element are obtained.

• 3. Global finite element model: to constitute the global finite element model representing whole physical domain, the element (algebraic) equations obtained in previous step are assembled by imposing the inter-element continuity and balance conditions.

• 4. Solution of the finite element model: to get the solution of the global finite element model any of the direct or iterative methods of solving a system of algebraic equations can be used after employing the boundary conditions.

A detailed description of Galerkin finite element method for solving non-dimensional ordinary differential equations governing the boundary layer flow problems are given in the research article (Seth et al. 2017).

4 Validation of approximate solution

In order to validate our approximate solution, we have compared the numerical values of skin friction and Nusselt number obtained via analytical (OHAM) and numerical (FEM) approaches which are provided in Tables 5 and 6. Further, we have compared our computed results with the results obtained by Ishfaq et al. (2016) in Table 2. For this purpose, we have reduced our problem to that of Ishfaq et al. (2016) by taking $n = 1, Sc = 10, Nb = 0.1$ and nullifying the rest of the parameters. From these tables one can conclude that both the approximate solutions indicate an excellent agreement, which validates the accuracy and cogency of our computed results.

Table 2 Comparison of local Nusselt number $Nu_xRe_x^{-1/2}$ with the value of Table 3 of Ishfaq et al. (2016)

5 Results and discussion

This article deals with mixed convection flow of a nanofluid over a stretchable surface with Navier’s slip condition and moving free stream. The revised Buongiorno’s nanofluid model is used to investigate the flow characteristics. All the boundary layer solution, i.e., velocity, temperature and nanoparticle volume fraction are obtained using the methods briefed in previous section. Effect of various active parameters on the flow field variables are presented in graphical form for better understanding. Moreover, the physical quantities of engineering interest, viz. local skin friction coefficient $Cf_xRe_x^{1/2}$ and local Nusselt number $Nu_xRe_x^{-1/2}$ are provided in tabular form. The OHAM solutions are obtained by taking optimal convergence control variables $h_\mathrm{f}, \,h_\theta$ and $h_\phi$ at 6th order of approximation from Table 1. In order to carry out numerical and analytical simulation the default values of flow-controlling parameters were taken as $n=2.0,\, M=2.0,\, \lambda =10,\, Nr=0.2, \, \gamma =0.5,\, Pr=6.2, \, Nb=0.2, \, Nt=0.2, \, Ec=0.1, \, Sc=3.0$ and $s=0.1$, until otherwise specified particularly. In each of the figures except Fig. 2, there are two sets of curves: one with dash lines and the other with solid lines. These two sets of curves are plotted for two different values of flow parameters specified thereat.

5.1 Nanofluid velocity profile

The formation of momentum boundary layer and velocity behavior within the layer are presented in Figs. 2, 3, 4 and 5. Figure 2 is included in the article to describe the behavior of momentum boundary layer as well as the velocity variation corresponding to stagnation parameter $\gamma$. As we know that $\gamma$ is responsible for relative velocities of stretching sheet and free stream. $\gamma < 1$ indicates that the surface stretching velocity is faster than the velocity of free stream, $\gamma =1$ indicates that both, surface stretching velocity and fluid in the free stream are in unison and $\gamma > 1$ represents the case when nanofluid in the free stream is moving faster than the stretching rate of surface. It is clear from the figure that the velocity of nanofluids increases with increasing value of $\gamma$, but the boundary layer width is observed to shrink for increasing value of $\gamma$. Another observation is worth pointing that in general for $\gamma =1$, i.e., when free stream and stretching velocities are same, there should be no boundary layer, but for the current problem, formation of boundary layer can be seen which is solely the contribution of buoyancy forces acting on the fluid. Figure 3 is plotted for various values of mixed convection parameter $\lambda$ corresponding to $\gamma =0.5$ and $\gamma =1.5$. The velocity of nanofluid has an increasing nature towards mixed convection parameter, which is theoretically correct as increase in $\lambda$ means enhanced buoyancy forces which assist the fluid motion. Effect of M on velocity field for both cases of stagnation parameters, i.e., for $\gamma <1$ and $\gamma >1$ is shown in Fig. 4. In both situations $f'(\eta )$ tend to decrease throughout the boundary layer. The applied magnetic field in a moving fluid generates an electromagnetic body force whose tendency is to inhibit the fluid motion, thus reducing the fluid velocity and boundary layer width in effect. This characteristic of the applied magnetic field is illustrated in Fig. 4. The effect of Navier’s slip occurring at the solid–fluid interface with or without buoyancy forces is presented in Fig. 5. In general the existence of slip between the fluid and the surface causes a dampening in the motion of fluid which is also visible from dashed lines of Fig. 4. But the solid lines which are plotted for different values of s when $\lambda \ne 0$ suggest that the slip velocity acts as assisting parameter for nanofluid motion and enhances the motion significantly.

Fig. 2

Velocity profile for $\gamma$

Fig. 3

Velocity profile for $\lambda$ and $\gamma$

Fig. 4

Velocity profile for M and $\gamma$

Fig. 5

Velocity profiles for $\lambda$ and s

Fig. 6

Temperature profile for s and $\lambda$

Fig. 7

Temperature profile for $\gamma$ and Ec

Fig. 8

Temperature profile for Sc and Nt

Fig. 9

Temperature profile for Pr and Nb

5.2 Nanofluid temperature profile

The temperature variation in the thermal boundary layer with respect to some flow parameters are depicted through plots (Figs. 6, 7, 8 and 9). Figure 6 explains the nature of slip velocity on temperature with and without the buoyancy forces. The dashed line curves which represent the temperature behavior towards s, in absence of buoyancy forces reveal that, temperature rises as more and more fluid slips through the surface. Exactly opposite but slightly weaker phenomena has been encountered when buoyancy forces were in action. Figure 7 is plotted for a set of values of Ec under two different values of $\gamma$. The curves with dashed lines are plotted for $\gamma =0.5$, whereas curves with solid lines correspond to $\gamma =1.5$. These curves suggest that an enhancement in the stagnation parameter leads to decrements in the temperature. The increasing value of Ec indicates the increasing effect of viscous and Joule dissipation. It is a well-known fact that in a moving fluid, due to viscous forces acting between two adjacent fluid layers a frictional heat is generated, similarly when an electrically conducting fluid moves in presence of magnetic field it generates heat, which helps to raise the temperature of the nanofluid throughout the boundary layer. In Fig. 8 there are two sets of curves of temperature, one for $Sc=3$ and the second one for $Sc=10$ and each set contains five curves corresponding to the thermophoresis parameter $Nt = 0.1, 0.2, 0.3, 0.4, 0.5$. The term “thermophoresis” is particle analogous phenomenon to the well-known “Soret effect” in liquid mixtures, which states that particles (species concentration) can diffuse due to presence of temperature gradient. The increasing value of Nt corresponds to a stronger thermophoresis phenomena, which leads nanoparticles to diffuse quickly from the hot sheet into the boundary layer, these nanoparticles transport temperature with them throughout the boundary layer. It can be seen that an increase in the Sc is accompanied by a rising temperature. The effect of Brownian diffusion parameter on temperature in the present scenario is almost insignificant as compared to that of Khan and Pop (2010). But Fig. 9 suggests that in revised nanofluid model the contribution of Brownian diffusion of nanoparticles possesses marginally an opposite nature. The same result is also reported in the research article of Halim et al. (2017). This figure also includes the curves corresponding to two different values of Pr. Curves corresponding to higher values of Pr are the lower ones. The results plotted are quite obvious, as the fluids having higher Prandtl number have small thermal diffusivity.

Fig. 10

Nanoparticle volume fraction profile for s and $\lambda$

Fig. 11

Nanoparticle volume fraction profile for Ec and $\gamma$

Fig. 12

Nanoparticle volume fraction profile for Pr and Nb

Fig. 13

Nanoparticle volume fraction profiles for Sc and Nt

5.3 Nanoparticle volume fraction profile

The analysis of nanoparticle volume fraction concentration in nanofluid as well as its boundary layer formation is depicted through graphs for active flow parameters and presented in Figs. 10, 11, 12 and 13. It is interesting to note that in these figures all the curves start with a negative value and then obtain a positive peak value and then vanish as we move towards free stream. The physical explanation to these characteristics is that the nanoparticle concentration near the solid surface is lower than that in free stream and it is higher within its boundary layer. These figures indicate that the higher concentration of nanoparticles is in the central region of the boundary layer. The effect of velocity slip on nanoparticles distribution is reported in Fig. 10 for two different conditions $\lambda =0.0$ and $\lambda =10$. Nanoparticles distribution displays behavior similar to that observed in Fig. 6 as it moves towards free stream. Figure 11 analyzes the effect of Eckert number Ec for $\gamma = 0.5$ and $\gamma =1.5$. It is concluded from this figure that Eckert number has the tendency to reduce the nanoparticle migration within the vicinity of surface, but it flips the nature of $\phi (\eta )$ before attaining the ambient free stream boundary condition. However, the effect of $\gamma$ is to reduce the the concentration of nanoparticles in its boundary layer before it changes its nature near the wall. Figure 12 tells the effects of Pr and Nb. Both active parameters tend to enhance the nanoparticle concentration $\phi (\eta )$ near the surface, but quickly change their nature and start to dilute nanoparticle concentration $\phi (\eta )$ as $\eta \rightarrow \infty$. In Fig. 13 it appears that as Nt increases, i.e., as thermophoresis phenomena strengthens, the transport of nanoparticles weakens near the sheet before its nature gets flipped to enhance transportation of nanoparticles in the boundary layer. The Schmidt number, however, plays an opposite role in nanoparticle distribution. As we know that Schmidt number represents the relative strength of momentum diffusivity to nanoparticles diffusivity. A higher Schmidt number corresponds to either a higher momentum diffusivity which leads to lower nanofluid velocity, thus reducing the nanoparticle migration through convection or a weaker molecular (nanoparticle) diffusivity which leads to a weaker penetration depth of nanoparticles.

5.4 Quantities of physical interests

Numerical values of skin friction coefficient and Nusselt number corresponding to active flow parameters obtained by OHAM as well as FEM are listed in Tables 5 and 6. From Table 5 it can be noted that the skin friction coefficient decreases for increasing values of $n,\, s$ and M on the other hand $Cf_xRe_x^{1/2}$ tends to enhance with increasing values of $\lambda$. However, $Cf_xRe_x^{1/2}$ tends to decrease as stagnation parameter increases from 0 to 1, i.e., until the sheet velocity is greater than the free stream velocity, but it starts increasing as the formation of momentum boundary layer is reversed. Table 6 values suggest that the active control parameters, namely, $M,\, Nb, \,Nt$ and Ec play a dampening role in the heat transfer process. Although the impact of Nb on Nusselt number is almost negligible contradictory to the result of Khan and Pop (2010), on the other hand, $\gamma ,\, Pr$ and Sc enhances the rate of heat transfer at the surface.

5.5 Estimation of skin friction coefficient and Nusselt number: a quadratic multiple regression model

A quadratic regression estimate of the skin friction coefficient and Nusselt number is presented in this section. The multiple quadratic regression model for skin friction coefficient is given for a set of 100 values of $s, \, n$ and $\gamma$ generated randomly from the intervals $[0,0.5],\, [0,2]$ and [0, 2], respectively. On the other hand, the multiple quadratic regression model for the Nusselt number is given for a set of 100 values of $Nb, \, Nt$ and $\gamma$ generated randomly from the interval $[0.1,0.5],\, [0.1,0.5]$ and [0, 2]. All the other parameters are kept constant as specified.

The estimated quadratic regression model for ${Cf}_x{Re}_x^{1/2}$ and ${Nu}_x{Re}_x^{-1/2}$ are given as follows

$$\begin{aligned} Cf_\mathrm{est}= & {} Cf+b_1{s}+b_2{n}+b_3{\gamma }+b_4{s}^2+b_5{n}^2+b_6{\gamma }^2+b_7{s}\,{n}+b_8{s}{\gamma } +b_9{n}{\gamma } \end{aligned}$$

(29)

$$\begin{aligned} Nu_\mathrm{est}= & {} {Nu}+c_1{Nb}+c_2{Nt}+c_3 {\gamma }+c_4{Nb}^2+c_5{Nt}^2+c_6{\gamma }^2+c_7{Nb}\,{Nt}\nonumber \\&+\,c_8{Nb}{\gamma }+c_9{Nt}{\gamma } \end{aligned}$$

(30)

Table 3 contains the quadratic regression coefficients corresponding to ${Cf}_x{Re}_x^{1/2}$ for different values of $\lambda$ and M and Table 4 contains the values of quadratic regression coefficients corresponding to ${Nu}_x{Re}_x^{-1/2}$ for different values of $\lambda$ and Pr. The maximum relative error bounds $\varepsilon = {|Cf_\mathrm{est} - Cf|}/{|Cf|}$ and $\varepsilon _1 = {|Nu_\mathrm{est} - Nu|}/{|Nu|}$ are also obtained. As one can see from Table 3 that the coefficients of s and $\gamma$ are large as compared to n which suggest that a small variation in s and $\gamma$ will result in a large perturbation in ${Cf}_x{Re}_x^{1/2}$. Similarly Table 4 values suggest that the coefficients of Nt and $\gamma$ are large. Thus, a small variation in Nt and $\gamma$ will result in maximum deflection in ${Nu}_x{Re}_x^{-1/2}$. From Table 4 it can be seen that the coefficient of Nb is very small as compared to the case in Khan and Pop (2010). A close observation of Table 4 values suggest that the coefficient of Nb when $\lambda =0$ is negative, but in presence of buoyancy forces, i.e., when $\lambda \ne 0$ the coefficient $c_1$ possesses positive value. Thus we can conclude that in the current analysis, due to presence of buoyancy forces, Nb has a gradually increasing effect on Nusselt number, opposite to what reported by Kuznetsov and Nield (2014). This observation of Nusselt number is also justified from 6.

Table 3 Quadratic regression coefficients and error bound for the estimated ${Cf}_x{Re}_x^{1/2}$ with variations in $\lambda$ and M

Table 4 Quadratic regression coefficients and error bound for the estimated ${Nu}_x{Re}_x^{-1/2}$ with variations in $\lambda$ and Pr

Table 5 Skin friction coefficient $Cf_xRe_x^{1/2}$

Table 6 Nusselt number $Nu_xRe_x^{-1/2}$

6 Conclusion

Throughout the investigation our focus has been devoted to address the velocity slip effect on mixed convection stagnation point flow towards a stretching surface. To analyze the effects of various flow controlling parameters, the approximate solutions were obtained analytically as well as numerically. The analytical solution has been obtained with the help of OHAM, while numerical solution has been obtained using Galerkin finite element technique. The solutions obtained via these two different approaches are in full agreement. The flow characteristics were discussed using graphs and tables. A statistical analysis is carried out on the data of skin friction and Nusselt number corresponding to some key flow-controlling parameters to devise an expression for estimating the skin friction coefficient and Nusselt number. Some important findings of the entire study worthy of attention are as follows:

• The velocity of the nanofluid increases with increasing value of stagnation parameter, but the width of its boundary layer reduces significantly.

• The velocity slip tends to enhance the nanofluid velocity in presence of buoyancy forces, while it has a negative impact on velocity when no buoyancy forces were present. Exactly opposite effect was observed in temperature and nanoparticle distribution.

• In all the situations, the temperature as well as its boundary layer width decreases with increasing value of stagnation parameter. The Brownian diffusion exhibit negligible effect on temperature field.

• The concentration of nanoparticle volume fraction is found to be higher in the middle of its boundary layer. Stagnation parameter tends to dilute the nanoparticles concentration, whereas Eckert number enhances the nanoparticles concentration.

• As per the expression of skin friction coefficient, the impact of velocity slip and stagnation parameter is very prominent on skin friction coefficient. The Nusselt number is highly sensitive for thermophoresis parameter and stagnation parameter for fixed value of Prandtl number while the Brownian diffusion parameter has almost negligible impact.