Exact and heuristic algorithms for minimizing Tardy/Lost penalties on a single-machine scheduling problem

Abstract

This paper addresses minimizing Tardy/Lost penalties with common due dates on a single machine. According to this penalty criterion, if tardiness of a job exceeds a predefined value, the job will be lost and penalized by a fixed value. The problem is formulated as an integer programming model, and a heuristic algorithm is constructed. Then, using the proposed dominance rules and lower bounds, we develop two dynamic programming algorithms as well as a branch and bound. Experimental results show that the heuristic algorithm has an average optimality gap less than 2 % in all problem sizes. Instances up to 250 jobs with low variety of process times are optimally solved and for high process time varieties, the algorithms solved all instances up to 75 jobs.

1 Introduction

In this study, we analyze minimizing total Tardy/Lost penalties on a single machine about two common due dates. Every job $i \left( {1\le i\le n} \right)$ has a processing time, $p_{i}$, and two common due dates, namely $d_{1}$ and $d_{2}$. In the case that a job finishes before the first due date, $d_{1}$, no penalty is assigned; if the completion time is between $d_{1}$ and $d_{2}$, the job will be penalized by a tardiness weight, $w_{i}$; and finally, the job will be lost if it is completed after the second due date and a fixed amount of penalty, $s_{i}$, will be incurred. We can formulate the Tardy/Lost objective function as in Eq. (1), where $C{_{i}}$ is the completion time of job i. It is assumed that $s_{i} >w_{i} \left( {d_{2} -d_{1} } \right)$ which means penalty for losing a job is greater than the maximum possible tardiness penalty for the same job, and this difference is denoted by parameter $u_{i}$.

$$\begin{aligned} Z_{i} = \left\{ {\begin{array}{*{20}l} 0 &{}\quad {\mathrm{if}\;C_{i} \le d_{1} } \\ w_i(C_i-d_1) &{}\quad {\mathrm{if}\;d_{1} < C_{i} \le d_{2} } \\ s_i=w_i(d_2-d_1)+u_i &{}\quad \mathrm{if}\; C_i > d_2 \\ \end{array} } \right. \end{aligned}$$

(1)

Figure 1 shows the Tardy/Lost penalty function for job i based on its completion time. The problem is denoted by $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\sum _{i\in R_{1} } {w_{i} T_{i} +\sum _{i\in R_{2} } {s_{i} } }$, where $R_{1}$ and $R_{2}$ indicate the sets of tardy and lost jobs, respectively. For the sake of brevity, we use $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\mathrm{TL}$ in the rest of this paper, where TL indicates the Tardy/Lost performance criteria.

To determine time complexity of this problem, we can set $d_{2} \ge \sum _{i=1}^n {p_{i} }$ and simplify it to the problem of minimizing weighted tardiness with common due date. Yuan (1992) showed that minimizing weighed tardiness with common due date on a single machine is ordinary NP-hard. According to this, the problem considered in this study is at least NP-hard in ordinary sense.

Fig. 1

Tardy/Lost penalty function with common due dates

Objective functions of real-life manufacturing problems are often much more complex than the well-known scheduling performance measures. Depending on the type of contractual penalties and expected goodwill of future revenue losses incurred, many types of non-linear tardiness penalty functions may arise. Tardy/Lost measure combines the futures of two parameters; weighted tardiness and weighted number of tardy jobs. On the other hand, the Tardy/Lost performance measure can be considered as a special case for scheduling problems with order acceptance assumption. Here, the objective is minimizing weighted tardiness on a single machine and common due date, where the rejection cost for a job i can be defined as $(d_{2} -d_{1} )w_{i}$. Order acceptance assumption has been widely investigated in the literature. Engels and Karger (2003) investigated the problem of minimizing weighted completion times and rejection penalties and developed some approximation algorithms. The survey papers by Slotnick (2011) and Shabtay et al. (2013) study a number of scheduling problems with order acceptance.

From a practical point of view, the Tardy/Lost penalty function is applicable in delivery contracts, most of which are arranged based on two due dates. If an order is early, then no penalty is considered; the order will be penalized if its delivery time exceeds the first due date. The penalty increases in proportion to the delivery time until the second due date is reached. If the delivery happens later than the second due date, we will lose the order and a maximum fixed penalty occurs. Other applications of Tardy/Lost measure are perishable goods and food industries.

Minimizing weighted tardiness is a special case of Tardy/Lost performance measure which has been widely investigated in scheduling area. The problem $1| |\sum {w_{i} T_{i} }$ is NP-hard in a strong sense (Lenstra et al. 1977) and is optimally solvable in pseudo-polynomial time for a fixed number of distinct due dates (Kolliopoulos and Steiner 2006). Cheng et al. (2005) presented an $O(n{^2})$ time approximation algorithm for the problem as well as a pseudo-polynomial algorithm when all job due dates have equal slacks. Kolliopoulos and Steiner (2006) considered the problem with a fixed number of due dates and designed a pseudo-polynomial algorithm. Karakostas et al. (2009) studied the same problem and designed a dynamic programming algorithm, as well as an approximation scheme. Koulamas (2010) considered the latest theoretical developments for problem $1| |\sum {T_{i} }$ and reviewed some exact algorithms, fully polynomial time approximation schemes, heuristic algorithms, special cases, and generalizations of the problem.

In a special case of problem $1| |\sum {w_{i} } T_{i}$, where due date is common for all jobs, Lawler and Moore (1969) provided a pseudo-polynomial dynamic programming algorithm in $O({n{^2}d}$) time and Fathi and Nuttle (1990) developed a 2-approximation algorithm in $O ( {n{^2}}$) time. Kellerer and Strusevich (2006) converted a dynamic programming algorithm to an FPTAS of $O({{n{^6}\log W}/{\varepsilon {^3}) }}$ time complexity, where W is the sum of tardiness weights; later, Kianfar and Moslehi (2013) studied the same problem and developed a more effective FPTAS in $O({{n}{^3}/\varepsilon } )$ time.

According to Table 1, some of the most common performance measures in scheduling literature are special cases for Tardy/Lost measure. The third column of this table describes how the parameters of TL measure should be adjusted in each case.

Table 1 Penalty functions derived from TL measure

Tardy/Lost performance measure is a kind of regular measure which is continuous and non-decreasing in completion times of jobs. Detienne et al. (2012) studied a single-machine problem, whose objective is to minimize a regular step total cost function and they proposed an exact approach based on Lagrangian relaxation. Zhou and Cai (1997) examined two types of regular performance measures, the total cost, and the maximum cost, with general cost functions. In the paper by Shabtay (2008), two continuous and non-decreasing objective functions are considered that include penalties due to earliness, tardiness, number of tardy jobs, and due date assignments. The research by Ventura and Radhakrishnan (2003) was focused on scheduling jobs with varying processing times and distinct due dates on a single machine. Carrasco et al. (2013) studied convex non-decreasing cost functions for single-machine problems subject to precedence constraints. Colin and Quinino (2005) proposed a pseudo-polynomial time algorithm to find a solution within some tolerance of optimality for the same problem. The objective function considered by Baptiste and Pape (2005) was minimizing a regular sum objective function $\sum _i {f_{i} (C_{i} )}$ that corresponds to the cost of the completion of job i at time $C_{i}$. They introduced lower bounds and dominance properties for this problem and described a branch-and-bound procedure with constraint propagation. Chandra et al. (2014) developed a binary branch and bound for single-machine problem of minimizing the maximum scheduling cost that is non-decreasing with job completion time.

Pinedo (1995) indicates that, in practice, the penalty function associated with a scheduling problem may follow from a function, in which early jobs are assigned no penalty and those that are finished after their due dates are assigned a penalty that increases at a given rate. Within the penalty function, the job reaches a point, where the penalty assignment changes and increases at a much slower pace. The function identified by Pinedo (1995) is general; however, two more specific functions that react similarly are the deferral cost function (Lawler 1964) and the late work criterion.

Deferral cost functions have been studied by Kahlbacher (1993) who considered general penalty functions monotonous with respect to absolute lateness. He examined several specific cases of the penalty function for situations, in which machine idle times are allowed or not allowed. Federgruen and Mosheiov (1994) considered a class of single-machine scheduling problems with a common due date and general earliness and tardiness penalties. In this study, some polynomial greedy algorithms were proposed and for convex cost structures, they also examined the worst-case ratio bound if the due date is non-restrictive. Baptiste and Sadykov (2009) considered the objective of minimizing a piecewise linear function. They introduced a new Mixed Integer Programming (MIP) model based on time interval decomposition.

The problem of late work minimization on a single machine, as a special case for Tardy/Lost measure, has been addressed in many studies. Potts and Van Wassenhove (1992b) proposed a polynomial time algorithm based on the similarity between tardiness and late work parameters. In another study (Potts and Van Wassenhove 1992a), they developed a branch-and-bound algorithm for the problem which formed a family of approximation algorithms based on truncated enumeration. The results concerning late work are partially reviewed in Chen et al. (1998) and Leung (2004), but Sterna (2011) addresses the first complete review of the topic. Kethley and Alidaee (2002) modified the definition of the late work criterion by introducing two due dates for each job, called due date and deadline. They called the proposed performance criterion as “modified Total Weighted Late Work” which is a special case for Tardy/Lost penalty function if we set $u_{i} =0$ in Eq. (1).

The main contribution of this research is introducing a new general penalty function, namely Tardy/Lost, for scheduling problems. By adjusting parameters, Tardy/Lost can be converted into some traditional penalty functions, such as weighted tardiness, tardiness with order acceptance assumption, late work, and penalties applied in delivery contracts. From solution point of view, this paper proposes both exact and heuristic methods for a novel problem, in which exact solutions outperform commercial software CPLEX 12 in test instances.

The rest of this paper is organized as follows. In Sects. 2 and 3, we propose a mathematical model and a heuristic algorithm, respectively. Section 4 deals with some dominance rules and lower bounds for problem $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\mathrm{TL}$ which later will be used in designing dynamic programming and branch-and-bound algorithms of Sects. 5 and 6. In the next section, we examine the performance of the proposed methods using experimental tests and concluding remarks will be presented in Sect. 8.

2 Mathematical model

To formulate a mixed integer programming model for problem $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\mathrm{TL}$, jobs are partitioned into four groups of early, tardy, lost, and straddling. In each optimal solution, all tardy jobs except the first one must be sorted by WSPT (Weighted Shortest Processing Time) ordering. The first tardy job in any optimal schedule may not belong to WSPT, and we call it straddling job. The straddling job is started before or at due date $d_{1}$ and is finished after $d_{1}$. If the straddling job $\alpha$ is finished after $d_{2}$, no job belongs to the set of straddling and job $\alpha$ will be considered as lost. However, in the next sections of this paper, it is assumed that there is exactly one straddling job in each schedule and the straddling job may be finished after $d_{2}$.

We renumber jobs according to WSPT ordering and define groups of early, tardy, lost, and straddling jobs as groups 1–4, respectively. Decision variables used in this model are as follows.

$Z_{i}$ is the amount of penalty related to job i.

$X_{i,k}$ is the binary variable that takes value 1 if job i belongs to group k and otherwise is 0.

In the following, we present a mixed integer programming (MIP) model by Eqs. (2) to (10).

$$\begin{aligned}&\mathrm{Min} \,\,\,Z=\sum _{i=1}^n {Z_{i} }\end{aligned}$$

(2)

$$\begin{aligned}&\sum _{k=1}^4 {X_{i,k} } =1 \quad \forall i=1,2, \ldots ,n\end{aligned}$$

(3)

$$\begin{aligned}&\sum _{i=1}^n {X_{i,4} } \le 1\end{aligned}$$

(4)

$$\begin{aligned}&\sum _{i=1}^n {\left( {p_{i} . X_{i,1} } \right) } \le d_{1}\end{aligned}$$

(5)

$$\begin{aligned}&\sum _{i=1}^n {\left( {p_{i} . \left( {X_{i,1} +X_{i,2} +X_{i,4} } \right) } \right) } \le d_{2}\end{aligned}$$

(6)

$$\begin{aligned}&Z_{i} +M_{1} \left( {1-X_{i,2} } \right) \ge w_{i} \left[ {\sum _{j=1}^n {\left( {p_{j} . \left( {X_{j,1} +X_{j,4} } \right) } \right) } +\sum _{j\le i} {\left( {p_{j} . X_{j,2} } \right) -d_{1} } } \right] \quad \forall i \end{aligned}$$

(7)

$$\begin{aligned}&Z_{i} +M_{2} \left( {1-X_{i,3} } \right) \ge s_{i}\quad \forall i \end{aligned}$$

(8)

$$\begin{aligned}&Z_{i} +M_{3} \left( {1-X_{i,4} } \right) \ge w_{i} \left[ {\sum _{j=1}^n {\left( {p_{j} . X_{j,1} } \right) } +p_{i} -d_{1} } \right] \quad \forall i \end{aligned}$$

(9)

$$\begin{aligned}&X_{i,k} \in \left\{ {0,1} \right\} \quad \forall i=1, \ldots ,n\quad k=1,\ldots ,4. \end{aligned}$$

(10)

Equation (2) indicates the objective function as sum of penalties related to all jobs. Equation (3) assigns each job to one of the previously defined groups. and from Eq. (4). at most one job can be straddling in each schedule. Relation (5) ensures that sum process times of early jobs cannot exceed $d_{1}$, while (6) restricts sum process times of early, tardy, and straddling jobs to $d_{2}$. Equations (7) to (9), respectively, calculate the penalties related to tardy, lost, and straddling jobs. $M_{1}, M_{2}$, and $M_{3}$ are big integers, and supposing, $w_{\max }$, $p_{\max }$, and $s_{\max }$ represent the maximum values of tardiness weights, process times, and lost penalties, we can define $M_{1} =w_{\max } \left( {d_{2} -d_{1} } \right)$, $M_{2} =s_{\max }$, and $M_{3} =w_{\max } .p_{\max }$.

The above model is original and includes 5n variables as well as $4n+3$ constraints. The number of variables and constraints is significantly small compared with typical models of single-machine scheduling. The following example illustrates the solution of the mathematical model for a small instance.

Example 1

Suppose an instance of problem $1|d_{i}^{1} =d_{1},d_{i}^{2} =d_{2} |\mathrm{TL}$ with 5 jobs. Here, ${d}_{1} =13$ and ${d}_{2} =21$, and other parameters are described in Table 2. The optimal sequence $\left( {1,4,3,2,5} \right)$ will be obtained using the above MIP model, where ${x}_{1,1} ={x}_{2,2} = {x}_{3,4} = {x}_{4,1} = {x}_{5,3} =1$ and other x’s are equal to zero. Figure 2 shows completion times of the jobs in the optimal solution. In this solution, jobs 1 and 4 are early, job 3 is straddling, job 2 is tardy, and job 5 is lost. The penalties related to jobs 1–5 are ${Z}_{1} = {Z}_{4} =0, {Z}_{3} =8, {Z}_{2} =12$, and ${Z}_{5} =18$ resulting the total penalty $Z=38$.

Table 2 Parameters of jobs in Example 1

Fig. 2

Optimal sequence for Example 1

3 MTLR heuristic algorithm

¹

In this section, we propose a heuristic algorithm to find near optimal solutions for problem $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\mathrm{TL}$. Define the ratio of lost penalty to processing time of a job as penalty ratio. The algorithm tries to schedule lost jobs based on these ratios, and, then, schedules tardy jobs, because lost penalties are greater than tardiness penalties and are considered first. In this procedure, four schedules are built and the best one is selected as output of the algorithm.

This algorithm is composed of two phases, where lost jobs are scheduled in the first phase and tardy jobs are scheduled in the second one. In each iteration of the first phase, a job with minimum $s_{i} /p_{i}$ ratio is selected among the set of unscheduled jobs U and will be placed into first idle position from the end of schedule. Moreover, if there exist some jobs able to fill remaining time interval until $d_{2}$, the algorithm schedules the one with minimum penalty and saves the obtained secondary schedule, $\hat{{G}}_{1}$, besides primary schedule $G_{1}$. Considering ${s_{i} }/{\min (C_{i} -d_{2},p_{i} )}$ instead of $s_{i} /p_{i}$ as ratio for choosing lost jobs creates two other primary and secondary schedules $G_{2}$ and $\hat{{G}}_{2}$. $\{ {U_{1},U_{2},\hat{{U}}_{1},~\mathrm{and}~\hat{{U}}_{2} } \}$ are the sets of unscheduled jobs in sequences $G_{1}, G_{2}, \hat{{G}}_{1}$, and $\hat{{G}}_{2}$; in addition, $\{ {j_{1},j_{2} ,\hat{{j}}_{1},~\mathrm{and}~\hat{{j}}_{2} }\}$ are the selected jobs going to be inserted in each iteration of these four schedules.

In the second phase, MTLR selects unscheduled jobs based on minimum ${w_{i} }/{\min (C_{i} -d_{1},p_{i} )}$ ratios and assigns them as tardy jobs in idle positions from the end of schedules $G_{1} ,\hat{{G}}_{1},G_{2}$, and $\hat{{G}}_{2}$. This makes four complete schedules for the problem, and algorithm MTLR returns the best solution among them as final answer. The time complexity of this algorithm is $O(n{^2})$, and its steps are as follows.

• 1. Set $C_{1} =P_{\mathrm{sum}} =\sum _{i=1}^n {p_{i} }$, $G_{1} =\varnothing$, $Z_{1} =0$, $\hat{{Z}}_{1} =\infty$ and $U_{1} =\left\{ {1,2, \ldots ,n} \right\}$.

• 2. While $C_{1} >d_{2}$ repeat steps 2.1 and 2.2.

  • 2.1 Select job $j_{1} =\mathop {\mathrm{Arg} \min }\limits _{i\in U_{1} } {\{s_{i} }/{p_{i} \}}$ and schedule it in first free position from the end of $G_{1}$. Set $U_{1} =U_{1} |\{j_{1} \}$, $C_{1} =C_{1} -p_{j_{1} }$, $G_{1} =\left( {j_{1},\left( {G_{1} } \right) } \right)$ and $Z_{1} =Z_{1} +s_{j_{1} }$.

  • 2.2 Select job $\hat{{j}}_{1} =\mathop {Arg\min }\limits _{i\in U_{1},p_{i} \ge C_{1} -d_{2} } \{s_{i}\}$ if exists and if $Z_{1} +s_{\hat{{j}}_{1} } <\hat{{Z}}_{1}$, then set $\hat{{G}}_{1} =({\hat{{j}}_{1},( {G_{1} })})$, $\hat{{C}}_{1} =C_{1} -p_{\hat{{j}}_{1} }$, $\hat{{U}}_{1} =U_{1} |\{\hat{{j}}_{1} \}$ and $\hat{{Z}}_{1} =Z_{1} +s_{\hat{{j}}_{1} }$.

• 3. Repeat steps 1 and 2 letting $j_{2} =\mathop {\mathrm{Arg}\min }\limits _{i\in U_{2} } \left\{ {{s_{i} }/{\min (C_{i} -d_{1},p_{i} )}} \right\}$ and create partial schedules $G_{2}$ and $\hat{{G}}_{2}$ with total penalties $Z_{2}$ and $\hat{{Z}}_{2}$, respectively.

• 4. While $C_{1} >d_{1}$ select job $j_{1} =\mathop {\mathrm{Arg}\min }\limits _{i\in U_{1} } \left\{ {{w_{i} }/{\min \left( {p_{i},C_{1} -d_{1} } \right) }} \right\}$. Set $G_{1} =\left( {j_{1},\left( {G_{1} } \right) } \right) C_{1} =C_{1} -p_{j_{1} }$, $U_{1} =U_{1} |\{j_{1} \}$ and $Z_{1} =Z_{1} +w_{j_{1} } \left( {C_{1} -d_{1} } \right)$.

• 5. Repeat step 4 for schedules $\hat{{G}}_{1}, G_{2}$, and $\hat{{G}}_{2}$.

• 6. Return the best solution among schedules $G_{1}, \hat{{G}}_{1}, G_{2}$, and $\hat{{G}}_{2}$.

4 Dominance rules and lower bounds

In this section, some dominance rules and lower bounds are proposed for problem $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\mathrm{TL}$which later will be used in designing dynamic programming and branch-and-bound algorithms. Suppose that groups of early, tardy, and lost jobs are indicated by $\sigma _{E}, \sigma _{T}$, and $\sigma _{L}$.

Dominance rule DR1  Let $i\in \sigma _{E}$ and $j\in \sigma _{T}$ be two arbitrary jobs in a sequence satisfying relations $p_{i} \ge p_{j}$ and $w_{i} \le w_{j}$. Then, swapping jobs i and j will not increase the total penalty.

Proof

The proof is done by comparing total penalty before and after swapping jobs i and j. Figure 3 shows these two cases, where $\pi _{1},\pi _{2}$, and $\pi _{3}$, respectively, denote groups sequenced before, between, and after jobs i and j. Amount of penalty related to groups $\pi _{1}$ and $\pi _{3}$ remains unchanged during swap and completion times of jobs in $\pi _{2}$ will not increase. Let $Z_{\pi _{2} }^{bef}$ and $Z_{\pi _{2} }^{aft}$ denote penalty of jobs in group $\pi _{2}$ in these two cases. Therefore, we have

$$\begin{aligned} Z^{\mathrm{bef}}= & {} Z_{\pi _{1} } +Z_{\pi _{2} }^{\mathrm{bef}} +Z_{\pi _{3} } +w_{j} \left( {C-d_{1} } \right) \\ Z^{\mathrm{aft}}= & {} Z_{\pi _{1} } +Z_{\pi _{2} }^{\mathrm{aft}} +Z_{\pi _{3} } +w_{i} \left( {C-d_{1} } \right) \\\Rightarrow & {} Z^{\mathrm{{aft}}}-Z^{\mathrm{bef}}=\left( {Z_{\pi _{2} }^{\mathrm{aft}} -Z_{\pi _{2} }^{\mathrm{bef}} } \right) +\left( {w_{i} -w_{j} } \right) \left( {C-d_{1} } \right) \le 0 \end{aligned}$$

and this finalizes the proof. $\square$

Fig. 3

Sequences related to the proof of DR1

Dominance rule DR2  Let $i\in \sigma _{T}$ and $j\in \sigma _{L}$ be two arbitrary jobs in a sequence satisfying relations $p_{i} \ge p_{j}$ and$\left( {w_{i} -w_{j} } \right) . t+\psi _{i,j} \ge 0$. Then, swapping jobs i and j will not increase the total penalty. Here, t is the start time of job i before swapping and parameter $\psi _{i,j}$ is calculated as $\psi _{i,j} =w_{i} ({p_{i} -d_{1} })-w_{j} ({p_{j} -d_{1} })+s_{j} -s_{i}$.

Proof

The proof is done similar to the proof of DR1.

Dominance rule DR3  Let $i\in \sigma _{E}$ and $j\in \sigma _{L}$ be two jobs in a sequence satisfying relations $p_{i} \ge p_{j}$ and $s_{i} \le s_{j}$. Then, swapping jobs i and j will not increase the total penalty. $\square$

Proof

The proof is done similar to the proof of DR1.

Lower bound LB1  This lower bound is composed of two parts; one for lost jobs ($\mathrm{LB}_{L} )$ and the other for tardy jobs ($\mathrm{LB}_{T} )$. Steps of the algorithm for calculating $\mathrm{LB}_{L}$ are as follows.

Algorithm LB_L

• 1. Let $U=\{1,2, \ldots ,n\}$ be a set of unscheduled jobs. Set $C=P_{\mathrm{sum}}$and $\mathrm{LB}_{L} =0$.

• 2. Select a job i from U with minimum ${s_{i} }/{p_{i} }$ and set $\mathrm{LB}_{L} =\mathrm{LB}_{L} +\frac{s_{i} }{p_{i} }\min \left( {C-d_{1} ,p_{i}}\right) .$

• 3. Set $C=C-p_{i}$ and $U=U|\{i\}$ and if $C>d_{2}$ go back to step 2.

To calculate $\mathrm{LB}_{T}$, create an ordered set $\Omega$ of artificial jobs via rearranging process times and tardiness weights of the real jobs, such that for each jobs i and $i+$1 in set $\Omega$, we have $p_{i} \ge p_{i+1}$ and $w_{i} \le w_{i+1}$. Jobs are selected from the beginning of set $\Omega$ and are scheduled into the tardiness interval from $d_{2}$ toward $d_{1}$. If last scheduled job passes across $d_{1}$, then tardiness penalty is only calculated for part of the job which falls inside the tardiness interval. The following algorithm describes this part of the lower bound.

Algorithm LB_T

• 1. Set $C=d_{2}$, $i=1$, $\mathrm{LB}_{T} =0$ and $\Omega =\left\{ {\left( {1,2,\ldots ,i,\ldots ,n} \right) |\quad \forall i p_{i} \ge p_{i+1}, w_{i} \le w_{i+1} } \right\}$.

• 2. Select i$^{\mathrm {th}}$ artificial job from $\Omega$ and set $\mathrm{LB}_{T} =\mathrm{LB}_{T} +\frac{w_{i} }{p_{i} }\left( {C-d_{1} } \right) . \min \left\{ {C-d_{1},p_{i} } \right\}$.

• 3. Set $C=C-p_{i}$, $i=i+1$ and if $C>d_{1}$, then go back to step 2.

Finally, the lower bound will be calculated as $\mathrm{LB}1=\mathrm{LB}_{T} +\mathrm{LB}_{L}$. $\square$

Proof

Consider minimization of lost penalties as minimizing objects’ weights in a knapsack problem, where objects can be split and the knapsack must be filled up. Suppose the knapsack size is $\sum _{i=1}^n {p_{i} } -d_{2}$, and in addition, $p_{i}$ and $w_{i}$ correspond for size and weight of object i, respectively. Algorithm LB_L selects jobs with minimum penalty ratios, and the ability of splitting jobs guarantee that this algorithm gives a lower bound for the problem of minimizing lost penalties.

Based on the proof of Theorem 2 in reference (Fathi and Nuttle 1990), algorithm LB_T gives a lower bound for common due date weighted tardiness problem. The only point is that, algorithm LB_T schedules tardy jobs from time $d_{2}$, but last tardy job in optimal sequence of problem $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\mathrm{TL}$ may finish before $d_{2}$. To show that the proposed algorithm gives a lower bound in this case, consider three sequences in Fig. 4.

Fig. 4

Sequences used for proving lower bound LB1

Let $\sigma _{1}$ to $\sigma _{4}$ be groups of jobs, and according to the definition of artificial jobs in algorithm LB_T, job $k_{2}$ has the biggest process time, and we split this job into two jobs in the artificial sequence (b) from Fig. 4. Considering $w_{k_{2} } =w_{{k}'_{2} } =w_{{k}''_{2} }$, we have $Z_{\sigma _{3} } \le Z_{\sigma _{1} } +s_{k_{1} } {\left( {p_{k_{1} } -\gamma } \right) }/{p_{k_{1} } }$ that implies

$$\begin{aligned} Z_{\sigma _{3} } +s_{k_{1} } \left( {\gamma /{p_{k_{1} } }} \right) \le Z_{\sigma _{1} } +s_{k_{1} }. \end{aligned}$$

(11)

From $\frac{w_{{k}'_{2} } }{p_{k_{2} } }=\frac{w_{k_{2} } }{p_{k_{2} } }\le \frac{w_{i} }{p_{i} } \forall i=1, \ldots ,n$, we will conclude

$$\begin{aligned} w_{{k}'_{2} } \left( {d_{2} -d_{1} } \right) \left( {\gamma /{p_{k_{2} } }} \right) \le w_{k_{1} } \left( {d_{2} -d_{1} } \right) \left( {\gamma /{p_{k_{1} } }} \right) \le s_{k_{1} } \left( {\gamma /{p_{k_{1} } }} \right) . \end{aligned}$$

(12)

By (11) and (12), we get $w_{{k}'_{2} } \left( {d_{2} -d_{1} } \right) \left( {\gamma /{p_{k_{2} } }} \right) +Z_{\sigma _{3} } \le Z_{\sigma _{1} } +s_{k_{1} }$, and because of $w_{{k}''_{2} } \le w_{i} \forall i$   we have

$$\begin{aligned} w_{{k}'_{2} } \left( {d_{2} -d_{1} } \right) \left( {\gamma /{p_{k_{2} } }} \right) +Z_{\sigma _{3} } +Z_{{k}''_{2} } +Z_{\sigma _{1} } \le Z_{\sigma _{2} } +Z_{\sigma _{1} } +s_{k_{1} }. \end{aligned}$$

(13)

Now, we will show $Z_{k_{2} } \le Z_{{k}''_{2} } +w_{{k}'_{2} } \left( {d_{2} -d_{1} } \right) \left( {\gamma /{p_{k_{2} } }} \right)$ which completes the proof.

$$\begin{aligned} Z_{{k}''_{2} } +w_{{k}'_{2} }\,\, ({d_{2} -d_{1} }) ({\upgamma /{p_{k_{2} } }})= & {} w_{k_{2} } \,\, ({d_{2} -\upgamma -\,d_{1} }) +w_{{k}'_{2} }\,\, ({d_{2} -d_{1} }) ({\upgamma /{p_{k_{2} } }}) \nonumber \\= & {} w_{k_{2} }\,\, ({d_{2} -d_{1}}) +w_{k_{2} } .\upgamma .\left( {\frac{d_{2} -d_{1} }{p_{k_{2} } }-1} \right) \nonumber \\\ge & {} w_{k_{2} }\,\, ({d_{2} -d_{1} }) = Z_{k_{2} }. \end{aligned}$$

(14)

$\square$

Lower bound LB2  In this lower bound, the same as $\mathrm{LB}1$, penalties of tardy and lost jobs are calculated separately, and then, we add them up to make the final lower bound. Penalty related to lost jobs is achieved by algorithm $\mathrm{LB}\_L$, but we use the approximation algorithm from (Fathi and Nuttle 1990) to create a lower bound for tardy jobs. Fathi and Nuttle (1990) propose an approximation algorithm with worst-case ratio bound 2 for problem $1|d_{i} =d|w_{i} T_{i}$. If we divide the penalty from this algorithm by 2, we will get a lower bound for tardy jobs in our problem. In the following, the procedure is described as algorithm $L{B}'\_T$.

Algorithm LB’_T

• 1. Set $C=d_{2}$, $i=1$, $L{B}'_{T} =0$, and renumber jobs according to WSPT order.

• 2. Select job i and calculate $L{B}'_{T} =L{B}'_{T} +\frac{w_{i} }{p_{i} }\left( {C-d_{1} } \right) . \min \left\{ {C-d_{1},p_{i}}\right\} .$

• 3. Set $C=C-p_{i}$, $i=i+1$ and if $C>d_{1}$, then go back to step 2.

• 4. Return $L{B}'_{T} ={L{B}'_{T} }/2$

Therefore, the final lower bound LB2 will be calculated as $\mathrm{LB}2=L{B}'_{T} +\mathrm{LB}_{L}$.

5 Dynamic programming algorithms

In this section, we will propose two dynamic programming algorithms for problem $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\mathrm{TL}$. Suppose that jobs are renumbered according to WSPT before developing these DP algorithms. Each optimal schedule for the considered problem includes four parts as: (1) a group of early jobs with any arbitrary order, (2) a straddling job, (3) a group of tardy jobs with WSPT order, and (4) a group of lost jobs with arbitrary order.

5.1 Algorithm DP1

In this dynamic programming algorithm, each state from state space $\nu _{k}^{\left( {\alpha ,C_{\alpha } } \right) }$ indicates a partial sequence for first k jobs excluding straddling job $\alpha$ that finishes at time $C_{\alpha }$. Each state is denoted by a vector $\left[ {t_{1},t_{2},f} \right]$, where $t_{1}$ and $t_{2}$ show sum of process times for early and tardy groups of jobs, respectively, and f is the penalty for corresponding partial sequence.

Figure 5 shows a state $\left[ {t_{1},t_{2},f} \right]$ from state space $\nu _{k-1}^{\left( {\alpha ,C_{\alpha } } \right) }$ as well as three states derived by adding the upcoming job j to different groups of early, tardy, and lost jobs.

Fig. 5

Details of creating new states in DP1

Let $Z_{(\alpha ,C_{\alpha } )}^{*}$ denote optimal penalty for the problem when job $\alpha$ is straddling with completion time $C_{\alpha }$. Steps of the algorithm are as follows.

• 1. For each $\alpha \in \left\{ {1,2, \ldots ,n} \right\}$and each $C_{\alpha } \in \left[ {d_{1} +1, d_{1} +p_{\alpha } } \right]$.

•   1.1  Set $\nu _{0}^{\left( {\alpha ,C_{\alpha } } \right) } =\left\{ {\left[ {0,0,0} \right] } \right\}$.

•    1.2  For each $k\in \left\{ {1,2, \ldots ,\alpha -1,\alpha +1 ,\ldots , n} \right\}$ consider all states $\left[ {t_{1},t_{2},f} \right]$ in $\nu _{k-1}^{\left( {\alpha ,C_{\alpha } } \right) }$.

  •   $\bullet$  (job  k  is early) If $t_{1} +p_{k} \le C_{\alpha } -p_{\alpha }$ and DR1 and DR3 do not eliminate the new state for job k, then add state $\left[ {t_{1} +p_{k},t_{2},f} \right]$to $\nu _{k}^{\left( {\alpha ,C_{\alpha } } \right) }$.

  •    $\bullet$  (job  k  is tardy) If $C_{\alpha } +t_{2} +p_{k} \le d_{2}$ and DR1, DR2, LB1, and LB2 do not eliminate the new state for job k, then add state $\left[ {t_{1},t_{2} +p_{k},f+w_{k} \left( {C_{\alpha } +t_{2} +p_{k} } \right) } \right]$to $\nu _{k}^{\left( {\alpha ,C_{\alpha } } \right) }$.

  •   $\bullet$  (job  k  is lost) If $\sum _{i=1}^k {p_{i} } -t_{1} -t_{2} <P_{\mathrm{sum}} -d_{2}$ and DR2, DR3, LB1, and LB2 do not eliminate the new state for job k, then add state $\left[ {t_{1},t_{2},f+s_{k} } \right]$to $\nu _{k}^{\left( {\alpha ,C_{\alpha } } \right) }$.

  •    $\bullet$  For all the states $\left[ {t_{1},t_{2},f} \right] \in \nu _{k}^{\left( {\alpha ,C_{\alpha } } \right) }$ with equal values for $t_{1}$ and $t_{2}$, keep at most one state having the minimum value of f.

  •    $\bullet$  Delete the state space $\nu _{k-1}^{\left( {\alpha ,C_{\alpha } } \right) }$.

   1.3  Set $Z_{(\alpha , C_\alpha )}^{*} =\mathop {\min }\limits _{[t_1,t_2,f] \in \nu _{n-1}^{ {\alpha ,C_{\alpha } } } } \left\{ f \right\} +Z_{\alpha }$.

• 2. Return $Z=\mathop {\min }\limits _{\alpha ,C_{\alpha } } Z_{(\alpha , C_\alpha )}^{*}$ as optimal solution.

Now, we describe the approach of implementing lower bounds in DP1. Suppose job k is going to be included into group of early jobs from state $\left[ {t_{1},t_{2},f} \right]$. If (15) holds, we can eliminate the new state. Values $\delta _{T}$ and $\delta _{L}$ denote remaining time intervals for scheduling tardy and lost jobs, respectively, and are calculated as (16). Value for $Z_{heu}$ comes from algorithm MTLR.

$$\begin{aligned} f+\mathrm{LB}_{T} \left[ {\delta _{T} } \right] +\mathrm{LB}_{L} \left[ {\delta _{L} } \right] \ge Z_{heu} \end{aligned}$$

(15)

$$\begin{aligned} {\delta }'_{L}= & {} P_{\mathrm{sum}} -\max \left\{ {C_{\alpha },d_{2} } \right\} -\sum _{i=1}^{k-1} {p_{i} } -t_{1} -t_{2} \nonumber \\ {\delta }'_{T}= & {} d_{2} -C_{\alpha } -t_{2} +\max \left\{ {-{\delta }',0} \right\} \nonumber \\ \delta _{L}= & {} \max \left\{ {{\delta }'_{L},0} \right\} \nonumber \\ \delta _{T}= & {} \max \left\{ {{\delta }'_{T},0}. \right\} \end{aligned}$$

(16)

To calculate the time complexity of DP1, consider the maximum number of states in each state space $\nu _{k}^{\left( {\alpha ,C_{\alpha } } \right) }$ as $d_{1}.\left( {d_{2} -d_{1} } \right)$. Step 1.2 iterates by a factor of total feasible states, $\sum _{k=1}^{n-1} {\left| {\nu _{k}^{\left( {\alpha ,C_{\alpha } } \right) } } \right| }$, and is $O\left( {nd_{1} \left( {d_{2} -d_{1} } \right) } \right)$. Similarly, we can show that complexity of step 1.3 is $O\left( {d_{1} \left( {d_{2} -d_{1} } \right) } \right)$. Step 1 iterates at most $P_{\mathrm{sum}} =\sum _{i=1}^n {p_{i} }$ times by selecting different $\alpha$ and $C_{\alpha }$ values, and its complexity is $O\left( {nP_{\mathrm{sum}} d_{1} \left( {d_{2} -d_{1} } \right) } \right)$. Finally, considering that step 2 is implemented in $O\left( {P_{\mathrm{sum}} } \right)$, we conclude the overall time complexity of DP1 as $O\left( {nP_{\mathrm{sum}} d_{1} \left( {d_{2} -d_{1} } \right) } \right)$.

5.2 Algorithm DP2

The basis of this algorithm is similar to DP1 and their only difference is in selecting straddling job. In contrast with the previous dynamic programming, we do not need to predefine a job as straddling at each iteration, and DP2 is able to distinguish suitable straddling job in each iteration of the algorithm. This algorithm considers the straddling job as a member of first group (group of early jobs) that makes minimum penalty if finishes at time $C_{\alpha }$.

During an iteration, straddling job may change, and we can only determine the correct straddling job after scheduling all jobs. Algorithm DP2 keeps at most two states with equal $t_{1}$ and $t_{2}$ values in each iteration; the former, $[{t_{1},t_{2} ,\alpha ,f,f_{\left( \alpha \right) } }]$, calculates minimum total penalty and the later, $[ {t_{1},t_{2},{\alpha }',{f}',{f}'_{\left( {{\alpha }'} \right) } }]$, gives minimum total penalty excluding straddling job. In this notation, f and $f_{\left( \alpha \right) }$ denote the total penalty and total penalty excluding straddling job, respectively.

In DP2, if a job is going to be scheduled in the group of early jobs and generates smaller penalty in comparison with the current straddling job, then the current straddling job will be considered as an early job and the new job takes the straddling place.

Let $[ {t_{1},t_{2},\alpha _{k-1},f,f_{\left( {\alpha _{k-1} } \right) } } ]$ be a state from the previous iteration, and DP2 is going to add job k to this state. Here, the following cases may arise, and we describe the new penalties $f^{new}$ and $f_{(\alpha )}^{new}$ generated in each case.

• 1. Job k is early and the straddling job is not changed: $f^{\mathrm{new}}=f, f_{(\alpha _{k} )}^{\mathrm{new}} =f_{(\alpha _{k-1} )}$.

• 2. Job k is early, the straddling job is changed from $\alpha _{k-1}$ to $\alpha _{k}$ and $C_{\alpha } \le d_{2}$: $f^{\mathrm{new}}=f+\left( {w_{\alpha _{k} } -w_{\alpha _{k-1} } } \right) \left( {C_{\alpha } -d_{1} } \right) , f_{(\alpha _{k} )}^{\mathrm{new}} =f_{(\alpha _{k-1} )}$.

• 3. Job k is early, the straddling job is changed from $\alpha _{k-1}$ to $\alpha _{k}$ and $C_{\alpha } >d_{2}$: $f^{\mathrm{new}}=f+s_{\alpha _{k} } -s_{\alpha _{k-1} }, f_{(\alpha _{k} )}^{\mathrm{new}} =f_{(\alpha _{k-1} )}$.

• 4. Job k is tardy: $f^{\mathrm{new}}{=}f{+}w{ }_{k}\left( {C_{\alpha } {+}t_{2} {+}p_{k} {-}d_{1} } \right) , f_{(\alpha _{k} )}^{\mathrm{new}} =f_{(\alpha _{k{-}1} )} +w{ }_{k}\left( {C_{\alpha } +t_{2} {+}p_{k} {-}d_{1} } \right)$.

• 5. Job k is lost : $f^{\mathrm{new}}=f+s_{k}, f_{(\alpha _{k} )}^{\mathrm{new}} =f_{(\alpha _{k-1} )} +s_{k}$.

Steps of this algorithm are as follows.

• 1. For each $C_{\alpha } \in \left[ {d_{1} +1,\min \left( {d_{1} +p_{\max },P_{\mathrm{sum}} } \right) } \right]$. 1.1.  Set $\nu _{0}^{\left( {C_{\alpha } } \right) } =\left\{ {\left[ {0,0,0,0,0} \right] } \right\}$. 1.2.  For each $k\in \left\{ {1,2, \ldots , n} \right\} \quad t_{1} \in \left\{ {0,1,\ldots ,C_{\alpha } } \right\}$ and each $t_{2} \in \big \{ 0,1,\ldots ,\max \left( {0,d_{2} {-}C_{\alpha } } \right) \big \}$consider all states $[ {t_{1},t_{2},\alpha _{k-1} ,f,f_{\left( {\alpha _{k-1} } \right) } }]$ and $[ {t_{1} ,t_{2},{\alpha }'_{k-1},{f}',{f}'_{\left( {{\alpha }'_{k-1} } \right) } }]$ in $\nu _{k-1}^{\left( {C_{\alpha } } \right) }$.

•    1.2.1  (job   k is early) If $t_{1} +p_{k} \le C_{\alpha }$ and DR1 and DR3 do not eliminate new state for job k,

  •   $\bullet$  If straddling job is not changed, add states $[ {t_{1} +p_{k},t_{2},\alpha _{k-1},f,f_{\left( {\alpha _{k-1} } \right) } } ]$ and $[ {t_{1} +p_{k},t_{2},{\alpha }'_{k-1} ,{f}',{f}'_{\left( {{\alpha }'_{k-1} } \right) } }]$ to state space $\nu _{k}^{\left( {C_{\alpha } } \right) }$.

  •   $\bullet$  If $C_{\alpha } \le d_{2}$ and straddling job changes, add states $[ t_{1} +p_{k},t_{2},\alpha _{k},f+({w_{\alpha }{_{_{}k} } -w_{\alpha _{k-1} } })( {C_{\alpha } -d_{1} } ),f_{( {\alpha _{k-1} } )} ]$ and $[ t_{1} +p_{k},t_{2},{\alpha }'_{k},f+( {w_{{\alpha }'}{_{_k} } -w_{{\alpha }'_{k{-}1} } } )\left( {C_{\alpha } {-}d_{1} } \right) ,{f}'_{\left( {{\alpha }'_{k-1} } \right) } ]$ to state space $\nu _{k}^{\left( {C_{\alpha } } \right) }$.

  • $\bullet$ If $C_{\alpha } >d_{2}$ and straddling job changes, add states $[t_{1} +p_{k},t_{2},\alpha _{k},f+s_{\alpha }{_{_k} } -s_{\alpha _{k-1} },f_{\left( {\alpha _{k-1} } \right) } ]$ and $[t_{1} +p_{k},t_{2},{\alpha }'_{k},f+s_{{\alpha }'}{_{_k}}-s_{{\alpha }'_{k-1} },f'_{\left( {{\alpha }'_{k-1} } \right) } ]$ to state space $\nu _{k}^{\left( {C_{\alpha } } \right) }$.

•    1.2.2  (job k is tardy) If $C_{\alpha } +t_{2} +p_{k} \le d_{2}$ and $\sum _{i=1}^k {p_{i} } -t_{1} \le P_{\mathrm{sum}} -C_{\alpha }$ and also DR1, DR2, LB1, and LB2 do not eliminate the new state for job k, then add states $[t_{1},t_{2} +p_{k},\alpha _{k-1},f+w_{k} \left( {C_{\alpha } +t_{2} +p_{k} -d_{1} } \right) ,f_{\left( {\alpha _{k-1} } \right) } +w_{k} \left( C_{\alpha } +t_{2} +p_{k} \right. \left. -d_{1} \right) ]$ and $[ t_{1},t_{2} +p_{k},{\alpha }'_{k-1} ,{f}'+w_{k} \left( {C_{\alpha } +t_{2} +p_{k} -d_{1} } \right) ,{f}'_{\left( {{\alpha }'_{k-1} } \right) } +w_{k} \left( C_{\alpha } +t_{2}\right. \left. +p_{k} -d_{1}\right) ]$ to $\nu _{k}^{\left( {C_{\alpha } } \right) }$.

•    1.2.3  (job k is lost) If $\sum \nolimits _{i=1}^k {p_{i} } -t_{1} -t_{2} <P_{\mathrm{sum}} -d_{2}$ and $\sum _{i=1}^k {p_{i} } -t_{1} \le P_{\mathrm{sum}} -C_{\alpha }$ and also DR2, DR3, LB1, and LB2 do not eliminate the new state for job k, then add states $[{t_{1},t_{2},\alpha _{k-1},f+s_{k} ,f_{\left( {\alpha _{k-1} } \right) } +s_{k} }]$ and $[ {t_{1},t_{2},{\alpha }'_{k-1},{f}'+s_{k},{f}'_{\left( {{\alpha }'_{k-1} } \right) } +s_{k} }]$ to $\nu _{k}^{\left( {C_{\alpha } } \right) }$.

•    1.2.4  For all the states $[ {t_{1},t_{2},\alpha _{k} ,f,f_{\left( {\alpha _{k} } \right) } }]\in v_{k}^{\left( {C_{\alpha } } \right) }$ with equal values for $t_{1}$ and $t_{2}$, keep at most one state having the minimum value of f and for all the states $[{t_{1},t_{2},{\alpha }'_{k} ,{f}',{f}'_{\left( {{\alpha }'_{k} } \right) } }]\in v_{k}^{\left( {C_{\alpha } } \right) }$ with equal values for $t_{1}$ and $t_{2}$, keep at most one state having the minimum value of ${f}'_{\left( {{\alpha }'_{k} } \right) }$.

•    1.2.5  Delete state space $\nu _{k-1}^{\left( {C_{\alpha } } \right) }$.

  1.3.  Set $Z_{C_{\alpha } }^{*} =\min \left( {\mathop {\min }\limits _{[ {t_{1},t_{2},\alpha _{n},f,f_{(\alpha _{n} )} }]\in \nu _{n}^{\left( {C_{\alpha } } \right) } } \left\{ f \right\} , \mathop {\min }\limits _{[ {t_{1},t_{2},{\alpha }'_{n} ,{f}',{f}'_{({\alpha }'_{n} )} } ]\in \nu _{n}^{\left( {C_{\alpha } } \right) } } \left\{ {{f}'} \right\} }\right)$.

• 2. Return $Z=\mathop {\min }\limits _{C_{\alpha } } Z_{C_{\alpha } }^{*}$ as optimal solution.

While implementing the dominance rules in DP2, it must be noted that we cannot use them on straddling jobs, because these jobs may change during step 1.2.1. To examine lower bounds, suppose, job k is considered to be added into group of early jobs from a state $[{t_{1},t_{2},\alpha _{k-1},f,f_{\left( {\alpha _{k-1} } \right) } }]$. If (17) holds, we discard the new state. Here, $Z_{C_{\alpha } }^{\min }$ denotes minimum penalty caused by an unknown straddling job that completes at time $C_{\alpha }$ and is calculated by (18). From the fact that, in DP2, there is no need to prefix a job as straddling, its complexity is O(n) times less than DP1, and, hence, is $O\left( {P_{\mathrm{sum}} d_{1} \left( {d_{2} -d_{1} } \right) } \right)$.

$$\begin{aligned}&f_{\left( {\alpha _{k-1} } \right) } +Z_{C_{\alpha } }^{\min } +\mathrm{LB}_{T} \left[ {\delta _{T} } \right] +\mathrm{LB}_{L} \left[ {\delta _{L} } \right] \ge Z_{\mathrm{heu}}\end{aligned}$$

(17)

$$\begin{aligned}&Z_{C_{\alpha } }^{\min } =\left\{ {{\begin{array}{ll} {\mathop {\min }\limits _{i} \left\{ {w_{i} } \right\} .\left( {C_{\alpha } -d_{1} } \right) \quad \mathrm{if}\; C_{\alpha } \le d_{2} } \\ {\mathop {\min }\limits _{i} \left\{ {s_{i} } \right\} \qquad \qquad \qquad \qquad \!\!\mathrm{if} \; C_{\alpha } >d_{2} }. \\ \end{array} }} \right. \end{aligned}$$

(18)

6 Branch-and-bound algorithm

This section introduces a branch and bound algorithm for problem $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\mathrm{TL}$. This algorithm prefixes a job as straddling as well as its completion time, and, then, schedules other jobs into groups of early, tardy, and lost (groups 1–3, respectively) based on depth first search tree. Jobs are renumbered and selected for scheduling by WSPT order.

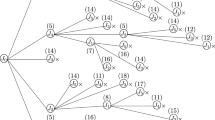
Figure 6 shows the depth first tree used for problem $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\mathrm{TL}$ with four jobs, where job 2 is straddling. Each level is related to one job, excluding the straddling job, and two numbers in each node show order of creating nodes and the group number, in which job is added, respectively. According to this figure, we first add job 1 to group 3, and then, jobs 3 and 4 are added to group 3, respectively.

Fig. 6

Part of the search tree for algorithm BB1

Details of this branch-and-bound algorithm are described as follows. Variables $t_{1}, t_{2}$, and $t_{3}$ show total process time of jobs in groups 1–3. In this algorithm, we first assign jobs to group 3 and then add them to groups 2 and 1, because experiments show this type of assignment increases $\hat{{Z}}$ rapidly and improves the efficiency of lower bounds.

• 1. Calculate the upper bound UB from algorithm MTLR. For each $\alpha =1,2, \ldots ,n$ and each $C_{\alpha } =\left[ {d_{1} +1,\min \left\{ {d_{1} +p_{\alpha },P_{\mathrm{sum}} } \right\} } \right]$. 1.1.  Set $t_{1} =t_{2} =t_{3} =0$ and if $C_{\alpha } \le d_{2}$, then $\hat{{Z}}=w_{\alpha } \left( {C_{\alpha } -d_{1} } \right)$ else $\hat{{Z}}=s_{\alpha }$. 1.2.  Assign jobs to a depth first tree of Fig. 6.

•    1.2.1  If current job $\hat{{i}}$ is a candidate for group 1.

  •    $\bullet$  If $t_{1} +p_{\hat{{i}}} >C_{\alpha } -p_{\alpha }$, then fathom current node and return to step 1.2.

  •    $\bullet$  Check DR1 and DR2 for job $\hat{{i}}$ and other tardy or lost jobs. If current node is fathomed, then return to step 1.2 else set $t_{1} =t_{1} +p_{i}$.

•    1.2.2.  If current job $\hat{{i}}$ is a candidate for group 2.

  •    $\bullet$  If $C_{\alpha } +t_{2} +p_{\hat{{i}}} >d_{2}$ or $C_{\alpha } +t_{2} +t_{3} +p_{i} >P_{\mathrm{sum}}$, then fathom current node and return to step 1.2.

  •    $\bullet$  Check LB1 and LB2 as well as DR1 and DR3 for job $\hat{{i}}$ and other early or lost jobs. If current node is fathomed, then return to step 1.2.

  •    $\bullet$  Set $t_{2} =t_{2} +p_{\hat{{i}}}$ and $\hat{{Z}}=\hat{{Z}}+w_{\hat{{i}}} \left( {C_{\alpha } +t_{2} -d_{1} } \right)$.

•    1.2.3  If current job $\hat{{i}}$ is a candidate for group 3.

  •    $\bullet$  If $t_{3} \ge P_{\mathrm{sum}} -d_{2}$, then fathom current node and return to step 1.2.

  •    $\bullet$  Check LB1 and LB2 as well as DR2 and DR3 for job $\hat{{i}}$ and other early or lost jobs. If current node is fathomed, then return to step 1.2.

  •    $\bullet$  Set $t_{3} =t_{3} +p_{\hat{{i}}}$ and $\hat{{Z}}=\hat{{Z}}+s_{\hat{{i}}}$.

  1.3  If a complete schedule with total penalty $\hat{{Z}}$ is achieved and $\hat{{Z}}<UB$, then set $UB=\hat{{Z}}$ and save this schedule as the best schedule found until now.

• 2. Return the final UB as optimal solution.

We can use the idea of letting the branch-and-bound algorithm to choose straddling job, but experiments indicate this idea increases run times in all instances, and hence, here, we discard this idea.

7 Computational results

In this section, we examine the results of the mathematical model, heuristic algorithm, dynamic programming, and branch-and-bound algorithms on a number of randomly generated test problems. Computational experiments were performed on Intel Core$^\mathrm{TM}$ i7-2600 CPU 3.4GHz with 4 GB RAM. On this system, CPLEX 12 was used as a mixed integer programming solver and the algorithms were coded in Visual studio C$++$ 2008.

We generate random instances for $n\in \left\{ {30, 50, 75, 100, 150, 200, 250} \right\}$. Processing times, $p_{i}$, and tardiness weights, $w_{i}$, are drown from uniform distributions [1, 10] or [1, 100]. Using the method proposed in (Kethley and Alidaee 2002), due date $d_{1}$ is selected from uniform distribution between $P_{\mathrm{sum}} \left( {1-\tau _{1} -0.5R_{1} } \right)$ and $P_{\mathrm{sum}} \left( {1-\tau _{1} +0.5R_{1} } \right)$, and $d_{2}$ is from uniform distribution between $d_{1} +\left( {P_{\mathrm{sum}} -d_{1} } \right) \left( {1-\tau _{2} -0.5R_{2} } \right)$ and $d_{1} +\left( {P_{\mathrm{sum}} -d_{1} } \right) \left( {1-\tau _{2} +0.5R_{2} } \right)$, where $\tau _{1} \in \left\{ {0.4, 0.8} \right\}$, $\tau _{2} \in \left\{ {0.2, 0.8} \right\}$, $R_{1} =0.2$, and $R_{2} =0.4$. Lost penalty steps, $u_{i}$, are generated from one of uniform distributions $U\left[ {0,0.5w_{i} \left( {d_{2} -d_{1} } \right) } \right]$ or $U\left[ {w_{i} \left( {d_{2} -d_{1} } \right) ,3w_{i} \left( {d_{2} -d_{1} } \right) } \right]$.

According to the above parameters, 32 instance groups are created by combining parameters $p_{i},w_{i},\tau _{1},\tau _{2}$, and $u_{i}$. For any given number of jobs, n, 20 random test instances are generated in each instance group. Table 3 shows the characteristics of these groups were L and H which show low and high levels for each parameter, respectively.

Table 3 Properties related to 32 groups of instances

Table 11 (see Appendix) shows a summary of computational results obtained from running proposed methods on test instances in groups G1 to G16. The first two columns show group number and the number of jobs in each instance. The next two columns indicate the average and maximum gap between heuristic solutions and optimal ones. The results show that in more than 95 % of cases, average and maximum gaps are less than 2 and 4 %, respectively.

The next two columns show the average run times and number of instances solved by MIP model. The model is implemented by CPLEX 12 and is able to optimally solve instances up to 50 jobs in 1 h time limit.

Results of algorithm DP1 are provided in columns 7 to 14. In column 9, the percentage of fathomed states by lower bounds and dominance rules out of all created states are given. This ratio varies between 35 and 65 % in different instance groups and DP1 is able to solve instances up to 50 jobs. Columns 15 to 22 of Table 11 contain the results of running algorithm DP2. These results indicate that DP2 is able to optimally solve all instances up to 250 jobs with $p_{i} \in [1, 10]$ and instances up to 75 jobs with $p_{i} \in [1, 100]$ in reasonable times. The last columns in this table are about algorithm BB1 and show that this algorithm is able to solve instances up to 50 jobs with 55–65 % percent of fathomed nodes.

Figure 7 shows the average gap from optimal solution for algorithm MTLR in different instance sizes. This average error is less than 0.8 % and decreases by any increase in the size of instances. This shows good performance of MTLR in generating near optimal solutions for problem $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\mathrm{TL}$. Running times of this algorithm are less than 0.1 s in all the cases, and hence, are not reported.

Fig. 7

Gap percentages for MTLR algorithm

In Table 4, we examine how changing the problem parameters influence optimality gap of algorithm MTLR. As it is seen, the algorithm performs better when the variation of processing times is low (i.e. $p_{i} \in [1,10])$. By increasing the variation of $w_{i}$ and $u_{i}$ parameters, the average gap decreases, because of that the algorithm can categorize jobs into the groups E, T, and L more accurately under high variation of these two parameters.

Parameter $\tau _{1}$ has no significant effect on the performance of heuristic algorithm, but when $\tau _{2}$ increases, more number of jobs will be lost, and high penalties of the lost jobs cause an increase in optimality gap of algorithm MTLR.

Table 4 Problem parameters impact on MTLR error percentage

Computational results show that all 30 job instances are solved by the mathematical model in average run time of 18.39 s. However, in the case of 50 job instances, the model is able to solve 298 instances out of 320 within 1 h time limit, and the average run time for solved instances is 1647.48 s.

Table 5 shows the impact of varying parameters on run times of mathematical model in 50 job instances. Variation of process times has a direct relation with run times, while increasing tardiness or lost penalties ($w_{i} 's$ or $u_{i} 's)$ will decrease the model run times in average. Changing the parameter $\tau _{1}$ has no significant effect on run times; however, results show a inverse relation between parameter $\tau _{2}$ and average run times. That is because if $\tau _{2}$ increases, the value of $d_{2}$ will decrease and less number of jobs can satisfy the fourth constraint of mathematical model, and hence, less number of jobs should be examined for laying in lost jobs’ group.

Table 5 Problem parameters impact on CPLEX run times

Algorithm DP1 is able to solve instances up to 250 jobs with low variation of process times (i.e. $p_{i} \in [1,10])$ and instances up to 50 jobs when process times are generated from U[1, 100]. Table 6 shows the number of solved instances out of 320, and Table 7 gives average of run times under low and high process time variation.

Table 6 Number of solved instances out of 320 solved by DP1

Table 7 Problem parameters impact on DP1 run times

Figure 8 shows the percentage of fathomed nods by dominance rules and lower bounds in DP1. According to this figure, LB1 has the best performance in small-size instances; however, by increasing the size of instances, more number of nodes is fathomed by dominance rules in average. DR1 fathoms more nodes in comparison with other dominance rules, because it works on early and tardy groups and jobs in these two groups are scheduled before lost jobs.

Fig. 8

Percentage of fathomed nodes in DP1

Algorithm DP2 solves all instances up to 75 jobs. Based on Table 8, in groups with low variety of process times, DP2 is able to solve instances up to 250 jobs in less than 32 s. In case of high variety for process times, instances up to 75 jobs are solved in average 183 s, but larger instances are not solved due to system memory limitations.

Table 8 Problem parameters impact on DP2 run times

Figure 9 shows the percentage of fathomed nodes by dominance rules and lower bounds in DP2. Here, LB2 has the best performance on instances with less than 100 jobs; however, by increasing the size of instances, more percentage of nodes is fathomed by dominance rules. This shows the efficiency of LB1 in small- and medium-size instances and dominance rules in large-size instances.

Fig. 9

Percentage of fathomed nodes in DP2

Tables 9 and 10 give the number of solved instances by BB1 and average run times for instances with low and high variation of process times. For instances with $p_{i} \in [1,10]$, algorithm BB1 is able to solve all instances up to 50 jobs in average run time 49.76 s. In case $p_{i} \in [1,100]$, all instances up to 30 jobs are solved in average 9.39 s.

Table 9 Number of solved instances out of 320 solved by BB1

Table 10 Problem parameters impact on BB1 run times

The percentage of fathomed nodes in BB1 is shown in Fig. 10, where LB1 has the best performance on fathoming nodes and such a way that it cuts more than 60 % of nodes in all problem sizes.

Fig. 10

Percentage of fathomed nodes in BB1

8 Conclusions

In this paper, we studied minimizing Tardy/Lost penalties on a single machine with common due dates. We examined time complexity of the problem and proposed a MIP model which classifies jobs into four groups of early, tardy, straddling, and lost jobs. Then, a heuristic algorithm was developed and, later, was used as upper bound in dynamic programming and branch-and-bound algorithms.

In Sect. 4, we introduced three dominance rules and two lower bounds, and in the next section, two dynamic programming algorithms were developed. These DPs are pseudo-polynomial with time complexities $O\left( {nP_{\mathrm{sum}} d_{1} \left( {d_{2} -d_{1} } \right) } \right)$ and $O\left( {P_{\mathrm{sum}} d_{1} \left( {d_{2} -d_{1} } \right) } \right)$. Then, we proposed a branch-and-bound algorithm based on depth first search tree.

To evaluate the proposed methods, we generated 32 groups of test instances with 30–250 jobs. Experiments indicated that increasing the variety of process times will make instances harder and cause algorithms need more time to solve them. For instances with 75 jobs or less, LB1 shows the best performance in cutting down search trees; but with increasing the size of instances, dominance rules show a better performance in comparison with LBs.

Average optimality gap of MTLR algorithm was less than 2 % for all instances, which proves the efficiency of this algorithm in finding near optimal solutions for problem $1|d_{i}^{1} =d_{1}, d_{i}^{2} =d_{2} |\mathrm{TL}$. In overall, DP2 is the best algorithm for finding optimal solutions. This algorithm solves all instances with low variety of process times in less than 32 s and for high process time varieties, the algorithm solves all instances up to 75 jobs in less than 183 s.

The proposed Tardy/Lost penalty function can be considered as a general form for some well-known performance measures, such as late work, weighted tardiness, and tardiness with order acceptance assumption. Therefore, efficient solution approaches can also be applied in the case of these problems. As future researches, we suggest using meta-heuristics or constraint programming methods.

Appendix

See Table 11.

Table 11 Summary of running proposed methods on test instances