Orbital maneuvers to reach and explore a triple asteroid

Abstract

The objective of the present paper is to study orbital maneuvers to perform a mission to a triple asteroid. First, a genetic algorithm is used to find multi-impulsive maneuvers to go from the Earth to the asteroid, with minimum fuel consumption. After that, swing-by maneuvers with the two smaller bodies of the triple system are simulated and mapped to show the possible gains of energy that can be accomplished with the use of this technique. This study is made using the “patched conics approximation” and the “restricted three-body problem”, to determine the accuracy of the approximated model. The system of asteroids 2001SN$_{263}$ is used as an example for the calculations.

1 Introduction

In astrodynamics, depending on the mission, the trajectory of the spacecraft can be controlled by orbital maneuvers. It is possible to find in the literature many publications showing how to make those maneuvers with minimum fuel consumption (Hohmann 1925; Hoelker and Silber 1959; Shternfeld 1959; Prussing and Chiu 1986). Besides the exclusive use of fuel, several alternatives have been considered to help to perform the maneuver with fuel savings, many times using the gravity field of other celestial bodies (Felipe and Prado 1999, 2004). The use of genetic algorithms to find optimal solutions for orbital maneuvers is also common in the literature (Santos et al. 2012; Santos and Formiga 2014). In the present paper, this technique is used to study the problem of sending a spacecraft from the Earth to the triple asteroid 2001SN$_{263}$ to encounter the system. After that, a study is conducted to show the potential of the Swing-By maneuvers to reduce the fuel expenditure in maneuvers around those three bodies. This maneuver is common in planetary missions and can be used to make the spacecraft to move around the three small bodies of this system. This technique uses the gravitational attraction of one body to modify the spacecraft energy, in order to reach a given goal. A description of this procedure is available in several references (Allen 2003; Battin 1987; Dowling et al. 1991; Formiga and Santos 2014; Formiga and Prado 2014). By dividing the trajectory in a series of two-body problems, it is possible to simplify the calculations. An important point to be considered is the accuracy of this method. This topic is addressed in the present paper, for this specific system of bodies. This study is very important, because the results are very much dependent on the particular system of primaries. Several studies are available in the literature on this topic, in terms of practical missions or theoretical results, like the ones presented in D’Amario et al. (1982), Farquhar and Dunham (1981), Flandro (1966), Helton et al. (2002), Longuski and Williams (1991), Strange and Longuski (2002), Petropoulos and Longuski (2000), Petropoulos et al. (1999), Striepe and Braun (1981), Gomes and Prado (2008, 2010), Sukhanov et al. (2010), Sukhanov and Prado (2004), Swenson (1991), Prado and Broucke (1995a, b, 1996), Prado (2005, 2007), Machuy et al. (2007).

The present study is made to determine the differences in the mean variations of energy obtained when using the patched conics model and the restricted three-body problem. The $\alpha$–$\gamma$ and $\alpha$–$\beta$ systems are considered, in order to see the accuracy of the patched conics model in those particular systems. Another contribution of the present paper is the use of the Tisserand’s criterion to validate the results.

Table 1 Physical data and distance of close approaches in the triple system 2001SN$_{263}$

2 The 2001SN$_{263}$ System

The asteroid 2001SN$_{263}$ (Araújo et al. 2012) was discovered in February 2008. Its orbit around the Sun has semi-major axis of 1.99 AU, eccentricity of 0.48 and inclination of 6.7 degrees. The initial conditions used in the simulations are shown in Table 1 and the geometry of the system in Fig. 1. The components of the system are: a central body $\alpha$ ($M_{1})$, with radius near 1.3 km, and two secondary bodies: $\beta$ and $\gamma$. $\beta$ is located in an orbit with semi-major axis of 16.63 km and eccentricity of 0.015. $\gamma$ has an orbit with semi-major axis 3.80 km and eccentricity 0.016 (Araújo et al. 2012). The masses are: $\alpha$ = 917.47 $\times$ 10$^{10}$ kg; $\beta$ = 24.04 $\times$ 10$^{10}$ kg and $\gamma$ = 9.77 04 $\times$ 10$^{10}$ kg. Table 1 also shows the periapsis distance of the maneuvers studied here.

Fig. 1

Geometry of trajectories passing by the 2001SN$_{263 }$system

3 “Patched conics” mathematical model

The system under study is assumed to be dominated by two main bodies that are in circular orbits around their center of mass. The spacecraft has negligible mass and is moving under the gravitational attraction of those two primaries. Then, the problem can be studied using the model given by the “Restricted Three-Body Problem”.

Using the approximations given by the “Patched Conics” model, the whole maneuver is assumed to be divided in three phases, where each one can be modeled by the “Two-Body” celestial mechanics. In the first part of the motion the spacecraft is moving around the largest body, before the close approach with $M_{2}$ (the smaller of the two primary bodies). In this phase, the effects of $M_{2}$ are neglected and the system $M_{1}$–$M_{3}$ is assumed to form a “two-body” system, where $M_{3 }$ is the spacecraft, which has negligible mass. In the second part of the motion it is assumed that $M_{1}$ is too far and the system $M_{2}$–$M_{3}$ makes a new “two-body” problem. In the third step of the maneuver, $M_{2}$ is neglected one more time and the system $M_{1}$–$M_{3}$ makes another “two-body” problem. The difference is that the orbit of $M_{3}$ around $M_{1}$ is now different from the one in the first part of the motion. Figure 2 shows the geometry of the close approach,$P_{1}$ with $P_{1}$ and $P_{2}$ the initial and final points of the maneuver, respectively.

Figure 2 also shows the variables used to identify the close approach trajectory: $r_{\mathrm{ap}}$ (the periapsis distance), $\vec {v}_{\infty }^{-}$ (velocities of the spacecraft ($M_{3})$ with respect to $M_{2}$, before and after the maneuver), $\vec {v}_{\infty }^{+}$ (velocity of $M_{3}$ with respect to $M_{1})$, $\delta$ (half of the angle of curvature due to the close approach), $\psi$ (angle of approach) and $\theta$ (true anomaly of the spacecraft around the primary body).

The orbital elements (a = semi-major axis, e = eccentricity), energy (E), angular momentum (C) and velocity of the spacecraft with respect to $M_{1}$ are modified by the passage near $M_{2}$. The values for the orbit before the encounter are given by Eqs. (1)–(4).

$$\begin{aligned} a=\frac{r_a +r_p }{2} \end{aligned}$$

(1)

$$\begin{aligned} e=1-\frac{r_p }{a} \end{aligned}$$

(2)

$$\begin{aligned} E=-\frac{\mu }{2a} \end{aligned}$$

(3)

$$\begin{aligned} C=\sqrt{\mu .a(1-e^2)} \end{aligned}$$

(4)

where $r_{\mathrm{p}}$ is the periapsis of the orbit, $r_{\mathrm{a}}$ is the respective apoapsis and $\mu$ is the gravitational parameter. Two different systems are used (see Table 2) in the present paper: $\alpha$–$\beta$ and $\alpha$–$\gamma$.

Fig. 2

The geometry of the close approach between a spacecraft and $M_{2}$

Table 2 Gravitational parameters of the two systems formed with the triple asteroid

The magnitude of the velocity of the spacecraft with respect to the main body when the approach starts $(v_i)$ obtained using Eq. (5)

$$\begin{aligned} \left| {v_i } \right| =\sqrt{\mu \left( {\frac{2}{r_{\mathrm{sp}} }-\frac{1}{a}}\right) }, \end{aligned}$$

(5)

where $r_{\mathrm{sp}}$ is the $M_{1}-M_{3 }$ distance. The variations of velocity, energy and angular momentum are obtained by Eqs. (6)–(9).

$$\begin{aligned} \Delta v = {\vec v_0} - {\vec v_1} = 2\left| {{{\vec v}_\infty }} \right| \sin \delta \end{aligned}$$

(6)

$$\begin{aligned} \Delta E=E_+ -E_- =-2v_2 v_\infty \sin \delta \sin \psi \end{aligned}$$

(7)

$$\begin{aligned} \Delta C=\frac{\Delta E}{\omega }, \end{aligned}$$

(8)

where

$$\begin{aligned} \delta =\sin ^{-1}\left[ {\frac{1}{1+\frac{r_{\mathrm{ap}\, v_\infty ^{2}} }{\mu }}} \right] \end{aligned}$$

(9)

with $\vec {v}_{2}$ the velocity of $M_{2}$ with respect to $M_{1}$; $\vec {v}_{i}$ the velocities of $M_{3}$ with respect to $M_{1}$, before and after the maneuver in the inertial frame, respectively; $v_\infty$ is the magnitude of the velocity of the spacecraft with respect to $M_{2}$ when the approach starts; $\psi$ is the angle of approach; $\omega$ is the angular velocity of the primaries; $\delta$ is half of the deflection angle and $E_{-}$, $E_{+}$ are the energy before and after the maneuver, respectively. To obtain the semi-major axis and eccentricity of the orbit of the spacecraft after the close approach it is possible to use Eqs. (10) and (11).

$$\begin{aligned} a_o =-\frac{\mu }{2E} \end{aligned}$$

(10)

$$\begin{aligned} e_0 =\sqrt{1-\frac{C^2}{\mu a}} \end{aligned}$$

(11)

In this paper, the average energy variations given by both the approximated model (“patched-conics”) and the more realistic “restricted three-body problem” are obtained.

4 Rendezvous trajectories for the triple system

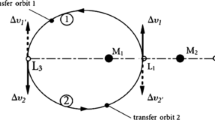
The first step is to calculate an interplanetary mission to encounter the triple system SN2001$_{263}$. The second step is to determine the location of the target body (body 2—point P2). After that, the Lambert problem formulation is used to transfer the spacecraft from the first body (Earth) to the second body (2001SN$_{263})$, as shown in Fig. 3. This maneuver is made using multiple impulses ($\Delta V$) (Santos et al. 2012), which means that a series of Lambert problems are used to connect every two points. Conceptually, the transfer of a satellite with minimum fuel consumption can be defined as: to change the state (position, velocity and mass) of a spacecraft from the initial conditions ($r_{0}$, $v_{0}$ and $M_{0})$, at the time $t_{0}$, to the final conditions ($r_{{f}}$, $v_{{f}}$ and $M_{{f}})$, at the time $t_{{f}}$($t_{{f}} \quad \ge$ $t_{0})$. It is very important to do this task using the lowest possible fuel consumption ($\Delta V = M_{0} - M_{{f}})$.

Fig. 3

Rendezvous maneuvers with four impulses to the triple system 2001SN$_{263}$ showing the solution provided by the genetic algorithm method (axes in normalized units)

In this paper, a genetic algorithm is used to solve this problem, which is a stochastic global search method inspired in the natural genetic and biological evolution. The genetic algorithm operates on a population of potential solutions by applying the principle of survival of the fittest to produce better and better approximations of the optimal solutions (Santos et al. 2012; Santos and Formiga 2014). The best parameters for the solutions searched here constitute of a population that comprises 800 individuals and up to 200 generations, but several situations were made with different population sizes and quantities in the objective function. The population number was adjusted and it was verified which values provided the best results. The final maneuver divides the four impulses in the way shown in Fig. 3.

5 The restricted three-body problem

The dimensionless canonical system of units is used (Szebehely 1967). It means that the mass of the smaller asteroid is $\upmu = M_{2}/(M_{1}+M_{2})$, where $M_{1}$ and $M_{2}$ are the real masses of $M_{1}$ and $M_{2}$, respectively. The mass of $M_{1}$ is ($1-\upmu )$, so the total mass of the system is one. The unit of distances is the $M_{1}-M_{2 }$ distance. The mean angular velocity of the motion of the primaries is one. The equations of motion are (Szebehely 1967):

$$\begin{aligned} \begin{aligned}&\ddot{x} - 2\dot{y} = x - \frac{{\partial V}}{{\partial x}} = \frac{{\partial \Omega }}{{\partial x}}\\&\ddot{y} - 2\dot{x} = y - \frac{{\partial V}}{{\partial y}} = \frac{{\partial \Omega }}{{\partial y}} \end{aligned} \end{aligned}$$

(12)

where

$$\begin{aligned} \mathrm{{\Omega }} = \frac{1}{2}\left( {{{\dot{x}}^2} + {{\dot{y}}^2}} \right) + \frac{{\left( {1 - \mu } \right) }}{{{r_1}}} + \frac{\mu }{{{r_2}}} \end{aligned}$$

with $r_{1}$ is the $M_{3}-M_{1}$ distance and $r_{2}$ the $M_{3}-M_{2 }$ distance. The energy and angular momentum are obtained from Eqs. (13) and (14).

$$\begin{aligned} E = \frac{{{{\left( {x + \dot{y}} \right) }^2} + {{\left( {\dot{x} - y} \right) }^2}}}{2} - \frac{{\left( {1 - \mu } \right) }}{{{r_1}}} + \frac{\mu }{{{r_2}}} \end{aligned}$$

(13)

$$\begin{aligned} C = {x^2} + {y^2} + x\dot{y} - y\dot{x}, \end{aligned}$$

(14)

where x and y are the coordinates of the spacecraft in the rotating system; E is the energy and C is the angular momentum.

Fig. 4

Tisserand’s parameter considering several distances of close approach and $\Psi =180^{\circ }$ a $r_{\mathrm{ap}}=1.5 R_{\gamma }$, b $r_{\mathrm{ap}}=2 R_{\gamma }$

6 Using the Tisserand’s criterion

The close approach can strongly modify the trajectory of the particle. The Tisserand’s criterion is a method that can be used to identify those news trajectories and it was created by Francois Felix Tisserand. It is expressed as an equation that must be obeyed by the orbital elements before and after the passage. It was used in several references to validate their results (Kresák 1954; Radzievskii and Tomanov 1986). This criterion says that two particles are probably the same if they satisfy Eq. (15).

$$\begin{aligned} \frac{1}{{\bar{{a}}}_{{i}} }+2\sqrt{{\bar{{a}}}_{{i}} ( {1-{e}_{{i}} ^2})} \cos {i}_{{i}} \approx \frac{1}{{\bar{{a}}}_{\mathrm{o}} }+2\sqrt{{\bar{{a}}}_{{o}} ( {1-{e}_0 ^2})} \cos { i}_0, \end{aligned}$$

(15)

where the particle has orbital elements ${\bar{{a}}}_{{i}}$, e$_{{i}}$ and i$_{{i}}$ before the maneuver and ${\bar{{a}}}_{{o}}$, e$_{{o}}$ and i$_{{o}}$ after that. Figure 4 shows the Tisserand’s parameter before and after the close approach for both models: the “Patched-Conics” (PC) and the “Restricted Three-Body Problem” (3PB). Several close approach distances with the body $\gamma$ were used, as well as two values for the periapsis distance: $r_{\mathrm{ap}} = 1.5 R_{\upgamma }$ and $r_{\mathrm{ap}} = 2.0 R_{\upgamma }$. This study was made for several ranges for the angle of approach $\Psi$ and periapsis distance. Figure 4 shows only the case $\Psi =180{^{\circ }}$, using 2550 simulations, as an example. Other values have similar results. Figure 4 shows that the results follow the Tisserand’s criterion, because the values before and after the close approach are very similar for both dynamics, which means that the models are working correctly. These coefficients were calculated before and after the maneuver by the PC and the 3PB models, considering several values of $V_{\infty }$, the velocity of approach of M3 with respect to M2, before the maneuver.

7 Numerical study of the energy variation

A numerical comparison is now performed using both models: “Patched-Conics” (PC) and the “Restricted Three-Body Problem” (3PB) to know the differences between them in this particular system. Near 450,000 simulations were made for each $r_{\mathrm{ap}}$ (periapsis distance). Different values for the velocity and angle of approach were used.

The results are shown in Table 3 for $r_{\mathrm{ap}} = 1.2R_\upgamma$ (radius of $\gamma$), where $\vert \Delta Em\vert =\vert \Delta Em\mathrm{PC}-\Delta Em3c\vert$; $\Delta Em3c$ is the result given by the restricted three-body problem, $\Delta Em\mathrm{PC}$ is the result given by the “patched conics approach”, $\Delta Em$ is the mean variation between the models; Cji and Cjf are the initial and final Jacobian constants, respectively; Vi and Vj are the initial and final velocities, both in the canonical units.

Table 3 Numerical results of energy variation between the two models

Figures 5 and 6 present the differences of energy between the two models, $\Delta Em$, as a function of the velocity and angle of approach. The mass ratio for both systems are: $\alpha$–$\gamma$ = 0.0105366 and $\alpha$–$\beta$ = 0.0255335. The initial conditions were divided in seven intervals for the angle of approach and ten intervals for the velocity of approach. Table 4 shows this division.

Figure 5 shows the results for the $\alpha$–$\gamma$ system and Fig. 6 for the $\alpha$–$\beta$ system. The differences in the variations of energy decreases with the increase of the velocity of approach. The difference in the variations of energy is about 4 % in the first velocity range, decreasing after that.

Some aspects that can be noted from the results are shown below.

• 1. $\Delta Em$ (mean variation between the models) range is very different, depending on the initial conditions. This fact indicates that more detailed studies must be done for each specific system of primaries to know the regions of initial conditions where it is more adequate to use the “Patched Conics” model;

• 2. $\Delta Em$ values decreases with the evolution of the periapsis distance, because when the spacecraft passes far from the secondary body the details of the better dynamics (restricted three-body problem) have little effects in the results;

• 3. $\Delta Em$ values are larger for maneuvers close to the maximum variation of energy ($\Psi = 270{^{\circ }})$, in particular when compared to the case of zero variation of energy ($\Psi = 180{^{\circ }})$. This is expected, because the difference in the variation of energy is nearly proportional to the effects of the maneuver.

• 4. $\Delta Em$ values are low when there are increases in the approach velocity. This information is important when a spacecraft needs to approach a planet, but do not want to modify its energy.

A summary of the results are shown in Table 5, which displays the absolute numbers in canonical units. In general, it is possible to say that the “Patched-Conics” is a good approximation for a first study, but for some initial conditions, $\Delta Em$ can increase and the use of the “Restricted Three-Body Problem” can be important.

Fig. 5

Variation of energy as a function of the velocity of approach for the $\alpha$–$\gamma$ system considering a periapsis distance of twice the radius of $\gamma$

Fig. 6

Variation of energy as a function of the velocity of approach for the $\alpha$–$\beta$ system considering a periapsis distance of twice the radius of $\beta$

Table 4 Velocity range (x-axis)

Table 5 Overall average differences of $\Delta Em$ (canonical units)

8 Conclusions

In the present paper, a numerical procedure was developed to measure the energy gains of a close approach between a spacecraft and both smaller bodies of the triple asteroid system 2001SN$_{263}$. The average difference is measured between two models: the “Patched Conics” approximated model and the more realistic “Restricted Three-Body Problem”. Several simulations were performed to evaluate those effects, in order to estimate the accuracy of the “Patched Conics” model. Several velocities and angles of approach ranges were used. The results have shown the possible energy gains and that the accuracy of the approximated method improves when the periapsis distance increases, since the effects of the close approaches are smaller. In the regions closer to the body, where practical applications are more interesting, with the periapsis distance less than four times the radius of the secondary body, the overall average differences of $\Delta Em$ does not exceed 1 %. It means that the approximated method is good enough for a first estimate and the methodology presented here to evaluate those effects is useful. The results have also shown that the “Patched-Conics” approach gives better estimates in regions of low energy variations, as when higher velocities of approach and/or large periapsis distances are involved. The research performed here indicates where numerical integrations are required for a better accuracy.