Optimal chemotherapy schedules from tumor entropy

Abstract

We propose a model for the dynamics of an heterogeneous tumor, which consists of sensitive and resistant cells. The model is analyzed and validated using a cellular automaton whose local rules are classic and widely accepted in Biology. We then extend the model to a tumor under therapy. We consider Shannon’s entropy for the tumor and analyze the problem of minimizing this entropy. From this minimization problem, we find viable therapies that maintain at low level the entropy of the tumor. These therapies could provide a valuable tool for designing protocols for disease control, maintaining a very low growth level, while the tumor remains composed mainly of sensitive cells.

1 Introduction

Cancer is one of the leading causes of death worldwide. At present, around 9 million people die from cancer each year and experts expect that number to rise to 11.4 million by the year 2030. Cancer is not just one disease but rather a generic term for a large class of diseases. These diseases are distinguished by an abnormal and autonomous cellular growth. Such cells grow to form a conglomerate called tumor. The main purpose of traditional therapies, such as chemotherapy, is the elimination of the largest possible number of malignant cells, with the implicit intention of the eradicating (curing) the tumor, even when such an outcome, based on extensive clinical experience, is highly improbable. This approach has serious side effects on patients and also it stimulates the development of resistant subpopulations (Boondirex et al. 2006; Gatenby and Gillies 2009; Norton and Simon 1977).

Mathematical modeling of cancer dynamics can contribute not only to the rational design of optimal treatment protocols involving combinations of surgery, chemotherapy and radiotherapy, but also to the development of new therapies, to better prognoses for patients and to more effective treatment plans.

Since 1954, many mathematical and computational models have been developed for studying the growth of tumors and other models pay tribute to the importance of leukemia research (leukemia is a type of cancer of the blood or bone marrow which does not form solid tumors) (Afenya and Calderón 1995; Clarkson 1972; Djulbegovic and Svetina 1985; Franziska et al. 2005; Moore and Li 2004; Noble et al. 2010; Todorov et al. 2012). Different models are used for boarding different questions such as modeling avascular and vascular tumor growth (Barrea and Hernández 2012a, b; Bonate and Howard 2011; Clarkson 1972; D’Onofrio et al. 2009; Gatenby and Gillies 2009) (either free or under the effect of a therapy), mechanical iterations between cells (D’Antonio et al. 2012; Kansal et al. 2000; Qi et al. 1993), dynamics and morphology of tissue invasion by cancer cells (Andasari et al. 2011; D’Antonio et al. 2012; Jiao and Torquato 2012; Tracqui 1995), angiogenesis dynamics (Barrea and Hernández 2013; D’Onofrio et al. 2009; Roose et al. 2007), competition between the immune system and tumor cells (Djulbegovic and Svetina 1985; Patanarapeelert et al. 2000), reaction and intra-cellular diffusion phenomena (Tracqui 1995). There are models which use either cellular automaton or agent-based modeling (Boondirex et al. 2006; D’Antonio et al. 2012; Jiao and Torquato 2012; Kansal et al. 2000; Patanarapeelert et al. 2000; Qi et al. 1993; Reis et al. 2009; Smolle 1998; Tracqui 1995; Wolfram 1984). Other models use ordinary or partial differential equations to study the tumor dynamics (Andasari et al. 2011; Byrne 2012; Cornelis et al. 2013; Liu et al. 2013; O’Neill et al. 2010; Roose et al. 2007; Wise et al. 2008). Some discrete models also exist (Gatenby and Gillies 2009).

At the present, a widely accepted model is the so-called Gompertz model, which was proposed by the English mathematician Benjamin Gompertz in 1825 (Mueller et al. 1995). Gompertz worked on modeling the dynamics of certain growth processes and his model was found to be a valuable tool for scientists in many disciplines. In 1964, Laird (1965) showed that unperturbed tumor growth in a test tube followed a Gompertzian kinetics, very similar to the profiles produced by the sigmoid $E_{\max }$ model which is quite familiar to most pharmacokineticists (Bonate and Howard 2011). Since then, many interdisciplinary studies have validated the Gompertzian models and were used to optimize chemotherapy and limit the development of resistance cells (Barrea and Hernández 2012a, b, 2013; Bonate and Howard 2011; D’Onofrio et al. 2009; Gatenby and Gillies 2009; Gonzalez and Rondón 2006; Gonzales et al. 2003; McCall and Petrovski 1999; Martin and Teo 1994; Norton 1988; Yamano 2009). Needless to say, since more than one hundred different diseases fall under the label of “cancer”, it would not be reasonable to expect that a single mathematical model could simulate well the dynamics of all the tumors that can beset different parts of the human body. Nevertheless, clinical studies have proved that eight out of ten tumors have a Gompertzian growth (Martin and Teo 1994).

Current therapies are mainly aimed at eradicating the tumor, but they all have severe negative consequences. For instance, therapy frequently fails due to the emergence of resistant populations. This occurs because the tumor is formed by sensitive and resistant cells and the sensitive cells proliferate at the expense of the resistant ones. Then, even if therapy is able to remove all of the sensitive cells, the resistant population can freely proliferate due to the lack of competition. We are interested in finding therapies that maintain under control the population of sensitive cells.

The organization of this article is as follows: in Sect. 2, the Gompertz model is generalized to model the interaction of two populations, sensitive and resistant, in a competitive setting. In Sect. 2.1, we present the competition model and analyze the attractors and equilibrium points. In Sect. 2.2, this model is validated by comparing simulations generated by a universal cellular automaton with clinical results. As a result, the Gompertzian growth is interpreted as a normally distributed stochastic process. Finally, in Sect. 2.3, a model for the dynamics of a tumor subject to multi-drug chemotherapy is presented. Section 3 is devoted to formulate the chemotherapy optimization problem. In Sect. 4, an optimization problem is proposed by assigning Shannon’s entropy to the tumor. The solution of this optimization problem provides protocols which maintain tumor entropy under control. These protocols, which assure that the disease does not progress, are subject to certain clinical restrictions such as maximum instantaneous dose, maximum cumulative dose, maximum size of the tumor, toxic side effects. Finally, Sect. 5 is devoted to the conclusions and possible further research.

Fig. 1

Typical graph of a Gompertz’s function

2 The model

In the sequel, we shall consider tumors constituted by heterogeneous lineages of cancer cells, having different sensitivities to therapy. Next, we formulate a competitive model for the dynamics of an heterogeneous tumor.

2.1 Competitive Gompertzian model

As noted in the introduction, Gompertz’s equation can be used to model the dynamics of a large variety of tumors (see Fig. 1). This model has the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm{d}N}{\mathrm{d}t}=\lambda N\ln \left( \frac{N_\infty }{N}\right) ,\\ N(0)=N_0, \end{array}\right. } \end{aligned}$$

(1)

where $N(t)\ge 0$ is the average quantity of tumor cells at time t,  $N_\infty$ denotes the carrying capacity of the tumor and $\lambda$ is a growth parameter. Note that $\lim _{t\rightarrow \infty }N(t)=N_\infty$ (in fact the analytic solution of (1) is $N(t)=N_\infty \mathrm{e}^{-d\mathrm{e}^{-\lambda t}}$, where $d=-\ln (N_0/N_\infty )).$

However, as a result of the large microenvironment’s heterogeneity in space and time, the tumor is usually composed of two main subpopulations of cells (Gatenby and Gillies 2009; Norton and Simon 1977): a population $N_\mathrm{s},$ sensitive to the therapy and a resistant one, $N_\mathrm{r}.$ Resistant cells are typically present in small numbers because they are less fit than the sensitive cells. Sensitive cells have a higher rate of replication, which results in competitive effects that cannot be accounted by model (1). As traditional therapies have as their main purpose the elimination of the largest possible quantity of malignant cells (which are mainly sensitive), the resistant population can proliferate freely because it does not have to compete with any fitter population, and therefore the therapies fail. Hence, if we wish to find therapies that are sustainable over time, competition between the populations $N_\mathrm{s}$ and $N_\mathrm{r}$ must be taken into account.

We assume that there is no Lotka–Volterra competition between sensitive and resistant populations (Simmons and Krantz 1972), and assume instead, interference competition. This means that the mere presence of one population affects the other one. Thus, for instance, the presence of one population makes it less likely for the other to access the available resources. We propose the following competition model:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm{d}N_\mathrm{s}}{\mathrm{d}t}=L_1N_\mathrm{s}\ln \left( \frac{N_{\infty }}{N_\mathrm{s}+\alpha N_\mathrm{r}}\right) ,\\ \frac{\mathrm{d}N_\mathrm{r}}{\mathrm{d}t}=L_2N_\mathrm{r}\ln \left( \frac{N_{\infty }}{\beta N_\mathrm{s}+N_\mathrm{r}}\right) ,\\ N_\mathrm{s}(0)=N_{\mathrm{s}_0},\\ N_\mathrm{r}(0)=N_{\mathrm{r}_0,} \end{array}\right. } \end{aligned}$$

(2)

where $N_\infty$ is the carrying capacity of the tumor, $L_1$ and $L_2$ are positive growth parameters and the parameters $\alpha > 0$ and $\beta > 0$ quantify the competition between $N_\mathrm{s}$ and $N_\mathrm{r}$. The remainder of the subsection is devoted to find the equilibrium points of system (2).

2.1.1 Equilibrium points of system (2)

We begin by defining the set $E_0\doteq \{(0,0),(0,N_\infty ),(N_\infty ,0)\}$ whose elements are clearly equilibrium points for all parameters $\alpha ,\beta >0$. It is easy to prove that these points are attractors.

Now, we will consider two cases: (A) $\alpha \beta =1$ and (B) $\alpha \beta \ne 1.$

(A) Suppose $\alpha \beta =1.$ In this case, there are no other equilibrium points than those in $E_0,$ except when $\alpha =\beta =1,$ in which case all elements in the set $E_2\doteq \{(x^*,y^*)\in {\mathbb {R}}^{2}_{\ge 0}:x^*+y^*=N_\infty \}$ are also equilibrium points. We shall prove that all points of $E_2$ are also attractors. For that, let $x\doteq N_\mathrm{s}, y\doteq N_\mathrm{r}$ and define $F(x,y)\doteq L_1x\ln \left( \frac{N_\infty }{x+y}\right) ,$ $G(x,y)\doteq L_2y\ln \left( \frac{N_\infty }{x+y}\right) .$ Then, the Jacobian matrix of system (2) is

$$\begin{aligned} J(x,y)=\left[ \begin{array}{cc} F_x(x,y) &{}\quad F_y(x,y) \\ G_x(x,y) &{}\quad G_y(x,y) \end{array}\right] , \end{aligned}$$

where $F_x=L_1\ln \left( \frac{N_\infty }{x+y}\right) -\frac{L_1x}{(x+y)},$ $F_y=\frac{-L_1x}{x+y},$ $G_x=\frac{-L_2y}{x+y}$ and $G_y=L_2\ln \left( \frac{N_\infty }{x+y}\right) -\frac{L_2y}{(x+y)}.$ Thus, for any $(x^*,y^*)\in E_2$, it follows that

$$\begin{aligned} \hbox {det}(J(x^*,y^*)-\lambda I)= & {} \left( \frac{-L_1x^*}{N_\infty }- \lambda \right) \left( \frac{-L_2(N_\infty -x^*)}{N_\infty }-\lambda \right) \\&-\frac{L_1L_2x^*}{N^2_{\infty }}(N_\infty -x^*) \\= & {} \left[ \left( \frac{L_1x^*}{N_\infty }+\frac{L_2(N_\infty -x^*)}{N_\infty }\right) +\lambda \right] \lambda . \end{aligned}$$

Hence, the eigenvalues of J are $\lambda _1=0$ and $\lambda _2=\frac{-1}{N_\infty }[L_1x^*+L_2(N_\infty -x^*)].$ Since $|\lambda _2|>|\lambda _1|$ and $Re(\lambda _2)<0$, the equilibrium points are in fact attractors.

(B) Suppose now $\alpha \beta \ne 1.$ Then, it is easy to prove that:

• If $\alpha =1$ or $\beta =1$, the set of equilibrium points is $E_0.$

• If $\alpha \ne 1$ and $\beta \ne 1$, the set of equilibrium point is $E_0\bigcup \left\{ N_\infty \left( \tfrac{\alpha -1}{\alpha \beta -1},\tfrac{\beta -1}{\alpha \beta -1}\right) \right\}$ with $(\alpha ,\beta )\in (0,1)^2\bigcup (1,\infty )^2$ and all equilibrium points are also attractors.

2.2 Validation of models (1) and (2)

This subsection is devoted to validate models (1) and (2). There is a large number of cellular automaton for studying different aspects of tumoral growth (Patanarapeelert et al. 2000; Qi et al. 1993; Reis et al. 2009; Smolle 1998; Tracqui 1995). Although some of the local rules used by those cellular automaton do not have solid biological support, if one is interested in modeling tumoral growth, a few widely known characteristics and rules of the tumoral cells can be used. Among those rules, we mention:

• Tumor growth is restricted by the tissue carrying capacity. This restriction may arise from limitations of nutrients that are available for the proliferation of cancer cells, from increasing accumulation of waste products which causes a decrease in the cancer cell proliferation rate or from the effects of mechanical confinement pressure. There is strong experimental evidence that the proportion of resting cells increases as the growth of the tumor progresses (Gonzalez and Rondón 2006). Resting cells are those which never undergo division.

• Since tumor cells evade the normal chemical signals producing apoptosis, they do not kill themselves and therefore we shall think of them as living indefinitely. Although these cells may die due to necrosis, our automaton does not include necrosis dynamics. This is so because the dynamics of the necrotic core is extremely complex and yet to be well understood.

• Tumor cells do not obey chemical signals and under suitable conditions they divide indefinitely.

In our model, tumor cells move on the (x, y) plane over an $n\times n$ lattice ${\mathfrak {L}}.$ Also, each cell will be in one and only one of the following states: (i) $A_\mathrm{S}$: Active-Sensitive, (ii) $A_\mathrm{R}$: Active-Resistant, (iii) $R_\mathrm{S}$: Resting-Sensitive and (iv) $R_\mathrm{R}$: Resting-Resistant. We shall use a Moore neighborhood with radius equal to one.

The local rules are:

LR1::

Active cells, of $A_\mathrm{S}$ or $A_\mathrm{R}$ type are checked for division attempt. Division happens with probabilities:

$$\begin{aligned} P_\mathrm{S}(t)=r_\mathrm{S}\left( 1-\frac{W(t)}{N_\infty }\right) \end{aligned}$$

(3)

and

$$\begin{aligned} P_\mathrm{R}(t)=r_\mathrm{R}\left( 1-\frac{W(t)}{N_\infty }\right) , \end{aligned}$$

(4)

where W(t) is the number of tumor cells at time t according to the cellular automaton, $N_\infty$ is as in models (1) and (2) and $r_\mathrm{S}$ and $r_\mathrm{R}$ are parameters quantifying the proliferative activity of the sensitive and resistant populations, respectively. If a cell divides, the new cell occupies any of the empty sites in its neighborhood with identical probability. If a cell divides but it cannot find an empty space, then it turns into a resting cell.

LR2::

An $A_\mathrm{S}$-type cell can mutate into an $A_\mathrm{R}$-type cell with a given probability $p_\mathrm{m}$.

LR3::

If an active cell is surrounded by eight cells, then it is transformed into a resting cell.

LR4::

A resting cell is transformed into an active cell if it is surrounded by $N_{\max }<8$ cells.

Figure 2 depicts a simulated tumor growth and experimental data taken from Laird (1965). The parameters used here were $r_\mathrm{S}=0.28,$ $r_\mathrm{R}=0.12$ and $N_\infty =1275\times 10^6$.

Fig. 2

Three simulations of the cellular automaton (solid). Experimental data (circle) for mouse El$_4$ tumor at high dose (Laird 1965)

2.2.1 Validating model (1)

In this case, we suppose that the tumor is homogeneous, therefore $p_\mathrm{m}=0$ and the number of resistant cells, $W_\mathrm{R}(t)$, is zero for all t. Then, the number of sensitive cells, $W_\mathrm{S}(t),$ is equal to W(t) for all t. From (1), it follows that

$$\begin{aligned} \ln (\ln N(t)-\ln N(t-1))=\ln (d(\mathrm{e}^{\lambda }-1))-\lambda t, \end{aligned}$$

(5)

where $d=-\ln \left( \tfrac{N_0}{N_\infty }\right)$. In light of Eq. (5), it is reasonable to think that Gompertz’s model provides a good fitting if the graph of $\ln (\ln \langle W(t)\rangle -\ln \langle W(t-1)\rangle )$ obtained from the data appears to follow a straight line. If this is the case, then knowing $\langle W(0)\rangle$ one can estimate $\lambda$ and d (and therefore $N_\infty$) form (5). A simulation of the cellular automaton was run with $\langle W(0)\rangle =1$ and parameters $r_\mathrm{S}=0.85$, $r_\mathrm{R}=0.3,$ $p_\mathrm{m}=10^{-3}$ and $N_{\infty }=600$. Then, only the first 54 observations were considered for estimating d and $\lambda$ via least squares (see Fig. 3). We obtained $d= 6.4026$ (and therefore $N_\infty =N_0\mathrm{e}^d=603.4119$). Figure 3b shows the cellular automaton simulations (circle) and the resulting Gompertz’s model solution (solid line).

Fig. 3

a Realizations of $\ln (\ln \langle W(t)\rangle -\ln \langle W(t-1)\rangle )$ (circles) and regression line (solid). b Simulation result with the cellular automaton (circles) and the tumor growth according to the model (1) with parameters $d=6.4026,$ $N_\infty =603.4119$ and $\lambda =0.0846$ (solid)

Fig. 4

Plots of the distributions of W(t) with $10^4$ realizations (red) and Gaussian densities $N(N_\infty p_t,4N_\infty p_t(1-p_t))$ (blue) at times $t=10$ (a); $t=17$ (b); $t=22$ (c) and $t=34$ (d) (color figure online)

Remark 1

It is quite interesting to note that in the context of cellular automaton realizations, for any time t,  the variable W(t) has approximately a normal distribution with mean $\langle W(t)\rangle =N_\infty p_t$ and standard deviation $\sigma (t)=2\sqrt{N_\infty p_t(1-p_t)},$ where $p_t=\mathrm{e}^{-d\mathrm{e}^{-\lambda t}}$ (see Fig. 4). Consequently, we interpret model (1) in the following way: tumoral growth is a stochastic process W(t) which at time t has approximately a normal distribution with mean $\langle W(t)\rangle =N_\infty p_t=N(t)$ and standard deviation $\sigma (t)=2\sqrt{N_\infty p_t(1-p_t)}.$ Since $\lim _{t\rightarrow \infty }p_t=1$ it follows that $\lim _{t\rightarrow \infty }\sigma (t)=0$ and $\lim _{t\rightarrow \infty }\langle W(t)\rangle =N_\infty .$

Fig. 5

Number of cells obtained from model (2) and from the cellular automaton

2.2.2 Validating model (2)

Consider now an heterogeneous tumor, composed of two different cell lineages: one subpopulation is sensitive and the other is resistant to therapy. We assume that sensitive cells are transformed into resistant cells via random mutations. These mutations are quantified by the probability $p_\mathrm{m}$ mentioned in the local rule LR2 of the cellular automaton.

Next, we present a general procedure for estimating the parameters used in model (2) from data provided by the cellular automaton.

Parameter estimation Let $\varvec{N}:[0,\infty )\times {\mathbb {R}}_+^7\longrightarrow {\mathbb {R}}^{2}$ be defined by $\varvec{N}(t;x_1,\ldots ,x_7)=(N_\mathrm{s}(t;x_1,\ldots ,x_7),N_\mathrm{r}(t;x_1,\ldots ,x_7)),$ where $N_\mathrm{s}(\cdot )$ and $N_\mathrm{r}(\cdot )$ are the solutions of (2) with $x_1\doteq N_\mathrm{r}(0),$ $x_2\doteq N_\mathrm{s}(0),$ $x_3\doteq L_1,$ $x_4\doteq L_2,$ $x_5\doteq \alpha ,$ $x_6\doteq \beta$ and $x_7\doteq N_\infty .$ Let $\tilde{\varvec{N}}(\vec {x}):{\mathbb {R}}_+^7\longrightarrow {\mathbb {R}}^{180}$ be defined by $[\tilde{\varvec{N}}(\vec {x})]_i\doteq N_\mathrm{s}(i-1;\vec {x})+N_\mathrm{r}(i-1;\vec {x}),i=1,\ldots ,180$, where $\vec {x}\doteq (x_1,\ldots ,x_7)$. The parameters used in model (2) are then estimated by the components of the vector $\vec {x}^{*}\in {\mathbb {R}}^7$ solving

$$\begin{aligned} \vec {x}^*= \underset{\vec {x}\in {\mathbb {R}}^{7}_{+}}{\text {argmin}} \Vert \tilde{\varvec{N}}(\vec {x})-\tilde{W}\Vert ^2, \end{aligned}$$

(6)

where $\tilde{W}\doteq (W(0),\dots ,W(T))$, with W(t) being the number of cells at time t obtained by the cellular automaton realization and $\Vert \cdot \Vert$ is the Euclidean norm in ${\mathbb {R}}^T={\mathbb {R}}^{180}$.

In our case, solving problem (6) resulted in $x_1^*=42.8367,$ $x_2^*=110.4854$ and the parameters $x_3^*=0.0834,$ $x_4^*=0.0345,$ $x_5^*=1.000,$ $x_6^*=0.9881$ and $x_7^*=601.2633.$

Figure 5 shows the total number of tumor cells which are obtained both with the cellular automaton and the continuous model (2) with parameters estimated from the automaton realizations, as above. For the cellular automaton realizations, we used $N_\infty =600,$ $r_\mathrm{S}=0.85,$ $r_\mathrm{R}=0.45,$ $p_\mathrm{m}=10^{-3}$ and $P_\mathrm{S}(t)$ and $P_\mathrm{R}(t)$ as given in (3) and (4). Also we took $W(0)=130,$ $W_\mathrm{r}(0)=10$ and terminal time $T=180.$ From the continuous models, we have $N(T)=603.3473,$ $N_\mathrm{s}(T)=575.5221$ and $N_\mathrm{r}(T)=27.8252,$ while for cellular automaton $W(T)=601, W_\mathrm{s}(T)=575$ and $W_\mathrm{r}(T)=26.$ Summing up, we have considered Gompertz’s model (1) to describe the growth of an homogeneous tumor. Model (2) was formulated for modeling the competition between two subpopulations of an heterogeneous tumor, one subpopulation being sensitive to therapy whereas the other one is resistant. A cellular automaton was then built for validating models (1) and (2). Numerical results show that by appropriately estimating the parameters, a Gompertzian model can adequately describe the growth of an homogeneous tumor while the modified Gompertzian model (2) can successfully describe the dynamics of a tumor with two competing subpopulation of cells. We also showed that the Gompertzian tumor growth can be seen as a stochastic process, W(t) with mean $N_\infty p_t$ and standard deviation $2\sqrt{N_\infty p_t(1-p_t)},$ where $N_\infty$ is carrying capacity of the tumor and $p_t=\mathrm{e}^{-d\mathrm{e}^{\lambda t}}.$

In the next subsection, we shall build an appropriate mathematical framework for the dynamics of an heterogeneous tumor under multi-drug therapy. The model takes into account the exponential decay of drug concentrations in the body, a phenomenon that is well documented by Pharmacokinetic and Pharmacodynamic studies (Bonate and Howard 2011).

2.3 Modeling the dynamics of an heterogeneous tumor under chemotherapy

Chemotherapy is a cancer treatment based on the administration of drugs. A chemotherapy treatment is given in cycles and the length of the treatment (i.e. the number of cycles) depends on a variety of factors. A cycle consists of a chemotherapy treatment period in which the patient is supplied with n doses of drugs at prescribed times $t_1,\ldots ,t_n$ (called the protocol) followed by a rest period for allowing the body and blood counts to recover before the next cycle. Drugs may be administered all on a single day, during several consecutive days or continuously. A treatment period could last minutes, hours, or days, depending on the specific protocol. The rest period may be of a week, two weeks or a month. Finally, the number of cycles is mainly determined by the evolution of the disease, which in turn depends on several factors.

In the case of multi-drug treatments, each dose is a cocktail of d drugs with concentrations levels $C_{ij}$, $i=1,2,\ldots ,n$, $j=1,2,\ldots ,d$, in the plasma blood. Let us denote by C the matrix $(C_{ij}).$

There are several models to describe the tumor’s response to treatment, but one of the most widely used is the Gompertz growth model with linear cell-loss effect (Barrea and Hernández 2012a, b; Boondirex et al. 2006; Patanarapeelert et al. 2000), given by

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm{d}N}{\mathrm{d}t}=N\left[ \lambda \ln \left( \frac{N_\infty }{N}\right) -\alpha (C,t)\right] ,\\ N(0)=N_0, \end{array}\right. } \end{aligned}$$

(7)

where the time t is measured in days, $\alpha (C,t)=\sum _{j=1}^{d}\sum _{i=1}^{c}\kappa _jC_{ij}\mathrm{e}^{-\mu _j\Delta _it}$, $\kappa _j$ is a parameter measuring the effectiveness of drug j, $\mu _j$ represents the decay of drug j in the body ($\mu _j=-\ln (1/2)/\tau _j,$ where $\tau _j$ is the half-life of the drug j in the plasma), $c=c(t)$ is the only non-negative integer such that $t\in [t_c,t_{c+1})$ if $t<t_n$ and $c=n$ if $t\ge t_n$, and $\Delta _it=t-t_i$.

For an heterogeneous tumor under therapy, we propose the following model:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\mathrm{d}N_\mathrm{s}}{\mathrm{d}t}=L_1N_\mathrm{s} \left[ \ln \left( \frac{N_{\infty }}{N_\mathrm{s}+ \alpha N_\mathrm{r}}\right) -\alpha _\mathrm{s}(C,t)\right] ,\\ \frac{\mathrm{d}N_\mathrm{r}}{\mathrm{d}t}=L_2N_\mathrm{r} \left[ \ln \left( \frac{N_{\infty }}{\beta N_\mathrm{s} +N_\mathrm{r}}\right) -\alpha _\mathrm{r}(C,t)\right] ,\\ N_\mathrm{s}(0)=N_{s_0},\\ N_\mathrm{r}(0)=N_{r_0.} \end{array}\right. } \end{aligned}$$

(8)

The functions $\alpha _\mathrm{s}$ and $\alpha _\mathrm{r}$ are defined similarly as the function $\alpha$ above. These functions involve different parameters corresponding to each one of both subpopulations.

In what follows $N=N(t,C)$ shall always denote the total number of tumor cells. i.e. either the solution of (7) or $N(\cdot )=N_\mathrm{s}(\cdot )+N_\mathrm{r}(\cdot )$, when referring to model (8).

Although restrictions for chemotherapy treatment vary from drug to drug as well as with the type of cancer, they all have the following general form:

$(R_1)$ Maximum instantaneous dose: there is a non- negative number $C^{\max }_j$, $1\le j\le d$, such that

$$\begin{aligned} C^{\max }_j-C_{ij}\ge 0,\quad \forall i=1,2,\ldots ,n,\ \forall j=1,2,\ldots ,d. \end{aligned}$$

$(R_2)$ Maximum cumulative dose: there is a non-negative number $C^{\mathrm{{cum}}}_j$, $1\le j\le d$, such that

$$\begin{aligned} C^{\mathrm{{cum}}}_j-\sum _{i=1}^n C_{ij}\ge 0,\quad \forall j=1,2,\ldots ,d. \end{aligned}$$

$(R_3)$ Maximum tumor size: there is a non-negative number $N_{\max }$ such that

$$\begin{aligned} N_{\max }-N(t_{i},C)\ge 0,\quad \forall i=1,2,\ldots ,n. \end{aligned}$$

$(R_4)$ Toxic side effects: there exist $K\in \mathbb {N}$ and non-negative numbers $C^{sc}_k$ and $\eta _{kj}$, for $k=1,\ldots ,K$ and $j=1,\ldots ,d$, such that

$$\begin{aligned} C^{sc}_k-\sum _{j=1}^d\eta _{kj}C_{ij}\ge 0,\quad \forall \, i=1,2,\ldots ,n,\ \forall \, k=1,2,\ldots ,K. \end{aligned}$$

Here, the factors $\eta _{kj}$ quantify the risk of damage on the organ or tissue k by the drug j.

We denote by $\Omega$ the set of all real $n\times d$ matrices C satisfying restrictions $R_1$–$R_4$. In the sequel, for simplicity of notation, we will suppress the dependency on C and denote N(t, C) simply by N(t).

3 Chemotherapy optimization problem

As previously mentioned, since traditional cancer chemotherapies seek to eradicate the disease, the therapies often fail because they remove most of the sensitive cells, leaving a tumor composed mainly of resistant cells. The current paradigm is radically different and researchers now seek therapies suitable for controlling the disease, which does not mean to eradicate the tumor but rather to avoid its growth. In light of this paradigm, we start building a theoretical framework that will lead us to the formulation of a new optimization problem. To begin with, once the disease is detected, it is desirable that the tumor does not increase its size. Therefore, if at time $t_0$ (the beginning of a cycle) the initial number of cancer cells is $N(t_0)=N_0,$ controlling the disease means complying with the restriction

$$\begin{aligned} N(t)\le N_0,\quad \forall t\in [t_0,T], \end{aligned}$$

(9)

where $T-t_0$ is the length of the cycle plus the respective rest period, when chemotherapy is not administered.

Consider now an heterogeneous tumor constituted by L different subpopulations with different sensitivities to the drugs. We denote $N_\ell (t)$, $\ell =1,\ldots ,L$, the number of cells in each subpopulation at time t. Thus, if N(t) is the total number of tumoral cells at time t, then $N(t)=\sum _{\ell =1}^{L}N_\ell (t)$. The Shannon’s entropy of the tumor is defined as: $S(t)\doteq -\sum _{\ell =1}^L p_\ell (t)\ln (p_\ell (t))$, where $p_\ell (t)\doteq \frac{N_\ell (t)}{N(t)}$. Clearly, the entropy is a function of time and therapy, i.e., $S=S(t,C)$, since $N=N(t,C)$.

Before applying chemotherapy, the entropy is low because the tumor is composed mainly by sensitive cells. As the tumor grows freely, its entropy decreases because the growth rate of the sensitive cells is smaller than the growth rate of the resistant cells. On the other hand, when drugs are administered to the patient, the sensitive subpopulation tends to lose a higher proportion of cells and therefore the entropy of the tumor increases. This analysis could lead us to think that to control a tumor it is perhaps reasonable to look for therapies C that maintain the functional $J(C)\doteq |S(T)-S(t_0)|$ as low as possible. But that is not the case. In fact, assuming that the tumor is composed only by two subpopulations (a sensitive subpopulation $N_\mathrm{s}$ and second one, $N_\mathrm{r}$, resistant to chemotherapy), it is possible that $S(T)=S(t_0)$ while $\frac{N_\mathrm{s}(T)}{N(T)}=\frac{N_\mathrm{r}(t_0)}{N(t_0)}$ which in turn implies $\frac{N_\mathrm{r}(T)}{N(T)}=\frac{N_\mathrm{s}(t_0)}{N(t_0)}$ (see Fig. 6). Thus, it is not only important to maintain $|S(T)-S(t_0)|$ low but also the difference between both proportions of cells at the initial and final times. The following proposition will lead us to the formulation of an adequate cost functional.

Fig. 6

Entropy dynamics with high dose of chemotherapy

Proposition 1

If S(t) is Shannon’ entropy,  then for all T and $t_0$ it follows that

$$\begin{aligned} |S(T)-S(t_0)|\le \sum _{\ell =1}^L\left| \ln \left( \frac{p_\ell (t_0)}{p_\ell (T)}\right) \right| . \end{aligned}$$

(10)

Proof

Observe that

$$\begin{aligned} |S(T)-S(t_0)|= & {} \left| -\sum _{\ell =1}^Lp_\ell (T) \ln (p_\ell (T))+\sum _{\ell =1}^Lp_g(t_0)\ln (p_\ell (t_0))\right| \\\le & {} \sum _{\ell =1}^L|-p_\ell (T)\ln (p_\ell (T)) +p_\ell (t_0)\ln (p_\ell (t_0))|. \end{aligned}$$

Thus, inequality (10) follows by showing that $|-x\ln (x)+y\ln (y)|\le |-\ln (x)+\ln (y)|$ $\forall x,y\in (0,1).$ To prove that, we use the following result, which is very easy to check: if f and g are continuous real-valued functions defined on an interval (a, b) and $|g'(x)|\ge |f'(x)|\; \forall x\in (a,b)$, then $|g(y)-g(x)|\ge |f(y)-f(x)|\,\forall x,y\in (a,b)$. Take $(a,b)=(0,1)$, $g(x)\doteq \ln x$ and $f(x)\doteq x\ln x$. Then, $g'(x)=\frac{1}{x}$ and $f'(x)=\ln x + 1$. Therefore, $|g'(x)|-|f'(x)|=\left| \frac{1}{x}\right| -|1+\ln x|\,\forall x\in (0,1)$. Now, we consider two cases: (i) $x\ge \mathrm{e}^{-1}$ and (ii) $x<\mathrm{e}^{-1}$. (i) In this case, $f'(x)\ge 0$ and therefore $|g'(x)|-|f'(x)|=\underbrace{\frac{1}{x}-1}_{\ge 0}+\underbrace{(-\ln x)}_{\ge 0}\ge 0$. (ii) In this case, $f'(x)\le 0$ and therefore $|g'(x)|-|f'(x)|=\frac{1}{x}+1+\ln x\ge \frac{1}{x}+1+\frac{x-1}{x}=2\ge 0$ (where we used the fact that $\frac{x-1}{x}\le \ln x$ for all $x>0$). This completes the proof of the proposition. $\square$

Proposition 1 inspires us to define the functional

$$\begin{aligned} J(C,T)\doteq d(S(T),S(t_0)), \end{aligned}$$

where

$$\begin{aligned} d(S(T),S(t_0))\doteq \sum _{\ell =1}^L\left| \ln \left( \frac{p_\ell (t_0)}{p_\ell (T)}\right) \right| . \end{aligned}$$

In this metric, it follows that $d(S(T),S(t_0))=0$ if and only if $p_\ell (T)=p_\ell (t_0)$, $\forall \ell =1,\ldots ,L$. Hence, if T is fixed, we formulate the problem:

$$\begin{aligned} C^*=\underset{{C\in \Omega }}{\text {argmin}}\;J(C,T). \end{aligned}$$

(11)

In case the optimal rest period is also to be found, then we formulate the following optimal problem:

$$\begin{aligned} (C^*,T^*)=\underset{{(C,T)\in \Omega \times {\mathbb {R}}^+}}{\text {argmin}}J(C,T). \end{aligned}$$

(12)

In the following section, several numerical results are presented. We shall assume that the tumor is constituted by two subpopulations: a subpopulation $N_\mathrm{s}$ sensitive to chemotherapy and a resistant one, $N_\mathrm{r}$. Generalizations to an arbitrary number of subpopulations are quite straight forward.

4 Numerical results

A common chemotherapy treatment used in bladder cancer is known as MVAC [by the initials of the drugs used: Methotrexate, Vinblastine, Doxorubicin (also called adriamycin) and Cisplatin]. In what follows, we shall use the information contained in the following tables about the parameters characterizing a bladder cancer under MVAC chemotherapy. These values were taken from references (Martin and Teo 1994; McCall and Petrovski 1999; Petrovski and McCall 2001; Von der Maase et al. 2000). In the framework of problem (11), we assume a rest period of 30 days. In problem (12), on the other hand, the rest period is free (Table 1).

Table 1 Tumor’s parameters

Fig. 7

a Growth of the tumor and entropy after a cycle has been applied. b Dynamics of $N_\mathrm{s}/N$ cycle by cycle. c Dynamics of $N_\mathrm{s}$ and $N_\mathrm{r}$ cycle by cycle. d Dynamics of N cycle by cycle

Figure 7a shows the evolution of the tumor and the entropy over a period of 100 days. Note that Shannon’s entropy grows as the size of the tumor decreases. Figure 7b depicts the dynamics of $N_\mathrm{s}/N$ cycle by cycle when the standard chemotherapy is implemented. Note that already at the beginning of the fourth cycle one already has $N_\mathrm{s}/N\approx 0$. Finally, in Fig. 7c, d, we observe that the resistant population prevails over the sensitive population and thus standard chemotherapy fails. Computational techniques for solving optimal problems (11) and (12) typically require combining a discretization technique with an optimization method. We assumed $t_0=0$ and $T=52,$ so that the patient received 30 rest days at the end of each cycle. Also, we assumed $N_0=10^9,N_{\mathrm{s}_0}=0.9999\,N_0$ and $N_{\mathrm{r}_0}=0.0001\,N_0$. For discretization purposes, we divided the interval [0, T] into $r=10^4$ equal subintervals and approximated system (8) by finite differences.

In both optimization problems, (11) and (12), we proceeded in the same way. We begun by solving the optimization problem, which lead to an optimal protocol $C_1$. Next, we repeated the process 11 times and generated a sequence of optimal protocols $C_1,\ldots ,C_{11}$. Protocol $C_2$ was obtained by solving the optimization problem with initial conditions $N_{\mathrm{s}_{0}}=N_\mathrm{s}(T)$ and $N_{\mathrm{r}_{0}}=N_\mathrm{r}(T)$. These conditions were obtained using the protocol $C=C_1$. The other protocols were obtained in a similar fashion.

Next, we solved problems (11) and (12). In each problem, we considered two cases: (i) $L_1=0.0011$, $L_2=0.00055$ and $\alpha =\beta =1$ and (ii) $L_1=L_2=0.11$, $\alpha =10$ and $\beta =0.1.$ The obtained results are depicted in Figs. 8 and 9.

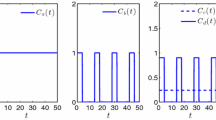
Solving problem (11): We proceeded as described above to obtain the optimal therapies $C_1,\ldots ,C_{11}$. In Fig. 8a, b, it can be observed that after 11 cycles (${\approx }1.5$ years) one has $N_\mathrm{s}/N>0.9990$. On the other hand, Fig. 7b shows that using a standard protocol, the ratio $N_\mathrm{s}/N$ is approximately equal to 0 at cycle 5 and it remains so afterwards.

Solving problem (12): In regard to problem (12), we also found optimal therapies $\tilde{C}_1,\ldots ,\tilde{C}_{11}$. All the optimal therapies obtained have break time periods greater than 80 days. Thus, for instance, in the first optimal therapy one has that $T=81.6739$ for case (i) and $T=88.8593$ for case (ii) (see Fig. 9c, d). However, the ratio $N_\mathrm{s}/N$ remains as good as the ratios obtained for problem (11) (see Fig. 8a, b). In both problems, we observe that the optimal therapies indicate that the drugs should be supplied in decreasing quantities (see Fig. 9). It is interesting to note that although these results are in accordance with some clinical experience, the optimal protocols obtained from problems (11) and (12) require much lower doses than standard protocols. For example, if $C^a_{ij}\doteq C_1$, $C^b_{ij}\doteq C_6$, $C^c_{ij}\doteq \tilde{C}_1$ and $C^d_{ij}\doteq \tilde{C}_6$ are the optimal protocols corresponding to Fig. 9a–d, respectively, then we have $\sum _{i}\sum _{j}C^a_{ij}=72.8738$ mg, $\sum _{i}\sum _{j}C^b_{ij}= 72.8212$ mg, $\sum _{i}\sum _{j}C^c_{ij}=72.8670$ mg and $\sum _{i}\sum _{j}C^d_{ij}=72.7912$ mg, while with a standard schedule, $C_{ij}$, it is necessary to deliver a total of 199 mg (see Table 2), i.e. standard protocol requires a much larger quantity of drugs than the optimal protocols and yet, it may fail). Solutions of problems (11) and (12) provide similar therapies but break time periods are significantly larger.

Fig. 8

Dynamic of $N_\mathrm{s}/N$ with different parameter values: a $L_1=0.0011$, $L_2=0.00055$ and $\alpha =\beta =1$. b $L_1=L_2=0.11$, $\alpha =10$ and $\beta =0.1$. c Same parameters as in a and T free. d Same parameters as in b and T free

Fig. 9

a Protocol $C_1$ obtained from problem (11) with $L_1=0.0011$, $L_2=0.00055$, $\alpha =\beta =1$ and $T=52$. b Protocol $C_6$ obtained from problem (11) with $L_1=L_2=0.11$, $\alpha =10$, $\beta =0.1$ and $T=52$. c Protocol $\tilde{C}_1$ obtained from problem (12) with the same values as in part a; here, $T=81.6739$. d Protocol $\tilde{C}_1$ obtained from problem (12) with the same values as in b; here, now $T=88.8593$

5 Conclusions

In this work, we proposed a model (2) to describe the competition between two subpopulations of tumor cells: a subpopulation sensitive to chemotherapy and a resistant subpopulation. The model was validated by a cellular automaton defined with the rules LR1–LR4. Next, we extended the model to include the effects of chemotherapy (8). Standard chemotherapy fails when the tumor is heterogeneous. This is so because resistant cells survive after chemotherapy treatment and the tumor continues to grow. Current research is focusing on alternative therapies that are able to maintain under control the size of the tumor over time. In light of this new paradigm, we formulated optimization problems (11) and (12) subject to the constraints $C\in \Omega$ and $(C,T)\in \Omega \times {\mathbb {R}}^+$, respectively. In problem (11), we sought therapies minimizing the distance d between S(T) and $S(t_0),$ where S is the Shannon’s entropy of the tumor. This approach ensured that the tumor continues to be treatable for a considerable longer period of time. This is so because $N_\mathrm{s}$ remains greater than $N_\mathrm{r}$ and the disease does not grow over a significantly longer period of time. In fact, as it can be seen in Fig. 9, using optimal protocols we obtained that $N_\mathrm{s}/N>0.9984$ even after eleven cycles, while with the standard protocol $N_\mathrm{s}/N$ is very close to 0 already in the fifth cycle. An appropriate analysis can also be made in terms of the entropy. If the tumor grows freely, its entropy decreases. Initially, the tumor has a low entropy (since most of the tumoral cells are sensitive). Then, if the objectives are to avoid the growth of the tumor and to maintain the entropy low, higher doses must be supplied at the beginning of the therapy whereas much lower doses are to be supplied at the end of it. Finally, these optimal therapies could provide a valuable tool for designing protocols for disease control, maintaining a very low growth level, while the tumor remains composed mainly of sensitive cells.

Table 2 Standard schedule (drug concentrations are measured in mg)