Double stratification effects on mixed convection flow of couple stress fluid in a non-Darcy porous medium with heat and mass fluxes

Abstract

This paper analyzes the flow, heat, and mass transfer characteristics of the mixed convection on a vertical plate with uniform and constant heat and mass fluxes in a doubly stratified non-Darcy porous medium saturated with couple stress fluid. The nonlinear governing equations and their associated boundary conditions are initially cast into dimensionless forms by pseudo-similarity variables. The resulting system of equations is then solved numerically using the Keller-box method. The numerical results are compared and found to be in good agreement with previously published results on special cases of the problem. The obtained results are displayed graphically to illustrate the effect of the couple stress, mixed convection, stratification parameters, and Forchheimer number on the dimensionless velocity, wall temperature, and wall concentration. The numerical values of heat and mass transfer rates for different values of governing parameters are also tabulated.

1 Introduction

In recent years, the study of convective heat transfer from surfaces embedded in porous media has been an active field of research as it plays a crucial role in diverse applications. The interest for such studies is motivated by several thermal engineering applications, such as geothermal systems, the storage of nuclear wastes, oil extraction, ground water pollution, thermal insulation, and chemical catalytic reactors, etc. Considerable work has been reported on flow, heat, and mass transfer in Darcian porous media. However, Darcy’s law is valid only for slow flows through porous media with low permeability. At higher flow rates, there is a departure from the linear law and inertial effects become important. The simultaneous effects of fluid inertia force and boundary viscous resistance on the flow and heat transfer in a porous medium were analyzed in case of free convection by Soundalgekar (1976) and in case of mixed convection (Ranganathan and Viskanta 1984). From their reports, it was found that both boundary and inertia effects exhibit a significant influence on velocity distribution and heat transfer and thus these effects cannot be ignored. The Darcy–Forchheimer model describes the effect of inertia as well as viscous forces in porous media. Recently, Patil and Chamkha (2013) have investigated the heat and mass transfer from mixed convection flow of polar fluid along a plate in porous media with chemical reaction. A detailed review of convective heat transfer in Darcian and non-Darcian porous medium can be found in the book by Nield and Bejan (2013). Most recently, Srinivasacharya and Kaladhar (2014) presented the mixed convection flow of couple stress fluid in a non-Darcy porous medium with soret and dufour effects.

Analysis of heat and mass transfer in non-Newtonian fluids is significant in engineering applications such as thermal design of industrial equipment dealing with molten plastics, polymeric liquids, foodstuffs, or slurries. The examples of such fluids are blood at low shear rate, lubricants containing small amount of polymer additives, electro-rheological fluids, paints, fiber solutions, and synthetic fluids, etc. Generally, the non-Newtonian fluid models describe the nonlinear relationship between stress and the rate of strain. The fluid model introduced by Stokes (1966) exhibits couple stress, body couples, and nonsymmetric tensors. The main effect of couple stresses introduces a size-dependent effect that is not present in the classical viscous theories. Muthuraj et al. (2013) studied the heat and mass transfer effects on MHD flow of a couple-stress fluid in a horizontal wavy channel with viscous dissipation and porous medium. Hayat et al. (2013) analyzed the stagnation-point flow of couple stress fluid with melting heat transfer. The analytical study of Hall and Ion-slip effects on mixed convection flow of couple stress fluid between parallel disks have been presented by Srinivasacharya and Kaladhar (2013). Makinde and Eegunjobi (2013) studied the entropy generation in a couple stress fluid flow through a vertical channel filled with saturated porous media. Approximate solution of couple stress fluid with expanding or contracting porous channel has been presented by Najeeb et al. (2013). Recently, Hayat et al. (2015) presented the effects of hall and convective conditions on peristaltic flow of couple-stress fluid in an inclined asymmetric channel. Most recently, Khan et al. (2015) presented the exact solutions for MHD heat transfer flow of couple stress fluid.

Stratification of fluid arises due to temperature variations, concentration differences or the presence of different fluids. In practical situations where the heat and mass transfer mechanisms run parallel, it is interesting to analyze the effect of double stratification (stratification of the medium with respect to the thermal and concentration fields) on the convective transport in a fluid. The analysis of mixed convection in a doubly stratified medium is a fundamentally interesting and important problem because of its broad range of engineering applications. The applications include heat rejection into the environment such as lakes, rivers, and the seas; thermal energy storage systems such as solar ponds and heat transfer from thermal sources such as the condensers of power plants. Although the effect of stratification of the medium on the heat removal process in a fluid is important, very little work has been reported in the literature. This phenomenon was first shown theoretically by Prandtl (1952) for an infinite wall and later on Jaluria and Himasekhar (1983) presented in the case of semi-infinite walls. Murthy et al. (2004) presented the effect of double stratification on free convection in Darcian porous medium. Magnetic effect on free convection in a non-Darcy porous medium saturated with doubly stratified power-law fluid has been studied numerically by Srinivasacharya et al. (2011). Most recently, Srinivasacharya and Surender (2015) presented the effect of double stratification on mixed convection boundary layer flow of a nano fluid in a porous medium.

The aim of this investigation was to consider the effects of thermal and concentration stratification on the mixed convection heat and mass transfer along a vertical plate in a non-Darcy porous medium saturated with couple stress fluid with heat and mass fluxes. This type of investigation is useful in understanding heat and mass transfer characteristics around a hot radioactive subsurface storage site or around a cooling magmatic intrusion where the theory of convection heat and mass transport is involved. Many researchers presented the study of heat and mass transfer in non-Darcy porous medium in case of Newtonian fluid but not much attention has been given to non-Newtonian fluids (Couple stress fluid). Hence, these boundary conditions are physically realistic, have more practical relevance, also have great deal of applications mentioned above motivated the author to start this paper. The Keller-box method (Cebeci and Bradshaw 1984) is employed to solve the nonlinear system of equations. The results are compared with relevant results in the existing literature and are found to be in good agreement. The effects of couple stress parameter, mixed convection, thermal and mass stratification parameters, and the non-Darcy parameter are examined and displayed through graphs.

2 Mathematical formulation

Consider the steady mixed convection heat and mass transfer along a vertical plate embedded in a stable, a doubly stratified couple stress fluid saturated non-Darcy porous medium. The porous medium is considered to be homogeneous and isotropic (i.e. uniform with a constant porosity and permeability) and is saturated with a fluid which is in local thermodynamic equilibrium with the solid matrix. The fluid has constant properties except the density in the buoyancy term of the balance of momentum equation. The fluid flow is moderate, so the pressure drop is proportional to the linear combination of fluid velocity and the square of velocity. The fluid flow is moderate and the permeability of the medium is low so that the Forchheimer flow model is applicable and the boundary effect is neglected.

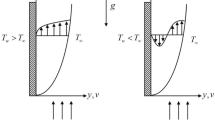
The free stream velocity which is parallel to the vertical plate is $\displaystyle {u_\infty }$, temperature is $T_{\infty ,0}$, and concentration is $C_{\infty ,0}$. Choose the coordinate system such that x-axis is along the vertical plate and y-axis normal to the plate. The physical model and coordinate system are shown in Fig. 1. The plate is maintained at uniform and constant heat and mass fluxes $q_\mathrm{w}$ and $m_\mathrm{w}$, respectively. The ambient medium is assumed to be vertically linearly stratified with respect to both temperature and concentration in the form $T_\infty (x)=T_{\infty ,0}+Ax$ and $C_\infty (x) =C_{\infty ,0}+Bx$, respectively, where A and B are constants and varied to alter the intensity of stratification in the medium.

Fig. 1

Physical model and coordinate system

By employing the laminar boundary layer flow assumptions, Boussinesq and boundary-layer approximations hold and using the Darcy–Forchheimer model and Dupuit–Forchheimer relationship, the governing equations for the couple stress fluid are given by

$$\begin{aligned} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 \end{aligned}$$

(1)

$$\begin{aligned} \frac{\rho }{\varepsilon ^2}\left( u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)= & {} \frac{\mu }{\varepsilon } \frac{\partial ^2 u}{\partial y^2}+\rho g (\beta _\mathrm{T}(T-T_{\infty })+\beta _\mathrm{C}(C-C_{\infty }))+\frac{\mu }{K_\mathrm{p}}(u_\infty -u)\nonumber \\&+\frac{\rho b}{K_\mathrm{p}}(u_\infty ^2-u^2)-\eta _1 \frac{\partial ^4 u}{\partial y^4} \end{aligned}$$

(2)

$$\begin{aligned} u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{\partial ^2 T}{\partial y^2} \end{aligned}$$

(3)

$$\begin{aligned} u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}=D\frac{\partial ^2 C}{\partial y^2}, \end{aligned}$$

(4)

where u and v are the velocity components in x and y directions, respectively, T is the temperature, C is the concentration, g is the acceleration due to gravity, $\rho$ is the density, $\mu$ is the dynamic coefficient of viscosity, b is the Forchheimer constant, $K_\mathrm{p}$ is the permeability, $\varepsilon$ is the porosity, $\beta _\mathrm{T}$ is the coefficient of thermal expansion, $\beta _\mathrm{C}$ is the coefficient of solutal expansions, $\alpha$ is the thermal diffusivity of the medium, D is the solutal diffusivity of the medium, and $\eta _1$ is the couple stress fluid parameter. The subscript $\infty$ indicates the condition at the outer edge of the boundary layer.

The boundary conditions are

$$\begin{aligned} u=0, \quad v=0, \quad v_x-u_y=0, \quad q_\mathrm{w}=-k \frac{\partial T}{\partial y}, \quad m_\mathrm{w}=-D\frac{\partial C}{\partial y} \quad at\,y=0 \end{aligned}$$

(5a)

$$\begin{aligned} u=u_\infty , \quad v_x-u_y=0, \quad T=T_{\infty }(x), \quad C=C_{\infty }(x) \quad as\,y\rightarrow \infty , \end{aligned}$$

(5b)

where the boundary condition $v_x-u_y=0$ implies that the couple stress fluid is irrotational at the boundaries (Type A condition for Couple stress fluid; Stokes 1966), and k is the thermal conductivity of the fluid.

In view of the continuity Eq. (1), we introduce the stream function $\psi$ by

$$\begin{aligned} u=\frac{\partial \psi }{\partial y}, \quad v=-\frac{\partial \psi }{\partial x} \end{aligned}$$

(6)

substituting (6) in (2)–(4) and then using the following transformations,

$$\begin{aligned} \left. \begin{array}{l} \xi =\displaystyle {\frac{x}{L}}, \quad \eta =\displaystyle {\left( \frac{Re}{\xi }\right) ^{1/2}\frac{y}{L}}, \quad \psi =\frac{L u_\infty }{Re^{1/2}}\xi ^{1/2} f \\ \displaystyle {\theta =\frac{T-T_{\infty }(x)}{\frac{q_\mathrm{w} L}{k}\xi ^{1/2}}Re^{1/2}}, \quad \displaystyle {\phi =\frac{C-C_{\infty }(x)}{\frac{m_\mathrm{w} L}{D}\xi ^{1/2}}Re^{1/2}} \end{array} \right. \end{aligned}$$

(7)

we get the following non-linear system of differential equations

$$\begin{aligned}&Re S^2 f^v -\frac{\xi }{\varepsilon } f'''-\frac{\xi }{2\varepsilon ^2} ff''-\xi ^2 R_i (\theta +N \phi )-\frac{\xi ^2}{Da Re}(1-f') -\frac{Fs}{Da}\xi ^2 (1-f'^2)\nonumber \\&\quad =\frac{\xi ^2}{\varepsilon ^2}\left[ f''\frac{\partial f}{\partial \xi }-f'\frac{\partial f'}{\partial \xi }\right] \end{aligned}$$

(8)

$$\begin{aligned} \frac{1}{Pr}\theta ''+\frac{1}{2}f\theta '-\frac{1}{2}f' \theta -\varepsilon _1 \xi ^{1/2} f'=\xi \left[ f'\frac{\partial \theta }{\partial \xi }-\theta '\frac{\partial f}{\partial \xi }\right] \end{aligned}$$

(9)

$$\begin{aligned} \frac{1}{Sc}\phi ''+\frac{1}{2}f\phi '-\frac{1}{2}f'\phi -\varepsilon _2 \xi ^{1/2} f'=\xi \left[ f'\frac{\partial \phi }{\partial \xi }-\phi '\frac{\partial f}{\partial \xi }\right] , \end{aligned}$$

(10)

where the primes indicate partial differentiation with respect to $\eta$ alone, $Pr={\frac{\nu }{\alpha }}$ is the Prandtl number, $Gr={\frac{g \beta _\mathrm{T}q_\mathrm{w} L^4}{k \nu ^2}}$ is the thermal Grashof number, $Sc={\frac{\nu }{D}}$ is the Schmidt number, ${Re = \frac{u_\infty L}{\nu }}$ is the Reynolds number, $\eta _1$ is the couple stress fluid parameter, and $N = {\frac{\beta _\mathrm{C} m_\mathrm{w} k}{\beta _\mathrm{T} q_\mathrm{w} D}}$ is the buoyancy ratio. $N>0$ indicates aiding buoyancy where both the thermal and solutal buoyancies are in the same direction and $N < 0$ indicates opposing buoyancy where the solutal buoyancy is in the opposite direction to the thermal buoyancy. When $N = 0$, the flow is driven by thermal buoyancy alone. ${Fs=\frac{b}{L}}$ is the Forchheimer number, which can be applied to all types of porous materials, as long as the permeability and non-Darcy coefficient can be determined experimentally, or empirically when no experimental data are available. ${Da=\frac{K_\mathrm{p}}{L^2}}$ is the Darcy number; it is a dimensionless group used in the study of the flow of fluids in porous media. $\varepsilon _1={\frac{Ak}{q_\mathrm{w}}Re^{1/2}}$ and $\varepsilon _2={\frac{BD}{m_\mathrm{w}}Re^{1/2}}$ are the thermal and solutal stratification parameters. ${Ri=\frac{Gr}{Re^2}}$ is the mixed convection parameter. ${S=\frac{1}{L} \sqrt{\frac{\eta _1}{\mu }}}$ is the couple stress parameter, the effects of couple-stress are significant for large values of $S (=l/L)$, where $l = \sqrt{\frac{\eta _1}{\mu }}$ is the material constant. If l is a function of the molecular dimensions of the liquid, it will vary greatly for different liquids. For example, the length of a polymer chain may be a million times the diameter of water molecule. Therefore, there are all the reasons to expect that couple-stresses appear in noticeable magnitudes in liquids with large molecules.

Boundary conditions (5a, 5b) in terms of f, g, $\theta$, $\phi$ become

$$\begin{aligned} f(\xi ,0)= f'(\xi ,0)= f''(\xi ,0)=0, \quad \theta '(\xi ,0)= \phi '(\xi ,0)=-1\end{aligned}$$

(11a)

$$\begin{aligned} f'(\xi ,\infty )=1, \quad \ f''(\xi ,\infty )=\theta (\xi ,\infty )=\phi (\xi ,\infty )=0 \end{aligned}$$

(11b)

The heat and mass transfers from the plate respectively are given by

$$\begin{aligned} \displaystyle {q_\mathrm{w}=-k\left[ \frac{\partial T}{\partial y}\right] _{y=0}}, \quad \displaystyle {m_\mathrm{w}=-D\left[ \frac{\partial C}{\partial y}\right] _{y=0}} \end{aligned}$$

(12)

The local Nusselt number $\displaystyle {Nu_x=\frac{q_\mathrm{w} x}{k(T_\mathrm{w}-T_{\infty ,0})}}$ and local Sherwood number $\displaystyle {Sh_x}$ = $\displaystyle {\frac{m_\mathrm{w} x}{D(C_\mathrm{w}-C_{\infty ,0})}}$ are given by

$$\begin{aligned} \frac{Nu_x}{Re_x^{1/2}}= \frac{1}{\theta (\xi ,0)+\varepsilon _1 \xi ^{1/2}}, \quad \frac{Sh_x}{Re_x^{1/2}}= \frac{1}{\phi (\xi ,0)+\varepsilon _2 \xi ^{1/2}}, \end{aligned}$$

(13)

where $\displaystyle {Re_x=\frac{u_\infty x}{\nu }}$ is the local Reynolds number.

3 Results and discussions

The flow Eq. (8) is coupled with the energy and concentration Eqs. (9) and (10), constituting nonlinear non-homogeneous differential equations for which closed form solutions cannot be obtained and hence we have to solve the problem numerically. Hence the governing boundary layer Eqs. (8)–(10) have been solved numerically using the Keller-box implicit method discussed in the book by Cebeci and Bradshaw (1984). This method has been proven to be adequate and give accurate results for boundary layer equations. In the present study, the boundary conditions for $\eta$ at $\infty$ are replaced by a sufficiently large value of $\eta$ where the velocity approaches one, temperature and concentration profiles approach zero. We have taken $\eta =8$ and a grid size of $\eta$ of 0.01. We have computed the solutions for the dimensionless velocity, temperature, and concentration function as shown graphically in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16. The effects of mixed convection parameter $R_i$, stratification parameters, $\varepsilon _1$ and $\varepsilon _2$, and the couple stress parameter S have been discussed. In the present study, we have adopted the following default parameter values for the numerical computations: $Re=100$, $Pr=0.71$, $Sc=0.22$, $Da=0.1$, and $\xi =0.1$. These values are used throughout the computations, unless otherwise indicated.

Fig. 2

Effect of mixed convection parameter $R_i$ on velocity when $S = 0.5, \varepsilon _1 = 0.1, \varepsilon _2 = 0.1$

Fig. 3

Effect of mixed convection parameter $R_i$ on temperature when $S = 0.5, \varepsilon _1 = 0.1, \varepsilon _2 = 0.1$

Fig. 4

Effect of mixed convection parameter $R_i$ on concentration when $S = 0.5, \varepsilon _1 = 0.1, \varepsilon _2 = 0.1$

Fig. 5

Effect of thermal stratification parameter $\varepsilon _1$ on velocity when $S = 0.5, R_i = 2.0, \varepsilon _2 = 0.1$

Fig. 6

Effect of thermal stratification parameter $\varepsilon _1$ on temperature when $S = 0.5, R_i = 2.0, \varepsilon _2 = 0.1$

Fig. 7

Effect of thermal stratification parameter $\varepsilon _1$ on concentration when $S = 0.5, R_i = 2.0, \varepsilon _2 = 0.1$

Fig. 8

Effect of solutal stratification parameter $\varepsilon _2$ on velocity when $S = 0.5, R_i = 2.0, \varepsilon _1 = 0.05$

Fig. 9

Effect of solutal stratification parameter $\varepsilon _2$ on temperature at $S = 0.5, R_i = 2.0, \varepsilon _1 = 0.05$

Fig. 10

Effect of solutal stratification parameter $\varepsilon _2$ on concentration at $S = 0.5, R_i = 2.0, \varepsilon _1 = 0.05$

Fig. 11

Effect of couple stress parameter S on velocity when $R_i = 2.0, \varepsilon _1 = 0.1, \varepsilon _2 = 0.1$

Fig. 12

Effect of couple stress parameter S on temperature at $R_i = 2.0, \varepsilon _1 = 0.1, \varepsilon _2 = 0.1$

Fig. 13

Effect of couple stress parameter S on concentration at $R_i = 2.0, \varepsilon _1 = 0.1, \varepsilon _2 = 0.1$

Fig. 14

Velocity profile for different values of Fs when $R_i = 2.0, \varepsilon _1 = 0.1, \varepsilon _2 = 0.1, S = 0.5$

Fig. 15

Temperature profile for different values of Fs at $R_i = 2.0, \varepsilon _1 = 0.1, \varepsilon _2 = 0.1, S = 0.5$

Fig. 16

Concentration profile for different values of Fs at $R_i = 2.0, \varepsilon _1 = 0.1, \varepsilon _2 = 0.1, S = 0.5$

In the absence of couple stress parameter S, buoyancy ratio N, mixed convection parameter $R_i$, stratification parameters $\varepsilon _1$, $\varepsilon _2$, and $Da \rightarrow \infty$, the results have been compared with that of previous work by Lee et al. (1987) and it is found that they are in good agreement, as shown in Table 1. Therefore, the developed code can be used with great confidence to study the present problem.

Table 1 Comparison of ${Nu_x/Re_x^{1/2}=\frac{1}{\theta (\xi ,0)}}$ for mixed convection with a vertical flat plate and Newtonian fluids (Lee et al. 1987)

Figure 2 displays the dimensionless velocity profile for various values of the $R_i$ with fixed values of S, $\varepsilon _1$, $\varepsilon _2$, and Fs. It can be observed that as the value of $R_i$ increases, the dimensionless velocity rises. Compared with the limiting case of $R_i$ = 0.0 (i.e. pure forced convection), an increase in the value of $R_i$ gives rise to a higher velocity. Since a greater value of $R_i$ indicates a greater buoyancy effects in mixed convection flow leads to an acceleration of the fluid flow. Figure 3 depicts the variation of temperature for selected values of $R_i$. The results indicate that the dimensionless temperature reduces with the increase of $R_i$. The temperature in case of mixed convection is less compared to that of pure forced convection. As $R_i$ (i.e. buoyancy effects) increase, the convection cooling effect increases and hence the temperature reduces. The effect of $R_i$ on the dimensionless concentration is depicted in Fig. 4. It is clear that the concentration of the fluid decreases with the increase of $R_i$. This is due to the fact that the buoyancy force acts like pressure gradient which decelerates the fluid within the boundary layer. Hence, the temperature and concentration in case of forced convection is more than that of the corresponding mixed convection case.

Figure 5 represent the non-dimensional velocity for different values of thermal stratification parameter $\varepsilon _1$ for fixed values of $\varepsilon _2$, $R_i$, S and Fs. It can be noted that the velocity of the fluid decreases with the increase of thermal stratification parameter. This is because thermal stratification reduces the effective convective potential between the heated plate and the ambient fluid in the medium. Hence, the thermal stratification effect reduces the velocity in the boundary layer. The dimensionless temperature for different values of thermal stratification parameter for $S = 0.5$, $R_i$ = 2, and $\varepsilon _2 =$ 0.1 is shown in Fig. 6. It is obvious that the temperature of the fluid decreases with the increase of thermal stratification parameter. When the thermal stratification effect is taken into consideration, the effective temperature difference between the plate and the ambient fluid will decrease; therefore, the thermal boundary layer is thickened and the temperature is reduced. Figure 7 depicts the dimensionless concentration for different values of thermal stratification parameter for $S = 0.5$, $R_i$ = 2, and $\varepsilon _2=$ 0.1. It is seen that the concentration of the fluid increases with the increase of thermal stratification parameter. It can be noted that the effect of the stratification on temperature is the formation of a region with a temperature deficit (i.e., a negative dimensionless temperature). This is in tune with the observation made in the references (Jaluria and Gebhart 1974; Hayat et al. 2006).

The dimensionless velocity component for different values of solutal stratification parameter $\varepsilon _2$ with fixed values of $S = 0.5$, $R_i = 2$, $\varepsilon _1 =$ 0.05, and $Fs = 0.6$ is depicted in Fig. 8. It is observed that the velocity of the fluid decreases with the increase of solutal stratification parameter. The dimensionless temperature for different values of solutal stratification parameter for $S = 0.5$, $R_i = 2$, and $\varepsilon _1 =$ 0.05 is displayed in Fig. 9. It is noted that the temperature of the fluid increases with the increase of solutal stratification parameter. Figure 10 demonstrates the dimensionless concentration for different values of solutal stratification parameter with $S = 0.5$, $R_i = 2$, $\varepsilon _1 =$ 0.05, and $Fs = 0.6$. It is clear that the concentration of the fluid decreases with the increase of thermal stratification parameter. Hence, comparing with the unstratified fluid (i.e. $\varepsilon _1 = \varepsilon _2=0$), an increase in the stratification parameters, $\varepsilon _1$ and $\varepsilon _2$ causes a reduction in the velocity boundary layer thickness. It is also observed that the non dimensional temperature and concentration values would become less inside the boundary layer for different values of the stratification parameters depending on the values of other parameters. This is because the fluids near the plate can have temperature or concentration lower than the ambient medium.

In Figs. 11, 12 and 13, the effects of the couple stress parameter S on the dimensionless velocity, temperature, and concentration profiles are presented for fixed values of $R_i = 2.0$, $\varepsilon _1 =$ 0.1, $\varepsilon _2$ = 0.1, and $Fs = 0.6$. As S increases, it can be observed from Fig. 11 that the maximum velocity decreases in amplitude and the location of the maximum velocity moves far away from the wall. It is noted that couple stress parameter is dependent upon the couple stress viscosity and this couple stress viscosity acts as a retarding agent which makes the fluid more denser resulting into a decrease in the velocity of the fluid. It is clear from Fig. 12 that the temperature increases with the increase of couple stress fluid parameter S. It can be seen from Fig. 13 that the concentration of the fluid increases with the increase of couple stress fluid parameter S. Temperature and concentration in case of couple stress fluid are more than that of viscous fluid. Hence, the presence of couple stresses in the fluid decreases the velocity and increases temperature and concentration.

The dimensionless velocity component for different values of Forchheimer number Fs with $\varepsilon _1 = 0.1$, $\varepsilon _2 = 0.1$, Ri = 2.0, and $S = 0.5$ is depicted in Fig. 14. It shows the effects of Forchheimer (inertial porous) number on the velocity. In the absence of Forchheimer number (i.e., when Fs = 0), the present investigation reduces to a mixed convection heat and mass transfer in a doubly stratified couple stress fluid saturated porous medium. It is observed from Fig. 14 that velocity of the fluid decreases with increase in the value of the non-Darcy parameter Fs. The increase in non-Darcy parameter implies that the porous medium is offering more resistance to the fluid flow. This results in reduction of the velocity profile. The dimensionless temperature for different values of Forchheimer number Fs for $\varepsilon _1 = 0.1$, $\varepsilon _2 = 0.1$, Ri = 2.0, and $S = 0.5$ is displayed in Fig. 15. An increase in Forchheimer number Fs, increases the temperature. Since as the fluid is decelerated, energy is dissipated as heat which leads to increases the temperature. As such the temperature is minimized for the lowest value of Fs and maximized for the highest value of Fs as shown in Fig. 15. Figure 16 demonstrates the dimensionless concentration for different values of Forchheimer number with $\varepsilon _1 = 0.1$, $\varepsilon _2 = 0.1$, Ri = 2.0, and $S = 0.5$. It is clear that the concentration of the fluid increases with the increase of Forchheimer number. The increase in non-Darcy parameter reduces the intensity of the flow and increases the thermal and concentration boundary layer thickness.

The effect of $R_i$ and Fs on the non-dimensional heat and mass transfer coefficients with variation of the thermal stratification parameter $\varepsilon _1$ and solutal stratification parameter $\varepsilon _2$ for fixed $S=0.5$ is presented in Table 2. It can be noticed that the heat transfer coefficient is increasing and the mass transfer coefficient decreases with the increase of $\varepsilon _1$ for fixed values of $R_i$, Fs, and $\varepsilon _2$. Physically, positive values of the stratification parameter have the tendency to decrease the boundary layer thickness due to the reduction in the temperature difference between the plate and the free stream. This causes increases in the Nusselt number as shown in Table 2. The decrease in the mass transfer coefficient causes with the increase of $\varepsilon _1$ for fixed values of $R_i$, Fs, and $\varepsilon _2$ due to the effective mass transfer between the plate and the ambient medium decreases as the thermally stratified effect increases. The reverse trend can be seen in the case of $\varepsilon _2$. The effects of buoyancy parameter $R_i$ on the non-dimensional heat and mass transfer coefficients against the thermal stratification parameter $\varepsilon _1$, solutal stratification parameter $\varepsilon _2$, and Fs are presented in Table 2. It can be observed that, for fixed values of Fs, $\varepsilon _1$ and $\varepsilon _2$, the non-dimensional heat and mass transfer coefficients increase with the increase of $R_i$. Hence the mixed convection parameter has an important role in controlling the temperature and concentration. Finally, the effects of Forchheimer number Fs on the rate of heat and mass transfer are shown in this table. The behavior of these parameters is self-evident from the Table 2 and hence is not discussed for brevity.

Table 2 Effect of mixed convection parameter ($R_i$), Forchheimer (Fs), Stratification parameters ($\varepsilon _1, \varepsilon _2$) on heat and mass transfer coefficients with $S=0.5$

4 Conclusions

In this study, a boundary layer analysis for mixed convection in a doubly stratified couple stress fluid in the presence of uniform wall temperature and concentration is presented. Using the pseudo-similarity variables, the governing equations are transformed into a set of non-similar parabolic equations where numerical solution has been presented for a wide range of parameters. The main findings are summarized as follows:

• 1. An increase in $R_i$ enhances the velocity, non-dimensional heat, and mass transfer coefficients but reduces the temperature and concentration profiles in boundary layer.

• 2. An increase in thermal stratification parameter $\varepsilon _1$ reduces the velocity, temperature profiles, and non-dimensional mass transfer coefficient but increases the non-dimensional heat transfer coefficient, concentration profile in the boundary layer.

• 3. An increase in the solutal stratification parameter, there is a reduction in velocity, concentration distributions and the dimensionless heat transfer coefficient but there is an increase in the temperature distribution and on the non-dimensional mass transfer coefficient in the boundary layer.

• 4. It is noticed that the presence of couple stresses in the fluid decreases the velocity and increases the temperature and concentration.

• 5. The higher values of the Forchheimer number Fs indicate lower velocity, higher rate of heat and mass transfers, higher wall temperature, and concentration distributions.