Constrained Nonlinear Predictive Control Using Neural Networks and Teaching–Learning-Based Optimization

Abstract

In this work, an efficient constrained nonlinear predictive control algorithm, based on the meta-heuristic optimization strategy, is proposed. The aim is to develop a predictive control algorithm having a simple design and implementation procedure on the one hand, and that can give satisfactory performance with a large class of nonlinear systems on the other hand. To achieve this goal, a feedforward multilayer neural network is used to predict the future outputs of the system, and the optimization problem of predictive control is resolved using teaching–learning-based optimization strategy. Due to their interesting proprieties, feedforward neural networks are widely used in nonlinear systems identification and control. Indeed, they have a simple structure and can accurately approximate any nonlinear mapping. The teaching–learning-based optimization is used in a large number of applications in different fields of engineering and has gained wide acceptance among the optimization researchers community. Unlike other metaheuristic algorithms, this algorithm requires only common controlling parameters like population size and number of generations for its working; it does not require any algorithm-specific parameters. To assess the effectiveness of the proposed control algorithm, the control of the model of the continuous stirred tank rector and the 2-DOF manipulator robot model is considered. A comparative study, using the conventional PID controller, the fuzzy logic control, the computed torque control and the neural network-based model predictive control using particle swarm optimization, is carried out. To further demonstrate the effectiveness of the proposed controller, the control algorithm is numerically implemented and applied to a system with fast dynamics, namely the induction motor. The obtained results, through the simulation and the experimental study, indicate that the proposed controller presents better control performance than the other controllers. Furthermore, the experimental study shows that the developed control strategy can be effectively used to control, in real time, systems with fast dynamics.

1 Introduction

Model-based predictive control (MPC) is a modern and successful control strategy that is characterized by its ability to control constrained multivariable systems. To obtain the optimal control sequence, it uses an explicit model to predict the system future behaviour over a given horizon and then minimizes a given constrained cost function. Usually, this cost function is a quadratic function of the error between the predicted response and the reference trajectory and includes in most cases the control energy (Camacho and Bordons 2007; Maciejowski 2002; Katz et al. 2018).

Due to its industrial success, considering a wide range of complex systems, a lot of attention was given to this control strategy and several control algorithms, based on linear models, were developed. Richalet et al. (1978) have proposed the model algorithmic control (MAC) technique. Two years later, a step response model-based predictive control, called dynamic matrix control (DMC), has been developed by Cutler and Ramaker (1980). Ydstie (1984) proposed the extended horizon adaptive control (EHAC). Taking into account the disturbances effect, the EHAC algorithm has been improved by De Keyser and Van Cauwenberghe (1985). After that, the famous generalized predictive control (GPC) was introduced (Clarke et al. 1987a, b). Since then, several techniques and improvement on the developed algorithms have been proposed (Kansha and Chiu 2009; Li and Wang 2017; Li et al. 2017). The success of the MPC strategy is related to its capability of handling different types of constraints and its ability to handle multivariables systems, systems with no-minimum phase behaviour and systems with variable or unknown time delays.

Although linear MPC techniques give satisfactory performance in many practical applications (Lucia et al. 2014; Han and Qiao 2014; Subramanian et al. 2018), in the case of highly nonlinear process, severe degradation in control performance can be observed. To ensure higher performance, MPC methods that use a nonlinear prediction model must be investigated. In fact, a lot of attention was given to nonlinear MPC (NMPC), and several control techniques were proposed (Mazinan 2012; Lu et al. 2015; Thangavel et al. 2018; Abdennour et al. 2002). The main difficulties in designing NMPC are obtaining an adequate nonlinear model for the system to be controlled, and online solving the nonlinear and the non-convex optimization problem. Obviously, the efficiency and computational requirement of the controller depend extremely on the accuracy and simplicity of the used model. In fact, there is no clearly suitable modelling approach to represent general nonlinear systems. Among the various nonlinear models developed and used in predictive control, we can find: Volterra series (Maner et al. 1994; Gruber et al. 2013; Diaz-Mendoza and Budman 2009), fuzzy models (Lu et al. 2015; Ait Sahed et al. 2016; Huang et al. 2000), neuronal models (Mazinan 2012; Patan 2018; Han et al. 2013), etc. Due to their flexibility, simplicity and good performances, artificial neural networks (ANN) were extensively used in modelling (Mohammadi et al. 2018; Mahmoudi et al. 2016; Ghorbani et al. 2017) and controlling nonlinear systems (Vargas et al. 2019; Qin et al. 2020; Yuan et al. 2019; Kumpati et al. 1997; Narendra and Parthasarathy 1989). Moreover, it has been shown that neural networks can approximate any given function with arbitrary precision ( Kumpati et al. 1997).

Solving the non-convex optimization problem of nonlinear constrained predictive control is difficult and time-consuming task. Since an analytical solution cannot be obtained, several suboptimal methods were used to deal with this optimization problem (Botto et al. 1999; Liu et al. 1998; Soloway and Haley 1996; Sorensen et al. 1999). To obtain a convex quadratic optimization problem, some of the suboptimal methods use prediction models of particular structure (Botto et al. 1999; Liu and Kadirkamanathan 1998). Some others are based on numerical optimization algorithms, which are known to have a slow convergence rate and could easily be trapped in local minima (Soloway and Haley 1996; Sorensen et al. 1999). An optimization strategy that could mitigate the non-convex and nonlinear optimization problem of predictive control is based on the meta-heuristic algorithms. These algorithms, such as genetic algorithms (GA) (Sarimveis and Bafas 2003; Li et al. 2012), particle swarm optimization (PSO) (Mazinan 2012; Coelho et al. 2005; Zhixiang et al. 2008), artificial bee colony (ABC) (Ait Sahed et al. 2015,2016) and evolutionary algorithm (EA) (Zimmer et al. 2015), are easy to implement, have good performance and could locate adequate solutions in a reasonable time. In fact, a lot of researches have been conducted on solving the NMPC optimization problem using meta-heuristic algorithms (Ait Sahed et al. 2016; Jiang et al. 2012; Wang et al. 2019).

A relatively recent efficient optimization method, called, teaching–learning-based optimization (TLBO), was designed for solving complex, constrained and nonlinear optimization problems (Rao et al. 2011,2012). It is based on classroom teaching–learning process in the form of two phases, a teacher phase, where students learn from their teacher, and a learners phase, where the students learn by interacting between themselves. Furthermore, this algorithm was found to be more efficient than several other meta-heuristic algorithms such as ABC, multimembered evolutionary strategy (M-ES), particle evolutionary swarm optimization (PESO), cultural differential evolution (CDE), co-evolutionary differential evolution (CoDE) and genetic algorithm (Rao et al. 2011; Rao and Waghmare 2014; Patel and Savsani 2016). Another interesting advantage of using the TLBO algorithm is the fact that, except the common control parameters (population size and number of generations), and unlike to other meta-heuristic algorithms, this algorithm does not require any algorithm-specific parameters (Rao 2016). A bad choice of any value of the specific parameters of the meta-heuristic algorithms leads to a slow convergence rate and could easily be trapped in local minima. Therefore, before implementing a meta-heuristic algorithm which depends on some specific parameters, an optimization step of these parameters is necessary. However, this is not required in the case of the TLBO algorithm.

In this work, a TLBO-based neural network model predictive controller (NNMPC-TLBO) is proposed. The aim is to develop a simple and an efficient controller that can be used to control any nonlinear system. The proposed control algorithm uses a simple static neural network, namely the multilayer perceptron (MLP), as a prediction model of the system to be controlled, and the TLBO strategy to solve the obtained constrained optimization problem. The efficiency and performance of the developed control algorithm are assessed by considering the control of two nonlinear systems: the continuous stirred tank reactor (CSTR) model and the two-degree-of-freedom manipulator robot model. To further demonstrate the effectiveness of the proposed controller, the control algorithm is numerically implemented and applied to the speed control of an induction motor. Furthermore, a comparative study with the conventional PID, the fuzzy logic control (FLC), the computed torque control (CTC) and the PSO-based neural network model predictive controller (NNMPC-PSO) controllers is carried out. The paper is organized as follows. The TLBO algorithm is described in Sect. 2. The proposed NNMPC-TLBO algorithm is presented in Sect. 3. In Sect. 4, the simulation results are given and discussed, while the experimental results are presented in Sect. 5. Finally, some conclusions are given in Sect. 6.

2 Teaching–Learning-Based Optimization Algorithm

TLBO is a teaching–learning process inspired algorithm that was proposed by Rao et al. (2011; 2012). Like other meta-heuristic methods, TLBO is a population-based method that uses a population of solutions to search for the global solution. The population is considered as a group of learners, and the search process is divided into two phases: the teacher and the learners phases. In the teacher phase, the learners learn from their teacher, while in the learners phase, the learners learn by interacting between themselves. The taught subjects are considered to be the cost function variables, and the fitness value of the optimization problem is considered as the learners’ results. The teacher is considered to be the best solution in the entire population.

2.1 Teacher Phase

The algorithm starts with the teacher phase where the learners learn from their teacher. Assuming that m subjects (variables) exist with n learners (population size), at any iteration i, this phase can be decomposed into five sub-steps:

• 1. A teacher is selected from the population by choosing the best learner $X_{j\ k_\mathrm{best}}^i (j=1,2,...,m,k=1,2,...,n)$ in each subject.

• 2. The learner mean result $M_{ji}$, for each subject j, is calculated using the following equation:

  $$\begin{aligned} M_{ji}=\frac{\sum ^n_{l=1}X_{jl}^i}{n}. \end{aligned}$$

  (1)

• 3. The distance between the teacher and the learners mean result, named the difference mean, is evaluated, for each subject, as follows:

  $$\begin{aligned} d_{j\ k}^i=r_i(X_{j\ k_\mathrm{best}}^i-T_F M_{ji}) \end{aligned}$$

  (2)

  where $r_i$ is a random number between 0 and 1, $T_F$ is a random integer number, called the teaching factor, and its purpose is to determine the changed mean value. According to Rao (2016), good performances are obtained when $T_F$ is chosen to be 1 or 2, where $T_F=\mathrm{round}(1+\mathrm{rand}(0,1))$.

• 4. The existing solutions are updated by adding the difference mean to each one of them:

  $$\begin{aligned} Xnew_{j\ k}^i=X_{j\ k}^i+d_{j\ k}^i. \end{aligned}$$

  (3)

• 5. Finally, greedy selection is applied between the old and new updated solution $(Xnew_{j\ k}^i\ and\ X_{j\ k}^i)$ in order to only keep the best solution.

2.2 Learners Phase

It is the phase where the learners try to improve themselves by interacting with each other. The learner $X_A$ chooses randomly to interact with the learner $X_B$ and learn from him. This phase can be decomposed into three sub-steps:

• 1. Choose randomly q pairs of solutions such that $F_A^i \ne F_B^i$, where $F_A^i$ and $F_B^i$ are the objective function values of $X_A$ and $X_B$ at the $i^th$ iteration, respectively.

• 2. For each pair, update the solutions using the following equations (in case of a minimization problem):

  $$\begin{aligned} Xnew_{j\ A}^i= & {} X_{j\ A}^i+r_i(X_{j\ A}^i-X_{j\ B}^i),\quad \hbox { if } F_A^i<F_B^i\nonumber \\ \end{aligned}$$

  (4)
  $$\begin{aligned} Xnew_{j\ A}^i= & {} X_{j\ A}^i+r_i(X_{j\ B}^i-X_{j\ A}^i),\quad \hbox { if }\ F_B^i<F_A^i.\nonumber \\ \end{aligned}$$

  (5)

• 3. For each updated solution, evaluate the objective function. Accept the updated solution only if it enhances the solution.

2.3 Initialization Step

Before starting the TLBO algorithm, an initialization step is required to initialize the following parameters:

• The dimension m of the optimization problem ($m\ =$ number of optimized variables).

• The population size n. The choice of the population size has a large impact on the meta-heuristic algorithms performance. So, choosing the population size depending on some factors, two of them are the converging speed and the solution accuracy (Chen et al. 2014; Bolufé-Rohler and Chen 2013).

• The maximum number of iterations $k_{\max }$. The choice of this parameter value depends on the chosen sampling time.

• The admissible maximum and minimum values for each variable $X_{j_{\min }}$ and $X_{j_{\max }}$.

• The initial solutions $X_{j\ k}^1$ are randomly chosen using the following equation:

  $$\begin{aligned} X_{j\ k}^1=rand(0,1)\cdot (X_{j_{\max }}-X_{j_{\min }})+X_{j_{\min }}. \end{aligned}$$

  (6)

• The minimum value of the termination criterion $\varepsilon$.

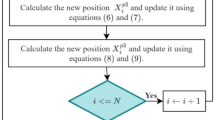
To illustrate the TLBO algorithm, a flowchart is given in Fig. 1.

Fig. 1

TLBO algorithm flow chart

3 Neural Network Model Predictive Control based on TLBO Algorithm

3.1 Principle

Two main steps are common to almost all MPC algorithms: the explicit model used to predict the future process behaviour and the optimization problem from which a control sequence is derived. The different steps to design a MPC law are given as follows:

• At each sampling time, a reference trajectory is specified over a given prediction horizon.

• Using the system model, the future values of the system outputs are computed over a given prediction horizon.

• A future control sequence is calculated, over a given control horizon, by minimizing a given cost function.

• Only the first element of the calculated control sequence is to be applied on the system.

The NMPC optimization problem is generally defined as follows:

$$\begin{aligned} \begin{aligned}&\min _{u(k)}J(\varDelta u(k),\hat{y}(k),c(k))\\&\quad =\sum _{i=N_1}^{N_2} \bigg [\Big (\hat{y}(k+i/k)-c(k+i)\Big )^TQ\\&\qquad \Big (\hat{y}(k+i/k)-c(k+i)\Big ) \bigg ]\\&\qquad +\sum _{i=1}^{N_u}\bigg [\varDelta u^T(k+i-1)R\varDelta u(k+i-1)\bigg ] \end{aligned} \end{aligned}$$

(7)

subject to

$$\begin{aligned}&\varDelta u(k+i-1)=0\quad \text {for} \quad i>N_u\\&y_{\min }<\hat{y}(k)<y_{\max }\\&u_{\min }<u(k)<u_{\max }\\&\varDelta u_{\min }<\varDelta u(k)<\varDelta u_{\max }\quad \text {for} \quad i \le N_u\end{aligned}$$

where

u(k) is the control input.

$\varDelta u(k)$ is the control increment, and it is defined by:

$$\begin{aligned}\varDelta u(k)= & {} u(k)-u(k-1)\quad \text {for}\quad i\le N_u \\ \varDelta u(k)= & {} 0\quad \text {for}\quad i>N_u \end{aligned}$$

$N_1$ and $N_2$ are the minimum and the maximum prediction horizon.

$N_u$ is the control horizon.

Q and R are positive definite matrix and positive semi-definite matrix, respectively.

$\hat{y}(k)$ is the estimated value of the system output at time k.

c(k) is the reference trajectory value at time k.

3.2 Constraints Handling

Predictive control is known by its ability to efficiently and directly handle the constraints by incorporating theme in the formulation of the optimization problem. Inputs and outputs constraints are due to physical limitations, safety reasons, economical and environmental objectives. Several approaches can be envisaged to handle these constraints (Coello 2002; Michalewicz and Schoenauer 1996; Koziel et al. 1999). In the proposed NNMPC-TLBO algorithm, the input constraints are directly handled by bounding the search space, while for handling the output ones, the penalty function approach is used. This penalty approach is based on adding new variables, called slack variables, to the cost function, that will heavily penalize any constraints violation. Using this approach, the optimization problem given in Eq. 7 will be reformulated to have the following expression:

$$\begin{aligned} \begin{aligned}&\min _{u(k)}J(\varDelta u(k),\hat{y}(k),c(k))\\&\quad =\sum _{i=N_1}^{N_2} \bigg [ \Big (\hat{y}(k+i/k)-c(k+i)\Big )^T\varGamma _y\\&\qquad \Big (\hat{y}(k+i/k)-c(k+i)\Big ) \bigg ]\\&\qquad +\sum _{i=1}^{N_u}\bigg [\varDelta u^T(k+i-1)R\varDelta u(k+i-1)\bigg ] \end{aligned} \end{aligned}$$

(8)

subject to

$$\begin{aligned}&\varDelta u(k+i-1)=0\quad \text {for} \quad i>N_u\\&u_{\min }<u(k)<u_{\max }\\&\varDelta u_{\min }<\varDelta u(k)<\varDelta u_{\max }\quad \text {for} \quad i \le N_u\end{aligned}$$

where the output-dependent weight function $\varGamma _y (y)$ was chosen to replace the imposed output constraint, and it has the following expression:

$$\begin{aligned} \begin{bmatrix} \varGamma _{y_1}(y_1) &{} 0 &{} \dots &{} 0 \\ 0 &{} \varGamma _{y_2}(y_2) &{} \dots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \dots &{} \varGamma _{y_n}(y_n) \end{bmatrix} \end{aligned}$$

where

$$\begin{aligned} \varGamma _{y_i}(y_i)=\left\{ \begin{array}{ll} \varGamma _{y_i}(0)&{} \quad \text {if} \quad y_{min_i} \le y_i \le y_{max_i} \\ \varGamma _{y_i}(0) [ 1+C_{i_y}] &{}\quad \text {if} \quad y_i<y_{min_i} \text { or } y_i>y_{max_i} \end{array} \right. . \end{aligned}$$

$i=1,2,\dots ,n$ (n is the outputs number).

$y(k)=[y_1 (k),y_2 (k),\dots ,y_n (k)]^T$.

$C_{i_y}$ is used to define the penalization degree: $C_{i_y}=0$ indicates no constraint, while $C_{i_y}=\infty$ indicates hard constraint.

In population-based algorithms, the input constraints can be systematically handled by bounding the search space to the inputs admissible values. The inputs constraints to be handled are:

• constraints on the input increment:

  $$\begin{aligned} \varDelta u_{\min }<\varDelta u(k)<\varDelta u_{\max } \end{aligned}$$

  (9)

• constraints on the input magnitude:

  $$\begin{aligned}&u_{\min }< u(k)<u_{\max }\nonumber \\&u_{\min }-u(k-1)< u(k)-u(k-1)<u_{\max }-u(k-1)\nonumber \\&\quad \rightarrow u_{\min }-u(k-1)<\varDelta u(k)<u_{\max }-u(k-1).\nonumber \\ \end{aligned}$$

  (10)

Hence, from Eqs. 9 and 10, the upper and the lower bounds of the input increments will be given by:

$$\begin{aligned} L_{\min }(k)<\varDelta u(k)<L_{\max }(k) \end{aligned}$$

where

$$\begin{aligned} L_{\min }(k)= & {} \left\{ \begin{array}{ll} \varDelta u_{\min } &{}\qquad \text {if} \qquad \varDelta u_{\min }> u_{\min }- u(k-1)\\ u_{\min }- u(k-1) &{}\qquad \text {otherwise} \end{array} \right. \\ L_{\max }(k)= & {} \left\{ \begin{array}{ll} \varDelta u_{\max } &{}\qquad \text {if} \qquad \varDelta u_{\max }< u_{\max }- u(k-1)\\ u_{\max }- u(k-1)&{} \qquad \text {otherwise}. \end{array} \right. \end{aligned}$$

3.3 Control Algorithm

Assuming that the MPC parameters ($N_u$, $N_1$, $N_2$ and $C_{i_y}$), the TLBO parameters (m, n and $k_{\max }$) and the neural network model have been established, the proposed NNMPC-TLBO algorithm can be described by the following steps:

• Step 1: Initialization

  • Let us take the control inputs, at the sampling time k, for the ith iteration, as $X_{j\ k}^i$ ,$(j=1,\dots ,m)$, where m denotes the number of control inputs.

  • For $j=1: m$

    • For $k=1: n$

      .:

      Choose the initial solution $X_{j\ k}^1$ using Eq. 6.

    • End

  • End

  • $i=1$

• Step 2: Reference trajectory

  • Specify the reference trajectory between $k+N_1$ and $k+ N_2$.

• Step 3: Teacher phase

  • Step 3_1: Determination of the teacher

    • For $k=1: n$

      .:

      1.Calculate the predicted values of the system outputs using the prediction model.

      .:

      2.Evaluate the objective function $F_k^i$ using Eq. 8.

    • End

    • $F_{k_{best}}=F_1^i$

    • For $k=2: n$

      .:

      If $F_k^i<F_{k_{best}}$

      .:

      $F_{k_{best}}=F_k^i$

      .:

      $X_{j\ k_{best}}= X_{j\ k}^i$

      .:

      End if

    • End

  • Step 3_2: Mean result calculation

    • For $j=1: m$

      • Calculate the mean result $M_{ji}$ using Eq. 1.

    • End

  • Step 3_3: difference mean calculation

    • For $j=1: m$

      .:

      For $k=1: n$

         Calculate $d_{jk}^i$ using Eq. 2.

      .:

      End

    • End

  • Step 3_4: Solution updating

    • For $j=1: m$

      .:

      For $k=1: n$

         Calculate the new solutions $Xnew_{j\ k}^i$ using Eq. 3.

      .:

      End

    • End

  • Step 3_5: Greedy selection

    • For $k=1: n$

      .:

      1.Using $Xnew_{j\ k}^i$, calculate the predicted values of the system outputs using the prediction model.

      .:

      2.Evaluate the objective function $new\_F_k^i$ using Eq. 8.

      .:

      If $new\_F_k^i < F_k^i$

         $F_k^i=new\_F_k^i$

         $X_{j\ k}^i=Xnew_{j\ k}^i$

      .:

      End if

      .:

      If$F_k^i<F_{k_{best}}$

         $F_{k_{best}}=F_k^i$

         $X_{j\ k_{best}}=X_{j\ k}^i$

      .:

      End if

    • End

• Step 4: Learner phase

  • Step 4_1: choosing the pairs to interact

    • Choose randomly q pairs of solutions such that $F_A^i\ne F_B^i$, where $F_A^i$ and $F_B^i$ are the objective function values of $X_A$ and $X_B$, respectively.

  • Step 4_2: Solutions updating

    • For $h=1: q$

         Update the solution $Xnew_{j\ k}^i$ using Eqs. 4 and 5.

    • End

  • Step 4_3: evaluating the new solutions

    • For $k=1: n$

      .:

      1.Using $Xnew_{j\ k}^i$, calculate the predicted values of the system outputs using the prediction model.

      .:

      2.Evaluate the objective function $new\_F_k^i$ using Eq. 8.

    • End

    • For $k=1: n$

      .:

      If $new\_F_k^i < F_k^i$

         $F_k^i=new\_F_k^i$

         $X_{j\ k}^i=Xnew_{j\ k}^i$

      .:

      End if

      .:

      If $F_k^i<F_{k_{best}}$

         $F_{k_{best}}=F_k^i$

         $X_{j\ k_{best}}=X_{j\ k}^i$

      .:

      End if

    • End

• Step 5: iterative process

  • if $F_{k_{best}}< \varepsilon$ or $i>k_{\max }$

       $i=1$

       Go to step 6.

  • else

       $i=i+1$

       Go back to step 3.

  • End if

• Step 6:

  • 1. Apply the obtained control value (the first element of $X_{j\ k_{best}}$ on the system.

  • 2. Wait for the next sampling time, and then go back to step 2.

4 Simulation Study

The efficiency of the proposed NNMPC-TLBO control algorithm is investigated in this section, by considering the control of the models of two highly nonlinear systems. The obtained results are then compared to those obtained using the NNMPC-PSO, the conventional PID controller, the computed torque control and the fuzzy logic controller. The first system is the continuous stirred tank reactor; it is a highly nonlinear chemical process. The second one is the two-degree-of-freedom manipulator robot; it is a coupled multi-input multi-output mechanical system.

4.1 Continuous Stirred Tank Reactor

The CSTR is a chemical process where a product A will be converted to another product B via an exothermic chemical reaction. The reactor volume v is constant, and the mixture is considered perfect with a uniform temperature T. The reactor operates continuously, its output (the mixture concentration $C_a$) changes nonlinearly according to the mixture temperature T, and the temperature changes according to the system input coolant flow $q_c$. This process is depicted in Fig. 2.

Fig. 2

Continuous Stirred Tank Reactor

The CSTR is described by the following equations:

$$\begin{aligned} \begin{aligned} \dot{C}_a(t)=&\frac{q}{v}\big (C_{a0}-C_a(t)\big )-k_0C_a(t)e^{\frac{-E}{RT(t)}}\\ \dot{T}(t)=&\frac{q}{v}\big (T_0-T(t)\big )+k_1C_a(t)e^{\frac{-E}{RT(t)}}\\ {}&+k_2q_c(t)\bigg (1-e^{\frac{-k_3}{q_c(t)}}\big (T_{c0}-T(t)\big ) \bigg ) \end{aligned} \end{aligned}$$

(11)

where

$$\begin{aligned} k_1=-\frac{\varDelta H k_0}{\rho C_p},\quad k_2=\frac{\rho _c C_{pc}}{\rho C_p v},\quad k_3=\frac{h_a}{\rho _c C_{pc}} \end{aligned}$$

where v is the reactor volume expressed in litre, $C_{a0}$ is the initial mixture concentration expressed in mol/l, $T_0$ is the initial temperature expressed in Kelvin, $T_{c0}$ is the initial jacket temperature expressed in Kelvin, $T_c$ is the jacket temperature expressed in Kelvin, $C_a(t)$ is the mixture concentration expressed in mol/l, T(t) is the mixture temperature expressed in Kelvin and $q_c(t)$ is the coolant flow expressed in l/min.

The constants values are given in Table 1.

Table 1 CSTR constants values

4.1.1 Process Identification

The first step of any MPC design is obtaining a model for the system to be controlled. This model is used to predict the future values of the system outputs. In the proposed NNMPC-TLBO controller, a static MLP with the following configuration is used.

• The input layer contains four inputs : $\big (q_c (k),\ q_c (k-1),\ C_a(k-1),\ C_a (k-2)\big )$.

• One hidden layer containing ten neurons with a sigmoid activation function.

• The output layer, which contains a single neuron with a linear activation function, gives the estimated output $\hat{C}_a (k)$.

Two different datasets, which cover all possible system working regimes, are generated using the system model expressed in equation (11). The first one is used to train the neural network, and the second one is used to test the trained model. Figure 3 gives the system and the model outputs which are superposed and the modelling error which is quite small. The values of the root mean square of the modelling error (RMSE) and the correlation coefficient ($R^2$), which are 6.909e-5 and 0.99999943, respectively, show the good accuracy of the obtained model.

Fig. 3

Test results of the obtained model

Fig. 4

CSTR control block diagram

Table 2 PSO parameters values

4.1.2 Controller Implementation

Four controllers are designed to control the mixture concentration $C_a (t)$, namely the proposed NNMPC-TLBO, the NNMPC-PSO, the fuzzy logic controller (FLC) and the conventional PID controller. In case of the first two controllers, the control block diagram is given in Fig. 4. The parameters of the PSO algorithm used in the second controller are gathered in Table 2. The design procedure and the parameters values of the FLC and the PID controllers can be found in Benrabah et al. (2019). Both NNMPC controllers use the same control parameters values given in Table 3. In this case, no constraint on the output was imposed. The obtained control results are given in Fig. 5, when the reference trajectory moves to 0.08, 0.11, 0.14, 0.11 and 0.08 mol/l. For each controller and for the same initial conditions, the average values, over a thousand runs, of the mean squared error (MSE), the mean absolute error (MAE) and the RMSE are given in Table 4. The execution time is very important in order to evaluate the computing efficiency and the real-time applicability of the proposed controller. Starting the NNMPC-TLBO and the NNMPC-PSO from the same initial conditions, the required time to obtain a value of the control signal is evaluated for both controllers and given in Table 5.

Table 3 MPC parameters values

Table 4 MSE, MAE and RMSE values for each controller

Fig. 5

Control results of the CSTR model using NNMPC-TLBO, NNMPC-PSO, FLC and PID controllers

From Fig. 5 and Table 4, it can be seen that a good tracking accuracy of the reference trajectory is obtained for both NNMPC-TLBO and NNMPC-PSO controllers. However, in case of the FLC and the PID controllers, a degradation in the control performance for large amplitude of the reference trajectory is observed. Comparing the MSE, the MAE and the RMSE values given in Table 4, we note that the proposed controller is more efficient in this experiment than the NNMPC-PSO, the FLC and the PID controllers. From Table 5, we notice that the computing time of the NNMPC-TLBO is lower than that of the NNMPC-PSO.

In a second case, an output constraint limiting the overshoot to no more than $2\%$ is imposed. Since the FLC and the PID controllers cannot handle constraints, the comparison is only made between the NNMPC-TLBO and NNMPC-PSO. The NNMPC-TLBO and NNMPC-PSO are implemented using the parameters values given in Tables 2 and 3. The constraints handling parameter $C_{1_y}$ is taken equal to 100. The obtained results are summarized in Fig. 6. Table 6 gives the maximal values of the process output and the maximal values of the control input, for both controllers, when the reference trajectory moves to 0.08, 0.11 and 0.14 mol/l. Using the same initial conditions, the average values, over a thousand runs, of the computing time, the MSE, the MAE and the RMSE are given in Table 7.

Table 5 Computing time for NNMPC-TLBO and NNMPC-PSO algorithms

Fig. 6

Control results using NNMPC-TLBO and NNMPC-PSO controllers for the case of imposed output constraints

Table 6 Input and output CSTR limits values using both NNMPC_TLBO and NNMPC_PSO controllers

Table 7 Computing time, MSE, MAE and RMSE values in case of an imposed output constraint

It can be observed from Fig. 6 and Table 6 that the imposed constraints are respected for both controllers, and the obtained overshoots for the NNMPC-TLBO controller when the reference trajectory is set to 0.11 mol/l or 0.14 mol/l are smaller than those obtained in the case of the NNMPC-PSO controller. Comparing the computing time, MSE, MAE and RMSE values given in Table 7, we note that the proposed algorithm is faster and more efficient than the NNMPC-PSO controller.

4.2 Two-Degree-of-Freedom Manipulator Robot

The dynamic model of the considered manipulator (Fig. 7), is expressed as follows (Lin. 2007):

$$\begin{aligned} \begin{bmatrix} Q_{11} &{} Q_{12} \\ Q_{21} &{} Q_{22} \end{bmatrix} \begin{bmatrix} \ddot{\theta }_1 \\ \ddot{\theta }_2 \end{bmatrix} + \begin{bmatrix} P_{11}\\ P_{21} \end{bmatrix} + \begin{bmatrix} f_1\\ f_2 \end{bmatrix} + \begin{bmatrix} g_{1q}\\ g_{2q} \end{bmatrix} = \begin{bmatrix} \tau _{f_{in1}}\\ \tau _{f_{in2}} \end{bmatrix}\nonumber \\ \end{aligned}$$

(12)

where

$\tau _{f_{in1}}$, $\tau _{f_{in1}}$ are the control torques for joints 1 and 2, respectively,

$$\begin{aligned} Q_{11}=&I_1+I_2+m_1 l_{c1}^2+m_2 l_1^2+m_2 l_{c2}^2+ 2m_2 l_1 l_{c2} \cos {\theta _2} \\&+ m_{33} (l_1^2+l_2^2+2l_1 l_2 \cos {\theta _2}).\\ Q_{12}=&I_2+m_2 l_{c2}^2+m_2 l_1 l_{c2}\cos {\theta _2}+m_{33} (l_2^2+l_1 l_2 \cos {\theta _2}).\\ Q_{21}=&Q_{12}.\\ Q_{22}=&I_2+m_2 l_{c2}^2+m_{33} l_2^2.\\ P_{11}=&-l_1 (2\dot{\theta }_1+\dot{\theta }_2)\dot{\theta }_2 \sin {\theta _2}(l_{c2} m_2+l_2 m_{33}).\\ P_{21}=&l_1 l_{c2} \dot{\theta }_1^2\sin {\theta _2} (m_2+m_{33}).\\ f_1\ =&b_{1q} \dot{\theta }_1.\\ f_2\ =&b_{2q} \dot{\theta }_2.\\ g_{1q}=&m_1 l_{c1} g\cos {\theta _1}+m_2 g (l_{c2} \cos {(\theta _1 + \theta _2)}+ l_1 \cos {\theta _1})\\&+m_{33} g (l_2 \cos {(\theta _1 + \theta _2)} + l_1 \cos {\theta _1}).\\ g_{2q}=&(m_2+m_{33})g l_{c2} \cos {(\theta _1 + \theta _2)}. \end{aligned}$$

Fig. 7

Two-degree-of-freedom planar robotic manipulator

The numerical values for the different constants are given in Table 8.

Table 8 Parameters values of the considered manipulator

4.2.1 System Identification

Two static MLPs are used to emulate the dynamics of the considered manipulator. Their structure is defined as follows:

• Both MLPs have the same input vector, which is given by:

  $$\begin{aligned} \begin{aligned}{}[&\tau _{f_{in1}}(k),\tau _{f_{in1}}(k-1),\tau _{f_{in2}}(k),\tau _{f_{in2}}(k-1),\theta _1(k),\\&\theta _1(k-1),\theta _2(k),\theta _2 (k-1) ]. \end{aligned} \end{aligned}$$

• Each MLP has one hidden layer containing 20 neurons with a sigmoid activation function.

• Each MLP has one neuron in the output layer with a linear activation function.

• The first MLP gives the estimated value $\hat{\theta }_1(k)$ of joint1 angle, while the second one gives the estimated value $\hat{\theta }_2(k)$ of joint2 angle.

The neuronal models are trained using the dataset generated from the state model given in Eq. 12. Figures 8 and 9 show the test results of the obtained models, where it can be seen that the modelling error is quite small. The values of the RMSE and $R^2$ for the model of $\theta _1$ and the model of $\theta _2$ are : 0.00200654, 0.99999950718, 0.00211524 and 0.99999277711, respectively. The RMSE values are close to zero, and $R^2$ values are close to one, which indicates that the obtained models have good accuracy.

Fig. 8

Joint1 NN model validation result

Fig. 9

Joint2 NN model validation result

4.2.2 Controller Implementation

Three controllers, namely computed torque control (CTC), NNMPC-TLBO and NNMPC-PSO, were designed to control the angular positions of joints 1 and 2 of the considered manipulator. The CTC control law is given by:

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \tau _{f_{in1}}\\ \tau _{f_{in2}} \end{bmatrix} =&\begin{bmatrix} Q_{11} &{} Q_{12} \\ Q_{21} &{} Q_{22} \end{bmatrix} \bigg ( \begin{bmatrix} \ddot{\theta }_{d_1} \\ \ddot{\theta }_{d_2} \end{bmatrix} + k_v \begin{bmatrix} \dot{\theta }_{d_1}-\dot{\theta }_1 \\ \dot{\theta }_{d_2}-\dot{\theta }_2 \end{bmatrix} + k_p \begin{bmatrix} \theta _{d_1}-\theta _1 \\ \theta _{d_2}-\theta _2 \end{bmatrix} \bigg ) \\ {}&+ \begin{bmatrix} P_{11}\\ P_{21} \end{bmatrix} + \begin{bmatrix} f_1\\ f_2 \end{bmatrix} + \begin{bmatrix} g_{1q}\\ g_{2q} \end{bmatrix} \end{aligned} \end{aligned}$$

where $\theta _{d_1}$ and $\theta _{d_2}$ are the desired references trajectories. The $k_v$ and $k_p$ values, optimized using the PSO algorithm, are 26.3077 and 2.6853e+02, respectively. The control block diagram of the NNMPC-TLBO and NNMPC-PSO is given in Fig. 10, and the design parameters for both controllers are given in Table 9. The parameters of the PSO algorithm are given in Table 2.

The efficiency of the proposed controller is evaluated by considering the two following cases.

Fig. 10

Robot manipulator control block diagram

Table 9 MPC parameters values

In the first case, no outputs constraints are imposed and two different reference trajectories are used. The obtained results are shown in Fig. 11 for the multistep trajectory and Fig. 12 for the sinusoidal trajectory.

Fig. 11

Control performance using NNMPC-TLBO, NNMPC-PSO and CTC controllers with a multistep trajectory

Fig. 12

Control performance using NNMPC-TLBO, NNMPC-PSO and CTC controllers with a sinusoidal trajectory

A good tracking accuracy of the reference trajectories is obtained for all controllers. However, the tracking error of the proposed controller is slightly smaller than that of the other controllers.

To see the difference in the control performance between the three controllers, the same experiment is repeated thousand times, and at each run, the population of the PSO and TLBO algorithm is randomly initialized. The average values of the MSE, the MAE and the RMSE are given in Table 10, where it can be seen that the NNMPC-TLBO controller has better tracking accuracy than the NNMPC-PSO and the CTC controllers. The computing time for both NNMPC-TLBO and NNMPC-PSO algorithms is calculated and given in Table 11, and it can be seen that the computing time of the proposed controller is smaller than that of the NNMPC-PSO algorithm.

Table 10 MSE, MAE and RMSE values using NNMPC-TLBO, NNMPC-PSO and CTC controllers

Table 11 Computing time for NNMPC-TLBO and NNMPC-PSO algorithms in case of reference and multistep trajectories

In the second case, output constraints, limiting the overshoot to no more than $1\%$, are imposed. The design parameters given in Table 9 are used for both controllers. The output-dependent weight function $\varGamma _{y} (y)$ has the following parameters: $C_{1_y}=100, C_{2_y}=100$. Figure 13 gives the obtained control performance, and Table 12 gives the average values, over thousand runs, of the computing time, the MSE, the MAE and the RMSE. From Fig. 13 and Table 12, it can be concluded that the TLBO-based controller has better control performance than the PSO-based controller.

Fig. 13

Control performance using NNMPC-TLBO and NNMPC-PSO controllers with output constraints

Table 12 Computing time, MSE, MAE and RMSE values using NNMPC-TLBO and NNMPC-PSO controllers with output constraints

Remark The following set-up has been used to calculate all computing times cited above:

• 1. MATLAB environment.

• 2. Desktop computer with the following hardware:

  • Intel(R) Core(TM) i7-7700 CPU @ 3.60 GHz.

  • 4.00 Go of RAM

  • Windows 10 Pro x64.

5 Experimental Study

To further demonstrate the effectiveness of the proposed controller, the experimental set-up shown in Fig. 14 is used to control the speed of an induction motor. In addition to the three-phase squirrel-cage induction motor, this experimental set-up contains the following elements: a three-phase voltage source inverter, a TMS320F28335 DSP board and a single computer board RASPBERRY PI 3B+. The control algorithm is implemented in the single computer board RASPBERRY, and the DSP board is used to generate the six required pulse width modulated (PWM) signals and measure the motor speed. The control block diagram is given in Fig. 15.

Fig. 14

Experimental set-up

Fig. 15

The induction motor control block diagram

5.1 Identification of the System

A neural network model, for the considered induction motor, is derived using the experimental collected data. This model is a simple static MLP with an input layer containing four inputs $[v_1(k),v_2(k),v_3(k),\omega (k-1)]$, a hidden layer of four neurons with sigmoid activation function and an output layer that contains one linear neuron representing the estimated angular speed $\hat{\omega }(k)$. $v_1 (k)$, $v_2 (k)$ and $v_3 (k)$ are the applied voltages on the motor at the sampling time k and $\omega (k-1)$ is the measured angular speed of the motor. The response of the obtained model to the input test is given in Fig. 16, where it can be seen the modelling error is quite small. The RMSE and the $R^2$ values of the obtained model are 11.19669 and 0.99976, respectively. Since the amplitude of the system output ranges between − 1500 and 1500 tr/min, the RMSE value is acceptable. The $R^2$ value is close to one, which indicates that the model has good accuracy.

Fig. 16

Model testing results for the induction motor

Table 13 Values of the design parameters

Fig. 17

NNMPC-TLBO controller performance for the case of a multistep trajectory

5.2 Controller Implementation

The controller is implemented using the design parameters given in Table 13 and the obtained neural network model. The control objective is to force the motor speed to track two different reference trajectories: the sinusoidal and the multistep trajectories. The results are given in Figs. 17 and 18.

Figures 17 and 18 show that good tracking accuracy is obtained for both trajectories, and the maximal value for the overshoot does not exceed 4%. For both (step and sinusoidal) reference trajectories, the maximum values of the computing time are 5.225 ms and 6.402 ms, respectively, which indicates that the proposed controller can be implemented in real time to control systems with fast dynamics.

Fig. 18

NNMPC-TLBO controller performance for the case of a sinusoidal trajectory

Fig. 19

NNMPC-TLBO controller performance in the presence of output constraints

Table 14 MSE, MAE and RMSE using NNMPC-TLBO controller

In a second experiment, to further reduce the observed overshoot, a constraint on the output limiting the overshoot to no more than 2% is included. A multistep reference trajectory and the parameter $C_y=100$ of the output-dependent weight function $\varGamma _y(y)$ are used in this experiment. The obtained control results are given in Fig. 19, where it can be seen that the overshoot value does not exceed 2% and the maximum value of the computing time is 5.839ms.

Table 14 gives the values of the MSE, the MAE and the RMSE for the released experiments. From this table, we can conclude that the proposed controller gives good control performances and the imposed constraints are respected.

6 Conclusion

An efficient constrained nonlinear predictive control algorithm, called neural network model predictive control using teaching–learning-based optimization, has been proposed. This controller uses a neural network model to predict the future values of the system outputs and the TLBO method to solve the resulting optimization problem. Neural networks are known for their simplicity and precision in approximating any nonlinear mapping, and the TLBO method does not require any algorithm-specific parameters. Although the proposed controller incorporate in its design the imposed constraints, its structure is simple and can be easily implemented to control, in real time, nonlinear systems with fast dynamics. It has been shown, using both simulation and experimental studies, that the proposed controller gives good control performance in terms of the tracking accuracy, computing time, constraints handling and the overshoot amplitude. The NNMPC-TLBO algorithm can be successfully used to control different classes of nonlinear systems. Indeed, the control of a highly nonlinear chemical process, a coupled multivariable mechanical system and an electrical machine were considered.