Nonlinear Neuro-Adaptive Control for MPPT Applied to Photovoltaic Systems

Abstract

This paper presents an intelligent control technique using a nonlinear neuro-adaptive method. This method is based on a nonlinear model describing the dynamics of the boost converter, the PV array and the load for maximum power point tracking (MPPT) under varying environmental conditions. The proposed approach consisted of a radial basis function-neuro observer for online estimation of unknown PV system parameters (i.e., irradiation and temperature) and an online trained neuronal controller that ensures a satisfactory MPPT, whatever be the position of the photovoltaic panel. The real-time implementation of the proposed controller is achieved using Arduino Mega board. The performance of the proposed MPPT method is analyzed under different operating conditions and compared to those provided by the P&O method. Simulation results using MATLAB/Simulink software coupled to experimental results demonstrate the feasibility and the robustness of the proposed controller.

1 Introduction

Renewable energy capacity has increased these last years due to its main objective to alleviate the problem of pollution caused by traditional energy source (Kenne et al. 2017). Solar energy has particularly captivated more attention in recent decades (Le Feuvre and Wieczorek 2011; Yin et al. 2015; Parra et al. 2015). The lowest environmental impact and the significant presence of solar radiation on the earth make photovoltaic (PV) systems one of the most interesting solutions to electricity generation (Sajadian and Ahmadi 2017; Chen et al. 2016; Mills and Wiser 2013). Indeed, the electricity produced by photovoltaic cells is an unstable energy because it depends on diverse factors such as the temperature, the level of solar irradiation, shadow, dirt, spectral characteristics of sunlight, and so on. It is therefore important to operate the photovoltaic system at the point of maximum power in order to increase its efficiency. Accordingly, the MPPT controller is one of the viable solutions to improve the productivity of PV systems under variable weather conditions.

The literature contains several approaches for MPPT in photovoltaic systems. These techniques include Hill Climbing (HC) (Kamarzaman and Tan 2013; Liu et al. 2008), perturb and observe (P&O) (Femia et al. 2009, 2005; Rezaei and Asadi 2005), incremental conductance (IC) (Li and Wang 2009; Reisi et al. 2013; Rajabi and Hassan Hosseini 2019), fractional open-circuit voltage (Mutoh et al. 2002; Yuvarajan and Xuc 2003), fractional short-circuit current (Kobayashi et al. 2004; Bekker and Beukes 2004), neural network (Hiyama et al. 1995, fuzzy logic methods (Won et al. 1994), and genetic algorithms (Larbes et al. 2009). These methods differ in several aspects such as oscillation around the MPP, required sensors, convergence speed, complexity, cost and correct tracking.

There are several advantages such as fast tracking, robust operation, nonlinear systems tolerant and on-line training. Therefore, various artificial neural network-based PV MPPT techniques have been elaborated (Cha et al. 1997; Singh et al. 2014).

Nevertheless, the number of sensors required to implement any MPPT technique affects the decision process since these sensors induce the major burden for the overall PV system cost (Giraud and Salameh 1999; Mathew and Selvakumar 2011; Veerachary et al. 2003; Bendib et al. 2014). The cost, in addition to the lack of robustness of irradiance/temperature sensors, is the main limit for the artificial neural network-based MPPT methods (Mathew and Selvakumar 2011; Baek et al. 2010; Ko et al. 2008; Al-Amoudi and Zhang 2000; Pachauri and Chauhan 2014), especially when a wide PV plant, involving several hundreds of PV panels, is considered.

In this work, an intelligent control technique based on adaptive neural network for maximum power point tracking during unexpected changes in atmospheric conditions is proposed. The idea is to evolve a sensorless controller that does not require climatic variable sensors (i.e., temperature and solar radiation) and to provide a satisfactory MPPT, whatever the position of the photovoltaic panel. Specifically, a sensorless nonlinear neuro-adaptive controller is designed using the RBF-neural network observer technique based on a nonlinear model describing the whole system, including the PV arrays, and the boost converter. The proposed adaptive controller involves online estimation of the model uncertain parameters that depend on radiation and temperature. Based on the obtained simulation results in Matlab/Simulink environment, the adaptive neuro-controller actually tracks effectively and efficiently the maximum power point. Additionally, experimental implementation using an Arduino Mega board is carried out.

The remainder of the work is organized as follows: Sect. 2 presents in detail the elements of a PV conversion system. In Sect. 3, the proposed approach is introduced, and the stability is investigated. Sections 4 and 5 present, respectively, the simulation and experimental results. The conclusions are given in Sect. 6.

2 PV System Model

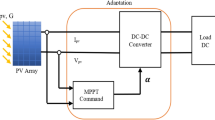
Figure 1 shows the basic structure of a photovoltaic system. It consists of a DC/DC converter, a photovoltaic generator, a load and the proposed MPPT control unit. The main function of the converter is to interface the output of the photovoltaic generator to the load and to track the MPP.

Fig. 1

Photovoltaic system made up of a PV array, a DC/DC converter and the proposed MPPT control algorithm

Photovoltaics is the direct conversion of light into electrical energy. Figure 2 shows the equivalent circuit of a photovoltaic cell (Rekioua and Matagne 2012; Safari and Mekhilef 2011; Moura and Chang 2013; Tan et al. 2010). In the PV system control literature, this circuit has been considered as a sufficiently good representation of the physical system for the purposes of MPPT control design (Masters 2004; Vachtsevanos and Kalaitzakis 1987; Villalva et al. 2009; Kwon et al. 2008; Tchouani Njomo et al. 2020). The solar cell terminal current is expressed as follows:

$$\begin{aligned} I_{\mathrm{Po}}= & {} I_{\mathrm{Pho}}-I_{\mathrm{Do}}-I_{\mathrm{Sho}} \end{aligned}$$

(1)

where $I_{\mathrm{Pho}}$ is the photocurrent (current generated by radiation), $I_{\mathrm{Do}}$ is the current through the diode, and $I_{\mathrm{Sho}}$ is the current through the parallel resistor.

Fig. 2

Electrical model of a photovoltaic cell

The relationship between the current $I_{\mathrm{Pho}}$ and the voltage $V_{\mathrm{Po}}$ of equivalent circuit of the photovoltaic cell is given by:

$$\begin{aligned} I_{\mathrm{Po}}= & {} I_{\mathrm{Pho}}-I_{\mathrm{so}}\left[ \exp \left( \frac{V_{\mathrm{Po}}+I_{\mathrm{Po}}R_{\mathrm{so}}}{nV_{T}}\right) -1\right] \nonumber \\&\quad -\frac{V_{\mathrm{Po}}+I_{\mathrm{Po}}R_{\mathrm{so}}}{R_{\mathrm{Sho}}} \end{aligned}$$

(2)

The relation between the current $I_{\mathrm{Po}}$ and the voltage $V_{\mathrm{Po}}$ in the ideal conditions ($R_{\mathrm{so}}=0$, $R_{\mathrm{Sho}}=\infty$) is described by the following equation:

$$\begin{aligned} I_{\mathrm{Po}}= & {} I_{\mathrm{Pho}}-I_{\mathrm{so}}[\exp (BV_{\mathrm{Po}})-1] \end{aligned}$$

(3)

$$\begin{aligned} B= & {} \frac{q}{nKT} \end{aligned}$$

(4)

where $I_{\mathrm{so}}$ is the cell reverse saturation current; K is the Boltzmann’s constant; T is the cell temperature, and q is the electron charge. The generated photocurrent $I_{\mathrm{Pho}}$ is given by the following equation:

$$\begin{aligned} I_{\mathrm{Pho}}= & {} \left[ I_{\mathrm{SCR}}+K_{I}\left( T-T_{\mathrm{or}}\right) \right] \frac{G}{1000} \end{aligned}$$

(5)

The cell saturation current $I_{\mathrm{so}}$ can be shown as:

$$\begin{aligned} I_{\mathrm{so}}= & {} I_{\mathrm{sor}}\left[ \frac{T}{T_{\mathrm{or}}}\right] ^{3}\exp \left[ \frac{\mathrm{EG}}{nK}\left( \frac{1}{T_{\mathrm{or}}}-\frac{1}{T}\right) \right] \end{aligned}$$

(6)

where $I_{\mathrm{SCR}}$ is the short circuit current at 298.15 K and 1000 W/m$^{2}$, $T_{\mathrm{or}}$ is the reference temperature, G is the solar radiation, EG is the bandgap energy of the semiconductor, and $I_{\mathrm{sor}}$ is the nominal saturation current. A photovoltaic generator is composed of elementary photovoltaic cells connected in series-parallel manner in order to obtain the desired electronic characteristics such as power, short-circuit current or open-circuit voltage. This photovoltaic generator exhibits a nonlinear $V_{\mathrm{PV}}$–$I_{\mathrm{PV}}$ characteristics given, approximately and ideally, by the following equation:

$$\begin{aligned} I_{\mathrm{PV}}= & {} I_{\mathrm{php}}-I_{\mathrm{sp}}[\exp (A_{\mathrm{pv}}V_{\mathrm{PV}})-1] \end{aligned}$$

(7)

where $I_{\mathrm{PV}}$ and $V_{\mathrm{PV}}$ are, respectively, the current and voltage of photovoltaic generator. $I_{\mathrm{sp}}=N_{\mathrm{p}}I_{\mathrm{so}}$ is the saturation current of the photovoltaic generator, $I_{\mathrm{php}}= N_{\mathrm{p}}I_{\mathrm{Pho}}$ is the photocurrent of the photovoltaic generator, and $A_{\mathrm{pv}}=B/N_{\mathrm{s}}$ is photovoltaic generator constant. $N_{\mathrm{s}}$ is the number of PV connected in series, and $N_{\mathrm{p}}$ is the number of parallel parts.

The specifications of the PV module used in this paper are given in Table 1. The corresponding power value $P_{\mathrm{mp}}=V_{\mathrm{mp}}I_{\mathrm{mp}}$ is called MPP. The typical $I_{\mathrm{PV}}-V_{\mathrm{PV}}$ and $P_{\mathrm{PV}}-V_{\mathrm{PV}}$ characteristics of the MSX60 PV module are shown in Fig. 3. It can be seen from this figure that an increase in irradiance results in a power increment. However, an increase in PV temperature causes power decrement.

Table 1 Electrical characteristics of the MSX-60 photovoltaic

Fig. 3

Case of constant temperature and variable irradiation [current–voltage (a) and power–voltage characteristics (b)] and case of constant irradiation and variable temperature [current–voltage (c) and power–voltage characteristics (d)]

A DC/DC boost converter (Fig. 4) increases the PV voltage and provides a control actuator for MPPT. At the boost converter’s output, a capacitor maintains a roughly constant voltage (Krein et al. 1990).

Fig. 4

Circuit diagram of DC/DC boost converter model

Applying Kirchhoffś laws to the circuit of Fig. 4, one obtains the following dynamic model:

$$\begin{aligned} \frac{\mathrm{d}i_{L}}{\mathrm{d}t}= & {} -(1-k)\frac{Ri_{L}}{L}+\frac{1}{L}V_{\mathrm{PV}} \end{aligned}$$

(8)

$$\begin{aligned} \frac{\mathrm{d}V_{\mathrm{PV}}}{\mathrm{d}t}= & {} -\frac{1}{C}i_{L}+\frac{1}{C}I_{\mathrm{PV}} \end{aligned}$$

(9)

where $i_{L}$ denotes the inductor current, $V_{\mathrm{PV}}$ the PV voltage, $I_{\mathrm{PV}}$ the pv current, and k the duty ratio. For the control design purpose, it is more convenient to consider the following averaged model:

$$\begin{aligned} \frac{\mathrm{d}y_{1}}{\mathrm{d}t}= & {} -(1-k)\frac{Ry_{1}}{L}+\frac{1}{L}y_{2} \end{aligned}$$

(10)

$$\begin{aligned} \frac{\mathrm{d}y_{2}}{\mathrm{d}t}= & {} -\frac{1}{C}y_{1}+\frac{1}{C}I_{\mathrm{PV}} \end{aligned}$$

(11)

where $y_{1}$ and $y_{2}$ denote the averaged value, respectively, of the current $i_{L}$, and the input voltage $V_{\mathrm{PV}}$. The duty ratio k is the average value of the binary control k.

3 Design of Adaptive Controller for PV System

Combining (7) and (11) yields:

$$\begin{aligned}&\frac{\mathrm{d}y_{2}}{\mathrm{d}t}= -\frac{1}{C}y_{1}+\frac{1}{C}\rho _{1}(T,G)-\frac{1}{C}\varphi (T,V_{\mathrm{PV}})\rho _{2}(T) \end{aligned}$$

(12)

$$\begin{aligned}&\rho _{1}(T,G)= I_{\mathrm{php}} \end{aligned}$$

(13)

$$\begin{aligned}&\rho _{2}(T)= I_{\mathrm{sp}} \end{aligned}$$

(14)

$$\begin{aligned}&\varphi (T,V_{\mathrm{PV}})=\exp \left( A_{\mathrm{pv}}(T)V_{\mathrm{PV}}\right) -1. \end{aligned}$$

(15)

The parameters $\rho _{2}$ depends only on the temperature, while $\rho _{1}$ depends on temperature T and irradiation G. The function $\varphi$ depends on T. Because of the slowly fluctuating temperature, the effect of variation of $\varphi$ is very small compared to the effect of $\rho _{1}$ and $\rho _{2}$. Therefore, the following approximation can be made:

$$\begin{aligned} \varphi (T,V_{\mathrm{PV}})\approx & {} \exp \left[ A_{\mathrm{pv}}(T_{\mathrm{or}})V_{\mathrm{PV}}\right] -1\doteq \varphi (V_{\mathrm{PV}}) \end{aligned}$$

(16)

where $T_{\mathrm{or}}$ is a constant reference temperature. Combining (10), (12) and (15), we obtain the following average model of the PV system:

$$\begin{aligned} {\dot{y}}_{1}= & {} -(1-k)\frac{Ry_{1}}{L}+\frac{1}{L}y_{2} \end{aligned}$$

(17)

$$\begin{aligned} {\dot{y}}_{2}= & {} -\frac{1}{C}y_{1}+\frac{1}{C}\rho _{1}(T,G)-\frac{1}{C}\varphi (y_{2})\rho _{2}(T) \end{aligned}$$

(18)

Given that the energy produced by PV is heavily dependent on temperature and irradiation, it is absolutely essential that the sensors used to measure temperature and irradiation are reliable. Hence, to ensure maximum power point tracking (MPPT), the controller must enforce the voltage $y_{2}$ to track as possible the unknown voltage $V_{\max }$ which depends on both T and G given by the sensors. However, the periodic maintenance of the sensors can be very expensive. The price of the sensors increases with their precision. The proposed approach aims to reduce the cost of sensor maintenance (eliminate the temperature and irradiation sensors) and improve the MPPT technique. In fact, the MPP $(V_{\max },P_{\max })$ is reached when $\frac{\partial P_{\mathrm{PV}}}{\partial V_{\mathrm{PV}}}\mid _{V_{\mathrm{PV}}=V_{\max }}$ with $P_{\mathrm{PV}}=V_{\mathrm{PV}}I_{\mathrm{PV}}$.

The condition of a maximum power point can be described as

$$\begin{aligned} \frac{\partial P_{\mathrm{PV}}}{\partial V_{\mathrm{PV}}}= & {} I_{\mathrm{PV}}+V_{\mathrm{PV}}\frac{\partial I_{\mathrm{PV}}}{\partial V_{\mathrm{VP}}}=0 \end{aligned}$$

(19)

It follows, using (7), (13) and (14), that

$$\begin{aligned} \rho _{1}-\rho _{2}\left[ \left( 1+V_{\max }A_{\mathrm{PV}}(T_{r})\right) \exp \left( A_{\mathrm{PV}}(T_{r})V_{\max }\right) -1\right] =0\nonumber \\ \end{aligned}$$

(20)

If $\rho _{1}$ and $\rho _{2}$ are known, Eq. (19) will be used to generate the optimal value of $V_{\max }$. In this approach, $\rho _{1}$ and $\rho _{2}$ depending of T and G are supposed not be accessible to measurement. So we can estimate ${\hat{\rho }}_{1}$ and ${\hat{\rho }}_{2}$ using Eq. (18) rewritten as:

$$\begin{aligned} {\dot{y}}_{2}= & {} -\frac{1}{C}y_{1}+ F(y_{2},\rho _{1},\rho _{2},t) \end{aligned}$$

(21)

with $F(y_{2},\rho _{1},\rho _{2},t)=\frac{1}{C}\rho _{1}(T,G)-\frac{1}{C}\varphi (y_{2})\rho _{2}(T)$.

Hence, in Eq. (20), ${\dot{y}}_{2}$ is unknown ($I_{l}$ available in measurement), and it is not possible to use immediately Eq. (20) to estimate the unknown $\rho _{1}$ and $\rho _{2}$.

By applied the approach of neuro-observer as in Ahmed-Ali et al. (2009), it will be possible to estimate ${\hat{\rho }}_{1}$ and ${\hat{\rho }}_{2}$, and get $V_{\max }$.

3.1 Design RBF-Neuro Observer

The application of the Taylor formula to Eq. (21) gives

$$\begin{aligned} {\dot{V}}_{\mathrm{PV}}= & {} -\frac{1}{C}I_{l}+f(y,\rho _{1},\rho _{2},t)+\Delta f(V_{\mathrm{PV}},\rho _{1},\rho _{2},t) \end{aligned}$$

(22)

where the term $f(V_{\mathrm{PV}},\rho _{1},\rho _{2},t)$ can be approximated by RBF-NN and Eq. (21) becomes

$$\begin{aligned} {\dot{\hat{V}}}_{\mathrm{PV}}= & {} \!-\frac{1}{C}{\hat{I}}_{l}\!+\!\varUpsilon \left( \chi _{V_{\mathrm{PV}}},\omega ^{*}\right) \!+\!e_{f}\left( \chi _{V_{\mathrm{PV}}}\right) \!+\!\Delta f\left( V_{\mathrm{PV}},\rho _{1},\rho _{2},t\right) \nonumber \\= & {} -\,\frac{1}{C}{\hat{I}}_{l}+\sum \omega ^{*}_{j}\phi \left( \parallel \chi _{V_{\mathrm{PV}}}-\,C_{j}\parallel ,\nu _{j}\right) \nonumber \\&\quad +\,e_{f}(\chi _{V_{\mathrm{PV}}})+\Delta f(V_{\mathrm{PV}},\rho _{1},\rho _{2},t) \end{aligned}$$

(23)

with $\chi ^{T}_{V_{\mathrm{PV}}}=(V_{\mathrm{PV}}, I_{l})$ the input vector or RBF neural network. In the assumption that $e_{f}(\chi _{V_{\mathrm{PV}}})$ and the time-varying $\Delta f(V_{\mathrm{PV}},\rho _{1},\rho _{2},t)$ are unknown and bounded by unknown positive value as $\mid e_{f}(\chi _{V_{\mathrm{PV}}})+\Delta h(V_{\mathrm{PV}},\rho _{1},\rho _{2},t)\mid \le \zeta (t)$, we rewrite Eq. (23) as:

$$\begin{aligned} {\dot{\hat{V}}}_{\mathrm{PV}}= & {} -\frac{1}{C}{\hat{I}}_{l}+\varUpsilon \left( \chi _{V_{\mathrm{PV}}},{\hat{\omega }}\right) +p\left( V_{\mathrm{PV}},\hat{V_{\mathrm{PV}}},t\right) \end{aligned}$$

(24)

where the sliding robust terms $p(V_{\mathrm{PV}},\hat{V_{\mathrm{PV}}},t)=-{\hat{\zeta }}(t)\mathrm{sgn}(e_{2})$ are introduced to compensate the effect of the uncertainty $\Delta f(V_{\mathrm{PV}},\rho _{1},\rho _{2},t)$ which cannot be approximated by a static neural network.

By taking errors as $e_{1}={\hat{I}}_{l}-I_{l}$, $e_{2}={\hat{V}}_{\mathrm{PV}}-V_{\mathrm{PV}}$ deriving $e_{2}$ with respect to time, we obtain

$$\begin{aligned} {\dot{e}}_{2}= & {} {\dot{\hat{V}}}_{\mathrm{PV}}-{\dot{V}}_{\mathrm{PV}}\nonumber \\= & {} -\frac{1}{C}e_{1}+\sum {\hat{\omega }}_{j}\phi \left( \parallel \chi _{V_{\mathrm{PV}}}-C_{j}\parallel ,\nu _{j}\right) \nonumber \\&-\,\sum \omega ^{*}_{j}\phi \left( \parallel \chi _{V_{\mathrm{PV}}}-C_{j}\parallel ,\nu _{j}\right) +\zeta \left( V_{\mathrm{PV}},\hat{V_{\mathrm{PV}}},t\right) \nonumber \\&-\, e_{f}(\chi )-\Delta f\left( V_{\mathrm{PV}},\rho _{1},\rho _{2},t\right) \end{aligned}$$

(25)

By using Taylor series expansion, Eq. (25) becomes

$$\begin{aligned} {\dot{e}}_{2}= & {} -\frac{1}{C}e_{1}+\sum ({\hat{\omega }}_{j}-\omega ^{*}_{j})\frac{\partial \Upsilon }{\partial \omega }\mid _{\omega ={\hat{\omega }}}+\nonumber \\&+\, \zeta (V_{\mathrm{PV}},\hat{V_{\mathrm{PV}}},t)-e_{f}(\chi _{V_{\mathrm{PV}}})-\Delta f(V_{\mathrm{PV}},\rho _{1},\rho _{2},t) \end{aligned}$$

(26)

The Lyapunov candidate function is considered as follows:

$$\begin{aligned} \varPi= & {} \frac{1}{2}e^{2}_{2}+\frac{1}{2}\sum \left( {\hat{\omega }}_{j}-\omega ^{*}_{j}\right) ^{2} \end{aligned}$$

(27)

Hence,

$$\begin{aligned} {\dot{\varPi }}= & {} e_{2}{\dot{e}}_{2}+\sum {\dot{\hat{\omega }}}_{j}\left( {\hat{\omega }}_{j}-\omega ^{*}_{j}\right) \nonumber \\= & {} -\,\frac{1}{C}e_{1}e_{2}+\zeta \big (V_{\mathrm{PV}},\hat{V_{\mathrm{PV}}},t\big )-e_{2}\big (e_{f}\big (\chi _{V_{\mathrm{PV}}}\big )\nonumber \\&+\,\Delta f\big (V_{\mathrm{PV}},\rho _{1},\rho _{2},t\big )\big )\nonumber \\&+\, \sum \big ({\hat{\omega }}_{j}-\omega ^{*}_{j}\big )\left[ {\dot{\hat{\omega }}}_{j}+e_{2}\frac{\partial \varUpsilon }{\partial \omega _{j}}\mid _{\omega ={\hat{\omega }}}\right] \end{aligned}$$

(28)

By choosing

$$\begin{aligned} p(V_{\mathrm{PV}},\hat{V_{\mathrm{PV}}},t)= & {} -{\dot{\hat{\zeta }}}(t)\mathrm{sgn}(e_{2}) \end{aligned}$$

(29)

$$\begin{aligned} {\dot{\hat{\omega }}}_{j}= & {} \mathrm{Proj}\left[ -e_{2}\frac{\partial \varUpsilon }{\partial \omega _{j}} \mid _({\omega _{j}}={\hat{\omega }}_{j})\right] ,\quad j=1,\ldots ,N \nonumber \\= & {} {\left\{ \begin{array}{ll} -e_{2}\frac{\partial \varUpsilon }{\partial \omega _{j}} &{}\quad {\text {if}}\; \mid {\hat{\omega }}_{j} \mid < R_{\omega }\\ 0 &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(30)

$$\begin{aligned} {\dot{\hat{\zeta }}}(t)= & {} {\left\{ \begin{array}{ll} \alpha _{t} &{}\quad \text {if}\; e_{2}\ne 0\\ 0 &{} \quad \text {if}\; e_{2}=0 \end{array}\right. } \end{aligned}$$

(31)

with $\alpha (t)>0$, ${\hat{\zeta }}(0)=0$, and $\mathrm{Proj}(.)$ the well-known projection function on the compact set $\varOmega _{\omega }=\{\omega :\parallel \omega \parallel \le R_{\omega }\}$

$$\begin{aligned} {\dot{\varPi }} \le -\frac{1}{C}\mid e_{1}e_{2}\mid -{\dot{\hat{\zeta }}}(t)\mid e_{2}\mid . \end{aligned}$$

(32)

Hence, the error $e_{2}$ will converge to the origin.

Remark 1

The width $\nu _{j}$ and the center $C_{j}$ of the j-th hidden unit are chosen by clustering technique (Jain and Dubes 1988) as:

$$\begin{aligned} \nu _{ij}= & {} \frac{\ell _{i\max }-\ell _{i\min }}{N} \end{aligned}$$

(33)

$$\begin{aligned} C_{ij}= & {} \ell _{i\min }+\frac{2j-1}{2}\nu _{ij} \end{aligned}$$

(34)

where $\ell _{i\min }$ and $\ell _{i\max }$ are the lower and upper bounds of the i-th element of the RBF input vector $\ell$, respectively.

For the estimation of $\rho _{1}$ and $\rho _{2}$, Eq. (21) becomes

$$\begin{aligned} {\hat{Z}}= & {} \frac{\lambda }{P+\lambda }\left[ {\hat{\rho }}^{T}(t)D(V_{\mathrm{PV}})\right] \end{aligned}$$

(35)

with $D(V_{\mathrm{PV}})=[\frac{1}{c}; -\frac{1}{c}\varphi (V_{\mathrm{PV}})]$, and $\rho (t)= [{\hat{\rho }}_{1}; {\hat{\rho }}_{2}]$, ${\hat{Z}}=\frac{\lambda }{P+\lambda }[{\dot{\hat{V}}}_{\mathrm{PV}}+\frac{1}{C}{\hat{I}}_{l}]$.

Let us define $e_{0}={\hat{Z}}-Z$, ${\tilde{\rho }}(t)={\hat{\rho }}-\rho (t)$. The output estimation error satisfies

$$\begin{aligned} e_{0}= & {} \frac{\lambda }{P+\lambda }\left[ {\tilde{\rho }}^{T}(t)D(V_{\mathrm{PV}})\right] \end{aligned}$$

(36)

which implies that

$$\begin{aligned} {\dot{e}}_{0}= & {} -\lambda e_{0}+\lambda {\tilde{\rho }}^{T}(t)D(V_{\mathrm{PV}}). \end{aligned}$$

(37)

To apply the Lyapunov synthesis method, we select the Lyapunov function as

$$\begin{aligned} \varPi _{1}= & {} \frac{1}{2}e^{2}_{0}+\frac{1}{2}{\tilde{\rho }}^{T}\varGamma ^{-1}{\tilde{\rho }} \end{aligned}$$

(38)

where $\varGamma =\gamma I$ is a positive definite symmetric matrix that will ultimately appear in the adaptive law for updating ${\hat{\rho }}(t)$ as the learning rate or adaptive gain.

Computing the derivative of $\varPi _{1}$ yields:

$$\begin{aligned} {\dot{\varPi }}_{1}= & {} e_{0}{\dot{e}}_{0}+{\tilde{\rho }}^{T}\varGamma ^{-1}{\dot{\hat{\rho }}}\nonumber \\= & {} -\lambda e^{2}_{0}+\lambda e_{0}{\tilde{\rho }}^{T}(t)D(V_{\mathrm{PV}})+{\tilde{\rho }}^{T}\varGamma ^{-1}{\dot{\hat{\rho }}}\nonumber \\= & {} -\lambda e^{2}_{0}+{\tilde{\rho }}^{T}(t)[\varGamma ^{-1}{\dot{\hat{\rho }}}+\lambda e_{0}D(V_{\mathrm{PV}})] \end{aligned}$$

(39)

By choosing

$$\begin{aligned} {\dot{\hat{\rho }}}(t)= & {} \mathrm{proj}[-\lambda \varGamma D(V_{\mathrm{PV}})e_{0}] \end{aligned}$$

(40)

Equation (39) becomes

$$\begin{aligned} {\dot{\varPi }}_{1}= & {} -\lambda e^{2}_{0}<0 \end{aligned}$$

(41)

From ${\dot{\varPi }}_{1}<0$, one concludes from the Lyapunov stability theory that ${\hat{\rho }}(t)$ remains uniformly bounded, and ${\tilde{\rho }}(t)$ converges to zero in finite time according to Barbalat’s lemma (Slotin and Li 1991)

3.2 Controller Synthesis by Dynamic Inversion with Model Estimation

Recall that the control objective is to enforce the voltage $V_{\mathrm{PV}}$ to track the optimal point $V_{\max }$, despite the system parameter uncertainties. To this end, the controller design is performed using Eq. (20) rewritten in from Eq. (42)

$$\begin{aligned} {\dot{I}}_{l}= & {} H_{I_{l}}+Z_{I_{l}}k \end{aligned}$$

(42)

where the functions $H_{I_{l}}=-\frac{R}{L}I_{l}+\frac{1}{L}V_{\mathrm{PV}}$ and $Z_{I_{l}}=\frac{R}{L}I_{l}$ are both smooth functions available; k is the input control.

We observed that in Eq. (42) the derivative state ${\dot{I}}_{l}$ is not available. For this reason, the RBF neuro-observer use in Sect. 3.1 will also be applied to get this derivative state ${\dot{\hat{I}}}_{l}$. Hence, the control law is given by:

$$\begin{aligned} k= & {} \frac{1}{Z_{I_{l}}}[{\dot{\hat{I}}}_{l}-H_{I_{l}}] \end{aligned}$$

(43)

The block diagram of the proposed nonlinear adaptive MPPT control technique for PV systems is depicted in Fig. 5.

Fig. 5

Block diagram of the nonlinear neuro-adaptive MPPT control technique for PV systems

4 Simulation Results

To demonstrate the efficiency of the proposed approach, different simulations are performed in Matlab/Simulink environment. The DC/DC converter is fed with a MSX-60 (60 W) solar panel from Solarex. The boost converter parameters are $C=100\,\upmu$F and $L=0.1\,\upmu$H. A nominal value $R=4.9\,\Omega$ is considered for the resistive DC load. The diode of the boost converter has a snubber resistance of 500 $\Omega$, an internal resistance of 0.001 $\Omega$ and a forward voltage of 0.8 V. Internal and snubber resistances of the insulated-gate bipolar transistor(IGBT), used as the electronic switch of the boost converter are, 0.001 $\Omega$ and 0.1 M$\Omega$, respectively. The switching frequency is set to $50\,{\text {kH}}_{z}$. The control design parameters are: $\gamma _{1}=1e{-}3$, $\gamma _{2}= 0.1e{-}5$ , $\lambda =1$ rad/s.

First, the system performances are assessed under two different operating conditions: the tracking under abrupt change in irradiation and the tracking under abrupt change temperature condition.

• (a) System response to fast changing irradiation. During this test, a sun irradiation profile comprising various step changes is applied to the system, while a constant temperature of ${25}\,^{\circ }$C is maintained. It is observed in Fig. 6 that the controller senses and follows the changes by extracting the maximum power corresponding to the given sun condition. The captured PV power in this condition varies between 21,5 W and 56 W. These values correspond (see Fig. 3) to the maximum points on the curves associated with the considered radiations. Figure 7 shows the estimates of unknown parameters. It is seen that the unknown parameters are continuously adapted to the changing operating conditions.

• (b) System response to fast changing temperature. Now, a varying temperature profile, in which the changes are carried out between 25 and 65 $^{\circ }$C, is considered. The radiation is kept constant and equal to 1000 W/m$^{2}$. The behavior of the controlled system under this test is shown in Figs. 8 and 9. It is seen in Fig. 8 that the proposed controller well manages the PV power by keeping it at the corresponding maximum value for each temperature (see Fig. 3). Figure 9 shows that the estimates ${\hat{\rho }}_{1}$ and ${\hat{\rho }}_{2}$ of unknown parameters $\rho _{1}$ and $\rho _{2}$ are automatically readjusted in order to match the new operating conditions.

Fig. 6

The proposed MPPT controller during the irradiation change

Fig. 7

Estimates of unknown parameters in the presence of radiation variations

Fig. 8

The proposed MPPT controller during the temperature change

Fig. 9

Estimates of unknown parameters in the presence of temperature variations

Secondly, the proposed MPPT algorithm is tested under load variation, and the result is presented in Fig. 10. For this test, the load resistance is varied from 30 to 4.9 $\Omega$ at time $t=0.2$ s (STC: 1000 W/m$^{2}$, 25 $^{\circ }$C). It is observed in Fig. 10 that the load power increases rapidly from 13.3 to 46 W. Thus, the proposed technique is also able to work under load variation condition.

Fig. 10

Load power and load voltage under load variation

Fig. 11

Comparison of the proposed approach with P&O

Finally, a comparative study between the proposed nonlinear neuro-adaptive control approach and the P&O algorithm is established. To have a fair comparison, both algorithms run under the same conditions. For these test conditions, The power curves for both MPPT algorithms are presented in Fig. 11. It is depicted in this figure that the P&O method presents similar dynamic response compared to that of the proposed method. In contrary, power losses are significant, especially for lower values of irradiation, in the case of P&O method than that of the proposed one. The MPPs obtained in this figure are predictable from the MSX60 characteristics illustrated in Fig. 3. The instantaneous irradiation change imposed on the PV system can be much faster than a real scenario, but gives an idea of how long it takes for the proposed controller to react to an irradiation change. The comparison of quantitative results obtained from Fig. 11 is presented in Table 2. Root mean square error (RMSE) and efficiency are evaluated using the following equations:

$$\begin{aligned} {\text {RMSE}}= & {} \sqrt{\frac{\sum (P_{\mathrm{ac}}-P_{\mathrm{si}})^{2}}{N}} \end{aligned}$$

(44)

$$\begin{aligned} \eta= & {} \frac{P_{\mathrm{out}}}{P_{\mathrm{PV}}} \end{aligned}$$

(45)

where $P_{\mathrm{ac}}$ is the actual value of maximum power obtained from the characteristics as in Table 1. $P_{\mathrm{si}}$ is the simulated value of the maximum power for both proposed and P&O techniques; N is the number of samples. The analysis of these results coupled to the fact that temperature and irradiation sensors are not needed clearly demonstrates the superiority of the proposed MPPT algorithm compared to the P&O method.

Table 2 Qualitative comparison between the proposed method and P&O

Fig. 12

Experimental architecture

5 Experimental Results

To complete the validation of the proposed MPPT algorithm, experimental system architecture is adopted as shown in Fig. 12. The experimental device, shown in Fig. 13, is constructed using an MSX-60 solar panel, a personal computer, a BOOST DC/DC converter, a resistive load (0–1000 $\Omega$), a control circuit using Arduino Mega board and Hall-effect sensors of ACS 712 type. Two voltage dividers were exploited to obtain the array output voltage and the voltage across the load. An Arduino Mega board is used to execute the proposed MPPT algorithm and deliver the external PWM signal needed to control the BOOST converter. The analog current and voltage values of the solar PV array are fed to the 10-bit ADC module of the Arduino Mega board to be converted into the digital values using current and voltage sensors. The proposed nonlinear adaptive controller was implemented and compiled in the Matlab/Simulink. To control the whole system, the program is downloaded in real time on the Arduino board. The Matlab/Simulink model showing the implementation of the proposed controller using Arduino Mega board is illustrated in Fig. 14.

Fig. 13

Experimental setup for testing and verification of the results

Fig. 14

Experimental design of the proposed algorithm using Arduino under Matlab Simulink

Figure 15 shows the experimental results of the proposed controller. It is observed that the system starts with nearly constant irradiance. During this stable atmospheric conditions, the results confirm the ability of the proposed controller to ensure the stability and the efficiency of the system. At $t=1.36$ s, the irradiance is abruptly reduced. It is observed that during this sudden change, the proposed controller properly tracks the new maximum power point.

Fig. 15

Experimental results (voltage, current, power and duty ratio) of the proposed MPPT controller

6 Conclusion

In this paper, a new solution to the MPPT issue for PV systems is developed. The MPPT is achieved using an adaptive nonlinear controller based on an artificial neural network approach. The latter takes into account the boost converter nonlinear dynamics. The controller adaptive feature has been introduced to lessen the requirements of temperature and irradiation sensors and also to cope with the changing operating conditions. Simulations have been executed in MATLAB/Simulink environment, and a real-time implementation using Arduino board has been conducted. simulation results were compared to those obtained with the P&O technique. Based on both numerical and experimental results, the proposed control algorithm accurately tracks the maximum power point with a shorter time during abrupt changes in atmospheric conditions.