1 Introduction

The motion of a physical systems group such as robotic manipulators, ship, surface vessels and quad-rotor can be considered as mechanical systems with dynamic uncertainties and external disturbances (Dupree et al. 2011). Furthermore, the actuator saturation and full-state constraint and finite time control have been mentioned in Hu et al. (2019), Yang and Yang (2011), Guo et al. (2019), He et al. (2015), He and Dong (2017), He et al. (2015). Dealing with unknown parameters and disturbances, the terminal sliding mode control (SMC) is one of the remarkable solutions with the consideration of finite time convergence. In Mondal and Mahanta (2014), the non-singular terminal sliding surface was employed to obtain the adaptive terminal SMC for a manipulator system. The work in Galicki (2015) was also based on the non-singular terminal sliding manifold to investigate the finite time control, which seems to be effective in counteracting not only uncertain dynamics but also unbounded disturbances. Authors in Madani et al. (2016) have extended terminal sliding mode technique to establish control design for exoskeleton systems to ensure the trajectory of the closed-loop system can be driven onto the sliding surface in finite time. In order to tackle the challenges of external disturbance, the classical robust control design was investigated the input-state stability (ISS) with equivalent attraction region. However, in the situation that the external disturbance can be a combination of finite number of step signals and sinusoidal signals, the closed-loop system in Lu et al. (2019) is asymptotic stability. In Huang et al. (2018), the optimal gain matrices-based disturbance observer, combining with SMC, was presented for under-actuated manipulators. Authors in Wang et al. (2018) considered the frame of generalized proportional integral observer(GPIO) technique and continuous SMC to overcome the matched/mismatched time-varying disturbances guaranteeing a high tracking performance in compliantly actuated robots. SMC technique is not only employed for classical manipulators but also for different types including bilateral teleoperators (BTs) and mobile robotic systems (wheeled mobile robotics, tractor–trailer systems) (Liu et al. 2020; Nguyena et al. 2019; Binh et al. 2019). Several control schemes have been considered for manipulators to handle the input saturation disadvantage by integrating the additional terms into the control structure (Hu et al. 2019; Yang and Yang 2011; Guo et al. 2019; He et al. 2015). In Hu et al. (2019), a new desired trajectory has been proposed due to the actuator saturation. The additional term would be obtained after taking the derivative of initial Lyapunov candidate function along the state trajectory in the presence of actuator saturation (Hu et al. 2019). Furthermore, a new approach was given in Hu et al. (2019) to tackle not only the actuator constraints but also handling external disturbances. The given sliding manifold was realized the Sat function of joint variables. The equivalent SMC scheme was computed, and then, the boundedness of input signal was mentioned. This approach leads to adjust absolutely input bound by choosing appropriate several parameters. The work in He et al. (2015) gives a technique to tackle the actuator saturation using a modified Lyapunov candidate function. Due to the actuator saturation, the Lyapunov function would be integrated more in the quadratic form from the relation between the input signal from controller and the real signal applied to object. The control design was obtained after considering the Lyapunov function derivative along the system trajectory. In order to tackle the drawback of state constraints in manipulator, the framework of barrier Lyapunov function and Moore–Penrose inverse matrix, fuzzy-neural network technique was proposed in Guo et al. (2019), He et al. (2015), Hu et al. (2019). Furthermore, these techniques are also developed for the situation of output feedback control with the appropriate virtual control input (He et al. 2020; Yu et al. 2020). On the other hand, the uncertainties/disturbance terms in control design are approximated by neural network and fuzzy method (He et al. 2020; Yu et al. 2020). However, these aforementioned classical nonlinear control techniques have several challenges, such as appropriate Lyapunov function and additional terms dynamic (He et al. 2015; He and Dong 2017; He et al. 2015). Optimal control solution has the remarkable way that can solve above constraint problems by considering the constraint-based optimization (Yang et al. 2020; Sun et al. 2017; Vamvoudakis et al. 2014; Yu et al. 2018; Zhu et al. 2016; Lv et al. 2016; Sun et al. 2017; Li et al. 2020) and model predictive control (MPC) is one of the most effective solutions to tackle the these constraint problems for manipulators (Yu et al. 2018). The terminal controller as well as equivalent terminal region has been established for a nominal system of disturb manipulators with finite horizon cost function (Yu et al. 2018). This technique of robust MPC was also considered for wheeled mobile robotics (WMRs) with the consideration of kinematic model after adding more disturbance observer (DO) (Sun et al. 2017). This work has been extended for the inner loop model by backstepping technique (Yang et al. 2020). Thanks to the advantages of the event-triggering mechanism, the computation load of robust MPC has been reduced in control systems for uni-cycle (Sun et al. 2017). The optimal control algorithm has been mentioned in the work of Dupree et al. (2011) after using classical nonlinear control law. However, the online computation technique has not considered yet in Dupree et al. (2011). Furthermore, it is difficult to find the explicit solution of Riccati equation and partial differential HJB (Hamilton–Jacobi–Bellman) equation in general nonlinear systems (Vamvoudakis et al. 2014). The reinforcement learning strategy was established to obtain the controller by Q learning and temporal difference learning and then was developed to a novel stage by the approximate/adaptive dynamic programming (ADP), which has been the appropriate solution in recent years. Thanks to the neural network approximation technique, authors in Vamvoudakis et al. (2014) proposed the novel online ADP algorithm which enables to tune simultaneously both actor and critic terms. The training problem of critic neural network (NN) was determined by modified Levenberg–Marquardt technique to minimize the square residual error. Furthermore, the weights convergence and convergence problem were shown by the weights in actor and critic NN tuning the need of persistence of excitation (PE) condition (Vamvoudakis et al. 2014). Considering the approximate Bellman error, the proposed algorithm in Vamvoudakis et al. (2014) enables to online simultaneously adjusted with unknown drift term. Extending this work, by using the special cost function, a model-free adaptive reinforcement learning has been presented without any information of the system dynamics (Zhu et al. 2016). Furthermore, by integrating the additional identifier, the nonlinear systems were controlled by online adaptive reinforcement learning with completely unknown dynamics (Lv et al. 2016; Bhasin et al. 2013). However, these three above works have not mentioned for robotic systems as well as non-autonomous systems yet (Zhu et al. 2016; Lv et al. 2016; Bhasin et al. 2013). In the work of Li et al. (2020), under the consideration of approximation and discrete time systems, online ADP tracking control was proposed for the dynamic of mobile robots. Inspired by the above works and analysis from traditional nonlinear control technique to optimal control strategy, the work focuses on the frame of online adaptive reinforcement learning for manipulators and nonlinear control with main contribution which are described in the following:

  1. 1)

    In comparison with the previous papers (Dupree et al. 2011; Hu et al. 2019; Yang and Yang 2011; Guo et al. 2019; He et al. 2015; He and Dong 2017; He et al. 2015; Mondal and Mahanta 2014; Lu et al. 2019; Galicki 2015; Madani et al. 2016; Huang et al. 2018; Wang et al. 2018), which were presented classical nonlinear controller in manipulator control systems, an adaptive reinforcement learning (ARL)-based optimal control design is proposed for a uncertain manipulator system in this paper. Compared with the proposed optimal control in Dupree et al. (2011) using Kim–Lewis formula in special case of cost function, ARL-based optimal control design has the advantage in that it is able to deal with general performance index for non-autonomous system with appropriate transform.

  2. 2)

    Unlike the reinforcement learning scheme-based optimal control in Vamvoudakis et al. (2014), Zhu et al. (2016), Lv et al. (2016), Li et al. (2020), Bhasin et al. (2013) is considered for mathematical systems of a first-order continuous-time nonlinear autonomous system without any external disturbance, the contribution is described that the adaptive dynamic programming combining with the sliding variable and the robust integral of the sign of error (RISE) was employed for second-order uncertain/disturbed manipulators in the situation of trajectory tracking control and non-autonomous systems.

The remainder of this paper is organized as follows. The dynamic model of robotic manipulators and control objective are given in Sect. 2. The proposed adaptive reinforcement learning algorithm and theoretical analysis are presented in Sect. 3. The offline simulation is shown in Sect. 4. Finally, the conclusions are pointed out in Sect. 5.

2 Dynamic Model of Robot Manipulator

Consider the planar robot manipulator systems described by the following dynamic equation:

$$\begin{aligned} {\varvec{M}}\left( {\varvec{\eta }}\right) {\ddot{{\varvec{\eta }}}} + {\varvec{C}}\left( {\varvec{\eta }}, {\dot{{\varvec{\eta }}}}\right) \dot{{\varvec{\eta }}} + {\varvec{G}}\left( {\varvec{\eta }} \right) + {\varvec{F}}\left( {\dot{{\varvec{\eta }}}}\right) + {\varvec{d}}\left( {\varvec{t}}\right) = {\varvec{\tau }}({\varvec{t}}) \end{aligned}$$
(1)

where \({\varvec{M}}({\varvec{\eta }})\in {\mathbb {R}}^{\varvec{n}\times \varvec{n}}\) is a generalized inertia matrix, \(\varvec{C}(\varvec{\eta },{\dot{\varvec{\eta }}})\in {\mathbb {R}}^{\varvec{n}\times \varvec{n}}\) is a generalized centripetal-Coriolis matrix, \(\varvec{G}(\varvec{\eta })\in {\mathbb {R}}^{\varvec{n}}\) is a gravity vector, \(\varvec{F}({\dot{\varvec{\eta }}})\in {\mathbb {R}}^{\varvec{n}}\) is a generalized friction, \(\varvec{d}(\varvec{t})\) is a vector of disturbances, and \(\varvec{\tau }(\varvec{t})\) is the vector of control inputs. It is worth emphasizing that the above manipulator belongs to the class of Euler–Lagrange systems, which has the following special property (Guo et al. 2019):

Fig. 1
figure 1

2-DOF Planar Robot Manipulator

Full size image

Property 01: The inertia symmetric matrix \(\varvec{M}(\varvec{\eta })\) is positive definite and satisfies \(\forall \varvec{\xi } \in {\mathbb {R}}^{\varvec{n}}\):

$$\begin{aligned}&\varvec{a}\Vert \varvec{\xi } \Vert ^{\varvec{2}}\le \varvec{\xi }^{\varvec{TM}}(\varvec{\eta })\varvec{\xi } \le \ \varvec{b}(\varvec{\eta })\Vert \varvec{\xi } \Vert ^{\varvec{2}} \end{aligned}$$
(2)
$$\begin{aligned}&\varvec{\xi }^{\varvec{T}}({\dot{\varvec{M}}}(\varvec{\eta }) - \varvec{2C}(\varvec{\eta }, {\dot{\varvec{\eta }}})\varvec{\xi } = \varvec{0} \end{aligned}$$
(3)

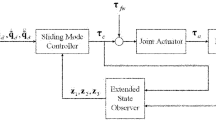
where \(\varvec{a}\in {\mathbb {R}}\) is a positive constant, and \(\varvec{b}(\varvec{\eta })\in {\mathbb {R}}\) is a positive function with respect to \(\varvec{\eta }\). Several following assumptions will be employed in considering the stability later (Fig. 1).

Assumption 1

If \(\varvec{\eta }(\varvec{t}),{\dot{\varvec{\eta }}}(\varvec{t}) \in {\mathcal {L}}_{\infty }\), then all these functions \(\varvec{C}(\varvec{\eta },{\dot{\varvec{\eta }}}), \varvec{F}({\dot{\varvec{\eta }}})\), \(\varvec{G}(\varvec{\eta })\) and the first and second partial derivatives of all functions of \(\varvec{M}(\varvec{\eta }), \varvec{C}(\varvec{\eta }, {\dot{\varvec{\eta }}})\), \(\varvec{G}(\varvec{\eta })\) with respect to \(\varvec{\eta }(\varvec{t})\) as well as of the elements of \(\varvec{C}(\varvec{\eta },{\dot{\varvec{\eta }}}),\varvec{F}({\dot{\varvec{\eta }}})\) with respect to \({\dot{\varvec{\eta }}}(\varvec{t})\) exist and are bounded.

Assumption 2

The desired trajectory \(\varvec{\eta }_{\varvec{d}}(\varvec{t})\) as well as the first, second, third and fourth time derivatives of it exists and is bounded.

Assumption 3

The vector of external disturbance term \(\varvec{d}(\varvec{t})\) and the derivatives with respect to time of \(\varvec{d}(\varvec{t})\) are bounded by known constants.

The control objective is to ensure the system tracks a desired time-varying trajectory \(\varvec{\eta }_{\varvec{d}}(\varvec{t})\) in the presence of dynamic uncertainties by using the frame of online adaptive reinforcement learning-based optimal control design and disturbance attenuation technique. Considering the sliding variable \(\varvec{s}\left( \varvec{t}\right) ={\dot{\varvec{e}}}_{\varvec{1}} + {\varvec{\lambda }}_{\varvec{1}}{\varvec{e}}_{\varvec{1}}, \left( \varvec{\lambda }_{\varvec{1}} \in {\mathbb {R}}^{\varvec{n} \times \varvec{n}} > 0, \varvec{e}_{\varvec{1}} \left( \varvec{t}\right) = \varvec{\eta }^{\varvec{ref}} - \varvec{\eta }\right) \), and the corresponding sliding surface is as follows:

$$\begin{aligned} \mathbf{M} = \left\{ \varvec{e}_{\varvec{1}}\left( \varvec{t}\right) \in {\mathbb {R}}^{\varvec{n}}:\varvec{s} \left( \varvec{t}\right) = \varvec{0}\right\} \end{aligned}$$
(4)

According to (1), the dynamic equation of the sliding variable \(\varvec{s}(\varvec{t})\) can be given as:

$$\begin{aligned} \varvec{M}\dot{\varvec{s}} = -\varvec{Cs}-\varvec{\tau } +\varvec{f}+\varvec{d} \end{aligned}$$
(5)

where \(\varvec{f}(\varvec{\eta }, \dot{\varvec{\eta }},\varvec{\eta }_{\varvec{ref}},\dot{\varvec{\eta }}_{\varvec{ref}}, \ddot{\varvec{\eta }}_{\varvec{ref}})\) is nonlinear function defined:

$$\begin{aligned} \varvec{f}=\varvec{M}(\ddot{\varvec{\eta }}^{\varvec{ref}}+\varvec{\alpha }_{\varvec{1}}{\dot{\varvec{e}}}_{\varvec{1}}) +\varvec{C}(\dot{\varvec{\eta }}^{\varvec{ref}}+\varvec{\alpha }_{\varvec{1}}\varvec{e}_{\varvec{1}})+\varvec{G}+\varvec{F} \end{aligned}$$
(6)

Remark 1

The role of the above sliding variable is considered to reduce the order of second-order uncertain/disturbed manipulator systems. It enables us to employ the adaptive reinforcement learning for a first-order continuous-time nonlinear autonomous system. Additionally, the external disturbance \(\varvec{d}(\varvec{t})\) and nonlinear function \(\varvec{f}\) are handled by RISE in the next section.

3 Adaptive Reinforcement Learning-Based Optimal Control Design

Assume that the dynamic model of robot manipulator is known, the control input can be designed as

$$\begin{aligned} \varvec{\tau } = \varvec{f}+\varvec{d} - \varvec{u} \end{aligned}$$
(7)

where the term \(\varvec{u}\) is designed by using optimal control algorithm and the remaining term \(\varvec{f}+\varvec{d}\) will be estimated later. Therefore, it can be seen that

$$\begin{aligned} \varvec{M}\dot{\varvec{s}}=-\varvec{Cs}+\varvec{u} \end{aligned}$$
(8)

According to (4) and (8), we obtain the following time-varying model

$$\begin{aligned} \dot{\varvec{x}} = \left[ \begin{array}{l} - \varvec{\lambda }_{\varvec{1}}\varvec{e}_{\varvec{1}} + \varvec{s}\\ - \varvec{M}\left( \varvec{\eta }^{\varvec{ref}} - \varvec{e}_{\varvec{1}},{\dot{\varvec{\eta }}}^{\varvec{ref}} + \varvec{\lambda }_{\varvec{1}}\varvec{e}_{\varvec{1}} - \varvec{s} \right) \varvec{s} \end{array}\right] +\left[ \begin{array}{l} \varvec{0}_{\varvec{n} \times \varvec{n}}\\ \varvec{M}^{-\varvec{1}} \end{array}\right] \varvec{u} \end{aligned}$$
(9)

where \(\varvec{x}=[\varvec{e}_{\varvec{1}}^{\varvec{T}}, \varvec{s}^{\varvec{T}}]^{\varvec{T}}\) and the infinite horizon cost function to be minimized is

$$\begin{aligned} \varvec{J}(\varvec{x}, \varvec{u}) = \int \limits _{\varvec{0}}^{\infty } \left( \frac{\varvec{1}}{\varvec{2}} \varvec{x}^{\varvec{T}}\varvec{Qx} +\frac{\varvec{1}}{\varvec{2}}\varvec{u}^{\varvec{T}}\varvec{Ru}\right) \varvec{dt} \end{aligned}$$
(10)

where \(\varvec{Q}\in {\mathbb {R}}^{\varvec{2n}\times \varvec{2n}}\) and \(\varvec{R}\in {\mathbb {R}}^{\varvec{n}\times \varvec{n}}\) are positive definite symmetric matrices. However, in order to deal with the problem of tracking control, some additional states are given. This work leads us to avoid the non-autonomous systems. Subsequently, the adaptive reinforcement learning is considered to find optimal control solution for autonomous affine state-space model with the assumption that the desired trajectory \(\varvec{\eta }^{\varvec{ref}(\varvec{t})}\) satisfies \(\dot{\varvec{\eta }}^{\varvec{ref}}(\varvec{t})=\varvec{f}^{\varvec{ref}}(\varvec{\eta }^{\varvec{ref}})\):

$$\begin{aligned} \dot{\varvec{X}}=\varvec{A}(\varvec{X})+\varvec{B}(\varvec{X})\varvec{u} \end{aligned}$$
(11)

where \(\varvec{X} = [\varvec{x}^{\varvec{T}},\varvec{\eta }^{\varvec{refT}},\dot{\varvec{\eta }}^{\varvec{refT}}]^{\varvec{T}}\)

$$\begin{aligned}&\varvec{A}(\varvec{X})=\begin{bmatrix} -\varvec{\lambda }_{\varvec{1}} \varvec{e}_{\varvec{1}}+\varvec{s}\\ \varvec{\Upsilon } \\ \varvec{f}^{\varvec{ref}}(\varvec{\eta }^{\varvec{ref}})\\ \dot{\varvec{f}}^{\varvec{ref}}(\varvec{\eta }^{\varvec{ref}}) \end{bmatrix},\\&\varvec{\Upsilon } = -\varvec{M}(\varvec{\eta }^{\varvec{ref}}-\varvec{e}_{\varvec{1}})^{-\varvec{1}} \varvec{C}(\varvec{\eta }^{\varvec{ref}}-\varvec{e}_{\varvec{1}}, \dot{\varvec{\eta }}^{\varvec{ref}}+\varvec{\lambda }_{\varvec{1}}\varvec{e}_{\varvec{1}}-\varvec{s})\varvec{s},\\&\varvec{B}(\varvec{X})=\begin{bmatrix} \varvec{0}_{\varvec{n}\times \varvec{n}}\\ \varvec{M}^{-\varvec{1}}\\ \varvec{0}_{\varvec{2n}\times \varvec{n}} \end{bmatrix}, \end{aligned}$$

Define the new infinite horizon integral cost function to be minimized is

$$\begin{aligned} \varvec{J}(\varvec{X},\varvec{u}) = \int \limits _{\varvec{t}}^{\infty } \left( \frac{\varvec{1}}{\varvec{2}} \varvec{X}^{\varvec{T}}\varvec{Q}_{\varvec{T}}\varvec{X} +\frac{\varvec{1}}{\varvec{2}}\varvec{u}^{\varvec{T}}\varvec{Ru} \right) \varvec{d}{\varvec{\tau }} \end{aligned}$$
(12)

where

$$\begin{aligned} \varvec{Q}_{\varvec{T}}=\begin{bmatrix} \varvec{Q} &{} \varvec{0}\\ \varvec{0} &{} \varvec{0} \end{bmatrix}. \end{aligned}$$
(13)

In order to guarantee the stability in optimal control design, we can consider the class of “Admissible Policy” described in Vamvoudakis et al. (2014), Zhu et al. (2016):

Definition 1

Vamvoudakis et al. (2014), Zhu et al. (2016), (Admissible Policy): A control input \(\varvec{\mu }(\varvec{X})\) is called as admissible in terms of (12) on \(\varvec{U}\), if \(\varvec{\mu }(\varvec{X})\) is continuous on \(\varvec{U}\) and the affine system (11) was stabilized by this control signal \(\varvec{\mu }(\varvec{X})\) on \(\varvec{U}\) and \(\varvec{J}(\varvec{X})\) is finite for any \(\varvec{X}\in \varvec{U}\).

The optimal control objective can now be considered finding an admissible control signal \(\varvec{\mu }^{*}\left( \varvec{X}\right) \) such that the cost function (12) associated with affine system (11) is minimized. According to the classical Hamilton–Jacobi–Bellman (HJB) equation theory (Bhasin et al. 2013), the optimal controller \(\varvec{u}^{*}\left( \varvec{X}\right) \) and equivalent optimal cost function \(\varvec{V}^{*}\left( \varvec{X}\right) \) are derived as:

$$\begin{aligned} \varvec{u}^*(\varvec{X})&=-\frac{\varvec{1}}{\varvec{2}}\varvec{R}^{-\varvec{1}}\varvec{B}^{\varvec{T}}(\varvec{X}) \frac{\partial \varvec{V}^{*}(\varvec{X})}{\partial \varvec{X}}^{\varvec{T}} \end{aligned}$$
(14)
$$\begin{aligned} \varvec{H}^{*}\left( \varvec{X}, \varvec{u}^{*},\frac{\partial \varvec{V}^{*}}{\partial \varvec{X}} \right)&=\frac{\partial \varvec{V}^{*}}{\partial \varvec{X}}\left( \varvec{AX} + \varvec{Bu}^{*}\right) + \frac{\varvec{1}}{\varvec{2}}\varvec{X}^{\varvec{T}}\varvec{Q}_{\varvec{T}}\varvec{X}\nonumber \\&\quad + \frac{\varvec{1}}{\varvec{2}}{\varvec{u}^{*}}^{\varvec{T}}\varvec{Ru}^{*} \end{aligned}$$
(15)

However, it is hard to directly solve the HJB equation as well as offline solution which requires complete knowledge of the mathematical model. Thus, the simultaneous learning-based online solution is considered by using neural networks to represent the optimal cost function and the equivalent optimal controller (Bhasin et al. 2013):

$$\begin{aligned} \varvec{V}(\varvec{X})&=\varvec{W}^{\varvec{T}}\varvec{\psi }(\varvec{X})+\varvec{\epsilon }_{\varvec{v}}(\varvec{X}), \end{aligned}$$
(16)
$$\begin{aligned} \varvec{u}^{*}\left( \varvec{X}\right)&= - \frac{\varvec{1}}{\varvec{2}}\varvec{R}^{-\varvec{1}}\varvec{B}^{\varvec{T}} \left( \varvec{X}\right) \nonumber \\&\quad \left( \left( \frac{\partial \varvec{\psi }}{\partial \varvec{x}}\right) ^{\varvec{T}}\varvec{W} + \left( \frac{\partial \varvec{\varepsilon }_{\varvec{\upsilon }} \left( \varvec{x}\right) }{\partial \varvec{x}}\right) ^{\varvec{T}}\right) \end{aligned}$$
(17)

where \(\varvec{W} \in {\mathbb {R}}^{\varvec{N}}\) is vector of unknown ideal NN weights, N is the number of neurons, \(\varvec{\psi } (\varvec{X})\in {\mathbb {R}}^{\varvec{N}}\) is a smooth NN activation function, and \(\varvec{\epsilon }_{\varvec{v}}(\varvec{X})\in {\mathbb {R}}\) is the function reconstruction error. The objective of establishing the NN (16) is to find the actor–critic NN updating laws \(\widehat{\varvec{W}_{\varvec{a}}}, \widehat{\varvec{W}_{\varvec{c}}}\) to approximate the actor and critic parts obtaining the optimal control law without solving the HJB equation. (For more details, see (Bhasin et al. 2013).) Moreover, the smooth NN activation function \(\varvec{\psi } (\varvec{X})\in {\mathbb {R}}^{\varvec{N}}\) is chosen depending on the description of manipulators (see chapter 4). In Bhasin et al. (2013), the Weierstrass approximation theorem enables us to uniformly approximate not only \(\varvec{V}^{*}\left( \varvec{X}\right) \) but also \(\frac{\partial \varvec{V}^{*}\left( \varvec{X}\right) }{\partial \varvec{X}}\) with \(\varvec{\varepsilon }_{\varvec{\upsilon }}\left( \varvec{x}\right) , \left( \frac{\partial \varvec{\varepsilon }_{\varvec{\upsilon }} \left( \varvec{x}\right) }{\partial \varvec{x}}\right) \rightarrow \varvec{0}\) as \(\varvec{N} \rightarrow \infty \). Consider to fix the number \(\varvec{N}\), the critic \(\hat{\varvec{V}}(\varvec{X})\) and the actor \(\hat{\varvec{u}}(\varvec{X})\) are employed to approximate the optimal cost function and the optimal controller as:

$$\begin{aligned}&\hat{\varvec{V}}(\varvec{X})=\hat{\varvec{W}}_{\varvec{c}}^{\varvec{T}}\psi (\varvec{X}) \end{aligned}$$
(18)
$$\begin{aligned}&\widehat{\varvec{u}}\left( \varvec{X}\right) = - \frac{\varvec{1}}{\varvec{2}}\varvec{R}^{-\varvec{1}}\varvec{B}^{\varvec{T}} \left( \varvec{X}\right) \left( \frac{\partial \varvec{\psi }}{\partial \varvec{x}}\right) ^{\varvec{T}} \widehat{\varvec{W}}_{\varvec{a}} \end{aligned}$$
(19)

The adaptation laws of critic \(\hat{\varvec{W}}_{\varvec{c}}\) and actor \(\hat{\varvec{W}}_{\varvec{a}}\) weights are simultaneously implemented to minimize the integral squared Bellman error and the squared Bellman error \(\delta _{hjb}\), respectively.

$$\begin{aligned} \varvec{\delta }_{\varvec{hjb}}&=\hat{\varvec{H}}\left( \varvec{X}, \hat{\varvec{u}}, \frac{\partial \hat{\varvec{V}}}{\partial \varvec{X}}\right) -\varvec{H}^{*}\left( \varvec{X}, \varvec{u}^{*},\frac{\partial \varvec{V}^{*}}{\partial \varvec{X}}\right) \nonumber \\&=\hat{\varvec{W}}_{\varvec{c}}^{\varvec{T}}\varvec{\sigma } +\frac{\varvec{1}}{\varvec{2}} \varvec{X}^{\varvec{T}}\varvec{Q}_{\varvec{T}}\varvec{X} +\frac{\varvec{1}}{\varvec{2}}\hat{\varvec{u}}^{\varvec{T}}\varvec{R}\hat{\varvec{u}} \end{aligned}$$
(20)

where \(\varvec{\sigma }(\varvec{X}, \hat{\varvec{u}})=\frac{\partial \varvec{\psi }}{\partial \varvec{x}} (\varvec{A}+\varvec{B}\hat{\varvec{u}})\) is the critic regression vector. Similar to the work in Bhasin et al. (2013), the adaptation law of critic weights is given:

$$\begin{aligned} \frac{d}{{dt}}{{\hat{\varvec{W}}}_c} = - {k_c}\lambda \frac{\varvec{\sigma } }{{1 + \nu \varvec{\sigma ^T} \lambda \varvec{\sigma } }}{\delta _{hjb}} \end{aligned}$$
(21)

where \(\nu ,k_c \in {\mathbb {R}}\) are constant positive gains, and \(\varvec{\lambda } \in {\mathbb {R}}^{\varvec{N}\times \varvec{N}}\) is a symmetric estimated gain matrix computed as follows

$$\begin{aligned} \frac{\varvec{d}}{\varvec{dt}}\varvec{\lambda }=-\varvec{k}_{\varvec{c}}\varvec{\lambda } \frac{\varvec{\lambda } \varvec{\sigma }^{\varvec{T}}}{\varvec{1}+\varvec{\nu } \varvec{\sigma }^{\varvec{T}}\varvec{\Psi } \varvec{\sigma }} \varvec{\lambda };\quad \varvec{\lambda }(\varvec{t}_{\varvec{s}}^{+}) =\varvec{\lambda }(\varvec{0})=\varvec{\varphi }_{\varvec{0}}\varvec{I} \end{aligned}$$
(22)

where \(t_s^+\) is resetting time satisfying \(\varvec{\alpha }_{\mathbf{min}} \left\{ \varvec{\lambda } \left( \varvec{t}\right) \right\} \le \varvec{\varphi }_{\varvec{1}}, \varvec{\varphi }_{\varvec{0}} > \varvec{\varphi }_{\varvec{1}}\). It can be seen that ensure \(\varvec{\lambda }(\varvec{t})\) is positive definite and prevent the covariance wind-up problem (Bhasin et al. 2013).

$$\begin{aligned} \varvec{\varphi }_{\varvec{1}}\varvec{I}\le \varvec{\lambda }(\varvec{t}) \le \varvec{\varphi }_{\varvec{0}}\varvec{I} \end{aligned}$$
(23)

Moreover, the actor adaptation law can be described as:

$$\begin{aligned} \frac{\varvec{d}}{\varvec{dt}}\widehat{\varvec{W}_{\varvec{a}}}&=-\frac{\varvec{k}_{\varvec{a1}}}{\sqrt{\varvec{1} + \varvec{\sigma }^{\varvec{T}}\varvec{\sigma }}} \frac{\partial \varvec{\psi }}{\partial \varvec{x}}\nonumber \\&\quad \varvec{BR}^{-\varvec{1}}\varvec{B}^{\varvec{T}}\frac{\partial \varvec{\psi }^{\varvec{T}}}{\partial \varvec{x}} \left( \widehat{\varvec{W}_{\varvec{a}}} - \widehat{\varvec{W}_{\varvec{c}}}\right) \varvec{\delta }_{\varvec{hjb}}\nonumber \\&\quad - \varvec{k}_{\varvec{a2}}\left( \widehat{\varvec{W}_{\varvec{a}}} - \widehat{\varvec{W}_{\varvec{c}}}\right) \end{aligned}$$
(24)

Remark 2

The approximate/adaptive reinforcement learning (ARL) control law (actor) and approximately optimal cost function (critic) are obtained in (19), (18), respectively. Based on the optimization principle, the updated law of actor and critic are carried out as in (24), (22). Compared with the optimal control law in Dupree et al. (2011), the ARL control algorithm has the advantage in that it is able to handle for general performance index. The convergences of estimated actor/critic weights \(\hat{\varvec{W}}_{\varvec{c}}\) and \(\hat{\varvec{W}}_{\varvec{a}}\) depend on the PE condition of \(\frac{\varvec{\sigma }}{\sqrt{\varvec{1} + \varvec{v}{\varvec{\sigma }^{\varvec{T}}\varvec{\lambda } \varvec{\sigma }}}} \in {\mathbb {R}}^{\varvec{N}}\) in Bhasin et al. (2013). Unlike the work in Bhasin et al. (2013), this algorithm does not mention the identifier design and focuses on the manipulator control design. Moreover, the learning technique in adaptation law (22), (24) is different from data-driven online integral reinforcement learning in Vamvoudakis et al. (2014), Zhu et al. (2016). In order to develop this adaptive reinforcement learning for manipulator systems in the trajectory tracking control problem, it is necessary to consider the manipulator dynamic as affine systems (11).

Consequently, the control design (7) is completed by implementing the estimation of \(\varvec{\epsilon } = \varvec{f} + \varvec{d}\), which is designed based on the robust integral of the sign of the error (RISE) framework (Dupree et al. 2011) as follows:

$$\begin{aligned} \epsilon _j(t)=(k_{sj}+1)s_j(t)-(k_{sj}+1)s_j(0)+\rho _j(t) \end{aligned}$$
(25)

where \(\rho (t) \in {\mathbb {R}}^n\) is computed by the following equation:

$$\begin{aligned} \frac{d}{{dt}}{\rho _j}=(k_{sj}+1)\lambda _{2j}s_j+\gamma _{1j}sgn(s_j) \end{aligned}$$
(26)

and \(\varvec{k}_{\varvec{s}} \in {\mathbb {R}}^{\varvec{n} \times \varvec{n}}, \varvec{\gamma }_{\varvec{1}} \in {\mathbb {R}}^{\varvec{n} \times \varvec{n}}, \varvec{\lambda }_{\varvec{2}} \in {\mathbb {R}}^{{n \times n}}\) are the positive diagonal matrices and \({\zeta _1} \in {\mathbb {R}} , {\zeta _2} \in {\mathbb {R}}\) are the positive control gains selected satisfying the sufficient condition as::

$$\begin{aligned} \gamma _{1j}>\zeta _1+\frac{1}{\lambda _{2j}}\zeta _2. \end{aligned}$$
(27)

Remark 3

In early works (Dupree et al. 2011), the optimal control design was considered for uncertain/disturbed mechanical systems by the RISE framework. The tracking control objective of this optimal control law is satisfied by appropriate assumptions 1-3 (Dupree et al. 2011). However, it should be noted that the work in Dupree et al. (2011) is extended by integrating adaptive reinforcement learning in the trajectory tracking problem with the consideration of non-autonomous systems, which are not directly applied on the adaptive reinforcement learning. It can be seen that the proposed control scheme in Dupree et al. (2011) only considered the optimal control in the special case of cost function. It leads to the optimal control problem which was easily implemented by using the formula of Dupree et al. (2011) for this special case. However, it is worth emphasizing that the method of Kim and Lewis in Dupree et al. (2011) is not able to carry out for general case. Compared with the proposed controller in Dupree et al. (2011), RISE-based uncertainties/disturbance estimation has the advantage in that it is able to combine with adaptive reinforcement learning algorithm for HJB equation to deal with general performance index. Moreover, this work deals with optimal control problem (9) for the general performance index (10) required the appropriate algorithm being adaptive reinforcement learning (ARL) for HJB equation. Additionally, due to the non-autonomous property of model (9), it is not able to directly carry out the model (9) by ARL strategy. Therefore, we proposed the transform method to obtain the modified autonomous system (11) developed by ARL algorithm. On the other hand, it should be noted that authors in Bhasin et al. (2013) considered an online ARL-based method for a first-order continuous-time nonlinear autonomous system without any external disturbance. However, unlike the work in Bhasin et al. (2013), a disturbed manipulator is described by a second-order continuous-time nonlinear systems (1). Therefore, in order to employ ARL strategy, the sliding variable is proposed in this work to reduce the order of manipulator model.

4 Simulation Results

In this section, to verify the effectiveness of the proposed tracking control algorithm, the simulation is carried out by a 2-DOF planar robot manipulator system, which is modeled by Euler–Lagrange formulation (1). In the case of 2-DOF planar robot manipulator systems \((n=2)\), the above matrices in (1) can be represented as follows:

$$\begin{aligned} \varvec{M}(\varvec{\eta })= & {} \begin{bmatrix} \varrho _1 + 2\varrho _2 \cos \eta _2 &{} \varrho _3 + \varrho _2 \cos \eta _2\\ \varrho _3 + \varrho _2 \cos \eta _2 &{} \varrho _3 \end{bmatrix},\nonumber \\ \varvec{G}(\varvec{\eta })= & {} \begin{bmatrix} \varrho _4 \cos \eta _1 + \varrho _5 \cos (\eta _1 + \eta _2)\\ \varrho _5 \cos (\eta _1 + \eta _2) \end{bmatrix}\nonumber \\ \varvec{C}(\varvec{\eta },\dot{\varvec{\eta }})= & {} \begin{bmatrix} -\varrho _2 \sin \eta _2\dot{\eta }_2 &{} -\varrho _2 \sin \eta _2(\dot{\eta }_1 + \dot{\eta }_2)\\ \varrho _2 \sin \eta _2\dot{\eta }_1 &{} 0 \end{bmatrix} \end{aligned}$$
(28)

where \(\varrho _i, i = 1...5\) are constant parameters depending on mechanical parameters and gravitational acceleration. In this simulation, these constant parameters are chosen as \(\varrho _1=5, \varrho _2=1, \varrho _3=1, \varrho _4=1.2g, \varrho _5=g\). The two simulation scenarios are considered to validate the performance of proposed controller as follows:

Case 1: The time-varying desired reference signal is defined as \(\varvec{\eta }_d=\begin{bmatrix} 3sin(t) \quad 3cos(t) \end{bmatrix}^T\) where the vector of disturbances is given as \(\ \varvec{d}(t)=\begin{bmatrix} 50sin(t) \quad 50cos(t) \end{bmatrix}^T\). For the control objective of general cost function, the optimal control problem is implemented with the arbitrary positive definite symmetric matrices in cost function (10) as:

$$\begin{aligned} \varvec{Q}=\begin{bmatrix} 40 &{} \quad 2 &{} \quad -4 &{} \quad 4\\ 2 &{} \quad 40 &{} \quad 4 &{} \quad -6\\ -4 &{} \quad 4 &{} \quad 4 &{}\quad 0\\ 4 &{} \quad -6 &{} \quad 0 &{} \quad 4\\ \end{bmatrix}, \quad \varvec{R}= \begin{bmatrix} 0.25 &{} \quad 0\\ 0 &{} \quad 0.25 \end{bmatrix} \end{aligned}$$

Moreover, due to the stability description of sliding surface, the design parameters in sliding variable \(\varvec{s}(\varvec{t}) ={\dot{\varvec{e}}}_{1} + \varvec{\lambda }_{\varvec{1}} \varvec{e}_{\varvec{1}}\) are chosen to satisfy that \(\varvec{\lambda }_{\varvec{1}} \in {\mathbb {R}}^{\varvec{n} \times \varvec{n}}\) is a constant positive definite matrix:

$$\begin{aligned} \varvec{\lambda }_1=\begin{bmatrix} 15.6 &{} \quad 10.6\\ 10.6 &{} \quad 10.4\\ \end{bmatrix} \end{aligned}$$

For the purpose of stability of the closed system as well as uncertainties/disturbance estimation, the remaining control gains in RISE framework are chosen satisfying (25), (26), (27) as:

$$\begin{aligned} \varvec{\lambda }_2=\begin{bmatrix} 60 &{} \quad 0\\ 0 &{} \quad 35\\ \end{bmatrix}, \quad \varvec{k}_s =\begin{bmatrix} 140 &{} \quad 0\\ 0 &{} \quad 20\\ \end{bmatrix}, \quad \gamma _{1j}=5 \end{aligned}$$

and the gains in actor–critic learning laws are selected guaranteeing (21)-(24) as:

$$\begin{aligned} k_c=800, \quad \nu =1, \quad k_{a1}=0.01, \quad k_{a2}=1, \end{aligned}$$

On the other hand, according to Dupree et al. (2011), the consideration of V in (16) can be calculated precisely as

$$\begin{aligned} V&= 2x_1^2 - 4{x_1}{x_2} + 3x_2^2 + 2.5x_3^2 + x_3^2 \cos \left( {{\eta _2}} \right) + {x_3}{x_4} \nonumber \\&\quad + {x_3}{x_4}\cos \left( {{\eta _2}} \right) + 0.5x_4^2 \end{aligned}$$
(29)

Although we can choose the arbitrary \(\varvec{\psi }(\varvec{X})\) in (16), however, for the comparison between result from experiences and result in (29), it leads to that the \(\varvec{\psi }(\varvec{X})\) was chosen as

$$\begin{aligned}&\varvec{\psi }(\varvec{X})\nonumber \\&\quad =\!{[x_1^2,{x_1}{x_2},x_2^2,x_3^2,x_3^2 \cos \left( {{\eta _2}} \right) , {x_3}{x_4},{x_3}{x_4}\cos \left( {{\eta _2}} \right) ,x_4^2]^T}\nonumber \\ \end{aligned}$$
(30)

and according to (29), exact values of \(\varvec{{\hat{W}}_c}\) in (18) and \(\varvec{{\hat{W}}_a}\) in (19) are

$$\begin{aligned} \varvec{{\hat{W}}_c}&=\begin{bmatrix} 2,&-4,&3,&2.5,&1,&1,&1,&0.5 \end{bmatrix}\nonumber \\ \varvec{{\hat{W}}_a}&=\begin{bmatrix} 2,&-4,&3,&2.5,&1,&1,&1,&0.5 \end{bmatrix} \end{aligned}$$
(31)
Fig. 2
figure 2

System states q(t) and its references \(q_d(t)=\eta _d \) with persistently excited input for the first 100 times

Full size image
Fig. 3
figure 3

Estimation of the total of external disturbance and nonlinear function by RISE control input

Full size image
Fig. 4
figure 4

The weight of NN for critic

Full size image
Fig. 5
figure 5

The weight of NN for actor

Full size image

In the simulation, the covariance matrix is initialized as

$$\begin{aligned} \varvec{\Psi }(\varvec{0}) = diag{\begin{bmatrix} 100&300&300&1&1&1&1&1 \end{bmatrix}} \end{aligned}$$

, while all the NN weights \(\varvec{W}_{\varvec{c}}, \varvec{W}_{\varvec{a}}\) are randomly initialized in \([-1,1]\), and the states and the its first time derivative are initialized to random matrices \(\varvec{q}(\varvec{0}),\dot{\varvec{q}}(\varvec{0}) \in {\mathbb {R}}^{\varvec{2}}\). It is necessary to guarantee PE conditions of the critic regression vector (in Remark 1) in using this developed algorithm. Unlike linear systems, where PE conditions of the regression translate to sufficient richness of the external input, there is no verifiable method exists to ensure PE regression translates in nonlinear regulation problems. To deal with this situation, a small exploratory signal consisting of sinusoids of varying frequencies is added to the control signal for first 100 times. Each experiment was performed 150 times, and data from experiments are displayed in Figs. 2, 4, 5 depicting the tracking states and the updating of NN weights \(\varvec{W}_{\varvec{c}}, \varvec{W}_{\varvec{a}}\), respectively. It is clear that the problem of tracking was satisfied after only about 2.5 times through Fig. 2. Meanwhile, the weights of NNs are compared to (31) as Table 1.

Table 1 Comparison between the proposed algorithm and exact values
Full size table

The highest error which is approximately 0.05 is a acceptable result although the time of convergence is still high. Furthermore, we obtain the tracking performance of the total of external disturbance \(\varvec{d} (t)\) and nonlinear function \(\varvec{f}(t)\), enabling the disturbance attenuation property of proposed control scheme in Fig. 3. These results proved the correctness of the algorithm.

Case 2: In this case, we consider for the different case of disturbance. The time-varying desired reference signal is defined as \(\varvec{\eta }_d=\begin{bmatrix} 3sin(t) \quad 3cos(t) \end{bmatrix}^T\) where the vector of random disturbances is given as \(\varvec{d}(t) =\begin{bmatrix} 10rand(1) \quad 10rand(1) \end{bmatrix}^T\). Based on the simulation method, the parameters are chosen as described in case 1, and our algorithm is effectively verified in tracking problem of the desired reference, weight convergence and disturbance attenuation as shown in Figs. 6, 7, 8, 9.

Fig. 6
figure 6

System states q(t) and its references \(q_d(t)=\eta _d \) with persistently excited input for the first 100 times

Full size image
Fig. 7
figure 7

Estimation of the total of external disturbance and nonlinear function by RISE control input

Full size image
Fig. 8
figure 8

The weight of NN for critic

Full size image
Fig. 9
figure 9

The weight of NN for actor

Full size image
Fig. 10
figure 10

Estimation of the total of external disturbance and nonlinear function by RISE control input

Full size image
Fig. 11
figure 11

The weight of NN for critic

Full size image
Fig. 12
figure 12

The weight of NN for actor

Full size image
Fig. 13
figure 13

System states q(t) and its references \(q_d(t)=\eta _d \) with persistently excited input for the first 100 times

Full size image

Case 3: In this case, we consider the different case of desired trajectory. The step function desired reference signal is defined as \(\varvec{\eta }_d=\begin{bmatrix} 2* 1(t) \quad 3* 1(t) \end{bmatrix}^T\) where the disturbance is given as \(\varvec{d}(t)= \begin{bmatrix} 50sin(t) \quad 50cos(t) \end{bmatrix}^T\). The parameters in simulation are chosen as mentioned in case 1. It should be noted that our algorithm is effective in tracking the desired reference, weight convergence and disturbance attenuation as described in Figs. 10, 11, 12, 13.

Remark 4

It is worth noting that the simulation results in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 illustrate the good behavior of trajectory tracking problem, the convergence in actor–critic neural network weights in the presence of dynamic uncertainties, external disturbances. This work is the remarkable extension of the work in Bhasin et al. (2013), which only mentions the first-order mathematical model without any disturbances. Additionally, the optimal control algorithm for manipulators was not considered the adaptive dynamic programming technique (Dupree et al. 2011).

5 Conclusions

This paper addresses the problem of adaptive reinforcement learning design for a second-order uncertain/disturbed manipulators in connection with sliding variable and RISE technique. Thanks to the online ADP algorithm based on the neural network, the solution of HJB equation was achieved by iteration algorithm to obtain the controller satisfying not only the weight convergence but also the trajectory tracking problem in the situation of non-autonomous closed systems. Offline simulations were developed to demonstrate the performance and effectiveness of the optimal control for manipulators.