Simultaneous Observation of the Wheel Torque and Tire Force as well as the Vehicle Speeds

Abstract

Individual torques at each vehicle wheel are important intermediate variables for the design of Advanced Driver Assistance Systems, and their knowledge stays an interesting research problem. In this study, a nonlinear high-gain unknown inputs state observer is designed to compute simultaneously longitudinal and transversal tire forces, resultant torques applied to wheels and the vehicle speeds. The necessary measurements are the usual rotation speed. Having validated the model of knowledge using a realistic vehicle simulator, the observer is tested under the same conditions and shows good performances for the vehicle state, tire forces and the unknown torques reconstruction.

1 Introduction

Due to the heavy tasks to improve safety, comfort and vehicle handling, advanced technologies have been used such as Antilock Brake System (ABS) and Direct Staking Control (DYC) as developed by Falcone et al. (2007), Mirzaei and Mirzaeinejad (2012) and Yang et al. (2009). Advanced Driver Assistant Systems designed for vehicle safety build effective automatic control strategies from a vehicle dynamical state whose components are either measured or estimated. Embedded measurements such as wheels rotation speeds, yaw rate or lateral acceleration are now generalized, but nowadays economic conditions lead to killing the production costs and at least ban the introduction of new components. Nevertheless, the scientific and technological progression is not stopped and it should be noted that the classical wheel bearings have evolved from a purely mechanical device to a mechatronic component that now integrates rotation speed measurements. Plied to the wheel would decrease from now hundred thousand euros to a small amount of euros. The present article anticipates the use of these newly affordable measurements by showing how it is possible to estimate the torques applied to the wheels as unknown inputs and the vehicle dynamic: longitudinal speed, lateral speed, yaw rate, yaw angle, sideslip angle, longitudinal and transversal tire forces.

Those estimated torques may be used in Active Driveline Torque Management, Pyabongkarn et al. (2010), in the Electronic Stability Control in complement of the existing brake-based actuation with the obvious economic and ecological advantages that energy is not necessarily lost during the actuation. These variables are now issued from procedures that use open-loop calibrated models. For example, the engine torques applied to the wheels are computed from the engine speed by using look-up tables and a powertrain model, Pfiffner et al. (2003). In the same way, the braking torque is computed from the measured pressure in the master cylinder and the “Electronic Brake Distribution” function that uses a model of brake disks friction.

Fig. 1

Vehicle variables for chassis: top view for longitudinal and transversal dynamics

This research anticipates that the estimated torque may be used in Active Driveline Torque Management [ADTM—Pyabongkarn et al. (2010)] in the ESC in complement of the existing brake-based actuation with the obvious economic and ecological advantages that energy is not necessarily lost during the actuation.

In engineering field, to improve the performance of the integrated technologies, numerous control strategies have been presented, such as fuzzy control (Li et al. 2015), robust control (Hu et al. 2016) and sliding mode control (Fang et al. 2011) and lateral dynamic control with delay (Zhu et al. 2015; Yang et al. 2016). Most of these controls assume that some variables are measured. But this is not generally the case because of very expensive sensors or absence of technology.

An alternative strategy based upon state observation theory is proposed in this work with the advantages of the closed-loop structure. This technology has been spread up in the industry under the “software sensor” denomination. Examples are the works of Doumiati et al. (2009) who present experimental embedded validations of tire/road force observer and Stéphant et al. (2007) who give a sideslip angle observer. Some works on observers assume that resultant torques applied to wheels are ”measured” (Ray 1997; M’Sirdi et al. 2008). But, in actual vehicles, these variables are estimated using the first solution.

The estimated state and unknown input can then be used as input of actual ADAS. The technique called ”high gain” can be applied without transformation of the initial system: In this case, the design of the observer is directly obtained from the system structure (Thau 1973; Kou et al. 1975; Gauthier et al. 1992; Raghavan and Hedrick 1994; Kreisselmeier and Engel 2003; Farza et al. 2005).

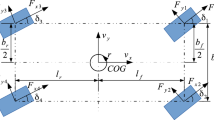
This work proposes to estimate simultaneously tire forces, vehicle speed and resultant torques applied to the wheel of a vehicle. The observer designed in Sect. 3 uses measurements of wheels rotation speeds and normal forces together with a nonlinear model of the vehicle defined and calibrated in Sect. 2. A vehicle simulator is used to validate the vehicle model (Sect. 4.3) and the designed observer (Sect. 4.4). It will be shown that the vehicle state observation is accurate in spite of the fact that resultant torques applied to the wheels are unknown. The different notations are indicated in “Appendix 6” and Fig. 1.

2 State-Space Model of Vehicle Dynamics

2.1 Chassis Dynamics

Considering the motion of the vehicle on a planar and horizontal road with neglected sprung masses, its configuration is composed of the coordinates $x_G$ and $y_G$ of its center of gravity together with the yaw angle $\psi$; these variables being defined in an earth-fixed reference frame ${\mathcal {W}} = \left\{ O_w,\mathbf {i}_w, \mathbf {j}_w\right\}$ (see top of Fig. 1 which is assumed to be inertial.

In this communication, the dynamics are considered from the viewpoint of the vehicle. The chassis dynamics model is thus hereafter represented in the mobile reference frame ${\mathcal {M}} = \left\{ G,\mathbf {i}, \mathbf {j}\right\}$. All variables are displayed in Fig.  1.

The motion is originated by the four forces applied at the tire/road interfaces. Each one of those forces is expressed in the wheel frame (see bottom of Fig.  1; $F_{xij}$ denotes the longitudinal component, $F_{yij}$) the lateral one and $F_{zij}$ is the normal one. $\delta _{ij}$ terms the steering angle of the $_{ij}$ wheel. It is generated by the steering driveline for the front wheels ($_{i}=_{F}$) and represents the effects of the toe angle for the two rear wheels. $M_V$ denotes the vehicle mass and $I_{zz}$ its yaw inertia. Applying Newton’s law in the mobile frame, the longitudinal ($V_x$), lateral ($V_y$) and yaw speeds ($\dot{\psi }$) evolve as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{V}_{x} = \displaystyle \frac{1}{M_V}\sum \limits _{i,j}\left( F_{xij}\cos (\delta _{ij})- F_{yij}\sin (\delta _{ij})\right) +\dot{\psi } V_{y}\\ \dot{V}_{y} = \displaystyle \frac{1}{M_V}\sum \limits _{i,j} \left( F_{xij}\sin (\delta _{ij}) + F_{yij}\cos (\delta _{ij})\right) - \dot{\psi } V_{x}\\ I_{zz}\ddot{\psi } = L_f\sum \limits _{j=R,L}\left( F_{xFj}\sin (\delta _{Fj})+F_{yFj}\sin (\delta _{Fj})\right) \\ \qquad \qquad -L_{r}\sum \limits _{j=R,L}\left( F_{xRj}\sin (\delta _{Rj})+F_{yRj}\sin (\delta _{Rj})\right) \\ \qquad \qquad +\sum \limits _{i=F,R}E_{iR}\left( F_{xiR}\cos (\delta _{iR})-F_{yiR}\sin (\delta _{iR})\right) \\ \qquad \qquad -\sum \limits _{i=F,R}E_{iL}\left( F_{xiL}\cos (\delta _{iL})-F_{yiL}\sin (\delta _{iL})\right) \end{array} \right. \end{aligned}$$

(1)

In the sequel, we propose to explicit the links between the forces and the variables that describe the motion in order to establish a state-space model of the motion. This is done by starting from the wheels.

2.2 Wheel Rotational Dynamics

The rotation of the $_{ij}$ wheel (Fig. 2) is generated by the longitudinal force $F_{xij}$ stemming from the road together with the resultant torque $T_{ij}$ induced by both the vehicle (engine and brakes for instance) and the environment (effects of the slope and aerodynamics effects). $I_{wij}$ being the wheel inertia, the moment equation around its rotation axis is:

$$\begin{aligned} \dot{\omega }_{ij} = \displaystyle \frac{1}{I_{wij}}\left( -R_{lij}\cdot F_{xij}+ T_{ij} \right) . \end{aligned}$$

(2)

In this expression, the moment of the longitudinal force is $\left( -R_{lij}.F_{xij}\right)$ where $R_{lij}$ is the “loaded radius” shown in Fig. 3 and defined by Gillespie Gillespie (1992) as “the distance from the center of tire contact to the wheel center.” It can be computed by (3) as the free radius $R_{0ij}$ minus the deflection deduced from both the tire vertical stiffness $k_{zij}$ and the normal load ($F_{zij}$).

$$\begin{aligned} R_{lij} \simeq R_{0ij} - \displaystyle \frac{F_{zij}}{k_{zij}} \end{aligned}$$

(3)

Fig. 2

Variables of the wheels dynamics

Fig. 3

Wheel and tire radii—Free, loaded and rolling radii

2.3 Slip Ratio

It is well known that the origin of the forces at the tire/road interfaces is linked with the deformation of the tire which is itself described by slip ratio.

The longitudinal slip ratio (LSR, $g_{lij}$) if defined by the normalized skidding speed between the wheel spin velocity ($\omega _{ij}$) and the equivalent spin velocity of a straight free rolling tire ($V_{xij}/R_{rij}$).

$$\begin{aligned} g_{lij} = -\displaystyle \frac{V_{ij}\cos (\beta _{ij})-\omega _{ii}R_{rij}}{V_{ij}\cos (\beta _{ij})} \end{aligned}$$

(4)

The LSR is positive during driving and negative for braking. The rolling radius ($R_\mathrm{r}$) is the radius of a rigid wheel whose centers are displaced of the same distance as the center of the (non-rigid) real tire while performing an equal number of turns (Fig. 3). This radius may be computed using the free radius $R_{0ij}$ and the vertical load applied to the wheel by equation (5) where $a_{ij}$ and $b_{ij}$ are parameters to be identified

$$\begin{aligned} R_{rij} \simeq R_{0ij} -\displaystyle \frac{F_{zij}}{a_{ij}F_{zij}+b_{ij}}. \end{aligned}$$

(5)

$\beta$ being the sideslip angle at the center of gravity (Fig. 1) and defined by:

$$\begin{aligned} \beta = \hbox {arctan}\left( \displaystyle \frac{V_{y}}{V_{x}}\right) , \end{aligned}$$

(6)

the norm of the speed of the center of each wheel speed is linked with the one of the centers of gravity by using kinematics relations:

$$\begin{aligned} \left\{ \begin{array}{lcl} V_\mathrm{FL} &{}=&{} V_{G}- \dot{\psi }\left( E_\mathrm{FL}- L_{f}\sin (\beta )\right) \\ V_\mathrm{FR} &{}=&{} V_{G}+ \dot{\psi }\left( E_\mathrm{FR}+ L_{f}\sin (\beta )\right) \\ V_\mathrm{RL} &{}=&{} V_{G}- \dot{\psi }\left( E_\mathrm{RL}+ L_{r}\sin (\beta )\right) \\ V_\mathrm{RR} &{}=&{} V_{G}+ \dot{\psi }\left( E_\mathrm{RR}- L_{r}\sin (\beta )\right) \end{array} \right. . \end{aligned}$$

(7)

The transversal slip ratio is defined as the tangent of the tire sideslip angle.

$$\begin{aligned} g_{tij} = \tan (\beta _{ij}) \end{aligned}$$

(8)

The sideslip angle (Fig. 1) of each wheel can be calculated using geometry and kinematics relations with the velocity of the center of gravity (Kiencke and Nielsen 2000):

$$\begin{aligned} \left\{ \begin{array}{rl} \beta _\mathrm{FL}=&{} \delta _\mathrm{FL} - \hbox {arctan} \left( \displaystyle \frac{V_G \sin (\beta ) + \dot{\psi }d_\mathrm{FL}\cos (\nu _\mathrm{FL})}{V_G \cos (\beta ) - \dot{\psi }d_\mathrm{FL}\sin (\nu _\mathrm{FL})}\right) , \\ \beta _\mathrm{FR}=&{} \delta _\mathrm{FR} - \hbox {arctan} \left( \displaystyle \frac{V_G \sin (\beta ) + \dot{\psi }d_\mathrm{FR}\sin (\nu _\mathrm{FR})}{V_G \cos (\beta ) + \dot{\psi }d_\mathrm{FR}\cos (\nu _\mathrm{FR})}\right) , \\ \beta _\mathrm{RL}=&{} \delta _\mathrm{RL} - \hbox {arctan} \left( \displaystyle \frac{V_G \sin (\beta ) - \dot{\psi }d_\mathrm{RL}\sin (\nu _\mathrm{RL})}{V_G \cos (\beta ) - \dot{\psi }d_\mathrm{RL}\cos (\nu _\mathrm{RL})}\right) , \\ \beta _\mathrm{RR}=&{} \delta _\mathrm{RR} - \hbox {arctan} \left( \displaystyle \frac{V_G \sin (\beta ) - \dot{\psi }d_\mathrm{RR}\cos (\nu _\mathrm{RR})}{V_G \cos (\beta ) + \dot{\psi }d_\mathrm{RR}\sin (\nu _\mathrm{RR})}\right) . \end{array} \right. \end{aligned}$$

(9)

In these expressions, $d_{ij}$ is the distance between the center of gravity and the wheel/road contact point and $\nu _{ij}$ denotes the angle between the vehicle coordinate systems and the wheel/road contact point. Those expressions are defined analytically by (10,11), and the $\nu _{ij}$ angles are displayed in Fig. 1.

$$\begin{aligned}&d_{ij}=\sqrt{L_{j}^{2}+E_{ij}^2} \end{aligned}$$

(10)

$$\begin{aligned}&\left\{ \begin{array}{lcl} \nu _\mathrm{FL}=\hbox {arctan}\left( \displaystyle \frac{E_\mathrm{FL}}{L_{f}}\right) \\ \nu _\mathrm{FR}=\hbox {arctan}\left( \displaystyle \frac{L_{f}}{E_\mathrm{FR}}\right) \\ \nu _\mathrm{RL}=\hbox {arctan}\left( \displaystyle \frac{L_{r}}{E_\mathrm{RL}}\right) \\ \nu _\mathrm{RR}=\hbox {arctan}\left( \displaystyle \frac{E_\mathrm{RR}}{L_{r}}\right) \end{array} \right. \end{aligned}$$

(11)

The resultant wheel slip is a ratio that combines longitudinal and transversal wheel slip phenomena.

$$\begin{aligned} g_{ij} = \sqrt{g_{lij}^{2} + g_{tij}^{2}} \end{aligned}$$

(12)

2.4 Tire/Road Contact Force Model

Among the numerous models of tire/road contact forces (Pacejka 2002), we propose to consider a simplified Burckhardt model (Burckhardt and Reimpell 1993) that is a good compromise between the number of parameters and the accuracy of the description. It is based on a nonlinear representation of the tire/road friction coefficient scaled by the normal force acting on the tire/road contact patch.

This tire/road friction coefficient is written as a function of the resultant slip ratio (12):

$$\begin{aligned} \mu _{ij}(g_{ij})= c_{1ij}(1 - \exp (-c_{2ij}g_{ij})) - c_{3ij}g_{ij} \end{aligned}$$

(13)

Coefficients $c_{1ij}$, $c_{2ij}$ and $c_{3ij}$ are representative of the road surface. An example of the representativity of this model where the results of the Burckhardt formula (13) is compared to data from a physical based model.

The forces are produced by contact between the road and tires. They are transmitted through the dynamics of wheels and vehicle. They are of major importance for the dynamic behavior of a road vehicle. Hence, accurate tire models are necessary components of models aimed at analyzing or simulating vehicle motion in real driving conditions. The driver can then control the vehicle trough this dynamic. A lot of work has been done in the area of tires model fitting and estimation. Many models have been previously used to describe the tire forces. Some of them are theoretical in the sense that they aim at modeling the physical processes that generates the forces. Other ones are empirically oriented, and their aim is to describe observed phenomena in a simple way. In this work, we consider the relaxation model which represents the forces is a model of the first order (Doumiati et al. 2008; Ouahi et al. 2015). The forces of the contact wheel/ground are formulated according to a differential equation of the first order, and the main parameter is the relaxation length $\sigma$. The relaxation length is the distance traveled by the tire during the settling time of the effort. In this model, the longitudinal and lateral force evolves as follows:

$$\begin{aligned} \left\{ \begin{array}{lcl} \dot{F}_{xij} &{}=&{} \displaystyle \frac{V_{x}}{\sigma _{xij}}(-F_{xij}+F_{x0ij})\\ \dot{F}_{yij} &{}=&{} \displaystyle \frac{V_{y}}{\sigma _{yij}}(-F_{yij}+F_{y0ij}) \end{array} \right. \end{aligned}$$

(14)

where $F_{x0ij}$ and $F_{y0ij}$ is calculated with a simplified model of Burckhardt. Among the numerous models of tire force, this study is altogether compact and thorough for the considered problem. Its expression (15) includes the normal load $F_{zij}$ and a nonlinear friction coefficient

$$\begin{aligned} \left\{ \begin{array}{lcl} F_{x0ij}&{}=&{} \displaystyle \frac{g_{lij}}{g_{ij}}\mu _{ij}(g_{ij})F_{zij}\\ F_{y0ij}&{}=&{}\displaystyle \frac{g_{tij}}{g_{ij}}\mu _{ij}(g_{ij})F_{zij} \end{array} \right. \end{aligned}$$

(15)

Finally, The vertical tire/road force is proportional to from a longitudinal and lateral acceleration and an equation of moment equilibrium. The vertical load applied to the wheel is ($F_{zij}$). This force could be estimated by equation

$$\begin{aligned} \left\{ \begin{array}{lcl} F_{z\mathrm{FL}}&{}=&{} \displaystyle \frac{L_{r} M_V g }{2L} - \displaystyle \frac{M_V h_g a_{x}}{2L}- \displaystyle \frac{L_{r} M_V h_g a_{y}}{ L E_\mathrm{FL}}\\ F_{z\mathrm{FR}}&{}=&{} \displaystyle \frac{L_{r} M_V g }{2L} - \displaystyle \frac{M_V h_g a_{x}}{2L}+ \displaystyle \frac{L_{r} M_V h_g a_{y}}{L E_\mathrm{FR}}\\ F_{z\mathrm{RL}}&{}=&{} \displaystyle \frac{L_f M_V g }{2L} + \displaystyle \frac{M_V h_g a_{x}}{2L}- \displaystyle \frac{L_f M_V h_g a_{y}}{L E_\mathrm{RL}}\\ F_{z\mathrm{RR}}&{}=&{} \displaystyle \frac{L_f M_V g }{2L} + \displaystyle \frac{M_V h_g a_{x}}{2L}+ \displaystyle \frac{L_f M_V h_g a_{y}}{L E_\mathrm{RR}}\\ \end{array} \right. \end{aligned}$$

(16)

where $L=L_f +L_{r}$.

2.5 State-Space Model of the Vehicle

By assembling the chassis dynamics (1), the wheels dynamics (2) and injecting the Burckhardt tire/road force model (14), it comes to the following state-space model of the vehicle:

$$\begin{aligned} \left\{ \begin{array}{lcl} \dot{\omega }_\mathrm{FL} &{}=&{} \frac{1}{I_{w\mathrm{FL}}} \displaystyle \left( -R_{l\mathrm{FL}}\cdot F_{x\mathrm{FL}} + T_\mathrm{FL} \right) \\ \dot{\omega }_\mathrm{FR} &{}=&{} \frac{1}{I_{w\mathrm{FR}}} \displaystyle \left( -R_{l\mathrm{FR}}\cdot F_{x\mathrm{FR}} + T_\mathrm{FR} \right) \\ \dot{\omega }_\mathrm{RL} &{}=&{} \frac{1}{I_{w\mathrm{RL}}} \displaystyle \left( -R_{l\mathrm{RL}}\cdot F_{x\mathrm{RL}} + T_\mathrm{RL} \right) \\ \dot{\omega }_\mathrm{RR} &{}=&{} \frac{1}{I_{w\mathrm{RR}}} \displaystyle \left( -R_{lRR}\cdot F_{x\mathrm{RR}} + T_\mathrm{RR} \right) \\ \dot{V}_{x} &{}= &{} \frac{1}{M_V}\sum \limits _{i,j}\left( F_{xij}\cos (\delta _{ij})- F_{yij}\sin (\delta _{ij})\right) +\dot{\psi } V_{y}\\ \dot{V}_{y} &{}=&{} \frac{1}{M_V}\sum \limits _{i,j} \left( F_{xij}\sin (\delta _{ij}) + F_{yij}\cos (\delta _{ij})\right) - \dot{\psi } V_{x}\\ \ddot{\psi } &{}=&{} \frac{1}{I_{zz}}\{ L_f\sum \limits _{j=R,L}\left( F_{x\mathrm{Fj}}\sin (\delta _{\mathrm{Fj}})+F_{y\mathrm{Fj}}\sin (\delta _{\mathrm{Fj}})\right) \\ &{} &{}-\, L_{r}\sum \limits _{j=R,L}\left( F_{x\mathrm{Rj}}\sin (\delta _{\mathrm{Rj}})+F_{y\mathrm{Rj}}\sin (\delta _{\mathrm{Rj}})\right) \\ &{} &{}+ \sum \limits _{i=F,R}E_{iR}\left( F_{xiR}\cos (\delta _{iR})-F_{yiR}\sin (\delta _{iR})\right) \\ &{} &{}-\sum \limits _{i=F,R}E_{iL}\left( F_{xiL}\cos (\delta _{iL})-F_{yiL}\sin (\delta _{iL})\right) \}\\ \dot{F}_{x\mathrm{FL}} &{}=&{} \displaystyle \frac{V_{x}}{\sigma _{x\mathrm{FL}}}(-F_{x\mathrm{FL}}+F_{x0\mathrm{FL}})\\ \dot{F}_{x\mathrm{FR}} &{}=&{} \displaystyle \frac{V_{x}}{\sigma _{x\mathrm{FR}}}(-F_{x\mathrm{FR}}+F_{x0\mathrm{FR}})\\ \dot{F}_{x\mathrm{RL}} &{}=&{} \displaystyle \frac{V_{x}}{\sigma _{x\mathrm{RL}}}(-F_{x\mathrm{RL}}+F_{x0\mathrm{RL}})\\ \dot{F}_{x\mathrm{RR}} &{}=&{} \displaystyle \frac{V_{x}}{\sigma _{x\mathrm{RR}}}(-F_{x\mathrm{RR}}+F_{x0\mathrm{RR}})\\ \dot{F}_{y\mathrm{FL}} &{}=&{} \displaystyle \frac{V_{y}}{\sigma _{y\mathrm{FL}}}(-F_{y\mathrm{FL}}+F_{y0\mathrm{FL}})\\ \dot{F}_{y\mathrm{FR}} &{}=&{} \displaystyle \frac{V_{y}}{\sigma _{y\mathrm{FR}}}(-F_{y\mathrm{FR}}+F_{y0\mathrm{FR}})\\ \dot{F}_{y\mathrm{RL}} &{}=&{} \displaystyle \frac{V_{x}}{\sigma _{y\mathrm{RL}}}(-F_{y\mathrm{RL}}+F_{y0\mathrm{RL}})\\ \dot{F}_{y\mathrm{RR}} &{}=&{} \displaystyle \frac{V_{x}}{\sigma _{y\mathrm{RR}}}(-F_{y\mathrm{RR}}+F_{y0\mathrm{RR}}) \end{array} \right. \end{aligned}$$

(17)

3 Design of a Software Sensor in the Form of a High-Gain Unknown Inputs Observer

3.1 Observer Principle

It often happens that all state variables of a system are not accessible to measurement or input not measurable because of very expensive sensors or absence of technology. The idea is to rebuild the state and the input not measurable from information available that is to say the output and known inputs.

The aim of an unknown input observer ($\mathcal {O}$) is to estimate simultaneously the state (x) and the unknown input ($\bar{u}$) applied to a physical system using measured input (u), measured output (y) and a knowledge model ($\Sigma$) of the system. The principle of this kind of observer is shown in Fig. 4.

Fig. 4

Unknown inputs observer principle

In the unknown inputs observer theory, our objective is to synthesize observers to simultaneously estimate the whole state as well as all unknown inputs.

Let us consider the nonlinear high-gain unknown inputs observer (47) proposed by Liu et al. (2006).

3.2 Model Formatting

The state-space variable of vehicle model (17) is:

$$\begin{aligned} x=\begin{pmatrix} x^1&X \end{pmatrix}^{\mathrm{T}} \end{aligned}$$

(18)

where the state is split into two parts $x^1 =(\omega _\mathrm{FL},\omega _\mathrm{FR},\omega _\mathrm{RL},\omega _\mathrm{RR})^{\mathrm{T}}$ and $X =(X1, X2)^{\mathrm{T}}$ with: $X1=(V_{x}, V_{y}, \dot{\psi }, F_{x\mathrm{FL}}, F_{x\mathrm{FR}}, F_{x\mathrm{RL}}, F_{x\mathrm{RR}})^{\mathrm{T}}$ and $X2 =(F_{y\mathrm{FL}}, F_{y\mathrm{FR}}, F_{y\mathrm{RL}}, F_{y\mathrm{RR}})^{\mathrm{T}}$.

Assuming that the rotational wheel speed is measured (for example, using ABS sensors), it is possible to build a measured output to this model.

$$\begin{aligned} y=(\omega _\mathrm{FL},\omega _\mathrm{FR},\omega _\mathrm{RL},\omega _\mathrm{RR})^{\mathrm{T}} \end{aligned}$$

(19)

Assuming that the steering geometry is known, it is possible to use the driver steering angle to compute the different wheel steering angles. The longitudinal and transversal accelerations are measured by interferometers. It gives a measured input described by:

$$\begin{aligned} u=(\delta _\mathrm{FL},\delta _\mathrm{FR},\delta _\mathrm{RL},\delta _\mathrm{RR},a_x,a_y)^{\mathrm{T}} \end{aligned}$$

(20)

Finally, an unknown input comprising the resulting torques applied to the wheels is defined.

$$\begin{aligned} \bar{u}=(T_\mathrm{FL},T_\mathrm{FR},T_\mathrm{RL},T_\mathrm{RR})^{\mathrm{T}} \end{aligned}$$

(21)

It should be noted that the number of unknown inputs is equal to the number of measures and that there is no input in the measurement equation.

Measurements are the usual wheel rotation speed. The model can now be expressed under a state equation (17).

$$\begin{aligned} \Sigma \left\{ \begin{array}{lcl} \dot{x} &{} =&{} f(x,u) + G(u) \bar{u} \\ y &{}=&{} Cx \end{array} \right. \end{aligned}$$

(22)

where the state is split into two parts

$$\begin{aligned} x^1 = y =(\omega _\mathrm{FL},\omega _\mathrm{FR},\omega _\mathrm{RL},\omega _\mathrm{RR})^{\mathrm{T}} \end{aligned}$$

is the measured one and X the other one.

The $f(x,u)=\begin{pmatrix} f^1(x,u)&f_X(x,u) \end{pmatrix}$ is the state function, the matrix $G(u)=\begin{pmatrix} G^1(u)&G_X(u) \end{pmatrix}$ and $C=\begin{pmatrix} I&0 \end{pmatrix}$

Such synthesis necessitates the adoption of appropriate assumptions which shall be given in due courses.

A nonlinear high-gain unknown inputs observer is designed (Liu et al. 2006). To build this kind of observer, some hypothesis must be checked:

• (1) The matrix $G^1$ must be full column rank (${\hbox {Rang}}(CG(u))={\hbox {Rang}}(G^1(u))$).

  $\exists \alpha , \beta > 0; \forall t\ge 0:$

  $0<\alpha ^2 I< (G^1(u))^{\mathrm{T}} (G^1(u))<\beta ^2 I$

• (2) The time derivative, $\varepsilon (t)$, of the unknown input $\bar{u}$ is a completely unknown function which is uniformly bounded. ${\hbox {sup}}||\varepsilon (t)|| \le \rho$ for $t\ge 0$ (where $\rho >0$ is a real number).

• (3) There exists a symmetric positive-definite matrix p(t) such that (detectability condition):

  • (a) $\exists \alpha _1, \alpha _2 > 0; \forall t\ge 0:$

    $\alpha _1 I_4 \le p(t) \le \alpha _2 I_4$

  • (b) $\exists \alpha _3 > 0,\forall u \in \mathbb {R}^{4}, \forall x^1 \in \mathbb {R}^{4}, \forall X \in \mathbb {R}^{4}:$

    $$\begin{aligned}&\dot{p}(t) + p(t)\frac{\partial f_X}{\partial X}(x^1,X,u) \\&\quad +\frac{\partial f_X}{\partial X}(x^1,X,u)^{\mathrm{T}} p(t) \le -\, \alpha _3 I_4 \end{aligned}$$

Now, let

$$\begin{aligned} \left\{ \begin{array}{lcl} \Upsilon ^1 &{} =&{} (G^1(u))(G^1(u))^+ \\ \Upsilon _X &{} =&{} (G_X(u))(G^1(u))^+ \\ \Upsilon &{} =&{} \begin{pmatrix} \Upsilon ^1 \\ \Upsilon _X \end{pmatrix} \end{array} \right. \end{aligned}$$

(23)

Consider the following change in coordinates,

$$\begin{aligned} \begin{pmatrix} \bar{x}^{1}_{1} \\ \bar{x}^{1}_{2}\\ \bar{X} \end{pmatrix} = \begin{pmatrix} I &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad I &{}\quad 0 \\ -\Upsilon &{}\quad 0 &{}\quad I \end{pmatrix} \begin{pmatrix} x^1 \\ \bar{u}\\ X \end{pmatrix} \end{aligned}$$

(24)

where I is the dimension appropriate.

For system (22), the formatted system is now written by (25)

$$\begin{aligned} \Sigma \left\{ \begin{array}{lcl} \dot{\bar{x}}^1 &{} =&{} \bar{f}^1(\bar{x}^{1}_{1},\bar{X},u) + \bar{G}^1(u) \bar{u}+ \bar{\varepsilon }(t) \\ \dot{\bar{X}} &{} =&{} \bar{f}_{\bar{X}}(\bar{x}^{1}_{1},\bar{X},u) + \dot{\Upsilon }_X \bar{x}^{1}_{1}\\ y &{}=&{} \bar{x}^{1}_{1} \end{array} \right. \end{aligned}$$

(25)

where $\bar{x}^1 = \begin{pmatrix} \bar{x}^{1}_{1} \\ \bar{x}^{1}_{2} \end{pmatrix}$, $\bar{X} = X- \Upsilon _X x^1$, $\bar{f}^1(\bar{x}^{1}_{1},\bar{X},u) = \begin{pmatrix} f^1(x,u) \\ 0 \end{pmatrix}$, $\bar{f}_{\bar{X}}(\bar{x}^{1}_{1},\bar{X},u) = f_X(x,u)- \Upsilon _X f^1(x,u)$, $\bar{G}^1(u) = \begin{pmatrix} 0 &{} G^1(u) \\ 0 &{} 0 \end{pmatrix}$ and $\bar{\varepsilon }(t) = \begin{pmatrix} 0 \\ \varepsilon (t) \end{pmatrix}$.

Now, let the following coordinate changes:

$$\begin{aligned} \begin{array}{lcl} z^{1}&{}=&{} \begin{pmatrix} z^{1}_{1} \\ z^{1}_{2}\end{pmatrix} \\ &{}=&{} \Lambda \bar{x}^1 \\ &{}=&{} \Phi (\bar{x}^1,u) \\ \end{array} \end{aligned}$$

(26)

where $\Lambda =\hbox {diag} \begin{pmatrix} I, G^{1}(u)\end{pmatrix}$

Before describing the dynamics of $z^{1}$, we note the following identity:

$$\begin{aligned} \Lambda \bar{G}(u) = A \Lambda \end{aligned}$$

(27)

where $A=\begin{pmatrix} 0 &{} I \\ 0 &{} 0 \end{pmatrix}$

The dynamic of $z^{1}$ is

$$\begin{aligned} \begin{array}{lcl} \dot{z}^{1}&{}=&{} \frac{\partial \Phi (\bar{x}^1,u)}{\partial \bar{x}^1}\dot{\bar{x}}^1 + \frac{\partial \Phi (\bar{x}^1,u)}{\partial u} \dot{u} \\ &{}=&{} Az +\Lambda \bar{f}^1(\bar{x}^{1}_{1},\bar{X},u) + \Lambda \bar{\varepsilon } +\frac{\partial \Phi (\bar{x}^1,u)}{\partial u}\dot{u} \\ &{}=&{} Az + \varphi (z,u) + \Lambda \bar{\varepsilon } \\ \end{array} \end{aligned}$$

(28)

The observer synthesis needs the following additional assumptions:

4) The function $\varphi (z,u)$ is globally Lipschitz with respect to z uniformly in u.

The initial observation problem becomes standard since the objective is now to design an observer for following the nonlinear systems

$$\begin{aligned} \Sigma \left\{ \begin{array}{lcl} \dot{z}^{1}&{}=&{} Az + \varphi (z^1,\bar{X},u) + \Lambda \bar{\varepsilon } \\ \dot{\bar{X}} &{} =&{} \bar{f}_{\bar{X}}(z^{1}_{1},\bar{X},u) + \dot{\Upsilon }_X z^{1}_{1}\\ y &{}=&{} z^{1}_{1}=C z^{1}\\ \end{array} \right. \end{aligned}$$

(29)

It should be noted that the number of unknown inputs is equal to the number of measures and that there is no input in the measurement equation.

3.3 Observer Synthesis

Before giving our candidate observer, one introduces the following notations.

• let $\Delta _{\theta }$ be the block diagonal matrix defined by:

  $$\begin{aligned} \Delta _{\theta }=\hbox {diag} \begin{pmatrix} I , \frac{I}{\theta } \end{pmatrix} \end{aligned}$$

  (30)

  where $\theta >0$ is a real number.

• Let S be the unique solution of the algebraic Lyapunov equation (31)

  $$\begin{aligned} S + A^{\mathrm{T}} S + SA - C^{\mathrm{T}}C =0 \end{aligned}$$

  (31)

  One can show that S is symmetric positive definite and in particular one has:

  $$\begin{aligned} S^{-1}C^{\mathrm{T}} = \begin{pmatrix} 2I \\ I \end{pmatrix} \end{aligned}$$

  (32)

A candidate observer for system (29) is:

$$\begin{aligned} \hat{ \Sigma }\left\{ \begin{array}{lcl} \dot{\hat{z}}^{1}&{}=&{} A\hat{z} + \varphi (\hat{z}^1,\hat{\bar{X}},u) - \theta \Delta _{\theta }^{-1} S^{-1}C^{\mathrm{T}} (\hat{z}^{1}_{1}-z^{1}_{1}) \\ \dot{\hat{\bar{X}}} &{} =&{} \bar{f}_{\bar{X}}(z^{1}_{1},\hat{\bar{X}},u) + \dot{\Upsilon }_X z^{1}_{1}\\ \end{array} \right. \end{aligned}$$

(33)

where $\hat{z}^1= \begin{pmatrix} \hat{z}^{1}_{1} \\ \hat{z}^{1}_{2} \end{pmatrix}$ and $\theta$ is the observer tuning parameter.

From the equation of the system ($\Sigma$) and ($\hat{\Sigma }$), the observation error is:

$$\begin{aligned} \left\{ \begin{array}{lcl} e^{1}&{}=&{} \hat{z} -z \\ e^{2}&{}=&{} \hat{X} -X \\ \end{array} \right. \end{aligned}$$

(34)

Lemma

Suppose the system (29) satisfied hypothesis (1), (2), (3) and (4), alors,

• (1) $\exists \bar{\theta }>0, \exists \lambda _1>0, \exists \lambda _2>0, \forall \theta>\bar{\theta }, \exists \mu (\theta ) >0, \exists M(\theta )$

  $$\begin{aligned}&||e^1(t)||\le \lambda _1 \theta \exp (-\mu (\theta )t)||e^2(0)|| \\&\quad +\lambda _2 \exp (-\alpha _3t)||e^2(0)|| +M(\theta )\rho \end{aligned}$$

• (2) $\exists \sigma >0$, on a $||e^2(t)||\le \sigma \exp (-\alpha _3t)||e^2(0)||$

Proof

Furthermore, one can easily check the following identities: $\Delta _{\theta }A \Delta _{\theta }^{-1}= \theta A$ and $C \Delta _{\theta }=C$.

Set

$$\begin{aligned} \left\{ \begin{array}{lcl} \bar{e}^{1}&{}=&{} \Delta _{\theta } e^{1} \\ \bar{e}^{2}&{}=&{} e^{2} \\ \end{array} \right. \end{aligned}$$

(35)

Using the theorem of average value for the second error, the dynamics errors are obtained by:

$$\begin{aligned} \left\{ \begin{array}{lcl} \dot{\bar{e}}^{1}&{}=&{} \theta \left( A- S^{-1}C^{\mathrm{T}} C\right) \bar{e}^{1}+\\ &{} &{} \Delta _{\theta }\left( \varphi (\hat{z}^1,\hat{\bar{X}},u)- \varphi (z^1,\bar{X},u)\right) -\Delta _{\theta } \Lambda \bar{\varepsilon }\\ \dot{\bar{e}}^{2}&{}=&{} \frac{\partial \bar{f}_{\bar{X}}}{\partial \bar{X}}(z^{1}_{1},\bar{X},u)\bar{e}^{2} \\ \end{array} \right. \end{aligned}$$

(36)

The Lyapunov function candidate is $V(\bar{e}^{1}, \bar{e}^{2}) = V_1(\bar{e}^{1}) + V_2(\bar{e}^{2})$, Where:

$$\begin{aligned} \left\{ \begin{array}{lcl} V_1(\bar{e}^{1})&{}=&{} (\bar{e}^{1})^{\mathrm{T}} S \bar{e}^{1} \\ V_2(\bar{e}^{2})&{}=&{} (\bar{e}^{2})^{\mathrm{T}} p(t) \bar{e}^{2} \\ \end{array} \right. \end{aligned}$$

(37)

One has:

$$\begin{aligned} \begin{array}{lcl} \dot{V}_1(\bar{e}^{1})&{}=&{} 2(\bar{e}^{1})^{\mathrm{T}} S \dot{\bar{e}}^{1} \\ &{}=&{} -\,\theta V_1(\bar{e}^{1}) - (\bar{e}^{1})^{\mathrm{T}} C^{\mathrm{T}} C \dot{\bar{e}}^{1}- 2 (\bar{e}^{1})^{\mathrm{T}} S \Delta _{\theta } \Lambda \bar{\varepsilon } \\ &{} &{} +\,2 (\bar{e}^{1})^{\mathrm{T}} S \Delta _{\theta }\left( \varphi (\hat{z}^1,\hat{\bar{X}},u)- \varphi (z^1,\bar{X},u)\right) \\ &{}\le &{} -\,\theta V_1(\bar{e}^{1}) + 2 ||\bar{e}|| ||S|| \left| \left| \Delta _{\theta } \Lambda \bar{\varepsilon }\right| \right| \\ &{} &{} +\,2 ||\bar{e}|| ||S|| \left| \left| \Delta _{\theta }\left( \varphi (\hat{z}^1,\hat{\bar{X}},u)- \varphi (z^1,\bar{X},u)\right) \right| \right| \\ \end{array} \end{aligned}$$

(38)

According to the Lipschitz condition on these function, one can easily show that:

$$\begin{aligned} \left| \left| \Delta _{\theta }\left( \varphi (\hat{z}^1,\hat{\bar{X}},u)- \varphi (z^1,\bar{X},u)\right) \right| \right| \le k_1 ||\bar{e}^{1}|| + k_2 ||\bar{e}^{2}|| \end{aligned}$$

(39)

According to the structures of $\bar{\varepsilon }$, one has:

$$\begin{aligned} \left| \left| \Delta _{\theta } \Lambda \bar{\varepsilon }\right| \right| = \left| \left| \frac{G^1(u) \varepsilon }{\theta }\right| \right| \le \frac{\beta \rho }{\theta } \end{aligned}$$

(40)

for some constants $\beta$ and $\rho$ which do not depend on $\theta$.

According to the previous developments, inequality (41) can be written as follows:

$$\begin{aligned} \dot{V}_1(\bar{e}^{1})\le & {} -(\theta -c_1) V_1(\bar{e}^{1}) \nonumber \\&+\, c_2\sqrt{V_1(\bar{e}^{1})}\sqrt{V_2(\bar{e}^{2})} + \frac{c_3 \rho }{\theta }\sqrt{V_1(\bar{e}^{1})} \end{aligned}$$

(41)

with: $c_1=\frac{2 K_1 ||S||}{\lambda _{min}(S)}$, $c_2$, $c_3$ for some constant real positive number $c_1=\frac{2 K_1 ||S||}{\lambda _{min}(S)}$, $c_2=\frac{2 K_2 ||S||}{\sqrt{\lambda _{min}(S)}}$, $c_3=\frac{2 \beta ||S||}{\sqrt{\lambda _{min}(S)}}$ ($\lambda _{min}(S)$ etant la plus petite valeur propre de (S) ) which do not depend on $\theta$.

Otherwise, under hypothesis (3), one can show that:

$$\begin{aligned} \dot{V}_2(\bar{e}^{2}) \le -\,\alpha _3 V_2(\bar{e}^{2}) \end{aligned}$$

(42)

or equivalently

$$\begin{aligned} ||e^2(t)||\le \sigma \exp (-\frac{\alpha _3t}{2})||e^2(0)|| \end{aligned}$$

(43)

with: $\sigma =\frac{\alpha _2}{\alpha _1}$.

We deduce

$$\begin{aligned} \begin{array}{lcl} \sqrt{V_1(\bar{e}^{1})} &{} \le &{} \exp \left( -\frac{(\theta -c_1)t}{2}\right) \sqrt{V_1(\bar{e}^{1}(0))} + \frac{c_2 \sigma }{\theta -c_1-\alpha _3} \\ &{} &{} \left( \exp (-\frac{\alpha _3t}{2})-\exp \left( -\frac{(\theta -c_1)t}{2}\right) \right) ||e^2(0)||\\ &{} &{} \frac{c_3 \rho }{\theta (\theta -c_1)}\left( 1-\exp \left( -\frac{(\theta -c_1)t}{2}\right) \right) \end{array}\nonumber \\ \end{aligned}$$

(44)

now choosing $\theta >1+c_1+\alpha _3$, we obtain:

$$\begin{aligned} \begin{array}{lcl} \sqrt{V_1(\bar{e}^{1})} &{} \le &{} \exp \left( -\frac{(\theta -c_1)t}{2}\right) \sqrt{V_1(\bar{e}^{1}(0))} + c_2 \sigma \\ &{} &{} \exp (-\frac{\alpha _3t}{2})||e^2(0)|| + \frac{c_3 \rho }{\theta (\theta -c_1)}\\ \end{array} \end{aligned}$$

(45)

We now use the fact that $||\bar{e}^1||\le ||e^1|| \le \theta ||\bar{e}^1||$ and obtain:

$$\begin{aligned} \begin{array}{lcl} ||e^1|| &{} \le &{} \frac{\lambda _{max}(S)\theta }{\lambda _{min}(S)} \exp \left( -\frac{(\theta -c_1)t}{2}\right) ||e^1(0)|| + \\ &{} &{} \frac{\theta c_2 \sigma }{\lambda _{min}(S)} \exp (-\frac{\alpha _3t}{2})||e^2(0)|| + \frac{c_3 \rho }{\lambda _{min}(S)(\theta -c_1)}\\ \end{array} \end{aligned}$$

(46)

Finally, set $\bar{\theta }= 1+c_1+\alpha _3$, $\lambda _1 =\frac{\lambda _{max}(S)}{\lambda _{min}(S)}$, $\lambda _2 = \frac{ c_2 \sigma }{\lambda _{min}(S)}$, $\mu (\theta )=\frac{(\theta -c_1)t}{2}$, $M(\theta )=\frac{c_3 }{\lambda _{min}(S)(\theta -c_1)}$. This ends the proof. $\square$

These expressions will be given in the new coordinates z in order to easily check hypothesis (1), (2), (3) and (4) as well as in the original coordinates x in order to easily recognize the structure of the resulting observers.

The observer for the system (22) is:

$$\begin{aligned} \hat{\Sigma } \left\{ \begin{array}{ll} \dot{\hat{x}}^1 &{} = f(\hat{x}^1, \tilde{X},u)+ G(u)\hat{\bar{u}} + 2 \theta D(u) (y - \hat{x}^1) \\ \hat{\bar{u}} &{} = \theta ^{2}(G^{1}(u))^{+}(y - \hat{x}^1) \end{array} \right. \end{aligned}$$

(47)

where $\hat{x}=\begin{pmatrix} \hat{x}^1 \\ \hat{X} \end{pmatrix}$ is estimation of the state vector, $\bar{u}$ is estimation of the unknown input, $D(u) = \begin{pmatrix} I \\ \Upsilon _X \end{pmatrix}$ and $\tilde{X} = \hat{X}- \Upsilon _X (\hat{x}^1 -x^1)$.

3.4 Summary for the Observer Applied to the Vehicle Model

To estimate simultaneously the state and the unknown inputs of the vehicle (17), the observer is explicitly:

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{\hat{\omega }}_\mathrm{FL} = \frac{1}{I_{w\mathrm{FL}}} \left( -R_{l\mathrm{FL}}\cdot \hat{F}_{x\mathrm{FL}} + \hat{T}_\mathrm{FL} \right) + 2\theta \left( \omega _\mathrm{FL}-\widehat{\omega }_\mathrm{FL}\right) \\ \dot{\hat{\omega }}_\mathrm{FR} = \frac{1}{I_{w\mathrm{FR}}} \left( -R_{l\mathrm{FR}}\cdot \hat{F}_{x\mathrm{FR}} + \hat{T}_\mathrm{FR} \right) + 2\theta \left( \omega _\mathrm{FR}-\widehat{\omega }_\mathrm{FR}\right) \\ \dot{\hat{\omega }}_\mathrm{RL} = \frac{1}{I_{w \mathrm{RL}}} \left( -R_{l \mathrm{RL}} \cdot \hat{F}_{x\mathrm{RL}} + \hat{T}_\mathrm{RL} \right) + 2\theta \left( \omega _\mathrm{RL}-\widehat{\omega }_\mathrm{RL}\right) \\ \dot{\hat{\omega }}_\mathrm{RR} = \frac{1}{I_{w\mathrm{RR}}} \left( -R_{l\mathrm{RR}} \cdot \hat{F}_{x\mathrm{RR}} + \hat{T}_\mathrm{RR} \right) + 2\theta \left( \omega _\mathrm{RL}-\widehat{\omega }_\mathrm{RL}\right) \\ \dot{\hat{V}}_{x} = \frac{1}{M_V}\sum \limits _{i,j}\left( \hat{F}_{xij}\cos (\delta _{ij})- \hat{F}_{yij}\sin (\delta _{ij})\right) +\dot{\hat{\psi }} \hat{V}_{y}\\ \dot{\hat{V}}_{y} = \frac{1}{M_V}\sum \limits _{i,j} \left( \hat{F}_{xij}\sin (\delta _{ij}) + \hat{F}_{yij}\cos (\delta _{ij})\right) - \dot{\hat{\psi }} \hat{V}_{x}\\ \ddot{\hat{\psi }} = \frac{1}{I_{zz}} \Bigg \{ L_f\sum \limits _{j=R,L}\left( \hat{F}_{x\mathrm{Fj}}\sin (\delta _{\mathrm{Fj}})+\hat{F}_{y\mathrm{Fj}}\sin (\delta _{\mathrm{Fj}})\right) \\ \qquad \quad - L_{r}\sum \limits _{j=R,L}\left( F_{x\mathrm{Rj}}\sin (\delta _{\mathrm{Rj}})+F_{y\mathrm{Rj}}\sin (\delta _{\mathrm{Rj}})\right) \\ \qquad \quad + \sum \limits _{i=F,R}E_{\mathrm{iR}}\left( \hat{F}_{x\mathrm{iR}}\cos (\delta _{\mathrm{iR}})-\hat{F}_{y\mathrm{iR}}\sin (\delta _{\mathrm{iR}})\right) \\ \qquad \quad -\,\sum \limits _{i=F,R}E_{iL}\left( \hat{F}_{x\mathrm{iL}}\cos (\delta _{\mathrm{iL}})-\hat{F}_{y\mathrm{iL}}\sin (\delta _{\mathrm{iL}})\right) \Bigg \}\\ \dot{\hat{F}}_{x\mathrm{FL}} = \displaystyle \frac{\hat{V}_{x}}{\sigma _{x\mathrm{FL}}}(-\hat{F}_{x\mathrm{FL}}+\hat{F}_{x0\mathrm{FL}})\\ \dot{\hat{F}}_{x\mathrm{FR}} = \displaystyle \frac{\hat{V}_{x}}{\sigma _{x\mathrm{FR}}}(-\hat{F}_{x\mathrm{FR}}+\hat{F}_{x0\mathrm{FR}})\\ \dot{\hat{F}}_{x\mathrm{RL}} = \displaystyle \frac{\hat{V}_{x}}{\sigma _{x\mathrm{RL}}}(-\hat{F}_{x\mathrm{RL}}+\hat{F}_{x0\mathrm{RL}})\\ \dot{\hat{F}}_{x\mathrm{RR}} = \displaystyle \frac{\hat{V}_{x}}{\sigma _{x\mathrm{RR}}}(-\hat{F}_{x\mathrm{RR}}+\hat{F}_{x0\mathrm{RR}})\\ \dot{\hat{F}}_{y\mathrm{FL}} = \displaystyle \frac{\hat{V}_{y}}{\sigma _{y\mathrm{FL}}}(-\hat{F}_{y\mathrm{FL}}+\hat{F}_{y0\mathrm{FL}})\\ \dot{\hat{F}}_{y\mathrm{FR}} = \displaystyle \frac{\hat{V}_{y}}{\sigma _{y\mathrm{FR}}}(-\hat{F}_{y\mathrm{FR}}+\hat{F}_{y0\mathrm{FR}})\\ \dot{\hat{F}}_{y\mathrm{RL}} = \displaystyle \frac{\hat{V}_{x}}{\sigma _{y\mathrm{RL}}}(-\hat{F}_{y\mathrm{RL}}+\hat{F}_{y0\mathrm{RL}})\\ \dot{\hat{F}}_{y\mathrm{RR}} = \displaystyle \frac{\hat{V}_{x}}{\sigma _{y\mathrm{RR}}}(-\hat{F}_{y\mathrm{RR}}+\hat{F}_{y0\mathrm{RR}})\\ \dot{\widehat{T}}_\mathrm{FL}= \theta ^2 I_{wFL}\left( \omega _\mathrm{FL}-\widehat{\omega }_\mathrm{FL}\right) \\ \dot{\widehat{T}}_\mathrm{FR}= \theta ^2 I_{wFR}\left( \omega _\mathrm{FR}-\widehat{\omega }_\mathrm{FR}\right) \\ \dot{\widehat{T}}_\mathrm{RL}= \theta ^2 I_{wRL}\left( \omega _\mathrm{RL}-\widehat{\omega }_\mathrm{RL}\right) \\ \dot{\widehat{T}}_\mathrm{RR}= \theta ^2 I_{w\mathrm{RR}}\left( \omega _\mathrm{RR}-\widehat{\omega }_\mathrm{RR}\right) \end{array} \right. \end{aligned}$$

(48)

4 Model and Observer Validation

The objective of this paper is to estimate non-measured variables by state-space observers deduced from available measurements interpreted by using the progression equation (17). A first step in this design consists to validate this model in the situations that will be studied. This is the subject of the following section.

4.1 Vehicle Simulator

Realistic simulators are useful intermediate between real experiments and simplified models which are used to design controllers or state observers.

Callas Lechner et al. (1997) is a realistic vehicle simulator software distributed by Oktal company (http://www.oktal.fr). It has been validated by some French car manufacturers and research institutions. The Callas model is a physical knowledge-based one and takes into account phenomena such as nonlinear vertical dynamics (suspension, tires), kinematics, elasto-kinematics, tire adhesion, aerodynamics $\ldots$ and the road profile. The validation tests that are shown in this section display the comparison between the behaviors of both a Callas model of a “Peugeot 406” car and the low-order state-space model (17). The relevance of those tests stems from the more complete physical description of the Callas model together with the fact that inner variables such as the torques and normal forces on all wheels are recorded. Those variables are the inputs of the model (17) to be validated. This is truly advantageous since the measurement of all those variables is rare and expensive, which is again a motivation of the present study that proposes to estimate indirectly the non-affordable measurements.

4.2 Simulation Conditions

In this paper, model and observer are evaluated using the following simulation conditions. The driver simulator is configured to perform a braking in turn. This kind of test is used to evaluate model’s performances in the case of coupling effects between longitudinal and transversal dynamics. The driver increases the steering wheel angle at 70 [km/h]. When a trajectory radius of 100 [m] is reached, a force of 40 [daN] is applied on the break pedal. Simulation conditions are shown in Fig. 5.

Fig. 5

Simulation conditions: vehicle position and force on brake pedal

Fig. 6

Rotational wheel speed calculated by the open-loop model with known torque. Callas reference and modeling error

For the following simulations, parameters of the nonlinear friction coefficient (13) are identified to match the friction curve during a braking and turning phase at wheel locked.

On all figures, only the front left ($ij=FL$) and the rear right ($ij=RR$) variables are shown. The front right (rear left) variables are similar to the front left variables (rear right).

4.3 Model Validation

Model validation is the first stage of a software sensor design. To do this, model (17) is used with all known inputs. $T_{ij}$ are extracted from Callas.

On the top of Fig. 6, the rotational speeds of wheels issued from Callas (”ref” label) and from the model (”BO” label) are shown. In the bottom, the modeling error is presented. On the rear right wheel, the maximum error is $1.7 \mathrm{rad} \mathrm{s}^{-1}\simeq 1.8 \mathrm{km}\,\mathrm{h}^{-1}]$. On the front left wheel, the maximum error is around $2.1 km\,\mathrm{h}^{-1}]$. This indicates that the model of rotational acceleration is correct when the resultant torque applied to the wheel is known.

4.4 Observer Validation

Fig. 7

Longitudinal speed of vehicle compared by the open-loop model and the unknown input observer. Callas reference, modeling error and observation error

On the top of Fig. 7, the longitudinal speed of vehicle estimation $\widehat{V}_x$ (”UIO” label) is compared to the Callas reference (”ref” label) and to the open-loop model with known torques (”BO” label). In the bottom, the observer and modeling error are presented. On the open-loop model, the maximum error is $0.3 \mathrm{m}\, \mathrm{s}^{-1}]$. On the unknown input observer, the maximum error is around $0.06 \mathrm{m} \mathrm{s}^{-1}]$. This figure indicates that observer results are better than the ones of the calibrated open-loop model.

Fig. 8

Lateral vehicle speed of vehicle calculated by the open-loop model with known torque and by the unknown input observer. Callas reference, modeling error and observation error

The top of Fig. 8 displays the results of the unknown input observer (48). The lateral vehicle speed of vehicle (chassis over ground speed) is presented. Callas reference is indicated by the label ref, open-loop model with known torque by the label BO and observed speed $\widehat{V}_y$ by observer. A maximum error of $0.16 \mathrm{ms}^{-1}$ shows that the speed estimation is accurate despite the lack of knowledge of torques applied to the wheels. Then, observer results are better than the ones of the calibrated open-loop model.

Fig. 9

Yaw angle calculated by the open-loop model with known torque and by the unknown input observer. Callas reference, modeling error and observation error

The top of Fig. 9 presents the observation the yaw angle compared with Callas reference and the one which was modelized by the open-loop model with known inputs. In the bottom, the observer and modeling errors are presented. One can see that the trends are good. The yaw angle $\psi$ estimation (”UIO” label) is compared to the Callas reference (”ref” label) and to the open-loop model with known torques (”BO” label). On the open-loop model, the maximum error is 4.92 deg. On the unknown input observer, the maximum error is around 0.37 deg.

In Fig. 10, the vehicle sideslip angle observed by the unknown inputs observer is compared to the Callas reference and the one which was modelized by the open-loop model with known inputs. First of all, the vehicle has small sideslip angle, because the curvature radius for the presented test is around 100 m for a speed of 70 km/h. The lateral acceleration is not important (less than 0.4 g). During the path at constant speed, open-loop model and observer give the same results. During the braking phase which begins at time 4 s, observer performance is better than the open-loop model.

Fig. 10

Vehicle sideslip angle computed by the open-loop model with known torque and by the unknown input observer. Callas reference, modeling error and observation error

On the top of Fig 11 the longitudinal tire/road forces issued from Callas (indicated by the ”ref” label) and from the observer (”UIO” label) are shown. In the bottom, the modeling error is presented. On the front left wheel, the maximum error is 13 daN. For the rear wheel, the maximum error is 7 daN. This indicates that model of longitudinal forces (14) is accurate when the resultant torque applied to the wheel is known. It should be noted that the relative error is around 2%.

Fig. 11

Longitudinal tire/road force calculated by the open-loop model with known torque. Callas reference and modeling error

Figure 12 presents the observer performances to compute the lateral tire/road contact forces. One can see that the trends are good. A relative error of about 10% can be noted.

Fig. 12

Lateral tire forces calculated by the unknown input observer. Callas reference and observation error

Fig. 13

Vertical tire/road force compared by the unknown input observer. Callas reference and observer error

Fig. 14

Resultant torque calculated by the unknown input observer. Callas reference and observation error

In the upper part of Fig. 13, the vertical tire/road forces issued both from Callas (”ref” label) and from the model (”UIO” label) are shown. In the bottom, the observer error is presented. On an average, the absolute value of the force error on all wheels is less than 17.13 daN for front lift wheels and $-11.45 \mathrm{daN}$ for the rear right ones.

Finally, Fig. 14 presents the unknown torque estimated by the observer confronted to the resultant torque applied to the wheels by the Callas simulator. On an average, performances of the observer are very accurate.

It is important to indicate here that the unknown input calculated is not directly the resultant torque (sum of braking and driving torque). Indeed, this unknown input is made up of:

• Effective resultant torque

• Errors on radius estimation

• Non-modelized torque

5 Conclusion

This paper has presented a nonlinear unknown inputs observer to estimate simultaneously torque, tire forces and vehicle speed from rotational wheel speed measurements. Having validated the model of knowledge using Callas as a realistic vehicle simulator, the observer has been tested under the same conditions and showed good performances for the reconstruction of the vehicle state and the unknown torques applied to the wheels.

This paper follows the work we have developed in Ouahi et al. (2010, 2011, 2013) which enables estimating the couple from measurements of wheel speed rotation.

Those estimated torques may be used in ADTM in the ESC in complement of the existing brake-based actuation with the obvious economic and ecological advantages that energy is not necessarily lost during the actuation.

6 Notations

• $i=F,R$ wheel or tire number (front, rear)

• $j=L,R$ wheel or tire number (left, right)

• $E_\mathrm{FL}$: Half-way front right (m)

• $E_\mathrm{FR}$: Half-way front left (m)

• $E_\mathrm{RL}$: Half-way rear right (m)

• $E_\mathrm{RR}$: Half-way rear left (m)

• $F_{zij}$: Normal force (i,j) (N)

• $F_{xij}$: Longitudinal tire/road force—tire (i,j) (N)

• $F_{yij}$ : Lateral tire/road force - tire (i,j) (N)

• $g_{ij}$ : Resultant slip ratio tire (i,j) $(-)$

• $g_{lij}$ : Longitudinal slip ratio tire (i,j) $(-)$

• $g_{tij}$ : Lateral slip ratio tire (i,j) $(-)$

• $I_{wij}$ : Inertia—wheel (i,j) $(\mathrm{kg} \mathrm{m}^{2})$

• $k_{zij}$ : Vertical stiffness—tire (i,j) $(\mathrm{N}\,\mathrm{m}^{-1})$

• $L_{f}$ : Distance from CG to front axle (m)

• $L_{r}$ : Distance from CG to rear axle (m)

• $R_{0ij}$: Nominal radius - tire (i,j) (m)

• $R_{rij}$: Rolling radius - tire (i,j) (m)

• $R_{lij}$: Loaded radius - tire (i,j) (m)

• $T_{ij}$: Torque applied to the wheel (i,j) (Nm)

• $V_{x}$: Longitudinal velocity $(\mathrm{ms}^{-1})$

• $V_{y}$: Lateral velocity $(\mathrm{ms}^{-1})$

• $\beta$: Center of gravity side slip angle (rad)

• $\beta _{ij}$: Wheel side slip angle (i,j) (rad)

• $\mu _{ij}$: Longitudinal friction coefficient tire (i,j) $(-)$

• $\omega$: Angular velocity $(\mathrm{N} \mathrm{rad}^{-1})$

• $\psi$: Angle rate (rad)

• $\sigma _{xij}$: Longitudinal relaxation - tire (i,j) (m)

• $\sigma _{yij}$: Lateral relaxation - tire (i,j) (m)

• $\theta$: Observer tuning parameter $(\mathrm{s}^{-1/2})$

• $M_{V}$: Total vehicle mass (kg)

• $\widehat{.}$ : Observed variable $(-)$