A Self-Adaptive Approach for Particle Swarm Optimization Applied to Wind Speed Forecasting

Abstract

Operational research has made meaningful contributions to practical forecasting in organizations. An area of substantial activity has been in nonlinear modeling. Based on Particle Swarm Optimization, we discuss a nonlinear method where a self-adaptive approach, named as Particle Swarm Optimization with aging and weakening factors, was applied to training a Focused Time Delay Neural Network. Three freely available benchmark datasets were used to demonstrate the features of the proposed approach compared to the Backpropagation algorithm, Differential Evolution and the Particle Swarm Optimization method when applied for training the artificial neural network. Even acknowledging that the effort in comparing methods across multiple empirical datasets is certainly substantial, the proposed algorithm was used to produce 30 min, 1, 3 and 6 h ahead predictions of wind speed at one site in Brazil. The use of the proposed algorithm goes further than only training the artificial neural network, but also searching the best number of hidden neurons and number of lags. The results have shown that the modified Particle Swarm Optimization algorithm obtained better results in all predictions horizons, and the use of it has remarkably reduced the training time.

1 Introduction

Energy markets demand higher levels of quality and service continuity from the energy suppliers, in such a way that decision tools became a major instrument to meet those demands. Applications in operation areas have proved particularly important, including the management of intermittent renewable sources and demand, supply chain planning, long-term scenario planning. Forecasting to support operations is the application area where operational research first contributed, and it remains important.

Wind energy continues to gain support throughout the world. Many countries have devoted much attention to the use of renewable energy sources to meet the growing of energy demand and ensure sustainable development (GWEC 2017). Wind generation is characterized by the variability in production and restricted control. Managing the variability of wind power generation is a key factor associated with the optimum integration of wind plants with the electrical grid network (Mao and Shaoshuai 2016; Ssekulima et al. 2016). As a result, the reliable and economical operation of power systems with high wind penetration requires wind power forecasts.

A review of the state of the art in short-term wind power forecasting is available in Giebel et al. (2011). Of particular relevance to this work is the conclusion that for forecast horizons of less than approximately six hours, statistical methods using local information are superior to physical models.

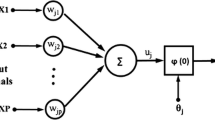
Statistical methods used for wind speed and power prediction usually are based on linear models despite the nonlinear nature of the wind. For this reason, we investigate a class of machine learning algorithms called artificial neural networks (ANN) which allow the processing of nonlinear features (Liu et al. 2015). ANN are models inspired by biological neural networks and generally are presented as systems of interconnected ‘neurons’ which exchange messages between each other. The connections have numeric weights (synaptic weights) that can be tuned based on experience, making neural nets adaptive to inputs and capable of learning.

Optimal selection of ANN parameters is an important open problem in the learning machine literature. Usually the selection is done through trial and error (TE) method, where the user manipulate variables in an attempt to sort through possibilities that may result in success. The method is costly and does not follow a standard process, making it strongly influenced by the user choices. To tackle this problem, we can use Particle Swarm Optimization (PSO) (Kennedy and Eberhart 1995), which does not differentiate between the variables that it optimizes. Therefore, it is possible to apply PSO to optimize all parameters of an ANN such as the number of layers, number of neurons in the input, hidden and output layer, synaptic weights, among others. However, as the number of parameter increases, PSO demands greater computational cost and has some drawbacks such as the local optimum and inactive particles.

The purpose of this article is to reach better or similar estimations to those obtained by models that use PSO, but with a significant reduction in the required computational cost. Therefore, we focus on the effect of Life Expectancy (LE) on the cultural diversity of a social animal colony. The LE is a statistical measure of how long an organism may live, and at a given age, life is expected to cease. LE is based on many features, e.g., the year of birth, current age and other demographic factors. Here we propose a simplified version of this concept, based on two constants called aging factor (AF) and weakening factor (WF). In nature, colony leaders are constantly challenged by new individuals. In this way, the community is always led by a strong leader. This paper transplants the above idea from nature to PSO and proposes the PSO with aging and weakening factors (PSO-AWF) algorithm. The proposed approach is compared to the Backpropagation (BP), Differential Evolution (DE) and the PSO method when applied for training the ANN.

The contributions of this paper are to: (1) propose a new lifespan controller that mimics a simplified version of the LE theory; (2) propose a new modified PSO algorithm called PSO-AWF that uses this new lifespan controller; (3) evaluate the effect of the lifespan controller applied to the PSO; (4) study of the search behavior of the proposed algorithm, PSO-AWF, as a learning method for an ANN solving regression problems.

The remainder of this paper is organized as follows. In Sect. 2, the problem is described in detail followed by a background review. The modeling of the proposed technique is presented in Sect. 3. Case studies are examined in Sect. 4 to validate the proposed model. In particular, the datasets are introduced in Sect. 4.1. In Sect. 4.2, for the sake of reproducibility of this paper, the parameter values are listed. The results and analysis of the PSO-AWF are shown in Sect. 4.3. Finally, the conclusions are given in Sect. 5.

2 Problem Formulation and Background Review

The prediction problem is outlined as follows, whereby the purpose of a potentially nonlinear function $f(\cdot )$ is to look $\varDelta$ samples ahead in time, estimating (or ) from the input vector (or ) containing time data comprising measurements $y_{t-\varDelta }$, $y_{t-\varDelta -1}$, $\ldots$. The predictor is written $\hat{y}_{\varDelta |t}=f(x_t)$. The aim in the context of a prediction problem is to find an estimate $\hat{f}(\cdot )$ of $f(\cdot )$, which minimizes the estimation error in the mean squared sense, i.e.,

$$\begin{aligned} \mathrm{MSE}_\varDelta = {\frac{1}{T}{\sum \limits _{{i = 1}}^T {{{\left( {{\hat{y}_{\varDelta |t}} - {{y}_t}} \right) }^2}} }}. \end{aligned}$$

(1)

The linear approximation of this problem is given by $\hat{f}(x_t)= Ax_t$, where (or ) is a coefficient matrix whose entries are to be determined. Many estimation schemes based on this approximation have been studied.

Alternatively, we can state the approximation in terms of a matrix of synaptic weights of a neural network that are computed by learning algorithms. One example of those learning algorithms is the BP. Williams and Hinton (1986) described several cases where BP works faster than earlier learning approaches, making it possible to use ANN to solve problems which had previously been insoluble. Today, the BP algorithm is considered a reference.

In this paper, we present an algorithm for short-term forecasting based on a Multilayer Perceptron (MLP) network with unit delays, named Focused Time Delay Neural Network (FTDNN). The FTDNN is a multilayer network without feedback, whose synaptic weights are adjusted in accordance with the conventional BP algorithm. As a typical feed-forward neural network, the signal travels through the FTDNN in only one direction, from the input to the output, whereby the neurons of the same layer are not connected. However, Time Delay Neural Networks (TDNN) are temporal networks that, along with the actual input x(t), have a line of unit delays (LAG) inserted in the input layer that represent the network memory, $x(t-1)$, $x(t-2)$,...,$x(t-\mathrm{LAG})$ (Engelbrecht 2007).

Although the BP is a consolidated learning technique (Chang et al. 2012; Mao et al. 2016), it has been verified that the application of DE and PSO as a learning algorithm is very efficient (Arce et al. 2016; Raza et al. 2016). Because of this, there has been interest in investigating the application of these tools in dynamic environments.

Proposed by Storn and Price (1997), DE is a stochastic, population-based search strategy for solving a wide variety of optimization problems. The optimization performance of the DE algorithm not only depends on the choice of three control parameters (i.e., mutation control parameter F, crossover control parameter CR and population size NP), but also on the choice of trial vector generation strategies (i.e., mutation and crossover strategies). A survey of the state of the art can be found in Das and Suganthan (2011).

PSO is an optimization technique inspired by the social cooperative and competitive behavior of bird flocking and fish schooling. PSO can be used to resolve nonlinear and multimodal problems, thereby being able to make different searches simultaneously. The PSO maintains a cloud of particles, in which each one represents a possible solution. The particles flow through a multidimensional space, where the position of each particle is adjusted in accordance with its own experience and those of its neighborhood.

Usually the initial speed v of each particle is zero or a random value. We describe the new speed $v_i(t+1)$ that drives the optimization process, and is used as a tool of communication between all particles, as follows.

$$\begin{aligned} v_{i}(t+1)= & {} v_{i}(t)+C_{1}R_{1}(Pbest_{i}(t)-x_{i}(t)) \nonumber \\&+ \,C_{2}R_{2}(Gbest(t)-x_{i}(t)), \end{aligned}$$

(2)

where $C_{1}$ and $C_{2}$ are, respectively, the social and cognitive constants, the best position of each particle is $Pbest_{i}$, the best position between all particles is Gbest(t), $R_{1}$ and $R_{2}$ are random numbers between [0,1]. The new position $x_{i}(t+1)$ is computed as

$$\begin{aligned} x_{i}(t+1)=x_{i}(t)+v_{i}(t+1). \end{aligned}$$

(3)

All particles would displace themselves up to an optimal point. During the search, if the best solution found (Gbest) is not the optimum solution, one of the particles could find a better solution and become the new Gbest. This cycle continues until the global optimum solution is found or a user restriction is encountered.

Innumerous PSO variants have attempted to eliminate some characteristics of the classical algorithm, such as inactive particles, rapid convergence and the risk of local optima clustering (Zhang et al. 2015). The existing PSO variants can be mainly classified into the following four categories. The first category of PSO variants achieves improvements by adjusting parameter configurations. Shi and Eberhart (1998) first introduced a new parameter, namely the inertia weight ($\omega$), to influence convergence. The velocity update rule is thus changed to

$$\begin{aligned} v_{i}(t+1)= & {} \omega v_{i}(t)+C_{1}R_{1}(Pbest_{i}(t)-x_{i}(t)) \nonumber \\&+ \, C_{2}R_{2}(Gbest(t)-x_{i}(t)). \end{aligned}$$

(4)

Linear decrease of $\omega$ was proposed by Shi and Eberhart (1999). In addition, the settings for other parameters have been tested. Further, by merely tuning parameters, particles are still attracted by Gbest. If Gbest is trapped in a local optimum, the problem of premature convergence remains.

The second category aims to increase diversity by defining neighborhood topologies. Kennedy and Mendes (2002) introduces the local version of PSO. The velocity update rule in Eq. 4 replaces Gbest for Lbest, which is the best position found by a particle in its neighborhood defined by a pre-given topology. To improve the robustness of PSO, structures have also been proposed by Beheshti et al. (2014) and Lim and Isa (2014). Chen et al. (2013) proposed an adaptive lifespan control of the leader of the swarm. It is characterized by assigning the leader with a growing age and a lifespan, and allowing the other individuals to challenge leadership when the leader becomes aged. In general, by introducing neighborhood structures, the PSO variants have an enhanced ability to prevent premature convergence. However, because the attraction of Gbest is weakened and other particles can also influence the adjustments of velocities and positions, this kind of PSO variant converges at a much lower speed.

The third category introduces multiswarm techniques to improve performance of PSO. The original PSO works better in simple and low-dimensional search space. Van den Bergh and Engelbrecht (2004) decomposed the search space and utilized multiple swarms to optimize different components of a solution vector cooperatively. In the Parallel Comprehensive Learning Particle Swarm Optimizer (PCLPSO) proposed by Åaban Glc and Kodaz (2015), multiple swarms based on the master–slave paradigm works cooperatively or concurrently. Liu et al. (2017) proposed a new Coevolutionary technique-based Multiswarm Particle Swarm Optimizer for Dynamic Multiobjective Optimization Problems (CMPSODMO) for the rapidly changing environments. The number of the swarms is determined by the number of the objective functions, which means that each function corresponds to a swarm. Usually, in PSO variants with multiple subpopulations, the subpopulations can be treated as a special type of neighborhood structure. In this sense, this category of PSO variants also faces the problem of slower convergence.

The fourth category is PSO hybridized with auxiliary search techniques to enhance performance. Various types of evolutionary computation paradigms have been used for this, including Genetic Algorithms (Garg 2016), Differential Evolution (Mao et al. 2017), Ant Colony Optimization (Elloumi et al. 2014), and others. Overall, integrating PSO with other optimization techniques is effective to improve performance, but the disadvantage is that the hybrid algorithms are usually much more complicated than the original PSO.

From the above discussions, it can be seen that preventing premature convergence while retaining the fast-converging feature of PSO is still a challenging task in PSO research. Most variants achieve the preservation of population diversity at the cost of slow convergence or complicated algorithmic structures. PSO-AWF avoids premature convergence, reducing the speed of convergence and maintaining the simplicity of the structure of PSO. PSO-AWF has the ability to jump out of local optima. Different from the local version PSO variants, however, PSO-AWF preserves the leader’s information. Only when the leader fails to lead, do the particles diverge from the current leader’s attraction. In this way, PSO-AWF can keep the fast-converging feature of PSO.

3 Particle Swarm Optimization with Aging and Weakening Factors

In social animal colonies, aging facilitates a leader to be replaced by a younger individual and hence likely creates more opportunities for diversity and improvements. Inspired by this phenomenon, this paper proposes a PSO whereby other bio-inspired characteristics are adopted, the aging and weakening process.

The phenomenon of aging has attracted the attention of biologists for approximately 150 years. As early as the 1880s, Weismann (1882) first argued that aging is necessary for evolution as it provides a mechanism to make room for the development of the next generation. Goldsmith (2006) advocated that aging is able to increase genetic diversity and therefore is helpful for the evolution of a species. An optimal lifespan plays an important role in improving the effectiveness of evolution. With recent development of the aging theories (Goldsmith 2004, 2006; Gavrilov and Gavrilova 2002), it would be interesting and worthwhile studying further the effect of aging on more evolutionary computation techniques.

In conventional PSO, the suitability of individuals is determined by their objective functional value only. In natural systems, age of an individual also plays a key role to determine its suitability. The essence of PSO-AWF is to provide a mechanism for promoting a suitable leader to lead the swarm through aging. Since all particles are attracted by Gbest in the original PSO, we can view Gbest as the leader of the swarm. The misleading effect of a leader positioned at a local optimum point is the main cause of premature convergence in the original PSO. To weaken such an effect, PSO-AWF assigns the entire swarm with a lifespan. Similar to the original PSO, particles still learn from the leader to update velocities and positions. However, if the lifespan of the particle is exhausted, new particles emerge to challenge and claim the leadership. In this way, the aging mechanism provides opportunities for other particles to lead the swarm and thus brings in diversity.

Aging is not the only feature that composes the LE of an individual. Here WF represents the other features from LE. WF plays a role whenever the particle ($x_{i}$) is not able to find a new result ($Pbest_{i}(t)$) better than the previous one ($Pbest_{i}(t-1)$). This way, even particles with the same age will have different LE and will cease to exist in different moments. The entirety of this section is summarized by the steps given as follows.

• 1. Initialization The initial positions ($x_i(t)$) of all particles are generated randomly within the n-dimensional search space, with velocities ($v_{i}(t)$) initialized to 0. The best particle among the swarm is selected as the leader (Gbest). The Particle Age (PA) of each particle is initialized to PA $= 0$;

• 2. Velocity and Position Updating Every particle follows the velocity update rule in Eq. 2 and the position update rule in Eq. 3 to adjust its velocity and position;

• 3. Updating Pbest and Gbest For all particles, if the newly generated position $x_{i}(t)$ is better than $Pbest_{i}$, then $x_{i}(t)$ becomes the new $Pbest_{i}$. In addition, if the best position is better than the Gbest, then the Gbest is updated to be the best position. In this sense, this step is similar to that of the conventional PSO, but it represents the best solutions generated by particles during their lifetime;

• 4. Lifespan Control After the positions of all particles are updated, the lifespans are adjusted by a lifespan controller. The PA$_{i}$ of the Gbest is set to zero. The rest of the swarm will follow the rule if Fitness$_{i}$ is worse than $Pbest_{i}$ then $\mathrm{PA}_{i}(t)=\mathrm{PA}_{i}(t-1)+\mathrm{AF}+\mathrm{WF}$ else $\mathrm{PA}_{i}(t)=\mathrm{PA}_{i}(t-1)+\mathrm{AF}$ end if where AF and WF are integers defined by the user. If the lifespan is exhausted, i.e., PA$_{i}>=$ LE, then delete the respective particle;

• 5. Generating Challengers When Generation $==$ Generation.max, a new swarm will be generated as defined in Step 1, and it is used to challenge Gbest;

• 6. Terminal Condition Check If the number of iterations is larger than the predefined maximum number, the algorithm terminates. Otherwise, go to Step 2 for a new round of iteration.

Note that PA$_{i}$ is incremented each iteration by the AF that reflects the particle time span, whereas the WF relates to the fitness of the particle. Therefore, the problem of inactive particles or those that may not be contributing to the search can be minimized. This way the number of particles varies during the search, reducing the computational cost.

4 Case Study

In this section, the search behavior of PSO-AWF in solving regression problems is studied using experiments. The effects of the lifespan controller will be analyzed. In particular, answers to the following two questions will be sought: (1) how PSO-AWF works on regression problems, and (2) how the parameters of the FTDNN model are best set.

4.1 The Datasets

This section introduces the dataset used in the experiments: three benchmark datasets, named Box–Jenkins Gas Furnace (BJ), Mackey–Glass Chaotic Time Series (MG) and Data set A: Laser Generated Data (LGD), and the Wind dataset (WS). They were used to test the performance of the proposed PSO-AWF. The benchmark time series are widely used as benchmark datasets in testing the performance of ANN.

The BJ dataset was recorded from the combustion process of a methane air mixture (Box and Jenkins 1970; Hyndman 2017). The original data included 296 samples of the CO$_{2}$ concentration output y(t) and gas flow rate input u(t). The amount of data used during the FTDNN learning process (training data) was 140 samples, and another 150 were defined as a testing set used to verify the training efficiency. The MG dataset is generated from the MackeyGlass time delay ordinary differential equation (Mackey and Glass 1977). The training data consist of 450 samples, and 500 were used as a test set. A detailed description of the LGD dataset can be found in Huebner et al. (1989). The training data consist of 400 samples, and another 400 as a test set. The number of samples used for the learning and test phases was chosen based on Yeh (2013) as well as other parameters that will be presented in the next section.

The WS features were measured at a 100 m height. The tower was located in the state of Pernambuco, Brazil. The available data are the averages of wind speed (v), wind direction (D), pressure (p), and temperature (T), recorded every 10 min from 17/08/2009 to 24/03/2013. Different from the benchmark datasets that are freely available and well known, the WS dataset is provided by a private company. There are no inconsistent data such as negative values or outliers, and independent of the year, its minimum and maximum values are close, as well as their distribution. Wind turbines usually start generating at wind speeds in the range of 3.0 to 4.0 m/s. In the evaluated site, approximately 95% of the time is favorable for wind power generation.

4.2 Parameter Settings

All benchmark datasets were used as input of a FTDNN to forecast the next step, with an input composed by: bias, x(t), $x(t-1)$, $x(t-2)$, and $x(t-3)$. The WS dataset was used as input of a FTDNN to forecast 30 min, 1, 3 and 6 h ahead, with an input composed by: bias, x(t),..., $x(t-LAG)$. The number of LAG was defined as 1, 3, 5 or 7 for the TE and LAG $\in {\mathbb {Z}}| 1\le$LAG$\le 7$ when PSO-AWF was used to define this parameter. All the datasets were normalized between 0.1 and 0.9 by cause of the adopted activation function, a sigmoid logistic.

For the BJ, MG and LGD datasets, the same set of values was used for the parameters: Number of generations (250, 500, 750 and 1000) and the Number of Neurons in the Hidden Layer (NNHL) (1, 2, 3, 4, and 5). Each combination between the number of generations and NNHL was repeated 50 times, generating a total of 12000 FTDNN, 4000 FTDNN for each training method. The PSO and PSO-AWF used the same number of particles (120). For the PSO-AWF parameters: LE was 150, AF was 1, and WF was 5. A new swarm with 120 particles was generated every 150 iterations.

As for the WS dataset, the number of generations was defined as 25. The NNHL was set as 3, 5, 7 and 11 when using TE and NNHL $\in {\mathbb {Z}}| 3\le$NNHL$\le 11$ using PSO-AWF. Each combination between the number of generations and NNHL was repeated twenty times with BP and twice using DE, PSO and PSO-AWF, generating a total of 39936 FTDNN, from which there were 30720 (BP), 3072 (DE), 3072 (PSO) and 3072 (PSO-AWF). The number of particles was the same (110) for the PSO and PSO-AWF. For the PSO-AWF parameters, the LE was 10, AF was 1, and WF was 2. A new swarm with 60 particles was generated every 10 iterations.

For all the datasets, the BP learning rate was 0.7 and the initial synaptic weights were random values between −10 and 10. The PSO and PSO-AWF inertia weight was linearly decreased from 0.9 to 0.5, $C_1 = C_2 = 1$, and the initial velocities were zero. DE/rand/1/bin with F $=0.5*(1+\mathrm{rand}())$, CR linear increased between 0.5 and 1.0, and the NP was the same used by the PSO and PSO-AWF.

The normalization range, the number of generations, the BP learning rate, and the initial velocities were chosen based on Yeh (2013), while the other parameters were randomly chosen under the assumption that the user has no expertise to set these parameters and as such they will be given in the search for better results.

4.3 Tests Results

Three test cases, assigned as TC1, TC2 and TC3, were performed with the time series as follows.

• TC1 Test all learning methods on the three benchmark datasets based on the FTDNN by trying different numbers of generations (250, 500, 750 or 1000) and NNHL (1, 2, 3, 4 or 5) chosen by TE;

• TC2 Test all learning methods on the WS dataset based on the FTDNN by trying different numbers of NNHL (3, 5, 7 or 11) and LAG (1, 3, 5 or 7) chosen by TE;

• TC3 Test the PSO-AWF algorithm on the WS dataset based on the FTDNN by trying different numbers of NNHL $\in \mathbb {Z}| 3\le$NNHL$\le 11$, and LAG $\in \mathbb {Z}| 1\le$LAG$\le 7$ chosen by the PSO-AWF.

The results obtained from TC1 were used to verify whether the PSO-AWF produces results faster with the same behavior as the PSO. On the other hand, the results from TC2 were used to determine the best ANN structure using the WS dataset, and finally, the results from TC3 were used to verify whether there is computational cost reduction when the PSO-AWF is used not only as a learning method but also to define the NNHL and LAG when compared to the TE results.

All tests results were evaluated by different measures that include the testing MSE (represented by MSE), RMSE, correlation coefficient, run time (represented by t) in seconds, and there were statistics in each category that included the average and standard deviation of the estimations.

Fig. 1

Taylor diagram displaying a statistical comparison with observations of three model’s estimates of the next step of the LGD time series (Color figure online)

4.3.1 Test Case 1

As a matter of space, only the detailed evaluation for the benchmark LGD dataset is presented next. A Taylor diagram (Taylor 2000) provides a method of graphically summarizing how closely a predicted pattern matches the observed data, quantified in terms of their correlation, centered Root Mean Square Difference (RMSD) error and the amplitude of their variations represented by their standard deviations.

Figure 1 shows a Taylor diagram which summarizes the relative skill with which regression models estimate the next step of the LGD time series. Statistics for four models were computed, and a colored dot was assigned to each model (BP, DE, PSO and PSO-AWF) considered. The position of each dot appearing on the plot quantifies how closely that model’s simulated pattern matches observations. Consider BP model, for example. Its pattern correlation with observations is about 0.83 (blue lines). The RMSD between the simulated and observed patterns is proportional to the distance to the point on the x-axis identified as measures. The green contours indicate the RMSD values, and it can be seen that in the case of BP model the centered RMS error is about 0.08. The standard deviation of the simulated pattern is proportional to the radial distance from the origin. For BP model, the standard deviation of the simulated data is greater than the observed standard deviation.

The relative merits of various models can be inferred from Fig. 1. Simulated patterns that agree well with observations will lay nearest the point marked measures on the x-axis. These models will have relatively high correlation and low RMSD error. Models laying on the same black dashed arc of the measure point will have the correct standard deviation (which indicates that the pattern variations are of the right amplitude). In Fig. 1, it can be seen that PSO and PSO-AWF models generally agree best with observations, each with about the same RMSD error and correlation with observations. However, both models have a slightly higher standard deviation than the observed.

BP model has a low pattern correlation, resulting in a relatively large centered RMSD error. DE model has a slightly better performance than BP but still with a low pattern correlation when compared with PSO and PSO-AWF. Note that although PSO and PSO-AWF models have about the same correlation with observations, this results in a smaller RMS error.

Now that we have a general view of each model, and the next graphic indicates the error. The box plot (Tukey 1977) is a standardized method of displaying the distribution of data based on the following information: minimum, first quartile, median, third quartile, and maximum. In the simplest box plot, the central rectangle spans the first quartile to the third quartile (the interquartile range or IQR). A segment inside the rectangle shows the median, and whiskers above and below the box show the locations of the minimum and maximum values.

Figure 2 shows a box plot that summarizes some characteristics of the distribution produced by each regression model that estimates the next step of the LGD time series. BP model has the largest minimum and maximum values, respectively, presented as the lower and upper whiskers. The outliers (blue dots) are spread in a wide range. The four sections of the box plot are uneven in size. This shows that the model has similar estimations at certain parts of the scale, but in other parts of it there is a high variability in the estimations. DE model has the smallest range, but the quartiles are the largest. PSO has a distribution that the estimations are varied along of the most negative quartile group. PSO-AWF model has the distribution with close median to zero and the smallest quartiles. Compared to the lower whisker, has a longer upper whisker which means that the estimations are varied along of the most positive quartile group, and very similar in the least positive quartile group.

Fig. 2

Box plot displaying a comparison of estimation errors of the three forecast models for the next step of the LGD time series (Color figure online)

Figure 3 shows a diagram which summarizes the relationship between maximum generation value with the MSE (bars) and run time (lines) with which regression models estimate the next step of the LGD time series. As expected, the run time is directly proportional to the number of generations; as we increase the number of generations (250, 500, 750, 1000), the run time also increases. The same behavior was found in the other two datasets. DE, PSO and PSO-AWF did not present any kind of trend between the MSE and the number of generations. However, BP decreased the MSE value as the number of generations increased.

Fig. 3

Performance of the FTDNN under different maximum generation values

To avoid countless repetitions of Figs 1, 2, and 3, Table 1 summarizes the computational results of the four training methods (BP, DE, PSO and PSO-AWF) using a FTDNN to forecast data from the BJ, MG and LGD datasets. In general, PSO-AWF outperforms PSO algorithms in CPU time, with an approximate MSE value for all three datasets forecasting with the FTDNN. BP has a better CPU time in all datasets; however, it is less efficient than the PSO and PSO-AWF algorithms, as the forecast is concerned. DE has a cpu time varying between the time ranges of PSO and PSO-AWF; however, it is less efficient than the other algorithms.

4.3.2 Test Case 2

Figure 4 shows a diagram which summarizes the relationship between training set size (10, 20 and 30%) with the MSE (bars), and run time (lines) with which regression models estimate the 30’, 1-, 3-, and 6-h step ahead of the WS time series. As expected, the run time is directly proportional to the training set size. DE, PSO and PSO-AWF did not present any kind of trend between the MSE and training set size. However, BP decreased the MSE value as training set size increased. This figure shows only the results using the speed (v) as input, but the same behavior was found with all the possible combinations of the wind speed and the other three features (D, p, T).

Table 1 Results of FTDNN among different hidden nodes

Table 2 summarizes the relationship between the most frequent training set size and the forecast horizon. The best computational results of the training method (PSO-AWF) using a FTDNN to forecast data from the WS dataset are presented. As a matter of space, only the PSO-AWF results are presented.

For 30’ ahead, the most frequent training set size was 10% for BP and PSO and 30% for PSO-AWF. In sequence, for 1h ahead, the most frequent training set was 20% for both BP and PSO and 10% for PSO-AWF. Finally, for 3 and 6 h ahead, the most frequent training set was 30% for BP and 10% for both PSO and PSO-AWF. It can be observed that BP model increased the size of the training set as the forecast horizon was increased. On the other hand, the size of the training set was the same (10%) in any forecasting horizon for PSO and PSO-AWF, except at 1 h, and 30 min ahead, respectively.

Figure 5 shows a diagram which summarizes the relationship between the input features of the WS dataset and the MSE (bars). The red lines are simple regressions used to represent MSE trends. As a matter of space, only the graphic results for 6 h ahead are presented. PSO and PSO-AWF presented roughly constant MSE results for forecast horizons of 30’ and 1 h, regardless of the features used as inputs. The 3 h ahead horizon presented a slight reduction in the MSE as the number of features used as an input increased. Finally, for 6 h the increase in the number of input features leads to the MSE decreasing. As far as BP model is concerned, as the number of input parameters increased, the MSE also increased for the horizons of 30’ and 1 h. The 3 h ahead horizon showed no consistent trends. Finally, for 6 h the increase in the number of input features led to the MSE decrease. In general, the increase in the forecast horizon requires more information.

Fig. 4

Relationship between the training set size with the MSE and run time

Table 2 Results of FTDNN among different training set sizes

Fig. 5

Relationship between the number of features used in the training set and the MSE

It was analyzed the influence of NNHL (3, 5, 7, 11) and LAG (1, 3, 5, 7) on the MSE for the time horizon of 30’, for each learning method (BP, PSO and PSO-AWF) with v as input, and training set size of 10%. PSO-AWF presented the same NNHL value for the three best results, and it was not possible to identify any trends for BP and PSO.

4.3.3 Test Case 3

Taking into account the results obtained by trial and error in Sect. 4.3.2, it is used v as the only input feature for 30’, 1 and 3 h forecast horizons, and combinations of v with the other features are employed as inputs for 6 h ahead, with training set size being always 10%.

It analyzed the influence of NNHL $\in \mathbb {Z}| 3\le$NNHL$\le 11$ and LAG $\in \mathbb {Z}| 1\le$LAG$\le 7$ on the MSE for each learning method (BP, DE, PSO and PSO-AWF). PSO-AWF shows that for 30’ and 1 h forecasts, LAG values tend to be small (often one), and the opposite was found to 3 and 6 h horizons where the most frequent value is 7. NNHL values for horizons of 1 and 6 h were high, and for 30’ and 3h it was not possible to observe any trends.

For the best results of each set of features used as input, the best result was using v, p and T. The behavior of the results was similar to those obtained through TE in Fig. 5. Regardless the sort of input set, the NNHL value was high (often 8), and the most frequent LAG value was 7.

It was verified whether the use of PSO-AWF to define the NNHL and LAG values produced better results than those obtained through TE, for each kind of inputs available (v, vp, vT, vD, vpT, vDp, vDT, vDpT) and training methods (BP, DE, PSO and PSO-AWF). PSO-AWF has obtained the best result among all and was present in seven of the eight best solutions, from which five of them have used the PSO-AWF as learning method and to find the NNHL and LAG values; the other 2, the PSO-AWF was used as a learning method only.

For all forecast horizons, it was verified whether the use of PSO-AWF to choose the NNHL and LAG values produced better results than those obtained through TE. Even with the search being wider (NNHL from 3, 5, 7 and 11 to NNHL $\in \mathbb {Z}| 3\le$NNHL$\le 11$ and LAG from 1,3,5 and 7 to LAG $\in \mathbb {Z}| 1\le$LAG$\le 7$); the restriction on the training set size (always 10%); the reduction in rounds from 32 to 10; and for the 30’, 1, and 3 h horizons the restriction of features used as inputs (always only v), PSO-AWF obtained the best result among all.

For a better understanding, the run time is no longer treated as the average, but as the accumulated time by test cases 2 and 3. In TC2 where only v was considered as input and the training set size 10%, we have for BP, DE, PSO and PSO-AWF approximately 0.16, 8.04, 7.93 and 3.96 hours by TE, respectively. Extrapolating this scenario to the same conditions used by PSO-AWF, where NNHL = [3,11] and LAG = [1,7], we have 0.64, 33.17, 31.24 and 15.6 hours. In TC3, PSO-AWF spent about 12.85 hours to accomplish the same task. A reduction of almost 58.9% when compared to PSO, and 17.6% to PSO-AWF when using TE to find NNHL and LAG.

5 Conclusions

A new PSO variant called PSO-AWF has been developed. PSO-AWF is characterized by assigning every particle in the swarm with a growing age and a lifespan. The lifespan is adaptively tuned according to the individual particles’ fitness.

On the benchmarks datasets BJ, MG and LGD, the proposed PSO-AWF was found to outperform BP, DE and PSO in terms of MSE and run time, respectively, for TE FTDNN. The number of neurons of the TE FTDNN hidden layer varied for each dataset. With the WS dataset, PSO-AWF presented a similar behavior as those found with the benchmarks datasets. The effectiveness of PSO-AWF FTDNN was always superior to that of TE FTDNN (in the minimal MSE). The computation time of PSO-AWF FTDNN was also better than that of TE FTDNN.

With regard to the benchmark datasets, it was observed that in general it was easier for the particles to improve the quality of the swarm. In this case, the particles had a long lifespan and the search behavior of PSO-AWF was very similar to that of the original PSO. Therefore, the fast-converging feature of the original PSO can be preserved. On the other hand, as the WS dataset is concerned, when the particle reaches a local optimum, it fails to improve the quality of the swarm and ages quickly.

In both cases, new particles emerge to replace the old ones and bring in diversity. Therefore, PSO-AWF has the ability to escape from local optima and prevent premature convergence. The difference between PSO and PSO-AWF is how fast this happens, and this is directly related to the dataset characteristics.

For future research, it is encouraged to investigate the aging mechanism on other evolutionary computing techniques. Also, the use of others datasets and functions would provide more information about PSO-AWF behavior. Investigation of the aging effects on ensemble machine learning problems is also promising for future work. As these problems require keeping multiple solutions concurrently, incorporating the aging mechanism with the multipopulation or species-conserving techniques would be helpful.