Observer-Based Predictive Control with One Free Control Move for NCSs with Data Loss

Abstract

In this paper, an efficient output feedback predictive control synthesis based on a prespecified observer for networked control systems is presented. The process of random packet loss between the controller and the actuator is described as Markov chain, and a missing data compensation strategy is induced to cope with the poor performance caused by fading links. The provided model predictive control algorithm optimizes an infinite-horizon objective and parameterizes the infinite-horizon control moves into a free control move followed by output feedback. Further, the corresponding constraints about recursive feasibility and stochastic stability are given by utilizing the linear matrix inequality technique. A numerical example is given to illustrate the applicability of the proposed method.

1 Introduction

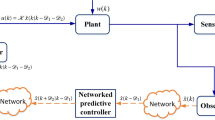
In recent decades, network has inevitably been introduced for information transmission in control zone since its excellent characteristics, i.e., low cost, simple installation and high reality (i.e., Franze et al. 2015; Franze and Tedesco 2014; Bai et al. 2012; Pin and Parisini 2011), which gives rise to the so-called networked control system. Here, it can be seen as a real-time feedback control system with control loops via networks. However, the insertion of network will bring a problem of data loss because of a series of complex factors by Zhang et al. (2012), which could be one of sources of poor performance and system instability. Many research papers have appeared. To mention a few, considering packet loss during wireless communication, two approaches are developed as well based on the Bernoulli packet loss model in Zhang (2015). For control signals transmitted by the controller to the plant, paper (Keller et al. 2016) proposes to estimate the switching disturbance from an augmented state version of the intermittent unknown input Kalman filter; recently, sufficient stochastic stability conditions are established. A self-triggered sampling scheme is proposed for a networked control system with consideration of data losses and communication delays in Chen and Qin (2015); the next sampling instant does not depend on online estimation of an event-triggered condition and the successive measurement of the state, which can be dynamically determined with respect to the transmitted packet. In paper Zhang et al. (2016), for random packet losses, a Bernoulli-distributed white sequence is used to describe packet dropouts among agents in a stochastic way, for deterministic packet losses, a switched system with stable and unstable subsystems is employed to model packet dropouts. It is easy to see that the above researches seldom are involved in the application of model predictive control.

Model predictive control(MPC), one of the advanced control technique, refers to a class of computer control algorithms that use an explicit process model to predict the future response of a plant in paper (Sun et al. 2009). It provides online solutions to optimal feedback control problems, so this method can be seen as a circular operation that a minimum problem is solved to calculated optional control inputs for a time horizon. Although many control sequences are calculated, only the first one is implemented, at next instant, the optimization problem is reformulated and solved with new measurements obtained from the system in paper (Zhao et al. 2010). Therefore, several industrial process models as well as many performance index of importance can be handled by predictive control, and for some references, the stable problem of MPC is studied in Hung et al. (2014), Roy et al. (2005), Yue et al. (2004), Chen et al. (2012) and Li et al. (2005); the MPC for stochastic system is investigated in Killian et al. (2015), Warren and Marlin (2003), Fleming (2015) and Zhang et al. (2014). Most above results show the advantages of MPC when the system states are measurable.

In the real industrial process, considering the complexity of physical plant, the assumption of available of system states will be optimistic. Thus, the output feedback strategy [refers to Ding and Pin (2014)] is widely practical than the state feedback designment. For developing the efficiency of the output feedback control, a series of research results will be given. A state observer that estimates plant states from the output when it is available via the communication network is used to generate a control signal; when the plant output is not available from the network, necessary and sufficient conditions for the exponential stability of the closed-loop system are derived in terms of the networked dwell time and the system parameters in Dritsas and Tzes (2007). Paper Mayne et al. (2006) proposes an efficient output feedback predictive control algorithm based on the state observer for uncertain discrete system. In Niu et al. (2009), an estimation method is introduced to cope with the effect of data dropout, and an output feedback control law is designed to guarantee the closed-loop stability. Aiming at the problem of predictive output feedback control for networked control systems with random communication delays and the analysis of closed-loop networked control systems, the predictive time-varying output feedback controller can guarantee system stability in Yang et al. (2014).

Considering the conservative of state feedback synthesis and the uncertainty networked problem, an efficient output feedback predictive control synthesis with (guaranteed stability) is presented in this paper, which is based on a prespecified estimator. The process of random packet loss between the controller and the actuator is modeled as Markov chain, and a missing data compensation strategy is induced to cope with the effectiveness of fading links. The provided synthesis research papers optimizes an infinite-horizon objective function, and specifically, the infinite-horizon control moves are parameterized as a free control move, while the use of a free control move is well practiced in current research papers. Further, the corresponding constraints about recursive feasibility and stochastic stability are given by a set of LMIs.

2 Problem Formulation

A nominal description plant sampled periodically with sampling interval $T_\mathrm{s}>0$ and described in discrete-time via

$$\begin{aligned} \left\{ \begin{aligned}&x(k+1)=Ax(k)+Bu(k)\\&y(k)=Cx(k) \end{aligned} \right. \end{aligned}$$

(1)

where x(k), u(k) and y(k) are plant states, actuator inputs and measured outputs, respectively. A, B and C are constant matrices with appropriate dimensions.

Here, due to the existence of links with missing data between controller and actuator, the stochastic variable $\theta (k)\epsilon R$ will be induced to describe the data status for instant k and the process of data loss satisfies discrete-time Markov chain with two states (1 for successful transmission, 0 for failure transmission). A natural assumption on $\theta (k)$ can be made as

$$\begin{aligned} \begin{aligned}&\textit{Prob} \left\{ \theta (k+1)=0| \theta (k)=1\right\} =\alpha \\&\textit{Prob} \left\{ \theta (k+1)=1| \theta (k)=0\right\} =\beta \end{aligned} \end{aligned}$$

(2)

To minimize the effects caused by fading channel, a compensation technique is applied to cope with the imperfect channel

$$\begin{aligned}&u(k)=\theta (k)v(k)+(1-\theta (k))\tau u(k-1) \end{aligned}$$

(3)

where v(k) are controller outputs, $\tau \in [0,1]$ is a forgetting factor. From (2), for successful transmission, $u(k)=v(k)$, otherwise, $u(k)=\tau u(k-1)$. As for h successive data loss, $u(k)=\tau ^{h}u(k-h)$. Then, by the model (1) and compensation strategy (2), the closed-loop model is rewritten as follows:

$$\begin{aligned}&x(k+1)=Ax(k)+\theta (k)Bv(k)+(1-\theta (k))\tau B u(k-1) \end{aligned}$$

(4)

Definition 1

For any initial state x(0), if the following inequality

$$\begin{aligned} E\left\{ \sum _{k=0}^{\infty }x(k)^{T}x(k)\big |x(0)\right\} < \infty \end{aligned}$$

is satisfied, the closed-loop system is stochastically stable.

As comparison, this paper firstly considers the case that the states are available, a state feedback scheme will be given. Then, it will extend the scheme to the case that the states are unavailable.

3 State Feedback Control Based on Available States

Suppose the states are measured fully, control data will be transmitted to the actuator via communication links, in which the data packets may loss. Paper (Zou et al. 2015) has talked about corresponding recursive feasibility and stability problem. Here it only gives the optimization conditions with one free control move and generalized contractiveness briefly, a state feedback control law $v(k+i|k)=F(k)x(k+i|k)$ will be obtained.

By (1), (3) and defining $z(k)=[x(k)^{T}~u(k-1)^{T}]^{T}$, the closed-loop system can be described as

$$\begin{aligned} z(k+1)= \begin{bmatrix} {A+ \theta (k) BF}&{(1- \theta (k))\tau B}\\ \theta (k) F&{(1- \theta (k)) \tau I} \end{bmatrix}z(k) \end{aligned}$$

(5)

which is an uncertainty stochastic system depending on the stochastic variable $\theta (k)$. The optimization problem concerned in this work is

$$\begin{aligned} \textit{min}_{u(k+i|k)} ~~~~ J_{0}^{\infty }(k)~~~~~~s.t~~(1),(3), (4), (5) \end{aligned}$$

(6)

where $J_{0}^{\infty }(k)=J_{0}^{1}(k)+J_{1}^{\infty }(k)$, $J_{0}^{1}(k)=z^{T}(k|k)Sz(k|k)+u^{T}(k|k)Ru(k|k)$, $J_{1}^{\infty }(k)=E\{\sum _{i=1}^{\infty }\{z^{T}(k+i|k)Sz(k+i|k)+u^{T}(k+i|k)Ru(k+i|k)\}$. $S=diag\{S_{1}~~0\}\},~S_{1}>0,~R>0$ are suitable weighting matrices. To derive an upper bound of objective $J_{0}^{\infty }(k)$, it chooses the quadratic Lyapunov function as

$$\begin{aligned}&V(x(k+i+1|k),u(k+i|k))=x^{T}(k+i+1|k)M_{\theta (k)}\nonumber \\&\quad \times x(k+i+1|k)+u^{T}(k+i|k)N_{\theta (k)}u(k+i|k)\nonumber \\&\quad S.t~~M_{\theta (k)}>0,N_{\theta (k)}>0 \end{aligned}$$

(7)

and follows the contractiveness condition:

$$\begin{aligned}&E\left\{ V(k+i+1|k)-V(k+i|k)\right\} \le \nonumber \\&\quad -E[z^{T}(k+i|k)Sz(k+i|k)+u^{T}(k+i|k)Ru(k+i|k)] \end{aligned}$$

(8)

For system stability, it has $x(\infty |k)=0$, so $V(\infty |k)=0$, then, by summing (8) from $i=1$ to $\infty$, it gets the following inequality:

$$\begin{aligned} \begin{aligned} \textit{max}~~J_{1}^{\infty } \le E\left\{ V(k+1|k)\right\} \end{aligned} \end{aligned}$$

(9)

let

$$\begin{aligned} \begin{aligned}&z^{T}(k|k)Sz(k|k)+u^{T}(k|k)Ru(k|k)+z^{T}(k+1|k)\\&\quad \times diag\{M_{\theta (k)},N_{\theta (k)}\}z(k+1|k)\le \gamma (k) \end{aligned} \end{aligned}$$

(10)

where $\gamma (k)$ is a nonnegative variable to be minimized.

Theorem 1

For the augmented closed-loop system (5), it assumes the control law can be transmitted successfully at instant k, the matrix S, R and factor $\tau$ are given, and the contractiveness condition (8) and the optimization problem (10) are satisfied to find u(k) and feedback F(k) to minimize the upper bound $\gamma (k)$. By $\gamma \varGamma ^{-1}= \bar{\varGamma }$, $\varGamma$ taking $\{M_{0}$,$M_{1}$,$N_{0}$,$N_{1}$,$W_{0}$,$W_{1}$,$T_{0}$,$T_{1}\}$ and $Y_{1}=F \bar{M}_{1}$.

(i) Constraint (10) is guaranteed by

$$\begin{aligned} \left[ \begin{array}{cccccccc} 1 &{} * &{} * &{} * &{} *\\ \varXi (k) &{} \bar{M}_{1} &{} * &{} * &{} *\\ u(k) &{} 0 &{} \bar{N}_{1} &{} * &{} * &{} \\ S_{1}^{1/2}x(k) &{} 0 &{} 0 &{} \gamma I &{} *\\ R^{1/2}u(k) &{} 0 &{} 0 &{} 0 &{} \gamma I\\ \end{array}\right] \ge 0 \end{aligned}$$

(11)

where the state $\varXi (k)= A(k)x(k)+\theta (k)Bv(k)+(1-\theta (k))Bu(k-1)$.

(ii) Considering the data loss, constraint (9) is satisfied by

$$\begin{aligned}&\left[ \begin{array}{cccccccc} \bar{M}_1 &{} *&{} * &{} * &{} * &{} *\\ 0 &{} \bar{N}_1 &{} * &{} * &{} * &{} *\\ {A \bar{M}_1^{T}+B Y_{1}} &{} 0 &{} \bar{W}_1 &{} * &{} * &{} *\\ Y_{1} &{} 0 &{} 0 &{} \bar{T}_1 &{} * &{} *\\ \bar{M}_1^T &{} 0 &{} 0 &{} 0 &{} \gamma S_1^{-1} &{} *\\ Y_{1} &{} 0 &{} 0 &{} 0 &{}0 &{} \gamma R^{-1} \end{array}\right] \ge 0 \end{aligned}$$

(12)

$$\begin{aligned}&\left[ \begin{array}{cccccccc} \bar{M}_0 &{} *&{} * &{} * &{} * &{} *\\ 0 &{}\bar{N}_0 &{} * &{} * &{} * &{} *\\ A \bar{M}_0^T &{} \tau B\bar{N}_0^T &{}\bar{W}_0 &{} * &{} * &{} *\\ 0 &{} \tau \bar{N}_0^T &{} 0 &{}\bar{T}_0 &{} * &{} *\\ \bar{M}_0^T &{} 0 &{} 0 &{} 0 &{} \gamma S_1^{-1} &{} *\\ 0 &{} \tau \bar{N}_0^T &{} 0 &{} 0 &{}0 &{} \gamma R^{-1} \end{array}\right] \ge 0 \end{aligned}$$

(13)

$$\begin{aligned}&\left[ \begin{array}{cccccccc} \bar{W}_1 &{} *&{} * &{} * &{} * &{} *\\ 0 &{} \bar{T}_1 &{} * &{} * &{} * &{} *\\ \alpha ^{1/2}\bar{W}_1^T &{} 0 &{}\bar{M}_0 &{} * &{} * &{} *\\ (1-\alpha )^{1/2}\bar{W}_1^T &{} 0 &{} 0 &{}\bar{M}_1 &{} * &{} *\\ 0 &{} \alpha ^{1/2}\bar{T}_1^T &{} 0 &{} 0 &{}\bar{N}_0 &{} *\\ 0 &{} (1-\alpha )^{1/2}\bar{T}_1^T &{} 0 &{} 0 &{}0 &{}\bar{N}_1 \end{array}\right] \ge 0 \end{aligned}$$

(14)

$$\begin{aligned}&\left[ \begin{array}{cccccccc} \bar{W}_0 &{} *&{} * &{} * &{} * &{} *\\ 0 &{} \bar{T}_0 &{} * &{} * &{} * &{} *\\ (1-\beta )^{1/2}\bar{W}_0^T &{} 0 &{}\bar{M}_0 &{} * &{} * &{} *\\ \beta ^{1/2}\bar{W}_0^T &{} 0 &{} 0 &{}\bar{M}_1 &{} * &{} *\\ 0 &{} (1-\beta )^{1/2}\bar{T}_0^T &{} 0 &{} 0 &{} \bar{T}_0 &{} *\\ 0 &{} \beta ^{1/2}\bar{T}_0^T &{} 0 &{} 0 &{}0 &{}\bar{T}_1 \end{array}\right] \ge 0 \end{aligned}$$

(15)

where the proof of Theorem 1 is similar to paper (Zou et al. 2015) and it only needs to make small changes.

Remark 1

In this section, it only gives some constraints about optimization conditions and generalized contractiveness briefly, which are different from paper Zou et al. (2015). And the other problem (i.e., recursive feasibility and stability) is not discussed. The above synthesis is just to be extended to the following output feedback.

4 Output Feedback Control Based on State Observer

Considering the complexity of physical plant, the states are not fully measured, but the output information of system is available. A state observer in Ding and Pin (2014) will be applied to the system:

$$\begin{aligned} \left\{ \begin{aligned}&\hat{x}(k+1)=A\hat{x}(k)+Bu(k)+ L(y(k)-C\hat{x}(k))\\&v(k)=F\hat{x}(k) \end{aligned} \right. \end{aligned}$$

(16)

where the observer gain L and feedback gain F are to be designed. It defines the estimation error as $e(k)=x(k)-\hat{x}(k)$, and then, based on the system (1) and state observer (16), the error dynamics can be derived as

$$\begin{aligned} \begin{aligned} e(k+1)=(A-LC)e(k) \end{aligned} \end{aligned}$$

(17)

Moreover, the control signals will be transmitted to the actuator via imperfect channel, and a compensation strategy (3) will remain to be utilized. Defining $\eta (k)=[\hat{x}^{T}(k)~~e^{T}(k)~~u^{T}(k-1)]^{T}$, the augmented closed-loop system based on (4), (16) and (17) can be derived as

$$\begin{aligned} \eta (k+1)=\begin{bmatrix} {A+ \theta (k) BF}&LC&{(1- \theta (k)) \tau B}\\ 0&A-LC&0\\ \theta (k) F&0&{(1- \theta (k))\tau I} \end{bmatrix}\eta (k) \end{aligned}$$

(18)

In the following, this paper will design an output feedback predictive control law such that (18) is stochastically stable, which includes an offline design of the observer gain and an online synthesis approach to find a real-time control law.

4.1 Offline Observer Design

In this section, an offline observer design will be developed, and it defines a quadratic function

$$\begin{aligned} \begin{aligned} \varepsilon (e(k))=e^{T}(k)P_{e}(k)e(k) \end{aligned} \end{aligned}$$

(19)

and imposing (19) subject to the following contractiveness condition:

$$\begin{aligned} \begin{aligned} \varepsilon (e(k+1))-\delta \varepsilon (e(k))\le 0 \end{aligned} \end{aligned}$$

(20)

where $\delta \in [0,1]$ is the decay rate. Then, the observer gain L(k) is provided by the following Theorem 2.

Theorem 2

For the decay rate $\delta$, if there exist $P_{e}(k)>0$ and $Y_{e}(k)= P_{e}(k)L(k)$ satisfying:

$$\begin{aligned} \left[ \begin{array}{cccccccc} \delta P_{e}(k) &{} *\\ P_{e}(k)A- Y_{e}(k)C &{} P_{e}(k) \end{array}\right] \ge 0 \end{aligned}$$

(21)

Then, the stability of error dynamics can be guaranteed. In addition, the observer gain is obtained by $L(k)=P_{e}(k)^{-1}Y_{e}(k)$ .

According to Theorem 2, it easily gets the observer gain $L(k) = P_{e}(k)^{-1}Y_{e}(k)$, which is time invariant. However, matrix $P_{e}(k)$ and $Y_{e}(k)$ are changes at each sampling time. For this, it can stochastically get a fixed value $(L,~P_{e0},~Y_{e0})$ and induce a time-varying scalar $\pi (k)$ satisfying $\pi (k)>0$. Thus, it has $P_{e}(k)=\pi (k)P_{e0}$ and $Y_{e}(k)=\pi (k)Y_{e0}$, which is inspired by Ding and Pin (2014), Dritsas and Tzes (2007), Mayne et al. (2006) and Niu et al. (2009).

Remark 2

Given the unavailable properties of system states, the state observer is to reconstruct the original system state. Here, it gives a simple scheme for design of observer, but it will be suitable to the system of unmeasured state. When $e(k)\rightarrow 0$ with $k\rightarrow \infty$, it has $x(k)\approx \hat{x}(k)$. To enhance the contractive speed of e(k), the user can choose suitable decay rate $\delta$.

Before further research, considering the estimation error is uncertain, and it gives the bound of e(k) at any time k by the following assumption.

Assumption 1

$e(1)^{T}P_{e0}e(1)\le \xi (1)$, the initial $\xi (1)$ is a prespecified constant. Then, at time $k > 0$, the bound of $e(k+1)$ is followed as:

$$\begin{aligned} \begin{aligned}&e(k+1)^{T}P_{e0}e(k+1)\le \xi (k+1) \end{aligned} \end{aligned}$$

(22)

And $\xi (k+1) = min \{\tilde{\xi }(k+1)/\pi (k-1), \delta \xi (k)\}$.

$$\begin{aligned} \begin{aligned} \tilde{\xi }(k+1)=&\,\gamma (k-1)\\&-\hat{x}^{T}(k-1)S_{1}\hat{x}(k-1)-u^{T}(k-1)Ru(k-1)\\&-u^{T}(k|k-1)(N_{\theta (k-1)}+R)u(k|k-1)\\&-\hat{x}^{T}(k)\times S_{1}\hat{x}(k)-\hat{x}^{T}(k+1|k-1)\\&M_{\theta (k-1)}\hat{x}(k+1|k-1) \end{aligned} \end{aligned}$$

where $\hat{x}(k+1|k-1)=(A+\theta (k-1)BF)\hat{x}(k)+(1-\theta (k-1))u(k-1)+L(y(k)-C\hat{x}(k))$.

4.2 Output Feedback Predictive Control Problem

On the one hand, when the system states are available, Sect. 3 has proposed a scheme for uncertainty system. On the other hand, the system states are not fully available. So part 4.1 designs an observer to achieve the reconstruction of system states. Here, it will develop an output feedback predictive control law with recursive feasibility and guaranteed stability. The objective function can be given as:

$$\begin{aligned} \begin{aligned} \textit{min}_{u(k+i|k)} J_{0}^{\infty }(k)~~ s.t \left\{ (3),(16),(17),(18),(21)\right\} \end{aligned} \end{aligned}$$

(23)

where $J_{0}^{\infty }(k)=J_{0}^{1}(k)+J_{1}^{\infty }(k)$, $J_{0}^{1}(k)=\eta ^{T}(k|k)S\eta (k|k)+u^{T}(k|k)Ru(k|k)$, $J_{1}^{\infty }(k)=E\{\sum _{i=1}^{\infty }\{\eta ^{T}(k+i|k)S\eta (k+i|k)+u^{T}(k+i|k)Ru(k+i|k)\}\}$, $S=diag\{S_{1},0,0\},S_{1}>0,R>0$ are suitable weighting matrices, To derive an upper bound on the objective (23), it chooses the quadratic Lyapunov function as

$$\begin{aligned}&V(\hat{x}(k+i+1|k),e(k+1+i|k),u(k+i|k))\nonumber \\&\quad =\hat{x}^{T}(k\!+\!i\!+\!1|k)M_{\theta (k)}\hat{x}(k\!+\!i\!+\!1|k)+e^{T}(k+1+i|k)\nonumber \\&\qquad \times P_{e}(k)e(k+i+1|k)+u^{T}(k+i|k)N_{\theta (k)}u(k+i|k) \nonumber \\&\quad S.t~~M_{\theta (k)}>0,P_{e}(k)>0,N_{\theta (k)}>0 \end{aligned}$$

(24)

Suppose $V(k+i+1|k)$ satisfies the following stability condition at each sampling time k:

$$\begin{aligned}&E\left\{ V(\hat{x}(k+i+1|k),e(k+1+i|k),u(k+i|k))\right. \nonumber \\&\qquad \left. -V(\hat{x}(k+i|k),e(k+i|k),u(k+i-1|k))\right\} \nonumber \\&\quad \le -E\left\{ \eta ^{T}(k+i|k)S\eta (k+i|k)+u^{T}(k+i|k)\right. \nonumber \\&\qquad \left. \times Ru(k+i|k)\right\} \end{aligned}$$

(25)

For stability, it has $\eta (\infty |k)=0$, hence $V(\infty |k)=0$, by summing (25) from $i=1$ to $\infty$, the following inequality condition is:

$$\begin{aligned} \textit{max}~~J_{1}^{\infty }(k) \le E\left\{ V(k+1|k)\right\} \end{aligned}$$

(26)

let

$$\begin{aligned}&\eta ^{T}(k|k)S\eta (k|k)+u^{T}(k|k)Ru(k|k)+\eta ^{T}(k+1|k)\nonumber \\&\quad \times diag\left\{ M_{\theta (k)}~P_{e}(k)~N_{\theta (k)}\right\} \eta (k+1|k) \le \gamma (k) \end{aligned}$$

(27)

where $\gamma (k)$ is a nonnegative variable to be minimized. Then, based on (27), the optimization problem can be developed as

$$\begin{aligned} \textit{min}_{u(k+i|k)}~~J_{0}^{\infty }(k) ~~~~~~s.t(3),(17),(18),(24),(27) \end{aligned}$$

(28)

Theorem 3

For the closed-loop system (18), it assumes the control signals can be transmitted at time k. The constant matrices {S, R} and factor {$\tau$, $\delta$} are given, the contractiveness condition (25) and the optimization problem (27) are satisfied to find u(k) and feedback F(k) , which minimizes the upper bound $\gamma (k)$. Then by taking $\gamma P_{e}^{-1}= \bar{P}_{e}$, $\gamma \varGamma ^{-1}= \bar{\varGamma }$, where $\varGamma$ taking $\{M_{0},M_{1},N_{0},N_{1},W_{0},W_{1},T_{0},T_{1}\}$ and $Y_{1}=F \bar{M}_{1}$.

(i) Constraint (29) is guaranteed by

$$\begin{aligned} \left[ \begin{array}{cccccccc} 1-\mu (k) &{} * &{} * &{} *\\ \varXi (k) &{} \bar{M}_{1} &{} * &{} *\\ u(k) &{} 0 &{} \bar{N}_{1} &{} * &{} * \\ S_{1}^{1/2}x(k) &{} 0 &{} 0 &{} \gamma I &{} *\\ R^{1/2}u(k) &{} 0 &{} 0 &{} 0 &{} \gamma I\\ \end{array}\right] \ge 0 \end{aligned}$$

(29)

with $\varXi (k)=A \hat{x}(k)+ Bu(k)+L(y(k)-C\hat{x}(k))$.

(ii) Considering the data dropouts, the contractiveness (25) is satisfied if

$$\begin{aligned}&\left[ \begin{array}{cccccccccc} \bar{M}_{1} &{} * &{} * &{} * &{} * &{} * &{} * &{} *\\ 0 &{} \bar{P}_{e} &{} * &{} * &{} * &{} * &{} * &{} * \\ 0 &{} 0 &{} \bar{N}_{1} &{} * &{} * &{} * &{} * &{} * \\ A \bar{M}_{1}^{T}+ BY_{1} &{} LC \bar{P}_{e}^{T} &{} 0 &{} \bar{W}_{1} &{} * &{} * &{} * &{} * \\ 0 &{} (A-LC)\bar{P}_{e}^{T} &{} 0 &{} 0 &{} \bar{U}_{1} &{} * &{} * &{} * \\ Y_{1} &{} 0 &{} 0 &{} 0 &{} 0 &{} \bar{T}_{1} &{} * &{} * \\ \bar{M}_{1}^{T} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \gamma S_{1}^{-1} &{} * \\ Y_{1} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \gamma R^{-1}\\ \end{array}\right] \ge 0\end{aligned}$$

(30)

$$\begin{aligned}&\left[ \begin{array}{ccc} \bar{W}_1 &{} * &{} *\\ 0 &{} \bar{U}_1 &{} *\\ 0 &{} 0 &{} \bar{T}_1\\ \alpha ^{1/2}\bar{W}_{1}^{T} &{} 0 &{} 0\\ 0 &{} \alpha ^{1/2}\bar{U}_{1}^{T} &{} 0\\ 0 &{} 0 &{} \alpha ^{1/2} \bar{T}_{1}^{T}\\ (1- \alpha )^{1/2} \bar{W}_{1}^{T} &{} 0 &{} 0\\ 0 &{} (1- \alpha )^{1/2} \bar{U}_{1}^{T} &{} 0\\ 0 &{} 0 &{} (1- \alpha )^{1/2} \bar{T}_{1}^{T}\\ \end{array}\right. \nonumber \\&\quad \left. \begin{array}{cccccc} * &{} * &{} * &{} * &{} *&{} * \\ * &{} * &{} * &{} * &{} * &{} *\\ * &{} * &{} * &{} * &{} * &{} *\\ \bar{M}_{0} &{} * &{} * &{} * &{} * &{} *\\ 0 &{} \bar{P}_{e} &{} * &{} * &{} * &{} *\\ 0 &{} 0 &{} \bar{N}_{0} &{} * &{} * &{} *\\ 0 &{} 0 &{} 0 &{} \bar{M}_{1} &{} * &{} *\\ 0 &{} 0 &{} 0 &{} 0 &{} \bar{P}_{e} &{} *\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \bar{N}_{1}\\ \end{array}\right] \ge 0 \end{aligned}$$

(31)

$$\begin{aligned}&\left[ \begin{array}{cccccccccc} \bar{M}_{0} &{} * &{} * &{} * &{} * &{} * &{} * &{} * \\ 0 &{} \bar{P}_{e} &{} * &{} * &{} * &{} * &{} * &{} * \\ 0 &{} 0 &{} \bar{N}_{0} &{} * &{} * &{} * &{} * &{} * \\ A \bar{M}_{0}^{T} &{} LC \bar{P}_{e}^{T} &{}\tau B \bar{N}_{0}^{T} &{} \bar{W}_{0} &{} * &{} * &{} * &{} * \\ 0 &{} (A-LC) \bar{P}_{e}^{T} &{} 0 &{} 0 &{} \bar{U}_{0} &{} * &{} * &{} * \\ 0 &{} 0 &{}\tau \bar{N}_{0}^{T} &{} 0 &{} 0 &{} \bar{T}_{0} &{} * &{} * \\ \bar{M}_{0}^{T} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \gamma S_{1}^{-1} &{} * \\ 0 &{} 0 &{}\tau \bar{N}_{0}^{T} &{} 0 &{} 0 &{} 0 &{} 0 &{} \gamma R^{-1}\\ \end{array}\right] \ge 0 \end{aligned}$$

(32)

$$\begin{aligned}&\left[ \begin{array}{ccc} \bar{W}_{0} &{} * &{} *\\ 0 &{} \bar{U}_{0} &{} *\\ 0 &{} 0 &{} \bar{T}_{0}\\ (1- \beta )^{1/2} \bar{W}_{0}^{T} &{} 0 &{} 0\\ 0 &{} (1- \beta )^{1/2} \bar{U}_{0}^{T} &{} 0\\ 0 &{} 0 &{} (1- \beta )^{1/2} \bar{T}_{0}^{T}\\ \beta ^{1/2} \bar{W}_{1}^{T} &{} 0 &{} 0\\ 0 &{} \beta ^{1/2} \bar{U}_{1}^{T} &{} 0\\ 0 &{} 0 &{} \beta ^{1/2} \bar{T}_{1}^{T}\\ \end{array}\right. \nonumber \\&\quad \left. \begin{array}{cccccc} * &{} * &{} * &{} * &{} *&{} * \\ * &{} * &{} * &{} * &{} * &{} *\\ * &{} * &{} * &{} * &{} * &{} *\\ \bar{M}_{0} &{} * &{} * &{} * &{} * &{} *\\ 0 &{} \bar{P}_{e} &{} * &{} * &{} * &{} *\\ 0 &{} 0 &{} \bar{N}_{0} &{} * &{} * &{} *\\ 0 &{} 0 &{} 0 &{} \bar{M}_{1} &{} * &{} *\\ 0 &{} 0 &{} 0 &{} 0 &{} \bar{P}_{e} &{} *\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \bar{N}_{1}\\ \end{array}\right] \ge 0 \end{aligned}$$

(33)

(iii) If (29), (30), (31),(32) and (33) are satisfied, then $e(k+1)^{T}P_{e0}e(k+1)\le \xi (k+1)$ for future time k and $\xi (k+1)$ is prespecified.

Proof

See “Appendix” for details. $\square$

Based on the above results, the whole output feedback predictive control problem can be described as:

$$\begin{aligned} \begin{aligned}&~~~\textit{min}_{ u(k),~\varGamma }~~~~~ \gamma (k) ~~s,t(18),(29)-(33)\\&\varGamma ~~ \textit{taking}~~\{M_{0},M_{1},N_{0},N_{1},,W_{0},W_{1},\\&~~~~~~~~~~~~~~~~~~~~~U_{0},U_{1},T_{0},T_{1}\} \end{aligned} \end{aligned}$$

(34)

Theorem 4

By the paper (Takács and Rohal’-Ilkiv 2012; Dughman and Rossiter 2015; James et al. 2013) and the closed-loop NCSs (18) with data loss, a feasible solution determined by the optimization problem (34) at initial time k is feasible for future time.

Proof

By the similar analysis with paper (Pin and Parisini 2011; Ding and Pin 2014; Zou et al. 2015), $\eta ^{T}diag\{M_{1},P_{e},N_{1}\}\eta \le \gamma (k)$ is always satisfied. Also the control signal can be transmitted successfully at initial instant by the assumption, that is, $\theta (k)=1$. So the solution $\{\varGamma (k)$,$\gamma (k)\}$ can be obtained from optional problem (34) at initial time k. At time $k+1$, it can construct a solution $\{\varGamma (k), ~~\gamma (k)\}$. Thus, to prove recursive feasibility, it only proves the inequality (29) (or (27)) is feasible at time $k+1$. Applying $P_{e}(k)=(P_{e0}\mu (k)\gamma (k))/\xi (k+1)$, it has

$$\begin{aligned}&\xi (k+2) \le (\xi (k+1)/(\mu (k)\gamma (k)))\times \left\{ \digamma (k+1)\right. \\&\quad \left. -\hat{x}^{T}(k+1)S_{1}\hat{x}(k+1)-u^{T}(k+1|k)(R+N_{\theta (k)})\right. \\&\quad \left. \times \, u(k+1|k)-\hat{x}^{T}(k+2|k)M_{\theta (k)}\hat{x}(k+2|k)\right\} \end{aligned}$$

$\square$

Then at time $k+1$, two cases will be considered.(i)$1\longrightarrow 1$, that is, $\theta (k)=1, \theta (k+1)=1$. It takes $u(k+1)=u(k+1|k)=F(k)\hat{x}(k+1)$ and $F(k+1)=F(k)$, then $\hat{x}(k+2|k)=\hat{x}(k+2|k+1)=\varXi (k+1)$. Furthermore, taking $\bar{M}_{\theta (k+1)}=\bar{M}_{\theta (k)}$ and $\gamma (k+1)=\gamma (k)$, it has $M_{\theta (k+1)}\le M_{\theta (k)}$. Thus

$$\begin{aligned} \begin{aligned}&\xi (k+2) \le (\xi (k+1)/(\mu (k)\gamma (k)))\times \{\gamma (k+1)\\&\quad -\hat{x}^{T}(k+1)S_{1}\hat{x}(k+1)-u^{T}(k+1)(R+N_{\theta (k)})\\&\quad \times u(k+1)-\varXi ^{T}(k+1)M_{\theta (k+1)}\varXi (k+1)\} \end{aligned} \end{aligned}$$

If it chooses $\mu (k+1)\xi (k+1)=\mu (k)\xi (k+2)$, then

$$\begin{aligned} \begin{aligned}&\hat{x}^{T}(k+1)S_{1}\hat{x}(k+1)+u^{T}(k+1)(R+N_{\theta (k)})u(k+1)\\&\quad +\varXi (k+1)^{T}M_{\theta (k+1)}\varXi (k+1) \le \gamma (k+1)\\&\quad -\mu (k+1)\gamma (k) \end{aligned} \end{aligned}$$

since the optional rule, $\gamma (k+1)\le \gamma (k)$, so it gets

$$\begin{aligned} \begin{aligned}&\hat{x}^{T}(k+1)S_{1}\hat{x}(k+1)+u^{T}(k+1)(R+N_{\theta (k)})u(k+1)\\&\quad +\varXi (k+1)^{T}M_{\theta (k+1)}\varXi (k+1) \le (1-\mu (k+1))\gamma (k) \end{aligned} \end{aligned}$$

which satisfies the (29) with k replaced $k+1$;

(ii) $1\longrightarrow 0$,that is, $\theta (k)=1, \theta (k+1)=0$, according to the compensation strategy, $u(k+1)$ take $\tau u(k)$ and $F(k+1)$ take F(k), so $\hat{x}(k+2|k)$ take $\hat{x}(k+2|k+1)=\hat{x}(k+2|k)=\varXi (k)$. Furthermore, if it takes $\bar{M}_{\theta (k+1)}=\bar{M}_{\theta (k)}$ and $\gamma (k+1)=\gamma (k)$, then $M_{\theta (k+1)}\le M_{\theta (k)}$. Thus

$$\begin{aligned} \begin{aligned}&\xi (k+2) \le (\xi (k+1)/(\mu (k)\gamma (k)))\times \{\gamma (k+1)\\&\quad -\hat{x}^{T}(k+1)S_{1}\hat{x}(k+1)-\tau u^{T}(k)(R+N_{\theta (k)})\\&\quad \times \tau u(k)-\varXi (k)^{T}M_{\theta (k+1)}\varXi (k)\} \end{aligned} \end{aligned}$$

If it chooses $\mu (k+1)\xi (k+1)=\mu (k)\xi (k+2)$, then

$$\begin{aligned} \begin{aligned}&\hat{x}^{T}(k+1)S_{1}\hat{x}(k+1)+\tau u^{T}(k)(R+N_{\theta (k)})\tau u(k)\\&\quad +\varXi (k)^{T}M_{\theta (k+1)}\varXi (k)\le \gamma (k+1)-\mu (k+1)\gamma (k) \end{aligned} \end{aligned}$$

since the optional rule, $\gamma (k+1)\le \gamma (k)$, so it gets

$$\begin{aligned} \begin{aligned}&\hat{x}^{T}(k+1)S_{1}\hat{x}(k+1)+u^{T}(k)(R+N_{\theta (k)})u(k)\\&\quad +\varXi (k)^{T}M_{\theta (k+1)}\varXi (k)\le (1-\mu (k+1))\gamma (k) \end{aligned} \end{aligned}$$

which also satisfy (27). Thus, the feasible solution $\{\varGamma (k)$,$\gamma (k)\}$ at instant k is feasible at time $k+1$; As for time $k+i(i\ge 2)$, similar conclusion can be obtained.

Theorem 5

For the closed-loop NCSs (18) with data loss with paper (Ravi et al. 2009), a feasible solution solved by the optimization problem Theorem 3 also drive the system stochastic stable.

Proof

For closed-loop NCSs (18), according to Theorem 4, if optimization problem is feasible at sampling instant $k_{0}$, then it is feasible for all future time $k>k_0$. Thus, $\gamma$ can be seen as a Lyapunov function of system (18), the evolution of $\gamma$ follows

$$\begin{aligned} \gamma (k+1)- \gamma (k) \le -\eta ^{T}(k)S\eta (k)-u^{T}(k)u(k) \end{aligned}$$

(35)

whenever the system state $\eta \ne 0$, $\gamma$ will decrease with the speed $\gamma (k+1)-\gamma (k) \le -\eta ^{T}(k)S\eta (k)$. Therefore, $\gamma (k)\le \gamma (k_0)$. According to the contractiveness (25), it has

$$\begin{aligned} \begin{aligned}&\varSigma _{i=0}^{\infty }E\{\eta ^{T}(k_{0}+i|k_{0})S\eta (k_{0}+i|k_{0})\\&\quad +u^{T}(k_{0}+i|k_{0})Ru(k_{0}+i|k_{0})\} \le \gamma (k_{0}) \end{aligned} \end{aligned}$$

(36)

choosing $k_{0}=0$, According to the above analysis, it gets $E\{\sum _{k=0}^{\infty }\eta ^{T}(k)S\eta (k)\}<\infty$, Taking $\varrho = \lambda _\mathrm{min}\{S\}$, which follows

$$\begin{aligned} E\left\{ \sum _{k=0}^{\infty }\eta ^{T}(k)\eta (k)\right\} \le (1/\varrho )E\left\{ \sum _{k=0}^{\infty }\eta ^{T}(k)S\eta (k)\right\} <\infty \end{aligned}$$

(37)

According to Definition 1, the stochastic stability of closed-loop system is obtained. Besides, the estimation error e(k) evolves by (34) such that $e(k)\rightarrow 0$ as $k\rightarrow \infty$, end. $\square$

5 Simulation Results

In this part, a DC servo control system is considered, which consists of a DC motor, load plate, speed and angle sensors. The model can be described as:

$$\begin{aligned} \left\{ \begin{aligned}&x(k+1)=Ax(k)+Bu(k)\\&y(k)=Cx(k) \end{aligned} \right. \end{aligned}$$

(38)

where

$$\begin{aligned} A=\begin{bmatrix} 1.12&0.213&-0.335\\ 1&0&0\\ 0&1&0 \end{bmatrix} \end{aligned}$$

and $B = [1 ~~0~~ 0]^{T}$,$C=[-0.1 -0.1 -0.1]$. Due to the system states are not available, it gets an observer gain $L=[5.0772~~4.6475~~3.0905]^{T}$ using the offline state observer Theorem 2, where decay rate $\delta =0.6$. For uncertainty communication links, it assumes the upper bound of data loss $h_\mathrm{max}=3$, and the data status description is shown in Fig. 1.

Fig. 1

Data status

To prove the effectiveness of the proposed design, it gives the corresponding simulation results. First, taking $S=I_{3},R=1$, it chooses the sampling instant $k=4$ as initial time, at current time, no data loss happen. For initial value, the estimation state $Xc4=[0.3~1~0.3]^{T}$, $X4=[0~1 ~0]^{T}$ and $U(4)=0$. Based on Theorem 3 and a forgetting factor $\tau =0.6$, it designs the different data missing rate when making simulations;

On the other hand, it takes the data missing rate $\alpha =0.05, \beta =0.92$, from the compensation strategy $u(k)=\theta (k)u(k)+(1-\theta (k))\tau u(k-1)$, it may be different effects when $\tau$ taking different values.

During the simulation, it firstly considers the different data loss rate, where $\alpha \in \{0.05,~~0.10,~~0.20\}$ and $\beta \in \{0.92,~~0.85,~~0.8\}$. Figures 2, 3 and  4 show the changes system state $\{x_1,~~x_2,~~x_3\}$ and observer state $\{x_{c1},~~x_{c2},~~x_{c3}\}$, respectively. Figure 5 represents the control inputs u at different data missing rate. It easily sees the system trajectories changes caused by data packet dropout, and for this, through the proposed theorem, it can get the suitable feedback gain K to drive the system stable; besides, the observer states can reconstruct the original states. The proposed theorems can be proved to cope with different data missing rate.

Furthermore, when data missing rate takes solid value at some time (from large-scale statistical probability, links could have constant rate at a period of time), it could get better control law with different factor. Figures 6, 7 and  8 show the system state trajectories $\{x_1,~~x_2,~~x_3\}$ and observer state $\{x_{c1},~~x_{c2},~~x_{c3}\}$, and Fig. 9 shows the changes of inputs u. It easily sees the different contractive speed of system state, so, a suitable forgetting factor will improve the efficiency of controller.

Fig. 2

Observer state $x_{c1}$, system state $x_1$

Fig. 3

Observer state $x_{c2}$, system state $x_2$

Fig. 4

Observer state $x_{c3}$, system state $x_3$

Fig. 5

System inputs u

Fig. 6

Observer state $x_{c1}$, system state $x_1$

Fig. 7

Observer state $x_{c2}$, system state $x_2$

Fig. 8

Observer state $x_{c3}$, system state $x_3$

Fig. 9

System inputs u

From above analysis, the following conclusions can be drawn:

• 1. A common state observer from Theorem 2 can realize the reconstruction of the original state, and estimation state follows the system state with a small error;

• 2. The control law computed can cope with the networks with data missing, where the missing rate varies;

• 3. For the compensation strategy, a smaller forgetting factor would improve the performance of controller by influence the convergence speed of system states.

Therefore, the proposed design of controller is effectiveness for NCSs.

6 Conclusion

Compared with state feedback synthesis, the problem of output feedback predictive control with one free control move for NCSs with data loss has been investigated in this paper. The random process of data missing is assumed to satisfy the Markov chain, and a compensation technique is used to minimize the effect by packet loss. Considering the unavailable states, a common observer is pre-design to reconstruct the original state, and an output feedback controller with one free control move satisfying the optional performance and stochastic stability is obtained. The effectiveness of the proposed method is proved by simulation results.

Appendix. Proof of Theorem 3

(i) According to (29), $\hat{x}(k|k)=\hat{x}(k)$, $e(k|k)=e(k)$, $\eta (k|k)=\eta (k)$ and the successful transmission at initial time k, then (27) can be described as

$$\begin{aligned} \begin{aligned}&\hat{x}^{T}(k)S_{1}\hat{x}(k)+u^{T}(k)Ru(k)+ \hat{x}^{T}(k+1)M_{1}\hat{x}(k+1)\\&\quad +u^{T}(k)N_{1}u(k)+ e^{T}(k+1)P_{e}(k)e(k+1)\le \gamma (k) \end{aligned} \end{aligned}$$

the error $e(k+1)=e(k+1|k)=(A_{0}- LC)e(k|k)$, according to the upper bound of e(k), $e^{T}(k+1)P_{e0}e(k+1) \le \xi (k+1)$ and $P_{e}(k)=(\mu (k) \gamma (k)P_{e0})/\xi (k+1)$, then the above inequality is equal to

$$\begin{aligned}&\hat{x}^{T}(k)S_{1}\hat{x}(k)+u^{T}(k)Ru(k)+ \hat{x}^{T}(k+1)M_{1}\hat{x}(k+1)\nonumber \\&\quad +u^{T}(k)N_{1}u(k)\le (1-\mu (k))\gamma (k) \end{aligned}$$

(39)

multiplying (39) by $\gamma ^{-1}$ and substituting $\gamma M_{1}^{-1}=\bar{M}_{1}$, $\gamma N_{1}=\bar{N}_{1}^{-1}$, using Schur complement, (29) is obtained.

(ii)Based on the quadratic Lyapunov function defined in (24), the contractiveness conditions (25) can be written as

$$\begin{aligned}&E\left\{ \eta ^{T}(k+i|k)\varPsi ^{T}diag \left\{ M_{\theta (k+i+1|\theta (k+i+1)},P_{e}(k),\right. \right. \nonumber \\&\quad \left. N_{\theta (k+i+1|k)|\theta (k+i|k)}\right\} \varPsi \eta (k+i|k)-\eta ^{T}(k+i|k)\nonumber \\&\quad \left. \times diag\left\{ M_{\theta (k+i|k)},P_{e}(k),M_{\theta (k+i|k)}\right\} \eta (k+i|k)\right\} \nonumber \\&\quad +E\left\{ \eta ^{T}(k+i|k)S\eta (k+i|k)+u^{T}(k+i|k)R\right. \nonumber \\&\quad \left. \times u(k+i|k) \right\} \le 0 \end{aligned}$$

(40)

where

$$\begin{aligned} \varPsi (k)=\begin{bmatrix} {A+ \theta (k) BF}&LC&{(1- \theta (k))\tau B}\\ 0&A-LC&0\\ \theta (k) F&0&{(1- \theta (k))\tau I} \end{bmatrix} \end{aligned}$$

(41)

If $\theta (k+i|k)=1$, $E_{\theta (k+i|k)=1}diag\{M_{\theta (k+i+1)}$, $P_{e}(k)$, $N_{\theta (k+i+1)}\}\alpha diag\{M_{0}$, $P_{e}$, $N_{0}\}+(1-\alpha )diag\{M_{1}$, $P_{e}$, $N_{1}\}$, the contractiveness condition is satisfied if and only if the following inequality holds

$$\begin{aligned}&\begin{aligned}&(a)~~\varPsi (k)_{\theta (k)=1}^{T}diag\left\{ W_{1},U_{1}, T_{1}\right\} \varPsi (k)_{\theta (k)=1}-diag\{M_{1},\\&\quad P_{e}, N_{1}\}+diag\left\{ S_{1}, 0, 0\right\} +[F~~0~~0]^{T}R[F~~0~~0] \le 0 \end{aligned}\\&\begin{aligned}&(b)~~\alpha diag\left\{ M_{0},P_{e},N_{0}\right\} +(1-\alpha )diag\left\{ M_{1},P_{e},N_{1}\right\} \\&\quad \le diag\left\{ W_{1},U_{1},T_{1}\right\} \end{aligned} \end{aligned}$$

Pre- and post-multiplying (a) by diag$\{\gamma ^{1/2}M_{1}^{-1}$,$\gamma ^{1/2}P_{e}^{-1}$, $\gamma ^{1/2}N_{1}^{-1}\}$, also pre- and post-multiplying (b) by $diag\{W_{1}^{-1}$, $U_{1}^{-1}$, $T_{1}^{-1}\}$, substituting $\gamma \varGamma ^{-1}=\bar{\varGamma }$, where $\varGamma$ takes $\{M_{1}$, $N_{1}$, $P_{e}$, $M_{0}$, $N_{0}$,$W_{1}$, $U_{1}$, $T_{1}$, $W_{0}$, $U_{0}$, $T_{0}\}$ and $Y_{1}=F \bar{M}_{1}$, according to Schur complement, (30) and (31) are obtained. If $\theta (k+i|k)=0$, using above similar procedure, (32) and (33) can be derived.

(iii) if (25) and (27) hold at sampling time k, then

$$\begin{aligned}&\begin{aligned}&\eta ^{T}(k+2|k)diag\left\{ M_{\theta (k)}, Pe(k), N_{\theta (k)}\right\} \eta (k+2|k)\\&\quad +\hat{x}^{T}(k+1|k)S_{1}\hat{x}(k+1|k)+u^{T}(k+1|k)Ru(k+1|k)\\&\quad \le \hat{x}^{T}(k+1|k)M_{\theta (k)}\hat{x}(k+1|k)+e^{T}(k+1|k)Pe(k)\\&\quad \times e(k+1|k)+u^{T}(k|k)N_{\theta (k)}u(k|k) \end{aligned}\\&\begin{aligned}&\hat{x}^{T}(k+1|k)M_{\theta (k)}\hat{x}(k+1|k)+e^{T}(k+1|k)Pe(k)\\&\quad \times e(k+1|k)+u^{T}(k|k)N_{\theta (k)}u(k|k)\le \digamma (k+1) \end{aligned} \end{aligned}$$

where $\digamma (k+1)\!=\!\gamma (k)\!-\!\hat{x}^{T}(k|k)S_{1}\hat{x}(k|k)\!-\!u^{T}(k|k)Ru(k|k)$, since $e(k+1|k)=e(k+1)$ and $\hat{x}(k+1|k)=\hat{x}(k+1)$. By above two inequalities, the following inequality can be obtained.

$$\begin{aligned} \begin{aligned}&e^{T}(k+2|k)Pe(k)e(k+2|k)\le \digamma (k+1)-\hat{x}^{T}(k+1)S_{1}\\&\quad \times \hat{x}(k+1)-u^{T}(k+1|k)(R+N_{\theta (k)})u(k+1|k)\\&\quad -\hat{x}^{T}(k+2|k)M_{\theta (k)}\hat{x}(k+2|k) \end{aligned} \end{aligned}$$

By $e(k+2|k)=e(k+2)=(A_{0}-LC)e(k+1)$ and $\tilde{x}(k+2)=\hat{x}(k+2|k)=(A+\theta (k)B F)\hat{x}(k+1)+ (1-\theta (k)) \tau u(k-1)+LCe(k+1)$. so it has

$$\begin{aligned} \begin{aligned}&e^{T}(k+2)Pe(k)e(k+2)\le \tilde{\xi }(k+2)= \digamma (k+1)\\&\quad -\hat{x}^{T}(k+1)S_{1}\hat{x}(k+1)-u^{T}(k+1|k)(R+N_{\theta (k)})\\&\quad \times u(k+1|k)-\hat{x}^{T}(k+2|k)M_{\theta (k)}\hat{x}(k+2|k) \end{aligned} \end{aligned}$$

where $\tilde{\xi }(k+2)$ follows the above assumption 1, besides, since $Pe(k)= \pi (k)P_{e0}$. Then

$$\begin{aligned} \begin{aligned} e^{T}(k+2)P_{e0}e(k+2)\le \tilde{\xi }(k+2)/ \pi (k) \end{aligned} \end{aligned}$$

from above results and Theorem 2, it gets the upper bound of estimation error at time $k+2$

$$\begin{aligned} \begin{aligned}&e^{T}(k+2)P_{e0}e(k+2)\le \xi (k+2)\\&\quad =min\left\{ \tilde{\xi }(k+2)/\pi (k);\delta \eta (k+1)\right\} \end{aligned} \end{aligned}$$

For any $k>1$, with similar analysis, we get $e^{T}(k+1)P_{e0}e(k+1)\le \xi (k+1)$.