Abstract
A van Leer-type numerical scheme for the model of a general fluid in a nozzle with variable cross section is presented. The model is nonconservative, making it hard for standard numerical schemes. Exact solutions of local Riemann problems are incorporated in the construction of this scheme. The scheme can work well in regions of resonance, where multiple waves are colliding. Numerical tests are conducted, where we compare the errors and orders of accuracy for approximating exact solutions between this scheme and a Godunov-type scheme. Results from numerical tests show that this van Leer-type scheme has a much better accuracy than the Godunov-type scheme.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we build a van Leer-type scheme for approximating solutions of the following model of a general fluid flow in a nozzle with variable cross section
where ρ = ρ(x, t), ε = ε(x, t), T = T(x, t), S = S(x, t), and p = p(x, t) denote the thermodynamic variables: density, internal energy, absolute temperature, specific entropy, and the pressure, respectively; u = u(x, t) is the velocity; e = e(x, t) = ε + u2/2 is the total energy; and \(a = a(x) > 0, x \in \mathbb {R}\) is the cross-sectional area.
The model (1.1) contains a nonconservative source term. To deal with this obstacle, one often supplements the system (1.1) with the trivial equation
and then, the system (1.1)–(1.2) can be re-written as a system of balance laws in nonconservative form. A formulation of weak solutions of this kind of systems was introduced in [16]. Numerical approximating nonconservative systems of balance laws is a challenging topic during the past decades. Often, nonconservative terms cause serious problems to standard schemes. For example, errors may not tend to zero when the mesh sizes tend to zero, or even numerical oscillations may appear quickly.
Motivated by our recent work [14], we will construct a van Leer-type scheme for (1.1). Note that in the literature, the second-order van Leer scheme can be seen as an important improvement of the first-order Godunov scheme for hyperbolic conservation laws. Therefore, we will also show that this van Leer-type scheme can provide us with a better accuracy than the Godunov-type scheme. It is interesting that this van Leer-type scheme can also give good approximations in the resonance cases where the exact solution contains several waves associated with different characteristic fields with coinciding shock speeds.
Throughout, we assume for simplicity that the fluid is polytropic and ideal so that the equation of state is given by
where γ > 1 is the adiabatic exponent.
We note that there are many works in the literature for the study on nonconservative systems of balance laws. Theoretical studies on nonconservative systems of balance laws were presented in [19, 20, 23,24,25, 27, 32,33,34]. Numerical treatments for balance laws in nonconservative form were studied in [7,8,9, 18]. Numerical schemes for shallow-water equations were considered in [3, 6, 13, 26, 28]. Numerical schemes for the model of a fluid flow in a nozzle with variable cross section were constructed in [5, 11, 15, 21, 22]. Generalized Riemann problems were considered in [4]. Numerical schemes for two-phase flow models were presented in [1, 2, 10, 12, 29,30,31]. The reader is referred to [17] for standard numerical schemes for hyperbolic systems of conservation laws (see also the references therein).
The organization of this paper is as follows. Basic properties of the model (1.1)–(1.2) are given in Section 2. In Section 3, the Riemann problem is revisited. Section 4 is devoted to the construction of the van Leer-type scheme for (1.1). Numerical tests are given in Section 5, where we compute the errors and orders of accuracy. Finally, we present several conclusions in Section 6.
2 Preliminaries
2.1 Nonstrict Hyperbolic Model
Using the thermodynamical identity, we can express the pressure p from (1.3) as a function of the density ρ and the specific entropy S
where Cv > 0 is the specific heat at constant volume and S∗ is constant. Note that for a polytropic and ideal fluid, γ and Cv are constants.
Thus, if we choose (p, S) as two independent thermodynamic variables, we can write
Therefore, for a smooth solution U = U(x, t) = (p(x, t),u(x, t),S(x, t),a(x))T, the system (1.1) can be re-written as a system of balance laws in nonconservative form
where
where c is the sound speed,
The characteristic equation is given by
Thus, we obtain four real eigenvalues
The corresponding eigenvectors can be chosen as
Therefore, the system (1.1) is hyperbolic, but not strictly hyperbolic. More precisely, λ0 and λ1 coincide on the hypersurface
λ0 and λ2 coincide on the hypersurface
λ0 and λ3 coincide on the hypersurface
These surfaces, referred to as strictly hyperbolic boundaries, separate the phase domain into four subdomains, denoted by \(G_{1}^{+}\), \(G_{2}^{+}\), \(G_{2}^{-}\), and \(G_{1}^{-}\), in which the system is strictly hyperbolic (see Fig. 1).
Hyperbolic boundaries and the four phases in the (p, u) −plane
The second and the zero characteristic fields are linearly degenerate, since
The first and the third characteristic fields are genuinely nonlinear, since
2.2 Rarefaction Waves
The k-rarefaction waves of the system (1.1) are the continuous piecewise-smooth self-similar weak solutions of (1.1) associated with nonlinear characteristic fields (λ k ,r k ), k = 1,3, which have the form
where V (ξ) :=Fan k (ξ;U−,U+) is a solution of the following ordinary differential equations
For k = 1, we determine V (ξ) = (p(ξ),u(ξ),S(ξ),a(ξ)) from (2.9) as follows
or, equivalently,
From (2.10), the forward1-rarefaction wave curve \(\mathcal {R}_{1}(U_{0})\) consisting of all right-hand states U = (p, u, ρ, a) that can be connected to a given left-hand state U0 = (p0,u0,ρ0,a0) by an 1-rarefaction wave is given by
Similarly, for k = 3, we have
Therefore, the backward3-rarefaction wave curve \(\mathcal {R}_{3}^{B}(U_{0})\) consisting of all left-hand states U = (p, u, ρ, a) that can be connected to a given right-hand state U0 = (p0,u0,ρ0,a0) by an 3-rarefaction wave is given by
2.3 Shocks and Admissibility Criterion
A discontinuity wave of (1.1) is a weak solution of the form
where U−,U+ are left- and right-hand states, respectively, and σ is the shock speed.
A shock wave always satisfies the Rankine-Hugoniot relation for the conservative equation ∂ t a = 0, which reads
The last relation leads to the following two cases:
-
(i)
either the cross section remained unchanged across the shock, i.e., [a] = 0, or
-
(ii)
the shock speed vanishes:
$$\sigma = 0. $$
If [a] = 0, then, the cross section is constant across the shock. We can eliminate this constant value in the governing equations (1.1) and obtain the usual gas dynamics equations. Thus, the Rankine-Hugoniot relations for the shock are given by
Transforming the relations (2.14) yields
If M = 0, then,
Thus, in this case, the discontinuity wave (2.13) is called the 2-contact discontinuity corresponding to the shock speed σ2(U−,U+) = u± = λ2(U±).
If M≠ 0, then, the relations (2.15) can be equivalently written
Then, we obtain
Shock waves associated with nonlinear characteristic fields, as indicated above, are required to fulfill the Lax shock inequalities
Observe that for a polytropic ideal gas (1.3), shock waves satisfying the Lax shock inequalities (2.18) are characterized as follows.
-
(a)
For a 1-Lax shock,
$$ M> 0, \quad u_{+} < u_{-}, \quad p_{+} > p_{-}. $$(2.19) -
(b)
For a 3-Lax shock,
$$ M< 0, \quad u_{-} > u_{+}, \quad p_{-} > p_{+}. $$(2.20)
From (2.18) and (2.19), the forward1-shock wave curve \(\mathcal {S}_{1}(U_{0})\) consisting of all right-hand states U = (p, u, ρ, a) that can be connected to a given left-hand state U0 = (p0,u0,ρ0,a0) by an 1-Lax shock wave is given by
From (2.18) and (2.20), the backward3-shock wave curve \(\mathcal {S}_{3}^{B}(U_{0})\) consisting of all left-hand states U = (p, u, ρ, a) that can be connected to a given right-hand state U0 = (p0,u0,ρ0,a0) by an 3-Lax shock wave is given by
For \(U_{R} \in \mathcal {S}_{1}(U_{L})\), we have the 1-shock speed
For \(U_{L} \in \mathcal {S}_{3}^{B}(U_{R})\), we have the 3-shock speed
From (2.23) and (2.24), we have the following lemma.
Lemma 2.1 ([32, Proposition 3.3])
1. The 1-shock speedσ1(U0,U)may change sign along the forward 1-shock wave curve\(\mathcal {S}_{1}(U_{0})\).More precisely, we have the following:
(i) If\(U_{0} \in G_{2}^{+} \cup G_{2}^{-} \cup G_{1}^{-}\),thenσ1(U0,U)remains negative:
(ii) If \(U_{0} \in G_{1}^{+}\), thenσ1(U0,U)vanishes onceat some point \(U = U^{\#} \in \mathcal {G}_{2}^{+}\)corresponding to a value
on the forward 1-shock wave curve \(\mathcal {S}_{1}(U_{0})\)such that
2. The 3-shock speed σ3(U, U0)may change sign along the backward 3-shock wave curve\(\mathcal {S}_{3}^{B}(U_{0})\). Moreprecisely, we have the following:
(i) If \(U_{0} \in G_{1}^{+} \cup G_{2}^{+} \cup G_{2}^{-}\),then σ3(U, U0)remains positive:
(ii) If \(U_{0} \in G_{1}^{-}\), thenσ3(U, U0)vanishes onceat some point \(U = U^{@} \in G_{2}^{-}\)corresponding to a value
on the backward 3-shock wave curve \(\mathcal {S}_{3}^{B}(U_{0})\)such that
Moreover, since \( \sigma _{1}(U_{-}, U_{+}) = u_{-} - \frac {M}{\rho _{-}} = u_{+} - \frac {M}{\rho _{+}}\) and M > 0, we imply that
Similarly, it holds that
From (2.11), (2.12), (2.21), and (2.22), we can therefore define the forward and backward wave curves in the nonlinear characteristic fields as follows.
These sets mean that: ∙ If \(U_{+} \in \mathcal {W}_{1}(U_{-})\), then there is the 1-wave (1-rarefaction wave or 1-shock wave) connecting U− to U+, denoted by
∙ If \(U_{-} \in \mathcal {W}_{3}^{B}(U_{+})\), then there is the 3-wave (3-rarefaction wave or 3-shock wave) connecting U− to U+, denoted by
2.4 Stationary Waves
Consider the case
This means that the shock wave is a contact wave associated with λ0. As shown in [32], the jump relations for this contact wave are given by
where h is specific enthalpy given by
We now describe the set of states U which can be connected to a given state U0 by a stationary contact wave (associated with λ0), where the cross section levels on both sides a0 and a are considered to be fixed. Substituting \(u = \frac {a_{0} \rho _{0} u_{0}}{a \rho }\) from the 1st equation of (2.30) into the 3rd equation of (2.30), we obtain the nonlinear equation
The domain of the function F(ρ) is given by
Consider the case u0 = 0. Then, the function F(ρ) has a unique root ρ = ρ0. Therefore, we obtain
Consider the case u0≠ 0. We have
so that
where
Moreover,
Thus, F(ρ) admits a zero if and only if
or, equivalently
where
If a > amin, the function F(ρ) has exactly two roots denoted by φ1(U0,a) and φ2(U0,a), which satisfy
The following lemma provides us with the existence of the above stationary waves.
Lemma 2.2 ([32, Lemma 3.1])
GivenU0 = (p0,u0,ρ0,a0)anda≠a0 such that u0 ≠ 0. There exists a stationarywave connectingU0to somestate U if and only ifa ≥ amin.More precisely, we have the following: (i) Ifa < amin,F(ρ)hasno roots; so there are no stationary waves. (ii) Ifa = amin,F(ρ)has onlyone rootρ = ρmax;so there is exactly one stationary wave connectingU0toUmax,where
(iii) If a > amin,F(ρ)hastwo distinct roots; so there are exactly two stationary waves connectingU0to thestate \({U_{0}^{s}}\)orthe state \({U_{0}^{b}}\),where
Using notations as Lemma 2.2, we have the following lemma.
Lemma 2.3
GivenU0 = (p0,u0,ρ0,a0)and a.
- (i):
-
It holds that
$$\begin{array}{@{}rcl@{}} && \rho_{\max} < \rho_{0}, \quad U_{0} \in G_{2}^{+} \cup G_{2}^{-},\\ && \rho_{\max} > \rho_{0}, \quad U_{0} \in G_{1}^{+} \cup G_{1}^{-}. \end{array} $$ - (ii):
-
It holds that
$$\begin{array}{@{}rcl@{}} && {U_{0}^{s}} \in G_{1}^{+}, \quad {U_{0}^{b}} \in G_{2}^{+} \quad \textit{for} \quad u_{0} > 0,\\ &&{U_{0}^{s}} \in G_{1}^{-}, \quad {U_{0}^{b}} \in G_{2}^{-} \quad \textit{for} \quad u_{0} < 0. \end{array} $$ - (iii):
-
It holds that
$$\begin{array}{@{}rcl@{}} && a_{\min} < a_{0}, \quad U_{0} \in G_{i}^{\pm}, \quad i = 1, 2\\ && a_{\min} = a_{0}, \quad U_{0} \in \mathcal{C}^{\pm},\\ && a_{\min} = 0, \quad u_{0} = 0. \end{array} $$ - (iv):
-
Ifa > a0,then
$$\varphi_{1}(U_{0}, a) < \rho_{0} < \varphi_{2}(U_{0}, a). $$ - (v):
-
If amin < a < a0,then
$$\begin{array}{@{}rcl@{}} && \rho_{0} < \varphi_{1}(U_{0}, a) < \varphi_{2}(U_{0}, a), \quad \textit{for} \quad U_{0} \in G_{1}^{\pm},\\ && \rho_{0} > \varphi_{2}(U_{0}, a) > \varphi_{1}(U_{0}, a), \quad \textit{for} \quad U_{0} \in G_{2}^{\pm}. \end{array} $$
It follows from Lemma 2.2 that there may be two possible stationary waves from a given state U0 to a state with a new level cross section a. Thus, it is necessary to impose some condition to select a unique physical stationary as follows.
- (MC):
-
Any stationary jump must not cross the sonic curve in the (p, u)-plane.
Observe that the admissibility criterion (MC) implies that:
-
If a > amin and \(U_{0} \in G_{1}^{\pm }\), then \({U_{0}^{s}}\) is selected.
-
If a > amin and \(U_{0} \in G_{2}^{\pm }\), then \({U_{0}^{b}}\) is selected.
3 The Riemann Problem Revisited
In this section, the Riemann problem for (1.1) is revisited (see [32]). We distinguish between four cases
-
Case A: \(U_{L} \in G_{1}^{+} \cup \mathcal {C}^{+}\) and a R > a L ;
-
Case B: \(U_{L} \in G_{2}^{+}\) and a R > a L ;
-
Case C: \(U_{R} \in G_{1}^{-} \cup \mathcal {C}^{-}\) and a L > a R ;
-
Case D: \(U_{R} \in G_{2}^{-}\) and a L > a R .
Notations 1
(i) W k (U i ,U j ) (S k (U i ,U j ),R k (U i ,U j )) denotes the kth-wave (kth-shock, kth-rarefaction wave, respectively) connecting the left-hand state U i to the right-hand state U j , k = 0,1,2,3; (ii) W m (U i ,U j ) ⊕ W n (U j ,U k ) indicates that there is an mth-wave from the left-hand state U i to the right-hand state U j , followed by an nth-wave from the left-hand state U j to the right-hand state U k , m, n ∈{1,2,3,4}. (iii) \(U_{0}^{\#}\) denotes the state such that \(\sigma _{1}(U_{0}, U_{0}^{\#}) = 0\). \(U_{0}^{@}\) denotes the state such that \(\sigma _{3}(U_{0}^{@},\)U0) = 0 (see Lemma 2.1). (iv) \({U_{0}^{s}}\), \({U_{0}^{b}} \) denote the states resulting from stationary waves from U0 (see Lemma 2.2).
3.1 Case A: \(U_{L} \in G_{1}^{+} \cup \mathcal {C}^{+}\) and a R > a L
3.1.1 Construction A1
The first part of the Riemann solution can be the stationary wave
i.e.,
where
If we take any \(U \in \mathcal {R}_{1}({U_{L}^{s}})\), then the second part of the Riemann solution can be a 1-rarefaction wave
i.e.,
On the other hand, if we take \(U \in \mathcal {S}_{1}({U_{L}^{s}})\) such that \(\sigma _{1}({U_{L}^{s}}, U) > 0\) (i.e., U is located above \(U_{L}^{s\#}\), see Lemma 2.1), then the second part of the Riemann solution can be a 1-shock wave
i.e.,
Thus, if \(U = (p, u, \rho , a_{R}) \in \mathcal {W}_{1}({U_{L}^{s}})\) such that U is located above \(U_{L}^{s \#}\), then the first two parts of the Riemann solution are
Therefore, we call the set
as the composite wave curveW0.W1(U L ,a R ). Obviously, W0.W1(U L ,a R ) is a part of the wave curve \(\mathcal {W}_{1}({U_{L}^{s}})\) (see Fig. 2). If we have an intersection in the (p, u)-plane
then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.1) can be seen as follows.
-
If \(U \in \mathcal {R}_{1}({U_{L}^{s}})\) and \(U^{*} \in \mathcal {R}_{3}^{B}(U_{R})\), then the form (3.1) yields
$$U_{\text{Rie}}(x/t; U_{L}, U_{R}) = \left\{\begin{array}{llllllll} U_{L} & \text{if~} x/t < 0,\\ {U_{L}^{s}} & \text{if~} 0 < x/t < \lambda_{1}({U_{L}^{s}}),\\ \text{Fan}_{1}(x/t; {U_{L}^{s}}, U) &\text{if~} \lambda_{1}({U_{L}^{s}}) \le x/t \le \lambda_{1}(U),\\ U & \text{if~} \lambda_{1}(U) < x/t < \lambda_{2}(U) = \lambda_{2}(U^{*}),\\ U^{*} &\text{if~} \lambda_{2}(U^{*}) < x/t < \lambda_{3}(U^{*}),\\ \text{Fan}_{3}(x/t; U^{*}, U_{R}) & \text{if~} \lambda_{3}(U^{*}) \le x/t \le \lambda_{3}(U_{R}),\\ U_{R} &\text{if~} x/t >\lambda_{3}(U_{R}). \end{array}\right.$$Fig. 2 
The composite wave curves: W0.W1(U L ,a R ), W0.S1.W0(U L ,a R ), and S1.W0(U L ,a R ) in the (p, u)-plane
-
If \(U \in \mathcal {R}_{1}({U_{L}^{s}})\) and \(U^{*} \in \mathcal {S}_{3}^{B}(U_{R})\), then the form (3.1) yields
$$U_{\text{Rie}}(x/t; U_{L}, U_{R}) = \left\{\begin{array}{llllllll} U_{L} & \text{if~} x/t < 0,\\ {U_{L}^{s}} & \text{if~} 0 < x/t < \lambda_{1}({U_{L}^{s}}),\\ \text{Fan}_{1}(x/t; {U_{L}^{s}}, U) &\text{if~} \lambda_{1}({U_{L}^{s}}) \le x/t \le \lambda_{1}(U),\\ U & \text{if~} \lambda_{1}(U) < x/t < \lambda_{2}(U) = \lambda_{2}(U^{*}),\\ U^{*} & \text{if~} \lambda_{2}(U^{*}) < x/t < \sigma_{3}(U^{*}, U_{R}),\\ U_{R} & \text{if~} x/t > \sigma_{3}(U^{*}, U_{R}). \end{array}\right.$$ -
If \(U \in \mathcal {S}_{1}({U_{L}^{s}})\) and \(U^{*} \in \mathcal {R}_{3}^{B}(U_{R})\), then the form (3.1) yields
$$U_{\text{Rie}}(x/t; U_{L}, U_{R}) = \left\{\begin{array}{llllllll} U_{L} &\text{if~} x/t < 0,\\ {U_{L}^{s}} &\text{if~} 0 < x/t < \sigma_{1}({U_{L}^{s}}, U),\\ U, & \text{if~} \sigma_{1}({U_{L}^{s}}, U) < x/t < \lambda_{2}(U) = \lambda_{2}(U^{*}),\\ U^{*} & \text{if~} \lambda_{2}(U^{*}) < x/t < \lambda_{3}(U^{*}),\\ \text{Fan}_{3}(x/t; U^{*}, U_{R}) &\text{if~} \lambda_{3}(U^{*}) \le x/t \le \lambda_{3}(U_{R}),\\ U_{R} & \text{if~} x/t > \lambda_{3}(U_{R}). \end{array}\right.$$ -
If \(U \in \mathcal {S}_{1}({U_{L}^{s}})\) and \(U^{*} \in \mathcal {S}_{3}^{B}(U_{R})\), then the form (3.1) yields
$$U_{\text{Rie}}(x/t; U_{L}, U_{R}) = \left\{\begin{array}{llllllll} U_{L} &\text{if~} x/t < 0,\\ {U_{L}^{s}} & \text{if~} 0 < x/t < \sigma_{1}({U_{L}^{s}}, U),\\ U & \text{if~} \sigma_{1}({U_{L}^{s}}, U) < x/t < \lambda_{2}(U) = \lambda_{2}(U^{*}),\\ U^{*} & \text{if~} \lambda_{2}(U^{*}) < x/t < \sigma_{3}(U^{*}, U_{R}),\\ U_{R} & \text{if~} x/t > \sigma_{3}(U^{*}, U_{R}). \end{array}\right. $$
Algorithm to Compute the Intersection Point \((p, u) = \mathcal {W}_{3}^{B}(U_{R}) \cap W_{0}.W_{1}(U_{L}, a_{R})\). Assume that \(U_{L}^{s\#}\) is located below the curve \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u) −plane.
Step 1
Set p1 = 0, \(p_{2} = p_{L}^{s\#}\);
Step 2
Compute \(p = \frac {p_{1} + p_{2}}{2}\); Compute u such that \((p,u) \in \mathcal {W}_{1}({U_{L}^{s}})\) in the (p, u)-plane;
Step 3
-
If (p, u) belongs to \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u) −plane, end;
-
If (p, u) is located above \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u) −plane, set p1 = p and return Step 2;
-
If (p, u) is located below \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u) −plane, set p2 = p and return Step 2.
3.1.2 Construction A2
Fix a cross section level a M between a L and a R . The first part of the Riemann solution can be a stationary wave
where
The second part of the Riemann solution is a 1-shock wave with zero speed
The third part is again a stationary wave
where
Because these three parts are discontinuity waves with same zero speed, we have a wave collision (resonant case), i.e., W0(U L ,ULs) ⊕ S1(ULs, ULs#) ⊕ W0(ULs#, ULs#b) is just a discontinuity wave with zero speed
We call the set
as the composite wave curveW0.S1.W0(U L ,a R ). It is not difficult to check that \(U_{L}^{\# b}\) and \(U_{L}^{s \#}\) are two end-points of W0.S1.W0(U L ,a R ) (see Fig. 2). Therefore, if we have an intersection in the (p, u)-plane
then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.4) can be seen as follows.
-
If \(U^{*} \in \mathcal {R}_{3}^{B}(U_{R})\), then the form (3.4) yields
$$U_{\text{Rie}}(x/t; U_{L}, U_{R}) = \left\{\begin{array}{llllllll} U_{L} & \text{if~} x/t < 0,\\ U_{L}^{s \# b} & \text{if~} 0 < x/t < \lambda_{2}(U_{L}^{s \# b}) = \lambda_{2}(U^{*}),\\ U^{*} & \text{if~} \lambda_{2}(U^{*}) < x/t < \lambda_{3}(U^{*}),\\ \text{Fan}_{3}(x/t; U^{*}, U_{R}) & \text{if~} \lambda_{3}(U^{*}) \le x/t \le \lambda_{3}(U_{R}),\\ U_{R} & \text{if~} x/t > \lambda_{3}(U_{R}). \end{array}\right.$$ -
If \(U^{*} \in \mathcal {S}_{3}^{B}(U_{R})\), then the form (3.4) yields
$$U_{\text{Rie}}(x/t; U_{L}, U_{R}) = \left\{\begin{array}{llllllll} U_{L} & \text{if~} x/t < 0,\\ U_{L}^{s \# b} & \text{if~} 0 < x/t < \lambda_{2}(U_{L}^{s \# b}) = \lambda_{2}(U^{*}),\\ U^{*} & \text{if~} \lambda_{2}(U^{*}) < x/t < \sigma_{3}(U^{*}, U_{R}),\\ U_{R} & \text{if~} x/t > \sigma_{3}(U^{*}, U_{R}). \end{array}\right.$$
Algorithm to Compute the Intersection Point \((p,u) = \mathcal {W}_{3}^{B}(U_{R}) \cap W_{0}.S_{1}.W_{0}\) (U L ,a R ). Assume that \(U_{L}^{s\#}\) is located above \(\mathcal {W}_{3}^{B}(U_{R})\) and \(U_{L}^{\#b}\) is located below \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u)-plane.
Step 1
Set a1 = a L , a2 = a R ;
Step 2
Compute \(a_{M} = \frac {a_{1} + a_{2}}{2}\); Compute \({U_{L}^{s}}\) as in (3.2); Compute \(U_{L}^{s\#}\); Compute \(U_{L}^{s\#b} = (p, u, \rho , a_{R})\) as in (3.3);
Step 3
-
If (p, u) belongs to \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u)-plane, end;
-
If (p, u) is located above \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u)-plane, set a2 = a M and return Step 2;
-
If (p, u) is located below \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u)-plane, set a1 = a M and return Step 2.
3.1.3 Construction A3
Take any state \(U = (p, u, \rho , a_{L}) \in \mathcal {S}_{1}(U_{L}) \cap G_{2}^{+}\) such that σ1(U L ,U) < 0, i.e., U is located between \(U_{L}^\#\) and \({U_{L}^{0}}\), where
Then, the first part of the Riemann solution can be a 1-shock wave with negative speed
Next, the second part of the Riemann solution can be a stationary wave
where
The set
is called the composite wave curve S1.W0(U L ,a R ). Obviously, \(U_{L}^{\# b}\) and \({U_{L}^{0}}\) are two end-points of S1.W0(U L ,a R ) (see Fig. 2). Therefore, if we have an intersection in the (p, u)-plane
then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.6) can be seen as follows. ∙\(U^{*} \in \mathcal {R}_{3}^{B}(U_{R})\), then the form (3.6) yields
∙\(U^{*} \in \mathcal {S}_{3}^{B}(U_{R})\), then the form (3.6) yields
Algorithm to Compute the State U and the Intersection Point \((p^{b}, u^{b}) = \mathcal {W}_{3}^{B}\)(U R ) ∩ S1.W0(U L ,a R ). Assume that \(U_{L}^{\#b}\) is located above \(\mathcal {W}_{3}^{B}(U_{R})\) and \({U_{L}^{0}}\) is located below \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u)-plane.
Step 1
Set \(p_{1} = p_{L}^{\#}\), \(p_{2} = {p_{L}^{0}}\);
Step 2
Compute \(p = \frac {p_{1} + p_{2}}{2}\); Compute \(U = (p,u, \rho , a_{L}) \in \mathcal {S}_{1}(U_{L})\); Compute Ub = (pb,ub,ρb,a R ) as in (3.5);
Step 3
-
If (pb,ub) belongs to \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u)-plane, end;
-
If (pb,ub) is located above \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u)-plane, set p1 = p and return Step 2;
-
If (pb,ub) is located below \(\mathcal {W}_{3}^{B}(U_{R})\) in the (p, u)-plane, set p2 = p and return Step 2.
3.2 Case B: U L ∈ G2+ and a R > a L
3.2.1 Construction B1
The first part of the Riemann solution can be the 1-rarefaction wave
where
The second part of the Riemann solution can be the stationary wave
where
Take any state \(U = (p, u, \rho , a_{R}) \in \mathcal {W}_{1}(U_{L}^{+s})\) such that U is located above \(U_{L}^{+s \#}\). Then, the third part of the Riemann solution can be a 1-wave
We call the set
as the composite wave curve R1.W0.W1(U L ,a R ) (see Fig. 3). If we have an intersection in the (p, u) −plane
then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.7) can be seen as follows. ∙ If \(U \in \mathcal R_{1}(U_{L}^{+s})\) and \(U^{*} \in \mathcal {R}_{3}^{B}(U_{R})\), then the form (3.7) yields
∙ If \(U \in \mathcal {R}_{1}(U_{L}^{+s})\) and \(U^{*} \in \mathcal {S}_{3}^{B}(U_{R})\), then the form (3.7) yields
∙ If \(U \in \mathcal S_{1}(U_{L}^{+s})\) and \(U^{*} \in \mathcal {R}_{3}^{B}(U_{R})\), then the form (3.7) yields
∙ If \(U \in \mathcal {S}_{1}(U_{L}^{+s})\) and \(U^{*} \in \mathcal {S}_{3}^{B}(U_{R})\), then the form (3.7) yields
The composite wave curves: R1.W0.W1(U L ,a R ), R1.W0.S1.W0(U L ,a R ) and W1.W0(U L ,a R ) in the (p, u)-plane
Algorithm to Compute the Intersection Point \((p, u) = \mathcal {W}_{3}^{B}(U_{R}) \cap R_{1}.W_{0}.W_{1}\)(U L ,a R ). Similar to case A, since \(R_{1}.W_{0}.W_{1}(U_{L}, a_{R}) \equiv W_{0}.W_{1}(U_{L}^{+}, a_{R})\).
3.2.2 Construction B2
The first part of the Riemann solution can be the 1-rarefaction wave
where
Fix a cross section a M between a L and a R . The second part of the Riemann solution can be a stationary wave
where
The third part of the Riemann solution can be a 1-shock wave with zero speed
The fourth part of the Riemann solution can be again a stationary wave
where
We call the set
as the composite wave curve R1.W0.S1.W0(U L ,a R ). It is not difficult to check that \(U_{L}^{+s\#}\) and \(U_{L}^{+b}\) are two end-points of R1.W0.S1.W0(U L ,a R ) (see Fig. 3). Therefore, if we have an intersection in the (p, u) −plane
then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.8) can be seen as follows. ∙ If \(U^{*} \in \mathcal {R}_{3}^{B}(U_{R})\), then the form (3.8) yields
∙ If \(U^{*} \in \mathcal {S}_{3}^{B}(U_{R})\), then the form (3.8) yields
Algorithm to Compute the Intersection Point \((p, u) = \mathcal {W}_{3}^{B}(U_{R}) \cap R_{1}.W_{0}.S_{1}.W_{0}\)(U L ,a R ). Similar to case A, since \(R_{1}.W_{0}.S_{1}.W_{0}(U_{L}, a_{R}) \equiv W_{0}.S_{1}.W_{0}(U_{L}^{+}, a_{R})\).
3.2.3 Construction B3
Take a state \(U = (p, u, \rho , a_{L}) \in \mathcal {W}_{1}(U_{L})\) such that \(U \in G_{2}^{+}\), i.e., U is located between \(U_{L}^{+}\) and \({U_{L}^{0}}\), where
Then, the first part of the Riemann solution can be a 1-wave
Next, the second part of the Riemann solution can be a stationary wave
where
We call the set
as the composite wave curve W1.W0(U L ,a R ). Obviously, \(U_{L}^{+b}\) and \({U_{L}^{0}}\) are two end-points of W1.W0(U L ,a R ) (see Fig. 3). Therefore, if we have an intersection in the (p, u) −plane
then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.9) can be seen as follows. ∙ If \(U \in \mathcal {R}_{1}(U_{L})\) and \(U^{*} \in \mathcal {R}_{3}^{B}(U_{R})\), then the form (3.9) yields
∙ If \(U \in \mathcal {R}_{1}(U_{L})\) and \(U^{*} \in \mathcal {S}_{3}^{B}(U_{R})\), then the form (3.9) yields
∙ If \(U \in \mathcal {S}_{1}(U_{L})\) and \(U^{*} \in \mathcal {R}_{3}^{B}(U_{R})\), then the form (3.9) yields
∙ If \(U \in \mathcal {S}_{1}(U_{L})\) and \(U^{*} \in \mathcal {S}_{3}^{B}(U_{R})\), then the form (3.9) yields
Algorithm to Compute the State U and the Intersection Point \((p^{b}, u^{b}) = \mathcal {W}_{3}^{B}\)(U R ) ∩ W1.W0(U L ,a R ). Similar to Construction A3, but the assignment \(p_{1} = p_{L}^{\#}\) in Step 1 is replaced by \(p_{1} = p_{L}^{+}\).
3.3 Case C: \(U_{R} \in G_{1}^{-} \cup \mathcal {C}^{-}\) and a L > a R
3.3.1 Construction C1
The last part of the Riemann solution can be the stationary wave
i.e.,
where
Take a state \(U = (p, u, \rho , a_{L}) \in \mathcal {W}_{3}({U_{R}^{s}})\) such that U is located below \(U_{R}^{s @}\). Then, the next part of the Riemann solution from the end can be a 3-wave
We call the set
as the backward composite wave curve \({W_{0}^{B}}.{W_{3}^{B}}(U_{R}, a_{L})\) (see Fig. 4). If the wave curve \(\mathcal {W}_{1}(U_{L})\) intersects \({W_{0}^{B}}.{W_{3}^{B}}(U_{R}, a_{L})\) at a point (p, u) in the (p, u)-plane, then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.10) can be seen as follows. ∙ If \(U \in \mathcal {R}_{3}^{B}({U_{R}^{s}})\) and \(U^{*} \in \mathcal {R}_{1}(U_{L})\), then the form (3.10) yields
∙ If \(U \in \mathcal {S}_{3}^{B}({U_{R}^{s}})\) and \(U^{*} \in \mathcal {R}_{1}(U_{L})\), then the form (3.10) yields
∙ If \(U \in \mathcal {R}_{3}^{B}({U_{R}^{s}})\) and \(U^{*} \in \mathcal {S}_{1}(U_{L})\), then the form (3.10) yields
∙ If \(U \in \mathcal {S}_{3}^{B}({U_{R}^{s}})\) and \(U^{*} \in \mathcal {S}_{1}(U_{L})\), then the form (3.10) yields
The composite wave curves: W0B.W3B(U R ,a L ), W0B.S3B.W0B(U R ,a L ) and S3B.W0B(U R ,a L ) in the (p, u)-plane
Algorithm to Compute the Intersection Point \((p, u) = \mathcal {W}_{1}(U_{L}) \cap {W_{0}^{B}}.{W_{3}^{B}}\)(U R ,a L ). Assume that \(U_{R}^{s@}\) is located above the curve \(\mathcal {W}_{1}(U_{L})\) in the (p, u) − plane.
Step 1
Set p1 = 0, \(p_{2} = p_{R}^{s@}\);
Step 2
Compute \(p = \frac {p_{1} + p_{2}}{2}\) and u such that \((p,u) \in \mathcal {W}_{3}^{B}({U_{R}^{s}})\) in the (p, u) −plane;
Step 3
-
If (p, u) belongs to \(\mathcal {W}_{1}(U_{L})\) in the (p, u)-plane, end;
-
If (p, u) is located above \(\mathcal {W}_{1}(U_{L})\) in the (p, u)-plane, set p2 = p and return Step 2;
-
If (p, u) is located below \(\mathcal {W}_{1}(U_{L})\) in the (p, u)-plane, set p1 = p and return Step 2.
3.3.2 Construction C2
Fix a cross section a M between a L and a R . The last part of the Riemann solution can be a stationary wave
where
The next part of the Riemann solution can be the 3-shock wave with zero speed
The next part of the Riemann solution can be again a stationary wave
where
Because these three parts are discontinuity waves with same zero speed, we have a wave collision (resonant case), i.e., W0(URs@b, URs@) ⊕ S3(URs@, URs) ⊕ W0(URs, U R ) is just a discontinuity wave with zero speed
We call the set
as the backward composite wave curve \({W_{0}^{B}}.{S_{3}^{B}}.{W_{0}^{B}}(U_{R}, a_{L})\). It is not difficult to check that \(U_{R}^{s@}\) and \(U_{R}^{@b}\) are two end-points of \({W_{0}^{B}}.{S_{3}^{B}}.{W_{0}^{B}}(U_{R}, a_{L})\) (see Fig. 4). If the wave curve \(\mathcal {W}_{1}(U_{L})\) intersects \({W_{0}^{B}}.{S_{3}^{B}}.{W_{0}^{B}}(U_{R}, a_{L})\) at a point (p, u) in the (p, u)-plane, then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.13) can be seen as follows. ∙ If \(U^{*} \in \mathcal {R}_{1}(U_{L})\), then the form (3.13) yields
∙ If \(U^{*} \in \mathcal {S}_{1}(U_{L})\), then the form (3.13) yields
Algorithm to Compute the Intersection Point \((p,u) = \mathcal {W}_{1}(U_{L}) \cap {W_{0}^{B}}.{S_{3}^{B}}.{W_{0}^{B}}\)(U R ,a L ). Assume that \(U_{R}^{s@}\) is located below \(\mathcal {W}_{1}(U_{L})\) and \(U_{R}^{@b}\) is located above \(\mathcal {W}_{1}(U_{L})\) in the (p, u) −plane.
Step 1
Set a1 = a L , a2 = a R ;
Step 2
Compute \(a_{M} = \frac {a_{1} + a_{2}}{2}\); Compute \({U_{R}^{s}}\) as in (3.11); Compute \(U_{R}^{s@}\); Compute \(U_{R}^{s@b} = (p,u,\)ρ, a L ) as in (3.12);
Step 3
-
If (p, u) belongs to \(\mathcal {W}_{1}(U_{L})\) in the (p, u)-plane, end;
-
If (p, u) is located above \(\mathcal {W}_{1}(U_{L})\) in the (p, u)-plane, set a1 = a M and return Step 2;
-
If (p, u) is located below \(\mathcal {W}_{1}(U_{L})\) in the (p, u)-plane, set a2 = a M and return Step 2.
3.3.3 Construction C3
Take a state \(U = (p,u,\rho , a_{R}) \in \mathcal {S}_{3}^{B}(U_{R})\) such that U is located between \(U_{R}^{@}\) and \({U_{R}^{0}}\), where
Then, the last part of the Riemann solution can be a 3-shock wave with positive speed
(see Lemma 2.1). The next part of the Riemann solution can be a stationary wave
where
We call the set
as the backward composite wave curve \({S_{3}^{B}}.{W_{0}^{B}}(U_{R}, a_{L})\). Obviously, \(U_{R}^{@b}\) and \({U_{R}^{0}}\) are two end-points of \({S_{3}^{B}}.{W_{0}^{B}}(U_{R}, a_{L})\) (see Fig. 4). If the wave curve \(\mathcal {W}_{1}(U_{L})\) intersects \({S_{3}^{B}}.W_{0}(U_{R}, a_{L})\) at a point (pb,ub) in the (p, u)-plane, then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.15) can be seen as follows. ∙ If \(U^{*} \in \mathcal {R}_{1}(U_{L})\), then the form (3.15) yields
∙ If \(U^{*} \in \mathcal {S}_{1}(U_{L})\), then the form (3.15) yields
Algorithm to Compute the State U and the Intersection Point \((p^{b}, u^{b}) = \mathcal {W}_{1}(U_{L})\)\( \cap {S_{3}^{B}}.W_{0}(U_{R}, a_{L})\). Assume that \(U_{R}^{@b}\) is located below \(\mathcal {W}_{1}(U_{L})\) and \({U_{R}^{0}}\) is located above \(\mathcal {W}_{1}(U_{L})\) in the (p, u)-plane.
Step 1
Set \(p_{1} = p_{R}^{@}\), \(p_{2} = {p_{R}^{0}}\);
Step 2
Compute \(p = \frac {p_{1} + p_{2}}{2}\); Compute \(U = (p,u, \rho , a_{R}) \in \mathcal {S}_{3}^{B}(U_{R})\); Compute Ub = (pb,ub,ρb,a L ) as in (3.14);
Step 3
-
If (pb,ub) belongs to \(\mathcal {W}_{1}(U_{L})\) in the (p, u)-plane, end;
-
If (pb,ub) is located above \(\mathcal {W}_{1}(U_{L})\) in the (p, u)-plane, set p2 = p and return Step 2;
-
If (pb,ub) is located below \(\mathcal {W}_{1}(U_{L})\) in the (p, u)-plane, set p1 = p and return Step 2.
3.4 Case D: U R ∈ G2− and a L > a R
3.4.1 Construction D1
The last part of the Riemann solution can be the 3-rarefaction wave
where
The next part of the Riemann solution can be the stationary wave
where
Take any state \(U = (p,u,\rho , a_{L}) \in \mathcal {W}_{3}^{B}(U_{R}^{-s})\) such that U is located below \(U_{R}^{-s @}\). Then, the next part of the Riemann solution can be a 3-wave
We call the set
as the backward composite wave curve \({R_{3}^{B}}.{W_{0}^{B}}.{W_{3}^{B}}(U_{R}, a_{L})\) (see Fig. 5). If the wave curve \(\mathcal {W}_{1}(U_{L})\) intersects \({R_{3}^{B}}.{W_{0}^{B}}.{W_{3}^{B}}(U_{R}, a_{L})\) at a point (p, u) in the (p, u) −plane, then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.16) can be seen as follows. ∙ If \(U \in \mathcal {R}_{3}^{B}(U_{R}^{-s})\) and \(U^{*} \in \mathcal {R}_{1}(U_{L})\), then the form (3.16) yields
∙ If \(U \in \mathcal {R}_{3}^{B}(U_{R}^{-s})\) and \(U^{*} \in \mathcal {S}_{1}(U_{L})\), then the form (3.16) yields
∙ If \(U \in \mathcal {S}_{3}^{B}(U_{R}^{-s})\) and \(U^{*} \in \mathcal {R}_{1}(U_{L})\), then the form (3.16) yields
∙ If \(U \in \mathcal {S}_{3}^{B}(U_{R}^{-s})\) and \(U^{*} \in \mathcal {S}_{1}(U_{L})\), then the form (3.16) yields
The backward composite wave curves: R3B.W0B.W3B(U R ,a L ), R3B.W0B.S3B.W0B(U R ,a L ), and W3B.W0B(U R ,a L ) in the (p, u)-plane
Algorithm to Compute the Intersection Point \((p, u) = \mathcal {W}_{1}(U_{L}) \cap {R_{3}^{B}}.W_{0}.{W_{3}^{B}}\)(U R ,a L ). Similar to case C, since \({R_{3}^{B}}.{W_{0}^{B}}.{W_{3}^{B}}(U_{R}, a_{L}) \equiv {W_{0}^{B}}.{W_{3}^{B}}(U_{R}^{-},\)a L ).
3.4.2 Construction D2
The last part of the Riemann solution can be the 3-rarefaction wave
where
Fix a cross section a M between a L and a R . The next backward part of the Riemann solution can be a stationary wave
where
The next backward part of the Riemann solution can be a 3-shock wave with zero speed
(see Lemma 2.1). The next backward part of the Riemann solution can be again a stationary wave
where
We call the set
as the backward composite wave curve \({R_{3}^{B}}.{W_{0}^{B}}.{S_{3}^{B}}.{W_{0}^{B}}(U_{R}, a_{L})\). It is not difficult to check that \(U_{R}^{-s@}\) and \(U_{R}^{-b}\) are two end-points of \({R_{3}^{B}}.{W_{0}^{B}}.{S_{3}^{B}}.{W_{0}^{B}}(U_{R}, a_{L})\) (see Fig. 5). If the wave curve \(\mathcal {W}_{1}(U_{L})\) intersects \({R_{3}^{B}}.{W_{0}^{B}}.{S_{3}^{B}}.{W_{0}^{B}}(U_{R}, a_{L})\) at a point (p, u) in the (p, u)-plane, then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.17) can be seen as follows. ∙ If \(U^{*} \in \mathcal {R}_{1}(U_{L})\), then the form (3.17) yields
∙ If \(U^{*} \in \mathcal {S}_{1}(U_{L})\), then the form (3.17) yields
Algorithm to Compute the Intersection Point \((p, u) = \mathcal {W}_{1}(U_{L}) \cap {R_{3}^{B}}.{W_{0}^{B}}.{S_{3}^{B}}.{W_{0}^{B}}\)(U R ,a L ). Similar to case C, since \({R_{3}^{B}}.{W_{0}^{B}}.{S_{3}^{B}}.{W_{0}^{B}}(U_{R}, a_{L}) \equiv {W_{0}^{B}}.{S_{3}^{B}}.{W_{0}^{B}}(U_{R}^{-}, a_{L}).\)
3.4.3 Construction D3
Take a state \(U = (p,u,\rho , a_{R}) \in \mathcal {W}_{3}^{B}(U_{R})\) such that \(U \in G_{2}^{-}\), i.e., U is located between \(U_{R}^{-}\) and \({U_{R}^{0}}\), where
Then, the last part of the Riemann solution can be a 3-wave
The next backward part of the Riemann solution can be a stationary wave
where
We call the set
as the backward composite wave curve \({W_{3}^{B}}.{W_{0}^{B}}(U_{R}, a_{L})\). Obviously, \(U_{R}^{-b}\) and \({U_{R}^{0}}\) are two end-points of \({W_{3}^{B}}.{W_{0}^{B}}(U_{R}, a_{L})\) (see Fig. 5). If the wave curve \(\mathcal {W}_{1}(U_{L})\) intersects \({W_{3}^{B}}.W_{0}(U_{R}, a_{L})\) at a point (pb,ub) in the (p, u)-plane, then the Riemann problem for (1.1) has a solution of the form
where
Explicitly, the form (3.18) can be seen as follows. ∙ If \(U \in \mathcal {R}_{3}^{B}(U_{R})\) and \(U^{*} \in \mathcal {R}_{1}(U_{L})\), then the form (3.18) yields
∙ If \(U \in \mathcal {R}_{3}^{B}(U_{R})\) and \(U^{*} \in \mathcal {S}_{1}(U_{L})\), then the form (3.18) yields
∙ If \(U \in \mathcal {S}_{3}^{B}(U_{R})\) and \(U^{*} \in \mathcal {R}_{1}(U_{L})\), then the form (3.18) yields
∙ If \(U \in \mathcal {S}_{3}^{B}(U_{R})\) and \(U^{*} \in \mathcal {S}_{1}(U_{L})\), then the form (3.18) yields
Algorithm to Compute the State U and the Intersection Point \((p^{b}, u^{b}) = \mathcal {W}_{1}(U_{L})\)\( \cap {W_{3}^{B}}.W_{0}(U_{R}, a_{L})\). Similar to Construction C3, but the assignment \(p_{1} = p_{R}^{@}\) in Step 1 is replaced by \(p_{1} = p_{R}^{-}\).
4 Building a van Leer-Type Numerical Scheme
Relying on the constructions of Riemann solutions in the previous section, we are now in a position to build up a van Leer-type scheme to compute the approximate solution of the Cauchy problem for (1.1). Let us set
Then, the system (1.1) can be written in the compact form
Accordingly, given the initial condition
then, the discrete initial values \(({U_{j}^{0}})_{j \in \mathbb {Z}}\) are given by
Suppose \(U^{n} = ({U^{n}_{j}})_{j \in \mathbb {Z}}\) at the time t n is known. Recently, the Godunov-type scheme has been built as follows
where \(U_{\text {Rie}} (\frac {x}{t}; U_{L}, U_{R})\) denotes the exact solution of the Riemann problem for (1.1) corresponding to the Riemann data (U L ,U R ). Now, in this paper, we build a van Leer-type scheme to compute the approximation \(U^{n + 1} = (U_{j}^{n + 1})_{j \in \mathbb {Z}}\) of U(⋅,tn+ 1) as follows: ∙ (Reconstruction Step) From the sequence Un, we construct a piecewise linear function Upl(x) defined by
where the slopes \({S_{j}^{n}} = (s_{j,1}^{n}, s_{j,2}^{n}, s_{j,3}^{n}, s_{j,4}^{n})\) are defined by
∙ (Evolution Step) We solve the Cauchy problem for (4.1) with the initial condition
to find the solution U(⋅,Δt). ∙ (Cell-averaging Step) We project (in the sense of \(\mathbb {L}^{2}\)) the solution U(⋅,Δt) onto the piecewise constant functions, i.e., we set
To make sure that the waves of local Riemann problems centered at xj− 1/2 and xj+ 1/2 do not interact, we use the following C.F.L. condition
In order to derive a more explicit form of the scheme, we integrate (4.1) over the rectangle (xj− 1/2,xj+ 1/2) × (0,Δt). We obtain
Using (4.3), (4.5), and (4.6), we get
Using the midpoint rule, we write
For approximating F(U(xj+ 1/2 ± 0,Δt/2)), we use a predictor-corrector scheme. Following an idea of Hancock (see [17], for example), we define values \(U_{j + 1/2, \pm }^{n + 1/2}\) at time Δt/2 by
where
Then, we solve the Riemann problem of (4.1) at the points xj+ 1/2, \(j \in \mathbb {Z}\) with piecewise constant initial data \(U_{j + 1/2, \pm }^{n + 1/2}\), whose solutions are noted as usual
The values U(xj+ 1/2 ± 0,Δt/2) in (4.9) are substituted by
Next, we approximate the right-hand side of (4.8) as follows.
Thus, the scheme (4.8) becomes
The updated values \(U_{j\pm 1/2, \mp }^{n + 1/2} \) can be interpreted as follows:
since
A similar argument can be made for \(U_{j-1/2, +}^{n + 1/2}\).
To complete the van Leer-type scheme (4.12), we will specify the values URie(0±;U L ,U R ) as follows.
Construction | URie(0−;U L ,U R ) | URie(0+;U L ,U R ) |
|---|---|---|
A1 (3.1) | U L | \({U_{L}^{s}}\) |
A2 (3.4) | U L | \(U_{L}^{s \# b}\) |
A3 (3.6) | U | U b |
B1 (3.7) | \( U_{L}^{+} \) | \(U_{L}^{+s} \) |
B2 (3.8) | \( U_{L}^{+} \) | \(U_{L}^{+ s \# b}\) |
B3 (3.9) | U | U b |
C1 (3.10) | \( {U_{R}^{s}} \) | U R |
C2 (3.13) | \( U_{R}^{s@b}\) | U R |
C3 (3.15) | U b | U |
D1 (3.16) | \( U_{R}^{-s} \) | \(U_{R}^{-}\) |
D2 (3.17) | \(U_{R}^{-s@b} \) | \( U_{R}^{-}\) |
D3 (3.18) | U b | U |
5 Numerical Experiments
This section is devoted to numerical tests by using MATLAB. For each test, by taking γ = 1.4 and CFL = 0.5, we plot the exact solution and its approximations corresponding to the Godunov-type scheme (4.2) and the van Leer-type scheme (4.12) at t = 0.02.
5.1 Approximations of Smooth Stationary Solutions
Test 1
Consider the Cauchy problem for system (1.1) with the initial data given as follows:
where
The exact solution in this test is just the smooth stationary wave
Figure 6 displays exact solution and its approximations for the mesh sizes h = 1/20, h = 1/80 by the van Leer-type scheme (4.12). The errors and orders for different mesh sizes h = 1/20, h = 1/40, h = 1/80, h = 1/160, h = 1/320, h = 1/640, and h = 1/1280 are reported in Table 1. The order of accuracy in this test is close to 2.
Exact solution and approximate solutions for the mesh sizes h = 1/20 and h = 1/80 by the van Leer-type scheme in test 1
5.2 Test for Simple Waves
Test 2
Consider the Riemann problem for system (1.1) with the initial data given as follows
Since p L = p R , u L = u R , and a L = a R , the exact solution for this test is just the 2-contact wave
see the left top of Fig. 7. Figure 7 displays exact solution and its approximations for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme. The errors and orders of accuracy of this test are reported in Table 2. We also evaluate from Table 2 that the L1-order of the van Leer-type scheme is approximately equal to 0.89, while the “second-order” van Leer scheme for usual gas dynamics equations has order of accuracy approximately equal to 2/3 for contact wave. Moreover, Fig. 7 and Table 2 show that the accuracy and the order of accuracy of the van Leer-type scheme are better than the Godunov-type scheme.
Exact solution and approximate solutions for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme in test 2
Test 3
Consider the Riemann problem for system (1.1) with the initial data
We can check that \(U_{L} \in \mathcal {S}_{3}^{B}(U_{R})\), so the exact solution for this test is just the 3-shock wave
(see the left top of Fig. 8). Figure 8 displays exact solution and its approximations for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme. The errors and orders of accuracy of this test are reported in Table 3. We can evaluate from Table 3 that the order is approximately equal to 1.07, while the “second-order” van Leer scheme for usual gas dynamics equations has order of accuracy approximately equal to 1.0 for shock wave. Moreover, we also see from Table 3 that the accuracy and the order of accuracy of the van Leer-type scheme are better than those of the Godunov-type scheme.
Exact solution and approximate solutions for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme in test 3
Test 4
Consider the Riemann problem for system (1.1) with the initial data given as follows
It is not difficult to check that \(U_{R} \in \mathcal {R}_{1}(U_{L})\); thus, the exact solution for this test is just the 1-rarefaction wave
(see the left top of Fig. 9). Figure 9 displays exact solution and its approximations for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme. The errors and orders of accuracy of this test are reported in Table 4. We can evaluate from Table 4 that the order is approximately equal to 1.00. This is consistent with the fact that the “second-order” van Leer scheme for usual gas dynamics equations has order of accuracy approximately equal to 2/3 for contact wave, and the order of accuracy is approximately equal to 1.0 for shock wave.
Exact solution and approximate solutions for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme in test 4
5.3 Tests for the Cases When Initial Data Belongs to Same Supersonic or Subsonic Region
Test 5
Let the Riemann data be given by
The exact solution of this test is computed by Construction D3
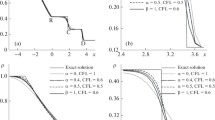
where U∗, Ub, and U are reported in Table 5. Figure 10 displays exact solution and its approximations for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme. We can see from this figure that the approximate solution corresponding to the van Leer-type scheme is closer to the exact solution than the one corresponding to the Godunov-type scheme. The errors and orders for different mesh sizes h = 1/40, h = 1/80, h = 1/160, h = 1/320, h = 1/640, and 1/1280 are reported in Table 6. We can evaluate from this table that the L1-order corresponding to the van Leer-type scheme is approximately equal to 0.98, while the one corresponding to the Godunov-type scheme is approximately equal to 0.64. So, the order of accuracy of the van Leer-type scheme is better than the one of the Godunov-type scheme.
Exact solution and approximate solutions for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme in test 5
5.4 Test Cases for Initial Data in Different Regions Without Resonance (No Wave Collisions)
Test 6
Let the Riemann data be given by
According to Construction C3, the exact solution is
where U∗, Ub, and U are reported in Table 7. Figure 11 displays exact solution and its approximations for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme. The errors and orders for this test are reported in Table 8. We can see from Table 8 and Fig. 11 that the accuracy and the order of accuracy of the van Leer-type scheme are better than those of the Godunov-type scheme.
Exact solution and approximate solutions for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme in test 6
5.5 Test Cases for Resonance
Test 7
Let the Riemann data be given by
The exact solution is constructed by Construction D2:
where U∗, \(U_{R}^{-s@b}\), \(U_{R}^{-s@}\), \(U_{R}^{-s}\), and \(U_{R}^{-}\) are reported in Table 9. Figure 12 displays exact solution and its approximations for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme. The errors and orders for different mesh sizes h = 1/40, h = 1/80, h = 1/160, h = 1/320, h = 1/640, and 1/1280 are reported in Table 10. We can see from Table 10 and Fig. 12 that the accuracy and the order of accuracy of the van Leer-type scheme are better than those of the Godunov-type scheme.
Exact solution and approximate solutions for the mesh size h = 1/640 corresponding to the Godunov-type scheme and the van Leer-type scheme in test 7
6 Conclusions and Discussions
Nonconservativeness often causes lots of inconvenience for standard numerical schemes in approximating solutions. This work deals with numerical approximations of solutions of a nonconservative system. A van Leer-type scheme is built and tested. Tests show that the scheme can work through for all types of data, and of the class of high-order numerical schemes. The proposed scheme can give very desirable results for approximating exact solutions, even in the resonance cases where the exact solution may contain several waves with coinciding shock speeds. Moreover, it has a much better accuracy than the Godunov-type scheme. Note that when we deal with non-smooth solutions, a high-order scheme may give orders of accuracy below 1. Further developments for numerical approximations of solutions of more complicated systems such as multi-phase flow models will be considered.
References
Ambroso, A., Chalons, C., Coquel, F., Galié, T.: Relaxation and numerical approximation of a two-fluid two-pressure diphasic model. Math. Mod. Numer. Anal. 43, 1063–1097 (2009)
Ambroso, A., Chalons, C., Raviart, P. -A.: A Godunov-type method for the seven-equation model of compressible two-phase flow. Comput. Fluids 54, 67–91 (2012)
Audusse, E., Bouchut, F., Bristeau, M. -O., Klein, R., Perthame, B.: A fast and stable well-balanced scheme with hydrostatic reconstruction for shallow water flows. SIAM J. Sci. Comput. 25, 2050–2065 (2004)
Ben-Artzi, M., Falcovitz, J.: Generalized Riemann Problems: from the Scalar Equation to Multidimensional Fluid Dynamics Recent Advances in Computational Sciences, vol. 1–49. World Sci. Publ., Hackensack (2008)
Bermúdez, A., López, X. L., Vázquez-Cendón, M. E.: Numerical solution of non-isothermal non-adiabatic flow of real gases in pipelines. J. Comput. Phys. 323, 126–148 (2016)
Bernetti, R., Titarev, V. A., Toro, E. F.: Exact solution of the Riemann problem for the shallow water equations with discontinuous bottom geometry. J. Comput. Phys. 227, 3212–3243 (2008)
Bouchut, F.: Nonlinear Stability of Finite Volume Methods for Hyperbolic Conservation Laws, and Well-Balanced Schemes for Sources. Frontiers in Mathematics Series, Birkhäuser (2004)
Botchorishvili, R., Perthame, B., Vasseur, A.: Equilibrium schemes for scalar conservation laws with stiff sources. Math. Comput. 72, 131–157 (2003)
Botchorishvili, R., Pironneau, O.: Finite volume schemes with equilibrium type discretization of source terms for scalar conservation laws. J. Comput. Phys. 187, 391–427 (2003)
Castro, C. E., Toro, E. F.: A Riemann solver and upwind methods for a two-phase flow model in non-conservative form. Internat. J. Numer. Methods Fluids 50, 275–307 (2006)
Cuong, D. H., Thanh, M. D.: A Godunov-type scheme for the isentropic model of a fluid flow in a nozzle with variable cross-section. Appl. Math. Comput. 256, 602–629 (2015)
Cuong, D. H., Thanh, M. D.: Building a Godunov-type numerical scheme for a model of two-phase flows. Comput. Fluids 148, 69–81 (2017)
Cuong, D.H., Thanh, M.D.: A well-balanced van Leer-type numerical scheme for shallow water equations with variable topography. Adv. Comput. Math. https://doi.org/10.1007/s10444-017-9521-4
Cuong, D. H., Thanh, M. D.: Constructing a Godunov-type scheme for the model of a general fluid flow in a nozzle with variable cross-section. Appl. Math. Comput. 305, 136–160 (2017)
Cuong, D. H., Thanh, M. D.: A high-resolution van Leer-type scheme for a model of fluid flows in a nozzle with variable cross-section. J. Korean Math. Soc. 54(1), 141–175 (2017)
Dal Maso, G., LeFloch, P. G., Murat, F.: Definition and weak stability of nonconservative products. J. Math. Pures Appl. 74, 483–548 (1995)
Godlewski, E., Raviart, P. A.: Numerical Approximation of Hyperbolic Systems of Conservation Laws. Springer, New York (1996)
Hou, T. Y., LeFloch, P. G.: Why nonconservative schemes converge to wrong solutions. Error Anal. Math. Comput. 62, 497–530 (1994)
Isaacson, E., Temple, B.: Nonlinear resonance in systems of conservation laws. SIAM J. Appl. Math. 52, 1260–1278 (1992)
Isaacson, E., Temple, B.: Convergence of the 22 Godunov method for a general resonant nonlinear balance law. SIAM J. Appl. Math. 55, 625–640 (1995)
Kröner, D., Thanh, M. D.: Numerical solutions to compressible flows in a nozzle with variable cross-section. SIAM J. Numer. Anal. 43, 796–824 (2005)
Kröner, D., LeFloch, P. G., Thanh, M. D.: The minimum entropy principle for fluid flows in a nozzle with discntinuous crosssection. Math. Mod. Numer. Anal. 42, 425–442 (2008)
LeFloch, P. G.: Shock waves for nonlinear hyperbolic systems in nonconservative form. Institute Math. Appl., Minneapolis. Preprint 593 (1989)
LeFloch, P. G., Thanh, M. D.: The Riemann problem for fluid flows in a nozzle with discontinuous cross-section. Comm. Math. Sci. 1, 763–797 (2003)
LeFloch, P. G., Thanh, M. D.: The Riemann problem for shallow water equations with discontinuous topography. Comm. Math. Sci. 5, 865–885 (2007)
LeFloch, P. G., Thanh, M. D.: A Godunov-type method for the shallow water equations with variable topography in the resonant regime. J. Comput. Phys. 230, 7631–7660 (2011)
Marchesin, D., Paes-Leme, P. J.: A Riemann problem in gas dynamics with bifurcation. Hyperbolic partial differential equations III. Comput. Math. Appl. (Part A) 12, 433–455 (1986)
Rosatti, G., Begnudelli, L.: The Riemann Problem for the one-dimensional, free-surface shallow water equations with a bed step: theoretical analysis and numerical simulations. J. Comput. Phys. 229, 760–787 (2010)
Schwendeman, D. W., Wahle, C. W., Kapila, A. K.: The Riemann problem and a high-resolution Godunov method for a model of compressible two-phase flow. J. Comput. Phys. 212, 490–526 (2006)
Saurel, R., Abgrall, R.: A multi-phase Godunov method for compressible multifluid and multiphase flows. J. Comput. Phys. 150, 425–467 (1999)
Tian, B., Toro, E. F., Castro, C. E.: A path-conservative method for a five-equation model of two-phase flow with an HLLC-type Riemann solver. Comput. Fluids 46, 122–132 (2011)
Thanh, M. D.: The Riemann problem for a non-isentropic fluid in a nozzle with discontinuous cross-sectional area. SIAM J. Appl. Math. 69, 1501–1519 (2009)
Thanh, M. D.: A phase decomposition approach and the Riemann problem for a model of two-phase flows. J. Math. Anal. Appl. 418, 569–594 (2014)
Thanh, M. D., Cuong, D. H.: Existence of solutions to the Riemann problem for a model of two-phase flows. Elect. J. Diff. Eqs. 2015(32), 1–18 (2015)
Acknowledgements
The authors are thankful to the referee for his/her very constructive comments and fruitful discussions.
Funding
This research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 101.02-2016.15.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Thanh, M.D., Cuong, D.H. A van Leer-Type Numerical Scheme for the Model of a General Fluid Flow in a Nozzle with Variable Cross Section. Acta Math Vietnam 43, 503–547 (2018). https://doi.org/10.1007/s40306-017-0242-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40306-017-0242-z