Disjunctive Ideals of Distributive Lattices

Abstract

Disjunctive ideals and strongly disjunctive ideals are introduced in lattices and normal lattices are also characterized in terms of annihilators. Some properties of disjunctive ideals are studied. The concept of normal prime ideals is introduced and their properties are studied. Some equivalent conditions are derived for the class of all strongly disjunctive ideals to become a sublattice of the ideal lattice.

1 Introduction

In 1968, the theory of relative annihilators was introduced in lattices by Mark Mandelker [9] and he characterized distributive lattices in terms of their relative annihilators. Later, many authors introduced the concept of annihilators in the structures of rings as well as lattices and characterized several algebraic structures in terms of annihilators. Speed [8] and Cornish [4, 5] made an extensive study of annihilators in distributive lattices. The main aim of this paper is to study some further properties of annihilators in the form of disjunctive ideals of distributive lattices.

In this note, the concepts of disjunctive ideals and strongly disjunctive ideals are introduced in terms of annihilators. Normal lattices are once again characterized in terms of annihilators. A set of equivalent conditions are derived for every ideal of a lattice to become a disjunctive ideal. The notion of normal prime ideals is introduced and proved that every normal prime ideal is a disjunctive ideal as well as a minimal prime ideal. Some properties of disjunctive ideals are observed with respect to inverse homomorphic images and cartesian products. The notion of weakly normal lattices is introduced and established a set of equivalent conditions for every weakly normal lattice to become a normal lattice. A set of equivalent conditions is derived for every ideal of a lattice to become a strongly disjunctive ideal. Finally, a set of equivalent conditions is deduced for the class of all strongly disjunctive ideals of a distributive lattice to become a sublattice of the ideal lattice.

2 Preliminaries

The reader is referred to [2] and [3] for the elementary notions and notations of distributive lattices. However, some of the preliminary definitions and results are presented for the ready reference of the reader.

For any element a of a distributive lattice (L, ∨, ∧, 0) with zero, we define the annihilator of a by the set (a)^∗={x ∈ L | x ∧ a = 0} and the principle ideal generated by a is written as (a]. The set $\mathcal {I}(L)$ of all ideals of (L, ∨,∧,0) forms a complete distributive lattice. A proper ideal P of a lattice L is called prime if for any x, y ∈ L, x ∧ y ∈ P implies x ∈ P or y ∈ P. A prime ideal is called minimal if it is the minimal element in the partial ordered set of all prime ideals. A prime ideal P is minimal if and only if to each x ∈ P there exists y ∉ P such that x ∧ y = 0. A proper ideal M of a lattice is called maximal if there exists no proper ideal N such that M ⊆ N. The properties of minimal prime ideals are exclusively studied by J. Kist [7] in commutative semi-groups and later these ideals are used by Cornish [4].

A distributive lattice with 0 is called normal [4] if every prime ideal contains a unique minimal prime ideal. A distributive lattice L with 0 is normal if and only if for all x, y ∈ L, (x)^∗ ∨ (y)^∗ = L whenever x ∧ y = 0. Normal lattices were extensively studied by W.H. Cornish [4]. In his study, he characterized normal lattices with the help of annihilators and minimal prime ideals. Some examples of normal lattices are as follows:(1) the lattice of all zero sets in a completely regular space, and (2) the generalized stone lattices. Example (1) is considered in [1, pp. 107, 108] and quoted by Cornish in [4, pp. 214]. Example (2) is considered by Katrinak [6] and it is proved in [5, Proposition 5.4]. Throughout this note, L stands for a bounded distributive lattice with 0 and 1, unless otherwise mentioned.

3 Disjunctive ideals

In this section, the concept of disjunctive ideals is introduced in lattices. Normal lattices are characterized. A set of equivalent conditions is derived for every ideal of a lattice to become a disjunctive ideal.

Definition 3.1

For any non-empty subset A of L, define

$$A^{\circ } = \{x\in L~|~(a)^{*}\vee (x)^{*} = L\text{ for all }a\in A\}. $$

Clearly {0}^∘ = L and L ^∘={0}. For any a ∈ L, we denote ({a})^∘ by (a)^∘. Then it is obvious that (0)^∘ = L and (1)^∘={0}.

Proposition 3.2

For any non-empty subset A of L, A ^∘ is an ideal in L.

Proof

Clearly 0 ∈ A ^∘. Let x, y ∈ A ^∘. For any a ∈ A, we get (x ∨ y)^∗ ∨ (a)^∗={(x)^∗∩(y)^∗}∨(a)^∗={(x)^∗ ∨ (a)^∗}∩{(y)^∗ ∨ (a)^∗}=L ∩ L = L. Hence x ∨ y ∈ A ^∘. Again, let x ∈ A ^∘ and y ≤ x. Then we get (x)^∗ ∨ (a)^∗ = L for any a ∈ A and (x)^∗⊆(y)^∗. For any c ∈ A, we then get L = (x)^∗ ∨ (a)^∗⊆(y)^∗ ∨ (a)^∗. Hence y ∈ A ^∘. Therefore A ^∘ is an ideal in L. □

The following lemma is a direct consequence of the above definition.

Lemma 3.3

For any two non-empty subsets A and B of L, we have the following:

• 1. $A^{\circ } = \bigcap \limits _{a\in A}(a)^{\circ },$,

• 2. A ∩ A ^∘ = {0},,

• 3. A ⊆ B implies B^∘ ⊆A ^∘,,

• 4. A ⊆ A ^∘∘,,

• 5. A ^∘∘∘ = A ^∘,,

• 6. A ^∘ = L if and only if A = {0},.

In case of ideals, we have the following result.

Proposition 3.4

For any two ideals I, J of L, (I∨J) ^∘ = I ^∘ ∩J ^∘.

Proof

Clearly (I ∨ J)^∘ ⊆ I ^∘∩J ^∘. Conversely, let x ∈ I ^∘∩J ^∘. Let c ∈ I ∨ J be an arbitrary element. Then c = i ∨ j for some i ∈ I and j ∈ J. Now (x)^∗ ∨ (c)^∗ = (x)^∗ ∨ (i ∨ j)^∗ = (x)^∗∨{(i)^∗∩(j)^∗}={(x)^∗ ∨ (i)^∗}∩{(x)^∗ ∨ (j)^∗}=L ∩ L = L. Therefore x ∈ (I ∨ J)^∘. □

The following corollary is a direct consequence of the above results.

Corollary 3.5

For any a, b ∈ L, we have the following:

• 1. a ≤ b implies (b)^∘ ⊆ (a) ^∘,

• 2. (a ∨ b)^∘ = (a) ^∘ ∩ (b) ^∘,

• 3. (a)^∘ = L if and only if a = 0.

For any ideal I of a distributive lattice L, it can be easily observed that I ^∘ ⊆ I ^∗. However, we derive a set of equivalent conditions for every ideal to satisfy the reverse inclusion which is not true in general.

Theorem 3.6

The following conditions are equivalent in a lattice L.

• 1. L is normal,

• 2. For any ideals I, J of L, I ∩ J = {0} if and only if I ⊆ J ^∘,

• 3. For any ideal I of L, I ^∘ = I ^∗,

• 4. For any a ∈ L, (a) ^∘ = (a) ^∗.

Proof

• (1)⇒(2): Assume that L is normal. Suppose I ∩ J = {0}. Let x ∈ I. For any a ∈ J, we get x ∧ a ∈ I ∩ J = {0}. Hence x ∧ a = 0. Since L is normal, we get (x)^∗ ∨ (a)^∗ = L. Thus it concludes that x ∈ J ^∘. Therefore I ⊆ J ^∘. Conversely, suppose that I ⊆ J ^∘. Let x ∈ I ∩ J. Then x ∈ I ⊆ J ^∘. Hence x ∈ J ∩ J ^∘={0}. Therefore I ∩ J = {0}.

• (2)⇒(3): Assume the condition (2). Let I be an ideal of L. Clearly I ^∘ ⊆ I ^∗. Conversely, let x ∈ I ^∗. Then, for any a ∈ I, we have the following consequence:

  $$\begin{array}{@{}rcl@{}} x\wedge a = 0 & \Rightarrow & (x]\cap (a] = (0]\\[.5pt] & \Rightarrow & (x]\subseteq (a)^{\circ }\hspace{1 cm}\text{ by condition (2) }\\[.5pt] & \Rightarrow & (x]\subseteq \bigcap \limits_{a\in I}(a)^{\circ }\\[.5pt] & \Rightarrow & x\in I^{\circ }. \end{array} $$

  Hence it concludes I ^∗ ⊆ I ^∘. Therefore I ^∗ = I ^∘.

• (3)⇒(4): It is obvious.

• (4)⇒(1): Let x, y ∈ L be such that x ∧ y = 0. Then x ∈ (y)^∗ = (y)^∘. Hence (x)^∗ ∨ (y)^∗ = L. Therefore L is normal.

□

The concept of disjunctive ideals is now introduced in lattices.

Definition 3.7

An ideal I of a lattice L is called disjunctive if for all x, y ∈ L, (x)^∘ = (y)^∘ and x ∈ I imply that y ∈ I.

Clearly, each (x)^∘, x ∈ L is a disjunctive ideal. It is evident that any ideal I is a disjunctive ideal if it satisfies (x)^∘∘ ⊆ I for all x ∈ I. By Theorem 3.6, it can be easily observed that the disjunctive ideals are equivalent to α-ideals of Cornish [4] in the case of normal lattices.

Theorem 3.8

The following conditions are equivalent in a lattice L:

• 1. Every ideal is a disjunctive ideal.

• 2. Every principal ideal is a disjunctive ideal.

• 3. Every prime ideal is a disjunctive ideal.

• 4. For a, b ∈ L,(a) ^∘ = (b) ^∘ implies (a] = (b].

Proof

• (1)⇒(2): It is clear.

• (2)⇒(3): Assume that every principal ideal is a disjunctive ideal. Let P be a prime ideal of L. Suppose (a)^∘ = (b)^∘ and a ∈ P. Then clearly (a]⊆P. Since (a)^∘ = (b)^∘ and (a] is a disjunctive ideal, we get that b ∈ (a]⊆P. Therefore, P is a disjunctive ideal.

• (3)⇒(4): Assume that every prime ideal of A is a disjunctive ideal. Let a, b ∈ A such that (a)^∘ = (b)^∘. Suppose (a]≠(b]. Without loss of generality assume that $(a]\nsubseteq (b]$. Let ${\Sigma } = \{~I\in \mathcal {I}(L)~|~ a\wedge b\in I\text { and } a\notin I~\}$. It is clear that (a ∧ b] ∈ Σ. Let {I _i } _i∈Δ be a chain in Σ. Then clearly $\bigcup _{i\in {\Delta }} I_{i}$ is an ideal, $a\wedge b\in \bigcup _{i\in {\Delta }} I_{i}$ and $a\notin \bigcup _{i\in {\Delta }} I_{i}$. Hence, $\bigcup _{i\in {\Delta }} I_{i}$ is an upper bound for {I _i } _i∈Δ in Σ. Therefore, by Zorn’s Lemma, Σ has a maximal element, say P. We now prove that P is a prime ideal in L. Let x, y ∈ L such that x ∉ P and y ∉ P. Hence P⊂P∨(x] and P⊂P∨(y]. Therefore, by the maximality of P, P∨(x] and P∨(y] are not in Σ. Hence a ∈ P∨(x] and a ∈ P∨(y]. So we have the following consequence

  $$\begin{array}{@{}rcl@{}} a & \in & \{~P\vee (x]~\}\cap \{~P\vee (y]~\}\\ & = & P\vee \{~(x]\cap (y]~\}\\ & = & P\vee (x\wedge y] \end{array} $$

  If x ∧ y ∈ P, then a ∈ P∨(x ∧ y]=P, which is a contradiction to that a ∉ P. Thus we get x ∧ y ∉ P. Hence P is a prime ideal. Therefore, by hypothesis (3), we can get that P is a disjunctive ideal of L. Since P ∈ Σ, we get that a ∧ b ∈ P and a ∉ P. Since P is prime, we get b ∈ P. Since b ∈ P and P is disjunctive, we get a ∈ P, which is a contradiction to a ∉ P. Therefore, it concludes that (a] = (b].

• (4)⇒(1): Assume the condition (4). Let I be an arbitrary ideal of L. Suppose a, b ∈ L are such that (a)^∘ = (b)^∘. Then by condition (4), we get (a] = (b]. Suppose a ∈ I. Then b ∈ (b] = (a]⊆I. Therefore I is a disjunctive ideal of L.

□

The notion of normal prime ideal is now introduced in a lattice.

Definition 3.9

A prime ideal P of a lattice L is called a normal prime ideal if to each x ∈ P, there exists x ^′∉P such that (x)^∘ ∨ (x ^′)^∘ = L.

Proposition 3.10

Every normal prime ideal is a minimal prime ideal.

Proof

Let P be a normal prime ideal of a lattice L. Suppose x ∈ P. Since P is normal, there exists x ^′∉P such that (x)^∘ ∨ (x ^′)^∘ = L. Hence, we get L = (x)^∘ ∨ (x ^′)^∘⊆(x ∧ x ^′)^∘. Thus by Corollary 3.5(3), we get that x ∧ x ^′=0. Therefore, P is a minimal prime ideal of L. □

In general, the converse of the above Proposition 3.10 is not true. It can be seen in the following example.

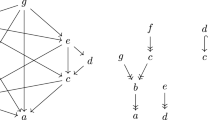
Example 3.11

Consider the following distributive lattice L = {0, a, b, c, 1} whose Hasse diagram is given by:

Consider the prime ideal P = {0, a}. It can be easily observed that P is a minimal prime ideal but not a normal prime ideal.

However, in the following, we derive a sufficient condition for every minimal prime ideal to become a normal prime ideal.

Proposition 3.12

If L is a normal lattice, then every minimal prime ideal of L is a normal prime ideal.

Proof

Assume that L is normal and P a minimal prime ideal of L. Let x ∈ P. Then there exists x ^′∉P such that x ∧ x ^′=0. Since L is normal, we get (x)^∘ ∨ (x ^′)^∘ = (x)^∗ ∨ (x ^′)^∗ = L. Therefore, P is normal in L. □

Proposition 3.13

Let P be a normal prime ideal of a lattice L. Then for each x ∈ L, we have the following property:

$$x\notin P~\Leftrightarrow ~(x)^{\circ }\subseteq P.$$

Proof

Let P be a normal prime ideal of L and x ∈ L. Suppose x ∉ P. Then clearly (x)^∘ ⊆ P. Conversely, assume that (x)^∘ ⊆ P. Suppose x ∈ P. Since P is normal, there exists x ^′∉P such that (x)^∘ ∨ (x ^′)^∘ = L. Hence L = (x)^∘ ∨ (x ^′)^∘⊆(x)^∗ ∨ (x ^′)^∗. Then x ^′∈(x)^∘ ⊆ P, which is a contradiction. Therefore x ∉ P. □

Theorem 3.14

Every normal prime ideal is a disjunctive ideal.

Proof

Let P be a normal prime ideal of L. Suppose x, y ∈ L are such that (x)^∘ = (y)^∘ and x ∈ P. Since P is normal, there exists x ^′∉P such that (x)^∘ ∨ (x ^′)^∘ = L. Hence L = (x)^∘ ∨ (x ^′)^∘ = (y)^∘ ∨ (x ^′)^∘⊆(y ∧ x ^′)^∘. Hence by Corollary 3.5(3), we get y ∧ x ^′ = 0 ∈ P. Since P is prime and x ^′∉P, it yields that y ∈ P. Therefore, P is a disjunctive ideal. □

In what follows, we prove a necessary and sufficient condition for the inverse image of a disjunctive ideal to become again a disjunctive ideal.

Theorem 3.15

Let f be a homomorphism of a lattice (L, ∨, ∧) onto another lattice (L ^′ , ∨, ∧). If J is a disjunctive ideal of L ^′ , then the following conditions are equivalent:

• 1. f ⁻¹ (J) is a disjunctive ideal in L,

• 2. For each x ∈ L ^′ , f ⁻¹ ((x) ^∘ ) is a disjunctive ideal in L.

Proof

• (1)⇒(2): Assume that f ⁻¹(J) is a disjunctive ideal in L for each disjunctive ideal J of L ^′. Since (x)^∘ is a disjunctive ideal in L ^′ for each x ∈ L ^′, we get from (1) that f ⁻¹((x)^∘) is a disjunctive ideal in L.

• (2)⇒(1): Assume that f ⁻¹((x)^∘) is a disjunctive ideal in L for each x ∈ L ^′. Let J be a disjunctive ideal of L ^′. Then clearly f ⁻¹(J) is an ideal in L. Let x, y ∈ L be such that (x)^∘ = (y)^∘ and x ∈ f ⁻¹(J). Then f(x)∈J. For any a ∈ L ^′, we get the following consequence:

  $$\begin{array}{@{}rcl@{}} a\in (f(x))^{\circ } & \Leftrightarrow & f(x)\in (a)^{\circ }\\ & \Leftrightarrow & x\in f^{-1}((a)^{\circ })\\ & \Leftrightarrow & y\in f^{-1}((a)^{\circ })\hspace{0.5 cm}\text{ since }f^{-1}((a)^{\circ })\text{ is disjunctive in }L \\ & \Leftrightarrow & f(y)\in (a)^{\circ }\\ & \Leftrightarrow & a\in (f(y))^{\circ }. \end{array} $$

  Hence, it concludes (f(x))^∘ = (f(y))^∘. Since f(x)∈J and J is a disjunctive ideal, we get f(y)∈J. Hence y ∈ f ⁻¹(J). Therefore f ⁻¹(J) is a disjunctive ideal in L.

□

We now discuss some properties of direct products of disjunctive ideals of lattices. First, we need the following lemma whose proof is routine.

Lemma 3.16

Let L ₁ and L ₂ be two distributive lattices. For any a∈L ₁ , b ∈ L ₂ and (a,b)∈L ₁ × L ₂ , we have the following:

• 1. (a, b) ^∗ = (a) ^∗ ×(b) ^∗,

• 2. (a,b) ^∗ ∨(c, d) ^∗ = (a∨c, b∨d) ^∗,

• 3. (a,b) ^∘ = (a) ^∘ × (b) ^∘.

Theorem 3.17

Let L=L ₁ × L ₂ be the product of the distributive lattices L ₁ and L ₂ . If I ₁ and I ₂ are disjunctive ideals of L ₁ and L ₂ , respectively, then I ₁ ×I ₂ is a disjunctive ideal of the product lattice L ₁ × L ₂ . Conversely, every disjunctive ideal of L ₁ × L ₂ can be expressed as I = I ₁ ×I ₂ where I ₁ and I ₂ are disjunctive ideals of L ₁ and L ₂ , respectively.

Proof

Let I ₁ and I ₂ be the disjunctive ideals of L ₁ and L ₂, respectively. Then clearly, I ₁×I ₂ is an ideal of L ₁×L ₂. Let a, c ∈ L ₁ and b, d ∈ L ₂ be such that (a, b)^∘ = (c, d)^∘ and (a, b)∈I ₁×I ₂. Then a ∈ I ₁ and b ∈ I ₂. Since (a, b)^∘ = (c, d)^∘, we get (a)^∘×(b)^∘ = (c)^∘×(d)^∘ and hence (a)^∘ = (c)^∘ and (b)^∘ = (d)^∘. Since I ₁ is a disjunctive ideal and a ∈ I ₁, we get that c ∈ I ₁. Similarly, we get d ∈ I ₂. Hence it concludes that (c, d)∈I ₁×I ₂. Therefore, I ₁×I ₂ is a disjunctive ideal in L ₁×L ₂.

Conversely, let I be a disjunctive ideal of L ₁×L ₂. Consider I ₁={a ∈ L ₁ | (a, b)∈I for some b ∈ L ₂}. Clearly, I ₁ is an ideal in L ₁. Let x, y ∈ L ₁ be such that (x)^∘ = (y)^∘ and x ∈ I ₁. Then (x, a)∈I for some a ∈ L ₂. Since (x)^∘ = (y)^∘, we get (x, a)^∘ = (x)^∘×(a)^∘ = (y)^∘×(a)^∘ = (y, a)^∘. Since I is a disjunctive ideal in L ₁×L ₂, we get (y, a)∈I. Hence it concludes that y ∈ I ₁. Therefore, I ₁ is a disjunctive ideal in L ₁. Similarly, we can obtain that I ₂ is a disjunctive ideal in L ₂.

We now prove that I = I ₁×I ₂. Clearly, I ⊆ I ₁×I ₂. Conversely, let (a ₁, a ₂)∈I ₁×I ₂. Then a ₁∈I ₁ and a ₂∈I ₂. Hence (a ₁, b ₁)∈I and (b ₂, a ₂)∈I for some b ₂∈L ₁ and b ₁∈L ₂. Hence, we get (a ₁, 0) = (1, 0)∧(a ₁, b ₁)∈I and also (0, a ₂)=(0,1)∧(b ₂, a ₂)∈I. Thus (a ₁, a ₂)=(a ₁,0)∨(0, a ₂)∈I. Therefore I ₁×I ₂ ⊆ I. □

We now introduce the concept of weakly normal lattices.

Definition 3.18

A distributive lattice L with 0 is called weakly normal if it satisfies (x)^∗ ∨ (y)^∗ = (x)^∘ ∨ (y)^∘ for all x, y ∈ L.

It is evident that every normal lattice is weakly normal. In general, the converse is not true. However, in the following, a set of equivalent conditions is derived for every weakly normal lattice to become normal.

Theorem 3.19

Let L be a weakly normal lattice. Then the following conditions are equivalent:

• 1. L is normal,

• 2. For x, y ∈ L, (x) ^∘ ∨(y) ^∘ = (x ∧ y) ^∘,

• 3. For x, y ∈ L, x ∧ y = 0 implies (x) ^∘ ∨(y) ^∘ = L.

Proof

• (1)⇒(2): Let L be a weakly normal lattice. Assume that L is a normal lattice. Let x, y ∈ L. Since L is a normal lattice, by Theorem 3.6, we get (x)^∘ ∨ (y)^∘ = (x)^∗ ∨ (y)^∗ = (x ∧ y)^∗ = (x ∧ y)^∘.

• (2)⇒(3): It is clear.

• (3)⇒(1): Assume that (3) is valid. Let x, y ∈ L be such that x ∧ y = 0. Then L = (x)^∘ ∨ (y)^∘⊆(x)^∗ ∨ (y)^∗. Hence L is normal.

□

4 Strongly disjunctive ideals

In this section, a concept of strongly disjunctive ideals is introduced in lattices. A set of equivalent conditions is derived for the class of all strongly disjunctive ideals to become a sublattice of the ideal lattice.

Definition 4.1

For any ideal I of a lattice L, define β(I) as follows:

$$\beta (I) = \{x\in L~|~(x)^{\circ }\vee I = L\}.$$

The following lemma is an immediate consequence of the above definition.

Lemma 4.2

For any ideals I, J of L, it holds that

• 1. β (I) ⊆ I,

• 2. I⊆J implies β(I)⊆β(J),

• 3. β(I∩J)=β(I)∩β(J).

Proof

The proof of the identities (2) and (3) is routine. It is sufficient to prove the identity (1). For that, let x ∈ β(I). Then (x)^∘ ∨ I = L. Hence x = a ∨ b for some a ∈ (x)^∘⊆(x)^∗ and b ∈ I. Then we get x ∧ a = 0 and x ∧ b ∈ I. Thus, we can conclude that x = x ∧ x = x∧(a ∨ b)=(x ∧ a)∨(x ∧ b)=0∨(x ∧ b)=x ∧ b ∈ I. Therefore β(I) ⊆ I. □

Proposition 4.3

For any ideal I of a lattice L, β(I) is an ideal in L.

Proof

Clearly 0 ∈ β(I). Let x, y ∈ β(I). Then (x)^∘ ∨ I = (y)^∘ ∨ I = L. Hence (x ∨ y)^∘ ∨ I = {(x)^∘∩(y)^∘}∨I = {(x)^∘ ∨ I}∩{(y)^∘ ∨ I}=L. Hence x ∨ y ∈ β(I). Again let x ∈ β(I) and y ≤ x. Then L = (x)^∘ ∨ I⊆(y)^∘ ∨ I. Thus y ∈ β(I). Therefore, β(I) is an ideal in L. □

Definition 4.4

An ideal I of a lattice L is called a strongly disjunctive ideal if I = β(I).

Proposition 4.5

Every strongly disjunctive ideal is a disjunctive ideal.

Proof

Let I be a strongly disjunctive ideal of a lattice L. Let x, y ∈ L be such that (x)^∘ = (y)^∘ and x ∈ I = β(I). Then it is clear that (x)^∘ ∨ I = L. Hence (y)^∘ ∨ I = L and so y ∈ β(I)=I. Thus I is a disjunctive ideal of L. □

In general, the converse of the above proposition is not true. However, we can derive a set of equivalent conditions for every ideal of a lattice to become strongly disjunctive.

Theorem 4.6

Consider the following conditions in a lattice L:

• 1. Every prime ideal is normal.

• 2. Every ideal is strongly disjunctive.

• 3. Every prime ideal is strongly disjunctive.

Then (1)⇒(2)⇒(3). If L is a weakly normal lattice, then all the above conditions are equivalent.

Proof

• (1)⇒(2): Assume that every prime ideal is normal. Let I be an ideal of L. Clearly β(I) ⊆ I. Conversely, let x ∈ I. Suppose (x)^∘ ∨ I ≠ L. Then there exists a prime ideal P such that (x)^∘ ∨ I ⊆ P. Hence (x)^∘ ⊆ P and x ∈ I ⊆ P. Since P is normal and (x)^∘ ⊆ P, by Proposition 3.13, we get that x ∉ P, which is a contradiction to that x ∈ P. Hence (x)^∘ ∨ I = L. Thus it yields that x ∈ β(I). Therefore, I is strongly disjunctive.

• (2)⇒(3): It is obvious.

• (3)⇒(1): Suppose that L is weakly normal. Assume that every prime ideal is strongly disjunctive. Let P be a prime ideal of L. Then by our assumption, β(P)=P. Let x ∈ P. Then (x)^∘ ∨ P = L. Hence a ∨ b = 1 for some a ∈ (x)^∘ and b ∈ P. Since a ∈ (x)^∘ and L is weakly normal, we get (x)^∘ ∨ (a)^∘ = (x)^∗ ∨ (a)^∗ = L. Suppose a ∈ P. Then 1=a ∨ b ∈ P, which is a contradiction. Therefore, a ∉ P and hence P is a normal prime ideal.

□

Theorem 4.7

The following conditions are equivalent in a lattice L:

• 1. (x)^∘ ∨(x) ^∘∘ = L for all x ∈ L,

• 2. Every ideal of the form I = I ^∘∘ is strongly disjunctive,

• 3. For each x ∈ L, (x) ^∘∘ is strongly disjunctive.

Proof

• (1)⇒(2): Assume that the condition (1) holds in L. Let I be an ideal in L such that I = I ^∘∘. Clearly β(I) ⊆ I. Conversely, let x ∈ I. Clearly (x)^∘∘ ⊆ I ^∘∘. Hence we get L = (x)^∘ ∨ (x)^∘∘⊆(x)^∘ ∨ I ^∘∘ = (x)^∘ ∨ I. Thus it yields that x ∈ β(I). Therefore, I is strongly disjunctive.

• (2)⇒(3): It is obvious.

• (3)⇒(1): Assume the condition (3). Then we get β((x)^∘∘)=(x)^∘∘. Since x ∈ (x)^∘∘, we get (x)^∘ ∨ (x)^∘∘ = L. Hence the proof is complete.

□

Definition 4.8

For any maximal ideal M of a lattice L, define ${\Omega } (M) \,=\, \{x\in L~|~(x)^{\circ }\!\nsubseteq \! M\}$.

Lemma 4.9

For any maximal ideal M,Ω(M) is an ideal contained in M.

Proof

Clearly 0 ∈ Ω(M). Let x, y ∈ Ω (M). Then $(x)^{\circ }\nsubseteq M$ and $(y)^{\circ }\nsubseteq M$. Since M is prime, we get $(x\vee y)^{\circ } = (x)^{\circ }\cap (y)^{\circ }\nsubseteq M$. Hence x ∨ y ∈ Ω (M). Let x ∈ Ω (M) and y ≤ x. Then $(x)^{\circ }\nsubseteq M$ and (x)^∘⊆(y)^∘. Thus we get $(y)^{\circ }\nsubseteq M$ and hence y ∈ Ω (M). Therefore, Ω(M) is an ideal of L. Now, let x ∈ Ω (M). Then $(x)^{\circ }\nsubseteq M$. Hence there exists a ∈ (x)^∘ such that a ∉ M. Since a ∈ (x)^∘, we get L = (a)^∗ ∨ (x)^∗⊆(a ∧ x)^∗. Thus a ∧ x = 0 ∈ M. Since M is prime and a ∉ M, it concludes that x ∈ M. Therefore Ω(M) ⊆ M. □

By μ we denote the set of all maximal ideals of a lattice L. For any ideal I of a lattice L, let μ(I)={M ∈ μ | I ⊆ M}.

Theorem 4.10

For any ideal I of a lattice $L, \beta (I) = \bigcap _{M\in \mu (I)}{\Omega } (M)$.

Proof

Let x ∈ β(I) and I ⊆ M where M ∈ μ. Then L = (x)^∘ ∨ I⊆(x)^∘ ∨ M. Suppose (x)^∘ ⊆ M, then M = L, which is a contradiction. Hence $(x)^{\circ }\nsubseteq M$. Thus x ∈ Ω (M) for all M ∈ μ(I). Therefore $\beta (I)\subseteq \bigcap _{M\in \mu (I)}{\Omega } (M)$. Conversely, let $x\in \bigcap _{M\in \mu (I)}{\Omega } (M)$. Then x ∈ Ω (M) for all M ∈ μ(I). Suppose (x)^∘ ∨ I ≠ L. Then there exists a maximal ideal M ₀ such that (x)^∘ ∨ I ⊆ M ₀. Hence (x)^∘ ⊆ M ₀ and I ⊆ M. Since I ⊆ M ₀, by hypothesis, we get x ∈ Ω (M ₀). Hence $(x)^{\circ }\nsubseteq M_{0}$, which is a contradiction. Therefore (x)^∘ ∨ I = L. Thus x ∈ β(I). Hence $\bigcap _{M\in \mu (I)}{\Omega } (M)\subseteq \beta (I)$. □

By the above Theorem 4.10, it can be easily observed that β(I)⊆Ω(M) for every M ∈ μ(I). In what follows, a set of equivalent conditions is derived for the class of all strongly disjunctive ideals of a lattice to become a sublattice of the ideal lattice $\mathcal {I}(L)$ of the lattice L.

Theorem 4.11

The following conditions are equivalent in a lattice L:

• 1. For any M ∈ μ, Ω(M) is maximal,

• 2. For any $I, J\in \mathcal {I}(L)$ , I∨J = L implies β(I) ∨ β(J) = L,

• 3. For any $I, J\in \mathcal {I}(L)$ , β(I)∨β(J)=β(I∨J),

• 4. For any two distinct maximal ideals M, N, Ω(M) ∨ Ω(N) = L,

• 5. For any M ∈ μ, M is the unique member of μ such that Ω(M) ⊆ M.

Proof

• (1)⇒(2): Assume the condition (1). Then it is clear that Ω(M)=M for all M ∈ μ. Let $I, J\in \mathcal {I}(L)$ be such that I ∨ J = L. Suppose β(I)∨β(J)≠L. Then there exists a maximal ideal M such that β(I)∨β(J) ⊆ M. Hence β(I) ⊆ M and β(J) ⊆ M. Now

  $$\begin{array}{@{}rcl@{}} \beta (I)\subseteq M & \Rightarrow & \bigcap \limits_{M\in \mu (I)} {\Omega} (M)\subseteq M\\ & \Rightarrow & {\Omega} (M_{i})\subseteq M\hspace{0.1 cm}\mathrm{ for\, some } \, M_{i}\in \mu (I)\hspace{0.1 cm}(\mathrm{since }\, M \, \mathrm{ is\, prime})\\ & \Rightarrow & M_{i}\subseteq M\hspace{0.8 cm}\mathrm{ by\, condition (1) }\\ & \Rightarrow & I\subseteq M. \end{array} $$

  Similarly, we can get J ⊆ M. Hence L = I ∨ J ⊆ M, which is a contradiction. Therefore β(I)∨β(J)=L.

• (2)⇒(3): Assume the condition (2). Let $I, J\in \mathcal {I}(L)$. Clearly β(I)∨β(J) ⊆ β(I ∨ J). Let x ∈ β(I ∨ J). Then ((x)^∘ ∨ I)∨((x)^∘ ∨ J)=(x)^∘ ∨ I ∨ J = L. Hence by condition (2), we get β((x)^∘ ∨ J)∨β((x)^∘ ∨ J)=L. Thus x ∈ β((x)^∘ ∨ I)∨β((x)^∘ ∨ J). Hence x = r ∨ s for some r ∈ β((x)^∘ ∨ I) and s ∈ β((x)^∘ ∨ J). Now

  $$\begin{array}{@{}rcl@{}} r\in \beta ((x)^{\circ }\vee I) & \Rightarrow & (r)^{\circ }\vee (x)^{\circ }\vee I = L\\ & \Rightarrow & L = ((r)^{\circ }\vee (x)^{\circ })\vee I\subseteq (r\wedge x)^{\circ }\vee I\\ & \Rightarrow & (r\wedge x)^{\circ }\vee I = L\\ & \Rightarrow & r\wedge x\in \beta (I). \end{array} $$

  Similarly, we can get s ∧ x ∈ β(J). Hence

  $$\begin{array}{@{}rcl@{}} x & = & x\wedge x\\ & = & x\wedge (r\vee s)\\ & = & (x\wedge r)\vee (x\wedge s)\in \beta (I)\vee \beta (J). \end{array} $$

  Then β(I ∨ J) ⊆ β(I)∨β(J). Therefore β(I)∨β(J)=β(I ∨ J).

• (3)⇒(4): Assume the condition (3). Let M, N be two distinct maximal ideals of L. Choose x ∈ M−N and y ∈ N−M. Now

  $$\begin{array}{@{}rcl@{}} x\notin N & \Rightarrow & \mathrm{there\,\,\, exists }~x_{1}\in N\,\mathrm{ such \,\,\, that }\,x\vee x_{1} = 1,\\ y\notin M & \Rightarrow & \mathrm{there \,\,\,exists }~y_{1}\in M\,\mathrm{ such\,\,\, that }\,y\vee y_{1} = 1. \end{array} $$

  Then (x ∨ y ₁)∨(y ∨ x ₁)=(x ∨ x ₁)∨(y ∨ y ₁)=1. Now

  $$\begin{array}{@{}rcl@{}} L & = & \beta (L)\\ & = & \beta ((1])\\ & = & \beta (((x\vee y_{1})\vee (y\vee x_{1})])\\ & = & \beta ((x\vee y_{1}])\vee \beta ((y\vee x_{1}])\hspace{0.7 cm}\text{ by condition (3) }\\ & \subseteq & {\Omega} (M)\vee {\Omega} (N)\hspace{0.5 cm}\text{since} \, (x\vee y_{1}]\subseteq M, (y\vee x_{1}]\subseteq N. \end{array} $$

  Therefore Ω(M) ∨ Ω (N)=L.

• (4)⇒(5): Assume the condition (4). Let M ∈ μ. Suppose N ∈ μ is such that N ≠ M and Ω(N) ⊆ M. Since Ω(M) ⊆ M by our hypothesis, we get L = Ω(M) ∨ Ω (N)=M, which is a contradiction. Therefore M is the unique maximal ideal such that Ω(M) is contained in M.

• (5)⇒(1): Let M ∈ μ. Suppose Ω(M) is not maximal. Let M ₀ be a maximal ideal of L such that Ω(M) ⊆ M ₀. We have always Ω(M ₀)⊆M ₀, which is a contradiction to the hypothesis.

□