1 Introduction

“How did cooperative behavior evolve” is a fundamental question in biology and the social sciences [1]. A great deal of game-theoretic research has been devoted to explain the prevalence of cooperation in biological systems as well as in human society. One reason for the vast literature from members of the game theory community on this topic is that their methods do not work for the underlying game, the Prisoner’s Dilemma (PD) game, which pits cooperative behavior against its nemesis of defection. In particular, defection strictly dominates cooperation since defectors always have higher payoffs by enjoying the benefits from cooperators without paying. That is, the only rational option in the PD game is to defect although it is to everyone’s advantage for all players to cooperate.

In the last decades, several mechanisms have been proposed to promote cooperation. Cooperation can be rational when the payoffs of the PD game are modified by assuming some relatedness between the players, by them playing the game an uncertain number of times, by extending the model to a game based on reputation, or introducing incentive mechanisms such as reward and punishment. These predictions are often based on applying either static (e.g., Nash equilibrium analysis and evolutionarily stable strategy) or dynamic methods (e.g., replicator equation) from game theory that assumes a large population of agents paired at random to play the game. Population interactions that are structured either spatially or socially also enhance the evolution of cooperation as do the stochastic effects of finite populations.

In this paper, we review recent studies on the evolution of cooperation. In particular, we focus on game mechanisms that can promote cooperation in groups of genetically unrelated individuals. These mechanisms include direct reciprocity in repeated games and incentive mechanisms such as reward and punishment. The rest of this paper is organized as follows. Section 2 introduces some basic games, equilibrium notations, and dynamic methods in game theory. Section 3 focuses on the repeated game and discusses strategies based on direct reciprocity. Section 4 considers the effects of reward and punishment in one-shot game. Section 5 summarizes and discusses the effects of these two types of mechanisms.

2 Game theory and Evolutionary Dynamics

2.1 Basic Games

2.1.1 The Prisoner’s Dilemma Game

A paradigm for modelling human cooperation is the Prisoner’s Dilemma (PD) game [2,3,4]. The standard PD game is a two-player game, where each player has two strategies, cooperation (\(\mathrm{C}\)) and defection (\(\mathrm{D}\)). The payoff matrix for the PD game is shown in Eq. (1). Two players are offered a certain payoff, \(R\) (i.e., reward), for mutual cooperation, and a lower payoff, \(P\) (i.e., punishment), for mutual defection. If one player cooperates while the other defects, then the cooperator gets the lowest payoff, \(S\) (i.e., sucker’s payoff), and the defector gains the highest payoff, \(T\)(i.e., the temptation of defection). Thus, the payoffs satisfy \(T>R>P>S\). A further common assumption is \(2R>S+T>2P\), which means that mutual cooperation is the best outcome and mutual defection is the worst outcome.

$$\begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {\text{C}} & {\text{D}} \\ \end{array} } \\ {\begin{array}{*{20}c} {\text{C}} \\ {\text{D}} \\ \end{array} } & {\left( {\begin{array}{*{20}c} R & S \\ T & P \\ \end{array} } \right)} \\ \end{array} .$$
(1)

In the one-shot PD game, \(\mathrm{D}\) strictly dominates \(\mathrm{C}\) because a player is better off defecting than cooperating no matter what the opponent does. So mutual defection is the only rational outcome.

We further introduce a simplified version of the PD game, the Donation game [3, 4]. This game has been widely used to study the evolution of cooperation. In this game, \(\mathrm{C}\) means that a donor pays a cost, \(c\), for a recipient to get a benefit, \(b\), where \(b>c\),\(\mathrm{D}\) means that the donor pays no cost and distributes no benefit. The payoff matrix is then given by

$$\begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {\text{C}} & {\text{D}} \\ \end{array} } \\ {\begin{array}{*{20}c} {\text{C}} \\ {\text{D}} \\ \end{array} } & {\left( {\begin{array}{*{20}c} {b - c} & { - c} \\ b & 0 \\ \end{array} } \right)} \\ \end{array} .$$
(2)

Similarly as the standard PD game, \(\mathrm{D}\) is a dominant strategy for both players and mutual cooperation leads to a higher average payoff.

2.1.2 The Public Goods Game

The public goods game (PGG) is a generalization of the PD game [4]. In a PGG, each player in a group of size \(n\) is given a fixed endowment, \(c\), and chooses how much of that endowment to put into a common pool. The total amount in the pool is multiplied by a factor \(r\) with \(1<r<n\) and then redistributed evenly to each player in the group. Denote the contribution of player \(i\) by \({x}_{i}\), with \(0 \leqslant {x}_{i} \leqslant c\). The payoff of player \(i\) is then the remainder of his/her endowment \(c-{x}_{i}\) plus what he/she receives from the public pool, which has the form

$${u}_{i}\left(\mathbf{x}\right)=c-{x}_{i}+\frac{r{\sum }_{j=1}^{n}{x}_{j}}{n}=c-\left(1-\frac{r}{n}\right){x}_{i}+\frac{r{\sum }_{j\ne i}{x}_{j}}{n}.$$
(3)

Furthermore, the average payoff of the group is

$$\overline{u }\left(\mathbf{x}\right)=\frac{1}{n}{\sum }_{i=1}^{n}{u}_{i}\left(\mathbf{x}\right)=c+\frac{(r-1)}{n}{\sum }_{i=1}^{n}{x}_{i}.$$
(4)

Thus, it is to the group’s advantage if all players contribute their total endowment because \(r>1\), but each player, given the contributions of the others, does best by contributing nothing because \(r<n\).

To show the relation between PGG and PD game, we consider a two-player PGG with discrete choices. We define \(\mathrm{C}\) as contributing all the endowment and \(\mathrm{D}\) as contributing nothing. Thus, the payoff matrix for this two-player PGG can be written as

$$\begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {{\text{C}}\;\;\;\;\;\;} & {\;\;{\text{D}}} \\ \end{array} } \\ {\begin{array}{*{20}c} \begin{gathered} {\text{C}} \hfill \\ \hfill \\ \end{gathered} \\ {\text{D}} \\ \end{array} } & {\left( {\begin{array}{*{20}c} {cr} & \frac{cr}{2} \\ {c\left( {1 + \frac{r}{2}} \right)} & c \\ \end{array} } \right)} \\ \end{array} .$$
(5)

This simplified PGG is a special case of the PD game, where \(\mathrm{D}\) is the only dominant strategy.

2.2 Equilibrium Analysis

2.2.1 Nash Equilibrium

The most commonly used equilibrium notation in game theory is the Nash equilibrium (NE). In a game, if each player has chosen a strategy and no player can benefit by changing his/her strategy while the other players keep theirs unchanged, then the set of strategy choices is called a Nash equilibrium [5].

Consider a 2-person \(n\)-strategy symmetric game, where for each player \(S=\{{s}_{1},{s}_{2},\cdots ,{s}_{n}\}\) is the strategy set. A strategy pair \(({s}_{i}, {s}_{i})\) is a NE if \(u({s}_{j}, {s}_{i}) \leqslant u({s}_{i}, {s}_{i})\) for any \(j\ne i\), where \(u({s}_{j}, {s}_{i})\) is the payoff to the player using strategy \(j\) when the other player adopts strategy \(i\).

It has been shown that every game has at least one Nash equilibrium [5], but in general there are many. Trying to select the “best” equilibrium for each game is a difficult problem. Methods to do this have been suggested by Harsanyi and Selten [6], inventing the risk dominant equilibrium, and by many other researchers.

2.2.2 Evolutionarily Stable Strategy

One well-known refinement for NE is the evolutionarily stable strategy (ESS). More than 40 years have passed since the concept of ESS was introduced by Maynard Smith, evolutionary game theory has become a powerful tool to analyze evolutionary processes and human behaviors [7, 8].

A strategy is called evolutionarily stable if all the members of the population adopted it, then no other strategy could invade the population. In a 2-person symmetric game, a strategy \({s}_{i}\) is an ESS if for any \(j\ne i\), \((\mathrm{i})\) \(u({s}_{j}, {s}_{i}) \leqslant u({s}_{i}, {s}_{i})\), and \((\mathrm{ii})\) \(u({s}_{j}, {s}_{j}) \leqslant u({s}_{i}, {s}_{j})\) when \(u\left({s}_{j}, {s}_{i}\right)=u({s}_{i}, {s}_{i})\). Condition \((\mathrm{i})\) is the NE condition and condition \((\mathrm{ii})\) guarantees that the strategy is evolutionarily stable that can prevent the invasion of other strategies.

We now provide a biological explanation for ESS. Consider that mutations occur in a population of strategy \({s}_{i}\), where the frequency of mutate strategy \({s}_{j}\) is \(x\). Thus, the expected payoffs for the resident strategy \({s}_{i}\) and the mutate strategy \({s}_{j}\) are \(u({s}_{i})=(1-x)u({s}_{i}, {s}_{i})+xu({s}_{i},{s}_{j})\) and \(u({s}_{j})=(1-x)u({s}_{j},{s}_{i})+xu({s}_{j},{s}_{j})\), respectively. If \({s}_{i}\) is an ESS, then we always have \(u({s}_{i})>u({s}_{j})\) in the limit of \(x\to 0\). This implies that any mutate strategy cannot invade the population under the influence of natural selection.

2.2.3 Quantal Response Equilibrium

The definition of NE relies on perfect rationality, where at a NE all players are using the best response strategies given the strategies of the others. However, people in reality are bounded rational and may make mistakes in decision making. In the context of bounded rationality, one important equilibrium notation is the quantal response equilibrium (QRE) introduced by McKelvey and Palfrey [9]. In a QRE, players do not always choose best responses. Instead, they make decisions based on a probabilistic choice model and assume other players do so as well. A general interpretation of this model is that players observe randomly perturbed payoffs of strategies and choose optimally according to those noisy observations [9,10,11,12,13]. For a given error structure, QRE is defined as a fixed point of this process.

For instance, in a 2-person \(n\)-strategy symmetric game, the set of QRE at noise level \(\lambda\) is defined as

$${\pi }_{\lambda }=\left\{\mathbf{x}=\left({x}_{1},\dots ,{x}_{n}\right)|{x}_{i}=\sigma \left(\lambda \mathbf{u}\left(\mathbf{x}\right)\right)\right\},$$
(6)

where \(\mathbf{u}\left(\mathbf{x}\right)=({u}_{1}\left(\mathbf{x}\right),\cdots ,{u}_{n}\left(\mathbf{x}\right))\) is the vector for the expected payoffs of the \(n\) strategies. The quantal response function has one free parameter \(\lambda\), whose inverse \(1/\lambda\) has been interpreted as the temperature, or the intensity of noise. At \(\lambda =0\), players have no information about the game and each strategy is chosen with equal probability. As \(\lambda\) approaches infinity, players achieve full information about the game and choose best responses. In particular, if \(\sigma\) satisfies continuity and cumulativity, then the limit set \(\underset{\lambda \to \infty }{\mathrm{lim}}{\pi }_{\lambda }\) consists of NE only [14].

McKelvey and Palfrey [9] then defined an equilibrium selection from the set of Nash equilibria by tracing the branch of the QRE correspondence starting at the centroid of the strategy simplex (the only QRE when \(\lambda =0\)) and following this branch to its terminus at \(\lambda =+\infty\). If \(\sigma\) satisfies \({C}^{2}\) continuity, monotonicity and cumulativity, then the graph of QRE correspondence generically includes a unique branch that starts at the centroid of the strategy simplex and converges to a unique Nash equilibrium as noises vanish [15, 16]. This equilibrium is called the limiting QRE of the game.

2.3 Evolutionary Dynamics

In addition to static equilibrium analysis, dynamic approaches have been widely used to study the evolution of strategies or behaviors. Dynamic approaches in game theory could be roughly classified into two categories. Evolutionary game theory considers the behavior of large populations, where individuals choose which actions to play genetically or using simple myopic rules (e.g., imitation, best response). In contrast, learning models focus on the behavior of small groups in repeated games. Individuals make decisions according to explicit learning rules, which could be simple myopic rules (called heuristic learning or adaptive learning) or more complicated Bayesian rules (called coordinated Bayesian learning or rational learning). The heuristic learning is close to the spirit of evolutionary approach. In contrast, in the Bayesian learning, individuals play the best response to their beliefs about other individuals’ strategies and update the beliefs over rounds. For instance, a representative class of Bayesian learning methods is homotopy approaches, such as the tracing procedure of Harsanyi and Selten [6] or the QRE of McKelvey and Palfrey [9], see also McKelvey and Palfrey [11], Turocy [13], and Zhang [15].

In this paper, we mainly focus on the evolutionary game method. One well-known evolutionary dynamics is the replicator dynamics [7, 17, 18]. Replicator dynamics was first motivated biologically in the context of evolution and is still applied in this field. Later, economists related replicator dynamics to learning [19,20,21] and defined several equilibrium notions [22, 23].

Replicator dynamics describes the evolution of the frequencies of strategies. It assumes that the per capita growth rate of each strategy is proportional to its payoff and the evolutionary success of a strategy is measured quantitatively by the difference between its payoff and the average payoff of the population. When a strategy has payoff above the average, then this strategy is expected to spread.

Consider a symmetric game and denote the frequency of strategy \({s}_{i}\) in the population by \({x}_{i}\). The replicator dynamics are then written as

$$\frac{\text{d}{x}_{i}}{\text{d}t}={x}_{i}({u}_{i}\left(\mathbf{x}\right)-\overline{u }\left(\mathbf{x}\right)),$$
(7)

where \({u}_{i}\left(\mathbf{x}\right)={\sum }_{j=1}^{n}{x}_{j}u({s}_{i},{s}_{j})\) is the expected payoff for strategy \(i\) and \(\overline{u }\left(\mathbf{x}\right)={\sum }_{i=1}^{n}{x}_{i}{u}_{i}\left(\mathbf{x}\right)\) is the average payoff of the population.

A state \({\mathbf{x}}^{\boldsymbol{*}}=({x}_{1}^{*},\cdots ,{x}_{n}^{*})\) is called evolutionarily stable if it is an asymptotically stable fixed point of the replicator dynamics. The stability analyses of replicator dynamics were given in the framework of population games [17, 18, 21, 24,25,26], asymmetric games [7, 27,28,29,30,31], and genetically structured population [7, 32,33,34]. In a symmetric game, a symmetric NE must be a fixed point of the replicator dynamics, and any stable fixed point must be a NE. In particular, in the case of two strategies, a stable fixed point corresponds to an ESS [17].

Other common evolutionary game dynamics include replicatory-mutator dynamics, adaptive dynamics, birth-death/death-birth process, exploration dynamics, Fermi update, best response dynamics, fictitious play, perturbed best response dynamics, logit dynamics, stochastic dynamics, and learning-mutation dynamics. Table 1 summarizes the biological or economic context of these dynamics and related equilibrium notations. More details can be found in Hofbauer and Sigmund [17] and Sandholm [12].

Table 1 Evolutionary dynamics. This table provides biological and economic contexts and related equilibrium notations for different evolutionary dynamics. Details for dynamics 1,2,3,6 can be found in Hofbauer and Sigmund [17]. Details for dynamics 1, 4, 5, 6, 7, 8 can be found in Sandholm [12]
Full size table

3 Repeated Game

The two basic games introduced in Sect. 2.1, the PD game and PGG, are one-shot, where the only NE/ESS is defection (\(\mathrm{D}\)). However, most of interactions in our daily life (e.g., with colleagues or friends) are not one-shot. We now consider that the game is repeatedly played between the two players. Furthermore, we assume that the two players do not know how many rounds their game will last. They only know that after every round, a further round can occur with a probability \(w<1\), i.e., the expected number of rounds is \(t=1/(1-w)\). If the number of rounds is known to the both players, then backward induction predicts that rational players ought to play \(\mathrm{D}\) in each round.

We note that strategies in the repeated game can be very complicated because the choice in a round could depend on what happens in previous rounds. In fact, in the repeated PD game, there is no strategy that can strictly dominate all other strategies. For instance, if the coplayer uses an unconditional strategy such as always defects (AllD) or always cooperates (AllC), then the best response is to play \(\mathrm{D}\). However, if the coplayer uses a conditional strategy that punishes defection, then it is better to play \(\mathrm{C}\) in every round. In this section, we will introduce some typical strategies in the repeated social dilemma games and discuss their evolutionary stabilities against defection.

3.1 Evolution of Cooperation in the Repeated PD Game

One of the most famous strategy in the repeated PD game is tit-for-tat (TFT). A player using this strategy chooses \(\mathrm{C}\) in the first round and then does whatever the opponent did in the previous round. TFT was first introduced by Rapoport, and it is both the simplest and the most successful strategy in Axelrod's computer tournaments [2, 35]. The success of TFT may attribute to four reasons. First, it is never the first to defect. Thus, cooperation can be sustained when both players are using TFT. Second, it is provocable into retaliation by a defection of the other. As a result, TFT will be not by exploited by defective strategies. Third, it is forgiving after just one act of retaliation. Thus, if the coplayer switches back to \(\mathrm{C}\), then the TFT player resumes to \(\mathrm{C}\) forthwith. Finally, it never tries to get more than its coplayer. In fact, in the repeated PD game, the only way to do better than the coplayer is to choose \(\mathrm{D}\). However, if both players want to get a higher payoff, then they will fall into mutual defection. Subsequent empirical studies found that the success of TFT is not limited to human society but that it also extends to animal populations [36].

However, TFT has an Achilles' heel, it cannot correct mistakes. When players may make mistakes in decision making, the expected payoff for two TFT players in an infinitely repeated PD is same as random players (see Fig. 1a). This implies that TFT is evolutionarily unstable in an uncertain world. In the next few years, evolutionary game method has been applied to find the “best” strategy in the repeated PD game. The evolution of strategies has been analyzed by adaptive dynamics and replicatory dynamics in the set of reactive strategies and stochastic strategies [37,38,39,40,41,42,43].

Fig. 1
figure 1

TFT, GTFT, and WSLS in repeated PD games with errors. (a) TFT cannot correct mistakes. (b) GTFT can correct mistakes in few rounds. (c) WSLS can exploit AllC. (d) WSLS is a deterministic corrector

Full size image

A reactive strategy is written as a 3D vector \((x, {p}_{\text{C}},{p}_{\text{D}})\), where \(x\) is the probability of cooperating in the first round and \(p_{\text{C}}\), and \(p_{\text{D}}\) are the conditional probabilities of playing C after the coplayer choosing \(\mathrm{C}\) and \(\mathrm{D}\), respectively. For instance, AllC, AllD, and TFT can be denoted by \((\mathrm{1,1},1)\), \((\mathrm{0,0},0)\), and \((\mathrm{1,1},0),\) respectively. Adaptive dynamics show that in the set of reactive strategies, there is no evolutionary tendency towards TFT. Once a cooperative population has been established, TFT will be replaced by a more generous strategy, \((\mathrm{1,1},p)\). This strategy is called generous tit-for-tat (GTFT). A GTFT player starts with \(\mathrm{C}\), choose C when the coplayer has cooperated and chooses \(\mathrm{C}\) with probability \(p\) when the coplayer has defected. Comparing with TFT, GTFT is more forgiving when faced with \(\mathrm{D}\). Thus, mistakes can be corrected in few rounds. Specifically, when the error probability is small, the expected payoff for two GTFT players per round is very close to the full reward for mutual cooperation (see Fig. 1b).

A memory-one strategy is written as a 5D vector \((x, {p}_{\text{CC}},{p}_{\text{CD}}, {p}_{\text{DC}},{p}_{\text{DD}})\), where \(x\) is the probability of cooperating in the first round and \({p}_{\text{CC}},\) \({p}_{\text{CD}},\) \({p}_{\text{DC}}\) and \({p}_{\text{DD}}\) are the conditional probabilities of playing \(\mathrm{C}\) after \(\mathrm{CC},\mathrm{ CD},\mathrm{ DC}\) and \(\mathrm{DD}\) interactions, respectively (see Table 2). Thus, reactive strategies form a 3D subset of the memory-one strategies. Evolutionary simulation based on selection and mutation shows that in the set of memory-one strategies, a GTFT population will be replaced by AllC through neutral drift, and the AllC population will be undermined by either AllD or a new strategy, (1,1,0,0,1) [41]. This strategy is called Win-Stay Lose-Shift (WSLS). In the repeated donation game, a WSLS player starts with \(\mathrm{C}\), repeats the previous action if the payoff > 0 and switches if the payoff  \(\leqslant 0\). Comparing with GTFT, WSLS has three advantages. First, it can exploit AllC (see Fig. 1c). Second, it can against the invasion of ALLD if \(b/2>c\)(in contrast, GTFT cannot defeat AllD when \(p\) is large). Finally, it is a deterministic corrector, where a mistake can be correct in 2 rounds (see Fig. 1d).

Table 2 Typical memory-one strategies in the repeated PD game. A memory-one strategy is written as a 5D vector \((x, {p}_{\text{CC}},{p}_{\text{CD}}, {p}_{\text{DC}},{p}_{\text{DD}})\), where \(x\) is the probability of cooperating in the first round and \({p}_{\text{CC}},\) \({p}_{\text{CD}},\) \({p}_{\text{DC}}\) and \({p}_{\text{DD}}\) are the conditional probabilities of playing \(\mathrm{C}\) after \(\mathrm{CC}\), \(\mathrm{CD}\), \(\mathrm{DC}\) and \(\mathrm{DD}\) interactions, respectively. The ESS condition is condition that the strategy can prevent the invasion of \(\mathrm{AllD}\) in the repeated donation game (with parameters \(b, c,\) and \(w\))
Full size table

We now let natural selection to design a strategy in the set of memory-one strategies. As shown in Fig. 2, a TFT population can be established if the initial cooperation rate is higher, after which TFT will be replaced by more generous strategies such as GTFT and AllC; finally, the population will be undermined by WSLS or AllD. However, there are two remaining questions for the evolution of cooperation in repeated games. First, AllD and TFT are bistable under deterministic evolutionary dynamics (e.g., replicator dynamics). If the population evolves to AllD, how does TFT establish a regime of cooperation? Second, the AllC population can be invaded by both AllD and WSLS. How to prevent the evolutionary trend from AllC to AllD?

Fig. 2
figure 2

Evolutionary cycles. In the set of memory-one strategies, natural selection favors AllD and WSLS in the long run

Full size image

For the first question, there are two possible explanations. The first explanation is that TFT can invade AllD through random mutation [40, 44,45,46,47]. In the limit of weak selection, natural selection can favor the invasion and replacement of the AllD strategy by TFT if the payoff of the PD game satisfies a one-third law [3, 47]. The second explanation is that suspicious tit-for-tat (STFT) can invade the AllD population through neutral drift. When most of the players become STFT, TFT-like strategies will obtain a higher payoff. The population will then evolve to a conditional cooperative regime, which cannot be invaded by non-cooperative strategies [4, 48]. For the second question, incentive mechanisms such as reward and punishment are often used to sustain cooperation, and this point will be discussed in Sect. 4.

3.2 More on Repeated Game Strategies

Recently, Press and Dyson revealed that the repeated PD game (and PGG) includes a special class of memory-one strategies, zero-determinant (ZD) strategy [42]. A player using a ZD strategy can unilaterally enforce a linear relation between the two players’ payoffs [37, 38, 42, 43, 137]. Furthermore, a subset of ZD strategies allows for implicit forms of extortion, where a player using extortionate strategies can enforce a unilateral claim to an unfair share of rewards such that the partner’s best response is to be fully cooperative. Thus, extortioners cannot be outperformed by any opponent in a pairwise encounter. Experimental studies showed that computers using such strategies can defeat each of their human opponents in repeated PD game, but extortion resulted in lower payoffs than generosity [49]. This is because human subjects showed a strong concern for fairness. They often punished extortion by refusing to fully cooperate, thereby reducing their own, and even more so, the extortioner’s gains. However, when the repeated game is sufficiently long, human subjects’ cooperation rates increased after they realized that punishment cannot change the behavioral pattern of their (computer) partners [50]. As a result, the extortionate strategy earns more than the generous strategy.

We note that strategies such as TFT, GTFT, WSLS, and ZD can be generalized to games with continues strategies and games with more than 2 players. Some researchers have examined models of continuous PD game (or equivalently, 2-person PGG) based on the linear reactive strategy method. They found that cooperative strategies such as TFT and GTFT are more difficult to invade a non-cooperative equilibrium than in the discrete PD game [51,52,53]. TFT and WSLS have also been generalized to \(n\)-person PD game (or equivalently, PGG with discrete choices) [46, 54,55,56]. In an \(n\)-person PD, a TFTk (\(0<k<n\)) strategist cooperates if at least \(k\) individuals cooperated in the previous round [46, 54, 55], and a WSLS strategist cooperates if all them group members cooperated or defected in the previous round [56]. Both TFTm−1 and WSLS can sustain cooperation in sizable group, and sometimes large group size can facilitate the evolution of cooperation [46, 56]. Finally, Hilbe et al. [49] showed that multiplayer social dilemma games also include ZD like strategies. They distinguished several subclasses of ZD strategies, e.g., fair strategies ensure that the own payoff matches the average payoff of the group, extortionate strategies allow a player to perform above average, and generous strategies let a player perform below average.

Finally, we summarize recent empirical results for strategies in the multi-player repeated PD games and PGG. On the one hand, a strategy called “moody conditional cooperation” was observed in experiments based on the multiplayer spatial PD game [57,58,59,60,61]. The definition of this strategy comprises two main ingredients. The first is conditional cooperation, i.e. people cooperate more when more of their neighbors cooperated in the previous round. The second is that the probability that they display condition cooperation depends on whether they cooperated or defected in the previous round. If defected, then this player is less likely to cooperate in this round. On the other hand, conditional cooperative strategies have been widely observed in repeated PGG experiments, where a conditional cooperator changes his/her contribution in the next round in the direction of the group average contribution of the current round [62,63,64,65,66]. Experimental studies have revealed that about half of the individuals in the repeated PGG can be classified as conditional cooperator [49, 62, 63]. Recent experiments based on PGG with institutionalized incentives show that this proportion seems to be independent of the incentive modes. The proportion of individuals displaying conditional cooperative behavior is stabilized at around 50% in all nine treatments [66].

3.3 Separable PD Game

For the repeated PD game, one of the key assumptions is that the interaction between a pair of individuals will be repeated for several rounds [2, 4, 67, 68]. In most of real-world interactions, people are able to stop the interaction with their coplayers. Some researchers then considered a variant of the repeated PD game, the separable PD game. In this game, players can choose to keep or stop the interaction after they know the choices of their coplayers. At the end of each round, all single subjects form new interaction pairs through random meeting in the next round. Based on individual self-interest in the PD game, both cooperators and defectors prefer a coplayer who cooperates. Thus, if players are able to unilaterally terminate the interactions with their coplayers, then a simple rule will be followed by all individuals: I would like to keep my opponent if he/she is a cooperator; and if my opponent is a defector, I will stop the interaction with him/her and seek a new partner instead (see Fig. 3). This class of conditional dissociation strategies is called “out-for-tat” (OFT) [56, 69,70,71,72,73,74,75, 138]. Since OFT means that an individual displaying cooperation (\(\mathrm{C}\)) will respond to defection (\(\mathrm{D}\)) by merely leaving, OFT will not tolerate defection but, unlike TFT, it does not seek revenge.

Fig. 3
figure 3

Separable PD game with OFT players. OFT-cooperators and OFT-defectors are marked by blue and red balls, respectively. At the end of a round, \(\mathrm{C}\)-\(\mathrm{D}\) pairs and \(\mathrm{D}\)-\(\mathrm{D}\) pairs will be broken since all individuals immediately stop the interaction with a defector. In a \(\mathrm{C}\)-\(\mathrm{C}\) pair, both individuals are willing to continue. Thus, the \(\mathrm{C}\)-\(\mathrm{C}\) pair will be terminated with probability \(w\) (as in the repeated PD game). All single individuals will be paired with a new partner through random meeting in the next round

Full size image

Theoretical analysis based on evolutionary game method shows that OFT leads to the stable coexistence of \(\mathrm{C}\) and \(\mathrm{D}\). Furthermore, when all individuals use OFT, non-OFT strategies (e.g., AllD, TFT) cannot successfully invade this population [14, 56, 70, 73, 76]. Empirical studies confirmed that most of subjects in separable PD game adopted OFT-like strategies, and the cooperation rate stabilized at about 60% in the repeated play.

In addition to stop the interaction with the current coplayer, another class of studies allows abstaining from a game [71, 74, 77, 78], with players choosing between an outside option (i.e., to be a loner) and the PD game. In such case, cooperators, defectors and loners can coexist if the payoff of the outside option is higher than the payoff of mutual defection. However, replicator dynamics show that voluntary participation usually does not lead to a stable equilibrium, but to an unending limit cycle [77, 78].

4 Reward and Punishment

Although direct reciprocity provides satisfactory explanations of cooperation in social dilemma games with repeated interactions, the sustaining of cooperation in one-shot interaction (or game between strangers) remains a problem [79, 80]. Examples such as the PD game and PGG (see Sect. 2.1) show that self-interested players should prefer a free-rider strategy, whereas it is to everyone’s advantage for all players to contribute [4]. In real-life situations that include this sort of dilemma between individual rationality and collective advantage, incentives are often used to promote cooperation, where contributors may be rewarded and free-riders may be punished. In fact, positive and negative incentives exist not only in human societies but also in animal behavior [81]. Understanding the consequences of such ‘carrots and sticks’ in boosting cooperation is a core topic in the economics and management sciences (see [82,83,84] for three recent review papers).

4.1 Peer Incentive

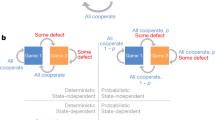
Several types of incentives have been proposed to promote cooperation in social dilemma games. Most of these investigations addressed so-called peer (or decentralized) incentives. In this scenario, players are allowed to reward and/or punish others at a cost to themselves. A typical social dilemma game with peer incentives is a two-stage game, where in the first stage players play the social dilemma game and in the second stage they can reward and/or punish their group members based on the result of the first stage (see Fig. 4a).

Fig. 4
figure 4

Peer incentives and institutional incentives. (a) A social dilemma game with peer incentives can be formalized as a two-stage game. (b) A social dilemma game with institutional incentives can be formalized as a three-stage game

Full size image

The social dilemma game with peer incentives can be simplified as a two-stage asymmetric game [4, 85, 86]. To show this, we consider a two-player donation game with peer incentives, where one player is donor and the other is recipient. In the first stage, the donor has two possible strategies, \(\mathrm{C}\) and \(\mathrm{D}\), and in the second stage, the recipient has three strategies, no action (No), \(\mathrm{R}\) (reward), and \(\mathrm{P}\) (punishment). We assume that players are pro-social in the sense that they only reward cooperators and punish defectors. Denote the cost of incentive by \({C}_{I}\) and the amounts of reward and punishment by \(\mathrm{R}\) and \(\mathrm{P}\), respectively. The payoff matrix of this two-stage game can be written as

$$\begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {\text{No }} & {\text{R }} & {\text{ P}} \\ \end{array} } \\ {\begin{array}{*{20}c} {\text{C}} \\ {\text{D}} \\ \end{array} } & {\left( {\begin{array}{*{20}c} { - c,b} & { - c + R,b - C_{I} } & { - c,b} \\ {0,0} & {0,0} & { - P, - C_{I} } \\ \end{array} } \right)} \\ \end{array} ,$$
(8)

where the rows are the strategies of the donor and columns are the strategies of the recipient.

It is clear that the defective state (\(\mathrm{D},\mathrm{ No}\)) is a NE, and the cooperative state (\(\mathrm{C},\mathrm{ P}\)) becomes a NE if\(P>c\). The subgame perfect NE of this game can be derived by backward induction. Since the incentive is costly, rational players will not choose \(\mathrm{R}\) and \(\mathrm{P}\) in the second stage. Thus, the subgame perfect NE in this game is same as the game without peer incentives, i.e., (\(\mathrm{D}\),\(\mathrm{No}\)). Evolutionary game theory analysis based on replicator dynamics also shows that the cooperative state (\(\mathrm{C},\mathrm{ P}\)) is evolutionarily unstable in one-shot game [85,86,87,88,89,90,91,92,93,94]. However, when subjects may make mistakes in decision making, intermediate errors can increase cooperation in for games with peer punishment [16, 95]. Furthermore, if the game is played repeatedly, incentive may help to enhance the effects of direct reciprocity and indirect reciprocity [4, 85, 86]. In particular, punishment promotes cooperation better than reward in the case of indirect reciprocity (i.e., players may know the historical behaviors of their coplayers), where the cooperative state can be evolutionarily stable.

Laboratory experiments confirmed that peer punishment can curb free-riding in human populations [96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112]. However, peer punishment suffers from several drawbacks. First, the use of incentives is costly, which then raises an issue of second-order free-riding. In fact, the incentive system itself is a common good that can be exploited, and the use of punishment is individually disadvantageous [99, 112]. Second, punishment decreases the total welfare. As a result, the average payoff for group with punishment often less than group without punishment [103, 104]. Finally, punishment often some players abuse sanctioning opportunities by engaging in antisocial punishment, which harms cooperators [97,98,99, 106, 107].

In contrast, the effect of peer reward is controversial. Some experimental studies showed that reward can promote cooperation if the reward-to-cost ratio (i.e., \({R/C}_{I}\)) is greater than one. However, given the budget-balanced condition (i.e., \({R/C}_{I}=1\)), peer reward alone is relatively inefficient in promote cooperation [110, 113].

4.2 Institutional Incentive

In the institutional incentive scenario, it is not individuals who reward or punish. Rather, an institution rewards and punishes individuals based on their contributions. The use of institutional incentives is a common feature in many parts of human society such as government institutions and businesses. It can overcome the problem of second-order free-riding and avoid antisocial punishment. However, this approach is more wasteful than peer incentives because subjects have to pay a fee to maintain the institution even if no one is being rewarded or punished (which can be viewed as paying for the upkeep of a police force).

A social dilemma game with institutional incentives can be formalized as a three-stage game. In the first stage, players can decide to pay for the incentive institution. In the second stage, they play the social dilemma game. In the third stage, the institution will reward or punish each player based on his/her behaviors in the two-stage game, where the amount of incentive depends on the total payment in the first stage. In particular, players do not need to make decisions in the third stage.

We consider an \(n\)-person PGG with institutional incentives [114,115,116,117,118,119,120,121,122]. For simplicity, we first assume that the institutional incentive is compulsory, where each player is forced to pay \({C}_{I}\) in the first stage. Thus, the total amount of incentive is \({C}_{I}n\). In the second stage, they play PGG with discrete choices. Specifically, each player can decide whether to contribute a fixed amount \({c}_{0}\) knowing that this amount will be multiplied by \(r>1\) and divided equally among all \(n\) players in the group. If \({n}_{\text{C}}\) is the number of those players who contribute (i.e. cooperators) and \({n}_{\text{D}}\) the number of those who do not (i.e. defectors), then the payoffs of a cooperator and a defector are \((rc{n}_{\text{C}})\)/\(n-c\) and \(rc{n}_{\text{C}}\)/\(n\), respectively.

In the case of institutional reward (IR), the incentive is shared among the \({n}_{{C}}\) cooperators. Thus, each cooperator obtains a reward of \({C}_{I}n\)/\({n}_{\text{C}}\). In the case of institutional punishment (IP), each defector analogously receives a punishment of \({C}_{I}n\)/\({n}_{\text{D}}\). Payoff for cooperators and defectors in IR are

$$\begin{aligned} u_{\text{C}} & = \frac{{rcn_{\text{C}} }}{n} - c - C_{I} + \frac{{C_{I} n}}{{n_{\text{C}} }}, \\ u_{\text{D}} & = \frac{{rcn_{C} }}{n} - C_{I} , \\ \end{aligned}$$
(9)

and in IP are

$$\begin{aligned} u_{\text{C}} & = \frac{{rcn_{\text{C}} }}{n} - c - C_{I} , \\ u_{\text{D}} & = \frac{{rcn_{\text{C}} }}{n} - C_{I} - \frac{{C_{I} n}}{{n_{\text{D}} }}. \\ \end{aligned}$$
(10)

Theoretical studies based on evolutionary game theory have revealed that the effect of institutional incentives on cooperation can be understood in terms of the incentive size [114, 115, 118, 119, 123, 124]. If \({C}_{I}<\frac{c}{n}-\frac{rc}{{n}^{2}}\), then both reward and punishment have no effect on promoting cooperation, and selfish players maintain a free-riding strategy. If \({C}_{I}>c-\frac{rc}{n}\), then both reward and punishment compel all players to cooperate. If \(\frac{c}{n}-\frac{rc}{{n}^{2}}<{C}_{I}<c-\frac{rc}{n}\), then full contribution and free-riding are bistable under punishment, and reward can cause only the stable coexistence of free-riders and cooperators. Experimental results are consistent with the theoretical prediction, where an intermediate size of punishment is sufficient to support high cooperation level, but reward can maintain stable cooperation only for a large incentive size [66, 113, 125,126,127,128,129].

4.2.1 Compulsory Institution vs Voluntary Institution

In the above model, every player has to pay for the incentive institution before contributing to the PGG. In fact, this payment can be seen as an entry fee for the PGG. If the payment is voluntary (e.g., players may choose not to pay for the incentive institution in the first stage), then the issue of second-order free-riding is raised because the incentive institution itself is a common good that can be exploited. Previous studies show that IP with voluntary payment is functional if punishment is also imposed on second-order free-riders, i.e. subjects who cooperate but do not pay for the institution should also be punished [121, 127, 129]. By contrast, if IR is budget-balanced, then rational players will not pay for the institution [94, 123].

Since the entry fee in our model is compulsory, a subsequent question is whether people will choose such an incentive institution. One experimental study showed that comparing with standard PGG or PGG with peer punishment, people are more likely to choose institutional punishment if the institution punishes both first-order and second-order free-riders [129]. Another experimental study indicated that approximately half of the subjects would like to pay 20% of their wealth for a reward mechanism before playing the PGG [130]. These findings suggest that the incentive institution could be sustainable.

4.2.2 Absolute Incentive vs Relative Incentive

In PD game or PGG with discrete choices, a reasonable incentive institution should reward cooperators and punish defectors. However, in PGG with continuous choices, it is difficult to determine who should be rewarded or punished.

Incentive institutions considered in the previous studies could be roughly classified into two types. One type is characterized as an absolute incentive institution, where the institution punishes (or rewards) all individuals whose contribution is less (or higher) than a predefined threshold [114, 118, 121, 123, 127, 129]. A similar institution is that the reward (or punishment) amount increases (decreases) with the absolute contribution, see e.g., Galbiati and Vertova [140] and Putterman et al. [126]. Both theoretical and experimental studies indicated that absolute punishment can eliminate extremely selfish behaviors in a cooperative population [121, 127, 129]. In contrast, absolute reward is relatively ineffective in moving the equilibrium from the selfish one to the cooperative one [114, 118].

Another type is characterized as a relative incentive institution, where individuals who contribute an amount lower than the group average are more likely to be punished, and those who contribute higher than the group average are more likely to be rewarded [66, 115, 125, 128, 131,132,133,134]. A similar institution would be that the reward (or punishment) amount increases (decreases) with the relative contribution, see e.g., Falkinger et al. [135]. For relative punishment, a full contribution becomes a Nash equilibrium if the institution punishes the lowest contributor such that his or her payoff is slightly lower than that of the second lowest contributor [131]. In contrast, relative reward can promote cooperation only if lower contributors also have the chance to win the reward [136].

5 Summary

In this paper, we provide a review of sustaining cooperation in groups of unrelated individuals from the perspective of game theory. We mainly focus on two mechanisms, direct reciprocity and incentives.

Direct reciprocity relies on the repeated interaction. In the framework of direct reciprocity, a vast amount of strategies can help to promote cooperation. In the repeated PD game, strategies that can sustain full cooperation including GRIM, TFT, and some strategies in the set of ZD strategies. However, when subjects may make mistakes in decision making, the above strategies can no longer sustain cooperation because they cannot correct mistakes. Evolutionary game analysis shows that successful strategies in repeated PD with errors are GTFT and WSLS. Finally, when subjects are able to stop the interaction with their coplayers, OTF performs better than TFT, where an OFT player responds to defection by breaking the interaction rather than seeking revenge. However, OFT cannot sustain full cooperation, it leads to the stable coexistence of \(\mathrm{C}\) and \(\mathrm{D}\). This implies that promoting cooperation in separable PD is a more difficult issue.

Comparing to direct reciprocity, incentive mechanism can promote cooperation even in one-shot interaction. Incentive mechanisms can be classified to two classes. One class is peer (or decentralized) incentives, where players can impose fines or bonuses on others at a cost to themselves. Another class is institutional (or centralized) incentives. In this scenario, it is not individuals who reward or punish but rather an institution that rewards and punishes individuals based on their contributions. Thus, Institutional incentives can overcome the problem of second-order free-riding, whereas peer incentives cannot.

Finally, when devising incentive systems, it is important to recognize that the effect of reward is not equivalent to punishment. Punishment can eliminate extremely selfish behaviors in a cooperative population but it does not work for the selfish population. In contrast, rewards alone are relatively ineffective in moving the equilibrium from the selfish one to the cooperative one. Finally, combining rewards and punishments has a very strong effect. Rewards can act as a catalyzer if the population consists of a majority of defectors.