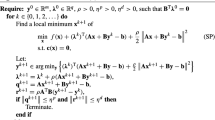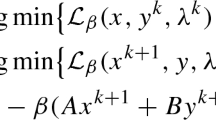1 Introduction

We consider the canonical linear programming (LP) model

$$\begin{aligned} \min \{ c^\mathrm{T}x \,|\, a_i^\mathrm{T} x\geqslant b_i, \; i=1, 2, \cdots , m \}, \end{aligned}$$
(1.1)

where \(c, a_i, \, i=1, \cdots , m\) are given vectors in \(\mathbb {R}^n\) and \(b_i\in \mathbb {R}\). As one of the most fundamental mathematical problems in operational research, LP has been intensively studied in the literature. The simplex and interior point methods represent two most important categories among different methods for LP, we refer to, e.g., [1–3] for reviews. The purpose of this short note is to show that the alternating direction method of multipliers (ADMM), which was originally proposed in [4] and has recently found many impressive applications in a broad spectrum of areas, can be easily used for the LP model (1.1). We thus aim at proposing the new ADMM approach to LP, which is completely different from the major simplex and interior point approaches in the literature.

To introduce ADMM, we consider a convex minimization problem with linear constraints and its objective function is the sum of two functions without coupled variables:

$$\begin{aligned} \min \left\{ {\varvec{\vartheta }}_1({\varvec{x}}_1) + {\varvec{\vartheta }}_2({\varvec{x}}_2) \,\big |\, \mathcal{A}_1{{\varvec{x}}_1} + \mathcal{A}_2{{\varvec{x}}_2} ={\varvec{b}}, \; {{\varvec{x}}_1}\in \mathcal{X}_1, {{\varvec{x}}_2}\in \mathcal{X}_2\right\} , \end{aligned}$$
(1.2)

where \(\mathcal{X}_i \subseteq \mathbb {R}^{s_i}\) are nonempty closed convex sets; \(\vartheta _i: \mathbb {R}^{s_i} \rightarrow \mathbb {R}\) are closed proper convex functions and \(\mathcal{A}_i \in \mathbb {R}^{t \times s_i}\) for \(i=1,2\); and \({\varvec{b}}\in \mathbb {R}^\mathrm{T}\). Note that we use bold letters in (1.2) because it may be in block-wise form. For example, \({\varvec{x}}_1\) may include more than one variable and \({\varvec{\vartheta }}_1\) may be the sum of more than one function.

Let \({\varvec{\lambda }}\in \mathbb {R}^\mathrm{T}\) and \(\beta \in \mathbb {R}\) denote the Lagrangian multiplier and penalty parameter of (1.2), respectively. Then, the augmented Lagrangian function of (1.2) is

$$\begin{aligned} \mathcal{L}_{\beta }({\varvec{x}}_1,{\varvec{x}}_2,{\varvec{\lambda }})= & {} {\varvec{\vartheta }}_1({\varvec{x}}_1) + {\varvec{\vartheta }}_2({\varvec{x}}_2) - {\varvec{\lambda }}^\mathrm{T}(\mathcal{A}_1{{\varvec{x}}_1} + \mathcal{A}_2{{\varvec{x}}_2} -{\varvec{b}})\nonumber \\&+\,\frac{\beta }{2}\Vert \mathcal{A}_1{{\varvec{x}}_1} + \mathcal{A}_2{{\varvec{x}}_2} -{\varvec{b}}\Vert ^2. \end{aligned}$$
(1.3)

When the ADMM proposed in [4] is applied to (1.2), the iterative scheme reads as

$$\begin{aligned} \left\{ \begin{array}{l} {\varvec{x}}_1^{k+1} = \mathrm{argmin} \bigl \{ \mathcal{L}_{\beta }({\varvec{x}}_1,{\varvec{x}}_2^k,{\varvec{\lambda }}^k)\; \big | \; {\varvec{x}}_1\in \mathcal{X}_1 \bigr \},\\ {\varvec{x}}_2^{k+1} =\mathrm{argmin} \bigl \{ \mathcal{L}_{\beta }({\varvec{x}}_1^{k+1},{\varvec{x}}_2,{\varvec{\lambda }}^k) \; \big | \; {\varvec{x}}_2\in \mathcal{X}_2 \bigr \},\\ {\varvec{\lambda }}^{k+1}={\varvec{\lambda }}^k- \beta (\mathcal{A}_1{\varvec{x}}^{k+1}+ \mathcal{A}_2{\varvec{x}}_2^{k+1}-{\varvec{b}}). \end{array}\right. \end{aligned}$$
(1.4)

We refer the reader to [5–7] for some recent review papers on ADMM; in particular, its applications in various fields such as image processing learning, statistical learning, computer vision, wireless network, and cloud computing. It worths to mention that these application models usually have nonlinear objective functions, but they are in separable form and thus the decomposition over variables often makes the subproblems in (1.4) extremely easy.

Next, we will show that after an appropriate reformulation, the LP model (1.1) can be solved by the ADMM scheme (1.4); this application results in a per-iteration complexity of O(mn) where m is the constraint number and n is the variable dimension. Moreover, at each iteration, there are m subproblems that are eligible for parallel computation, and they all have closed-form solutions. Indeed, each of these subproblems only requires O(n) flops. We refer to [8] for some augmented Lagrangian-based efforts to LP.

2 Reformulation

In this section, we reformulate the LP model (1.1) as a more favorable form so that the ADMM scheme (1.4) can be used conveniently. Without loss of generality, we assume m is odd, i.e., \(m=2l+1\) where l is an integer. For the case where m is even, we can add a dummy constraint to make m odd (or vice versa if m is assumed to be even).

Clearly, if we introduce auxiliary variables \(x_i \in \mathbb {R}^n\) for \(i=1,\cdots ,m\) and define

$$\begin{aligned} \theta _i(x_i)=c^\mathrm{T}x_i\;\; \hbox {and} \;\; X_i:=\{ x\in \mathbb {R}^n \, |\, a_i^\mathrm{T} x \geqslant b_i \},\; i=1,\cdots ,m, \end{aligned}$$

the LP model (1.1) can be written as

$$\begin{aligned} \begin{array}{rl} \min &{} \sum \limits _{i=1}^m \theta _i(x_i) \\ \quad \hbox {s.t.} &{} \left( \begin{array}{ccccccc} I &{} -I &{} &{} &{} &{} &{} \\ &{} I &{} -I &{} &{} &{} &{} \\ &{} &{} I &{} -I &{} &{} &{} \\ &{} &{} &{} \ddots &{} \ddots &{} &{} \\ &{} &{} &{} &{} \ddots &{} \ddots &{} \\ &{} &{} &{} &{} &{} I &{} -I \end{array}\right) \left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_{m-1} \\ x_m \end{array}\right) = 0. \\ &{} \;\; x_i\in X_i, \quad i=1,\cdots , m. \end{array} \end{aligned}$$
(2.1)

Let us denote by A the coefficient matrix in (2.1). Then we have

$$\begin{aligned} \mathcal{A}=(A_1, A_2, \cdots , A_m)=\left( \begin{array}{ccccccc} I &{} -I &{} &{} &{} &{} &{} \\ &{} I &{} -I &{} &{} &{} &{} \\ &{} &{} I &{} -I &{} &{} &{} \\ &{} &{} &{} \ddots &{} \ddots &{} &{} \\ &{} &{} &{} &{} \ddots &{} \ddots &{} \\ &{} &{} &{} &{} &{} I &{} -I \end{array}\right) _{(m-1)\times m \;\hbox {blocks}}, \end{aligned}$$

where \(A_i\)’s denote the columns of A. For these columns \(A_i\)’s, we have

$$\begin{aligned} A_i^\mathrm{T}A_j =\left\{ \begin{array}{ll} I, &{}\quad \hbox {if}\quad i=j=1 \quad \hbox {or} \quad i=j=m, \\ 2I, &{}\quad \hbox {if}\quad 1\ne i=j \ne m, \\ -I, &{}\quad \hbox {if}\quad |i-j|=1,\\ 0, &{}\quad \hbox {otherwise}. \end{array} \right. \end{aligned}$$

Further, let us regroup the variables, functions, and constraint sets in (2.1) as

$$\begin{aligned} {\varvec{x}}_1= & {} \left( \begin{array}{c}x_1\\ x_3 \\ \vdots \\ x_m\end{array} \right) , \quad {\varvec{x}}_2=\left( \begin{array}{c} x_2\\ x_4\\ \vdots \\ x_{m-1}\end{array} \right) , \quad \\&\mathcal{A}_1 =(A_1,A_3,\cdots , A_m), \quad \mathcal{A}_2 =(A_2,A_4,\cdots ,A_{m-1}),\\ {\varvec{\vartheta }}_1({\varvec{x}}_1)= & {} \theta _1(x_1) + \theta _3(x_3) + \cdots + \theta _m(x_m),\\&{\varvec{\vartheta }}_2({\varvec{x}}_2)= \theta _2(x_2) + \theta _4(x_4) + \cdots + \theta _{m-1}(x_{m-1}), \end{aligned}$$

and

$$\begin{aligned} \mathcal{X}_1=X_1\times X_3\times \cdots \times X_m, \qquad \mathcal{X}_2=X_2\times X_4\times \cdots \times X_{m-1}. \end{aligned}$$

Then, the model (2.1) is a special case of the block-wise model (1.2) with the specifications above and \({\varvec{b}}=0\). Thus, the ADMM scheme (1.4) is applicable. Note that we additionally have the following identities:

$$\begin{aligned} \mathcal{A}_1^\mathrm{T}\mathcal{A}_1 = \left( \begin{array}{ccccc} I &{} \quad &{}\quad &{}\quad &{} \\ &{}\quad 2I &{}\quad &{}\quad &{} \\ &{}\quad &{}\quad \ddots &{}\quad &{} \\ &{}\quad &{}\quad &{}\quad 2I &{} \\ &{} \quad &{}\quad &{}\quad &{} I \end{array}\right) _{\frac{m+1}{2}\; \hbox {blocks}}, \qquad \mathcal{A}_2^\mathrm{T}\mathcal{A}_2 = \left( \begin{array}{cccc} 2I &{}\quad &{}\quad &{} \\ &{}\quad 2I &{}\quad &{} \\ &{}\quad &{}\quad \ddots &{} \\ &{}\quad &{}\quad &{} 2I \end{array}\right) _{\frac{m-1}{2} \;\hbox {blocks}}, \end{aligned}$$

and

$$\begin{aligned} A_i^\mathrm{T}A_j= \left\{ \begin{array}{ll} 0, &{}\quad \hbox {if}\quad |i-j|>1, \\ -I, &{}\quad \hbox {if}\quad |i-j|=1, \end{array} \right. \end{aligned}$$
(2.2)

which are actually important facts that make the implementation of the ADMM scheme (1.4) extremely easy.

3 Application of ADMM for LP

Recall we assume \(m=2l+1\) in (1.1). Moreover, to implement the ADMM (1.4) to the reformulation (2.1), the Lagrange multiplier \({\varvec{\lambda }}\) can be denoted as

$$\begin{aligned} {\varvec{\lambda }}=\left( \begin{array}{c} \lambda _1\\ \lambda _2\\ \vdots \\ \lambda _{m-1}\end{array} \right) . \end{aligned}$$

3.1 Algorithm

Now, let us elucidate the k-th iteration of the ADMM scheme (1.4) when it is applied to solve the model (2.1). More specifically, starting from given \({\varvec{x}}_2^k\) and \({\varvec{\lambda }}^k\), the new iterate \(({\varvec{x}}_1^{k+1},{\varvec{x}}_2^{k+1}, {\varvec{\lambda }}^{k+1})\) is generated by the following steps.

Step 1 With given \(({\varvec{x}}_2^k, {\varvec{\lambda }}^k)\), obtain

$$\begin{aligned} {\varvec{x}}_1^{k+1} = \mathrm{argmin} \bigl \{ \mathcal{L}_{\beta }({\varvec{x}}_1,{\varvec{x}}_2^k,{\varvec{\lambda }}^k)\; \big | \; {\varvec{x}}_1\in \mathcal{X}_1 \bigr \} \end{aligned}$$

via

$$\begin{aligned} \left\{ \begin{array}{l} x_1^{k+1} =\mathrm{argmin}\left\{ \theta _1(x_1) + \frac{\beta }{2}\Vert x_1 - \left[ x_2^k + \frac{1}{\beta } \lambda _1^k\right] \Vert ^2 \,|\, x_1\in X_1\right\} , \\ \quad \hbox {For } p=1, \cdots , l-1, \hbox {do}\\ x_{2p+1}^{k+1} = \mathrm{argmin}\{\theta _{2p+1}(x_{2p+1}) +\beta \Vert x_{2p+1} - q_p\Vert ^2 | x_{2p+1}\in X_{2p+1} \}, \\ \quad \hbox {where} \quad q_p=\frac{1}{2} \left[ \left( x_{2p}^k + x_{2(p+1)}^k\right) + \frac{1}{\beta }\left( -\lambda _{2p}^k + \lambda _{2p+1}^k\right) \right] .\\ x_{2l+1}^{k+1} = \mathrm{argmin}\left\{ \theta _{2l+1}(x_{2l+1}) + \frac{\beta }{2}\Vert x_{2l+1} - \left[ x_{2l}^k - \frac{1}{\beta }\lambda _{2l}^k\right] \Vert ^2 | x_{2l+1}\in X_{2l+1}\right\} . \end{array} \right. \end{aligned}$$
(3.1a)

Step 2 With given \(({\varvec{x}}_1^{k+1}, {\varvec{\lambda }}^k)\), obtain

$$\begin{aligned} {\varvec{x}}_2^{k+1} = \mathrm{{argmin}} \bigl \{ \mathcal{L}_{\beta }({\varvec{x}}_1^{k+1},{\varvec{x}}_2,{\varvec{\lambda }}^k)\; \big | \; {\varvec{x}}_2\in \mathcal{X}_2 \bigr \} \end{aligned}$$

via

$$\begin{aligned} \left\{ \begin{array}{l} \hbox {For } p=1, \cdots , l, \hbox {do}\\ \quad x_{2p}^{k+1} = \mathrm{{argmin}}\{\theta _{2p}(x_{2p}) +\beta \Vert x_{2p} - q_p\Vert ^2 | x_{2p}\in X_{2p} \}, \\ \qquad \hbox {where} \quad q_p=\frac{1}{2} \left[ \left( x_{2p-1}^{k+1} + x_{2p+1}^{k+1}\right) + \frac{1}{\beta }\left( -\lambda _{2p-1}^k + \lambda _{2p}^k\right) \right] . \end{array} \right. \end{aligned}$$
(3.1b)

Step 3 Update the Lagrange multipliers \( {\varvec{\lambda }}^{k+1} = {\varvec{\lambda }}^k - \beta \left( \mathcal{A}_1{\varvec{x}}_1^{k+1} + \mathcal{A}_2{\varvec{x}}_2^{k+1}\right) \) via

$$\begin{aligned} \lambda _p^{k+1} =\lambda _p^k -\beta \left( x_p^{k+1} -x_{p+1}^{k+1}\right) , \quad p=1, 2, \cdots , m-1. \end{aligned}$$
(3.1c)

3.2 An Illustrative Example

Let us take the particular example of (1.1) with \(m=5\) and see how to implement the ADMM (1.4). That is, we consider the specific case of (2.1):

$$\begin{aligned} \begin{array}{cl} \min &{} \theta _1(x_1) + \theta _2(x_2) +\theta _3(x_3) +\theta _4(x_4) +\theta _5(x_5) \\ \hbox {s.t.} &{} \left( \begin{array}{rrrrr} I &{} -I &{} &{} &{} \\ &{} I &{} -I &{} &{} \\ &{} &{} I &{} -I &{} \\ &{} &{} &{} I &{} -I \\ \end{array}\right) \left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{array}\right) = 0 \\ &{} \;\; x_i\in X_i, \quad i=1,\cdots , 5. \end{array} \end{aligned}$$
(3.2)

For the coefficient matrix A in (3.2), we have

$$\begin{aligned} A_1= \left( \begin{array}{c} I \\ 0 \\ 0 \\ 0 \end{array} \right) ,\;\; A_2= \left( \begin{array}{c} -I \\ I \\ 0 \\ 0 \end{array} \right) , \;\; A_3= \left( \begin{array}{c} 0 \\ - I \\ I \\ 0 \end{array} \right) , \;\; A_4= \left( \begin{array}{c} 0 \\ 0 \\ - I \\ I \end{array} \right) \;\; \hbox {and} \;\; A_5= \left( \begin{array}{c} 0 \\ 0 \\ 0 \\ - I \end{array} \right) .\nonumber \\ \end{aligned}$$
(3.3)

We suggest regrouping this model as

$$\begin{aligned} \begin{array}{cccccc} \min &{}\bigl ( \theta _1(x_1) +\theta _3(x_3) +\theta _5(x_5) \bigr ) + \bigl ( \theta _2(x_2) + \theta _4(x_4)\bigr )\\ \hbox {s.t.} &{} \left( \begin{array}{rrr} I &{} &{} \\ &{} - I &{} \\ &{} I &{} \\ &{} &{} -I \end{array}\right) \left( \begin{array}{c} x_1 \\ x_3 \\ x_5 \end{array}\right) + \left( \begin{array}{rrr} -I &{} \\ I &{} \\ &{} -I \\ &{} I \end{array}\right) \left( \begin{array}{c} x_2 \\ x_4 \end{array}\right) = 0 \\ &{} x_1\in X_1,\, x_3\in X_3,\, x_5\in X_5; \qquad x_2\in X_2,\, x_4\in X_4. \end{array} \end{aligned}$$
(3.4)

Then, using these notation:

$$\begin{aligned} {\varvec{x}}_1=\left( \begin{array}{c}x_1\\ x_2 \\ x_3\end{array} \right) , \qquad {\varvec{x}}_2=\left( \begin{array}{c} x_2\\ x_4\end{array} \right) , \quad \mathcal{A}_1 =(A_1,A_3,A_5), \qquad \mathcal{A}_2 =(A_2,A_4),\nonumber \\ {\varvec{\vartheta }}_1({\varvec{x}}_1)= \theta _1(x_1) + \theta _3(x_3) + \theta _5(x_5), \qquad {\varvec{\vartheta }}_2({\varvec{x}}_2)= \theta _2(x_2) + \theta _4(x_4),\nonumber \\ \end{aligned}$$
(3.5)

and

$$\begin{aligned} \mathcal{X}_1=X_1\times X_3\times X_5, \qquad \mathcal{X}_2=X_2\times X_4, \end{aligned}$$

the model (3.2) is reformulated as a special case of (1.2) with

$$\begin{aligned} \mathcal{A}_1^\mathrm{T}\mathcal{A}_1 = \left( \begin{array}{ccc} I &{} &{} \\ &{} 2I &{} \\ &{} &{} I \end{array}\right) _{\frac{5+1}{2}\; \hbox {blocks}} \quad \hbox {and} \quad \mathcal{A}_2^\mathrm{T}\mathcal{A}_2 = \left( \begin{array}{cc} 2I &{} \\ &{} 2I \end{array}\right) _{\frac{5-1}{2} \;\hbox {blocks}}. \end{aligned}$$

To execute the k-th iteration of the ADMM (1.4) for the problem (3.4), we start with the given iterate

$$\begin{aligned} {\varvec{x}}_2^k=\left( \begin{array}{c} x_2^k\\ x_4^k\end{array} \right) \qquad \hbox {and}\qquad {\varvec{\lambda }}^{k} =\left( \begin{array}{c} \lambda _1^k\\ \lambda _2^k\\ \lambda _3^k\\ \lambda _4^k\end{array} \right) . \end{aligned}$$

Below, let us explain how to solve the resulting subproblems (3.1a) and (3.1b).

(1) Obtain \( {\varvec{x}}_1^{k+1} = \mathrm{argmin} \bigl \{ \mathcal{L}_{\beta }({\varvec{x}}_1,{\varvec{x}}_2^k,{\varvec{\lambda }}^k)\; \big | \; {\varvec{x}}_1\in \mathcal{X}_1 \bigr \}. \)

The first step of (1.4) is

$$\begin{aligned} \left( \begin{array}{c} x_1^{k+1} \\ x_3^{k+1} \\ x_5^{k+1} \end{array}\right)= & {} \mathrm{argmin} \left\{ \begin{array}{l} \theta _1(x_1) + \theta _3(x_3) + \theta _5(x_5) + \theta _2(x_2^k) + \theta _4(x_4^k) \\ - ({\varvec{\lambda }}^k)^\mathrm{T}\bigl ( A_1x_1 + A_3x_3 + A_5x_5 + (A_2x_2^k + A_4x_4^k)\bigr ) \\ + \frac{\beta }{2}\Vert A_1x_1 + A_3x_3 + A_5x_5 + (A_2x_2^k + A_4x_4^k) \Vert ^2 \end{array} \left| \begin{array}{c} x_1\in X_1, \\ x_3\in X_3, \\ x_5\in X_5 \end{array}\right. \right\} \nonumber \\= & {} \mathrm{argmin} \left\{ \begin{array}{l} \theta _1(x_1) + \theta _3(x_3) + \theta _5(x_5) \\ - ({\varvec{\lambda }}^k)^\mathrm{T}\bigl ( A_1x_1 + A_3x_3 + A_5x_5\bigr ) \\ + \frac{\beta }{2}\Vert \bigl (A_1x_1 + A_3x_3 + A_5x_5\bigr ) + (A_2x_2^k + A_4x_4^k)\Vert ^2 \end{array} \left| \begin{array}{c} x_1\in X_1, \\ x_3\in X_3, \\ x_5\in X_5 \end{array}\right. \right\} .\nonumber \\ \end{aligned}$$
(3.6)

Note that we get the second equation in (3.6) by ignoring some constant terms in its objective function. Notice that the first-order optimality condition of the optimization problem (3.6) is

$$\begin{aligned} \begin{array}{l} \left( x_1^{k+1},x_3^{k+1},x_5^{k+1}\right) \in {X}_1\times {X}_3\times {X}_5, \quad \left( \begin{array}{c} \theta _1(x_1) - \theta _1(x_1^{k+1}) \\ +\theta _3(x_3) - \theta _3(x_3^{k+1}) \\ +\theta _5(x_5) - \theta _5(x_5^{k+1}) \end{array}\right) + \left( \begin{array}{c} x_1 - x_1^{k+1} \\ x_3 - x_3^{k+1} \\ x_5 - x_5^{k+1} \end{array}\right) ^\mathrm{T} \\ \qquad \times \left\{ \left( \begin{array}{c} -A_1^\mathrm{T}{\varvec{\lambda }}^k \\ -A_3^\mathrm{T}{\varvec{\lambda }}^k \\ -A_5^\mathrm{T}{\varvec{\lambda }}^k \end{array}\right) + \beta \left( \begin{array}{c} A_1^\mathrm{T} \\ A_3^\mathrm{T} \\ A_5^\mathrm{T} \end{array}\right) \bigg [\big (A_1x_1^{k+1} + A_3x_3^{k+1} + A_5x_5^{k+1}\big ) + \big (A_2x_2^k + A_4x_4^k\big )\bigg ] \right\} \\ \quad \geqslant 0,\; \forall \, (x_1,x_3,x_5) \in {X}_1\times {X}_3\times {X}_5. \end{array} \end{aligned}$$

It follows from the orthogonal property (2.2) that \( (x_1^{k+1}, x_3^{k+1}, x_5^{k+1}) \in {X}_1\times {X}_3\times {X}_5\), and

$$\begin{aligned} \left\{ \begin{array}{ll} \theta _1(x_1) - \theta _1(x_1^{k+1}) + (x_1 - x_1^{k+1})^\mathrm{T} \bigl \{ -A_1^\mathrm{T}{\varvec{\lambda }}^k + \beta A_1^\mathrm{T} \bigl [A_1x_1^{k+1}+ A_2x_2^k\bigr ] \bigr \} \geqslant 0, \;\; &{}\quad \forall x_1\in \mathcal{X}_1, \\ \theta _3(x_3) - \theta _3(x_3^{k+1}) + (x_3 - x_3^{k+1})^\mathrm{T} \bigl \{ -A_3^\mathrm{T}{\varvec{\lambda }}^k + \beta A_3^\mathrm{T} \bigl [A_3x_3^{k+1}+ (A_2x_2^k + A_4x_4^k)\bigr ] \bigr \} \geqslant 0, &{}\quad \forall x_3\in \mathcal{X}_3, \\ \theta _5(x_5) - \theta _5(x_5^{k+1}) + (x_5 - x_5^{k+1})^\mathrm{T} \bigl \{ -A_5^\mathrm{T}{\varvec{\lambda }}^k + \beta A_5^\mathrm{T} \bigl [A_5x_5^{k+1}+ A_4x_4^k\bigr ] \bigr \} \geqslant 0, &{}\quad \forall x_5\in \mathcal{X}_5. \end{array} \right. \end{aligned}$$

According to the structure \(A_j\) in (3.3), we further have \( (x_1^{k+1}, x_3^{k+1}, x_5^{k+1}) \in {X}_1\times {X}_3\times {X}_5\) and

$$\begin{aligned} \left\{ \begin{array}{rll} \theta _1(x_1)-\theta _1(x_1^{k+1}) &{} +\; (x_1-x_1^{k+1})^\mathrm{T} \bigl \{ - \lambda _1^k + \beta [x_1^{k+1}- x_2^k] \bigr \}\geqslant 0, &{}\quad \forall x_1\in X_1, \\ \theta _3(x_3)-\theta _3(x_3^{k+1}) &{} +\; (x_3-x_3^{k+1})^\mathrm{T} \bigl \{ (\lambda _2^k - \lambda _3^k) + \beta [2x_3^{k+1}- (x_2^k + x_4^k)] \bigr \}\geqslant 0, &{}\quad \forall x_3\in X_3, \\ \theta _5(x_5)-\theta _5(x_5^{k+1}) &{} + \;(x_5-x_5^{k+1})^\mathrm{T} \bigl \{\lambda _4^k +\beta [x_5^{k+1}-x_4^k] \bigr \}\geqslant 0, &{}\quad \forall x_5\in X_5. \end{array} \right. \end{aligned}$$

Based on these inequalities, the solution of (3.6) can be obtained via

$$\begin{aligned} \left\{ \begin{array}{rcl} x_1^{k+1} &{} = &{} \mathrm{argmin}\{ \theta _1(x_1) + \frac{\beta }{2}\Vert x_1 - [x_2^k + \frac{1}{\beta } \lambda _1^k]\Vert ^2\, \big | \, x_1\in X_1\}, \\ x_3^{k+1} &{} = &{} \mathrm{argmin}\{ \theta _3(x_3) +\beta \Vert x_3 - \frac{1}{2} [(x_2^k + x_4^k) + \frac{1}{\beta }(-\lambda _2^k + \lambda _3^k)]\Vert ^2 \,\big |\, x_3\in X_3\}, \\ x_5^{k+1} &{} = &{} \mathrm{argmin}\{ \theta _5(x_5) + \frac{\beta }{2}\Vert x_5 - [x_4^k - \frac{1}{\beta }\lambda _4^k]\Vert ^2 \, \big |\, x_5\in X_5\}. \end{array} \right. \nonumber \\ \end{aligned}$$
(3.7)

This is just the concrete form of (3.1a) for the case where \(l=2\).

(2) Obtain \( {\varvec{x}}_2^{k+1} = \mathrm{argmin} \bigl \{ \mathcal{L}_{\beta }({\varvec{x}}_1^{k+1},{\varvec{x}}_2,{\varvec{\lambda }}^k)\; \big | \; {\varvec{x}}_2\in \mathcal{X}_2 \bigr \}. \)

The second step of the k-th iteration of (1.4) is

$$\begin{aligned} \left( \begin{array}{c} x_2^{k+1} \\ x_4^{k+1} \end{array}\right)= & {} \mathrm{{argmin}} \left\{ \begin{array}{l} \bigl (\theta _1(x_1^{k+1}) + \theta _3(x_3^{k+1}) + \theta _5(x_5^{k+1})\bigr ) + \bigl (\theta _2(x_2) + \theta _4(x_4) \bigr ) \\ - ({\varvec{\lambda }}^k)^\mathrm{T}\bigl ( (A_1x_1^{k+1} + A_3x_3^{k+1} + A_5x_5^{k+1} + (A_2x_2 + A_4x_4)\bigr ) \\ + \frac{\beta }{2}\Vert \bigl (A_1x_1^{k+1} + A_3x_3^{k+1} + A_5x_5^{k+1}\bigr ) + (A_2x_2 + A_4x_4 ) \Vert ^2 \end{array} \left| \begin{array}{c} x_2\in X_2, \\ x_4\in X_4, \end{array}\right. \right\} \nonumber \\= & {} \mathrm{{argmin}} \left\{ \begin{array}{l} \theta _2(x_2) + \theta _4(x_4) - ({\varvec{\lambda }}^k)^\mathrm{T}\bigl ( A_2x_2 + A_4x_4 \bigr ) + \\ \frac{\beta }{2}\Vert \bigl (A_1x_1^{k+1} + A_3x_3^{k+1} + A_5x_5^{k+1}\bigr ) + \bigl (A_2x_2 + A_4x_4 \bigr )\Vert ^2 \end{array} \left| \begin{array}{c} x_2\in X_2, \\ x_4\in X_4 \end{array}\right. \right\} .\nonumber \\ \end{aligned}$$
(3.8)

Again, we get the second equation in (3.8) by ignoring some constant terms in its objective function. Since the first-order optimality condition of the optimization problem (3.8) is

$$\begin{aligned} \begin{array}{l} \left( x_2^{k+1},x_4^{k+1}\right) \in {X}_2\times {X}_4, \quad \left( \begin{array}{c} \theta _2(x_2) - \theta _2\left( x_2^{k+1}\right) \\ +\theta _4(x_4) - \theta _4\left( x_4^{k+1}\right) \end{array}\right) + \left( \begin{array}{c} x_2 - x_2^{k+1} \\ x_4 - x_4^{k+1} \end{array}\right) ^\mathrm{T} \\ \qquad \times \left\{ \left( \begin{array}{c} -A_2^\mathrm{T}{\varvec{\lambda }}^k \\ -A_4^\mathrm{T}{\varvec{\lambda }}^k \end{array}\right) + \beta \left( \begin{array}{c} A_2^\mathrm{T} \\ A_4^\mathrm{T} \end{array}\right) \left[ \left( A_2x_2^{k+1} + A_4x_4^{k+1}\right) +\left( A_1x_1^{k+1} + A_3x_3^{k+1} + A_5x_5^{k+1}\right) \right] \right\} \\ \quad \geqslant 0,\; \forall \, (x_2,x_4)\in {X}_2\times {X}_4, \end{array} \end{aligned}$$

it follows from the orthogonal property (2.2) that \( (x_2^{k+1}, x_4^{k+1}) \in {X}_2\times {X}_4\), and

$$\begin{aligned} \left\{ \begin{array}{ll} \theta _2(x_2) - \theta _2(x_2^{k+1}) + (x_2 - x_2^{k+1})^\mathrm{T} \bigl \{ -A_2^\mathrm{T}{\varvec{\lambda }}^k + \beta A_2^\mathrm{T} \bigl [A_2x_2^{k+1}+ (A_1x_1^{k+1} + A_3x_3^{k+1}) \bigr ] \bigr \} \geqslant 0, &{}\quad \forall x_2\in \mathcal{X}_2, \\ \theta _4(x_4) - \theta _4(x_4^{k+1}) + (x_4 - x_4^{k+1})^\mathrm{T} \bigl \{ -A_4^\mathrm{T}{\varvec{\lambda }}^k + \beta A_4^\mathrm{T} \bigl [A_4x_4^{k+1}+ (A_3x_3^{k+1} + A_5x_5^{k+1}) \bigr ] \bigr \} \geqslant 0, &{}\quad \forall x_4\in \mathcal{X}_4. \end{array} \right. \end{aligned}$$

According to the structure \(A_j\) in (3.3), we further have \( (x_2^{k+1}, x_4^{k+1}) \in {X}_2\times {X}_4\), and

$$\begin{aligned} \left\{ \begin{array}{rll} \theta _2(x_2)-\theta _2(x_2^{k+1}) &{} +\; (x_2-x_2^{k+1})^\mathrm{T} \bigl \{ (\lambda _1^k - \lambda _2^k) + \beta [2x_2^{k+1}- (x_1^{k+1}+ x_3^{k+1})] \bigr \}\geqslant 0, &{}\quad \forall x_2\in X_2, \\ \theta _4(x_4)-\theta _4(x_4^{k+1}) &{} + \;(x_4-x_4^{k+1})^\mathrm{T} \bigl \{(\lambda _3^k - \lambda _4^k) +\beta [2x_4^{k+1}- (x_3^{k+1} + x_5^{k+1})] \bigr \}\geqslant 0, &{}\quad \forall x_4\in X_4. \end{array} \right. \end{aligned}$$

Thus, the solution of (3.8) can be obtained via

$$\begin{aligned} \left\{ \begin{array}{rcl} x_2^{k+1} &{} = &{} \mathrm{argmin}\{ \theta _2(x_2) +\beta \Vert x_2 - \frac{1}{2} [(x_1^{k+1} + x_3^{k+1}) + \frac{1}{\beta }(-\lambda _1^k + \lambda _2^k)]\Vert ^2 \, \big |\, x_2\in X_2\}, \\ x_4^{k+1} &{} = &{} \mathrm{argmin}\{ \theta _4(x_4) +\beta \Vert x_4 - \frac{1}{2} [(x_3^{k+1} + x_5^{k+1}) + \frac{1}{\beta }(-\lambda _3^k + \lambda _4^k)]\Vert ^2 \, \big |\, x_4\in X_4\}. \end{array} \right. \nonumber \\ \end{aligned}$$
(3.9)

This is just the concrete form of (3.1b) for the case where \(l=2\).

3.3 Subproblems

Recall that when the LP model (1.1) is considered, we have

$$\begin{aligned} X_i= \{ x\in \mathbb {R}^n \, |\, a_i^\mathrm{T} x \geqslant b_i \}, \quad i=1, \cdots , m, \end{aligned}$$

in (2.1). It is thus clear that when the ADMM scheme (1.4) is used to solve (1.1), the computation at each iteration is dominated by the subproblems in form of

$$\begin{aligned} \min \{ \Vert x_i- q_i\Vert ^2 \, |\, x_i\in \mathbb {R}^n, a_i^\mathrm{T}x_i \geqslant b_i \}, \quad i=1, \cdots , m, \end{aligned}$$

where \(a_i, q_i\in \mathbb {R}^n\) are given vectors and \(b_i\in \mathbb {R}\) is a given scalar. In this subsection, we discuss how to solve these subproblems. The main result is summarized in the following theorem.

Theorem 3.1

For given \(a, q\in \mathbb {R}^n\) and \(b\in \mathbb {R}\), we have

$$\begin{aligned} \mathrm{argmin} \{ \Vert x- q\Vert ^2 \, |\, x\in \mathbb {R}^n, a^\mathrm{T}x \geqslant b \}= q + \left( \frac{b-a^\mathrm{T}q}{a^\mathrm{T}a}\right) _+ a. \end{aligned}$$
(3.10)

Proof

First, for any \(q\in \mathbb {R}^n\), we know that

$$\begin{aligned} q_1=p_+, \qquad q_2= (-p)_+ \end{aligned}$$

are the unique decompositions satisfying the following conditions:

$$\begin{aligned} q=q_1 - q_2, \qquad 0 \leqslant q_1\, \perp \, q_2 \geqslant 0. \end{aligned}$$
(3.11)

Note that the Lagrangian function of the minimization problem in (3.10) is

$$\begin{aligned} L(x,\lambda ) = \Vert x- q\Vert ^2 - \lambda ( a^\mathrm{T}x - b). \end{aligned}$$

The first-order optimality condition is

$$\begin{aligned}&2 (x-q) -\lambda a =0, \end{aligned}$$
(3.12a)
$$\begin{aligned}&0 \leqslant \lambda \, \perp \, a^\mathrm{T}x -b \geqslant 0. \end{aligned}$$
(3.12b)

Left multiplying \(a^\mathrm{T}\) to (3.12a), we get

$$\begin{aligned} \left( a^{\mathrm{T}x} -b\right) - \frac{1}{2} \lambda a^{\mathrm{T}a} = a^{\mathrm{T}q} -b. \end{aligned}$$

Using (3.12b) and (3.11), we get

$$\begin{aligned} a^\mathrm{T}x - b = \left( a^\mathrm{T}q-b\right) _+, \qquad \frac{1}{2} \lambda a^\mathrm{T}a = [-(a^\mathrm{T}q-b)]_+, \end{aligned}$$

and thus

$$\begin{aligned} \lambda = 2 \Bigl [ \frac{b-a^\mathrm{T}q}{a^\mathrm{T}a}\Bigr ]_+. \end{aligned}$$

Substituting it into (3.12a), we obtain the assertion (3.10) immediately.

This theorem thus shows that when the ADMM scheme (1.4) is applied to (1.1), all the resulting subproblems have closed-form solutions. This ADMM application is thus easy to be implemented. Moreover, as shown, at each iteration, there are m subproblems that are eligible for parallel computation; each of them only requires O(n) flops. We summarize this complexity result in the following theorem.

Theorem 3.2

When the ADMM scheme (1.4) is applied to (1.1) via the reformulation (2.1), at each iteration, there are m subproblems that are eligible for parallel computation; each of them only requires O(n) flops.

4 Extension

We can easily extend our previous analysis to the LP model with equality constraints:

$$\begin{aligned} \min \{ c^\mathrm{T}x \,|\, a_i^\mathrm{T} x= b_i, \; i=1, 2, \cdots , m, x\geqslant 0 \}. \end{aligned}$$
(4.1)

Indeed, we can reformulate (4.1) as

$$\begin{aligned} \begin{array}{rl} \min &{} \sum \limits _{i=1}^m \theta _i(x_i) \\ \hbox {s.t.} &{} \left( \begin{array}{cccccc} I &{}\quad &{} \quad &{}\quad &{}\quad &{} -I \\ &{} I &{}\quad &{}\quad &{} \quad &{} -I \\ &{} &{}\quad \ddots &{} \quad &{}\quad &{} \vdots \\ &{} &{}\quad &{}\quad I &{} \quad &{} -I \\ &{} &{}\quad &{} \quad &{}\quad I &{} -I \end{array}\right) \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_{m-1} \\ x_m\\ y \end{array}\right) = 0, \\ &{} \;\; x_i\in X_i =\{x\in \mathbb {R}^n \, |\, a_i^\mathrm{T}x= b_i\} , \quad i=1,\cdots , m, \\ &{} \;\; y\in Y =\{y\in \mathbb {R}^n \, |\, y\geqslant 0\} . \end{array} \end{aligned}$$
(4.2)

with \(\theta _i(x_i)=c^\mathrm{T}x_i\) for \(i=1,\cdots ,m\). Furthermore, (4.2) can be regrouped as

$$\begin{aligned} {\varvec{x}}_1=\left( \begin{array}{c}x_1\\ x_2 \\ \vdots \\ x_{m-1} \\ x_m\end{array} \right) , \quad {\varvec{x}}_2= y, \qquad \mathcal{A}_1= \left( \begin{array}{ccccc} I &{} &{} &{} &{} \\ &{} I &{} &{} &{} \\ &{} &{} \ddots &{} &{} \\ &{} &{} &{} I &{} \\ &{} &{} &{} &{} I \end{array}\right) \quad \hbox {and} \quad \mathcal{A}_2= \left( \begin{array}{c} -I \\ -I \\ \vdots \\ -I \\ -I \end{array}\right) , \end{aligned}$$

which is a special case of (1.2), and thus the ADMM scheme (1.4) can be applied. Note that for the case (4.2), \(\mathcal{A}_1\) is an identity matrix and \(\mathcal{A}_2\) can be viewed a “one column” matrix. Thus, as the analysis in Sect. 3, the resulting subproblems are all easy. Indeed, these subproblems have the forms of

$$\begin{aligned} \min \{ \Vert x- q\Vert ^2 \, |\, x\in \mathbb {R}^n, a^\mathrm{T}x = b \} \qquad \hbox {or} \qquad \min \{ \Vert x- q\Vert ^2 \, |\, x\in \mathbb {R}^n_+ \} , \end{aligned}$$

whose closed-form solutions can be given by

$$\begin{aligned} q + \left( \frac{b-a^\mathrm{T}q}{a^\mathrm{T}a}\right) a \qquad \hbox {or} \qquad q_+ , \end{aligned}$$

respectively. Similarly as the analysis in Sect. 3, the ADMM scheme (1.4) for (4.1) also needs to solve m subproblems that are eligible for parallel computation, and each of them only requires O(n) flops.

Remark 4.1

Note that one can artificially treat each \(x_i \in \mathbb {R}\) as one block of variable and each \(c_ix_i\) as one function; thus the direct extension of ADMM for a multiple-block (more than two block) can be applied to solve (4.1). However, as proved in [9], the direct extension of ADMM is not necessarily convergent.

Finally, we mention that we can extend our techniques for the LP models (1.1) and (4.1) to a more general model

$$\begin{aligned} \min \left\{ \theta (x) \,|\, x\in \prod _{i=1}^m X_i \right\} , \end{aligned}$$
(4.3)

where \(\theta (x):\mathbb {R}^n\rightarrow \mathbb {R}\) is a convex (not necessarily linear) function and \(X_i\)’s are closed convex nonempty sets that are not necessarily polyhedrons given by linear equalities or inequalities. This model (4.3) includes more applications such as the feasibility set problems and some image restoration models. We omit the detail for succinctness.

5 Conclusions

We show that the ADMM can be used to solve the canonical LP model. The iteration is easy to implement; the resulting per-iteration complexity is O(mn) where m is the constraint number and n is the variable dimension. The ADMM approach is completely different from the dominating simplex and interior point approaches in the literature. This is also a new application of ADMM that is different from most of its known applications in the literature. To use the ADMM, we need to introduce auxiliary variables and reformulate the LP model. The storage for variables is thus increased by m times accordingly. But, the decomposed m subproblems at each iteration are eligible for parallel computation, and each of them has a closed-form solution which can be obtained by O(n) flops. Thus, this new ADMM approach is particularly suitable for the LP scenario where there are many constraints and parallel computing infrastructure is available.