1 Introduction

Sparsity constrained optimization (SCO) is to minimize a general nonlinear function subject to sparsity constraint. It has wide applications in signal and image processing, machine learning, pattern recognition and computer vision, and so on. Recent years have witnessed a growing interest in the theory and algorithm for SCO, especially for SCO caused by the sparse recovery from linear or nonlinear observations.

SCO is actually a combinatorial optimization problem and it is generally NP-hard even for quadratic objective function [1]. So, usually continuous optimization theory is unable to cope with SCO and the research on existence of solutions to SCO is difficult. Negahban et al. [2] introduced the concept of restricted strong convexity (RSC) in convex optimization problem, and showed it is a sufficient condition for existence of unique solution for the convex program in a restricted region. Agarwal et al. [3] modified RSC and introduced the notions of restricted strong smoothness (RSS) that suffice to establish global linear convergence of a first-order method for the above problem. Later, various variants of RSC and RSS were developed and used in [4–7] to guarantee the existence of unique solution and corresponding error bound holding for SCO. Bahmani et al. [8] proposed stable restricted Hessian (SRH) for twice continuously differentiable objective functions and stable restricted linearization (SRL) for nonsmooth objective functions, and obtained that they are sufficient conditions to achieve the true unique solution to SCO in a finite number of iterations. Here, we should point out that these conditions can be regarded as some extensions or relaxations of restricted isometry property (RIP) by Candès and Tao [9] in compressed sensing (CS) [9, 10], where RIP suffices to guarantee that the \(l_0\)-minimization associated with CS from linear observations has a unique solution and is polynomially solvable. Recently, Beck and Eldar [11] introduced and analyzed three kinds of first-order necessary optimality conditions for the existence of solutions to SCO: basic feasibility, L-stationarity and coordinate-wise optimality. Basic feasibility is an extension of the necessary condition that gradient is zero for unconstrained optimization. L-stationarity is based on the notion of fixed-point equation for convex constrained problems and used to derive the iterative hard thresholding (IHT) algorithm for SCO.

In this paper, we try to investigate the existence of solutions of SCO by using the concepts of tangent cone and normal cone, which are very useful in characterizing feasible region and establishing optimality condition for constrained optimization problems. We first give the expressions of the Bouligand and Clarke tangent cones and normal cones of sparsity constraint. Then we establish the concepts of N-stationarity and T-stationarity for SCO, and analyze the relationship and differences among basic feasibility, L-stationarity, N-stationarity, and T-stationarity. Our analysis shows that they play an important role in optimality theory and algorithm design for SCO. Further, we give the second-order necessary and sufficient optimality conditions under the sense of Clarke tangent cone for the existence of local optimal solutions to SCO. Especially, we conclude the existence theorems for global optimal solutions to SCO with least squares objective function from sparse recovery of linear observations. At last, we extend these results to SCO with nonnegative constraint.

This paper is organized as follows. Section 2 studies the first- and second-order optimality conditions for sparsity constrained optimization. Section 3 extends the corresponding results in Sect. 2 to SCO with nonnegative constraint. The last section gives some concluding remarks.

2 Optimality Conditions

In this section, we study the first- and second-order necessary optimality conditions of the following SCO problem

$$\begin{aligned} \min ~~f(x),~~~~~\mathrm{s.t.}~~\Vert x\Vert _0\leqslant s, \end{aligned}$$
(2.1)

where \(f(x):\mathbb {R}^n\rightarrow \mathbb {R}\) is a continuously differentiable or twice continuously differentiable function. \(\Vert x\Vert _0\) is the \(l_0\)-norm of \(x\in \mathbb {R}^n\), which refers to the number of nonzero elements in the vector x. \(s<n\) is a positive integer. Let \(S\triangleq \{x\in \mathbb {R}^n:~\Vert x\Vert _0\leqslant s\}\) be the feasible region of (2.1).

We first consider the projection on sparse set S, named support projection. For \(\varOmega \subset \mathbb {R}^n\) being nonempty and closed, we call the mapping \(\text {P}_\varOmega : \mathbb {R}^n\rightarrow \varOmega \) the projector onto \(\varOmega \) if

$$\begin{aligned} \mathrm{P}_{\varOmega }(x):=\mathrm{argmin}_{y\in \varOmega }\Vert x-y\Vert . \end{aligned}$$

It is well known that the support projection \(\mathrm{P}_{S}(x)\) sets all but s largest absolute value components of x to zero. Carefully speaking, letting \(I_s(x):=\{j_1,j_2,\cdots ,j_s\}\subseteq \{1,2,\cdots ,n\}\) of indices of x with \(\min _{i\in I_s(x)}|x_i|\geqslant \max _{i\notin I_s(x)}|x_i|\), we have

$$\begin{aligned} \mathrm{P}_S(x)=\left\{ ~y\in \mathbb {R}^{n}: y_i= x_i,i\in I_s(x);~y_i= 0,i \notin I_s(x)~\right\} . \end{aligned}$$

As S is nonconvex, the support projection \(\mathrm{P}_{S}(x)\) is not single-valued. Letting \( M _i(x)\) denote the ith largest element of x, we have

$$\begin{aligned} M _1(x)\geqslant M _2(x)\geqslant \cdots \geqslant M _n(x). \end{aligned}$$

Denote \(|x|=\left( |x_1|, \cdots , |x_n|\right) ^\mathrm{T}\). If \( M _s(|x|)=0\) or \( M _s(|x|)> M _{s+1}(|x|)\), then \(\mathrm{P}_{S}(x)\) is single-valued, in such case,

$$\begin{aligned} \left( \mathrm{P}_S(x)\right) _i=\left\{ \begin{array}{l@{\quad }l} x_i,\quad &{} |x_i|\geqslant M _s(|x|), \\ 0,\quad &{} \mathrm {otherwise}. \end{array} \right. \end{aligned}$$

Otherwise,

$$\begin{aligned} \left( \mathrm{P}_S(x)\right) _i=\left\{ \begin{array}{l@{\quad }l} x_i, \quad &{} |x_i|> M _s(|x|), \\ x_i ~\mathrm {or} ~0, \quad &{} |x_i|= M _s(|x|), \\ 0, \quad &{} \mathrm {otherwise}. \end{array} \right. \end{aligned}$$

If there are more than one \(x_i\) such that \(|x_i|= M _s(|x|)\), only one element can be selected either randomly or according to some predefined ordering to be assigned itself, while others are assigned zeros.

2.1 Tangent Cone and Normal Cone

Recalling that for any nonempty set \(\varOmega \subseteq \mathbb {R}^{n}\), its Bouligand tangent cone \(\mathrm {T}^B_{\varOmega }(\bar{x})\), Clarke tangent cone \(\mathrm {T}^C_{\varOmega }(\bar{x})\) and corresponding Normal Cones \(\mathrm {N}^B_{\varOmega }(\bar{x})\) and \(\mathrm {N}^C_{\varOmega }(\bar{x})\) at point \(\bar{x}\in \varOmega \) are defined as [12]:

$$\begin{aligned}&\displaystyle \mathrm {T}^B_{\varOmega }(\bar{x}):= \left\{ ~d\in \mathbb {R}^{n}: \ \begin{array}{r}\exists ~\{x^k\}\subset \varOmega , \underset{k\rightarrow \infty }{\lim }x^k=\bar{x},~\lambda _k\geqslant 0,~k\in \mathbb {N}~ ~\text {such that}\nonumber \\ \underset{k\rightarrow \infty }{\lim }\lambda _k(x^k-\bar{x})=d~\end{array}\right\} ,\quad \\&\displaystyle \mathrm {T}^C_{\varOmega }(\bar{x}):= \left\{ ~d\in \mathbb {R}^{n}: \ \begin{array}{r} ~\text {For}~\forall ~\{x^k\}\subset \varOmega ,~\forall ~\{\lambda _k\}\subset \mathbb {R}_+ ~\text {with}~\underset{k\rightarrow \infty }{\lim }x^k=\bar{x},\nonumber \\ ~\underset{k\rightarrow \infty }{\lim }\lambda _k=0,~\exists ~\{y^k\}~\text {such that}\\ \underset{k\rightarrow \infty }{\lim }y^k=d~\text {and}~x^k+\lambda _{k}y^k\in \varOmega ,~ k\in \mathbb {N}~ \end{array}\right\} ,\\&\displaystyle \mathrm {N}^B_{\varOmega }(\bar{x}):= \left\{ ~d\in \mathbb {R}^{n}: \ \langle d, z\rangle \leqslant 0,~\forall ~z\in \mathrm {T}^B_{\varOmega }(\bar{x})~\right\} ,\nonumber \\&\displaystyle \mathrm {N}^C_{\varOmega }(\bar{x}):= \left\{ ~d\in \mathbb {R}^{n}: \ \langle d, z\rangle \leqslant 0,~\forall ~z\in \mathrm {T}^C_{\varOmega }(\bar{x})~\right\} . \end{aligned}$$
(2.2)

The following two theorems give the expressions of Bouligand and Clarke tangent cones and normal cones of sparse set S.

Theorem 2.1

For any \(\bar{x}\in S\) and letting \(\varGamma =\mathrm{supp}(\bar{x})\), the Bouligand tangent cone and corresponding normal cone of  S at \(\bar{x}\) are respectively

$$\begin{aligned} \mathrm {T}^B_{S}(\bar{x})= & {} \{~d\in \mathbb {R}^{n}:~\Vert d\Vert _0\leqslant s,~\Vert \bar{x}+\mu d\Vert _0\leqslant s~,\forall ~\mu \in \mathbb {R}~\} \end{aligned}$$
(2.3)
$$\begin{aligned}= & {} \bigcup _{\varUpsilon }~\mathrm{span}\left\{ ~{e}_i,~~ i\in \varUpsilon \supseteq \varGamma , |\varUpsilon |\leqslant s ~\right\} , \end{aligned}$$
(2.4)
$$\begin{aligned} \mathrm {N}^B_{S}(\bar{x})= & {} \left\{ \begin{array}{ll} \left\{ ~d\in \mathbb {R}^{n}:~d_i=0,~ i\in \varGamma ~\right\} =\mathrm{span}\left\{ ~{e}_i,~~ i\notin \varGamma ~\right\} , &{} \quad \mathrm{if}~~|\varGamma |=s,\\ \{0\}, &{}\quad \mathrm{if}~~|\varGamma |<s, \end{array}\right. \end{aligned}$$
(2.5)

where \({e}_i\in \mathbb {R}^{n}\) is a vector whose ith component is one and others are zeros, \(\mathrm{span}\{{e}_i,i\in \varGamma \}\) denotes the subspace of  \(\mathbb {R}^{n}\) spanned by \(\{~{e}_i:~i\in \varGamma \}\), and

$$\begin{aligned} \mathrm{supp}(x)=\{i\in \{1,\cdots ,n\}:~ x_i\ne 0\}. \end{aligned}$$

Proof

Denote the set of the right hand of (2.3) as D. It is not difficult to verify that D is equal to (2.4), and thus we only prove (2.3). First we prove \(\mathrm {T}^B_{S}(\bar{x})\subseteq D\). For any \(d\in \mathrm {T}^B_{S}(\bar{x})\), there is \(\lim _{k\rightarrow \infty }x^k=\bar{x},~x^k\in S,~\lambda _k\geqslant 0\) satisfies \(d=\lim _{k\rightarrow \infty }\lambda _k(x^k-\bar{x})\). Since \(\lim _{k\rightarrow \infty }x^k=\bar{x}\), there is \(k_0\) when \(k\geqslant k_0\), \(\varGamma \subseteq \mathrm{supp}(x^k)\). In addition, \(d=\lim _{k\rightarrow \infty }\lambda _k(x^k-\bar{x})\) derives \(\mathrm{supp}(d)\subseteq \mathrm{supp}(x^k)\), which combining with \(\Vert x^k\Vert _0\leqslant s\) when \(k\geqslant k_0\) and \(\varGamma \subseteq \mathrm{supp}(x^k)\) yields that \(\Vert d\Vert _0\leqslant s\) and \(\Vert \bar{x}+\mu d\Vert _0\leqslant s~,\forall ~\mu \in \mathbb {R}\). Next we prove \(\mathrm {T}^B_{S}(\bar{x})\supseteq D\). For any \(\Vert d\Vert _0\leqslant s, \Vert \bar{x}+\mu d\Vert _0\leqslant s~,\forall ~\mu \in \mathbb {R}\), we take any sequence \(\{\lambda _k\}\) such that \(\lambda _k>0\) and \(\lambda _k\rightarrow +\infty \). Then by defining \(\{x^k\}\) with \(x^k=\bar{x}+d/\lambda _k\), evidently \(x^k\in S\), \(\lim _{k\rightarrow \infty }x^k=\bar{x}\), and \(d=\lim _{k\rightarrow \infty }\lambda _k(x^k-\bar{x}),\) which implies \(d\in \mathrm {T}^B_{S}(\bar{x})\).

For (2.5), by the definition of \(\mathrm {N}^B_{S}(\bar{x})\), we obtain

$$\begin{aligned} \mathrm {N}^B_{S}(\bar{x})= & {} \{~d\in \mathbb {R}^{n}:~\langle d, z\rangle \leqslant 0,~\forall ~z\in \mathrm {T}^B_{S}(\bar{x})~\}\nonumber \\= & {} \{~d\in \mathbb {R}^{n}:~\langle d, z\rangle \leqslant 0,~\Vert z\Vert _0\leqslant s, \Vert \bar{x}+\mu z\Vert _0\leqslant s~,\forall ~\mu \in \mathbb {R}~\}.\quad \end{aligned}$$
(2.6)

If \(|\varGamma |=s\), it yields \(\mathrm{supp}(z)\subseteq \varGamma \) for any \(z\in \mathrm {T}^B_{S}(\bar{x})\). Then

$$\begin{aligned} d\in \mathrm {N}^B_{S}(\bar{x})\Longleftrightarrow & {} \langle d, z\rangle \leqslant 0, \quad \forall ~\mathrm{supp}(z)\subseteq \varGamma \Longleftrightarrow d_i\left\{ \begin{array}{ll} =0, &{}\quad i\in \varGamma , \\ \in \mathbb {R}, &{}\quad i\notin \varGamma . \end{array}\right. \\\Longleftrightarrow & {} d\in \mathrm{span}\left\{ ~{e}_i,~~ i\notin \varGamma ~\right\} . \end{aligned}$$

If \(|\varGamma |<s\), we will prove \( \mathrm {N}^B_{S}(\bar{x})=\{0\}\). Assuming \(d\in \mathrm {N}^B_{S}(\bar{x})\), we take \(z=d_{i_0}{e}_{i_0}\), \(\forall ~i_0\in \{1,2,\cdots ,n\}\), then \(z\in \mathrm {T}^B_{S}(\bar{x})\) because of \(|\varGamma |<s\). By \(\langle d, z\rangle =d_{i_0}^2\leqslant 0\), we can obtain \(d_{i_0}=0\). The arbitrariness of \(i_0\) yields that \(d=0\), henceforth \( \mathrm {N}^B_{S}(\bar{x})=\{0\}\).

Theorem 2.2

For any \(\bar{x}\in S\) and letting \(\varGamma =\mathrm{supp}(\bar{x})\), the Clarke tangent cone and corresponding normal cone of S at \(\bar{x}\) are, respectively,

$$\begin{aligned} \mathrm {T}^C_{S}(\bar{x})= & {} \{~d\in \mathbb {R}^{n}:~\mathrm{supp}(d)\subseteq \varGamma ~\}=\mathrm{span}\left\{ ~{e}_i,~~ i\in \varGamma ~\right\} , \end{aligned}$$
(2.7)
$$\begin{aligned} \mathrm {N}^C_{S}(\bar{x})= & {} \mathrm{span}\left\{ ~{e}_i,~~ i\notin \varGamma ~\right\} . \end{aligned}$$
(2.8)

Proof

Obviously, \(\mathrm{span}\left\{ ~{e}_i,~~ i\in \varGamma ~\right\} =\{~d\in \mathbb {R}^{n}:~\mathrm{supp}(d)\subseteq \varGamma ~\}\).

We first prove \(\mathrm {T}^C_{S}(\bar{x})\subseteq \{~d\in \mathbb {R}^{n}:~\mathrm{supp}(d)\subseteq \varGamma ~\}\). For any \(~d\in \mathrm {T}^C_{S}(\bar{x})\), we have \(\forall ~\{x^k\}\subset S,~\forall ~\{\lambda _k\}\subset \mathbb {R}_+ \) with \(\lim _{k\rightarrow \infty }x^k=\bar{x},~\lim _{k\rightarrow \infty }\lambda _k=0,\) there is a sequence \(\{y^k\}\) such that \(\lim _{k\rightarrow \infty }y^k=d\) and \(x^k+\lambda _{k}y^k\in S,~ k=1,2,\cdots \). Assume that \(\mathrm{supp}(d)\nsubseteq \varGamma \), namely there is an \(i_0\in \mathrm{supp}(d)\) but \(i_0\notin \varGamma \). Since \(\lim _{k\rightarrow \infty }y^k=d\), it must have \(y^{k}_{i_0}\rightarrow d_{i_0}\) which requires \(y^{k}_{i_0}\ne 0\) when \(k\geqslant k_0\). By the arbitrariness of \(\{x^k\}\), we take \(\{x^k\}\subset S\) such that \(\lim _{k\rightarrow \infty }x^k=\bar{x}\), \(\mathrm{supp}(x^k)=\varGamma \cup \varGamma _k\) with \(|\varGamma \cup \varGamma _k|=s\), where \(\varGamma _k\subset \{1,2,\cdots ,n\}\backslash \varGamma \), and \(i_0\notin \varGamma _k\). Because \(\{y^k\}\) is fixed and the arbitrariness of \(\{\lambda _k\}\), we can take \(\{\lambda _k\}\) such that

$$\begin{aligned} \lambda _k=\min _{i\in \varGamma \cup \varGamma _k}\frac{|x^k_i|}{|y^k_i|+k}. \end{aligned}$$

Then \(\lambda _k(\ne 0)\rightarrow 0\) as \(k\rightarrow \infty \). And thus \(\forall i\in \varGamma \cup \varGamma _k\), it follows

$$\begin{aligned} |x^k_i+\lambda _ky_i^k|\geqslant |x^k_i|-\lambda _k|y_i^k|= & {} |x^k_i|-|y_i^k|\min _{i\in \varGamma \cup \varGamma _k}\frac{|x^k_i|}{|y^k_i|+k}>0. \end{aligned}$$

Moreover, from \(i_0\notin \varGamma \cup \varGamma _k\) deriving \(x^{k}_{i_0}=0,y^{k}_{i_0}\ne 0\), we must have \(\Vert x^k+\lambda ^{\prime }_ky^k\Vert _0\geqslant s+1\) for \(k\geqslant k_0\), which is contradicted to \(x^k+\lambda ^{\prime }_ky^k\in S\) for any \(k=1,2,\cdots \). Therefore \(\mathrm{supp}(d)\subseteq \varGamma \).

Next we prove \(\mathrm {T}^C_{S}(\bar{x})\supseteq \{~d\in \mathbb {R}^{n}:~\mathrm{supp}(d)\subseteq \varGamma ~\}\). For any \(d\in \mathbb {R}^{n}\) such that \(\mathrm{supp}(d)\subseteq \varGamma \) and \(\forall ~\{x^k\}\subset S,~\forall ~\{\lambda _k\}\subset \mathbb {R}_+ \) with \(\lim _{k\rightarrow \infty }x^k=\bar{x},~\lim _{k\rightarrow \infty }\lambda _k=0,\) we have \(\mathrm{supp}(d)\subseteq \varGamma \subseteq \mathrm{supp}(x^k)\) for any \(k\geqslant k_0\). Let

$$\begin{aligned}\begin{array}{ll} y^{k}=0, &{} \quad k=1,2,\cdots ,k_0, \\ y^{k}=x^{k}-\bar{x}+d, &{}\quad k=k_0+1,\quad k_0+2,\cdots , \end{array} \end{aligned}$$

which brings out \(x^k+\lambda _ky^k\in S\) for \(k=1,2,\cdots \) due to \(x^k\in S\). In addition, \(\lim _{k\rightarrow \infty }y^k=\lim _{k\rightarrow \infty }x^k-\bar{x}+d=d\). Hence \(d\in \mathrm {T}^C_{S}(\bar{x})\).

Finally (2.8) holding is obvious. Then the whole proof is completed.

Remark 2.3

Clearly for any \(\bar{x}\in S\), Bouligand tangent cone \(\mathrm {T}^B_{S}(\bar{x})\) is closed but nonconvex, while Clarke tangent cone \(\mathrm {T}^C_{S}(\bar{x})\) is closed and convex. In addition, \(\mathrm {T}^C_{S}(\bar{x})\subseteq \mathrm {T}^B_{S}(\bar{x})\).

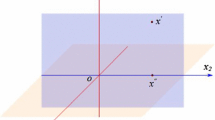
To end this subsection, we give a plot to illustrate the Bouligand and Clarke tangent cones in three dimensional space (Fig. 1). One can easily verify \(\mathrm {T}^B_{S}(x^{\prime })=\mathrm {T}^C_{S}(x^{\prime })=\{x\in \mathbb {R}^3|~x_1=0\}\), \(\mathrm {T}^B_{S}(x'')=\{x\in \mathbb {R}^3|~x_1=0\}\cup \{x\in \mathbb {R}^3|~x_3=0\}\) and \(\mathrm {T}^C_{S}(x'')=\{x\in \mathbb {R}^3|~x_1=x_3=0\}\).

Fig. 1
figure 1

Bouligand tangent cone and Clarke tangent cone in three dimensional space, where \(S=\{x\in \mathbb {R}^3|~\Vert x\Vert _0\leqslant 2\}\) and \(x^{\prime }=(0,1,1)^\mathrm{T},x''=(0,1,0)^\mathrm{T}\)

Full size image

2.2 First-Order Optimality Conditions

When f(x) is continuously differentiable on \(\mathbb {R}^{n}\), we give the definitions of \(\mathrm {N}\)-stationarity and \(\mathrm {T}\)-stationarity of problem (2.1) based on the expressions of tangent cone and normal cone.

Definition 2.4

A vector \(x^*\in S\) is called an \(\mathrm {N}^\sharp \)-stationary point and \(\mathrm {T}^\sharp \)-stationary point of (2.1) if it respectively satisfies the relation

$$\begin{aligned} \mathrm {N}^\sharp {\text {-}}\mathrm{stationary~point:}~~~~~~~~0~~\in & {} \nabla f(x^*)+\mathrm {N}^\sharp _{S}(x^*), \end{aligned}$$
(2.9)
$$\begin{aligned} \mathrm {T}^\sharp {\text {-}}\mathrm{stationary~point:}~~~~~~~~0~~= & {} \Vert \nabla ^{\sharp }_S f(x^*)\Vert , \end{aligned}$$
(2.10)

where \(\nabla ^{\sharp }_S f(x^*)=\mathrm{argmin}\{~\Vert d+\nabla f(x^*)\Vert :~d\in \mathrm {T}^\sharp _S(x^*)~\}\), \(\sharp \in \{B,C\}\) stands for the sense of Bouligand tangent cone or Clarke tangent cone.

Note that \(\mathrm {N}^\sharp \)-stationary point is called the critical point of nonconvex optimization problem by Attouch et al. [13], \(\mathrm {T}^\sharp \)-stationary point is the zero point of projection gradient of objective function introduced by Calamai and Mo\(\grave{r}\)e in [14]. Recall that \(x^*\in S\) is defined in [11] as an L-stationary point of (2.1) if

$$\begin{aligned} x^*\in \mathrm {P}_{S}(x^*-\nabla f(x^*)/L), \quad \forall ~ L>0. \end{aligned}$$
(2.11)

L-stationary point with \(L=1\) is called a fixed point in [15].

It is well known that L-stationarity, \(\mathrm {N}^\sharp \)-stationarity and \(\mathrm {T}^\sharp \)-stationarity are equivalent in convex constrained optimization problems. But for SCO problem, it is not the case observed from the following theorem.

Theorem 2.5

Under the concept of Bouligand tangent cone, we consider problem (2.1). For \(L>0\), if the vector \(x^*\in S\) satisfies \(\Vert x^*\Vert _0=s\), then

$$\begin{aligned} L\text {-stationary point}~~~\Longrightarrow ~~~\mathrm {N}^B\text {-stationary point}~~~\Longleftrightarrow ~~~\mathrm {T}^B\text {-stationary point} ; \end{aligned}$$

if the vector \(x^*\in S\) satisfies \(\Vert x^*\Vert _0<s\), then

$$\begin{aligned} L\text {-stationary point}~~\Longleftrightarrow & {} ~~\mathrm {N}^B\text {-stationary point}~~\Longleftrightarrow ~~\mathrm {T}^B\text {-stationary point}\\\Longleftrightarrow & {} ~~\nabla f(x^*)=0. \end{aligned}$$

Proof

Denote \(\varGamma ^*=\mathrm{supp}(x^*)\). If \(x^*\) is an L-stationary point of problem (2.1), then from Lemma 2.2 in [11], it holds for any \(L>0\),

$$\begin{aligned} x^*\in \mathrm {P}_{S} (x^*- \nabla f(x^*)/L )~\Longleftrightarrow ~\left| (\nabla f(x^*))_i\right| ~\left\{ \begin{array}{ll} =0, &{} \quad i\in \varGamma ^*,\\ \leqslant L M _s(|x^*|), &{} \quad i\notin \varGamma ^*. \end{array} \right. \qquad \end{aligned}$$
(2.12)

Case 1 First we consider the case \(\Vert x^*\Vert _0= s\). Under such circumstance, if \(x^*\) is an \(\mathrm {N}^B\)-stationary point of problem (2.1), then by (2.5) in Theorem 2.1, we have

$$\begin{aligned} -\nabla f(x^*)\in \mathrm {N}^B_S(x^*)~\Longleftrightarrow ~(\nabla f(x^*))_i~\left\{ \begin{array}{ll} =0, &{} \quad i\in \varGamma ^*,\\ \in \mathbb {R}, &{}\quad i\notin \varGamma ^*. \end{array} \right. \end{aligned}$$
(2.13)

Moreover, \(\Vert x^*\Vert _0= s\) produces

$$\begin{aligned} \nabla ^{B}_S f(x^*)= & {} \mathrm{argmin}\{~\Vert d+\nabla f(x^*)\Vert :~d\in \mathrm {T}^B_S(x^*)~\}\nonumber \\= & {} \mathrm{argmin}\{~\Vert d+\nabla f(x^*)\Vert :~\Vert d\Vert _0\leqslant s,~\Vert x^*+\mu d\Vert _0\leqslant s~,\forall ~\mu \in \mathbb {R}~\}\nonumber \\= & {} \mathrm{argmin}\{~\Vert d+\nabla f(x^*)\Vert :~\mathrm{supp}(d)\subseteq \varGamma ^*~\}, \end{aligned}$$
(2.14)

where the third equality holds due to \(\Vert x^*\Vert _0= s\). (2.14) is equivalent to

$$\begin{aligned} (\nabla ^{B}_S f(x^*))_i=\left\{ \begin{array}{ll} -(\nabla f(x^*))_i, &{}\quad i\in \varGamma ^*, \\ 0, &{} \quad i\notin \varGamma ^*. \end{array} \right. \end{aligned}$$

Therefore, if \(x^*\) is a \(\mathrm {T}^B\)-stationary point of problem (2.1), then from above

$$\begin{aligned} \nabla ^{B}_{S} f(x^*)=0~\Longleftrightarrow ~\big (\nabla f(x^*)\big )_i~\left\{ \begin{array}{ll} =0, &{} i\in \varGamma ^*,\\ \in \mathbb {R}, &{} i\notin \varGamma ^*. \end{array} \right. \end{aligned}$$
(2.15)

Henceforth, from (2.12), (2.13) and (2.15), one can easily check that when \(\Vert x^*\Vert _0= s\),

$$\begin{aligned} L\text {-stationary point}~~~\Longrightarrow ~~~\mathrm {N}^B\text {-stationary point}~~~\Longleftrightarrow ~~~\mathrm {T}^B\text {-stationary point}. \end{aligned}$$

Case  2 Now we consider the case \(\Vert x^*\Vert _0<s\). Under such circumstance, \( M _s(|x^*|)=0\), and thus if \(x^*\) is an L-stationary point of problem (2.1), then from (2.12), it holds

$$\begin{aligned} x^*\in \mathrm {P}_{S}(x^*- \nabla f(x^*)/L)~\Longleftrightarrow ~\nabla f(x^*)=0. \end{aligned}$$
(2.16)

Then when \(\Vert x^*\Vert _0<s\), \(\mathrm {N}^B_{S}(x^*)=\{0\}\) from (2.5), which implies \(\nabla f(x^*)=0\). Therefore, if \(x^*\) is an \(\mathrm {N}^B\)-stationary point of problem (2.1), then

$$\begin{aligned} 0\in \nabla f(x^*)+\mathrm {N}^B_{S}(x^*)~\Longleftrightarrow ~\nabla f(x^*)=0. \end{aligned}$$
(2.17)

Finally, we prove \(\nabla f(x^*)=0\Longleftrightarrow \nabla ^{B}_S f(x^*)=0\) when \(\Vert x^*\Vert _0<s\). On the one hand, if \(\nabla f(x^*)=0\), then

$$\begin{aligned} \nabla ^{B}_S f(x^*)= & {} \mathrm{argmin}\{~\Vert d+\nabla f(x^*)\Vert :~\Vert d\Vert _0\leqslant s,~\Vert x^*+\mu d\Vert _0\leqslant s~,\forall ~\mu \in \mathbb {R}~\}\\= & {} \mathrm{argmin}\{~\Vert d\Vert :~\Vert d\Vert _0\leqslant s,~\Vert x^*+\mu d\Vert _0\leqslant s~,\forall ~\mu \in \mathbb {R}~\}=0. \end{aligned}$$

On the other hand, if \(\nabla ^{B}_S f(x^*)=0\), then

$$\begin{aligned} 0=\nabla ^{B}_S f(x^*)=\mathrm{argmin}\{~\Vert d+\nabla f(x^*)\Vert :~\Vert d\Vert _0\leqslant s,~\Vert x^*+\mu d\Vert _0\leqslant s~,\forall ~\mu \in \mathbb {R}~\} \end{aligned}$$

leads to \(\Vert \nabla f(x^*)\Vert \leqslant \Vert d+\nabla f(x^*)\Vert \) for any \(\Vert d\Vert _0\leqslant s,~\Vert x^*+\mu d\Vert _0\leqslant s~,\forall ~\mu \in \mathbb {R}\). Particularly, for any \(i_0\in \{1,2,\cdots ,n\}\), we take d with \(\mathrm{supp}(d)=\{i_0\}\). Apparently, \(\Vert x^*+\mu d\Vert _0\leqslant s~,\forall ~\mu \in \mathbb {R}\) owing to \(\Vert x^*\Vert _0<s\). Then by valuing \(d_{i_0}=-(\nabla f(x^*))_{i_0}\) and \(d_{i}=0,~i\ne i_0\), we immediately get \((\nabla f(x^*))_{i_0}=0\) because of \(\Vert \nabla f(x^*)\Vert \leqslant \Vert \nabla f(x^*)-(\nabla f(x^*))_{i_0}\Vert \). Then by the arbitrariness of \(i_0\), it holds \(\nabla f(x^*)=0\). Therefore, if \(x^*\) is a \(\mathrm {T}^B\)-stationary point of problem (2.1), then

$$\begin{aligned} \nabla ^{B}_S f(x^*)=0~\Longleftrightarrow ~\nabla f(x^*)=0. \end{aligned}$$
(2.18)

Henceforth, from (2.16), (2.17) and (2.18), one can easily check that when \(\Vert x^*\Vert _0<s\)

$$\begin{aligned} L\text {-stationary point}~~\Longleftrightarrow & {} ~~\mathrm {N}^B\text {-stationary point}~~\Longleftrightarrow ~~\mathrm {T}^B\text {-stationary point}\\\Longleftrightarrow & {} \nabla f(x^*)=0. \end{aligned}$$

Overall, the whole proof is finished.

Based on the proof of Theorem 2.5, we use Table 1 to illustrate the relationship among these three stationary points under the concept of Bouligand tangent cone.

Theorem 2.6

Under the concept of Clarke tangent cone, we consider problem (2.1). For \(L>0\), if \(x^*\in S\) then

$$\begin{aligned} L\text {-stationary point}~~~\Longrightarrow ~~~\mathrm {N}^C\text {-stationary point}~~~\Longleftrightarrow ~~~\mathrm {T}^C\text {-stationary point}. \end{aligned}$$

Proof

Denote \(\varGamma ^*=\mathrm{supp}(x^*)\). If \(x^*\) is an L-stationary point of problem (2.1), for any \(L>0\), we have (2.12).

If \(x^*\) is an \(\mathrm {N}^C\)-stationary point of problem (2.1), then by (2.8), we have

$$\begin{aligned} -\nabla f(x^*)\in \mathrm {N}^C_S(x^*)~\Longleftrightarrow ~\left( \nabla f\big (x^*\big )\right) _i~\left\{ \begin{array}{ll} =0, &{} \quad i\in \varGamma ^*,\\ \in \mathbb {R}, &{}\quad i\notin \varGamma ^*. \end{array} \right. \end{aligned}$$
(2.19)

Moreover, by (2.7), it follows

$$\begin{aligned} \nabla ^{C}_S f(x^*)= & {} \mathrm{argmin}\{~\Vert d+\nabla f(x^*)\Vert :~d\in \mathrm {T}^C_S(x^*)~\}\\= & {} \mathrm{argmin}\{~\Vert d+\nabla f(x^*)\Vert :~\mathrm{supp}(d)\subseteq \varGamma ^*~\}, \end{aligned}$$

which is equivalent to

$$\begin{aligned} \left( \nabla ^{C}_S f\big (x^*\big )\right) _i=\left\{ \begin{array}{ll} -(\nabla f(x^*))_i, &{} \quad i\in \varGamma ^*, \\ 0, &{} \quad i\notin \varGamma ^*. \end{array} \right. \end{aligned}$$

Therefore, if \(x^*\) is a \(\mathrm {T}^C\)-stationary point of problem (2.1), then from above

$$\begin{aligned} \nabla ^{C}_{S} f(x^*)=0~\Longleftrightarrow ~\left( \nabla f\big (x^*\big )\right) _i~\left\{ \begin{array}{ll} =0, &{} \quad i\in \varGamma ^*,\\ \in \mathbb {R}, &{} \quad i\notin \varGamma ^*. \end{array} \right. \end{aligned}$$
(2.20)

Henceforth, from (2.12), (2.19) and (2.20), one can easily check

$$\begin{aligned} L\text {-stationary point}~~~\Longrightarrow ~~~\mathrm {N}^C\text {-stationary point}~~~\Longleftrightarrow ~~~\mathrm {T}^C\text {-stationary point}. \end{aligned}$$

Overall, the whole proof is finished.

Based on the proof of Theorem 2.6, we use Table 2 to illustrate the relationship among these three stationary points under the concept of Clarke tangent cone.

Table 1 The relationship of the stationary points for (2.1) under Bouligand tangent cone
Full size table
Table 2 The relationship of the stationary points for (2.1) under Clarke tangent cone
Full size table

From Tables 1 and 2, we can see that \(\mathrm {N}^C\)-stationarity and \(\mathrm {T}^C\)-stationarity are weaker than \(\mathrm {N}^B\)-stationarity and \(\mathrm {T}^B\)-stationarity. While \(\mathrm {N}^B\)- and \(\mathrm {T}^B\)-stationarity coincide with basic feasibility property in [11] for problem (2.1), that is \(\nabla f(x^*)=0\) if \(\Vert x^*\Vert _0<s\), \(\nabla _i f(x^*)=0\) for \(i\in \mathrm {supp}(x^*)\) if \(\Vert x^*\Vert _0=s\). The following theorem shows that they are all the necessary optimality conditions for SCO under some assumptions.

Assumption 2.7

The gradient of the objective function f(x) is Lipschitz with constant \(L_f\) over \(\mathbb {R}^n\):

$$\begin{aligned} \Vert \nabla f(x)-\nabla f(y)\Vert \leqslant L_f\Vert x-y\Vert ,~~~\forall ~x, y\in \mathbb {R}^n. \end{aligned}$$
(2.21)

Theorem 2.8

If \(x^*\) be an optimal solution of (2.1), then \(x^*\) is an \(\mathrm {N}^B\)-stationary point and hence \(\mathrm {N}^C\)-stationary point. Further, if Assumption 2.7 holds and \(L>L_f\), then \(x^*\) is an L-stationary point of (2.1).

Proof

The first conclusion comes from the equivalence of \(\mathrm {N}^B\)-stationarity and basic feasibility and Theorem 2.1 in [11]. The second conclusion is also proven in Theorem 2.2 in [11], and here we give a short proof. Suppose to the contrary that there exists a vector

$$\begin{aligned} y\in \mathrm {P}_S(x^*- \nabla f(x^*)/L). \end{aligned}$$

It follows that

$$\begin{aligned} \Vert y-x^*+ \nabla f(x^*)/L\Vert ^2\leqslant \Vert x^*-x^*+ \nabla f(x^*)/L\Vert ^2, \end{aligned}$$

which yields that

$$\begin{aligned} \langle \nabla f(x^*), y-x^*\rangle \leqslant -(L/2)\Vert y-x^*\Vert ^2. \end{aligned}$$

By Lipschitz continuity property of \(\nabla f\) and \(L>L_f\), we have

$$\begin{aligned} f(y)\leqslant & {} f(x^*)+\langle \nabla f(x^*),y-x^*\rangle +(L_f/2)\Vert y-x^*\Vert ^2 \\\leqslant & {} f(x^*) +(L_f/2-L/2)\Vert y-x^*\Vert ^2\\< & {} f(x^*), \end{aligned}$$

contradicting the optimality of \(x^*\). This completes the proof.

This theorem indicates that \(L>L_f\) is sufficient to guarantee the optimal solution being an L-stationary point. Next example shows that it is not necessary for the case of \(\Vert x^*\Vert _0=s\), where \(x^*\) denotes a solution to SCO.

Example 2.9

Consider the problem

$$\begin{aligned}&\min \; f(x)=1.5x_1^2+3x_2^2+4x_1x_2-0.5x_1-12x_2 \nonumber \\&\mathrm{s.t.}\quad \Vert x\Vert _0\leqslant 1. \end{aligned}$$
(2.22)

The gradient of the objective function is Lipschitz with constant \(L_f={ \lambda }_{\max }\left( \begin{array}{cc} 3 &{} 4 \\ 4 &{} 6 \\ \end{array}\right) =8\). Obviously the optimal solution of the problem is \(x^{*}=(0,2)^\mathrm{T}\). By (2.12), \(x^{*}\) is an L-stationary point if and only if \(L\geqslant \frac{|\nabla _1 f(x^{*})|}{ M _1(|x^{*}|)}=\frac{15}{4}\). Therefore, the condition \(L>L_f\) is sufficient but not necessary to guarantee the optimal solution being an L-stationary point.

2.3 Second-Order Optimality Conditions

In this subsection, we will study the second-order necessary and sufficient optimality conditions of problem (2.1).

Theorem 2.10

(Second-Order Necessary Optimality) Assume f(x) is twice continuously differentiable on \(\mathbb {R}^n\). If \(x^{*}\in S\) is the optimal solution of (2.1), we have

$$\begin{aligned} d^\mathrm{T}\nabla ^{2}f(x^*)d\geqslant 0,~~~~\forall ~d \in \mathrm {T}_S^C(x^*), \end{aligned}$$
(2.23)

where \(\nabla ^{2}f(x^*)\) is the Hessian matrix of f at \(x^*\).

Proof

If \(x^{*}\in S\) is the optimal solution of (2.1), it is also an \(\mathrm {N}^C\)-stationary point from Theorem 2.8. From (2.7) and Table 2, one can easily verify that

$$\begin{aligned} d^\mathrm{T}\nabla f(x^*)=0,~~~~\forall ~d \in \mathrm {T}_S^C(x^*). \end{aligned}$$

Moreover, for any \(\tau >0\) and \(d \in \mathrm {T}_S^C(x^*)\), by the optimality of \(x^*\) and the equality above, we have

$$\begin{aligned} 0\leqslant & {} f(x^*+\tau d)-f(x^*)\\= & {} f(x^*)+\tau d^\mathrm{T}\nabla f(x^*)+\frac{\tau ^{2}}{2}d^\mathrm{T}\nabla ^{2}f(x^*)d+o(\Vert \tau d\Vert ^2)-f(x^*)\\= & {} \frac{\tau ^{2}}{2}d^\mathrm{T}\nabla ^{2}f(x^*)d+o(\Vert \tau d\Vert ^2), \end{aligned}$$

which implies that

$$\begin{aligned} d^\mathrm{T}\nabla ^{2}f(x^*)d\geqslant 0,~~~~\forall ~d \in \mathrm {T}_S^C(x^*). \end{aligned}$$

The desired result is acquired.

Theorem 2.11

(Second-Order-Sufficient Optimality) If \(x^{*}\in S\) with \(\varGamma ^*=\mathrm {supp}(x^*)\) is an \(\mathrm {N}^C\)-stationary point of (2.1) and \(\nabla ^{2}f(x^*)\) is restricted positive definite, that is

$$\begin{aligned} d^\mathrm{T}\nabla ^{2}f(x^*)d>0,~~~~\forall ~d \in \mathrm {T}_S^C(x^*), \quad d\ne 0, \end{aligned}$$
(2.24)

then \(x^{*}\) is the strictly locally optimal solution of (2.1) restricted on the subspace \(\mathbb {R}^n_{\varGamma ^*}\), where \(\mathbb {R}^n_{\varGamma ^*}:=\mathrm {span}\{{e}_i, ~i\in \varGamma ^*\}\). Moreover, there are \(\eta >0\) and \(\delta >0\), for any \(x\in B(x^*, \delta )\cap \mathbb {R}^n_{\varGamma ^*}\) such that

$$\begin{aligned} f(x)\geqslant f(x^*)+\eta \Vert x-x^*\Vert ^{2}. \end{aligned}$$
(2.25)

Proof

We only prove the second conclusion because it can yield the first one. From Table 2, one can easily check

$$\begin{aligned} d^\mathrm{T}\nabla f(x^*)=0,~~\forall ~d \in \mathrm {T}_S^C(x^*). \end{aligned}$$
(2.26)

Suppose the conclusion does not hold. There must be a sequence \(\{x^k\} \in B(x^*, \delta )\cap \mathbb {R}^n_{\varGamma ^*}\) with

$$\begin{aligned} \lim _{k\rightarrow \infty }x^k=x^*~~~\mathrm{and}~~~\mathrm{supp}(x^k)=\mathrm{supp}(x^*) \end{aligned}$$

such that

$$\begin{aligned} f(x^{k})- f(x^*)\leqslant \frac{1}{k}\Vert x^{k}-x^*\Vert ^{2}. \end{aligned}$$
(2.27)

Denote \(d^{k}=\frac{x^{k}-x^*}{\Vert x^{k}-x^*\Vert }\). Due to \(\Vert d^{k}\Vert =1\), there exists a convergent subsequence, without loss of generality, assuming \(d^{k}\rightarrow \bar{d}\). Then \(d^k \in \mathbb {R}^n_{\varGamma ^*}\) and \(\bar{d} \in \mathbb {R}^n_{\varGamma ^*}\) by \(\mathrm{supp}(x^k)=\mathrm{supp}(x^*)\). From (2.26) and \(\mathrm {T}_S^C(x^*)=\mathbb {R}^n_{\varGamma ^*}\), we get \(d^{k\mathrm{T}}\nabla f(x^*)=0\). It follows from (2.27) that

$$\begin{aligned} \frac{1}{k}\geqslant & {} \frac{1}{\Vert x^{k}-x^*\Vert ^{2}}\big ( f\big (x^{k}\big )- f\big (x^*\big )\big )\\= & {} \frac{1}{\Vert x^{k}-x^*\Vert ^{2}}\left( \big (x^{k}-x^*\big )^\mathrm{T}\nabla f(x^{*})+\frac{1}{2}\big (x^{k}-x^*\big )^\mathrm{T}\right. \\&\left. \times \nabla ^2f\big (x^*\big )\big (x^{k}-x^*\big )+o\big (\Vert x^{k}-x^*\Vert ^{2}\big )\right) \\= & {} \frac{1}{2}d^{k\mathrm{T}} \nabla ^2f(x^*)d^{k}+ \frac{1}{\Vert x^{k}-x^*\Vert }d^{k\mathrm{T}} \nabla f\big (x^*\big )+o(1)\\= & {} \frac{1}{2}d^{k\mathrm{T}} \nabla ^2f\big (x^*\big )d^{k}+o(1). \end{aligned}$$

Then by taking the limit of both sides of the above inequality, we obtain

$$\begin{aligned} 0=\lim _{k\rightarrow \infty }\frac{1}{k}\geqslant \lim _{k\rightarrow \infty } \left( \frac{1}{2}d^{k\mathrm{T}} \nabla ^2f(x^*)d^{k}+o(1) \right) =\frac{1}{2}\bar{d}^\mathrm{T} \nabla ^2f(x^*)\bar{d}>0, \quad \bar{d} \in \mathbb {R}^n_{\varGamma ^*}, \end{aligned}$$

which is contradicted. Therefore the conclusion does hold.

We next give an example to show that for problem (2.1), under the condition (2.24), the \(\mathrm {N}^C\)-stationary point may not be the local minimizer of f on S.

Example 2.12

Consider the problem

$$\begin{aligned} \min&f(x)=\frac{1}{2}\left( \big (x_1+1\big )^2+\big (x_2-1\big )^2+\big (x_3-1\big )^2\right) \\ \mathrm {s.t.}&\Vert x\Vert _0\leqslant 2. \end{aligned}$$

The gradient and Hessian matrix of f are \(\nabla f(x)=(x_1+1, x_2-1,x_3-1)^\mathrm{T}\) and \(\nabla ^2 f(x)=I\) respectively. From Table 2, \(\bar{x}=(0,0,1)^\mathrm{T}\) with \(\nabla f(\bar{x})=(1, -1, 0)^\mathrm{T}\) is an \(\mathrm {N}^C\)-stationary point of the above problem, but not the local minimizer because \(f((0,\varepsilon ,1)^\mathrm{T})<f(\bar{x})\), \(0<\varepsilon \leqslant 1\).

In the end of this section, we will give more details about the special case of \(f(x)\equiv \frac{1}{2}\Vert Ax-b\Vert ^2\), where \(A\in \mathbb {R}^{m\times n}\), \(b\in \mathbb {R}^m\), \(L_f=\lambda _{\max }(A^\mathrm{T}A)\) is the largest eigenvalue of \(A^\mathrm{T}A\). From Theorem 2.11, we easily derive the following result.

Corollary 2.13

Let \(f(x)\equiv \frac{1}{2}\Vert Ax-b\Vert ^2\). If \(x^{*}\in S\) with \(\varGamma ^*=\mathrm {supp}(x^*)\) is an \(\mathrm {N}^C\)-stationary point of (2.1) and

$$\begin{aligned} d^\mathrm{T}A^\mathrm{T}Ad>0,~~~~\forall ~d \in \mathrm {T}_S^C(x^*), \quad d\ne 0, \end{aligned}$$
(2.28)

then \(x^{*}\) is the globally optimal solution of (2.1) restricted on \(\mathbb {R}^n_{\varGamma ^*}\).

Note that condition (2.28) is weaker than s-regularity of matrix A in [11], which means that every s column of A is linearly independent. Using the s-regularity of matrix A, we can obtain the global uniqueness of solution of problem (2.1).

Corollary 2.14

Let \(f(x)\equiv \frac{1}{2}\Vert Ax-b\Vert ^2\). If matrix A is s-regular, the number of \(\mathrm {N}^C\)-stationary points is finite, and any \(\mathrm {N}^C\)-stationary point, say \(x^{*}\in S\) with \(\varGamma ^*=\mathrm {supp}(x^*)\), is uniquely global minimizer of problem (2.1) on \(\mathbb {R}^n_{\varGamma ^*}\).

Proof

Since \(x^*\) is an \(\mathrm {N}^C\)-stationary point of (2.1) and \(\varGamma ^*=\mathrm {supp}(x^*)\), we denote \(x^*=(x_{\varGamma ^*}^{*\mathrm{T}}, 0)^\mathrm{T}\) and let \(A_{\varGamma ^*}\) be the submatrix of A made up of the columns corresponding to the set \(\varGamma ^*\). By Tables 1 and 2, we have \(0=(\nabla f(x))_i=(A^\mathrm{T}(Ax-b))_i=0, \forall ~i\in \varGamma ^*\), namely,

$$\begin{aligned} A^\mathrm{T}_{\varGamma ^*}A_{\varGamma ^*}x^*_{\varGamma ^*}=A^\mathrm{T}_{\varGamma ^*}b. \end{aligned}$$

The s-regularity of A yields that \(x^*_{\varGamma ^*}=(A^\mathrm{T}_{\varGamma ^*}A_{\varGamma ^*})^{-1}A^\mathrm{T}_{\varGamma ^*}b\) is unique. Since the number of subsets \(\varGamma ^*\) of \(\{1, 2, \cdots , n\}\) with \(|\varGamma ^*|\leqslant s\) is finite, the number of \(\mathrm {N}^C\)-stationary points is finite.

The s-regularity of A implies that f(x) is strongly convex on subspace \(\mathbb {R}^n_{\varGamma ^*}\). By Corollary 2.13, every stationary point is uniquely global minimizer of (2.1) on subspace \(\mathbb {R}^n_{\varGamma ^*}\). This completes the proof.

Furthermore, we obtain the result on globally unique solution to SCO with \(f(x)\equiv \frac{1}{2}\Vert Ax-b\Vert ^2\).

Theorem 2.15

Let \(f(x)\equiv \frac{1}{2}\Vert Ax-b\Vert ^2\). If matrix A is s-regular, and both A and b guarantee a unique solution to

$$\begin{aligned} \varGamma _0\triangleq \mathop \mathrm{argmin}\limits _{|\varGamma |\leqslant s}~\Vert \varPi _{\varGamma }b\Vert , \end{aligned}$$
(2.29)

where \(\varPi _{\varGamma }b=A_{\varGamma }(A_{\varGamma }^\mathrm{T}A_{\varGamma })^{-1}A_{\varGamma }^\mathrm{T}b\), then problem (2.1) has a unique solution.

Proof

We will prove it by contradiction. Let x and y be two different solutions of (2.1) with \(\varGamma _1=\mathrm {supp}(x)\) and \(\varGamma _2=\mathrm {supp}(y)\). Denote \(x=(x^\mathrm{T}_{\varGamma _1},~0)^\mathrm{T}\) and \(y=(y^\mathrm{T}_{\varGamma _2},~0)^\mathrm{T}\). We easily verify that (2.1) is equivalent to

$$\begin{aligned} \min _{|\varGamma |\leqslant s}\min _{x_\varGamma } \Vert A_{\varGamma }x_{\varGamma }-b\Vert ^2. \end{aligned}$$

Since A is s-regular, we have \(\varGamma _1\ne \varGamma _2\) provided \(x\ne y\). It is easy to see that \(x_{\varGamma _1}=(A_{\varGamma _1}^\mathrm{T}A_{\varGamma _1})^{-1}A_{\varGamma _1}^\mathrm{T}b\), \(y_{\varGamma _2}=(A_{\varGamma _2}^\mathrm{T}A_{\varGamma _2})^{-1}A_{\varGamma _2}^\mathrm{T}b\). From \(\Vert Ax-b\Vert ^2=\Vert Ay-b\Vert ^2\), we have

$$\begin{aligned} \Vert A_{\varGamma _1}(A_{\varGamma _1}^\mathrm{T}A_{\varGamma _1})^{-1}A_{\varGamma _1}^\mathrm{T}b-b\Vert ^2=\Vert A_{\varGamma _2}(A_{\varGamma _2}^\mathrm{T}A_{\varGamma _2})^{-1}A_{\varGamma _2}^\mathrm{T}b-b\Vert ^2, \end{aligned}$$

that is

$$\begin{aligned} \Vert \varPi _{\varGamma _1}b-b\Vert ^2=\Vert \varPi _{\varGamma _2}b-b\Vert ^2. \end{aligned}$$

Because \(\Vert Ax-b\Vert ^2=\Vert Ay-b\Vert ^2\) is the optimal value of (2.29) and \(\varPi _{\varGamma }^\mathrm{T}=\varPi _{\varGamma }\) and \(\varPi _{\varGamma }^2=\varPi _{\varGamma }\), the above equation means

$$\begin{aligned} \Vert \varPi _{\varGamma _1}b\Vert =\Vert \varPi _{\varGamma _2}b\Vert =\min _{|\varGamma |\leqslant s}~\Vert \varPi _{\varGamma }b\Vert . \end{aligned}$$

Hence it violates the assumption.

3 Extensions

In this section, we mainly aim at specifying the results in Sect. 2 for SCO with nonnegative constraint:

$$\begin{aligned} \min ~~f(x),~~~~~\mathrm{s.t.}~~\Vert x\Vert _0\leqslant s, \quad x \geqslant 0. \end{aligned}$$
(3.1)

First, we give the explicit expression of the projection on \(S\cap \mathbb {R}_+^{n}\), which is named the nonnegative support projection.

Proposition 3.1

\(\mathrm{P}_{S\cap \mathbb {R}_+^{n}}(x)= \mathrm{P}_S\cdot \mathrm{P}_{\mathbb {R}_+^{n}}(x)\).

Proof

Denote \(I_+(x)=\{i:~x_i>0\}\), \(I_0(x)=\{i:~x_i=0\}\), \(I_-(x)=\{i:~x_i<0\}\), and let \(y\in \mathrm{P}_{S\cap \mathbb {R}_+^{n}}(x)\). For \(i\in I_0(x)\cup I_-(x)\), it is easy to see \(y_i=0\). There are two cases: Case 1, \(|I_+(x)|\leqslant s\), then \(y=\mathrm{P}_{\mathbb {R}_+^{n}}(x)=\mathrm{P}_S\cdot \mathrm{P}_{\mathbb {R}_+^{n}}(x)\). Case 2, \(|I_+(x)|> s\), we should choose no more than s coordinates from \(I_+(x)\) to minimize \(\Vert x-y\Vert \). For \(i,j\in I_+(x)\) and \(x_i>x_j\),

$$\begin{aligned} (x_i-x_i)^2+(x_j-x_j)^2< & {} (x_i-x_i)^2+(x_j-0)^2\\< & {} (x_i-0)^2+(x_j-x_j)^2<(x_i-0)^2+(x_j-0)^2. \end{aligned}$$

Then the projection on \(S\cap \mathbb {R}_+^{n}\) sets all but s largest elements of \(\mathrm{P}_{\mathbb {R}_+^{n}}(x)\) to zero, which is \(\mathrm{P}_S\cdot \mathrm{P}_{\mathbb {R}_+^{n}}(x)\).

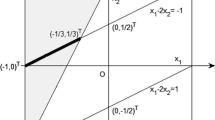
Notice that the order of the nonnegative support projection on \(S\cap \mathbb {R}_+^{n}\) can not be changed. For example \(x=(-2,1)^\mathrm{T}\), \(s=1\). \(\mathrm{P}_{S\cap \mathbb {R}_+^{2}}(x)= \mathrm{P}_S\cdot \mathrm{P}_{\mathbb {R}_+^{2}}(x)=(0,1)^\mathrm{T}\), while \(\mathrm{P}_{\mathbb {R}_+^{2}}\cdot \mathrm{P}_S(x)=(0,0)^\mathrm{T}\).

The direct result of Theorems 2.1 and 2.2 is the following theorem.

Theorem 3.2

For any \(\bar{x}\in S\cap \mathbb {R}^{n}_+\), by denoting  \(\mathbb {R}^{n}_+(\bar{x}):=\{~d\in \mathbb {R}^{n}:~d_i\geqslant 0,i\notin \mathrm {supp}(\bar{x})~\}\), it follows

$$\begin{aligned}&\mathrm {T}^B_{S\cap \mathbb {R}^{n}_+}(\bar{x})=\mathrm {T}^B_{S}(\bar{x})\cap \mathbb {R}^{n}_+(\bar{x}), ~~~~\mathrm {N}^B_{S\cap \mathbb {R}^{n}_+}(\bar{x})=\mathrm {N}^B_{S}(\bar{x})\cup (-\mathbb {R}^{n}_+(\bar{x})), \end{aligned}$$
(3.2)
$$\begin{aligned}&\mathrm {T}^C_{S\cap \mathbb {R}^{n}_+}(\bar{x})= \mathrm {T}^C_{S}(\bar{x}),\quad \mathrm {N}^C_{S\cap \mathbb {R}^{n}_+}(\bar{x})= \mathrm {N}^C_{S}(\bar{x}). \end{aligned}$$
(3.3)

Clearly, one can check that

$$\begin{aligned} \begin{array}{lll} \mathrm {T}^B_{S\cap \mathbb {R}^{n}_+}(\bar{x})\!=\!\mathrm {T}^B_{S}(\bar{x}), \quad \mathrm {N}^B_{S\cap \mathbb {R}^{n}_+}(\bar{x})\!=\!\mathrm {N}^B_{S}(\bar{x}), &{} \quad \hbox {if}~~ \Vert \bar{x}\Vert _0=s \quad \mathrm {and} \quad \bar{x}\geqslant 0,\\ \mathrm {T}^B_{S\cap \mathbb {R}^{n}_+}(\bar{x})\!=\!\mathrm {T}^B_{S}(\bar{x})\cap \mathbb {R}^{n}_+(\bar{x}),~~~~ \mathrm {N}^B_{S\cap \mathbb {R}^{n}_+}(\bar{x})=-\mathbb {R}^{n}_+(\bar{x}), &{} \quad \hbox {if}~~ \Vert \bar{x}\Vert _0<s \quad \mathrm {and} \quad \bar{x}\geqslant 0. \end{array} \end{aligned}$$

For problem (3.1), the corresponding definitions of L-stationary point, \(\mathrm {N}^\sharp \)-stationary point and \(\mathrm {T}^\sharp \)-stationary point can be obtained from Definition 2.3 in [11] and Definition 2.4, just by substituting \(S\cap \mathbb {R}_+ ^n\) for S.

$$\begin{aligned} L{\text {-}}\mathrm{stationary~point:}~~~~~~~~x^*\in & {} \mathrm {P}_{S\cap \mathbb {R}_+ ^n} (x^*- \nabla f(x^*)/L), \end{aligned}$$
(3.4)
$$\begin{aligned} \mathrm {N}^\sharp {\text {-}}\mathrm{stationary~point:}~~~~~~~~0~~\in & {} \nabla f(x^*)+\mathrm {N}^\sharp _{S\cap \mathbb {R}_+ ^n}(x^*), \end{aligned}$$
(3.5)
$$\begin{aligned} \mathrm {T}^\sharp {\text {-}}\mathrm{stationary~point:}~~~~~~~~0~~= & {} \Vert \nabla ^{\sharp }_{S\cap \mathbb {R}_+ ^n} f(x^*)\Vert . \end{aligned}$$
(3.6)

In order to facilitate the discussion next, we describe a more explicit representation of L-stationary point for (3.1).

Theorem 3.3

For \(L>0\), a vector \(x^*\in S\cap \mathbb {R}_+ ^n\) is L-stationary point of (3.1) if and only if

$$\begin{aligned} (\nabla f(x^*))_i\left\{ \begin{array}{lll} =0, &{} \quad \hbox {if}~~ i\in \mathrm {supp}(x^*),\\ \in [-L M _s (x^*),+\infty ), &{} \quad \hbox {if}~~ i \notin \mathrm {supp}(x^*). \end{array} \right. \end{aligned}$$
(3.7)

Proof

Suppose \(x^*\in S\cap \mathbb {R}_+ ^n\) is an L-stationary point, namely, satisfying (3.4). For simplicity, we write \(\nabla _i f(x^*)=(\nabla f(x^*))_i\). Note that the component of \(\mathrm {P}_{S\cap \mathbb {R}^n_+}(x^*- \nabla f(x^*)/L)\) is either zero or itself. If \(i\in \mathrm {supp}(x^*)\), then \(x^*_i =x^*_i -\nabla _i f(x^*)/L\), so that \(\nabla _i f(x^*)=0\); If \(i\notin \mathrm {supp}(x^*)\), there are two cases: either \(x^*_i - \nabla _i f(x^*)/L\leqslant 0\), that is \(\nabla _i f(x^*)\geqslant x^*_i= 0\), or \(0\leqslant x^*_i - \nabla _i f(x^*)/L\leqslant M _s (x^*)\), that is \(-L M _s (x^*)\leqslant \nabla _i f(x^*)\leqslant 0\).

On the contrary, assume (3.7) holds. If \(\Vert x^*\Vert _0 <s\), we get \( M _s (x^*)=0\), then for \(i\in \mathrm {supp}(x^*)\), \(\nabla _i f(x^*)=0\), then \(x^*-\nabla _i f(x^*)/L=x_i^*\) or for \(i\notin \mathrm {supp}(x^*)\), \(x_i^*- \nabla _i f(x^*)/L\leqslant 0\), therefore, (3.4) holds. If \(\Vert x^*\Vert _0 =s\), that is \( M _s (x^*)>0\). By (3.7), for \(i\in \mathrm {supp}(x^*)\), \( \nabla _i f(x^*)/L= 0\); for \(i\notin \mathrm {supp}(x^*)\), \(x^*- \nabla _i f(x^*)/L\leqslant 0\) or \(0\leqslant x_i^*- \nabla _i f(x^*)/L\leqslant M _s (x^*)\), so that (3.4) holds as well.

The following theorem is derived by Theorems 2.5, 2.6 and 3.3 directly.

Theorem 3.4

For the problem (3.1) and \(L>0\), the following assertions hold.

  1. (i)

    Under the concept of Bouligand tangent cone, if  \(\Vert x^*\Vert _0=s, x^*\geqslant 0\), then

    $$\begin{aligned} L\text {-stationary point}~~~\Longrightarrow ~~~\mathrm {N}^B\text {-stationary point}~~~\Longleftrightarrow ~~~\mathrm {T}^B\text {-stationary point}. \end{aligned}$$

    If  \(\Vert x^*\Vert _0<s, x^*\geqslant 0\), then

    $$\begin{aligned} L\text {-stationary point}~~~\Longleftrightarrow ~~~\mathrm {N}^B\text {-stationary point}~~~\Longleftrightarrow ~~~\mathrm {T}^B\text {-stationary point}. \end{aligned}$$
  2. (ii)

    Under the concept of Clarke tangent cone, if  \(\Vert x^*\Vert _0\leqslant s, x^*\geqslant 0\), then

    $$\begin{aligned} L\text {-stationary point}~~~\Longrightarrow ~~~\mathrm {N}^C\text {-stationary point}~~~\Longleftrightarrow ~~~\mathrm {T}^C\text {-stationary point}. \end{aligned}$$

Combining Theorems 3.3 and 3.4, we have the following table to illustrate the relationship among the three stationary points for (3.1) under the concepts of Bouligand and Clarke tangent cones (Table 3).

Table 3 The relationship of the stationary points for (3.1) under Bouligand and Clarke tangent cones
Full size table

Combining Theorems 2.10 and 2.11, we derive the following second-order optimality result.

Theorem 3.5

(Second-Order Optimality) Let f(x) be twice differentiable. If \(x^{*}\in S\cap \mathbb {R}^n_+\) with \(\varGamma ^*=\mathrm {supp}(x^*)\) is the optimal solution of (3.1), then (i) \(x^*\) is an \(\mathrm {N}^B\)-stationary point of (3.1) and hence an \(\mathrm {N}^C\)-stationary point; (ii) \(x^{*}\) is also an L-stationary point of (3.1) provided that Assumption 2.7 holds and \(L>L_f\); and (iii)

$$\begin{aligned} d^\mathrm{T}\nabla ^2f(x^*)d\geqslant 0,~~~~\forall ~d\in \mathrm {T}^C_{S\cap \mathbb {R}^n_+}(x^*). \end{aligned}$$
(3.8)

Conversely, if \(x^{*}\in S\cap \mathbb {R}^{n}_{+}\) is an \(\mathrm {N}^C\)-stationary point of (3.1) and satisfies

$$\begin{aligned} d^\mathrm{T}\nabla ^2f(x^*)d>0,~~~~\forall ~d\in \mathrm {T}^C_{S\cap \mathbb {R}^n_+}(x^*), \quad d\ne 0, \end{aligned}$$
(3.9)

then \(x^{*}\) is the strictly locally optimal solution of (3.1) restricted on \(\mathbb {R}^n_{\varGamma ^*}\cap \mathbb {R}^n_+\). Moreover, there are \(\gamma >0\) and \(\delta >0\), for any \(x\in B(x^*, \delta )\cap \mathbb {R}^n_{\varGamma ^*}\cap \mathbb {R}^{n}_{+}\), it holds

$$\begin{aligned} f(x)\geqslant f(x^*)+\gamma \Vert x-x^*\Vert ^{2}. \end{aligned}$$
(3.10)

In the same way, Corollaries 2.13 and 2.14 and Theorem 2.15 can be extended to the problem of (3.1) with the case of \(f(x)\equiv \frac{1}{2}\Vert Ax-b\Vert ^2\).

Theorem 3.6

Let \(f(x)\equiv \frac{1}{2}\Vert Ax-b\Vert ^2\). We have the following conclusions.

  1. (i)

    If \(x^{*}\in S\) with \(\varGamma ^*=\mathrm {supp}(x^*)\) is an \(\mathrm {N}^C\)- stationary point of (3.1) and \(d^\mathrm{T}A^\mathrm{T}Ad>0\), \(\forall ~d\in \mathrm {T}^C_{S\cap \mathbb {R}_+^n}(x^*)\), \(d\ne 0\), then \(x^{*}\) is the strictly globally optimal solution of (3.1) on \(\mathbb {R}^n_{\varGamma ^*}\cap \mathbb {R}^{n}_{+}\).

  2. (ii)

    If matrix A is s-regular, then the number of \(\mathrm {N}^C\)-stationary points of (3.1) is finite, and every \(\mathrm {N}^C\)-stationary point, say \(x^*\) with \(\varGamma ^*=\mathrm {supp}(x^*)\), is uniquely global minimizer of problem (3.1) on \(\mathbb {R}^n_{\varGamma ^*}\cap \mathbb {R}^{n}_{+}\). Furthermore, if both A and b guarantee a unique solution of \( \varGamma _0\triangleq \mathrm {argmin}_{|\varGamma |\leqslant s}~\Vert \varPi _{\varGamma }b\Vert , \) where \(\varPi _{\varGamma }b=A_{\varGamma }(A_{\varGamma }^\mathrm{T}A_{\varGamma })^{-1}A_{\varGamma }^\mathrm{T}b\), then problem (3.1) has a unique solution.

4 Conclusions

In this paper, we have established the first- and second-order optimality conditions for sparsity constrained optimization with the help of tangent cone and normal cone. Furthermore, we extended the results to sparsity constrained optimization with nonnegative constraint. However, there are many practical problems with both sparsity constraint and other additional constraints, such as [16–19]. In the future, we will use the tangent cone and normal cone to consider the optimality conditions for this kind of problems and derive algorithms using the conditions.

This paper is based on the technical report [20] uploaded on http://arxiv.org/abs/1406.7178 on 27th Jun 2014. Over the past year, some results on optimality conditions for sparsity constrained optimization were found. Bauschke et al. [21] gave the expressions of proximal and Mordukhovich normal cones and Bouligand tangent cone to sparse set S. While in [20], we showed explicitly the Bouligand and Clarke tangent cones and normal cones to sparse set S by the definitions. Lu and Zhang [22] gave the first-order necessary optimality condition of a more general form of sparsity constrained optimization. If there is only the sparsity constraint, this condition turns out to be an \(\mathrm {N}^M\)-stability in the sense of Mordukhovich normal cone. For \(x^*\in S\) satisfying \(\Vert x^*\Vert _0=s\), \(\mathrm {N}^M\)-stability is equivalent to \(\mathrm {N}^B\)- and \(\mathrm {N}^C\)- stability for sparsity constrained optimization. Beck and Hallak extended the results in [11] to the optimization problem over sparse symmetric sets and gave three types of optimality conditions and the hierarchy between the optimality conditions using the orthogonal projection operator. And then they presented and analyzed algorithms satisfying the various optimality conditions.