Power Generalized Weibull Distribution Based on Record Values and Associated Inferences with Bladder Cancer Data Example

Abstract

The power generalized Weibull distribution has been proposed recently by [24] as an alternative to the gamma, Weibull and the exponentiated Weibull distributions. The power generalized Weibull family is suitable for modeling data that indicate nonmonotone hazard rates and can be used in survival analysis and reliability studies. Usefulness and flexibility of the family are illustrated by reanalyzing Efron’s data pertaining to a head-and-neck cancer clinical trial. These data involve censoring and indicate unimodal hazard rate. For this distribution, some recurrence relations are established for the single and product moments of upper record values. Further, using these relations, we have obtained means, variances and covariances of upper record values from samples of sizes up to 10 for various values of the parameters and present them in figures. Real data set is analyzed to illustrate the flexibility and importance of the model.

1 Introduction

Record values are used in many statistical applications, statistical modeling and inference involving data pertaining to weather, athletic events, economics, life testing studies and so on. For example, Guinness World Records, fastest time taken to recite the periodic table of the elements or shortest ever tennis matches both in terms of number of games and duration of time or fastest indoor marathon. There are lots of work published on value (see, [1, 9, 28, 30, 4, 5, 12]and [2, 3]).

[8] proposed the concept of record value and are widely used many real life situations such as industrial stress testing, meteorology, hydrology, sports and stock market analysis. For example, see [3] and [23, 25,26,27, 31, 13,14,15]. Recently, [16] and [29] obtained the relations for moments of record values for generalized Lindley and unit-Gompertz distributions, respectively.

The power generalized Weibull (PGW) distribution proposed by [24] with probability density function (pdf) of the form

$$\begin{aligned} f(x)=\frac{\tau }{\delta \xi ^{\tau }}x^{\tau -1}\left[ 1+\left( \frac{x}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }-1}e^{1-[1+(\frac{x}{\xi })^{\tau }]^{\frac{1}{\delta }}};~~~~x>0,~ \tau ,~\delta ,~\xi >0 \end{aligned}$$

(1.1)

and cumulative distribution function (cdf) is

$$\begin{aligned} F(x)=1-e^{1-[1+(\frac{x}{\xi })^{\tau }]^{\frac{1}{\delta }}};~~~~x>0,~~ \tau ,~\delta ,~\xi >0. \end{aligned}$$

(1.2)

The hazard function is given by

$$\begin{aligned} h(x)=\frac{f(x)}{1-F(x)}=\frac{\tau }{\delta \xi ^{\tau }}x^{\tau -1} \left[ 1+\left( \frac{x}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }-1},~~x>0. \end{aligned}$$

(1.3)

Fig. 1

Means of record values for $\tau =1(1)5$, $\xi =1$ and $\delta =0.5$

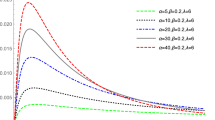
The pdf of power generalized Weibull family is hight-tailed at the left end, similar to that of the Exponential distribution. The hazard rates of the power generalized Weibull family can be constant, monotone, unimodal, bathtub shaped . [24] pointed out PGW $(\tau , \delta , \xi )$ distribution can be used to model reanalyzing Efron’s data pertaining to a head-and-neck cancer clinical trial. Note that by setting $\delta = 1$ and $\tau =1$, $\delta =1$, (1) reduces to the Weibull and exponential distributions, respectively. [24] obtained the first and second moments of this distribution are (Fig. 1)

$$\begin{aligned} E(X)=\delta \xi e(-1)^{1/\tau }\sum _{i=1}^{1/\tau } i \left( \begin{array}{c}1/\tau \\ i\end{array}\right) (-1)^{i}~\Gamma (i\tau ,~1) \end{aligned}$$

(1.4)

and

$$\begin{aligned} E(X^2)=\delta \xi ^{2} e(-1)^{2/\tau }\sum _{i=1}^{2/\tau } i \left( \begin{array}{c}2/\tau \\ i\end{array}\right) (-1)^{i}~\Gamma (i\tau ,~1). \end{aligned}$$

(1.5)

Moreover, the quantile function of PGW $(\tau , \delta , \xi )$ distribution is found to be

$$\begin{aligned} Q(p)=\xi \left\{ \left( 1-log(1-p)\right) ^{1/\delta }-1\right\} ^{1/\tau },~~0<p<1. \end{aligned}$$

The outline of this note is as follows. In Sect. 2, we describe the basic concept of record values. In Sect. 3, we derive relations for single and product moments of record values from PGW distribution. The maximum likelihood estimators and the asymptotic confidence intervals for the parameters based on asymptotic variance covariance matrix are provided in Sect. 4. In Sect. 5, the prediction of a future record value is discussed. In Sect. 6, we describe the computational procedure that will produce all the means and variances of record values as presented in Figs. 2–5. In Sect. 7, we present real data applications. Finally, in Sect. 8, we make some concluding remarks.

Fig. 2

Means of record values for $\tau =1(1)5$, $\xi =1$ and $\delta =1.0$

Fig. 3

Variance of record values for $\tau =1(1)3$, $\xi =1$ and $\delta =0.5$

Fig. 4

Variance of record values for $\tau =1(1)3$, $\xi =1$ and $\delta =1.0$

Fig. 5

Fitted densities for cancer data

2 Record Values

Let $\{X_{n}, n\ge 1\}$ be a sequence of identically independently distributed (iid) random variables with pdf f(x) and cumulative distribution function (cdf) F(x). The $j-$th order statistics of a sample $(X_{1}, X_{2},\ldots , X_{n})$ is denoted by $X_{j:n}$. For a fix $k\ge 1$, we define the sequence $\{U^{(k)}(n), n\ge 1\}$ of k upper record times of $X_{1},X_{1},\ldots$ as follows:

$$\begin{aligned} U^{(k)}(1)=1, U^{(k)}(n+1)=min\{j>U^{(k)}(n):X_{j:j+k+1}>X_{U^{(k)}(n):U^{(k)}(n)+k-1}\}. \end{aligned}$$

The sequences $\{Z_{n}^{(k)}, n\ge 1\}$ with $Z_{n}^{(k)}=X_{k:U^{(k)}(n)+k-1}$, $n=1, 2,\ldots ,$ are called the sequences of kth upper record values of $\{X_{n}, n\ge 1\}$. For convenience, we shall also take $Z_{0}^{(k)}=0.$ Note that $k=1$ we have $Y_{n}^{(1)}=X_{U(n)},~ n\ge 1$, i.e.,  record values of $\{X_{n},~ n\ge 1\}$.

The joint pdf of kth upper record values $Z_{1}^{(k)}, Z_{2}^{(k)},\ldots ,Z_{n}^{(k)}$ can be given as the joint pdf of kth upper record values of $\{-X_{n}, n\ge 1\}$, [25]

$$\begin{aligned}{} & {} f_{z_{1}^{(k)},\ldots ,z_{n}^{(k)}}(z_{1},\ldots , z_{n})=k^{n}\left( \prod _{i=1}^{n-1}\frac{f(z_{i})}{1-F(z_{i})}\right) [1-F(z_{n})]^{k-1}f(z_{n}),\\{} & {} \quad ~~z_{1}<z_{2}<\ldots <z_{n}. \end{aligned}$$

The marginal pdf of $X_{U(n)}^{(k)}$,  $n\ge 1$ is given by

$$\begin{aligned} f_{X_{n}^{(k)}}(x)=\frac{k^{n}}{(n-1)!}[-ln(\bar{F}(x))]^{n-1}[\bar{F}(x)]^{k-1}f(x) \end{aligned}$$

(2.1)

and the joint pdf of $X_{m}^{(k)}$ and $X_{n}^{(k)}$, $1\le m<n$, $n>2$ is given by

$$\begin{aligned}{} & {} f_{X_{m}^{(k)},X_{n}^{(k)}}(x,y)=\frac{k^{n}}{(m-1)!(n-m-1)!}[-ln(\bar{F}(x))]^{m-1}\nonumber \\{} & {} \quad \times [-ln\bar{F}(y)+ln\bar{F}(x)]^{n-m-1}[\bar{F}(y)]^{k-1}\frac{f(x)}{\bar{F}(x)}f(y),~x<y, \end{aligned}$$

(2.2)

where $~~~\bar{F}(x)=1-F(x).$

3 Moments of Record Values

Here, we provide the relations for single and product moments of upper record values from PGW distribution.

3.1 Relations for Single Moments

Theorem 3.2 gives a relation for single moments of kth upper record values and r a negative integer.

Theorem 3.1

For the fixed parameters $\tau , \delta >0$, $\xi >0$ $k, n=1, 2, \ldots$, and $r=0,1,2,\ldots$, we have

$$\begin{aligned} \mu _{U(n):k}^{(r)}= & {} \frac{k^{n}e^{k}\xi ^{r}}{(n-1)!}\sum _{l=0}^{n-1} \sum _{p=0}^{r/\tau }\left( \begin{array}{c}n-1\\ l\end{array}\right) \left( \begin{array}{c}r/\tau \\ p\end{array}\right) \frac{(-1)^{n-1-l+p-(r/\tau )}}{k^{l+p\delta +1}} \nonumber \\{} & {} \times \Gamma (\delta p+l+1,~k). \end{aligned}$$

(3.1)

Proof

Using (1.4), we have

$$\begin{aligned} \mu _{n:k}^{(r)}= & {} \frac{k^{n}}{(n-1)!}\int _{0}^{\infty }x^{r} [-ln(\bar{F}(x))]^{n-1}[\bar{F}(x)]^{k-1}f(x)dx\\= & {} \frac{\tau k^{n} e^{k}}{\delta \xi ^{\tau }(n-1)!} \int _{0}^{\infty }x^{r+\tau -1}\left[ 1+(x/\xi )^{\tau }\right] ^{1/\delta } \left[ \left\{ 1+(x/\xi )^{\tau }\right\} ^{1/\delta }-1\right] ^{n-1}\\{} & {} \times e^{-k\left[ 1+(x/\xi )^{\tau }\right] ^{1/\delta }}dx\\= & {} \frac{k^{n}e^{k}\xi ^{r}}{(n-1)!}\sum _{l=0}^{n-1}(-1)^{n-1-l} \left( \begin{array}{c}n-1\\ l\end{array}\right) \frac{1}{k^{l+1}}\int _{k}^{\infty } \left[ (z/k)^{\delta }-1\right] ^{r/\tau } e^{-z}z^{l}dz\\= & {} \frac{k^{n}e^{k}\xi ^{r}}{(n-1)!}\sum _{l=0}^{n-1} \sum _{p=0}^{j/\tau }(-1)^{n-1-l+p-(j/\tau )} \left( \begin{array}{c}n-1\\ l\end{array}\right) \left( \begin{array}{c}j/\tau \\ p\end{array}\right) \\{} & {} \times \frac{1}{k^{l+p\delta +1}}\int _{k}^{\infty }z^{\delta p+l}~e^{-z}dz, \end{aligned}$$

where $z=k\left[ 1+(x/\xi )^{\tau }\right] ^{1/\delta }$. The mean and variance kth record values are

$$\begin{aligned} \mu _{U(n):k}^{(1)}= & {} \frac{k^{n}e^{k}\xi }{(n-1)!}\sum _{l=0}^{n-1} \sum _{p=0}^{1/\tau }(-1)^{n-1-l+p-(1/\tau )} \left( \begin{array}{c}n-1\\ l\end{array}\right) \left( \begin{array}{c}1/\tau \\ p\end{array}\right) \nonumber \\{} & {} \times \frac{\Gamma (\delta p+l+1,~k)}{k^{l+p\delta +1}} \end{aligned}$$

(3.2)

and

$$\begin{aligned} \xi _{n:k}^{2}= & {} \mu _{n:k}^{(2)}-[\mu _{n:k}]^{2}\nonumber \\= & {} \frac{k^{n}e^{k}\xi ^{2}}{(n-1)!}\sum _{l=0}^{n-1} \sum _{p=0}^{2/\tau }(-1)^{n-1-l+p-(2/\tau )} \left( \begin{array}{c}n-1\\ l\end{array}\right) \left( \begin{array}{c}2/\tau \\ p\end{array}\right) \nonumber \\{} & {} \times \frac{\Gamma (\delta p+l+1,~k)}{k^{l+p\delta +1}}-[\mu _{n:k}]^{2}, \end{aligned}$$

(3.3)

respectively. $\square$

Theorem 3.2

For the fixed parameters $\tau , \delta >0$, $\xi >0$, $k, n=1, 2, \ldots$, and r a negative integer, we have

$$\begin{aligned} \mu _{U(n):k}^{(r)}= & {} \frac{k^{n}e^{k}\xi ^{r}}{(n-1)!}\sum _{l=0}^{n-1} \sum _{p=0}^{\infty }(-1)^{n-1-l+p-(r/\tau )} \left( \begin{array}{c}n-1\\ l\end{array}\right) \left( \begin{array}{c}r/\tau \\ p\end{array}\right) \nonumber \\{} & {} \times \frac{\Gamma (\delta p+l+1,~k)}{k^{l+p\delta +1}}. \end{aligned}$$

(3.4)

Proof

This proof is straightforward. $\square$

Theorem 3.3

Under the assumptions of equation (8), and convention $\mu _{n:k}^{(0)}=1$, $\mu _{0:k}^{(r)}=0,$ we have

$$\begin{aligned} \mu _{U(n+1):k}^{(r+\tau )}{=}\frac{1}{n}\mu _{U(n-1):k}^{(r+\tau )}{+}\left( \frac{(r+\tau )\delta }{\tau n}-\frac{1}{n}+1\right) \mu _{U(n):k}^{(r+\tau )}+\frac{(r+\tau )\delta \xi ^{\tau }}{\tau n}\mu _{U(n):k}^{(r)}.\nonumber \\ \end{aligned}$$

(3.5)

Proof

Clearly, from (1.1) and (1.2) , we see that

$$\begin{aligned} \left\{ 1+\left( \frac{x}{\xi }\right) ^{\tau }\right\} f(x)= & {} \frac{\tau }{\delta \xi ^{\tau }}x^{\tau -1}\bar{F}(x)[1-log\bar{F}(x)]\nonumber \\= & {} \frac{\tau }{\delta \xi ^{\tau }}x^{\tau -1}\bar{F}(x)+\frac{\tau }{\delta \xi ^{\tau }}x^{\tau -1}\bar{F}(x)[-log\bar{F}(x)]. \end{aligned}$$

(3.6)

Therefore, for $r=0,~1,~2,\ldots$, we have

$$\begin{aligned}{} & {} (n-1)!\left[ \frac{1}{\xi ^{r}}E\left( X_{U(n):k}^{r}\right) +\frac{1}{\xi ^{r+\tau }}E\left( X_{U(n):k}^{r+\tau }\right) \right] \\{} & {} \quad =\int _{0}^{\infty }\left\{ \left( \frac{x}{\xi }\right) ^{r}+\left( \frac{x}{\xi }\right) ^{r+\tau }\right\} [\bar{F}(x)]^{k-1}[-log\bar{F}(x)]^{n-1}f(x)dx\\{} & {} \quad =\int _{0}^{\infty }\left( \frac{x}{\xi }\right) ^{r}[\bar{F}(x)]^{k-1}[-log\bar{F}(x)]^{n-1}\left\{ 1+\left( \frac{x}{\xi }\right) ^{\tau }\right\} f(x)dx\\{} & {} \quad =\frac{\tau }{\delta \xi ^{r+\tau }}\int _{0}^{\infty }x^{r+\tau -1}[\bar{F}(x)]^{k}[-log\bar{F}(x)]^{n-1}dx\\{} & {} \qquad +\frac{\tau }{\delta \xi ^{r+\tau }}\int _{0}^{\infty }x^{r+\tau -1}[\bar{F}(x)]^{k}[-log\bar{F}(x)]^{n}dx. \end{aligned}$$

Integrating by parts, we get

$$\begin{aligned}{} & {} \frac{(r+\tau )\delta }{\tau }\left[ \xi ^{\tau }E\left( X_{U(n):k}^{r}\right) +E\left( X_{U(n):k}^{r+\tau }\right) \right] \\{} & {} \quad =\frac{n k^{n}}{n!}\int _{0}^{\infty }x^{r+\tau }[\bar{F}(x)]^{k-1}[-\log \bar{F}(x)]^{n}f(x)dx \\{} & {} \qquad -\frac{(n-1) k^{n}}{(n-1)!}\int _{0}^{\infty }x^{r+\tau }[\bar{F}(x)]^{k-1}[-\log \bar{F}(x)]^{n-1}f(x)dx \\{} & {} \qquad -\frac{ k^{n}}{(n-2)!}\int _{0}^{\infty }x^{r+\tau }[\bar{F}(x)]^{k-1}[-\log \bar{F}(x)]^{n-2}f(x)dx \\{} & {} \quad =nE\left( X_{U(n+1):k}^{r+\tau }\right) -E\left( X_{U(n-1):k}^{r+\tau }\right) -(n-1)E\left( X_{U(n):k}^{r+\tau }\right) . \end{aligned}$$

$\square$

Corollary 3.4

If $r=0$ in (3.5), we get

$$\begin{aligned} \mu _{U(n+1):k}^{(\tau )}=\frac{1}{n}\mu _{U(n-1):k}^{(\tau )}+\left( \frac{\delta -1}{ n}+1\right) \mu _{U(n):k}^{(\tau )}+\frac{\delta \xi ^{\tau }}{n}. \end{aligned}$$

(3.7)

Corollary 3.5

If $r=1$ in (3.5), we get

$$\begin{aligned} \mu _{U(n+1):k}^{(\tau +1)}=\frac{1}{n}\mu _{U(n-1):k}^{(\tau +1)}+\left( \frac{(\tau +1)\delta }{\tau n}-\frac{1}{n}+1\right) \mu _{U(n):k}^{(\tau +1)}+\frac{(\tau +1)\delta \xi ^{\tau }}{\tau n}\mu _{U(n):k}.\nonumber \\ \end{aligned}$$

(3.8)

3.2 Relations for Product Moments

Here, we present the relation for product moments of record values.

Theorem 3.6

For the PGW distribution given in (1) and for $1\le m < n$ and $r, s = 0, 1, 2,\ldots$,

$$\begin{aligned} \mu _{U(m,n):k}^{(r,s)}= & {} \frac{k^{n}e^{k}\xi ^{r+s}}{(m-1)!(n-m-1)!} \sum _{p=0}^{m-1}\sum _{q=0}^{n-m-1}\sum _{u=0}^{s/\tau }\sum _{v=0}^{r/\tau } \frac{(-1)^{r-1-p+q+u+v-((r+s)/\tau )}}{k^{s-r+\delta (u+v)+p+1}}\nonumber \\{} & {} \times \left( \begin{array}{c}m-1\\ p\end{array}\right) \left( \begin{array}{c}n-m-1\\ q\end{array}\right) \left( \begin{array}{c}s/\tau \\ u\end{array}\right) \left( \begin{array}{c}r/\tau \\ v\end{array}\right) \nonumber \\{} & {} \times \frac{\Gamma (n-m+\delta (u+v)+p+1)}{p+q+\delta v+1}\nonumber \\{} & {} \times {}_2 F_1\left( 1,~n-m+\delta (u+v)+p+1;~\delta v+p+q+2;~0\right) , \end{aligned}$$

(3.9)

where ${}_2 F_1(a,b;~c;~x)$ denotes the Gauss hypergeometric function defined by

$$\begin{aligned} {}_2 F_1(a,b;~c;~x)=\sum _{k=0}^{\infty }\frac{(a)_{k}~(b)_{k}}{(c)_{k}}\frac{x^{k}}{k!}, \end{aligned}$$

where $(e)_{k}=e(e+1)\ldots (e+k-1)$ denotes the ascending fractorial.

Proof

Using ( 1.5), we have

$$\begin{aligned} \mu _{U(m,n):k}^{(r,s)}= & {} \frac{k^{n}}{(m-1)!(n-m-1)!}\int _{0}^{\infty }\int _{x}^{\infty }x^{r}~y^{s}[-ln(\bar{F}(x))]^{m-1}\frac{f(x)}{[\bar{F}(x)]}\nonumber \\{} & {} \times [-ln(\bar{F}(y))+ln(\bar{F}(x))]^{n-m-1}[\bar{F}(x)]^{k-1}f(y)dydx \nonumber \\= & {} \frac{\tau ^{2}e^{k}k^{n}}{\delta ^{2}\xi ^{2\tau }(m-1)!(n-m-1)!}\int _{0}^{\infty }\int _{x}^{\infty }x^{r+\tau -1}y^{s+\tau -1} \nonumber \\{} & {} \times \left[ \left\{ 1+(x/\xi )^{\tau }\right\} ^{1/\delta }-1\right] ^{m-1} \nonumber \\{} & {} \times \left[ \left\{ 1+(y/\delta )\right\} ^{1/\delta }-\left\{ 1+(x/\delta )\right\} ^{1/\delta }\right] ^{n-m-1}e^{-k[1+(y/\xi )]^{1/\delta }} \nonumber \\{} & {} \times \left[ 1+(x/\delta )\right] ^{\frac{1}{\delta }-1}\left[ 1+(y/\delta )\right] ^{\frac{1}{\delta }-1}dydx \nonumber \\= & {} \frac{\tau ^{2}e^{k}k^{n}}{\delta ^{2}\xi ^{2\tau }(m-1)!(n-m-1)!}\sum _{p=0}^{m-1}\sum _{q=0}^{n-m-1}(-1)^{r-1-p+q}\left( \begin{array}{c}m-1\\ p\end{array}\right) \nonumber \\{} & {} \times \left( \begin{array}{c}n-m-1\\ q\end{array}\right) \int _{0}^{\infty }\int _{x}^{\infty }x^{r+\tau -1}y^{s+\tau -1}\left[ 1+(x/\xi )^{\tau }\right] ^{\frac{p+q+1}{\delta }-1} \nonumber \\{} & {} \times \left[ 1+(y/\xi )^{\tau }\right] ^{\frac{s-r-q}{\delta }-1}e^{-k\left[ 1+(y/\xi )^{\tau }\right] ^{1/\delta }}dydx \nonumber \\= & {} \frac{\tau e^{k}k^{n}\xi ^{s}}{\delta \xi ^{\tau }(m-1)!(n-m-1)!}\sum _{p=0}^{m-1}\sum _{q=0}^{n-m-1}\sum _{u=0}^{s/\tau }(-1)^{r-1-p+q+u-(s/\tau )} \nonumber \\{} & {} \times \left( \begin{array}{c}m-1\\ p\end{array}\right) \nonumber \\{} & {} \times \left( \begin{array}{c}n-m-1\\ q\end{array}\right) \left( \begin{array}{c}s/\tau \\ u\end{array}\right) \frac{1}{k^{s-r-q+\delta u}}\int _{0}^{\infty }x^{r+\tau -1}\left[ 1+(x/\xi )^{\tau }\right] ^{\frac{p+q+1}{\delta }-1} \nonumber \\{} & {} \times \int _{k\left[ 1+(x/\xi )^{\tau }\right] ^{1/\delta }}^{\infty } z^{s-r-q+\delta p-1}e^{-z}dzdx \nonumber \\= & {} \frac{\tau e^{k}k^{n}\xi ^{s}}{\delta \xi ^{\tau }(m-1)!(n-m-1)!}\sum _{p=0}^{m-1}\sum _{q=0}^{n-m-1}\sum _{u=0}^{s/\tau }(-1)^{r-1-p+q+u-(s/\tau )} \nonumber \\{} & {} \times \left( \begin{array}{c}m-1\\ p\end{array}\right) \nonumber \\{} & {} \times \left( \begin{array}{c}n-m-1\\ q\end{array}\right) \left( \begin{array}{c}s/\tau \\ u\end{array}\right) \frac{1}{k^{s-r-q+\delta u}}\int _{0}^{\infty }x^{r+\tau -1}\left[ 1+(x/\xi )^{\tau }\right] ^{\frac{p+q+1}{\delta }-1} \nonumber \\{} & {} \times \Gamma \left( \delta u+s-r-q,~~k\left[ 1+(x/\xi )^{\tau }\right] ^{1/\delta }\right) dx \nonumber \\= & {} \frac{\tau e^{k}k^{n}\xi ^{r+s}}{(m-1)!(n-m-1)!}\sum _{p=0}^{m-1}\sum _{q=0}^{n-m-1}\sum _{u=0}^{s/\tau }\sum _{v=0}^{r/\tau }(-1)^{r-1-p+q+u+v-((r+s)/\tau )} \nonumber \\{} & {} \times \left( \begin{array}{c}m-1\\ p\end{array}\right) \nonumber \\{} & {} \times \left( \begin{array}{c}n-m-1\\ q\end{array}\right) \left( \begin{array}{c}s/\tau \\ u\end{array}\right) \left( \begin{array}{c}r/\tau \\ v\end{array}\right) \frac{1}{k^{s-r+\delta ( u+v)+p+1}} \nonumber \\{} & {} \times \int _{0}^{\infty }w^{p+q+\delta v}\Gamma \left( s-r+\delta u,~w\right) dw. \end{aligned}$$

(3.10)

where $z=k\left[ 1+(y/\xi )^{\tau }\right] ^{1/\delta }$ and $w=k\left[ 1+(x/\xi )^{\tau }\right] ^{1/\delta }$. $\square$

Theorem 3.7

For $1\le m < n$ and $r = 0, 1, 2,\ldots$, and s a negative integer,

$$\begin{aligned} \mu _{U(m,n):k}^{(r,s)}= & {} \frac{k^{n}e^{k}\xi ^{r+s}}{(m-1)!(n-m-1)!}\sum _{p=0}^{m-1}\sum _{q=0}^{n-m-1}\sum _{u=0}^{\infty }\sum _{v=0}^{r/\tau }\frac{(-1)^{r-1-p+q+u+v-((r+s)/\tau )}}{k^{s-r+\delta (u+v)+p+1}} \nonumber \\{} & {} \times \left( \begin{array}{c}m-1\\ p\end{array}\right) \left( \begin{array}{c}n-m-1\\ q\end{array}\right) \left( \begin{array}{c}s/\tau \\ u\end{array}\right) \left( \begin{array}{c}r/\tau \\ v\end{array}\right) \nonumber \\{} & {} \times \frac{\Gamma (n-m+\delta (u+v)+p+1)}{p+q+\delta v+1} \nonumber \\{} & {} \times {}_2 F_1\left( 1,~n-m+\delta (u+v)+p+1;~\delta v+p+q+2;~0\right) . \end{aligned}$$

(3.11)

Proof

This proof is straightforward. $\square$

Theorem 3.8

For $1\le m < n$ and $s= 0, 1, 2,\ldots$, and and r a negative integer,

$$\begin{aligned} \mu _{U(m,n):k}^{(r,s)}= & {} \frac{k^{n}e^{k}\xi ^{r+s}}{(m-1)!(n-m-1)!}\sum _{p=0}^{m-1}\sum _{q=0}^{n-m-1}\sum _{u=0}^{s/\tau }\sum _{v=0}^{\infty }\frac{(-1)^{r-1-p+q+u+v-((r+s)/\tau )}}{k^{s-r+\delta (u+v)+p+1}} \nonumber \\{} & {} \times \left( \begin{array}{c}m-1\\ p\end{array}\right) \left( \begin{array}{c}n-m-1\\ q\end{array}\right) \left( \begin{array}{c}s/\tau \\ u\end{array}\right) \left( \begin{array}{c}r/\tau \\ v\end{array}\right) \nonumber \\{} & {} \times \frac{\Gamma (n-m+\delta (u+v)+p+1)}{p+q+\delta v+1} \nonumber \\{} & {} \times {}_2 F_1\left( 1,~n-m+\delta (u+v)+p+1;~\delta v+p+q+2;~0\right) . \end{aligned}$$

(3.12)

Proof

This proof is straightforward. $\square$

Theorem 3.9

For $1\le m < n$ and and both r and s negative integers,

$$\begin{aligned} \mu _{U(m,n):k}^{(r,s)}= & {} \frac{k^{n}e^{k}\xi ^{r+s}}{(m-1)!(n-m-1)!}\sum _{p=0}^{m-1}\sum _{q=0}^{n-m-1}\sum _{u=0}^{\infty }\sum _{v=0}^{\infty }\frac{(-1)^{r-1-p+q+u+v-((r+s)/\tau )}}{k^{s-r+\delta (u+v)+p+1}} \nonumber \\{} & {} \times \left( \begin{array}{c}m-1\\ p\end{array}\right) \left( \begin{array}{c}n-m-1\\ q\end{array}\right) \left( \begin{array}{c}s/\tau \\ u\end{array}\right) \left( \begin{array}{c}r/\tau \\ v\end{array}\right) \nonumber \\{} & {} \times \frac{\Gamma (n-m+\delta (u+v)+p+1)}{p+q+\delta v+1} \nonumber \\{} & {} \times {}_2 F_1\left( 1,~n-m+\delta (u+v)+p+1;~\delta v+p+q+2;~0\right) . \end{aligned}$$

(3.13)

Proof

This proof is straightforward. $\square$

Theorem 3.10

For the PGW distribution given in (1) and $1\le m\le n-2$,

$$\begin{aligned} \mu _{U(m+n,n):k}^{(r+\tau ,s)}= & {} \frac{(r+\tau )\delta \xi ^{\tau }}{\tau m} \mu _{U(m,n):k}^{(r,s)}+\frac{1}{m}\mu _{U(m-1,n-1):k}^{(r+\tau ,s)}-\frac{1}{m}\mu _{U(m,n-1):k}^{(r+\tau ,s)}\nonumber \\+ & {} \left( 1+\frac{(r+\tau )\delta }{m\tau }\right) \mu _{U(m,n):k}^{(r+\tau ,s)}. \end{aligned}$$

(3.14)

Proof

For $m\le n-1$, we have

$$\begin{aligned}{} & {} \frac{1}{\xi ^{r}}E\left( X_{U(m):k}^{(r)} X_{U(n):k}^{(s)}\right) +\frac{1}{\xi ^{r+\tau }}E\left( X_{U(m):k}^{r+\tau }X_{U(n):k}^{s}\right) \\{} & {} \quad =\frac{k^{n}}{(m-1)!(n-m-1)!}\int _{0}^{\infty }y^{s}[\bar{F}(y)]^{k-1}~f(y)~I(y)~dy, \end{aligned}$$

where

$$\begin{aligned} I(y)= & {} \int _{0}^{y}x^{r}[-\log (\bar{F}(x))^{m-1}]~[-\log (\bar{F}(y))\nonumber \\{} & {} +\log (\bar{F}(x))]^{n-m-1}~\frac{\left\{ 1+\left( \frac{x}{\xi }\right) ^{\tau }\right\} f(x)}{\bar{F}(x)}~dx \nonumber \\= & {} \frac{\tau }{\delta \xi ^{r+\tau }}\int _{0}^{y}x^{r+\tau -1}~[-\log (\bar{F}(x))^{m-1}][-\log (\bar{F}(y))\nonumber \\{} & {} +\log (\bar{F}(x))]^{n-m-1}[1-\log (\bar{F}(x))]~dx \nonumber \\= & {} \frac{\tau }{\delta \xi ^{r+\tau }}\int _{0}^{y}x^{r+\tau -1}~[-\log (\bar{F}(x))^{m-1}][-\log (\bar{F}(y))+\log (\bar{F}(x))]^{n-m-1}~dx \nonumber \\+ & {} \frac{\tau }{\delta \xi ^{r+\tau }}\int _{0}^{y}x^{r+\tau -1}~[-\log (\bar{F}(x))^{s}][-\log (\bar{F}(y))\nonumber \\{} & {} +\log (\bar{F}(x))]^{n-m-1}[1-\log (\bar{F}(x))]~dx. \end{aligned}$$

(3.15)

Upon integration by parts, we get

$$\begin{aligned}{} & {} \frac{1}{\xi ^{r}}E\left( X_{U(m):k}^{(r)} X_{U(n):k}^{(s)}\right) +\frac{1}{\xi ^{r+\tau }}E\left( X_{U(m):k}^{r+\tau }X_{U(n):k}^{s}\right) \\{} & {} \quad = \frac{\frac{\tau }{\delta \xi ^{r+\tau }}(r+\tau )^{-1}}{(m-1)!(n-m-1)!}\int _{0}^{\infty }\int _{0}^{y}y^{s}x^{r+\tau }[\bar{F}(y)]^{k-1}f(y)\\{} & {} \qquad \times \Bigg [(n-m-1)[-\log (\bar{F}(x))]^{m-1}[\log (\bar{F}(x))-\log (\bar{F}(y))]^{n-m-2}\frac{f(x)}{\bar{F}(x)}\\{} & {} \qquad -(m-1)[-\log (\bar{F}(x))]^{m-2}[\log (\bar{F}(x))-\log (\bar{F}(y))]^{n-m-1}\frac{f(x)}{\bar{F}(x)}\\{} & {} \qquad - m[-\log (\bar{F}(x))]^{m-1}[\log (\bar{F}(x))-\log (\bar{F}(y))]^{n-m-1}\frac{f(x)}{\bar{F}(x)}\\{} & {} \qquad + (n-m-1)[-\log (\bar{F}(x))]^{m}[\log (\bar{F}(x))-\log (\bar{F}(y))]^{n-m-2}\frac{f(x)}{\bar{F}(x)}\Bigg ]~dx~dy\\{} & {} \quad = \frac{\tau }{(r+\tau )\delta \xi ^{r+\tau }}\Big [-E\left( X_{U(m-1):k}^{r+\tau }X_{U(n-1):k}^{s}\right) +E\left( X_{U(m):k}^{r+\tau } X_{U(n-1):k}^{s}\right) \\{} & {} \qquad - m E\left( X_{U(m):k}^{r+\tau } X_{U(n):k}^{s}\right) +mE\left( X_{U(m+1):k}^{r+\tau }X_{U(n):k}^{s}\right) \Big ]. \end{aligned}$$

The result follows. $\square$

Corollary 3.11

Upon setting $r=0$ and $s=1$, we have the following relation for simple product moments for $m=1,2,\ldots ....,n-1$

$$\begin{aligned} \mu _{U(m+1,n):k}^{(\tau ,1)}= & {} \frac{\delta \xi ^{\tau }}{m}\mu _{U(m,n):k}+\frac{1}{m}\mu _{U(m-1,n-1):k}^{(\tau ,1)}-\frac{1}{m}\mu _{U(m,n-1):k}^{(\tau ,1)}\nonumber \\{} & {} +\left( 1+\frac{\delta }{m}\right) \mu _{U(m,n):k}^{(\tau ,1)}. \end{aligned}$$

(3.16)

Specially for $m=1$, we get

$$\begin{aligned} \mu _{U(2,n):k}^{(\tau ,1)}=\delta \xi ^{\tau }\mu _{U(1,n):k}-\mu _{U(1,n-1):k}^{(\tau ,1)}+(1+\delta )\mu _{U(1,n):k}^{(\tau ,1)}. \end{aligned}$$

4 Estimation of Model Parameters

4.1 Maximum Likelihood Estimation

Here, we obtain the maximum likelihood estimators (MLEs) of the parameters $\tau$, $\delta$ and $\xi$ of PGW distribution. Let $X_{1}, X_{2},\ldots$ be a sequence of iid random variables with cdf F(x) and pdf f(x) on positive support. Let $Y_{n}=max\{X_{1}, X_{2},\ldots , X_{n}\}$ for $n\ge 1$. The observation $X_{j},~ J\ge 1$, is a upper record values of this sequence, if it is greater than all preceding observations, that is $Y_{j}<Y_{j-1}$ for $j>1$.

The likelihood function based on the random sample of size n is obtained as:

$$\begin{aligned} L(\tau , \delta , \xi |\underline{x})=f(x_{U(n)}; \tau , \delta , \xi )\prod _{i=1}^{n-1}\frac{f(x_{U(i)}; \tau , \delta , \xi )}{1-F(x_{U(i)}; \tau , \delta , \xi )}. \end{aligned}$$

(4.1)

Using ( 1.1) and ( 1.2), then ( 3.4) can be rewritten as

$$\begin{aligned} L(\tau , \delta , \xi |\underline{x})=\left( \frac{\tau }{\delta \xi ^{\tau }}\right) ^{n} e^{1-\left[ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right] ^{1/\delta }}\prod _{i=1}^{n}x_{U(i)}^{\tau -1}\left[ 1+\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }-1}. \end{aligned}$$

(4.2)

The log likelihood function $l(\tau , \delta , \xi |\underline{x})=log L(\tau , \delta , \xi |\underline{x})$, dropping terms that do not involve $\tau$, $\delta$ and $\xi$, is

$$\begin{aligned} l(\tau , \delta , \xi |\underline{x})= & {} nlog\tau -nlog\delta -n\tau log\xi +1-\left[ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }} \nonumber \\{} & {} +(\tau -1)\sum _{i=1}^{n}log x_{U(i)}+\left( \frac{1}{\delta }-1\right) \sum _{i=1}^{n}log\left[ 1+\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }\right] .\qquad \end{aligned}$$

(4.3)

Differentiate (4.3) partially with respect to $\tau$, $\delta$ and $\xi$ and equate to zero, we get

$$\begin{aligned} 0=\frac{\partial l(\tau , \delta , \xi |\underline{x})}{\partial \tau }= & {} \frac{n}{\tau }-nlog \xi -\frac{1}{\delta } \left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }log\left( \frac{x_{U(n)}}{\xi }\right) \left[ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }-1} \nonumber \\+ & {} \sum _{i=1}^{n}log x_{U(i)}+\left( \frac{1}{\delta }-1\right) \sum _{i=1}^{n}\frac{\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }log\left( \frac{x_{U(i)}}{\xi }\right) }{\left[ 1+\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }\right] }, \end{aligned}$$

(4.4)

$$\begin{aligned} 0=\frac{\partial l(\tau , \delta , \xi |\underline{x})}{\partial \delta }= & {} -\frac{n}{\delta }-\left[ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }}log\left[ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right] \nonumber \\- & {} \frac{1}{\delta ^{2}}\sum _{i=1}^{n}log\left[ 1+\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }\right] \end{aligned}$$

(4.5)

and

$$\begin{aligned} 0=\frac{\partial l(\tau , \delta , \xi |\underline{x})}{\partial \xi }= & {} -\frac{n\tau }{\xi }+\frac{\tau }{\delta \xi }\left[ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }-1}\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau } \nonumber \\- & {} \left( \frac{1}{\delta }-1\right) \sum _{i=1}^{n}\frac{\tau \left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }}{\xi \left[ 1+\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }\right] }. \end{aligned}$$

(4.6)

The solutions of the above equations are the maximum likelihood estimators of the parameters $\tau$, $\delta$ and $\xi$, denoted $\hat{\tau }_{MLE}$, $\hat{\delta }_{MLE}$ and $\hat{\xi }_{MLE}$, respectively. It may be noted that equations (4.4), (4.5) and (4.6) cannot be solved simultaneously to provide a nice closed form for maximum likelihood estimators. Therefore, we propose to use non-linear minimization method (nlm) through R software. For details about the proposed method, readers may refer [20,21,22].

4.2 Approximate Confidence Intervals

Since the MLEs of the unknown parameters $\tau$, $\delta$ and $\xi$ cannot be derived in closed form, it is not easy to derive the exact distributions of the MLEs. Hence, we cannot obtain exact confidence intervals for the parameters. Using large sample approximation, the asymptotic distribution of the MLE is $[\sqrt{n}(\hat{\tau }_{MLE}-\tau ), \sqrt{n}(\hat{\delta }_{MLE}-\delta ), \sqrt{n}(\hat{\xi }_{MLE}-\xi )]\rightarrow N_{3}(0, \pi ^{-1}(\tau , \delta ,\xi ))$, (see [17]), where $\pi ^{-1}(\tau , \delta , \xi )$, defined by

$$\begin{aligned} \pi ^{-1}(\Theta )= & {} \left( \begin{array}{llll} &{}-\frac{\partial ^{2}l(\tau , \delta , \xi )}{\partial \tau ^{2}} &{}-\frac{\partial ^{2}l(\tau , \delta , \xi )}{\partial \tau \partial \delta } &{} -\frac{\partial ^{2}l(\tau , \delta , \xi )}{\partial \tau \partial \xi }\\ &{} -\frac{\partial ^{2}l(\delta , \tau , \xi )}{\partial \delta \partial \tau } &{}-\frac{\partial ^{2}l(\tau , \delta , \xi )}{\partial \delta ^{2}}&{} -\frac{\partial ^{2}l(\tau , \delta , \xi )}{\partial \delta \partial \xi } \\ &{} -\frac{\partial ^{2}l(\tau , \delta , \xi )}{\partial \xi \partial \tau } &{} -\frac{\partial ^{2}l(\tau , \delta , \xi )}{\partial \xi \partial \delta } &{} -\frac{\partial ^{2}l(\tau , \delta , \xi )}{\partial \xi ^{2}} \end{array}\right) ^{-1}_{(\tau , \delta , \xi )=(\hat{\tau }, \hat{\delta }, \hat{\xi })}\\= & {} \left( \begin{array}{llll} &{}Var(\hat{\tau }) &{} Cov(\hat{\tau }, \hat{\delta }) &{} Cov(\hat{\tau }, \hat{\xi })\\ &{} Cov(\hat{\delta }, \hat{\tau })&{}Var(\hat{\tau }) &{} Cov(\hat{\delta }, \hat{\xi })\\ &{} Cov(\hat{\xi }, \hat{\tau }) &{}Cov(\hat{\xi }, \hat{\delta } ) &{} Var(\hat{\xi }) \end{array}\right) . \end{aligned}$$

The derivatives in $\pi (\Theta )$ are given in

$$\begin{aligned}{} & {} \frac{\partial ^{2} \ell (\tau , \delta , \xi |\underline{x})}{\partial \tau ^{2}}\nonumber \\{} & {} \quad = -\frac{n}{\tau ^{2}}+\frac{z_{n}^{2}~u_{n}~(1+z_{n})^{\frac{1}{\delta }-1}}{\delta }\left\{ \left( \frac{1}{\delta }-1\right) ~u_{n}^{1/\tau }(1+u_{n})^{-1}+1\right\} \nonumber \\{} & {} \qquad +\left( \frac{1}{\delta }-1\right) \sum _{i=0}^{n} \frac{z_{i}^{2}~u_{i}^{2}}{(1+u_{i})^{2}}\left( \frac{1+u_{i}}{u_{i}}-1\right) , \end{aligned}$$

(4.7)

$$\begin{aligned}{} & {} \frac{\partial ^{2} \ell (\tau , \delta ,\xi |\underline{x})}{\partial \delta ^{2}} =\frac{n}{\delta ^{2}}-(log(1+u_{n}))^{2}(1+u_{n})^{1/\delta }+\frac{2}{\delta ^{3}}\sum _{i=1}^{n}log(1+u_{i}),\qquad \end{aligned}$$

(4.8)

$$\begin{aligned}{} & {} \frac{\partial ^{2} \ell (\tau , \delta ,\xi |\underline{x})}{\partial \xi ^{2}} = \frac{n\tau }{\xi ^{2}}-\frac{\tau ^{2}}{\delta \xi ^{2}}\left[ \left( \frac{1}{\delta }-1\right) u_{n}^{2}(1+u_{n})^{\frac{1}{\delta }-2}+u_{n}(1+u_{n})^{\frac{1}{\delta }-1}\right] \nonumber \\{} & {} \qquad +\frac{\tau ^{2}}{\xi ^{2}}\left( \frac{1}{\delta }-1\right) \sum _{i=1}^{n}\left[ \frac{u_{i}(1+u_{i})-u_{i}^{2}}{(1+u_{i})^{2}}\right] , \end{aligned}$$

(4.9)

$$\begin{aligned}{} & {} \frac{\partial ^{2} \ell (\tau , \delta ,\xi |\underline{x})}{\partial \tau ~\partial \delta }=-\frac{1}{\delta ^{2}}\sum _{i=1}^{n}\frac{u_{i}z_{i}}{(1+u_{i})} -\frac{u_{n}~z_{n}}{\delta ^{2}~(1+u_{n})}, \end{aligned}$$

(4.10)

$$\begin{aligned}{} & {} \frac{\partial ^{2} \ell (\tau , \delta ,\xi |\underline{x})}{\partial \tau ~\partial \xi }\nonumber \\{} & {} \quad = -\frac{n}{\xi }+\left( \frac{1}{\delta }-1\right) \left( \sum _{i=1}^{n}\frac{\left( \frac{\tau }{\xi }~u_{i}~z_{i}-\frac{1}{\xi }~u_{i}\right) (1+u_{i})}{(1+u_{i})^{2}}-\sum _{i=1}^{n}\frac{\tau ~u_{i}^{2}~z_{i}}{\xi ~(1+u_{i})^{2}}\right) \nonumber \\{} & {} \qquad + \frac{\left( \frac{\tau }{\xi }~u_{n}~z_{n}-\frac{1}{\xi }~u_{n}\right) (1+u_{n})}{\delta (1+u_{n})^{2}}-\frac{\tau ~u_{n}^{2}~z_{n}}{\delta \xi ~(1+u_{n})^{2}}, \end{aligned}$$

(4.11)

$$\begin{aligned}{} & {} \frac{\partial ^{2} \ell (\tau , \delta ,\xi |\underline{x})}{\partial \xi ~\partial \delta }=-\frac{1}{\delta ^{2}}\sum _{i=1}^{n}\frac{\tau ~u_{i}}{\xi ~(1+u_{i})}-\frac{\tau ~u_{n}}{\delta ^{2}\xi ~(1+u_{n})}, \end{aligned}$$

(4.12)

$$\begin{aligned}{} & {} \frac{\partial ^{2} \ell (\tau , \delta ,\xi |\underline{x})}{\partial \tau ~\partial \delta }\nonumber \\{} & {} \quad =-z_{n}u_{n}\left[ \frac{1}{1+u_{n}}\left\{ -\frac{(1+u_{n})^{1/\delta }}{\delta ^{2}}+\frac{log(1+u_{n})(1+u_{n})^{1/\delta }}{\delta }\right\} \right] , \end{aligned}$$

(4.13)

where

$$\begin{aligned} z_{i}= & {} log\left( \frac{x_{U(i)}}{\xi }\right) ,\\ z_{n}= & {} log\left( \frac{x_{U(n)}}{\xi }\right) ,\\ u_{i}= & {} \left( \frac{x_{U(i)}}{\xi }\right) ^{\tau } \end{aligned}$$

and

$$\begin{aligned} u_{n}=\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }. \end{aligned}$$

The above approach is used to derive approximate $100(1- \tau )\%$ confidence intervals of the parameters $\tau$ and $\delta$ of the forms

$$\begin{aligned}{} & {} \hat{\tau }\pm z_{\tau /2}\sqrt{var(\hat{\tau })},\\{} & {} \quad \hat{\delta }\pm z_{\tau /2}\sqrt{var(\hat{\delta })} \end{aligned}$$

and

$$\begin{aligned} \hat{\xi }\pm z_{\tau /2}\sqrt{var(\hat{\xi })}, \end{aligned}$$

where $z_{\tau /2}$ is the upper $(\tau /2)$th percentile of the standard normal distribution.

5 Prediction of Future Record Values

5.1 Maximum Likelihood Prediction

The likelihood function of $y=x_{U(m)}$ can be written (see Basak and Balakrishnan 2003) as

$$\begin{aligned} L(y; \Theta , \underline{x})=\prod _{i=1}^{n}g(x_{U(i)}; \Theta )\frac{[G(y, \Theta )-G(x_{U(n)}; \Theta )]^{m-n-1}}{\Gamma (m-n)}f(y; \Theta ), \end{aligned}$$

where

$$\begin{aligned} G(y, \Theta )=-log[1-F(y, \Theta )] \end{aligned}$$

and

$$\begin{aligned} g(x_{U(i)}; \Theta )= & {} \frac{f(x_{U(i)}; \tau , \delta , \lambda )}{S(x_{U(i)}; \tau , \delta , \lambda )}\\= & {} \frac{\tau }{\delta \xi ^{\tau }}~ x_{U(i)}^{\tau -1}\left[ 1+\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }-1}. \end{aligned}$$

For the data set, we shall compare the fits of PGW model with other models.

The predictive likelihood function for the PGW distribution is

$$\begin{aligned} L(y; \tau , \delta , \xi )= & {} \left( \frac{\tau }{\delta \xi ^{\xi }}\right) ^{n+1}\prod _{i=1}^{n}x_{U(i)}^{\tau -1}\left[ 1+\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }-1}\\{} & {} \times \frac{1}{\Gamma (m-n)}\left[ \left\{ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }}-\left\{ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }}\right] ^{m-n-1}\\{} & {} \times y^{\tau -1}\left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }-1}e^{1-\left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }}}. \end{aligned}$$

The log predictive likelihood is given by

$$\begin{aligned} log L= & {} (n+1)log\tau -(n+1)log\delta -(n+1)\tau log\xi +(\tau -1)\sum _{i=1}^{n}log~x_{U(i)} \nonumber \\{} & {} +\left( \frac{1}{\delta }-1\right) \sum _{i=1}^{n}log\left[ 1+\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }\right] -log \Gamma (m-n) \nonumber \\{} & {} +(m-n-1)log\left[ \left\{ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }}-\left\{ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }}\right] \nonumber \\{} & {} +(\tau -1)log y+\left( \frac{1}{\delta }-1\right) log\left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] +1-\left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }}.\nonumber \\ \end{aligned}$$

(5.1)

Differentiating (33) partially with respect to $\tau$ , $\delta$, $\xi$ and y and equate to zero, we get

$$\begin{aligned} 0=\frac{\partial log~L}{\partial \tau }= & {} \frac{n+1}{\tau }-(n+1)log\xi +\sum _{i=1}^{n}log x_{U(i)}\\{} & {} +\left( \frac{1}{\delta }-1\right) \sum _{i=1}^{n}\frac{\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }log\left( \frac{x_{U(i)}}{\xi }\right) }{\left[ 1+\left( \frac{x_{U(i)}}{\xi }\right) \right] }+(m+n-1) \\{} & {} \times \frac{\left( \frac{y}{\xi }\right) ^{\tau }~log \left( \frac{y}{\xi }\right) ~\left\{ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }-1}-\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }~log \left( \frac{x_{U(n)}}{\xi }\right) ~\left\{ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }-1}}{\delta \left[ \left\{ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }}-\left\{ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }-1}\right] } \\{} & {} +log y+\left( \frac{1}{\delta }-1\right) \frac{\left( \frac{y}{\xi }\right) ^{\tau }log\left( \frac{y}{\xi }\right) }{\left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] }+\frac{1}{\delta }\left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }-1}log \left( \frac{y}{\xi }\right) \left( \frac{y}{\xi }\right) ^{\tau } ,\\ 0=\frac{\partial log~L}{\partial \delta }= & {} -\frac{n+1}{\delta }-\frac{1}{\delta ^{2}}\sum _{i=1}^{n}log\left[ 1+\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }\right] +(m-n-1) \\{} & {} \times \frac{\left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }}log\left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] -\left[ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }}log\left[ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right] }{\left[ \left\{ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }}-\left\{ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }}\right] } \\{} & {} -\frac{1}{\delta ^{2}}log\left\{ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right\} -log\left\{ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right\} \left\{ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }},\\ 0=\frac{\partial log~L}{\partial \xi }= & {} -\frac{n+1}{\xi }-\left( \frac{1}{\delta }-1\right) \sum _{i=1}^{n}\frac{\tau \left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }}{\xi \left[ 1+\left( \frac{x_{U(i)}}{\xi }\right) ^{\tau }\right] }+(m-n-1) \\{} & {} \times \frac{\frac{\tau }{\delta \xi }\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\left\{ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right\} -\frac{\tau }{\delta \xi }\left( \frac{y}{\xi }\right) ^{\tau }\left\{ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right\} }{\left[ \left\{ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }}-\left\{ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }}\right] } \\{} & {} -\left( \frac{1}{\delta }-1\right) \frac{\tau \left( \frac{y}{\xi }\right) ^{\tau }}{\xi \left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] }+\frac{1}{\delta \xi }\left( \frac{y}{\xi }\right) ^{\tau } \left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }-1} \end{aligned}$$

and

$$\begin{aligned} 0=\frac{\partial log~L}{\partial y}= & {} (m-n-1)\frac{\frac{\tau }{\delta \xi }\left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }}\left( \frac{y}{\xi }\right) ^{\tau -1}}{\left[ \left\{ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }}-\left\{ 1+\left( \frac{x_{U(n)}}{\xi }\right) ^{\tau }\right\} ^{\frac{1}{\delta }}\right] } \\{} & {} +\frac{\tau -1}{y}+\left( \frac{1}{\delta }-1\right) \frac{\tau \left( \frac{y}{\xi }\right) ^{\tau -1}}{\xi \left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] }-\frac{\tau }{\delta \xi }\left( \frac{y}{\xi }\right) ^{\tau -1}\left[ 1+\left( \frac{y}{\xi }\right) ^{\tau }\right] ^{\frac{1}{\delta }-1}. \end{aligned}$$

Table 1 Prediction of 18-th upper record for data I

Table 2 Goodness-of-fit statistics, MLEs, standard errors (SE) (in parentheses) and the approximate confidence intervals (CI) for cancer data

Table 3 MLEs, standard error (in parentheses) and the approximate confidence intervals for cancer data

6 Numerical Results

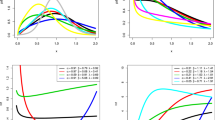
In Tables 1 and  2 , we have computed the values of means for $n=1, 2, \cdots 10$ and $\tau = 1(1)4$. One can see that the means are decreasing with respect to n but increasing with respect to $\tau$. In Table 3, we have computed the variances and covariances for different values m and n and for different values of $\tau$ and $\delta$. We can see that variances and covariances are decreased for both $\tau$ and $\delta$ values increase.

7 Data Analysis

In this section, the PGW distribution is fitted to real data set and compared with other some competitive models to illustrate the potentiality of the PGW distribution.

We compare the PGW distribution with Burr type III (Burr-III) distribution [7], Marshall–Olkin generalized exponential (MOGE) distribution [19], exponentiated exponential (EE) distribution [10], Weibull (W) distribution [32] and complementary exponential geometric (CEG) distribution (Louzada et al. 2011). Their density functions (for $x > 0$) are given by

$$\begin{aligned}{} & {} \text {Burr-III}: f(x; \tau , \delta , \lambda )=\frac{\tau \delta \lambda x^{-\delta -1}}{(1+x^{-\delta })^{\tau +1}}\left( 1-\left( 1+x^{-\delta } \right) ^{-\tau -1} \right) ^{\lambda -1}, \quad \\{} & {} x>0, \tau , \delta , \lambda> 0, \\{} & {} \quad \text {MOGE}: f(x; \tau , \delta , \lambda )=\frac{\tau \delta \lambda e^{-\lambda x}\left( 1-e^{-\lambda x} \right) ^{\delta -1}}{\left( \tau +\left( 1-\tau \right) \left( 1-e^{-\lambda x} \right) ^{\delta }\right) ^2}, \quad x>0,~ \tau , \delta , \lambda> 0,\\{} & {} \quad \text {EE}: f(x; \tau , \lambda )=\tau \lambda e^{-\lambda x} \left( 1- e^{-\lambda x} \right) ^{\tau - 1}, \qquad x>0, \tau , \lambda> 0,\\{} & {} \quad \text {W}:f(x; \tau , \lambda )=\tau \lambda ^\tau x^{\tau -1} {e^{-\left( \lambda x\right) } }^{\tau }, \quad x>0, \tau , \lambda> 0,\\{} & {} \quad \text {CEG}: f(x; \tau , \lambda )=\frac{\lambda ~\tau ~e^{-\lambda x}}{[\lambda +(1-\lambda )~e^{-\lambda x}]^{2}}, \lambda , \lambda >0. \end{aligned}$$

In order to compare the fits of the distributions, we consider some measures of goodness of fit statistics $-2L$ (where L denotes the log-likelihood function evaluated at the maximum likelihood estimates), Kolmogorov–Smirnov (K-S) statistic and the corresponding p-value, Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). The smaller these statistics are, the better the fit is.

The data set represents the remission times (in months) of a random sample of 128 bladder cancer patients. The data are:

0.08, 2.09, 3.48, 4.87, 6.94, 8.66, 13.11, 23.63, 0.20, 2.23, 3.52, 4.98, 6.97, 9.02, 13.29, 0.40, 2.26, 3.57, 5.06, 7.09, 9.22, 13.80, 25.74, 0.50, 2.46, 3.64, 5.09, 7.26, 9.47, 14.24, 25.82, 0.51, 2.54, 3.70, 5.17, 7.28, 9.74, 14.76, 26.31, 0.81, 2.62, 3.82, 5.32, 7.32, 10.06, 14.77, 32.15, 2.64, 3.88, 5.32, 7.39, 10.34, 14.83, 34.26, 0.90, 2.69, 4.18, 5.34, 7.59, 10.66, 15.96, 36.66, 1.05, 2.69, 4.23, 5.41, 7.62, 10.75, 16.62, 43.01, 1.19, 2.75, 4.26, 5.41, 7.63, 17.12, 46.12, 1.26, 2.83, 4.33, 5.49, 7.66, 11.25, 17.14, 79.05, 1.35, 2.87, 5.62, 7.87, 11.64, 17.36, 1.40, 3.02, 4.34, 5.71, 7.93, 11.79, 18.10, 1.46, 4.40, 5.85, 8.26, 11.98, 19.13, 1.76, 3.25, 4.50, 6.25, 8.37, 12.02, 2.02, 3.31, 4.51, 6.54, 8.53, 12.03, 20.28, 2.02, 3.36, 6.76,12.07, 21.73, 2.07, 3.36, 6.93, 8.65, 12.63, 22.69.

This data set was studied by [18] in survival data analysis, but no one has discussed this data set in considered model under upper record values. From this data set, we have extracted 17 upper records 0.08, 2.09, 3.48, 4.87, 6.94, 8.66, 13.11, 23.63, 25.74, 25.82, 26.31, 32.15, 34.26, 36.66, 43.01, 46.12, 79.05 for our data analysis. The simulation results are presented in Table 1. Also, we have implemented prediction procedures as mentioned the earlier section of the paper. Here our goal is to predict 18-th upper record values based on the 17 records considered in the parameter estimation.

In Table 1, we compare the fits of the PGW model with the Burr III, MOGE, EE, We and CEG models. The figures in these tables indicate that the PGW distribution has the lowest values for all the goodness-of-fit statistics, for the data set, among all fitted models. The histogram and the fitted MOAP-Ex distribution of both the data sets are displayed in Figures 3 and 5. Also, the plots of the estimated cdfs of the two data sets are displayed in Figures 4 and 6, respectively. The fitted pdf, cdf, sf and Q-Q plots of the MOAP-Ex distribution are shown in Figure 7 (Fig. 8).

Fig. 6

Fitted PP-plot for cancer data

Fig. 7

Fitted QQ-Plot for cancer data

Fig. 8

Fitted CDF plot and theoretical empirical plot for cancer data

8 Conclusion

In this paper, we considered the upper record values from power generalized Weibull distribution and obtained the relations for single and product moments of record values. We see that the moments of record values of the distribution are well behaved. However, we have only computed the means, variances and the covariances of the upper record values which are useful in determining best linear unbiased estimators (BLUEs) of location/scale parameters and best linear unbiased predictors (BLUPs) of censored failure times. This will encourage the study of the other properties of order statistics for a future research.