Accessing Individual Students Academic Performance Using Random Effect Analysis (Multilevel Analysis)

Abstract

Sometimes, people with interest in measuring quality of education take into account level in academic performance and various associated factors. Usually, an average academic performance is an accustomed way of assessment; however, this study examines on individual basis different factors that might have an impact on the academic performance of undergraduate students. Data on the semester weighted average of class of 2012 mathematics students were acquired from the Quality Assurance and Planning Unit and the Examination Office of the Department of Mathematics, Kwame Nkrumah University of Science and Technology. The main factors considered for this research were entry age, gender, entry aggregate, Ghana education service graded level of senior high school attended and geographical location. The statistical method considered was random effect. Since the interaction or variation around the slope was highly insignificant, the random intercept model was the better alternative ahead of the random intercept and slope model. Statistically, not all the parameter estimates are significant at $\alpha =0.05$ level of significance. It was observed that the difference in geographical location was not significant in the main effect model. Hence where a student comes from has no influence on their academic performance. However, entry aggregate, entry age and gender were all significant. Nevertheless, the geographical location with regard to the Northern Belt was significant in the linear trend with a standard deviation of approximately 0.712.

1 Introduction

Studies of academic performance may be able to explain to some extent what factors increase the likelihood of high academic performance and to possibly make recommendations to facilitate the removal of social, psychological and economic barriers to full participation in the educational system by all and sundry who have the ability and appetite to do so.

Some of the impetus for this study came from initiative to help the Department of Mathematics and its administration to monitor and evaluate the gradual progress of students from 1 to 4 years.

Most of the experts argue that the low socio-economic status has negative effect on the academic performance of students because the basic needs of students remain unfulfilled, making them unable to perform better academically [1]. Low socio-economic status causes environmental deficiencies which results in low self esteem of students [10].

Academic achievement is defined as level of expertise attained in the academic work in the school [6].

The root of national wealth is based on excellent technological knowledge and education. There is a strong correlation between a country’s development and the quality of education provided within that country [3].

To achieve quality education, frequency and proper measure of academic performance should be put in place. The basic purpose of any measurement system is to provide feedback relative to the goal that increases the chances of achieving the goals efficiently and effectively. If the performance measurement is right, the corresponding data generated will direct where one is and what lies ahead.

A study conducted by [5] concluded that overcrowdings abolish the quantity and quality of teaching and learning with serious implication for attainment of educational goals. If teachers and students interact properly, they have positive and good relationship which between students must be reflective, maximum productive, and it must reflect certain attitudes. If teacher and students does not build positive relationship, they cannot move together on the same way.

Sirohi [9] concluded in his study that 98.7 % of the students have poor study habits. Ansari [2] in his research on study habits and attitude of students observed that (a) study habits are positively correlated with the quality of classroom teaching; and (b) the study habits centered around shortcut methods like test and guess papers cannot ensure the desired level of success in an examination.

Kwame Nkrumah University of Science and Technology admission is based on results obtained in Senior High School (SHS). The results are therefore a pre-tool used in the admission process. Candidates who have the potential to excel in their field of interest in the University are the preferred targets of the admission committee officials.

In this work piece, semester weighted average (SWA) as a measurement of academic performance would be used as dependent variables. The SWA is basically a single score that represents a students performance in all the course taken in a semester and is calculated to represent a students quality of performance numerically. It is calculated by multiplying the marks obtained for each course by the credits of the particular course adding up the products and dividing by the total number of unit of credit for the course. To be able to critically access the up to date academic information of a student, cumulative weighted average (CWA) is calculated, which is used for the award of degree. The CWA therefore depends on SWA.

There is also a focus on the influence of identified factors such as students age, category of SHS attended, entry aggregate and geographical location.

The study is therefore longitudinal and the observations within one subject over time are correlated. The observations over time are nested within the subject where regression coefficients are allowed to differ between subjects. The development of certain variables over time are allowed to vary among subjects or, in other words, the slope with time is considered to be random which enable the analyst to not only describe the trend over time while taking into account the correlation that exists between massive measurements, but also to describe the variation in the baseline measurement and in the rate of change over time.

The study compares and chooses best model fit between the random effect model and the random intercept and slope model.

2 Methodology

2.1 Random Effect Analysis

Random effect analysis is also known as multilevel analysis or random coefficient analysis [4, 7, 8]. Multilevel analysis was initially developed in the social sciences, more specifically for educational research. This type of study design is characterized by a hierarchical structure. Students are nested within classes, and classes are nested within schools. Various levels can be distinguished. As this technique is suitable for correlated observations, it is obvious that it is also suitable for use in longitudinal studies. In longitudinal studies, the observations within one subject over time are correlated. The observations over time are nested within the subject. The basic idea behind the use of multilevel techniques in longitudinal studies is that the regression coefficients are allowed to differ between subjects. Therefore, the term random coefficient analysis is preferred to the term multilevel analysis.

2.2 Random Effect Analysis in Longitudinal Studies

The simplest form of random effect analysis is an analysis with only a random intercept. The corresponding statistical model with which to analyse a longitudinal relationship between an outcome variable Y and time is given in Eq. (2.1).

$$\begin{aligned} Y_{it} = \beta _{0i} +\beta _{1}t+\varepsilon _{it} \end{aligned}$$

(2.1)

where $Y_{it}$ are observations for subject i at time t, $\beta _{0i}$ is the random intercept, t is time, $\beta _{1}$ is the regression coefficient for time, and $\varepsilon _{it}$ is the error for subject i at time t. What is new about this model (compared to Eq. 2.2) is the random intercept $\beta _{0i}$, i.e., the intercept can vary between subjects. It is also possible that the intercept is not random, but that the development of a certain variable over time is allowed to vary among subjects or, in other words, the slope with time is considered to be random.

$$\begin{aligned} Y_{it} = \beta _{0} +\beta _{1i}t+\varepsilon _{it} \end{aligned}$$

(2.2)

where $Y_{it}$ are observations for subject i at time t, $\beta _{0}$ is the intercept, t is time, $\beta _{1i}$ is the random regression coefficient for time, and $\varepsilon _{it}$ is the error for subject i at time t. The most interesting possibility is the combination of a random intercept and a random slope with time, which is in Equation (below).

$$\begin{aligned} Y_{it} = \beta _{0i} +\beta _{1i}t+\varepsilon _{it} \end{aligned}$$

(2.3)

where $Y_{it}$ are observations for subject i at time t, $\beta _{0i}$ is the random intercept, t is time, $\beta _{1i}$ is the random regression coefficient for time, and $\varepsilon _{it}$ is the error for subject i at time t.

The assumption of random coefficient analysis is that the variation in intercept and variation in slopes are normally distributed with an average of zero and a certain variance. This variance is estimated by the statistical software package. The general idea of random coefficient analysis is that the unexplained variance in outcome variable Y is divided into different components. One of the components is related to the random intercept, and another component is related to random slopes.

For longitudinal studies, random effect models enable the analyst to not only describe the trend over time while taking into account the correlation that exists between massive measurements, but also to describe the variation in the baseline measurement and in the rate of change over time.

2.3 Nature of Data Collection

• Subjects are not assumed to be measured on the same number of time points, and the time points do not need to be necessarily equally spaced.

• Analyses can be conducted for subjects who may miss one or more of the measurement occasions, or who may be lost to follow-up at some point during study. In our example, a student may fall sick during the entire duration of a semester examination.

Random effect models, however, allow for the inclusion of time-varying and time-invariant covariates. Time-varying covariates are independent variables that co-vary with the dependent variable over time. For example, a researcher studying trends in students $Y_{i}$ performance over time might also want to capture data on the highest and lowest marks of the group or degree of performance of co-student at each measurement occasion. The background of the student is likely to be an important predictor for performance assessment which may also vary over time. Covariates such as gender and geographical location status either do not change over time or are less likely to change over time.

Random effects allow the research analyst to model the correlation structure of the data. Thus, the analyst does not need to assume that measurements taken at successive times in time are equally correlated, which is the correlation structure that underlies the ANOVA model. The analyst also does not need to assume measurements taken at successive points in time have an unstructured pattern of correlations, which is the structure that underlies the multivariate analysis of variance model. The former pattern is generally too restrictive, while the latter is too generic. With random effects model, analyst can fit a specific correlation structure to the data, such as an autoregressive structure, which assumes a decreasing correlation between successive measurements over time.

2.4 Random Intercept Model (REM)

The simplest regression model for longitudinal data is one in which measurements are obtained for a single dependent variable at successive time points. Let $Y_{ij}$ represent the measurement for the $i\hbox {th}$ individual at the $j\hbox {th}$ point in time,

$$\begin{aligned} Y_{ij}=\beta _{0}+\beta _{1}t_{ij}+\varepsilon _{ij} \end{aligned}$$

(2.4)

$\beta _{0}$ is the intercept, $\beta _{1}$ is the slope, that is the change in the outcome variable for every one-unit increase in time(semester) and $\varepsilon _{ij}$ is the error component. In this simple regression, the $\varepsilon _{ij}$’s are assumed to be correlated and to follow a normal distribution (ie. $\varepsilon _{ij}\sim N(0,\sigma ^2))$. $\beta _{0}$ represents the average value of the dependent variable when $\hbox {time}=0$ and $\beta _{1}$ represents the average change of the dependent variable for each one-unit increase in time(semester). There is a possibility that a student may start with a low SWA and then increase over semesters as shown in Fig. 1a or no change in SWA over semesters as shown in Fig. 1b or start with a high SWA and decrease over semester as in Fig. 1c.

The implication was that on average students who perform well are depicted by Fig. 1a, whereas Fig. 1c depicts that on average students are performing poorly.

Fig. 1

Possible average change in SWAs over semesters. a Slope 1. b Slope 2. c Slope 3

The simple random effect is the one which the intercept is allowed to vary across individuals (students):

$$\begin{aligned} Y_{ij}=\beta _{0}+\beta _{1}t_{ij}+\upsilon _{0i}+\varepsilon _{ij}, \end{aligned}$$

(2.5)

where $\upsilon _{0i}$ represent the influence on individual i on his/her repeated observations. Note that the individuals have no influence on their repeated outcome(SWA) and then all the $\upsilon _{0i}$ will be equal to zero $(\upsilon _{0i}=0)$, but that may not be true. Therefore, $\upsilon _{0i}$ may have negative or positive impact on their SWAs; therefore, $\upsilon _{0i}$ may deviate from zero. For better reflection of this model on the characteristic individual, the model is partition into within subjects and between subjects.

Within subjects

$$\begin{aligned} Y_{ij}=b_{oi}+b_{1}t_{ij}+\varepsilon _{ij}. \end{aligned}$$

(2.6)

Between subjects

$$\begin{aligned}&\displaystyle b_{oi}=\beta _{0}+\upsilon _{0i}, \end{aligned}$$

(2.7)

$$\begin{aligned}&\displaystyle b_{1i}=\beta _{1}. \end{aligned}$$

(2.8)

Equation (second above) indicates that the intercept for the ith individual is a function of a population intercept plus unique contribution for individual. We assume $\upsilon _{0i} \sim N(0,\sigma ^2)$. This model also indicates that each individual’s slope is equal to the population slope, $\beta _{1}$, equation(last one above).

When both the slope and the intercept are allowed to vary across individual, the model is:

$$\begin{aligned} Y_{i}=\beta _{0}+\beta _{1}t_{ij}+\upsilon _{0i}+\upsilon _{1i}t_{ij}+\varepsilon _{i}. \end{aligned}$$

(2.9)

The within-subject model is the same as

$$\begin{aligned} Y_{i}=b_{oi}+b_{1i}t_{ij}+\varepsilon _{i}. \end{aligned}$$

(2.10)

The between-subject models is:

$$\begin{aligned} b_{oi}= & {} \beta _{0}+\upsilon _{0i}, \end{aligned}$$

(2.11)

$$\begin{aligned} b_{1i}= & {} \beta _{1}+\upsilon _{1i}. \end{aligned}$$

(2.12)

The within-subject model indicates that the individual ith SWA at time j is influenced by their initial level $b_{0i}$ and the time trend or the slope $b_{1i}$. The between-subject indicates that the individual’s i’s initial level is determined by the population initial level $\beta _{0}$ plus the unique contribution of $\upsilon _{0i}$. Thus each individual has their own distinct initial level. Intercept for the ith individual is a function of a population intercept plus unique contribution for that individual. As well, the slope for the ith individual is a function of the population slope plus some unique contribution for that subject. We assume the variance–covariance matrix of the random effects. Correlation exists between the random slope and the random intercept, so that individuals have higher values for the intercept (i.e., higher or lower values for the slope). The resulting linear model can now be written as:

$$\begin{aligned} Y_{i}= & {} X_{i}\beta +Z_{i}b_{i}+\varepsilon _{1i} \nonumber \\ b_{i}\sim & {} N(0,D)\nonumber \\ \varepsilon _{1i}\sim & {} N\left( 0,\sigma ^2 I_{ni}\right) . \end{aligned}$$

(2.13)

Assumptions:

• $b_{1},\ldots , b_{N}$, $\varepsilon _{1},\ldots , \varepsilon _{N}$ b’s are independent

• $\varepsilon _{1} \sim N(0,\sigma ^2 I_{ni})$ is the measurement error

The variance of the measurement is given below

$$\begin{aligned} V(y_{i})=Z_{i}\sum _{\upsilon }Z_{i}^{\prime }+\sigma ^2 I_{ni}. \end{aligned}$$

(2.14)

This model implies that conditional on the random effects, the errors are uncorrelated, as is displayed. This is seen in the above equation (Equation above) since the error variance is multiplied by the identity matrix (i.e., all correlations of the error equal to zero).

2.5 Restricted Maximum Likelihood Estimation

Here we consider the case where the variance of a normal distribution $N(\mu , \sigma ^2)i$ is to be estimated based on a sample $Y_{1},\ldots , Y_{N}$ of N observations. Where the mean $\mu$ is known, the maximum likelihood estimation (MLE) for $\sigma ^2$ equals $\widehat{\sigma ^2}=\sum _i\frac{(Y_{i}-\mu )^2}{N}$ which is unbiased for $\sigma ^2$. When $\mu$ is not unknown, we get the same expression for the MLE but with $\mu$ replaced by the sample mean ${\overline{Y}}=\sum _{i}\frac{Y_{i}}{N}$,

$$\begin{aligned} E\left( \widehat{\sigma ^2}\right) =\frac{N-1}{N}\sigma ^2. \end{aligned}$$

(2.15)

The equation (as in above) indicate that the MLE is now biased downward due to the estimation of $\mu$ and the unbiased estimation of (as in above) yield the classical sample variance.

$$\begin{aligned} S^2=\sum _{i}\frac{\left( Y_{i}-{\overline{Y}}\right) ^2}{N-1}. \end{aligned}$$

(2.16)

To obtain an unbiased estimate for $\sigma ^2$ directly, we should use the following: let $Y=(Y_{1},\ldots , Y_{N}$ denote the vector for all measurement and $I_{N}$ be N-dimensional vector containing only ones and zeros. The distribution of Y is then $N(\mu I_{N},\sigma ^2 I_{N})$ where $I_{N}$ equals the identity matrix, if A is $N \times (N-1)$ any matrix with $N-1$ linear independent columns orthogonal to the vector $I_{N}$, vector U of $N-1$ which is the error contrast is defined by $U=A^{\mathrm{T}}A$. Maximizing the corresponding likelihood with respect to the only remaining parameter $\sigma ^2$ yields $\widehat{\sigma ^2}=\frac{Y_{\mathrm{T}}A(A^{\mathrm{T}}A)^{-1}A^{\mathrm{T}}Y}{{N-1}}$ which is equal to classical sample variance $S^{2}$. The resulting estimator is the RMLE since it restricts $(N-1)$ error contrasts.

2.6 The Random Intercepts Model

The random effect covariance matrix D is now scalar, and it will be denoted by $\sigma ^{2}_{b}$ and the matrix $Z_{i}$ are of the form $I_{n_{i}}$, a $n_{i}$-dimensional vector of ones. We will assume that all residual covariance matrices are of the form $\sum _{i}=\sigma ^2 I_{n_{i}}$, i.e., we assume conditional independent. The random intercept of subject i is given by

$$\begin{aligned} \widehat{b_{i}}= & {} \sigma ^{2}_{b} I_{n_{i}}^{\prime }\left( \sigma ^{2}_{b} I_{n_{i}} I_{n_{i}}^{\prime }\right) ^{-1}\left( y_{i}-X_{i}\beta \right) \nonumber \\= & {} \sigma ^{2}_{b} I_{n_{i}}^{\prime }\left( \frac{\sigma ^{2}_{b}}{\sigma ^{2}}-\frac{\sigma ^{2}_{b}}{\sigma ^{2}+n_{i}\sigma ^{2}_{b}}I_{n_{i}} I_{n_{i}}^{\prime }\right) \left( y_{i}-X_{i}\beta \right) \nonumber \\= & {} \frac{n_{i}\sigma ^{2}_{b}}{\sigma ^{2}+n_{i}\sigma ^{2}_{b}}\frac{1}{n_{i}}\sum _{j=1}^{n_{i}} \left( y_{i}-x_{ij}^{\prime }\beta \right) , \end{aligned}$$

(2.17)

where the vector $x_{ij}$ consists of the $j\hbox {th}$ row in the design matrix $X_{i}$ and $\frac{1}{n_{i}}\sum _{j=1}^{n_{i}} (y_{i}-x_{ij}^{\prime }\beta )$ is equal to the average residual. If $n_{i}$ is large for subject i a weight is put on the average residual yielding less shrinkage, the within-subject variability is large in comparison with the between-subject variability if more shrinkage is obtained.

3 Data Collection

The consecutive students’ semester weighted average (SWA) academic results of Class of 2012 Mathematics students at KNUST (i.e., eight semesters) were obtained. The obtained SWA(s) and their socio-demographic factor response variables were tallied and also coded in the Window Microsoft Excel (2010), R and the SAS version 9.1 for the analyses. The geographical locations of students were categorized into three zonal belts specifying their respective regions of origin. These include the Northern Belt (includes Northern, Upper East, Upper West) coded as N, Middle Belt (Ashanti, Brong Ahafo Regions, Eastern, Volta) was coded M, and Southern Belt (includes Greater Accra, Central and Western regions) was also coded as S. Similarly, the graded schools were categorized into A, B, C, D and P from Ghana Education Service (GES) specification. Grade A schools were coded as A, grade B schools were coded as B, grade C schools were coded as C, grade D schools were coded as D, and grade P schools were coded as P. There were ninety (90) students in the class of 2012 Mathematics students records sampled. Details of the analyses are discussed below.

3.1 Exploratory Data Analysis

Out of a total of 90 students, 15 students coded F were females representing 16.85 % and 74 students coded M were males representing 83.15 %. The gender of a student was not mentioned in the data and therefore was treated as missing.

Fig. 2

Gender profile for maths four students

Fig. 3

Geographical location for maths four students

Fig. 4

GES categories of schools in maths four

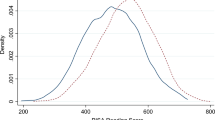
The profile of the male students in maths four as in Fig. 2 is denser than that of the females indicating a greater number of males than females. Majority of the males SWAs lies approximately between 52 and 66, whereas that of the females lies between 55 and 65. Statistically, the males recorded a maximum and a minimum SWA of 84.2 and 36.8, whereas the females recorded a maximum and a minimum SWA of 86.9 and 51.8 over the 8 semesters.

The geographical location of maths four students was grouped into three zonal belts specifying their respective regions of origin. These include the Northern Belt (includes Northern, Upper East, Upper West) coded as N, Middle Belt (Ashanti, Brong Ahafo Regions, Eastern, Volta) coded as M and Southern/Coastal Belt (includes Greater Accra, Central and Western regions) also coded as S. In general, majority of the students from maths four as in Fig. 3 reside in the Middle Belt of Ghana, whereas those from the Northern Belt contributed the least. The minimum SWA score was recorded by a student from the Southern Belt, whereas the maximum SWA score was recorded by a student from the Middle Belt. The distribution of the SWAs of students from the Middle Belt and Southern was very dense approximately between the 51–68 and 51–65 %, respectively. However, the distribution of students due to their population was scattered over the 8 semesters around the 50–72 mark. The geographical Location of four (4) students was not captured in the data and therefore was treated as missing.

It could be observed that out of the total of 90 students, 47 students (representing 55.29 %) attended a Grade A schools, 25 students (representing 29.41 %) attended Grade B school, 9 students (representing 10.59 %) attended a Grade C school.

All in all most of the students in maths four were from a Type A school with a Type C school having the least number of students as shown in Fig. 4. A student in Type B school recorded the highest SWA score of 86.9 % in semester 8. However, a student from a Type A school recorded the least SWA score over the 8 semesters.

Fig. 5

Maths four (4) students profile

In general most students started with a low SWA but managed to complete with a higher SWA as in Fig. 5. Students SWAs over the semesters lie between the 50 and the 70 mark, with semesters 8 and 5 approximately recording the highest and the least SWA of 86.9 and 30.8 %, respectively.

3.2 Random Intercept Model

The model below is exactly what we would use in deciding as to whether or not to select a random effect model for the data. The model contains only one parameter which is the random intercept effect. This partition the total variation in the data into two: within-individual and between-individual components

$$\begin{aligned} \hbox {SWA}_{ij}=\upsilon _{oi}+\varepsilon _{ij}, \end{aligned}$$

(3.1)

where

$$\begin{aligned} \upsilon _{0i} \sim N\left( 0,\sigma ^2_{r0}\right) \end{aligned}$$

and

$$\begin{aligned} \varepsilon _{ij} \sim N\left( 0,\sigma ^2\right) . \end{aligned}$$

A useful tool used in deciding whether a random effect model would be an appropriate choice for the data is the intraclass correlation coefficient (ICC), and it is represented mathematically as follows:

$$\begin{aligned} \hbox {ICC}=\frac{\widehat{\sigma ^2}_{\upsilon _{o}}}{\widehat{\sigma ^2}_{\upsilon _{o}}+\widehat{\sigma ^2}}, \end{aligned}$$

(3.2)

where $\widehat{\sigma ^2}$ is the residual variance.

From Table 1, $\widehat{\sigma ^2}_{\upsilon _{o}} = 39.876$ and $\widehat{\sigma ^2} = 19.939$.

Table 1 Covariance parameter estimates

Therefore, it implies that our $\hbox {ICC}=\frac{39.876}{39.876+19.939}=0.666$, indicating that approximately 67 % of the variation in the data is explained by allowing the intercept to vary across the individual students. The statistical significant value for the within-individual variation suggests the data structure is best captured by using random effect model. With a covariance value of 39.876 and a residual of 19.939, it is clear that there is a lot of variations in the academic performance of students at semester one (1).

Table 2 Random effect or mixed model random intercept

With regard to Table 2, the random intercept model is considered. It is a linear mixed model where only subject specific effect is the intercept. Statistically, not all the parameter estimates are significant at $\alpha =0.05$ level of significance. It was observed that geographical location was not significant. However, entry aggregate, entry age and gender were all significant. On the average, there is no significance difference in the SWA between the GES type of schools over a linear trend as well as the middle and southern belts with regard to the linear trends in the geographical location. Nevertheless, the geographical location with regard to the Northern Belt was significant in the linear trend with a standard deviation of approximately 0.712.

In the Type (III) tests, entry age, entry aggregate and linear trend in the geographical location of the students are significant.

3.3 Random Intercept and Slope Model

Again, consider the model below:

$$\begin{aligned} \hbox {SWA}_{ij}=\upsilon _{oi}+\upsilon _{1i}t_{ij}+\varepsilon _{ij}, \end{aligned}$$

(3.3)

where

$$\begin{aligned}&\upsilon _{0i} \sim N\left( 0,\sigma ^2_{r0}\right) ,\\&\upsilon _{1i} \sim N\left( 0,\sigma ^2_{r1}\right) , \end{aligned}$$

and

$$\begin{aligned} \varepsilon _{ij} \sim N\left( 0,\sigma ^2\right) . \end{aligned}$$

The ICC is computed using variance estimates for the random intercept and slope model as in the equation above as well as their covariances.

Table 3 Covariance parameter estimates

With regard to Table 3, $\hbox {ICC}=\frac{29.594-0.450 + 0.778}{29.594-0.450 + 0.778 + 15.613}=0.657$, indicating that approximately 65.7 % of the variation in the data is accounted for by allowing the intercept and slope to vary across individual students in maths four. The random intercept has a relatively large estimate with respect to the other variance components. This supports the fact that there is high difference between student’s variability based on SWAs at semester 1. The negative estimate of the covariance implies that students who start with a high SWA at semester 1 have a more tendency to exhibit reduction of SWA over the semesters. Variation within the slope and the semester was, however, not significant. Therefore, variations in students academic performance as the semester progresses are very minimal. Hence, they can be ignored in the final model.

In Table 4 in the Appendix, the random intercept and slope model together with some regressors and individual slopes are considered. It is a linear mixed model where only subject specific effect is the intercept. Again, not all the parameter estimates are significant at $\alpha =0.05$ level of significance. It was observed that geographical location in the main model as well as the linear trend in the GES categorization type of SHS school was not significant. However, the parameters intercept, entry age, gender and entry aggregate were all significant. On the average, there is no significance difference in the SWA between the geographical location(M,S) over a linear trend. Nevertheless, the geographical location with regard to the Northern Belt was significant in the linear trend with a standard deviation of approximately 0.749. Again, in the Type (III) tests, entry age, entry aggregate and linear trend in the geographical location of the students are significant.

4 Results and Discussion

The study attempts to find the factor(s) that can have impact or affect academic performance. A measure of academic performance used was SWA scores obtained over the eight. The main factors considered are entry age, gender, entry aggregate, GES graded level of SHS attended and geographical location. Whether these socio-demographic factors affect students academic performance is the researcher’s priority. The statistical model used here was the random effect model.

As part of the exploratory data analysis, it was observed that out of a total of 90 students, 15 students were females representing 16.85 % and 74 students were males representing 83.15 %. The geographical location of maths four students was grouped into three zonal belts specifying their respective regions of origin. These include the Northern Belt (includes Northern, Upper East, Upper West), Middle Belt (Ashanti, Brong Ahafo Regions, Eastern, Volta) and Southern/Coastal Belt (includes Greater Accra, Central and Western regions). Fifty of the students representing 58.14 % represented the Middle Belt. Also, ten (10) of the students representing 11.63 % represented the Northern Belt. Similarly, twenty-six of the students representing 30.23 % represented the Southern Belt. The geographical location of four students was not captured in the data and therefore was treated as missing. Again, the students were grouped according to the GES special SHS categorization with respect to the type of SHS attended and whether Grade A, B, C, D or P schools were specified. It could be observed that out of the total of 90 students, 47 students (representing 55.29 %) attended a Grade A schools, 25 students (representing 29.41 %) attended Grade B school, 9 students (representing 10.59 %) attended a Grade C school, 2 students (representing 2.35 %) attended both a Grade D school and a Grade P school respectively, while five students information failed to be captured and therefore was recorded as missing.

In longitudinal studies, the observations within one subject over time are correlated. The observations over time are nested within the subject. The basic idea behind the use of multilevel techniques in longitudinal studies is that the regression coefficients are allowed to differ between subjects. Therefore, the term random coefficient analysis is preferred to the term multilevel analysis. The simplest form of random effect analysis is an analysis with only a random intercept. It is also possible that the intercept is not random, but that the development of certain variable over time are allowed to vary among subjects or, in other words, the slope with time is considered to be random. For longitudinal studies, random effect models enable the analyst to not only describe the trend over time while taking into account of the correlation that exists between massive measurements, but also to describe the variation in the baseline measurement and in the rate of change over time.

Since the interaction or variation around the slope was highly insignificant, the random intercept model was the better alternative ahead of the random intercept and slope model. The random intercept model is a linear mixed model where only subject specific effect is the intercept. Statistically, not all the parameter estimates are significant at $\alpha =0.05$ level of significance. It was observed that the difference in geographical location was not significant in the main effect model. However, entry aggregate, entry age and gender were all significant. On the average, there is no significant difference in the SWA between the GES SHS categories type of schools over a linear trend as well as the middle and southern belts with regard to the linear trends in the geographical location. Nevertheless, the geographical location with regard to the Northern Belt was significant in the linear trend with a standard deviation of approximately 0.712.

5 Conclusion

Random Intercept and Slope Model has an $\hbox {ICC}=0.657$, indicating that approximately 65.7 % of the variation in the data is accounted for by allowing the intercept and slope to vary across individual students in maths four. The negative estimate of the covariance implies that students who start with a high SWA at semester 1 have a more tendency to exhibit reduction of SWA over the semesters. Variation within the slope and the semester was, however, not significant. Again, variations in students academic performance as the semester progresses are very minimal.

Random effect model produced an intraclass correlation coefficient (ICC) of 0.666, indicating that approximately 67 % of the variation in the data is explained by allowing the intercept to vary across the individual students. The statistically significant value for the within-individual variation suggests the data structure is best captured. Therefore, the random intercept model was the better alternative ahead of the random intercept and slope model.

It was observed that the difference in geographical location was not significant in the main effect model. However, entry aggregate, entry age and gender were all significant. Therefore, students with a very good entry aggregates tend to perform better than those with a fairly good ones. In terms of age, younger students tends to perform better than elderly students in the same class.

To crown it all, the geographical location with regard to the Northern Belt was significant in the linear trend with a standard deviation of approximately 0.712.

Appendix

See Table 4.

Table 4 Random effect or mixed model random intercept and slope