A Bayes analysis of autoregressive model having functional-coefficients and its application on exchange rate data

Abstract

The paper provides a Bayes analysis, based on free-knot spline technique, of the popular autoregressive model having functional-coefficients. The model was initially proposed by Chen and Tsay (1993). The technique of polynomial splines of different orders is used to approximate the functional-coefficients. A sample based approach using the Gibbs sampler algorithm with intermediate Metropolis steps is adopted to draw the posterior estimates for the parameters involved. Additionally, the technique of reversible jump Markov chain Monte Carlo is incorporated to update the location and number of knots in the polynomial spline. The paper then proceeds with the motive of obtaining both retrospective and prospective predictions based on the selected model. The complete procedure is illustrated by both simulated and a real dataset representing the exchange rate of Indian rupees relative to the US dollars.

1 Introduction

In the last few decades, the development of non-linear models has been a milestone for researchers in the time series. The non-linear models enjoy the properties where the linear models fail to explain the nature of a time series. One of the pioneer works is done by [5]. In this paper, the authors have suggested the functional-coefficients for an autoregressive (AR) model instead of the unknown AR constants. They allow the coefficients as a function of the modelled variable at some lag apart. For a sequence of time series observations {$y_t; t=1,2,\ldots , T$}, the general form of an autoregressive model having functional-coefficients (FCAR) can be written as

$$\begin{aligned} y_t = \theta _0 + \sum \limits _{i=1}^p g_i(y_{t-d}) y_{t-i} + \epsilon _t, \end{aligned}$$

(1)

where $\theta _0$ is the intercept, $g_i(.)$’s are unknown univariate measurable functions, d and p are suitably chosen positive integers known as the delay parameter and the AR order, respectively, and $\epsilon$’s are independently and identically distributed (i.i.d.) normal variates with mean zero and a constant variance. We shall refer to the model by FCAR(p, d) throughout the paper.

Some of the pioneering works on non-linear time series models include the threshold autoregressive (TAR) model by [20, 21] and exponential autoregressive (EXPAR) model by Haggan and Ozaki [14], etc. Besides, the FCAR model is also quite popular due to its non-linear and non-parametric aspects. The model is non-parametric due to the fact that its functional-coefficients are left unspecified. The popularity of the FCAR model can be seen because of its numerous applications and considerable number of uses in the literature over the last few decades (see, for example, Chen and Tsay [5], Cai et al. [4] and Fan and Yao [11], among others). Truly speaking, the model is quite flexible and rich to cover some of the commonly used linear as well as non-linear models. For example, if $g_i(x)=a_i$, a constant, for each $i=1,2,\ldots , p$, the model (1) reduces to the linear AR model. Similarly, if $g_i(x)=a_i I(x\le c) + b_i I(x > c)$ where I(.) is the usual indicator function, the model (1) changes into TAR model (see Tong [21]) and if $g_i(x)=a_i + b_i exp(-c_i x_i^2)$, it reduces to the EXPAR model proposed by Haggan and Ozaki [14]. The FCAR(p, d) model has been further extended by taking the distribution of error terms other than the normal with varying variance (see, for example, Chib and Greenberg [6] and [19]).

The functional-coefficients involved in the FCAR(p, d) model can be estimated in numerous ways. Some of the non-parametric methods discussed in the literature include local linear smoothing and spline smoothing, etc. (see, for example, Fan and Gijbels [10], DiMatteo et al. [9], Grégoire and Hamrouni [13] and Lindstrom [15]). A Bayesian approach based on free-knot spline has been discussed by [9] that requires a few well-placed knots to connect the polynomials of the spline where the number of knots and their locations can be estimated from the data. Free-knot spline technique reduces a non-parametric model into an ordinary linear form once the number and location of knots are determined. After achieving the linear form of the model, posterior summaries can be easily drawn for the parameters involved in the model just by supposing the conjugate normal priors for the spline coefficients. Normally, one can start with a combination of the preassigned number and location of knots at random and can achieve the level of smoothness comfortably (see, for example, Denison et al. [7] and Wang and Wu [28]). In the true sense, the procedure should be followed for the efficiency of the algorithm and to avoid the consideration of numerous knots.

The present work proposes to consider a complete Bayesian approach to analyze the FCAR(p, d) model with the help of free-knot spline technique. Bayesian analysis of time series models with functional-coefficients is frequently exercised by researchers in time series literature. Some of the recent works include [1, 16, 19, 27, 28], among others. We, however, follow the spline technique proposed by [28], where the authors have considered the integrated form of a time series model. The uniqueness of the proposed work lies in the fact that it allows the functional-coefficients of FCAR(p, d) model to be approximated by the polynomial splines of different orders. Consequently, the different orders provide the different levels of smoothness (see Wang and Wu [28]). The randomness involved in the knots allocation, with respect to their dimension and location, could be handled by the reversible jump Markov chain Monte Carlo (MCMC) method proposed by Green [12]. The complete analysis is performed by using the Gibbs sampler algorithm with intermediate Metropolis steps to estimate the rest of the parameters of FCAR(p, d) model (see [25]).

The proposed methodology is illustrated on a simulated and real datasets of the monthly exchange rate of Indian rupees relative to the US dollars from January 2011 to December 2020. Also, the short term retrospective and prospective predictions, for the exchange rate data, are given to see the predictive performance of the model under consideration. It may, however, be noted that to forecast smoothly the stationarity of a time series model is an essential requirement. In the present case of FCAR(p, d) model, such a requirement can be fulfilled by geometric ergodicity (see, for example, [5]). Following the Theorem 1.1 and 1.2 from [5], for the constants $n_i; i = 1, 2,\ldots , p$, if the function $g_i(.)$ is bounded such that $|g_i(.)|\le n_i$ and if all the roots of the characteristic polynomial ($\gamma ^p-n_1\gamma ^{p-1}-\cdots -n_p=0$) of (1) lie inside the unit circle, the FCAR(p, d) model is said to have the geometrical ergodicity, where $\gamma$ refers the eigenvalue. It is important to mention, here, that the characteristic polynomial of (1) could possibly be written by considering the functional coefficients $g_i(.)$’s as the constant coefficients of the general linear AR model or could be replaced by the utmost constant values taken by the functional coefficients (see [5]). This, however, provides a sufficient condition of ergodicity but for some of the special cases of model (1) (as discussed above), this condition becomes both necessary and sufficient.

The paper is organized as follows. Section 2, divided into several subsections, provides the complete Bayesian model formulation of the FCAR(p, d) model starting from the chosen priors to the posterior distributions. Separate subsections are provided to describe the considered MCMC sampling strategy and its complete implementation. An algorithm to update the functional-coefficients is provided separately. Since the specification of parameters p and d is a significant step in the analysis of FCAR(p, d) model, it is suggested to use the Bayesian information criterion (BIC) as the guiding principle. The BIC is briefly reviewed in Sect. 2.3 for completeness of the work. The section finally ends with a discussion on obtaining predictive samples for the intended retrospective and prospective predictions. Section 3 illustrates the proposed methodology for a simulated as well as a real dataset on the exchange rate of Indian rupees relative to the US dollars. The compatibility of the selected model is graphically shown and the predictive ability of the model is examined by the short term retrospective prediction of the exchange rates. At the end of this section, short-term prospective predictions are also provided using the selected model. A brief conclusion is given in the last section.

2 Bayesian model formulation

Consider a time series ${\underline{y}}: y_1, y_2,\ldots , y_T$ from the non-linear FCAR(p, d) model (1) at equally spaced time periods $t=1,2,\ldots , T$. It is our supposition that the negative values of y’s and $\epsilon$’s have not much effect on the conclusion drawn on the basis of model (1). Since the model (1) has a dependent characteristic on its own previous values up to the lag p, we assume that $y_t=\epsilon _t=0$ for $t\le 0$, which results in the conditional distribution of $y_t$ given $y_{t-1},\ldots , y_{t-p}$ in the form

$$\begin{aligned} f(y_t|y_{t-1},\ldots , y_{t-p}; \theta _0, \sigma ^2) \propto \frac{1}{\sigma } \times \exp \left( -\frac{1}{2\sigma ^2}(y_t - \theta _0 - \sum _{i=1}^{p} g_i(y_{t-d}) y_{t-i})^2\right) . \end{aligned}$$

(2)

The corresponding likelihood function for the model (1) from its conditional density (2) can be approximated by

$$\begin{aligned} f({\underline{y}}|\theta _0, \sigma ^2) \propto \left( \frac{1}{\sigma ^2}\right) ^{\frac{T-p^*}{2}} \times \exp \left( -\frac{1}{2\sigma ^2}\sum \limits _{t=p^*+1}^T(y_t-\theta _0-\sum \limits _{i=1}^p g_i(y_{t-d}) y_{t-i})^2\right) , \end{aligned}$$

(3)

where $p^*=\text {max}(p,d)$. This kind of approximation is very common in time series literature (see, for example, Box and Jenkins [3] and Wang and Wu [28], among others).

Next, we approximate, for each $i=1,2,\ldots , p$, the functional-coefficient $g_i(.)$ by an $m_i$-order polynomial spline with $k_i$ ordered interior knots $\xi _i = (\xi _{i1}, \xi _{i2},\ldots , \xi _{ik_i})'$, such that $A'$ shows the transpose of any arbitrary vector A. Thus,

$$\begin{aligned} g_i(x)\approx \sum \limits _{j=1}^{K_i} B_{ij}(x) \beta _{ij}=B'_i(x)\beta _i,\hspace{2cm} x\in [a,b], \end{aligned}$$

(4)

where $K_i=m_i + k_i$, $B_i(x) = (B_{i1}(x), B_{i2}(x),\ldots , B_{iK_i}(x))'$ is $K_i \times 1$ vector of B-spline bases, $\beta _i = (\beta _{i1}, \beta _{i2},\ldots , \beta _{iK_i})'$ is a $K_i \times 1$ vector of spline coefficients and the boundary knots are given by

$a=\min \limits _{1\le t \le T}\{y_t\}$ and $b=\max \limits _{1\le t \le T}\{y_t\}$.

For each functional coefficient $g_i(.)$, the B-spline bases may be recursively obtained by the general formula

$$\begin{aligned} B_l^0(x)=I(z_l\le x <z_{l+1}), \end{aligned}$$

(5)

and

$$\begin{aligned} B_l^q(x)=\frac{x-z_l}{z_{l+q}-z_l}B_l^{q-1}(x) + \frac{z_{l+q+1}-x}{z_{l+q+1}-z_{l+1}}B_{l+1}^{q-1}(x), \hspace{2cm} q\ge 1 \end{aligned}$$

(6)

where q denotes the degree of spline and $z_l$ represents the $l^{th}$ knot in a spline. We allow splines of different order and, hence, with different numbers and locations of knots in the equation (4). As stated earlier, this provides flexibility when the functional-coefficients have different levels of smoothness. Using (4), (3) can be further approximated as

$$\begin{aligned} f({\underline{y}}|\theta _0,\beta ,k,\xi ,\sigma ^2) \propto \left( \frac{1}{\sigma ^2}\right) ^{\frac{T-p^*}{2}} \!\!\times \!\! \exp \left( -\!\frac{1}{2\sigma ^2}\sum \limits _{t=p^*+1}^T(y_t-\theta _0\!-\!\sum \limits _{i=1}^p B'_i(y_{t-d})\beta _i y_{t-i})^2\right) \!,\nonumber \\ \end{aligned}$$

(7)

where $\beta = (\beta '_1, \beta '_2,\ldots , \beta '_p)'$, $k = (k_1, k_2,\ldots , k_p)'$ and $\xi = (\xi '_1, \xi '_2,\ldots , \xi '_p)'$ are the vectors of spline coefficients, knots and locations, respectively.

2.1 Prior and posterior distributions

To perform a Bayesian analysis, it is essential to choose suitable prior distributions for the parameters. Such prior distributions can be informative or non-informative based on the available a priori information. It may be noted that prior elicitation is not the main objective of the paper and, therefore, we consider some standard priors for the parameters under consideration. To begin with, let us consider for each $i=1,2,\ldots , p$, the following conjugate priors for the spline coefficients $\beta$, numbers k and locations $\xi$ of the knots (see also Wang and Wu [28]).

$$\begin{aligned} \pi _1(k_i)=\frac{\lambda _i^{k_i}}{k_i!} e^{-\lambda _i}; \hspace{1cm} \lambda _i \ge 1, \end{aligned}$$

(8)

$$\begin{aligned} \pi _2(\xi _i|k_i)=\frac{k_i!}{(b-a)^{k_i}} I\{a=\xi _{i0}< \xi _{i1}<\cdots< \xi _{ik_i} < \xi _{ik_i+1}=b\}, \end{aligned}$$

(9)

and

$$\begin{aligned} \beta _i|k_i,\xi _i,\sigma ^2,\tau _\beta \sim N_{K_i}(0, \tau _\beta \sigma ^2 I_{K_i}), \end{aligned}$$

(10)

where $I\{.\}$ denotes the indicator function that takes value either zero or one, $\tau _\beta$ is a hyperparameter and $I_{K_i}$ is the $K_i \times K_i$ identity matrix. We specify the inverse-gamma hyper-prior for $\tau _\beta$ with the two pre-specified hyperparameters r and $s^2_\tau$ given by,

$$\begin{aligned} \pi _3(\tau _\beta ) \propto \tau _\beta ^{-\frac{r}{2} -1} \exp \left( \frac{-s_\tau ^2}{2\tau _\beta }\right) . \end{aligned}$$

(11)

We have also considered the non-informative priors for the parameters $\theta _0$ and $\sigma ^2$ similar to [23] and the same are given by,

$$\begin{aligned} \pi _4(\theta _0) \propto U[-M, M]; \hspace{1cm} M > 0, \end{aligned}$$

(12)

and

$$\begin{aligned} \pi _5(\sigma ^2) \propto \frac{1}{\sigma ^2}. \end{aligned}$$

(13)

The set of hyperparameters, for each i, is ($\lambda _i, r, s_\tau ^2, M$). The prior distribution can be jointly represented as

$$\begin{aligned} \pi (\theta _0,\beta , \xi , k, \tau _\beta , \sigma ^2) \propto \left\{ \prod _{i=1}^{p} \pi _6(\beta _i|k_i,\xi _i,\sigma ^2,\tau _\beta ) \pi _2(\xi _i|k_i) \pi _1(k_i)\right\} \pi _3(\tau _\beta ) \pi _4(\theta _0) \pi _5(\sigma ^2),\nonumber \\ \end{aligned}$$

(14)

where $\pi _6(\beta _i|k_i,\xi _i,\sigma ^2,\tau _\beta )$ is used to denote the prior in (10). Now, the Bayes’ theorem enables us to write the posterior distribution, up to proportionality, by multiplying the likelihood function (7) and the prior distributions (8) to (13) as

$$\begin{aligned} p(\Theta |{\underline{y}}) \propto f({\underline{y}}|\Theta ) \times \pi (\Theta ), \end{aligned}$$

(15)

where $\Theta =(\theta _0,\beta , \xi , k, \tau _\beta , \sigma ^2)$. Obviously, this posterior distribution forms the basis for drawing the desired Bayesian inferences.

2.2 MCMC based sampling scheme

It can be seen that the posterior distribution (15) is not analytically tractable and, therefore, we shall propose to consider a MCMC based sampling scheme to draw the samples from the joint posterior density (15). For this purpose, we shall first calculate the conditional posterior density from (15) and then discuss the corresponding sampling scheme one by one. It may be noted that the scheme is actually the Gibbs sampler but some of the full conditionals are generated using the Metropolis algorithm or even using the updating steps offered by the reversible jump MCMC strategy. As such, the scheme can also be referred to as the hybrid Gibbs sampler with hybridization being introduced by the use of the Metropolis algorithm.

2.2.1 Sampling from the full conditionals of ($\beta _i, k_i, \xi _i$)

Combining the likelihood function (7) and the prior distributions from (8) to (10), the joint posterior of $(\beta _i, k_i, \xi _i)$, $i=1, 2,\ldots , p$, for the given remaining parameters, can be written as

$$\begin{aligned} p_1(\beta _i, k_i, \xi _i|{\underline{y}},\theta _0, \beta _{-i}, k_{-i}, \xi _{-i}, \tau _\beta , \sigma ^2) \propto \left( \frac{\tau _\beta ^{-1/2} \lambda _i}{b-a}\right) ^{k_i} \times (\sigma ^2)^{-k_i/2} \exp \left( \frac{-S_i}{2\sigma ^2}\right) \nonumber \\ \times \exp \left\{ \frac{-1}{2\sigma ^2}(\beta _i - \hat{\beta _i})' \Sigma _i^{-1} (\beta _i - \hat{\beta _i})\right\} ,\nonumber \\ \end{aligned}$$

(16)

where $\beta _{-i}, k_{-i}$ and $\xi _{-i}$ are obtained after removing $\beta _{i}, k_{i}$ and $\xi _{i}$ from the vectors $\beta , k$ and $\xi$, respectively. We took $Z_i$ as a $(T-p^*)\times 1$ vector with its $t^{th}$ component $y_{p^*+t} - \theta _0$ and $X_i$ as a $(T-p^*)\times K_i$ matrix with its tth row $B'_i(y_{p^*+t-d}) y_{p^*+t-i}$ such that,

$$\begin{aligned} \begin{aligned} \Sigma _i&= (\tau _\beta ^{-1} I_{K_i} + X'_i X_i)^{-1},\\ {\hat{\beta }}_i&= \Sigma _i X'_i Z_i,\\ \text {and} \hspace{1cm} S_i&= Z'_i Z_i - \hat{\beta '_i} \Sigma _i^{-1} \hat{\beta _i}. \end{aligned} \end{aligned}$$

(17)

Appendix A provides details regarding the derivation of (16). Hence, the full conditional distribution of $\beta _i$ can be easily obtained from the joint posterior (16) as

$$\begin{aligned} p_2(\beta _i|{\underline{y}}, \theta _0,\beta _{-i}, k, \xi , \tau _\beta , \sigma ^2) \propto (\sigma ^2)^{-K_i/2} |\Sigma _i|^{-1/2}\! \exp \left\{ \frac{-1}{2\sigma ^2} (\beta _i\! -\! \hat{\beta _i})' \Sigma _i^{-1} (\beta _i \!-\! \hat{\beta _i})\right\} .\nonumber \\ \end{aligned}$$

(18)

Now, the posterior samples for $\beta _i$ can be easily obtained from (18) as it follows a multivariate normal density with mean vector ${\hat{\beta }}_i$ and covariance matrix $\sigma ^2 \Sigma _i$. Similarly, the full conditional of ($k_i,\xi _i$) can be jointly obtained as,

$$\begin{aligned} p_3(k_i, \xi _i|{\underline{y}}, \theta _0,\beta _{i}, k_{-i}, \xi _{-i}, \tau _\beta , \sigma ^2) \propto \left( \frac{\tau _\beta ^{-1/2} \lambda _i}{b-a}\right) ^{k_i} \times |\Sigma _i|^{1/2} \exp \left( \frac{-S_i}{2\sigma ^2}\right) . \end{aligned}$$

(19)

Here, the numbers $k_i$ and $\xi _i$ can be updated using a sample based reversible jump MCMC approach. This approach is very popular among researchers working in the Bayesian curve fitting and free-knot splines technique (see, for example, Denison et al. [7], Biller [2], DiMatteo et al. [9] and Wang and Wu [28]). The method efficiently works on the basis of a three-step procedure, which are birth step (addition), death step (deletion) and move step (relocation) (see, for example, Green [12] and Denison et al. [7]). Movements of variables under the three steps are independent of each other and can be chosen randomly with probabilities $b_{k_i}$, $d_{k_i}$ and $\eta _{k_i}$, respectively, where

$$\begin{aligned} b_{k_i}\!=\!C. \min \left\{ 1, \frac{p(k_i + 1)}{p(k_i)}\right\} , \hspace{3mm}d_{k_i}=C. \min \left\{ 1, \frac{p(k_i \!-\! 1)}{p(k_i)}\right\} , \hspace{3mm} \eta _{k_i}=1-b_{k_i}-d_{k_i}\nonumber \\ \end{aligned}$$

(20)

and the constant C is a tuning parameter that controls the rate at which the variables move within the three different move-steps. The recommended range for C is generally [0, 0.5]. For the present case, we choose it as 0.4. This value of C, also suggested in the literature (see, for example, [7]), is seen to provide a good acceptance probability. One should ensure that the probabilities given in (20) must satisfy the following relationships: $b_{k_i} p(k_i) = d_{k_i +1} p(k_i +1)$ and in case of no change of knots, that is $k_i = 0$, we have $b_0 = 1$ and $d_0 = 0 = \eta _0$ (see, for example, [28]). Below, we provide the necessary details of three move-types one by one.

Birth step: In this move-type, we add a newly generated candidate knot from a randomly chosen sub-interval $(\xi _{ij}, \xi _{i,j+1})$. The key idea is to divide the interval (a, b) into $(k_i +1)$ sub-intervals by means of the quantity $k_i$ and to choose one of them at random. Next, we draw candidate value, say $\phi$, uniformly from $(\xi _{ij}, \xi _{i,j+1})$ as the location of newly added knot with a jump probability

$$\begin{aligned} \frac{b_{k_i}}{k_i + 1} \sum _{j=0}^{k_i} \frac{1}{\xi _{i, j+1} - \xi _{ij}} I\{\xi _{ij}< \phi < \xi _{i,j+1}\}. \end{aligned}$$

Death step: In this move-type, a candidate knot is randomly chosen from the set of existing knots and then deleted with a jump probability,

$$\begin{aligned} \frac{d_{k_i}}{k_i}. \end{aligned}$$

Move step: In the move step, a candidate knot $\xi _{ij}$ is selected uniformly from the set of existing $k_i$ knots and a candidate location $\xi ^*_{ij}$ is generated from a distribution with mean $\xi _{ij}$ and variance $\sigma ^2_m$. A truncated normal distribution on the interval $(\xi _{i,j-1}, \xi _{i,j+1})$ seems to be a good choice for the proposal distribution (see, for example, Wang and Wu [28]). Since, for the large value of $\sigma ^2_m$, the proposal density will tend to a uniform distribution over the interval $(\xi _{i,j-1}, \xi _{i,j+1})$ and, therefore, the algorithm will be similar to a standard Metropolis algorithm. Hence, the jump probability is given by

$$\begin{aligned} \frac{\eta _{k_i}}{k_i} \frac{1}{\xi _{i, j+1} - \xi _{i, j-1}}. \end{aligned}$$

Following Green [12], the acceptance probability in each of the three steps can be defined as

$\min (1, \text {posterior ratio} \times \text {proposal ratio})$,

where the posterior and the proposal ratios can be obtained by the method proposed by Denison et al. [7] and DiMatteo et al. [9]. In our case, this acceptance probability can be written as

$$\begin{aligned} \min \left\{ 1, A\left( \frac{|\Sigma _i^*|}{|\Sigma _i|}\right) ^{1/2} \exp \left( \frac{S_i-S_i^*}{2\sigma ^2}\right) \right\} , \end{aligned}$$

(21)

where $\Sigma _i$ and $S_i$ can be obtained from (17) and the components of A are given as under

$$\begin{aligned} A = {\left\{ \begin{array}{ll} \frac{k_i + 1}{\tau _\beta ^{1/2}} \frac{\xi _{i,j+1} - \xi _{ij}}{b-a}, & k_i^* = k_i + 1 \hspace{5mm} (\text {Birth step}),\\ \frac{\tau _\beta ^{1/2}}{k_i} \frac{b-a}{\xi _{i,j+1} - \xi _{i,j-1}}, & k_i^* = k_i - 1 \hspace{5mm} (\text {Death step}),\\ 1, & k_i^* = k_i \hspace{5mm} (\text {Move step}). \end{array}\right. } \end{aligned}$$

(22)

In the above expression, $k_i^*$ represents the number of knots in the candidate posterior distribution. It is important to mention that in the move step above, the posterior and the proposal ratios are both unity because by moving one knot to another knot any collection of the same number of knots has similar posterior probabilities and proposal distributions. A detailed derivation of the jump probabilities as well as acceptance probabilities, in each move-type, is provided in Appendix 2. The values of hyperparameters $\lambda _i$, in Poisson priors (8), and the order of splines $m_i$ are so chosen that the rates of acceptance for the above reversible jump MCMC sampler would be enough to avoid too many rejections and thereby to increase the efficiency of the sampler.

2.2.2 Sampling from the full conditional of $\tau _\beta$

Combining the prior distribution in (10) with the distribution of hyperparameter $\tau _\beta$ in (11), the full conditional of $\tau _\beta$ can be written up to proportionality as

$$\begin{aligned} p_4(\tau _\beta |{\underline{y}}, \theta _0, \beta , k, \xi , \sigma ^2) \propto \tau _\beta ^{-\frac{r+\sum \nolimits _{i=1}^{p} K_i}{2} -1} \exp \left[ -\dfrac{1}{2\tau _\beta }\left( s_\tau ^2 + \dfrac{\beta ' \beta }{\sigma ^2}\right) \right] . \end{aligned}$$

(23)

Obviously, the full conditional (23) represents the well known density of inverse-gamma distribution from which the sampling can be done routinely using any inverse-gamma generating routine (see, for example, [8]).

2.2.3 Sampling from the full conditional of $\sigma ^2$

The full conditional of $\sigma ^2$ can be obtained by considering the likelihood in (7) and the prior in (13). The same can be written as

$$\begin{aligned} & p_5(\sigma ^2|{\underline{y}},\theta _0,\beta ,k,\xi ,\tau _\beta ) \propto \left( \frac{1}{\sigma ^2}\right) ^{\frac{\left( T-p^*-\sum \limits _{i=1}^{p} K_i+2\right) }{2}}\nonumber \\ & \quad \times \exp \left( -\frac{1}{2\sigma ^2}\left[ \frac{\beta '\beta }{\tau _\beta } +\sum \limits _{t=p^*+1}^T(y_t-\theta _0-\sum \nolimits _{i=1}^p B'_i(y_{t-d})\beta _i y_{t-i})^2\right] \right) . \end{aligned}$$

(24)

Using a simple transformation $\lambda =\frac{1}{\sigma ^2}$, it can be seen that (24) represents the probability density function of a gamma distribution with the shape parameter $\frac{\left( T-p^*-\sum \nolimits _{i=1}^{p} K_i\right) }{2}$ and the scale parameter $\frac{\left( \frac{\beta '\beta }{\tau _\beta } +\sum \nolimits _{t=p^*+1}^T(y_t-\theta _0-\sum \nolimits _{i=1}^p B'_i(y_{t-d})\beta _i y_{t-i})^2\right) }{2}$. Thus, samples of $\sigma ^2$ can be easily obtained by using a gamma generating routine.

2.2.4 Sampling from the full conditional of $\theta _0$

Next, considering the likelihood function in (7) and the prior in (12), the full conditional of $\theta _0$ can be obtained as

$$\begin{aligned} & p_6(\theta _0|{\underline{y}},\beta ,k,\xi ,\tau _\beta ,\sigma ^2) \propto \exp \left( -\frac{1}{2\sigma ^2}\sum \limits _{t=p^*+1}^T(y_t-\theta _0-\sum \limits _{i=1}^p B'_i(y_{t-d})\beta _i y_{t-i})^2\right) \nonumber \\ & \quad \times I_{[-M,M]}(\theta _0), \end{aligned}$$

(25)

where I(.) is the indicator function that takes value unity if $\theta _0$ lies in the interval $[-M,M]$ and zero otherwise. It is to be noted that the full conditional (25) is not available in a nice closed form from the viewpoint of sample generation and, therefore, we propose the use of Metropolis algorithm to obtain the required samples of $\theta _0$ from (25). For this purpose, one can consider, among other choices, a univariate normal kernel as a proposal density with mean as the maximum likelihood (ML) estimate of $\theta _0$ (say) and the standard deviation as c times the Hessian based approximation at ML estimate of $\theta _0$. Both mean and standard deviation of normal kernel can be successively changed by using the current realization of $\theta _0$. This is expected to improve the acceptance rate of the Metropolis chain. Here, c is a scaling constant and its value is recommended between 0.5 and 1.0 (see also [22, 26]).

Once the full conditionals are made available from the viewpoint of sample generation, one can implement the proposed MCMC based hybrid algorithm on the posterior (15) by proceeding with a single long run of the chain, among many other possibilities. Results are available which ensure that after a sufficiently large number of iterations, the generated sequence converges in distribution to a random sample from the corresponding posterior distribution and the ergodic means converge almost surely to the corresponding posterior expectations. Once the convergence is monitored, the generated values can be picked up at a fixed gap to form a random sample of the desired size. It may be noted that the gaps so chosen make the serial correlation among the generating variates negligibly small and thereby giving independent samples. The selected samples can then be used to estimate any posterior characteristics of interest. For further details of the algorithm, one may refer to [25, 26], among others.

2.2.5 Algorithm to update the functional-coefficients

For each $i=1, 2,\ldots , p$, the functional-coefficient $g_i(.)$ can be updated as follows:

Step 1::

Choose $m_i$ and $\lambda _i$, to initialize the configuration, uniformly along the range [a, b] at least $(m_i + 1)$ points away from each other.

Step 2::

Set $k_i$ equal to the number of interior knots.

Step 3::

Generate random variable u from U[0, 1], and choose the move type in the following manner.

• (i) if $u\le b_{k_i}$, go to the birth step;

• (ii) if $b_{k_i} < u\le b_{k_i} + d_{k_i}$, go to the death step;

• (iii) otherwise go to the move step.

Step 4::

Sample $\beta _i$ from the full conditional (18).

Step 5::

Simulate $\tau _{\beta }$ from the full conditional (23).

2.3 Specification of the parameters p and d

Specification of the parameters p and d is an important step to exactly specify the proposed FCAR(p, d) model before implementing the MCMC algorithm. This is obviously equivalent to the model selection task that can be achieved by BIC, among others. The BIC is a Bayesian criterion of model selection that penalizes the model for its inherent complexity. Based on the likelihood function of an estimated model, the BIC can be defined as

$$\begin{aligned} \text {BIC} = -2log\hspace{2mm}(\text {ML}_d) + n \hspace{0.2mm}log(T-p^*), \end{aligned}$$

(26)

where n is the number of estimated parameters in the entertained model and $\hbox {ML}_{{d}}$ is the maximized likelihood. The above criterion, proposed by [18], is based on the information theory and formulated in the Bayesian context. In order to specify the most appropriate FCAR model, one can calculate the BIC values for different candidate models of FCAR given in (1) by choosing different values of p and d. The model corresponding to the least value of BIC is finally taken as the best candidate model among others for further analysis.

It is important to mention here that the likelihood function (3) is not easy to obtain the corresponding ML estimates in order to evaluate $\hbox {ML}_{{d}}$ due to the involvement of the non-linear function g(.). To evaluate the same, one can approximate the non-linear function g(.) by an unknown constant, say $\psi$, and then calculate the ML estimates by using, say, a non-linear function minimization routine available in R software. It may be further noted that the approximation of the non-linear function g(.) by an unknown constant $\psi$ provides a likelihood similar to that of a general linear AR model that finally leads to easy evaluation of the approximate ML estimates and hence the value of $\hbox {ML}_{{d}}$. Alternatively, one can use the posterior modes as an approximation to the ML estimates provided the considered priors are not strong enough to affect the posterior distribution significantly. This latter suggestion is given in the literature by a number of authors (see, for example, [17]) and it is likely to be in the Bayesian spirit as well.

2.4 Predictive samples

For the given set of observed data ${\underline{y}}: y_1, y_2,\ldots , y_T$, one often wishes to obtain the next observed value, that is, $y_{T+1}$. This can be obtained from the model (1) once the estimated values of the parameters are made available. Truly speaking, if the estimated posterior density is symmetric, one can use the posterior mean, median or mode of the corresponding parameter as the most logical estimate. Among these estimates, the posterior mode is unconditionally used even if the estimated posterior density is non-symmetrical. Accordingly, the functional-coefficients $g_i(.)$’s can be estimated after getting the desired posterior samples of $\beta , \xi$ and k as discussed in Sects. 2.2.1 and 2.2.5. The future observation $y_{T+1}$, given the observed informative data, can then be obtained using a normal distribution with mean

$$\begin{aligned} \mu _{T+1} = \theta _0 + \sum \limits _{i=1}^p g_i(y_{t+1-d}) y_{t+1-i} \end{aligned}$$

(27)

and variance $\sigma ^2$. Obviously, the next observation corresponding to the error term, $\epsilon _{T+1}$, can be simulated from a normal distribution with mean zero and variance equal to the corresponding posterior estimate of $\sigma ^2$ (see, for example, [24]).

3 Numerical illustration

3.1 Simulation study

To examine the empirical performance of the proposed methodology, let us proceed with a simulation study on the two simple forms of the general FCAR model, that is, FCAR(1,1) and FCAR(2,1). These models can be expressed, respectively, as

$$\begin{aligned} y_t= & \theta _0+g_1(y_{t-1})y_{t-1}+\epsilon _t, \end{aligned}$$

(28)

$$\begin{aligned} y_t= & \theta _0+g_1(y_{t-1})y_{t-1}+g_2(y_{t-1})y_{t-2}+\epsilon _t. \end{aligned}$$

(29)

In order to perform the simulation in the above two cases, one has to consider some arbitrary choices for the model parameters such as $\theta _0$=0.05, $g_1(y_{t-1})=(y_{t-1})exp(-y_{t-1}^2/2), g_2(y_{t-1})=-cos(1.5y_{t-1})/(y_{t-1}^2+1)$. Besides, the assumed error terms $\epsilon$’s are i.i.d. $N(0,0.4^2)$. We, however, considered the other choices for $\sigma ^2$ such as 0.01, 0.81 and 4; and obtained the estimated posterior densities of $\sigma ^2$ corresponding to these values in Fig. 10 and 11 for the two considered models FCAR(1,1) and FCAR(2,1) respectively (see Appendix 3). In each of the two cases, we have considered replicating the simulation 100 times for a random sample of size 500 each. In each replication, the hyperparameters’ values, that is, $\lambda _1=1$, $r=1$, $s^2_\tau = 1$ and $\sigma _m^2 = 10^5$ are chosen arbitrarily but approved by simulation experience and provide a good convergence rate in all the 100 replications. Such choices of hyperparameters are not completely arbitrary, rather guided by a literature survey (see, for example, [28]). Referring to Sect. 2.2.1, the value of the tuning parameter $\sigma _m^2 = 10^5$ ensures the uniformity to select the candidate knot from the interval $(\xi _{i,j-1},\xi _{i,j+1})$ as for the higher values (more than $10^5$), the posterior samples remain unaltered. It is important to note that in each replication, the ergodicity of $g_1(y_{t-1})$ and $g_2(y_{t-1})$ has been ensured numerically by imposing a bounded condition on these functions (see Appendix 4).

To estimate the functional-coefficients, which are estimated by the quadratic splines, the posterior samples are drawn from the full conditionals of ($k_i$, $\xi _i$) and $\beta _i$’s using the reversible jump MCMC sampler as discussed in Sects. 2.2.1 and 2.2.2. Further, for the intercept $\theta _0$, the hyperparameter M and the scaling constant c are assumed to be 100 and 0.6, respectively, in each of the two cases (see Sect. 2.2.4). Also, the posterior samples of $\sigma ^2$ can be easily obtained from (24) using a gamma generating routine in each case.

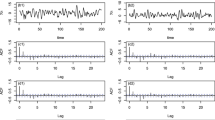
To obtain the desired posterior estimates of the parameters of the two models, (28) and (29), the proposed MCMC scheme (see Sect. 2.2) is implemented. Under the discussed initial setup, we have considered a long run of 5K iterations of the proposed MCMC scheme after observing a smooth convergence at about 2K iterations in its each replication. For each of the two models, the final posterior estimates are obtained by considering a random sample of size 1K, in each of the MCMC replications, after ignoring the initial transient behaviour and by maintaining a gap of 3. It was noted that a gap of 3 was sufficient to provide serial correlation negligibly small. The final posterior estimates are obtained as the “average” of 100 values of ‘posterior means’, ‘posterior medians’, ‘posterior modes’ and the ‘highest posterior density intervals’ with coverage probability 0.95 (0.95 HPD). Table 1 and Table 2 are providing the final posterior estimates (an average estimate of 100 replications) separately for FCAR(1,1) and FCAR(2,1) models respectively. Figure 2 demonstrates an estimate of functional-coefficient $g_1(.)$ of the FCAR(1,1) model along with 0.95 HPD region and the true function based on the average posterior estimate, for 100 replications, corresponding to each of the data point. A similar plot for the estimates of functional-coefficients $g_1(.)$ and $g_2(.)$ of the FCAR(2,1) model along with the corresponding 0.95 HPD regions and the true functions are provided in Fig. 3. The overall posterior estimates are quite satisfactory from the viewpoint of non-linear characteristic of FCAR model and their proximity with the true values of the parameters. In a single replication of FCAR(1,1) model, the trace plots of 10 equidistant grid points, which are picked up randomly from 500 observations, are demonstrated by Fig. 4a–j. Figure 4k–l show the ergodic plot and autocorrelation function (ACF) plot, respectively, for the FCAR(1,1) model. The ergodic plot advocates the convergence of the chain at about 2K iterations whereas, the ACF plot conveys the continuous decay of the autocorrelations of sample values at lag 100. It is to be noticed that Fig. 4k–l are obtained for a randomly chosen grid point (corresponding to $7^{th}$ observation in our case). The plots obtained in Fig. 4 are quite subjective and demonstrate the whole simulation procedure at just one sight. Moreover, in all other replications and at any arbitrarily chosen grid point, the behaviour is not going to be changed, in general. One may draw similar plots for FCAR(2,1) model as well, although the same are not provided due to paucity of space and left to the part of readers because of the ease of understanding of the proposed method.

The appropriateness of the model selection criterion is demonstrated by considering the simulated dataset of size 500 from the FCAR(1,1) model. Obviously, the BIC value should be least for a model from which the dataset is actually simulated. In order to investigate the same, let us obtain the BIC values for FCAR models with different nearby choices of p and d in each of the 100 replications. Figure 1 demonstrates the average of BIC values, for 100 replications, for different nearby choices of p and d of a general FCAR model. The height of each bar indicates the strength of BIC value for each considered model. Obviously, the BIC value is least corresponding to FCAR(1,1) model from which the dataset is actually simulated. This finding clearly indicates the appropriateness of the considered model selection criterion.

Table 1 Posterior summaries for the parameters of FCAR(1, 1) model corresponding to simulated dataset

Table 2 Posterior summaries for the parameters of FCAR(2, 1) model corresponding to simulated dataset

Fig. 1

Average BIC values based on the simulated dataset

Fig. 2

Estimated functional-coefficient (solid line) with 0.95 HPD interval (shaded region) of the functional coefficient $g_1(.)$ corresponding to FCAR(1,1) model. The corresponding true value of $g_1(.)$ is shown by means of dotted line

Fig. 3

Estimated functional-coefficients (solid lines) with 0.95 HPD intervals (shaded regions) of the functional-coefficients $g_1(.)$ and $g_2(.)$ corresponding to FCAR(2,1) model. The corresponding true values of $g_1(.)$ and $g_2(.)$ are shown by means of dotted lines

Fig. 4

(a)-(j) Trace plots of the estimated functional-coefficient $g_1(.)$ corresponding to FCAR(1,1) model for 5k iterations at 10 random grid points. (k) Ergodic plot of the estimated functional-coefficient $g_1(.)$ corresponding to FCAR(1,1) for 5K iterations. (l) ACF plot of the estimated functional-coefficient $g_1(.)$ corresponding to FCAR(1,1) model

3.2 Real data example

Let us now begin with a real data example on monthly exchange rate of Indian rupees relative to the US dollars from January 2011 to December 2020. The dataset has been taken from the website of Fusion Media Limited group of the British Virgin Islands (see http://in.investing.com/currencies/usd-inr-historical-data) and is reported in Table 3.

The time series plot for the dataset reported in Table 3 is shown in Fig. 5. One can observe that the time series exhibits an increasing pattern, which clearly advocates the non-stationary behaviour of the original dataset (see Fig. 5). To remove non-stationarity from the data, we considered the first difference from the original data and plotted the same as time series in Fig. 6. It can be seen that the first difference plot exhibits nearly a stable pattern at least with regard to its mean value and, therefore, considering the first difference appears logical for further analyses of the data. Moreover, since the stability in the stationarity pattern is examined only graphically (Fig. 6), it is pertinent to consider numerical evidence as well to examine stationarity before proceeding further. For this purpose, we considered the augmented Dickey-Fuller (ADF) test on the data and noted that the test was significant at 5% level (p-value close to 0.01). Obviously, the first differenced data ensures stationarity on the basis of objective consideration as well. For further details on the ADF test, one may refer to [23, 24], among others.

Selection of an appropriate model for further analysis is of utmost importance in order to retrieve the reliable results. We, therefore, implemented the methodology discussed in Sect. 2.3 to select an appropriate FCAR model by choosing the most appropriate values of its order p and delay parameter d. For this purpose, we begin by considering a few combinations of the AR order p and delay parameter d in the FCAR model (1) and then obtain the BIC value corresponding to each such model. We have considered 25 combinations of the FCAR model by using different values of $p (=1, 2, 3, 4, 5)$ and $d (=1, 2, 3, 4, 5)$. The BIC values for different d are then plotted against the variation of p in Fig. 7. The plot actually summarizes the numerical values of BIC for different considered combinations of p and d and the line combining similar plotting symbols is used for clarity of presentation and, of course, to display a trend. One may interpret that the BIC values show an increasing pattern as the order p increases for each value of the delay parameter d. Obviously, based on the values of BIC shown in Fig. 7, $p=1$ appears to be an appropriate choice as the corresponding BIC value is least.

Table 3 Monthly exchange rate of Indian rupees relative to the US dollars from January 2011 to December 2020

Fig. 5

Time series plot of exchange rate data of Indian rupees relative to the US dollars

Fig. 6

First differenced time series plot of exchange rate data of Indian rupees relative to the US dollars

Fig. 7

Plot of BIC values for different choices of parameters p and d

The choice of d, however, seems difficult on the basis of pictorial representation, since the BIC values corresponding to all the considered FCAR(1, d) models for different d appear to originate from the same point (see Fig. 7). Therefore, in order to provide a clear-cut conclusion, the numerical values of BIC corresponding to FCAR(1, d) models with different $d (=1, 2, 3, 4, 5)$ are shown in Table 4. Obviously, the BIC corresponding to FCAR(1, 1) model is least recommending for the use of FCAR(1, 1) for the considered dataset. It may, however, be noted that other BIC values (for $d (= 2, 3, 4, 5)$) are not too far away from the value corresponding to FCAR(1, 1) and, therefore, one can proclaim why not to consider recommending other values of d. The answer is obvious. First, the value corresponding to FCAR(1, 1) is the least and, second, the parsimony principle never allows us to go for complicated models unless there is a real requirement. Moreover, the second term in (26) is almost unaffected by a variation in d and it is only the first term that provides a minor variation. So our final conclusion certainly supports FCAR(1, 1) model for the considered dataset.

Let us now represent the selected FCAR(1, 1) model mathematically, for the differenced dataset, as

$$\begin{aligned} \Delta y_t = \theta _0+ g_1(\Delta y_{t-1}) \Delta y_{t-1} + \epsilon _t, \end{aligned}$$

(30)

where $\Delta y_t$ denotes the first difference data at time t. To perform the Bayesian analysis, for the selected FCAR (1, 1) model (30), we choose the quadratic spline for $g_1(.)$. It is needless to mention that all the forthcoming analyses will be performed on the first difference data where we have noticed a stationarity pattern in the time series. To begin with the Bayesian analysis, we assign numerical values to the hyperparameters defined in the Sect. 2.1 as $\lambda _1=1$, $r=1$ and $s^2_\tau = 1$ and $M=100$. Of course, there is no basis in the selection of these hyperparameters except using the suggestions given by [28] and [23, 24], etc. It is to be noted that these choices of hyperparameters approximately result into weakly informative priors in the sense that the resulting priors are more or less flat in an appreciable range and, as such, most of the inferences can be regarded as driven by the likelihood function only.

Table 4 BIC values for FCAR(1, d) models with different choices of $d \hspace{1mm}(=1, 2, 3, 4, 5)$

With these choices of the prior hyperparameters, the MCMC implementation was done as detailed in Sect. 2.2. The value of the tuning parameter, in the move step, can be taken large enough to make the proposal uniform over the random interval (see Sect. 2.2.1) and it is noted that $\sigma _m^2$=$10^5$ is an appropriate choice for this. The posterior samples of $\beta _i'$s, on the other hand, can be obtained easily by using the multivariate normal routine (see (18)). Also, the posterior samples of $\sigma ^2$ can be effortlessly obtained from (24) using the gamma generating routine for the current values of shape and scale parameters. Now, following the three move types, defined in Sect. 2.2, the posterior samples for the number of knots $k_i$’s and the locations $\xi _i$’s can be easily simulated and finally updated to get the functional-coefficient $g_i(.)$ (see also Sect. 2.2.5). A reversible jump MCMC based estimates of the functional-coefficient is shown in Fig. 8. These estimates are obtained exactly in a similar way as described for the simulated dataset. Figure 8 indicates that the estimated quadratic spline, corresponding to the functional coefficient $g_1(.)$, is continuous at point 0 and has a range approximately from $-0.0175$ to 0.025 with a coverage probability of 0.95. To be specific, the estimated spline meets the zero line at two different location points, which further justifies the consideration of quadratic spline as mentioned in the above paragraph. The trace plots at several grid points and ergodic plots can also be obtained similar to Fig. 4, though we skip such plots due to the paucity of space.

Fig. 8

Estimated functional-coefficient $g_1(.)$ (solid line) with 0.95 HPD (shaded region) for the differenced data

Next, the posterior samples of the intercept parameter $\theta _0$ can be obtained by implementing the Metropolis algorithm as discussed in Sect. 2.2.4. As mentioned, we fixed the value of the hyperparameter $M=100$ and chose the value of the scaling constant as $c=0.6$. This choice of $M=100$ can certainly be regarded as providing a vague choice of the prior and hence allowing the inferences to be data driven. Also, the choice of scaling constant, as mentioned above, was well within the permissible range and resulted in the maximum acceptance probability (see also [24]).

Under the above setup, the joint posterior density (15) was managed for MCMC implementation to get the desired posterior samples for drawing the sample based inferences. To draw such inferences, we considered a single long run of the chain up to 20K iterations although the convergence was noticed at about 8K iterations. Next, after ignoring the outcomes of the first 10K iterations, we picked up posterior samples of size 1K from the last 10K iterations by maintaining a gap of 10 in order to minimize serial correlation among the generating variates. The extracted posterior summaries for the relevant parameters of the selected FCAR(1, 1) model are given below in Table 5.

Table 5 Posterior summaries for the parameters of FCAR(1, 1) model corresponding to first difference data

A statistical interpretation of Table 5 can be easily made and is mostly fact-driven. It is obvious from the above posterior summaries that the estimated marginal posterior densities of $\theta _0$ and $\sigma ^2$ are quite close to symmetry. Since the above estimates are solely based on the simulated posterior samples from their respective full conditionals, the accuracy of the estimates conveys a strong message that the FCAR(1, 1) model is having an error term with (an almost) constant value of $\sigma ^2$ and, hence, the model is homoscedastic in nature. Moreover, approximately normal shape of the densities was also assessed, which is not given here due to the paucity of space.

To show the model compatibility with the data in hand, we relied on graphical tools which appeared to be more striking than other statistical tools. We, therefore, plotted the differenced time series (using solid line) along with the predictive samples of time series (using dotted lines). For such an assessment, we considered 10 predictive samples, each of size equal to that of the differenced data, and superimposed them on to a plot of differenced data time series. It may be noted that the 10 predictive samples were obtained on the basis of 10 posterior samples of the concerned parameters, which were picked up randomly from the converged set of simulated posterior samples (see Sect. 2.4). The corresponding plot is shown in Fig. 9. It can be easily confirmed that the predicted time series and the observed (differenced) time series exhibit similar pattern (see Fig. 9), which advocates the adequacy of the proposed model with the data in hand.

Fig. 9

Time series plots for the predictive datasets with superimposed differenced dataset (the dark line corresponds to the differenced data)

Let us come to the final objective of our study to investigate the predictive ability of the proposed FCAR(1, 1) model. For this purpose, we performed the retrospective predictions of the exchange rate for the period from July 2020 to December 2020 by considering only the data from January 2011 to June 2020 as an informative dataset. Obviously, we did not use the observed dataset from July 2020 to December 2020, rather kept them for a comparison with the values obtained from the retrospective predictions. It is important to mention here that the entire posterior analysis was repeated for the updated informative set of data. By updating the informative dataset, we mean to include the predicted observations one after another in the informative dataset until the last value is predicted. Moreover, at each stage of prediction, we used posterior mode to predict 1K predictive samples. The result of retrospective predictions is given in the form of predictive modes and predictive intervals with coverage probability 0.95 (0.95 PI) (see Table 6). These estimates are everywhere based on the entire 1K predictive samples.

Table 6 The retrospective predictions of exchange rate of Indian rupees relative to the US dollars from July 2020 to December 2020 based on FCAR(1, 1) model

Clearly, it can be seen that the predictive point estimates are not far away from their corresponding true values and they lie well within the estimated predictive intervals (see Table 6). Obviously, our analysis supports the FCAR (1, 1) model for the considered exchange rate dataset as the model based on retrospective predictions is in complete agreement with the true values of informative data.

Once the retrospective prediction is successfully observed with the proposed FCAR(1, 1) model, it is pertinent to look for the prospective prediction. Our objective was to predict the values from January, 2021 to June, 2021. Thus, for the prospective prediction, we considered the complete posterior analysis discussed earlier for the dataset reported in Table 3 with the posterior estimates given in Table 5. Using estimated posterior modes as given in Table 5, we obtained 1K predictive samples for predicting the corresponding value for January, 2021. The results are given in Table 7 in the form of predictive modes and 0.95 PI for January, 2021. Now adding the predictive mode for January, 2021 in the informative data, we repeated the entire procedure and obtained the corresponding predictive mode and 0.95 PI for February, 2021. This procedure was repeated until we obtained the predictive mode and 0.95 PI for the next four months, that is, up to June, 2021 (see Table 7). We do not provide a comparison of the prospective predictions with the actual values, but our belief conveys that the predicted results are close to the reality and the true values are reflected almost at the middle of our estimated 0.95 PIs although there can be slight differences in the point estimates.

Table 7 The prospective predictions of exchange rate of Indian rupees relative to the US dollars from January 2021 to June 2021 based on FCAR(1, 1) model

4 Conclusion

This paper discusses the Bayesian analysis of FCAR(p, d) model using a free-knot spline technique. The significance of the work can be realized from the fact that it not only provides the complete Bayesian analysis using a hybrid MCMC based strategy but also looks at several important aspects such as model compatibility, specification of both p and d of FCAR(p, d) model and, most importantly, both retrospective and prospective predictions. The first part obviously employs the Gibbs sampler algorithm with the intermediate Metropolis steps supported by the reversible jump MCMC technique. Numerical illustrations based on the simulated data as well as on a real dataset on the exchange rate of Indian rupees relative to the US dollars not only convey the ease of implementation of our methodology but also suggest that the proposed procedure has enough potential with regard to the prediction as well. It is expected that such an analysis will help the business analysts, investors and policy makers to come across an appropriate planning.

Appendices

Appendix 1

Derivation of the conditional joint posterior of $(\beta _i, k_i, \xi _i)$

Let us write the joint posterior of $(\beta _i, k_i, \xi _i)$, $i=1, 2,\ldots , p$, after combining the likelihood function (7) and the prior distributions ((8) to (10)), up to proportionality as

$$\begin{aligned} & \pi (\beta _i, k_i, \xi _i|{\underline{y}}, \theta _0, \beta _{-i}, k_{-i}, \xi _{-i}, \tau _\beta , \sigma ^2) \\ & \propto \exp \left( -\frac{1}{2\sigma ^2}\sum \limits _{t=p^*+1}^T(y_t-\theta _0-\sum \limits _{i=1}^p B'_i(y_{t-d})\beta _i y_{t-i})^2\right) \times \left( \frac{\lambda _i \tau _\beta ^{-1/2}}{b-a}\right) ^{k_i} \\ & \times (\sigma ^2)^{-k_i/2} \times \exp \left( -\frac{1}{2\sigma ^2\tau _\beta } \beta '_i \beta _i\right) , \\ & \propto \exp \left( -\frac{1}{2\sigma ^2}(Z_i -\beta _i X_i)'(Z_i -\beta _i X_i)\right) \times \left( \frac{\lambda _i \tau _\beta ^{-1/2}}{b-a}\right) ^{k_i} \\ & \times (\sigma ^2)^{-k_i/2} \times \exp \left( -\frac{1}{2\sigma ^2\tau _\beta } \beta '_i \beta _i\right) , \end{aligned}$$

where $Z_i$ and $X_i$ are defined in Sect. 2.2.1. Now expanding the first exponential term, in above expression, a more simplified version can be obtained as

$$\begin{aligned} & \pi (\beta _i, k_i, \xi _i|{\underline{y}},\theta _0, \beta _{-i}, k_{-i}, \xi _{-i}, \tau _\beta , \sigma ^2)\\ & \propto \exp \left( -\frac{1}{2\sigma ^2 \tau _\beta }\{\beta '_i \beta _i - Z'_i X_i \beta _i \tau _\beta - X'_i \beta '_i Z_i\tau _\beta + X'_i X_i \beta '_i \beta _i \tau _\beta )\}\right) \\ & \times \left( \frac{\lambda _i \tau _\beta ^{-1/2}}{b-a}\right) ^{k_i} \times (\sigma ^2)^{-k_i/2} \times \exp \left( -\frac{1}{2\sigma ^2} Z'_i Z_i\right) , \\ & \propto \exp \left( -\frac{1}{2\sigma ^2} \Sigma _i^{-1} \{\beta '_i \beta _i - \beta _i {\hat{\beta }}'_i -\beta '_i {\hat{\beta }}_i +{\hat{\beta }}'_i{\hat{\beta }}_i)\}\right) \times \left( \frac{\lambda _i \tau _\beta ^{-1/2}}{b-a}\right) ^{k_i}\\ & \times (\sigma ^2)^{-k_i/2} \times \exp \left( -\frac{1}{2\sigma ^2} \{Z'_i Z_i - {\hat{\beta }}'_i\Sigma _i^{-1}{\hat{\beta }}_i\}\right) ,\\ & \propto \exp \left( -\frac{1}{2\sigma ^2} (\beta _i - {\hat{\beta }}_i)' \Sigma _i^{-1} (\beta _i - {\hat{\beta }}_i)\right) \times \left( \frac{\lambda _i \tau _\beta ^{-1/2}}{b-a}\right) ^{k_i} \times (\sigma ^2)^{-k_i/2} \times \exp \left( -\frac{1}{2\sigma ^2} S_i\right) , \end{aligned}$$

where the mathematical form of $\Sigma _i$, ${\hat{\beta }}_i$ and $S_i$ are defined in equation (17) of Sect. 2.2.1.

Appendix 2

Derivations of jump probabilities and acceptance probabilities in the three move-types

Jump probability:

Let $M_{k_i}$ represents a model having $k_i$ interior knots and $M_{k_{i}+1}$ represents a model after adding an additional knot. The jump probability in birth step can be written as

$$\begin{aligned} q(M_{k_{i}+1}|M_{k_{i}})= & b_{k_{i}} \times \text {probability of selecting a subinterval out of} (k_i +1) \text {subintervals} \\ & \times \text {probability of drawing a candidate knot, say},\\ & \times \phi \text {uniformly from} (\xi _{ij}, \xi _{i, j+1})\\= & \frac{b_{k_i}}{k_i + 1} \sum _{j=0}^{k_i} \frac{1}{\xi _{i, j+1} - \xi _{ij}} I\{\xi _{ij}< \phi < \xi _{i,j+1}\}. \end{aligned}$$

The probability defined above is actually the mixture of uniform densities as $\phi$ can be drawn from any of $k_i$ different uniform distributions. Similarly, in the deletion process of death step, the model moves from $M_{k_{i}}$ to $M_{k_{i-1}}$ and hence the jump probability is given by

$$\begin{aligned} q(M_{k_{i}-1}|M_{k_{i}})= & d_{k_{i}} \times \text {probability of randomly chosing a knot out of} k_i \text {existing knots}\\= & \frac{d_{k_i}}{k_i}. \end{aligned}$$

The jump probability in move step can be defined as the probability of movement of the current model $M_{k_i}$ to the candidate model $M^*_{k_i}$ with the same number of knots $k_i$ and it can be given as

$$\begin{aligned} q(M^{*}_{k_{i}}|M_{k_{i}})= & \eta _{k_{i}} \times \text {probability of chosing a candidate knot} \xi _{ij} \text {randomly out of} k_i \text {existing} \\ & \times \text { knots probability of drawing a new location of candidate knot, say,} \\ & \xi ^*_{ij} \text {uniformly from} (\xi _{i,j-1}, \xi _{i, j+1})\\= & \frac{\eta _{k_i}}{k_i} \frac{1}{\xi _{i, j+1} - \xi _{i, j-1}}. \end{aligned}$$

Acceptance probability: The acceptance probability in all the three steps is defined earlier as

$\min (1, \text {posterior ratio} \times \text {proposal ratio})$.

In birth step, the posterior ratio is obtained from the full conditional (19) as

$$\begin{aligned} \frac{\pi (M_{k_{i}+1})}{\pi (M_{k_{i}})}= & \frac{\left( \frac{\tau _\beta ^{-1/2} \lambda _i}{b-a}\right) ^{k_{i}+1} \times |\Sigma ^*_i|^{1/2} \exp \left( \frac{-S^*_i}{2\sigma ^2}\right) }{\left( \frac{\tau _\beta ^{-1/2} \lambda _i}{b-a}\right) ^{k_i} \times |\Sigma _i|^{1/2} \exp \left( \frac{-S_i}{2\sigma ^2}\right) } \\= & \left( \frac{\tau _\beta ^{-1/2} \lambda _i}{b-a}\right) \times \left( \frac{|\Sigma ^*_i|}{|\Sigma _i|}\right) ^{1/2} \exp \left( \frac{S_i-S^*_i}{2\sigma ^2}\right) \end{aligned}$$

and the proposal ratio is given by

$$\begin{aligned} \frac{\pi ^*(M_{k_{i}+1})}{\pi ^*(M_{k_{i}})}= & \frac{d_{k_{i}+1}/(k_i +1)}{b_{k_i}/(k_i +1) \times \frac{1}{\xi _{i, j+1} - \xi _{ij}}}\\= & \frac{d_{k_{i}+1}}{b_{k_i}} \times (\xi _{i, j+1} - \xi _{ij})\\= & \frac{p(k_{i})}{p(k_{i}+1)} \times (\xi _{i, j+1} - \xi _{ij})\\= & \frac{(k_{i}+1)}{\lambda _{i}} \times (\xi _{i, j+1} - \xi _{ij}). \end{aligned}$$

The acceptance probability is, then, given by

$$\begin{aligned} \frac{\pi (M_{k_{i}+1})}{\pi (M_{k_{i}})} \times \frac{\pi ^*(M_{k_{i}+1})}{\pi ^*(M_{k_{i}})} = \frac{k_i + 1}{\tau _\beta ^{1/2}} \frac{\xi _{i,j+1} - \xi _{ij}}{b-a} \times \left( \frac{|\Sigma ^*_i|}{|\Sigma _i|}\right) ^{1/2} \exp \left( \frac{S_i-S^*_i}{2\sigma ^2}\right) . \end{aligned}$$

In death step, the posterior ratio is obtained from the full conditional (19) as

$$\begin{aligned} \frac{\pi (M_{k_{i}-1})}{\pi (M_{k_{i}})}= & \frac{\left( \frac{\tau _\beta ^{-1/2} \lambda _i}{b-a}\right) ^{k_{i}-1} \times |\Sigma ^*_i|^{1/2} \exp \left( \frac{-S^*_i}{2\sigma ^2}\right) }{\left( \frac{\tau _\beta ^{-1/2} \lambda _i}{b-a}\right) ^{k_i} \times |\Sigma _i|^{1/2} \exp \left( \frac{-S_i}{2\sigma ^2}\right) } \\= & \left( \frac{\tau _\beta ^{-1/2} \lambda _i}{b-a}\right) ^{-1} \times \left( \frac{|\Sigma ^*_i|}{|\Sigma _i|}\right) ^{1/2} \exp \left( \frac{S_i-S^*_i}{2\sigma ^2}\right) \end{aligned}$$

and the proposal ratio is given by

Fig. 10

Estimated posterior density plots of $\sigma ^2$, at different values, corresponding to FCAR(1,1) model

$$\begin{aligned} \frac{\pi ^*(M_{k_{i}-1})}{\pi ^*(M_{k_{i}})}= & \frac{b_{k_{i}-1}/k_i}{d_{k_i}/k_i} \times \frac{1}{\xi _{i, j+1} - \xi _{i, j-1}} \\= & \frac{p(k_{i})}{p(k_{i}-1)} \times \frac{1}{\xi _{i, j+1} - \xi _{i, j-1}}\\= & \frac{\lambda _{i}}{k_{i}} \times \frac{1}{\xi _{i, j+1} - \xi _{i, j-1}}. \end{aligned}$$

The acceptance probability is, therefore, given by

$$\begin{aligned} \frac{\pi (M_{k_{i}-1})}{\pi (M_{k_{i}})} \times \frac{\pi ^*(M_{k_{i}-1})}{\pi ^*(M_{k_{i}})} = \frac{\tau _\beta ^{1/2}}{k_i} \frac{b-a}{\xi _{i, j+1} - \xi _{i, j-1}} \times \left( \frac{|\Sigma ^*_i|}{|\Sigma _i|}\right) ^{1/2} \exp \left( \frac{S_i-S^*_i}{2\sigma ^2}\right) . \end{aligned}$$

Finally, in move step, the number of knots remain same and the only change is the relocation of a selected knot by the candidate knot. The posterior ratio is obtained from the full conditional (19) as

$$\begin{aligned} \frac{\pi (M^*_{k_{i}})}{\pi (M_{k_{i}})}= & \frac{\left( \frac{\tau _\beta ^{-1/2} \lambda _i}{b-a}\right) ^{k_{i}} \times |\Sigma ^*_i|^{1/2} \exp \left( \frac{-S^*_i}{2\sigma ^2}\right) }{\left( \frac{\tau _\beta ^{-1/2} \lambda _i}{b-a}\right) ^{k_i} \times |\Sigma _i|^{1/2} \exp \left( \frac{-S_i}{2\sigma ^2}\right) } \\= & \left( \frac{|\Sigma ^*_i|}{|\Sigma _i|}\right) ^{1/2} \exp \left( \frac{S_i-S^*_i}{2\sigma ^2}\right) . \end{aligned}$$

The proposal ratio in this case is given by

$$\begin{aligned} \frac{\pi ^*(M^*_{k_{i}})}{\pi ^*(M_{k_{i}})} = 1. \end{aligned}$$

Hence the acceptance probability is given by

$$\begin{aligned} \frac{\pi (M^*_{k_{i}})}{\pi (M_{k_{i}})} \times \frac{\pi ^*(M^*_{k_{i}})}{\pi ^*(M_{k_{i}})} = \left( \frac{|\Sigma ^*_i|}{|\Sigma _i|}\right) ^{1/2} \exp \left( \frac{S_i-S^*_i}{2\sigma ^2}\right) . \end{aligned}$$

Appendix 3

As discussed in Sect. 3.1, we have checked the performance of two considered models for different choices of error variance. We have performed the whole analysis for the values 0.01, 0.16, 0.81 and 4 of $\sigma ^2$ and have plotted the estimated posterior densities in Fig. 10 and Fig. 11 for FCAR(1,1) and FCAR(2,1) models respectively.

Fig. 11

Estimated posterior density plots of $\sigma ^2$, at different values, corresponding to FCAR(2,1) model

We can easily verify that the nature of plots are almost unchanged (close to symmetry) except for the value very close to zero (for $\sigma ^2$=0.01); which ultimately putting negligible effects on the predicted values and non-linearity of the model. We, however, considered $\sigma ^2$=0.16 in order to get the final posterior estimates of parameters and functional coefficients, for the two models, in the simulation study.

Appendix 4

Proof of boundedness for the proposed functions in simulation study

1) Proof of boundedness for the functional-coefficient $g_1(y_{t-1})$:

We have considered the following function for the non-linear functional-coefficient $g_1(y_{t-1})$:

$$\begin{aligned} g_1(x)=x\times exp(-x^{2}/2); \hspace{2cm} \forall \hspace{1cm} x\in {\mathbb {R}}. \end{aligned}$$

We know that any function $f:D \rightarrow R$, where D and R represent the possible domain and range of the function respectively, will be differentiable at any point $c\in D$, if and only if both the left-hand and the right-hand derivatives of the function are finite and equal, such that-

$$\begin{aligned} \lim _{h\rightarrow 0}\dfrac{f(c-h)-f(c)}{-h}=\lim _{h\rightarrow 0}\dfrac{f(c+h)-f(c)}{h}. \end{aligned}$$

It is important to mention that, for the considered function $g_1(.)$, domain (D) and range (R) are the set of real numbers ${\mathbb {R}}$. In order to show that the function is differentiable, we check the left-hand and the right-hand derivative of the function $g_1(.)$ at any arbitrary point, say, c. We can write the left-hand derivative as,

$$\begin{aligned} g_{1}'(c_{-})= & \lim _{h\rightarrow 0}\dfrac{g_1(c-h)-g_1(c)}{-h} \\= & \lim _{h\rightarrow 0}\left[ \dfrac{(c-h)e^{-(c-h)^{2}/2}-ce^{-c^{2}/2}}{-h}\right] \\= & \lim _{h\rightarrow 0}\left[ \dfrac{(c-h)^{2}e^{-(c-h)^{2}/2}-e^{-(c-h)^{2}/2}}{-1}\right] \\= & -e^{-c^{2}/2}(c^{2}-1). \end{aligned}$$

Similarly, the right-hand derivative can be written as,

$$\begin{aligned} g_{1}'(c_{+})= & \lim _{h\rightarrow 0}\dfrac{g_1(c+h)-g_1(c)}{h} \\= & \lim _{h\rightarrow 0}\left[ \dfrac{(c+h)e^{-(c+h)^{2}/2}-ce^{-c^{2}/2}}{h}\right] \\= & \lim _{h\rightarrow 0}\left[ \dfrac{-(c+h)^{2}e^{-(c+h)^{2}/2}+e^{-(c+h)^{2}/2}}{1}\right] \\= & -e^{-c^{2}/2}(c^{2}-1). \end{aligned}$$

One can see that both the left-hand and the right-hand derivatives, for the considered function, are finite and equal. Hence, the function $g_1(x)$ is differentiable. Moreover, the optimum points for the function $g_1(x)$ can also be obtained by calculating the first derivative and putting it equals to zero.

$$\begin{aligned} g_{1}'(x)= & e^{-x^{2}/2}- x^{2}e^{-x^{2}/2}\\= & e^{-x^{2}/2}\left( 1-x^{2}\right) . \end{aligned}$$

In above expression, the optimum points can be obtained by putting

$$\begin{aligned} 1-x^{2}=0 ; (\because e^{-x^{2}/2}\ne 0) \end{aligned}$$

$\Rightarrow x=\pm 1$.

Now, the value of the function can easily be obtained at the optimum points as,

$$\begin{aligned} g_1(-1)&= -e^{-1/2} \textrm{and}\\ g_1(1)&= e^{-1/2}\\ \Rightarrow -e^{-1/2}&\le g_1(x) \le e^{-1/2}. \end{aligned}$$

Hence, the function $g_1(x)$ is bounded on a closed interval $[-e^{-1/2}, e^{-1/2}]$ and, hence,

$$\begin{aligned} |g_1(x)|\le e^{-1/2} \hspace{0.5cm} \text {or} \hspace{0.5cm} (|g_1(x)|\le 0.6065). \end{aligned}$$

2) Proof of boundedness for the functional-coefficient $g_2(y_{t-1})$:

We have considered the following function for the non-linear functional-coefficient $g_2(y_{t-1})$:

$$\begin{aligned} g_2(x)=-cos(1.5x)/(x^2+1); \hspace{2cm} \forall \hspace{1cm} x\in {\mathbb {R}}. \end{aligned}$$

We know that any real-valued function f(x) defined on a subset S of the real numbers is said to be bounded if there exist a constant M, such that for all $x\in S$, the inequality $|f(x)|\le M$ holds, where M belongs to some positive real number ($\mathbb {R^+}$).

Now, we know that the range of the cos function lies in the interval $[-1,1]$. So, the range of cos(1.5x) also lies within the range $[-1,1]$ such that

$$\begin{aligned} \left| -cos(1.5x)\right| \le 1 \end{aligned}$$

Also, for all $x\in {\mathbb {R}}$,

$$\begin{aligned} \dfrac{1}{1+x^2}\le 1 \end{aligned}$$

$\Rightarrow \left| \dfrac{-cos(1.5x)}{1+x^2}\right| \le 1$

         $\Rightarrow -1 \le \dfrac{-cos(1.5x)}{1+x^2} \le 1$

Hence, the function $g_2(x)$ is a bounded function.