Modelling escalation in crime seriousness: a latent variable approach

Abstract

This paper investigates the use of latent variable models in assessing escalation in crime seriousness. It has two aims. The first is to contrast a mixed-effects approach to modelling crime escalation with a latent variable approach. The paper therefore examines whether there are specific subgroups of offenders with distinct seriousness trajectory shapes. The second is methodological—to compare mixed-effects modelling used in previous work on escalation with group-based trajectory modelling and growth mixture modelling (mixture of mixed-effects models). The availability of software is an issue, and comparisons of fit across software packages is not straightforward. We suggest that mixture models are necessary in modelling crime seriousness, that growth mixture models rather than group-based trajectory models provide the best fit to the data, and that R gives the best software environment for comparing models. Substantively, we identify three latent groups, with the largest group showing crime seriousness increases with criminal justice experience (measured through number of conviction occasions) and decreases with increasing age. The other two groups show more dramatic non-linear effects with age, and non-significant effects of criminal justice experience. Policy considerations of these results are briefly discussed.

1 Introduction

The term “escalation” has different meanings in the criminological literature. Some authors such as [9] and [35] use the term in relation to increasing frequency of offending; others (e.g., [4]) define escalation as a tendency to move to more serious offence types. In this paper we follow the second usage of the term and refer to escalation in crime seriousness. Surprisingly little quantitative work has been done in this area, with most work using crime type switching tables, fitting log-linear models or using methods such as the forward escalation coefficient. Liu et al. [21] provides a literature review.

In previous work, a linear mixed-effects model has been used to model escalation in offence seriousness over the criminal lifespan [21]. This paper took a multi-level modelling approach to the sequence of seriousness scores for each offender. This statistical approach modelled sequences of seriousness scores with time-varying covariates and accounted for between individual and within individual variability. The paper also identified that there are two temporal scales—age and conviction occasion, and so examined two types of escalation process—escalation associated with experience of the criminal justice process, and escalation associated with age and maturation. The resulting model suggested some interesting findings where ageing is associated with de-escalation, whereas increasing conviction occasions (court appearances) are associated with escalation. However, one potential criticism of this work is that it did not consider that there may be different subpopulations of offenders with different escalation processes. This paper therefore addresses this problem and considers a variety of models which allow for different escalation trajectories.

In the disciplines of psychology, medicine, and criminology, the work of Nagin and Land [31] has popularised the use of group-based trajectory modelling, which assumes that there are a number of latent subpopulations with different temporal trajectories present in the data. While in criminology such models have been used for offending frequency, there has been little work in estimating trajectories of crime severity over age and conviction history. This is therefore an important research area for criminologists which is necessary to understand how offenders develop their criminal careers in terms of the seriousness of crimes.

Despite the popularity of Nagin’s model for understanding trajectories, there are a number of alternative statistical terminologies that have also been used. In the psychological and sociological literature, the terms growth curve model and growth mixture modelling are commonly found. In addition, alternative terms such as the linear mixed-effects model, the heterogeneity model, and latent class linear mixed-effect model can also be found. The terminology is confusing, and sometimes these terms refer to the same underlying model, whereas others differ in important respects. However, they all are designed to study and model repeated observations over time, with many of these approaches taking account of within individual and between individual variation.

The second new development of this paper is to examine the effect of time spent in prison on crime escalation. We conceptualise this in terms of cumulative custodial sentence awarded, measuring cumulative sentence length up to the current conviction occasion. In effect, this means that there are now three types of escalation process—escalation associated with experience of the criminal justice process, escalation associated with age and maturation, and escalation associated with time spent in prison.

In Sect. 2, we provide a methodological review, disentangling the multitude of terms used in this area. We will group the current available statistical approaches on studying developmental trajectory into three main types of methodologies according to the assumptions made. In Sects. 3 and 4, we briefly discuss the conceptual issues involved in studying escalation, before introducing the Offenders Index dataset. Then in the following Sect. 5, we firstly examine the existence of heterogeneity for the distribution of random effects, then we apply two competing methods: group-based trajectory modelling and growth mixture modelling to assess the existence of subpopulations in assessing escalation over conviction history. We compare the results from our earlier study using a linear mixed-effects model with these two new approaches. In the last section, we discuss our results reaching some tentative substantive conclusions.

2 Competing approaches for modelling trajectories

As already mentioned, there are a variety of terminologies that are commonly used by researchers in studying developmental trajectories and longitudinal data. Indeed, it is often confusing for researchers from different disciplines to understand the links between these varying terminologies. Essentially, among these varying terminologies, there are three distinct statistical methodologies: mixed-effects modelling, mixture modelling, and mixtures of mixed models.

This section firstly reviews the statistical properties and software implementation options of each approach, and examines two existing comparison studies which examine these methods.

We now define the framework for our models. We let $Y_{it}$ represent the response variable, for observations $i=1,\ldots ,m$ at the time points $t=1,\ldots ,n_{i}$. Here m is the total number of cases, and $n_{i}$ is the number of observations for each case i.

The repeated outcomes for each i can be gathered into an vector of length $n_{i}$, ${\varvec{y}}_{i}=(Y_{i1},\ldots ,Y_{in_{i}})$. The responses for all i are stacked into a long vector of length n; thus ${\varvec{y}}=({\varvec{y}}_{1},\ldots ,{\varvec{y}}_{m})$, with $n=\sum _{i=1}^{m}n_{i}$.

2.1 Mixed-effects modelling

The linear mixed-effects (LME) model [7, 19] is a well developed and popular statistical approach for the analysis of longitudinal data, which is well described in many texts such as [34] and [45]. Another commonly used term is the growth curve model (GCM) [10, 38, 46, 47]. These two terminologies essentially refer to the same approach and estimate not only the overall growth or trajectory (fixed-effect) but also the amount of variation across individuals in the growth parameters (random intercept and random slopes).

The terminology of GCM is commonly used in the disciplines of sociology, psychology, and criminology and is used by the statistical package MPLUS. The conventional growth curve model is often in a form of an intercept plus variables representing the time effect (slopes), such as time and time squared which we refer to as growth factors. The variance of the intercept and the polynomial time parameters are represented by random effects which are multivariate normally distributed with means of 0 and an estimated variance–covariance matrix [7, Chap. 5]. It is commonly used in conjunction with time-constant explanatory variables to explain the variation in the growth random effects. Hwang and Takane [14] also pointed out that the conventional GCM assumes that the covariance matrix of repeated measurements is unstructured. Typically, GCM in the social sciences is normally used with a relatively small and equal number of time points for each subject.

The linear mixed-effects model represents a broader framework of modelling than the GCM. Typically, time-varying explanatory variables may also be included to explain within individual-level variation and the number of time points can vary across each subject. It can also provide a more flexible structure to define the covariance matrix, such as various forms of serial correlation within subjects over time. Therefore, GCM can be viewed as one type of model within linear mixed-effects modelling.

These two models therefore share a common approach to trajectory estimation—a mean trajectory for all cases is estimated through a polynomial function of time, and variability over cases is represented by random effects terms on the intercept, slope and higher order polynomial terms.

In this paper, the terminology of the linear mixed-effects (LME) model is preferred. The model can be defined as follows:

$$\begin{aligned} {Y}_{it}={\varvec{X}}_{it}^{'}{\varvec{\beta }} + {\varvec{Z}}_{it}^{'}{\varvec{u}}_{i} + \epsilon _{it}, \end{aligned}$$

(1)

where ${\varvec{X}}_{it}$ is a p-vector of fixed effects covariates, ${\varvec{\beta }}=(\beta _{1},\ldots ,\beta _{p})$ is a p-vector of unknown regression coefficients for the fixed effects. The fixed effects of ${\varvec{X}}_{it}$ can include both time varying and time constant covariates. ${\varvec{Z}}_{it}$ is a q-vector of random effects covariates, with a q-vector of unknown subject-specific coefficients ${\varvec{u}}_{i}=(u_{i1},\ldots ,u_{iq})$. It is common that ${\varvec{u}}_{i}=(u_{i1},u_{i2})$, where $u_{i1}$ is the random intercept and $u_{i2}$ is the random slope for time; with ${\varvec{u}}_{i}\sim MVN({\varvec{0}},{\varvec{V}})$ and with ${\varvec{V}}$ a two by two variance–covariance matrix of the ${\varvec{u}}_{i}$, with diagonal terms $var(u_{i1})= v_{11}$, and $var(u_{i2})=v_{22}$ , and an off-diagonal covariance $cov(u_{i1}, u_{i2})=v_{12}=v_{21}$. Hence, the two random terms have a correlation of $\frac{v_{12}}{\sqrt{ v_{11} v_{22}}}$. Finally, $\epsilon _{it}$ is the residual error term with $\epsilon _{it}\sim N(0, \tau ^{2})$.

However, the multivariate normality assumption on the random effects needs to be assessed when applying the mixed-effects modelling approach. Studies from Verbeke and Lesaffre [44] and Verbeke and Molenberghs [45] have pointed that lack of multivariate normality for the random effects can seriously influence estimates of the random effects and is very difficult to check. However, inference for the fixed effects is shown to be robust to the assumption of multivariate normally distributed errors, except in the special case when the error variance is correlated with a term representing interaction between a covariate and time [15]. Therefore, it will be important for us to examine whether heterogeneity exists in the underlying distribution of random effects estimated from the model.

2.2 Mixture modelling approach

The second common approach to trajectory estimation is through group-based trajectory modelling (GBTM) [29, 30], which is also known as latent class growth analysis (LCGA). This approach assumes that the population is composed of a mixture of distinct groups defined by their developmental trajectories. Thus, instead of assuming a multivariate normal distribution of random effects in the linear mixed-effects model, this approach uses a finite number of groups to approximate a continuous distribution of random effects. The groups can be considered to be latent classes. Each individual will have a probability of belonging to a specific trajectory class—thus variability between individuals is represented through the varying individual probabilities of class trajectory membership. Therefore, there is no specific inclusion of any underlying random effects, and homogeneity is assumed within each identified trajectory class. The terminology of group-based trajectory model (GBTM) is preferred in this paper.

An alternative way of thinking about the GBTM approach is to conceptualise it as a linear mixed-effects model but with a finite number of discrete random effects or mass points [18]. The unknown mass points interact with the growth factors of time, time-squared etc. to provide the equivalent of the random slopes in the mixed-effects model. This is sometimes known as the non-parametric maximum likelihood (NPML) approach to mixture modelling [1].

The model can be generalised from the linear mixed-effects model Eq. (1) in the following way. Assuming the existence of K classes, and given the latent class k with $k=1,\ldots ,K$, the model can be written as:

$$\begin{aligned} {Y}_{it|c_{i}=k}={\varvec{X}}_{1it}^{'}{\varvec{\beta }} + {\varvec{X}}_{2it}^{'}{\varvec{\alpha }}_{k}+ \epsilon _{it}, \end{aligned}$$

(2)

where ${\varvec{X}}_{1it}$ is a p-vector of common effect covariates, and ${\varvec{\beta }}=(\beta _{1},\ldots ,\beta _{p})$ is a p-vector of unknown regression coefficients that have common effects across all classes. Additionally, ${\varvec{X}}_{2it}$ is a q-vector of class-specific covariates, and ${\varvec{\alpha }}_{k}=(\alpha _{k1},\ldots ,\alpha _{kq})$ is a q-vector of unknown regression coefficients with the coefficients varying across classes. $\epsilon _{it}$ is the residual error term for each individual i at time t, where $\epsilon _{it}\sim N(0,\tau ^{2})$. Therefore, the residual variance $\tau ^{2}$ is assumed to have a common variance across different classes. However, this assumption can be extended by allowing class-specific residual variances ($\epsilon _{itk}$).

Thus, conceptually, there are now two types of covariates which can be included in the model. The first (${\varvec{\beta }}$) acts at the population level—the same as the fixed effect (${\varvec{\beta }}$) in Eq. (1), and assumes the effects are common for all individuals. The second (${\varvec{\alpha }}$) acts at the class-level, and so the effects here will vary across classes. Thus if time (slope) and powers of time are treated as class-specific covariates, then the shape of the developmental trajectory among each latent class of individuals will vary. In summary, the group-based trajectory approach can be more flexible as it allows risk factors (both time-varying and time-constant variables) to vary across each latent class of individuals. In the linear mixed-effects model, in contrast, there are no latent groups, and therefore varying effects of covariates cannot be estimated.

Implementations of this model for balanced data with the same number of time points per case are available through the SAS procedure PROC TRAJ [16], and via the MPLUS package, where the method is referred to as latent class growth analysis (LCGA). For unbalanced data (unequal number of repeated measurements within each observation), the lcmm package in R [37], the Latent Gold package [48] (using the latent regression option), and MPLUS (by fitting a two-level model with a latent factor though the command TWOLEVEL MIXTURE) are suitable options. The difference in terms of modelling assumptions between the lcmm package with the other two software packages is that both the Latent Gold package and MPLUS allow a class-specific residual variance ($\epsilon _{itk}$) if required, in contrast the lcmm package allows only a class-independent residual variance ($\epsilon _{it}$). All of these implementations allow covariates at both the class level and at the population level.

2.3 Mixtures of mixed models approach

While group-based trajectory modelling provides a framework to identify latent subpopulations and to estimate their distinct trajectories, the model assumes that each class-specific trajectory is a good representation for all members of its class. In other words, variation around the expected trajectory within a class is assumed to be zero. Additional models which we term “mixtures of mixed models” have therefore been proposed to relax this assumption.

The simplest extension is the heterogeneity model [44, 45] which is basically a form of finite mixture model [25, 43]. This model assumes that the population distribution of trajectories is composed of a discrete number of latent subpopulations, each following a conventional linear mixed-effects model. To avoid numerical convergence issues, their method assumes a common variance–covariance structure for the random effects in each class. In other words, the individuals’ variation around the expected trajectories within each class is the same.

A more flexible extension—the growth mixture model (GMM)—was proposed by Muthèn and Shedden [28], and relaxes the assumption of a common covariance matrix. For each class, a unique covariance matrix of growth factors and intercept can be estimated. Proust and Jacqmin-Gadda [36] have proposed an alternative terminology, the latent class linear mixed-effect model (LCLMM), which covers both the growth mixture model and the heterogeneity model when modelling continuous response variables.

Both methods can be thought either as an extension of the linear mixed-effects model to handle heterogeneous populations (with the number of classes $>$1), or as an extension of group-based trajectory modelling to account for correlation between repeated measures of the same subject and the variance within each subpopulation. The terminology of growth mixture model (GMM) is preferred in this paper.

The formal definition for GMM is as follows. Given the latent class k, the trajectory of the outcome is described using a linear mixed-effects model, and is given by:

$$\begin{aligned} Y_{it|c_{i}=k}={\varvec{X}}_{1it}^{'}{\varvec{\beta }} + {\varvec{X}}_{2it}^{'}{\varvec{\alpha }}_{k} + {\varvec{Z}}_{it}^{'}{\varvec{u}}_{i} + \epsilon _{it}. \end{aligned}$$

(3)

where the vectors of ${\varvec{X}}_{1it}$, ${\varvec{X}}_{2it}$, and ${\varvec{Z}}_{it}$ are defined as in Eq. 2. The term ${\varvec{u}}_{i}$ is a q-vector of the class-specific random effect coefficients, where the probability density of ${\varvec{u}}_{i}$ $Pr({\varvec{u}}_{i})=\sum _{k=1}^{K} \pi _{k}\Phi ({\varvec{\mu }}_{k}, {\varvec{V}}_{k})$, where ${\varvec{u}}_{i}$ is assumed to follow a mixture of K multivariate Gaussians with probabilities $\pi _{k}$ and with different means ${\varvec{\mu }}_{k}$ and covariance matrices ${\varvec{V}}_{k}$, with e.g. $\sum _{k=1}^{K}\pi _{k}{\varvec{\mu }}_{k}={\varvec{0}}$ for identifiability.¹ Therefore, when $k=1$, this model becomes the linear mixed-effects model (Eq. 1); alternatively, if the random effects are excluded (${\varvec{u}}_{ik}={\varvec{0}}$), it becomes the group-based trajectory model (Eq. 2).

A further extension to the GMM is to replace the assumption of multivariate normality of the class specific random effects above with a non-parametric alternative, estimating the random effects distributions within each class by a series of mass points with unknown masses and locations which are estimated from the data. This model is termed the non-parametric growth mixture model (NGMM) and has been considered by Kreuter and Muthèn [17] and Muthèn and Asparouhov [27].

Software implementations of the GMM model can be found in either MPLUS or in R. In MPLUS, both the MIXTURE and TWOLEVEL MIXTURE commands can be used. The MIXTURE command is for the analysis of balanced data. In contrast, the TWOLEVEL MIXTURE command can be used for unbalanced data with no time-dependent covariates. Additionally, an option to this command allows a single time-dependent covariate (through the command TWOLEVEL MIXTURE RANDOM). However, the setup of the coding is not straightforward. As an alternative, a more flexible implementation of GMM which allows both for unbalanced data and time-dependent covariates is provided by the lcmm package in R [37].

In this paper, R is our preferred software as it is more flexible for dealing with unbalanced data (see Appendix Table 5), also it allows both time-varying and time-constant variables. More importantly, the lcmm package provides a single framework for model comparison.

2.4 Other longitudinal latent variable models

Finally, in our review of longitudinal latent variable models for criminology, it is worth mentioning another class of models known as variously as latent transition [6], or latent Markov models [2]. These models assume that the profiles of the latent classes are constant over time, but that offenders will move or transit from one latent state to another at known points in time. Pennoni [33] has also suggested a local likelihood version of the latent class model which allows class membership to change at unknown time points. The term ‘hidden Markov model’ is also sometimes used when the focus is on long time series of observations and where the number of cases is small and the time sequence is long [2, p. 5]. These models have commonly been used in criminology to identify patterning in the types of offences committed and how offenders may transit from one type of offending to another as they age [3, 11]. Because the nature of these Markov models are rather different in concept to the models in Sects. 2.1–2.3 (which assume that class membership does not change over time), they will not be considered further in this paper.

2.5 Comparison studies

In comparing the above three approaches, there are two existing major studies.

Firstly, Kreuter and Muthèn [17] used four mixture modelling alternatives: the growth curve model, the group-based trajectory model (which they referred as latent class growth analysis), the growth mixture model (GMM) and the non-parametric GMM, to analyse conviction histories in two longitudinal criminological datasets (the Cambridge Study in Delinquent Development data and the Philadelphia cohort study data). They used both BIC and absolute standardised residuals for each response pattern as criteria for model selection. Their comparison methods focused on differences in overall fit, such as the average curve on convictions by age at offence, and significance of the age effects for each modelling approach. For the Cambridge data, they found that the four alternative models suggested no substantial differences in terms of number of classes, the characteristics of each class, the shape of curves over age and the proportion in each class. However, the four alternative approaches differed substantially for the Philadelphia cohort study. Their advice is essentially not to focus on one strategy, but to consider a variety of approaches before making inferences.

In contrast, the work of Bushway et al. [5] focused on examining and comparing estimates of the individual trajectories from the growth curve model (GCM) and the group-based trajectory models (GBTM) based on offending prevalence data from a criminal career and life course study (CCLS) in the Netherlands. In terms of their comparison method, they first estimated separate trajectories for each individual offender by a method they called the individual trajectory model (ITM). ITM simply takes a sequence of observed offences from each offender as a subsample and estimates the individual trajectory through a cubic regression function. They then computed Bayesian estimates of the individual trajectories from both the GCM and GBTM models. Finally they compared the Bayesian estimates to the estimates given by ITM using two statistical measures of bias: the signed difference (SDF) in the fitted probabilities of prevalence and the absolute value of the signed difference (ADF) of these probabilities, both of which were computed for each individual and at each age. Their comparison methods thus do not compare methods to the observed data, but rather assess bias towards ITM. They conclude that the average trajectories obtained from these three approaches are quite similar. On the other hand, for any given individual, these approaches tell very different stories, although GCM and GBTM are far more consistent relative to ITM.

Both of the above comparative studies also warn that care should be taken in assuming the existence of latent classes where none exist. Debates in this topic have been lively [32, 39, 40] and have been followed recently by a simulation study by Skarðhamar [41] suggesting that evidence for groups can be weak. However, Bushway et al. [5] also warn that GCM and GBTM may not detect classes with small numbers of cases which do not follow the general trend. Thus current practice suggests that mixture based models need to be used with care, but when well applied, can provide insight into underlying structure.

3 Conceptual issues in escalation

Liu et al. [21] reviewed a number of major studies on the topic of escalation from criminological literature, and found that mixed-effects models had not hitherto been used for modelling crime seriousness. Liu et al. [21] also identified various ways of measuring crime seriousness, discussed methodological approaches in assessing crime seriousness, and indicated that there were two types of temporal scales in crime escalation. This paper extends the work of Liu et al. [21], using an enlarged dataset and an additional covariate representing time spent in custody, but focuses instead on the use of the various forms of mixture models discussed above. Although the more detailed background information has been provided in our previous paper, we still need to briefly introduce how we measure escalation in seriousness.

Following Liu et al. [21], we used a recently developed measure of crime seriousness [12] based on court sentencing to assess escalation. This research developed a continuous score (score A in the report) for 405 separate offence codes, which, when logged, ranged from a score of 9.9 for murder down to a score of 0.0 for minor offences such as driving without lights. Any specific court conviction can consist of a number of offences brought to court at the same time. We took the seriousness of a court conviction to be the maximum seriousness score of the convicted offences at that court appearance. Thus we measure court conviction seriousness as the seriousness of the worst convicted offence rather than the total seriousness over all convicted offences in the court appearance. Liu et al. [21] makes the case as to why this is a sensible approach. Conceptually, we view offending history as consisting of major offences with other minor offences committed at the same time—for example, theft of a car and driving without insurance. The severity of the court conviction is therefore that of the major offence rather than the average of the severity of the major and associated minor offences.

4 Data and variables

4.1 Offenders index

Our dataset was based on that used by Liu et al. [21]. This was a 1 in 13 sample of all England and Wales offenders born in 1953 and followed through to 1999. The dataset contains details of all standard list offences for which an offender is found guilty and sentenced in a court in England and Wales—the 1953 birth cohort data will contain offending histories such as dates of conviction and types of offences, from age 10 (the age of criminal responsibility) up to age 46. Following Liu et al. [21] we removed offenders who had only a single court appearance, and also those who were convicted for the first time after age 37. The resulting dataset was larger than that used in [21] as improved matching of offences to seriousness scores meant that we discarded fewer unmatched cases. Our final dataset consisted of 4831 offenders with 4288 males (89 $\%$) and 543 females (11 $\%$).

Table 1 Offenders index 1953 birth cohort: number of court conviction appearances by gender from 1963 to 1999

Table 1 shows the characteristics of the final sample by gender and number of court conviction appearances. While the most common number of court appearances is two for both males and females, around 20 % of the sample have eight or more convictions.

4.2 Variables

We define a conviction occasion (sometimes shortened to ‘conviction’) to be a distinct court appearance where an offender has been found guilty of one or more offences. Thus, an offender with two conviction occasions will have two separate court convictions at different dates.

As described earlier, we define the seriousness of a conviction to be the maximum seriousness score for all offences at that conviction. We then model the individual sequence of seriousness scores over convictions. The observed sequences of seriousness in crime from the first conviction are longitudinal sequences measured at each conviction number.

We allow for both time varying and time constant covariates in our analysis. We include the following time varying covariates.

• Order of conviction This is the number of current and prior conviction occasions. This provides a partial indication of the effect of criminal justice experience on escalation.

• Age at conviction This is also a time varying covariate, and assesses the effect of maturation on escalation. It is measured at the date of sentence.

• Number of offences This is the number of separate offences at each conviction occasion. Liu et al. [21] showed that the expected maximum seriousness score for a conviction occasion increases with the number of offences at that occasion. A log transformation of this variable was used.

• Custodial sentence This is the cumulative custodial sentence length (in years) up but not including the current conviction occasion for each offender. This is a proxy measure for the time spent in prison; in general offenders serve between 40 and 50 % of sentences awarded [42].

We also include two time-constant covariates: gender (coded (1) male and (2) female) and age at onset (the age at the first conviction occasion).

5 Assessing the nature of heterogeneity among offenders

We now return to the models outlined in Sect. 2, and discuss how we might choose between the various alternatives. The simplest approach—the linear mixed-effects model—is based on the assumption of multivariate normality of the random effects, but [44] state that violation of this assumption may seriously influence the parameter estimates. Therefore, in this section, prior to any detailed modelling, we will be assessing this assumption through graphical diagnostics from the fitted of a basic linear mixed-effects model (including both random intercept and slope as well as controlling for the other variables listed in Sect. 4.2 ²).

In testing the multivariate normality of the estimated random effects ($\hat{u}_{i1}$ and $\hat{u}_{i2}$) we use a joint test proposed by [13], which combines two graphical methods.

The first graphical method is a correlation scatterplot of means against variances which are computed from the multivariate data, the second method is a Q–Q plot of Mahalanobis $d^{2}$ and Chi-square distribution quantiles. The joint visual examination of the two graphs can provide a more robust test on detecting non-multivariate normality in situations when one graph fails to detect but the other does. For example, the correlation scatterplot has power to detect non-normality which the Q–Q plot cannot detect for simulated skewed normally distributed data. In contrast, for data which comes from a mixture of normals with the same mean but heterogeneous variances, the Q–Q plot is likely to detect non-normality, whereas the correlation scatterplot supports normality. Therefore, the combination of these two tests are powerful graphical tools to detect non-normality.

We first define the correlation scatterplot. Let ${\varvec{X}}_{1},\ldots ,{\varvec{X}}_{n}$ be n i.i.d. random variables, where ${\varvec{X}}_{j}=(x_{j1},\ldots ,x_{jp})$ is a p-vector of realisations, with $j=1,\ldots ,n$. In this study, n is the total number of offenders, and $p=2$ representing the estimated random intercept and estimated random slope for each offender. Let $\overline{\varvec{X}}=(1/n)\sum _{j=1}^{n}{\varvec{X}}_{j}$, where $\overline{\varvec{X}}$ is a p-vector of means $\overline{\varvec{X}}=(\overline{x}_{1},\ldots ,\overline{x}_{p})$ and ${\varvec{S}}=(1/n)\sum _{j=1}^{n}\sum ({\varvec{X}}_{j}-\overline{\varvec{X}})({\varvec{X}}_{j}-\overline{\varvec{X}})^{-1}$, with ${\varvec{S}}=(s_{1},\ldots ,s_{p})$. If the n random variables are normally distributed then the value of ${\varvec{L}}^{'}\overline{{\varvec{X}}}$ and ${\varvec{L}}{'}{\varvec{S}}{\varvec{L}}$ are independent [22]. Normally, either ${\varvec{L}}={\varvec{1}}$ (i.e. a sum) or ${\varvec{L}}={\varvec{1/p}}$ (i.e. an average).

The ${\varvec{X}}_{j}$ are multivariate normally distributed if and only if ${\varvec{L}}^{'}\overline{\varvec{X}}$ and ${\varvec{L}}{'}{\varvec{S}}{\varvec{L}}$ are independent. Therefore, we can bootstrap M samples of realisations from ${\varvec{X}}_{1},\ldots ,{\varvec{X}}_{n}$ to compute M paired values of ${\varvec{L}}^{'}\overline{\varvec{X}}$ and ${\varvec{L}}{'}{\varvec{S}}{\varvec{L}}$. If ${\varvec{X}}_{j}$ is normally distributed then the scatterplot of ${\varvec{L}}^{'}\overline{\varvec{X}}$ against ${\varvec{L}}{'}{\varvec{S}}{\varvec{L}}$ should have no pattern of correlation.

The second graphical tool is the Q–Q plot of Mahalanobis distance $d^{2}$ [23] and is given by:

$$\begin{aligned} d_{j}^{2}=({\varvec{X}}_{j}-\overline{\varvec{X}})^{'} {\varvec{S}}^{-1} ({\varvec{X}}_{j}-\overline{\varvec{X}}). \end{aligned}$$

(4)

Given that ${\varvec{X}}_{j}$ is i.i.d. normally distributed, then the $d^{2}$ measures are Chi-square distributed. Therefore, the basic idea of this Q–Q plot of the distance $d^{2}$ is to display the graph of the Chi-square distribution quantiles $Q_{p}(\frac{j}{n+1})$ against $d_{j}^{2}$ which should display a approximately straight line on the diagonal if the data is multivariate normal.

These two graphical methods are applied to the data in this study, in order to test the multivariate normality assumption on the distribution of the estimated random slope (the order of conviction) and the random intercept in the linear mixed-effects model. This model controls for a range of fixed effect covariates - namely, age with one breakpoint (at ages 18), gender, number of offences at each conviction occasion (log transformed), and cumulative sentence length. 400 bootstrapped samples of the estimated random effects ($\hat{u}_{i1}$ and $\hat{u}_{i2}$) which were obtained from this mixed-effects model, and ${\varvec{L}}^{'}\overline{\varvec{X}}$ and ${\varvec{L}}{'}{\varvec{S}}{\varvec{L}}$ were computed, taking $L={\varvec{1}}$. The 400 paired statistics are graphed in Fig. 1a. It clearly suggests that there is a strong linear correlation between the means (${\varvec{L}}^{'}\overline{\varvec{X}}$) and variances (${\varvec{L}}{'}{\varvec{S}}{\varvec{L}}$) of the joint distribution of estimated random intercept and slope. As the variance is increasing with the mean, the plot rejects the assumption of multivariate normality. Figure 1b shows the Malahanobis Q–Q plot. It shows a curvilinear relationship rather than the expected straight line, which suggests that heterogeneity of the random effects is present with structure arising from a mixture of normals [13].

In summary, both the scatterplot and the Q–Q plot suggest that the joint distribution of estimated random intercept and slope does not follow a bivariate normal. However, a note of warning is needed. Work by Verbeke and Lesaffre [44] states that the test of heterogeneity on random effects is fundamentally difficult as both the random intercept and slopes are already estimated under the multivariate normality assumption. Therefore, the estimates of the random effects may be biased if this assumption is wrong. In addition, Verbeke and Molenberghs [45] suggests that Q–Q plots of the type suggested by Lange and Ryan [20] cannot differentiate a wrong distributional assumption for the random effects or the error terms from a wrong choice of covariates. However, Eberly and Thacheray [8] suggests that in the presence of a correctly specified mean model, the normality test of Lange and Ryan [20] detected non-normal random effect distributions with reasonable power that increased as the non-normality grew more pronounced. In the presence of a misspecified mean model, they go on to state that such plots are more useful as a general diagnostic procedure. Our conclusion is that there is sufficient evidence from these plots to justify the investigation of heterogeneity in more detail.

Fig. 1

a The scatterplot for ${\varvec{L}}^{'}\overline{\varvec{X}}$ vs. ${\varvec{L}}{'}{\varvec{S}}{\varvec{L}}$ of 400 bootstrapping samples from estimated random effects. b Q–Q plot of Mahalanobis $D^{2}$ vs. quantiles of $\chi _{2}^{2}$

Therefore, in the next stage, it is necessary to apply both types of mixture modelling approaches to investigate the heterogeneity in the population of offenders and to identify where possible potential latent types of offender in terms of their development of seriousness in crime.

6 Statistical modelling results

Our model-fitting strategy for mixture models is developed as follows. Firstly, we need to identify the effect of covariates as either class-specific (with different parameter estimates in each class) or class independent effects with the same estimates in each class. Our primary interest in this analysis is in identifying any potential differences in the effects of age at conviction and criminal justice experience between classes, and we therefore make the age and the order of conviction class-specific covariates, and make the number of offences, gender and custodial sentence length all class-independent covariates.

Secondly, the three statistical models described in Sect. 2 are applied, using the covariates described previously, trying two, three and four class models for the mixture based approaches. In terms of their goodness-of-fit, the three statistical models of their AIC/BIC are compared. The result of three-class GMM model which is preferred as the final model will be described.

6.1 Choice of non-linear effect

We propose that the effect of age or conviction order may be non-linear. For the effect of conviction order, a quadratic term is examined through the three statistical models. However, the quadratic term of conviction order is not significant (with p value $>$0.05) in any of the three statistical models. Therefore, there is no evidence of non-linearity over convictions.

For the effect of age, we used a breakpoint model with one breakpoint. This will give a flexible form of non-linearity for age which is consistent with earlier work on this dataset [21]. The breakpoint model for age assumes that the effect of age has different slopes for different values of age, with the age effect piece-wise linear and continuous. Such modelling terms are sometimes known as segmented regression model terms [26]. We estimate the breakpoint by a grid-point search, taking values of the breakpoint from 12 to 45 at 1 year intervals and taking that value of the breakpoint that minimises AIC or BIC. For the one breakpoint, the break was estimated at age 18.

6.2 Three statistical models for criminal career escalation

The three types of trajectory model each controlled for the class-independent covariates of gender, sentence length and the log of the number of offences at each conviction occasion, and the class-specific effects of order of conviction and age at conviction with one breakpoint (at age 18). The AIC and BIC values of the LME model, the GBTM with two and three classes, and the GMM with two and three class solutions are compared in Table 2.

Table 2 AIC and BIC values for various models by the LME model, the GBTM with two/three classes and the GMM with two/three classes

Table 2 clearly shows that both the GBTM and the GMM with two or three classes have smaller BICs/AICs than the LME model, indicating better goodness-of-fit by using a mixture approach than the straightforward LME model. Moreover, in terms of the difference between the two mixture modelling approaches, the GMM two-class model has smaller BIC/AIC (48,515.76/48,405.55) than the GBTM two-class model (49,251.88/49,167.61), and similarly the GMM three-class model also has smaller BIC/AIC (48,126.13/47,977.03) than the GBTM three-class model (48,604.29/48,487.60).

A model with a four-class solution has also been attempted by both GMM and GBTM. Although both the AIC and BIC are smaller, suggesting a better goodness-of-fit, the interpretation of the class-specific parameter estimates are far less clear. As we are concerned about interpretability, we do not consider the four-class solutions further.

Table 3 Growth mixture model with three-class solution

Table 3 shows the parameter estimates of the final growth mixture model for the three-class solution, which was computed through the lcmm package in R. In this particular package, Proust-Lima and Liquet [37] directly maximise the observed log-likelihood using a modified Marquardt optimisation algorithm [24], and the standard errors of the covariates are directly computed using the inverse of the observed Hessian matrix.

In Table 3, the class-independent effects show that females have a significantly lower crime seriousness score compared to males ($-$0.123) and that the effect of time spent in custody is small and non-significant ($-$0.002). The larger the number of offences within each conviction occasion the more likely the conviction is to be serious.

There are three classes of offenders, consisting of a large first class with 92 % of offenders (class one), and two smaller classes each with 4 % of offenders. Note that the percentages of class membership which are presented in this table are the averages of the estimated posterior class probabilities³ of each individual.

Class one consists of the majority of offenders. The intercept of 3.926 lies below the other two intercepts. Members of this class are generally de-escalating with age and escalating with their experience, although the age effect before age 18 ($-$0.002) is not statistically significant. The coefficients of the order of conviction (0.010) and the age at conviction after age 17 ($-$0.012) are very similar but with different signs. Therefore, the contradictory effects highlight that offenders with one conviction a year on average will show de-escalation, whereas those with a large number of convictions a year will show escalation. The variances of the random effects in this class are also small (0.039 and 0.012 for the intercept and slope respectively).

The second class is formed of a small subset of offenders (4 %). The estimate for the intercept lies between the other two intercepts, which gives the mean seriousness level at age 10 is 5.532. De-escalation with age dominates the effect of escalating with their experience, especially before age 18. For those aged 18 and older, again the coefficients of age ($-$0.027) and order of conviction (0.027) are having the same effect size but with different signs, showing increasing escalation with the number of distinct convictions. The variation among individual’s intercepts (0.130) and slopes (0.041) is larger than the first class.

The third class contains another 4 % of offenders, this small subset of offenders who have a very high estimate of seriousness at age 10 (8.210). The de-escalation is strongest up to age 17 ($-$0.584), and then becomes relative smaller but positive (0.041) for those aged 18 and older. However, the overall effect of age shows a strong de-escalation effect. The effect of experience (the order of conviction) is not significant. The model estimates for the third class show very interesting findings. Although class three contains 4 % of offenders, this group of offenders shows substantial variation within offenders, with variances of 3.990 and 1.261 for the random intercept and random slope respectively.

It is worth highlighting that a model with a four-class solution is basically splitting class three into two even smaller groups with very similar directional effects of the class-specific estimates in the two new groups, but with different magnitudes. Since the dataset used in this study is sizeable, then the AIC and BIC may not reach their minima until a large number of classes have been fitted. Recent guidance suggests that it is important to stop at a meaningful model with a smaller number of classes rather than searching for the best AIC/BIC with larger number of classes which is less interpretable [32]. Therefore, the GMM three-class model is preferred in this paper.

7 Comparison of the three statistical models

In this section, further examination of differences among the three statistical methodologies in terms of their goodness-of-fit are needed. Firstly, the goodness-of-fit of the three models (the LME model, the GBTM three-class model, the GMM three-class model) will be assessed through graphical tools by comparing the differences between the observed scores and the estimated scores at both marginal-level and individual cases. Then diagnostic measures such as AIC/BIC, and the Euclidean distance are used to compare the three models.

Fig. 2

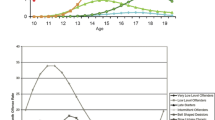
Comparison of the observed marginal seriousness scores and the estimated mean scores for the three models plotted against age at conviction. Offenders have been grouped into three classes by assigned class membership according to Table 3. Plot a for offenders who are classified in class 1; plot b for offenders who are classified in class 2; plot c for offenders who are classified in class 3

7.1 Graphical goodness-of-fit at marginal-level

We focus first of all on the marginal goodness-of-fit for all three statistical models within each class. The class membership which has been estimated from the three-class GMM model (Table 3) is assigned to each individual offender. The marginal means of observed seriousness scores and predicted scores from the LME model, the GBTM approach, the GMM approach are computed for each age of conviction and for each of the three classes. The reason to look at the marginal seriousness scores by age at conviction is to be able to present graphs of the marginal crime seriousness effects within the three groups by age, as the age escalation effects differ strongly between the groups. The plots of the observed scores and the fitted scores against age at conviction are shown in Fig. 2. It is important to clarify that in Fig. 2 different offenders will contribute to each observed mean point, as each offender has a different set of conviction ages.

Firstly, the character of each class is examined by looking at the observed mean scores. It is clearly shown that class 1—Plot (a)—indicates that the majority (92 %) of offenders appear to stay relatively constant in their crime severity, but with a small tendency to de-escalate with increasing age. Class two consists of 4 % of offenders who, if they offend in early adolescence, will start with a high serious offence, then de-escalate quickly between the ages of 14–16 followed by a gentle de-escalation at later ages. In contrast, class three shows remarkable diversity in crime seriousness especially between age 10–16 and from age 35 onwards. This group seems to consist of groups of offenders either involved with serious crimes at earlier age (between age 10–15), or late onset offenders with quite serious offences, or even those offenders who were most delinquent with high serious crimes at both an early age and from the late 30s onwards.

Secondly, the differences in fitted marginal means among the fitted three models are examined for each class. There is hardly any difference in class one between the three models. However, for the more complex offending patterns found in class two and class three, the differences among the three methods are starting to show. On average, for both class two and class three, estimates from the GMM appear to capture the more serious crimes more accurately and also can fit the observed mean more smoothly than the GBTM, and certainly better than the LME model, although the estimates from the GBTM also follow the mean observed trajectories well compared with the mean estimated scores from the LME model.

Fig. 3

Comparison of the observed seriousness scores and estimated scores for the three models for two individual offenders with varying number of convictions (labelled with offenders’ identification number) in class 1 (plots a, b), 2 (plots c, d) and 3 (plots e, f) (Table 3), plotted against order of conviction but labelled with age at conviction

7.2 Graphical goodness-of-fit for individual cases

From looking at Fig. 2, a clear story of the characteristics of each class has been observed, and some general marginal goodness-of-fit diagnostics have been presented. Therefore, the next step is to examine the individual offenders’ trajectories in crime seriousness and their fitted values over conviction occasions. The plots are prepared as follows. First a random sample of around 100 individuals within each class is taken. Then, within each class, two offenders were selected who represent some common offending patterns from these samples, and also represent the range of total number of convictions. For an individual offender, the sequence of seriousness score in crimes is presented by the order of conviction but labelled with the age at conviction (on the x-axis). Graphical output from class one is shown in Fig. 3 plots (a) and (b), plots (c) and (d) show cases from class two, and plots (e) and (f) show cases from class three.

First, examination of the two individual offenders from class one is undertaken (plots (a) and (b) in Fig. 3). As described before, class one consists of the majority of offenders who are relatively stable in their seriousness in crime. In comparing the fitted models for the two offenders, similar findings are found to those given by the marginal plot diagnostics in Fig. 2a—namely that the three models give very similar estimates. The plot (b) (offender 771101) indicates that complex offending patterns will cause difficulty for any model. Basically, offender 771101 is active in offending from age 12 to 40, with the seriousness of most of the offending at about 4.0 but with a few irregular episodes of high seriousness offending in between. The sudden changes of severity in such a case cannot be captured accurately by any of the three models. It is possible that this type of offending may need its own small latent class which is not represented in the three group solution.

Two individual offenders from the second class (class two) are now shown in plots (c) and (d) in Fig. 3. As mentioned previously, class two consists of offenders with median seriousness at early ages but de-escalating with increasing age, and also escalating with increasing experience. For this class, estimates from both the GMM and the GBTM are a better fit than the LME model.

Finally, two offenders from class three are examined in plots (e) and (f). Offenders in this class are general with high seriousness at early ages and also more diverse in terms of their range of crime seriousness. In particular, the GMM captures the high seriousness at the beginning of each trajectory better than the other two models, and adjusts better for changing crime severity. Thus, the conclusion is the same as for class two, with the GMM method performing more sensitively than the other two models. For this particular group of offenders, the common analytical issue is the sudden occurrence of the occasional high serious crime as part of the criminal history which occur more often in this class than for the offenders in the other two classes. This is represented in the model by the high estimates of $v_{11}$ and $v_{22}$.

7.3 Comparison of goodness-of-fit by diagnostic measures

The diagnostic measure which is used to examine the goodness-of-fit is the Euclidean distance. The Euclidean distance is a mathematical term which is used to measure the “ordinary” distance between two points or sequences, and is defined as follows:

$$\begin{aligned} D_{ik}({\varvec{y}}_{ik}, {\hat{\varvec{y}}}_{ik})= & {} \sqrt{(y_{ik1}-\hat{y}_{ik1})^{2}+\cdots +(y_{ikn_{i}}-\hat{y}_{ikn_{i}})^{2}}, \end{aligned}$$

(5)

where ${\varvec{y}}_{ik}$ is a vector of an observed sequence of seriousness scores for offender i assigned to class k, with length $n_{i}$, and the vector of estimated scores is given by $\hat{\varvec{y}}_{ik}$. The average Euclidean distances by class (assigned membership according to Table 3) for each fitted model are then shown in Table 4.

Table 4 The average Euclidean distance measures for the LME model, the GBTM with three classes and the GMM with three classes

Firstly, class one shows that the Euclidean distance measurements from LME and GBTM models are very similar. In fact, the GBTM three-class model has a slightly greater average distance than the LME model, indicating the LME model fits the data slightly better the GBTM for class one. In general, out of the three models, the GMM three-class model fits all three classes the best, with the smallest distance for class one (0.788), class two (2.933), and class three (1.600). In addition, the two mixture modelling approaches (the GBTM three-class and the GMM three-class) have improved the goodness-of-fit substantially for class three.

8 Conclusions

This study has attempted to assess the existence of heterogeneity in the population of offenders in terms of their seriousness of crimes. Three modelling approaches are used; the linear mixed effect model, the group-based trajectory model and the growth mixture model. These approaches all suggest that male offenders on average are more likely to be convicted of more serious offences than female offenders; in addition the larger the number of offences involved within a single conviction occasion the higher the seriousness level in this conviction occasion will be. In contrast, the effect of custodial sentence varies from model to model. However, models with a statistically significant custodial sentence effect all show a small and positive effect, indicating that offenders escalate with increasing time spent in prison, but the effects are small, with changes of 0.01 of a seriousness score point per year or less. For the preferred GMM three-class model the effect of length of custodial sentence is not significant.

This work contributes to some important policy implications on how to identify and selectively target a small group of potentially dangerous offenders. In general, most offenders in this sample are more likely to be involved with similar types of crimes with similar crime seriousness as this study showed. Moreover, offenders who started with a relatively high seriousness crime at an early age have a tendency to de-escalate with age. For those offenders, policy implications are clear: it is important for criminal justice professionals to focus on persistent offenders—those with large numbers of convictions in a short period of time—as these individuals are most likely to escalate. This work importantly also identifies a group of offenders (around 4 %) with high diversity and high seriousness in crime. For this type of offender, monitoring could be worthwhile as they are generalists in offending and more likely to be involved in occasional high seriousness crimes in between other offences compared to the other two types of offenders. They can be identified by early offending which escalates rapidly in seriousness at young age.

There is still some future work needed to be carried out based on this current study. For example, this work compared the three modelling approaches statistically and identified three types of offender according to their offending patterns. Offenders belonging to each class may share some common crime patterns in terms of the specific types of offences involved. Therefore, a future study can focus on the examination of each class of offender by considering various features of their criminal career, such as age at onset, type of first crime, sequence of crimes, length of criminal career, and diversity of offending. The other potential area of development would be the need to develop better searching methods for a model with a larger number of classes (perhaps allowing the detection of classes with a small number of cases).

Appendix

See Table 5.

Table 5 List of terminologies in mixed-effects and mixture modelling, and the available software for the analysis of a continuous response variable