Robust Cislunar Trajectory Optimization in the Presence of Stochastic Errors

Abstract

The focus of this research is the optimization of impulsive maneuvers in the circular restricted three body problem with stochastic error sources. Two and three impulse transfer trajectories with corrective maneuvers are designed to minimize an upper statistical bound for total $\Delta V$, including the sum of nominal impulsive $\Delta V$ plus the 3$\sigma$ upper bound for corrections. Error sources include an initial state dispersion, maneuver execution error, and random white disturbances modeled as process noise. Direct optimization is performed via nonlinear programming. At each step in the nonlinear program, the optimal location and number of trajectory correction maneuvers (TCM) is determined, simultaneously satisfying a set of position dispersion constraints along the trajectory. Analytical gradients of the nominal maneuver magnitude and trace of the TCM covariance are provided to the nonlinear program to avoid finite differencing and associated numerical errors. Partial derivatives of the TCM covariance require the propagation of second-order state transition tensors. This work incorporates process noise into the optimization problem by propagating the effect of the accumulated process noise covariance. As a result, populating analytical gradients requires the partial derivative of the accumulated process noise covariance, called the accumulated process noise covariance state sensitivity tensor, which is propagated similar to state transition tensors. Robust trajectory scenarios analyzed include a three impulse trajectory from low-Earth orbit (LEO) to a near-rectilinear halo orbit (NRHO), and a two impulse NRHO rendezvous.

1 Introduction

Optimization of deterministic impulsive maneuvers has been a topic of extensive study. Conway presents a thorough history and overview [1] of early influential works in trajectory optimization [2,3,4,5,6]. Indirect optimization formed a large portion of the early trajectory optimization approaches prior to the advance of significant personal computing power. Betts presents a survey of numerical methods for trajectory optimization to include nonlinear programming, optimal control problems, numerical analysis, shooting methods, transcription, dynamic programming, and genetic algorithms [7]. Trajectory optimization algorithms that connect multiple events via segments and incorporate node flexibility enable optimization trades across an entire mission [8, 9]. In two works by Ocampo forming the foundation for the COPERNICUS trajectory design tool [10], multiple impulses are simultaneously minimized while satisfying segment connectivity constraints as well as other constraint options [11, 12].

In some cases, a deterministically planned trajectory may appear to provide a minimum fuel path to a target. However, the same trajectory may exhibit sensitivities that result in excessively expensive corrective maneuvers if not properly planned. On the other hand, robust trajectories that take into account uncertainties may require more nominal energy to embark upon, but reduce the cost corrections. The search for a robust trajectory has taken numerous forms. In one of the earlier examples, Nishimura and Pfeiffer utilize a dynamic programming approach to develop trajectories with stochastic error sources that constrain trajectory corrections within a magnitude threshold and minimize dispersions at a target [13]. Jin et al. embedded a linear covariance analysis tool within a genetic algorithm to identify robust trajectories for rendezvous and proximity operations (RPO) that minimize nominal $\Delta V$ plus the sum of corrections [14]. Oguri and McMahon optimize trajectories in the presence of stochastic error sources to maximize the likelihood of a spacecraft’s ability to meet its mission operating parameters [15]. Geller et al. incorporate robustness into linear covariance analysis by triggering terminal RPO maneuvers with an event occurrence rather than at a specific time [16]. Jenson and Scheeres approach a robust optimization problem with maneuver execution error using indirect methods [17]. Boone and McMahon perform optimization of a nonlinear system with impulsive controls and stochastic constraints [18]. Greco et al. optimize interplanetary transfers under uncertainty by abandoning the concept of a reference trajectory and errors with respect to the reference in favor of a more general framework where each trajectory is a sample from a probability density function [19].

This paper begins by presenting supporting theory for the dynamical system, for the propagation of state transition matrices (STM) and second-order state transition tensors (STT), and a deterministic multiple-segment trajectory design problem formulation with deterministic cost and constraints (Sect. 2). Next, the theory for stochastic analysis along a nominal (mean) deterministic trajectory to manage a state dispersion via trajectory correction maneuvers (TCM) is presented (Sect. 3). The error sources incorporated are an initial state dispersion, maneuver execution error, and process noise. A stochastic constraint on the magnitude of the position dispersion at trajectory events and a total stochastic cost are introduced. A large part of the robust trajectory design method presented in this paper is designed to improve algorithm convergence. This includes utilizing analytical gradients of the stochastic cost and analytical gradients of the accumulated process noise covariance; important aspects of their derivation are presented in Appendix A. Utilizing the stochastic theory presented, Sect. 4 first shows a method to optimize the number and location of TCMs along a nominal trajectory to minimize the $3\sigma$ TCM cost and meet the position dispersion constraints. Next, a series of comparisons are made to demonstrate the sensitivity of the optimal TCM solution to variations in the magnitude of error sources. Section 5 presents a robust trajectory design method by combining multiple-segment trajectory design and TCM optimization. The robust cost that is minimized includes the deterministic $\Delta V$ plus the $3\sigma$ TCM cost to represent a total $\Delta V$ upper bound. Robust trajectory results appear in Sect. 6. Concluding remarks are made in Sect. 8.

In a previous work by the authors of this work, a robust trajectory design method was presented that incorporated a single optimal TCM along a nominal trajectory [20]. Results included two-body trajectories robust to initial state dispersion only. Similarities between this work and the prior work include the optimization of nominal cost plus a stochastic cost via nonlinear programming, multiple segment trajectory design, the use of STTs in the development of analytical gradients, and the incorporation of an initial state dispersion as an error source. This work represents numerous advancements and evolutions to the previous design method through the additional error sources incorporated, the incorporation and optimization of multiple TCMs, the derivation of the gradient of multiple TCMs, and the discovery of a robust LEO to powered lunar flyby to NRHO insertion trajectory with promising characteristics. Specifically, novel contributions of this work include:

• The simultaneous optimization of deterministic cost plus a stochastic cost estimate through the optimization of a nominal trajectory and TCM set via a nonlinear program.

• The fast TCM optimization method presented in Sect. 4.

• The propagation and manipulation of the QBM history alongside STM for incorporation in linear covariance analysis.

• The propagation and manipulation of the QBT history alongside the QBM for use in the derivation of the QBM analytical gradients.

• The development of a trajectory that could save up to 77.8 m/s in total upper bound maneuver requirement for a spacecraft traveling from LEO to the 9:2 synodic ratio L2 southern NRHO.

2 Supporting Theory

2.1 Dynamical System

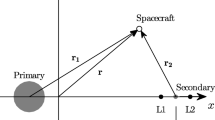
The Circular Restricted Three Body Problem (CR3BP) serves as the dynamical system for modeling a massless spacecraft’s motion (the third body) in the Earth-Moon system (the first and second bodies). Another CR3BP simplification is the circular motion of each of the two primary bodies, modeled as point masses, about their mutual barycenter. The coordinate frame used to describe the spacecraft’s motion rotates with the Earth-Moon system about the origin at the barycenter, the x axis pointing toward the moon and the z axis being the axis of rotation. The system’s units (distance and time) are generally nondimensionalized. Distance is scaled such that the distance between the Earth and the Moon is equal to 1 unit of nondimensional distance. Time is scaled by the system mean motion n such that the angular velocity of the system is 1 [21]:

$$\begin{aligned} n=\sqrt{\frac{G(m_{1}+m_{2})}{a^{3}}} \end{aligned}$$

(1)

The system mass parameter $\mu$ is defined as the ratio of the second body’s mass (or gravitational parameter) to total system mass:

$$\begin{aligned} \mu =\frac{\mu _{2}}{\mu _{1}+\mu _{2}} \end{aligned}$$

(2)

For the Earth–Moon system, $\mu =0.01215$. As a result, the position of the Earth is $(-\mu ,0,0)$ and the position of the Moon is $(1-\mu ,0,0)$. In the rotating frame, the equations defining the motion of the spacecraft are:

$$\begin{aligned} \ddot{x}= & {} 2{\dot{y}}+\frac{\partial U}{\partial x} \end{aligned}$$

(3)

$$\begin{aligned} \ddot{y}= & {} -2{\dot{x}}+\frac{\partial U}{\partial y} \end{aligned}$$

(4)

$$\begin{aligned} \ddot{z}= & {} \frac{\partial U}{\partial z} \end{aligned}$$

(5)

where U is the pseudo-potential function

$$\begin{aligned} U=\frac{1}{2}\left( x^{2}+y^{2}\right) +\frac{1-\mu }{r_{1}}+\frac{\mu }{r_{2}} \end{aligned}$$

(6)

and $r_{1}$ and $r_{2}$ are the distances from the spacecraft to primaries 1 and 2 respectively:

$$\begin{aligned} r_{1}= & {} \sqrt{\left( x+\mu \right) ^{2}+y^{2}+z^{2}} \end{aligned}$$

(7)

$$\begin{aligned} r_{2}= & {} \sqrt{\left( x-1+\mu \right) ^{2}+y^{2}+z^{2}} \end{aligned}$$

(8)

2.2 First-order Dynamics

The six-dimensional spacecraft state represents the spacecraft position and velocity along a nominal trajectory, $\varvec{x}=\left[ \begin{array}{cccccc} x&y&z&{\dot{x}}&{\dot{y}}&{\dot{z}}\end{array}\right]$. Error sources create a dispersion, $\delta \varvec{x}$, with respect to the nominal trajectory $\varvec{x}_{N}$. The dynamics of the dispersed state are a function of the nominal state and the dispersion:

$$\begin{aligned} \dot{\varvec{x}}=\dot{\varvec{x}}_{N}+\delta \dot{\varvec{x}}=\varvec{f}\left( \varvec{x}+\delta \varvec{x}\right) . \end{aligned}$$

(9)

A first-order Taylor series expansion (TSE) along the nominal trajectory provides an estimate for the dispersed state at a future time:

$$\begin{aligned} \varvec{x}\left( t\right) \approx \varvec{x}_{N}\left( t\right) +\Phi \left( t,t_{0}\right) \delta \varvec{x}\left( t_{0}\right) \end{aligned}$$

(10)

where $\Phi \left( t,t_{0}\right)$ is the state transition matrix (STM), which contains the first-order dynamics between $t_{0}$ and t along the reference trajectory [22]: $\Phi (t,t_{0})=\frac{\partial \varvec{x}(t)}{\partial \varvec{x}(t_{0})}$. The linear differential equations for propagating the STM are

$$\begin{aligned} {\dot{\Phi }}\left( t,t_{0}\right) =F\left( \varvec{x}_{N}\right) \Phi \left( t,t_{0}\right) \end{aligned}$$

(11)

where F represents the Jacobian

$$\begin{aligned} F\left( \varvec{x}_{N}\right) =\frac{\partial \varvec{f}}{\partial \varvec{x}}\bigg |_{\varvec{x}_{N}}. \end{aligned}$$

(12)

2.3 Second-order Dynamics

The second-order STT derivation begins in a similar way that the (first-order) STM does, via a TSE corresponding to the desired order. This derivation follows the work by Park and Scheeres [23]. The second-order TSE of the state dispersion at a future time is

$$\begin{aligned} \delta \varvec{x}_{i}(t)\approx \Phi _{i,p}\delta \varvec{x}_{p}^{0}+\frac{1}{2}\Phi _{i,pq}\delta \varvec{x}_{p}^{0}\delta \varvec{x}_{q}^{0}, \end{aligned}$$

(13)

where i, p, and q are standard index notation subscripts; indices following commas identify a partial derivative index. $\delta \varvec{x}_{p}^{0}$ and $\delta \varvec{x}_{q}^{0}$ are both the same values numerically with the index summation operation applied to different indices. $\Phi _{i,pq}$ represents the second-order STT. The second-order TSE of the system dynamics is

$$\begin{aligned} \delta \dot{\varvec{x}}_{i}(t)\approx F_{i,p}\delta \varvec{x}_{p}+\frac{1}{2}F_{i,pq}\delta \varvec{x}_{p}\delta \varvec{x}_{q} \end{aligned}$$

(14)

where $F_{i,p}$ is equivalent to Eq. 12 and $F_{i,pq}$ is the second partial derivative of the system dynamics:

$$\begin{aligned} F_{i,pq}=\frac{\partial F_{i,p}(\varvec{x})}{\partial \varvec{x}_{q}} \end{aligned}$$

(15)

Substituting Eq. 13 into Eq. 14 (and appropriately adjusting indices) results in

$$\begin{aligned} \delta \dot{\varvec{x}}_{i}(t)&=F_{i,m}\left( \Phi _{m,p}\delta \varvec{x}_{p}^{0}+\frac{1}{2}\Phi _{m,pq}\delta \varvec{x}_{p}^{0}\delta \varvec{x}_{q}^{0}\right) \nonumber \\&\quad +\frac{1}{2}F_{i,mn}\left( \Phi _{m,p}\delta \varvec{x}_{p}^{0}+\frac{1}{2}\Phi _{m,pq}\delta \varvec{x}_{p}^{0}\delta \varvec{x}_{q}^{0}\right) \left( \Phi _{n,p}\delta \varvec{x}_{p}^{0}+\frac{1}{2}\Phi _{n,pq}\delta \varvec{x}_{p}^{0}\delta \varvec{x}_{q}^{0}\right) \end{aligned}$$

(16)

The next step is taking the time derivative of Eq. 13

$$\begin{aligned} \delta \dot{\varvec{x}}_{i}(t)={\dot{\Phi }}_{i,p}\delta \varvec{x}_{p}^{0}+\frac{1}{2}{\dot{\Phi }}_{i,pq}\delta \varvec{x}_{p}^{0}\delta \varvec{x}_{q}^{0} \end{aligned}$$

(17)

and equating Eqs. 16 and 17, from which the terms of equivalent order are equated. The first-order terms are:

$$\begin{aligned} {\dot{\Phi }}_{i,p}=F_{i,m}\Phi _{m,p} \end{aligned}$$

(18)

which matches the traditional first-order STM time derivative equation. Collecting second-order terms reveals the second-order STT time derivative when common terms are canceled [23]:

$$\begin{aligned} {\dot{\Phi }}_{i,pq}=F_{i,m}\Phi _{m,pq}+F_{i,mn}\Phi _{m,p}\Phi _{n,q} \end{aligned}$$

(19)

with initial conditions

$$\begin{aligned} \Phi _{m,pq}\left( t_{0},t_{0}\right) =0_{6\times 6\times 6} \end{aligned}$$

(20)

Combining second-order STTs is a bit more involved than combining sequential STMs. The desired STT in many situations requires sequential combination and inversion. Combining a second-order STT from $t_{0}$ to $t_{1}$ with an STT from $t_{1}$ to $t_{2}$ requires STMs from the same two periods, $\Phi (t_{1},t_{0})$ and $\Phi \left( t_{2},t_{1}\right)$, and the corresponding second-order STTs, $\Phi _{II}(t_{1},t_{0})$ and $\Phi _{II}\left( t_{2},t_{1}\right)$. Equation 21 shows the operation using index notation [24]:

$$\begin{aligned} \Phi _{II}\left( t_{2},t_{0}\right) _{i,jk}=\Phi _{II}\left( t_{2},t_{1}\right) _{i,pq}\Phi \left( t_{1},t_{0}\right) _{p,j}\Phi \left( t_{1},t_{0}\right) _{q,k}+\Phi \left( t_{2},t_{1}\right) _{i,p}\Phi _{II}\left( t_{1},t_{0}\right) _{p,jk} \end{aligned}$$

(21)

Inverting a second-order STT requires the forward STT and inverse STM for the corresponding time period [24]:

$$\begin{aligned} \Phi \left( t_{0},t_{1}\right) _{i,jk}=-\Phi \left( t_{0},t_{1}\right) _{i,p}\Phi _{II}\left( t_{1},t_{0}\right) _{p,qm}\Phi \left( t_{0},t_{1}\right) _{q,j}\Phi \left( t_{0},t_{1}\right) _{m,k} \end{aligned}$$

(22)

2.4 Multiple Segment Deterministic Trajectory Setup

A multiple segment trajectory is a method of modeling a trajectory as a set of discrete dynamics and constraints. Each trajectory segment formulation is a boundary value problem that is designed to satisfy its endpoint constraints. Assembling the multi-segment problem involves discretizing a trajectory into n segments separated by $n+1$ nodes that are not necessarily evenly spaced in time. Each trajectory segment is defined by the six-dimensional state at the beginning of segment i, $\varvec{x}_{0,i}$ and the duration of the segment, $\Delta t_{i}$. The state at the end of segment i, $\varvec{x}_{f,i}$ is a function of the natural motion dynamics of the system, the state at the beginning of the segment, and the duration $\Delta t_{i}$. Numerical integration of the dynamics is used to obtain $\varvec{x}_{f,i}$.

$$\begin{aligned} \varvec{x}_{f,i}=f\left( \varvec{x}_{0,i},\Delta t_{i}\right) \end{aligned}$$

(23)

Each trajectory segment parameter vector $\varvec{s}_{i}$ is defined by its initial state and duration

$$\begin{aligned} \varvec{s}_{i}=\left[ \begin{array}{c} \varvec{x}_{0,i}\\ \Delta t_{i} \end{array}\right] \end{aligned}$$

(24)

and are each assembled into a parameter vector defining the trajectory:

$$\begin{aligned} \varvec{S}=\left[ \begin{array}{c} \varvec{s}_{1}\\ \vdots \\ \varvec{s}_{n} \end{array}\right] \end{aligned}$$

(25)

A history of the states, the state transition matrices ($\Phi$), and any other desired sensitivities are propagated and saved along the nominal trajectory at the time indices automatically chosen by the variable-step variable-order Adams–Bashforth–Moulton predictor-corrector method [25]. The multiple segment approach enables the propagation of all trajectory dynamics histories from the beginning of each segment. This results in an error reduction when computing an STM with arbitrary endpoints as it need not reference the beginning of the trajectory. The multiple segment approach also discretizes the nonlinear portions of the trajectory into smaller portions that can improve first-order numerical convergence when the first-order dynamics for a longer segment fail to result in convergence.

2.5 Deterministic Constraints

The segment connectivity constraint enforces natural motion (a coast) across node $i+1$ (between segments i and $i+1$) and involves constraining the final state of segment i with the initial state of segment $i+1$:

$$\begin{aligned} \varvec{x}_{f,i}=\varvec{x}_{0,i+1} \end{aligned}$$

(26)

An impulsive maneuver is allowed between segments by leaving the velocity elements unconstrained (or only constraining the position elements):

$$\begin{aligned} \varvec{r}_{f,i}=\varvec{r}_{0,i+1}. \end{aligned}$$

(27)

The problem initial conditions are applied at the initial state of the first segment, $\varvec{x}_{0,1}$. The simplest initial condition to implement is a given initial state in the CR3BP, $\varvec{X}_{0}$, whereby the equality constraint

$$\begin{aligned} \varvec{x}_{0,1}=\varvec{X}_{0} \end{aligned}$$

(28)

enforces the problem initial conditions. Constraining the final state ($n+1$th node) of the final (nth) segment ensures arrival to the target orbit.

$$\begin{aligned} \varvec{x}_{f,n}=\varvec{X}_{target}. \end{aligned}$$

(29)

The next deterministic constraint enables a flexible initial orbit departure and target orbit arrival. Rather than constraining a specific target orbit arrival position and risking a suboptimal injection into the target orbit, a combination of two constraints enables a flexible arrival to the target orbit. Equation 29 combined with allowing a $\Delta V$ at the beginning of the final segment (Eq. 27 where $i=n$ ) frees the arrival position along the target orbit, as long as only coasting meets a future state in the target orbit, $\varvec{X}_{target}$. The result is arriving to the target orbit while simultaneously optimizing the injection location. A similar combination enables a flexible departure from the initial orbit where the initial state constraint is followed by a coast duration and an impulsive $\Delta V$ at the end of the first segment (Eq. 27 where $i=1$).

The combination of constraints described in the previous paragraph directly constrain the initial and final elements of the state vector. While coast durations in the initial and final trajectory segments enable flexibility in the specific departure and arrival orbits, effectively five of the six classical orbital elements (COEs) are fixed with the true anomaly eligible for optimization. In scenarios where there is flexibility in the initial orbital plane, the combination of Eqs. 32, 33, and 34 free the initial orbital plane and constrain the initial orbit to be circular of a specific radius. As a result, the orbital plane (inclination and right ascension) and true anomaly are free to be optimized. The first constraint (Eq. 32) fixes the two-body orbital energy

$$\begin{aligned} \epsilon =\frac{\left( v_{sc}^{I}\right) ^{2}}{2}-\frac{\mu _{body}}{r_{sc/B}} \end{aligned}$$

(30)

with respect to the planetary body B to be equal to a desired value. $r_{sc/B}$ is the magnitude of the position vector with respect to B, $\varvec{r}_{sc/B}$, and

$$\begin{aligned} \varvec{r}_{sc/B}=\varvec{r}_{0,i}-\varvec{r}_{B} \end{aligned}$$

(31)

$v_{sc}^{I}$ is the velocity of the spacecraft in a non-rotating frame. In this case, the velocity elements of the parameter vector are in the CR3BP rotating frame and the rotating frame velocity needs to be included. Assuming the constraint is applied to the initial orbit:

$$\begin{aligned} \varvec{v}_{sc/B}^{I}=\varvec{v}_{0,1}+\omega _{S/I}\times \varvec{r}_{0,1} \end{aligned}$$

The constraint equation is

$$\begin{aligned} \epsilon _{initial}-\epsilon _{fixed}=0 \end{aligned}$$

(32)

where $\epsilon _{fixed}$ in this paper generally corresponds to an initial circular orbit of a desired altitude.

Equation 33 enforces a specific position vector magnitude with respect to B:

$$\begin{aligned} r_{sc/B}-r_{fixed_{B}}=0 \end{aligned}$$

(33)

Equation 34 enforces orthogonal position and velocity vectors (an apse, or a circular orbit):

$$\begin{aligned} \varvec{r}_{sc/B}^{\top }\varvec{v}_{sc}^{I}=0 \end{aligned}$$

(34)

Nominal 3 $\Delta V$ trajectories enable powered flyby scenarios, however, this scenario requires a flyby distance inequality constraint to produce a realistic result in some cases. The flyby distance constraint implementation chosen does not constrain the powered flyby as the apse; rather, the state history is searched for the point of closest body approach (typically the moon for this analysis), and a distance constraint is applied at this point.

$$\begin{aligned} \Vert \varvec{r}_{periapse}\Vert \ge d_{\text {min flyby}} \end{aligned}$$

(35)

2.6 Deterministic Cost

The deterministic cost to be minimized along a nominal trajectory is the sum of the magnitude of m nominal impulsive maneuvers:

$$\begin{aligned} J=\underset{j=1}{\overset{m}{\Sigma }}\Delta V. \end{aligned}$$

(36)

3 Stochastic Analysis Along a Nominal Trajectory

The trajectory parameter vector $\varvec{S}$ defines a nominal trajectory. Altering any quantity in the vector $\varvec{S}$ results in a new nominal trajectory that requires a new propagation and re-assessment of the deterministic cost and constraints. The state dispersion covariance defines the Gaussian statistics along the nominal trajectory, as a function of time and of the stochastic error sources. Unlike modifications to the nominal trajectory, modifications to the dispersion covariance analysis do not require the propagation of a new nominal trajectory (the exception being modifications to the upcoming process noise power spectral density (PSD) Q, which does require repropagation of the accumulated process noise covariance). As a result, a new dispersion covariance analysis happens quickly when only changing a dispersion covariance modifying event (initial dispersion, trajectory correction maneuver (TCM) execution time, maneuver execution error values).

Section 3 presents a fast linear covariance analysis-based method of TCM optimization along a nominal trajectory that only requires a series of matrix multiplications versus a new trajectory propagation. Following the description of the TCM optimization method, a series of examples illustrates the dependence of the result on the magnitude of specific stochastic parameters. The stochastic parameters considered are an initial state dispersion, nominal maneuver execution error, TCM execution error, and process noise.

3.1 Initial State Dispersion

An initial state dispersion represents errors in the trajectory initial state. The initial state dispersion is a zero mean multivariate normal distribution with position variance $\sigma _{r}^{2}$ and velocity variance $\sigma _{v}^{2}$ in each direction:

$$\begin{aligned} P_{0}=E\left[ \delta \varvec{x}\left( t_{0}\right) \delta \varvec{x}\left( t_{0}\right) ^{\top }\right] =\left[ \begin{array}{cc} \sigma _{r}^{2}I_{3\times 3} &{} 0_{3\times 3}\\ 0_{3\times 3} &{} \sigma _{v}^{2}I_{3\times 3} \end{array}\right] \end{aligned}$$

(37)

The dispersion along a nominal trajectory is propagated linearly using the STM

$$\begin{aligned} \delta \varvec{x}(t_{c})=\Phi (t_{c},t_{0})\delta \varvec{x}(t_{0}) \end{aligned}$$

(38)

Similarly, the state dispersion covariance is propagated linearly along the nominal trajectory to the next dispersion covariance modifying event:

$$\begin{aligned} P_{c}^{-}=E\left[ \delta \varvec{x}(t_{c})\delta \varvec{x}(t_{c})^{\top }\right] =\Phi \left( t_{c},t_{0}\right) P_{0}\Phi \left( t_{c},t_{0}\right) ^{\top } \end{aligned}$$

(39)

3.2 Trajectory Correction Maneuvers without Execution Error

The purpose of a TCM is to modify the dispersion at a target. In this analysis, the target is an upcoming nominal maneuver(s). Two types of TCMs are implemented: a position dispersion-correcting TCM (Eq. 41) and a velocity dispersion-correcting TCM (Eq. 46). A more detailed derivation of these equations are are presented by Kelly and Geller in [20].

The dispersion at $t_{c}$ along a nominal trajectory is propagated linearly using the STM to the target

$$\begin{aligned} \delta \varvec{x}(t_{n})=\Phi (t_{n},t_{c})\delta \varvec{x}(t_{c}). \end{aligned}$$

(40)

A position targeting TCM, $\delta \varvec{V}_{r}$, is designed to remove the position dispersion at a future target $\left( \delta \varvec{r}(t_{n})=0\right)$ via a velocity modification

$$\begin{aligned} \delta \varvec{V}_{r}=\left[ \begin{array}{ccc} -\Phi _{rv}(t_{n},t_{c})^{-1}\Phi _{rr}(t_{n},t_{c})&\,&-I_{3\times 3}\end{array}\right] \delta \varvec{x}(t_{c})=T\delta \varvec{x}(t_{c}) \end{aligned}$$

(41)

where $t_{c}$ represents TCM execution time and $t_{n}$ represents the target time along a nominal trajectory. The covariance of $\delta \varvec{V}_{r}$ is a function of the matrix T and the dispersion covariance at $t_{c}$ prior to the TCM, $P_{c}^{-}$:

$$\begin{aligned} E\left[ \delta \varvec{V}_{r}\delta \varvec{V}_{r}^{\top }\right] =TE\left[ \delta \varvec{x}\delta \varvec{x}^{\top }\right] T^{\top }=TP_{c}^{-}T^{\top }. \end{aligned}$$

(42)

An upper bound for the variance of the magnitude of a TCM is the square root of the sum of the squares (RSS) of the TCM covariance matrix diagonal terms:

$$\begin{aligned} \sigma _{\delta V_{r}}=\sqrt{\text {tr}\left( TP_{c}^{-}T^{\top }\right) }=\sqrt{\text {tr}\left( P_{TCM_{r}}\right) }. \end{aligned}$$

(43)

The TCM dispersion update is

$$\begin{aligned} \delta \varvec{x}_{c}^{+}=\delta \varvec{x}_{c}^{-}+\left[ \begin{array}{c} 0_{3\times 6}\\ T \end{array}\right] \delta \varvec{x}_{c}^{-} \end{aligned}$$

(44)

and the post-correction dispersion covariance follows, where I is the identity matrix and $N=\left[ \begin{array}{c} 0_{3\times 6}\\ T \end{array}\right]$:

$$\begin{aligned} P_{c}^{+}=E\left[ \left( \delta \varvec{x}_{c}^{-}+N\delta \varvec{x}_{c}^{-}\right) \left( \delta \varvec{x}_{c}^{-}+N\delta \varvec{x}_{c}^{-}\right) ^{\top }\right] =\left( I+N\right) P_{c}^{-}\left( I+N\right) ^{\top }. \end{aligned}$$

(45)

A velocity dispersion-correcting TCM directly corrects remaining velocity dispersion at a final time or nominal maneuver, $\delta \varvec{V}_{v}=-M_{v}\delta \varvec{x}\left( t_{n}\right)$.

$$\begin{aligned} \sigma _{\delta V_{v}}=\sqrt{\text {tr}\left( M_{v}P_{n}^{-}M_{v}^{\top }\right) }=\sqrt{\text {tr}\left( P_{TCM_{v}}\right) } \end{aligned}$$

(46)

where $M_{v}$ is $\left[ \begin{array}{cc} 0_{3\times 3}&I_{3\times 3}\end{array}\right]$, a mapping matrix that extracts the velocity dispersion covariance. The actual covariance update is not implemented as injection into the target orbit marks the end of the trajectory design.

3.3 Trajectory Correction Maneuvers with Execution Error

Realistically, TCMs do not perfectly mitigate a future position dispersion as they are not perfectly executed. TCM execution error is incorporated simultaneously with the TCM dispersion covariance update. The execution error model is normally distributed, zero mean, $\sigma _{R_{TCM}}^{2}$ variance per axis, resulting in the following TCM dispersion covariance update:

$$\begin{aligned} P_{c}^{+}=\left( I+N\right) P_{c}^{-}\left( I+N\right) ^{\top }+GR_{TCM}G \end{aligned}$$

(47)

where $R_{TCM}=\sigma _{R_{TCM}}^{2}I_{3\times 3}$ is the TCM execution error covariance and G is a $6\times 3$ matrix that maps the error to the velocity covariance sub-matrix. A more realistic model that is aligned with a specific mission’s hardware specifications, potentially capturing pointing error and/or thrust vector error, could be incorporated as future work without significant additional effort.

The TCM execution error also contributes to the stochastic cost of the TCM:

$$\begin{aligned} \sigma _{\delta V}=\sqrt{\text {tr}\left( P_{TCM}+R_{TCM}\right) }. \end{aligned}$$

(48)

3.4 Nominal Maneuver Execution Error

Nominal maneuvers along the nominal trajectory are also not executed perfectly and contribute to the dispersion covariance. The dispersion covariance update equation only includes the error term at the time of the nominal maneuver as it does not affect the covariance otherwise. The error model is also zero mean with a variance of $\sigma _{R_{\Delta V}}^{2}$ per axis where $R_{\Delta V}=\sigma _{R_{\Delta V}}^{2}I_{3\times 3}$ is the nominal maneuver execution error covariance. The dispersion covariance update equation for a nominal maneuver is

$$\begin{aligned} P_{\Delta V}^{+}=P_{\Delta V}^{-}+GR_{\Delta V}G^{\top } \end{aligned}$$

(49)

3.5 Corrected Nominal Maneuvers

Another option for affecting the future state dispersion covariance is combining a TCM with a nominal maneuver. Assuming the nominal maneuver is not performed at a location that has poor sensitivity in a specific direction for the TCM (i.e., correcting out of plane dispersion during the first maneuver in a Hohmann transfer), the effect of combining vector magnitudes results in savings in many cases. When a nominal maneuver, $\Delta \varvec{V}$, and a TCM, $\delta \varvec{V}_{r}$, are combined in a single maneuver, the corrected nominal maneuver vector, $\Delta \varvec{V}_{cr}$, is

$$\begin{aligned} \Delta \varvec{V}_{cr}=\Delta \varvec{V}+\delta \varvec{V}_{r} \end{aligned}$$

where the individual $\delta \varvec{V}_{r}$ components are modeled as zero mean Gaussian random variables with covariance matrix $P_{TCM_{r}}$. A first-order TSE of the magnitude of the corrected position-targeting maneuver, $\Vert \Delta \varvec{V}_{cr}\Vert$, helps to estimate the statistics of the correction magnitude $\Vert \delta \varvec{V}\Vert$:

$$\begin{aligned} \Vert \Delta \varvec{V}_{cr}\Vert \approx \Vert \Delta \varvec{V}\Vert +\frac{\partial \Vert \Delta \varvec{V}\Vert }{\partial \Delta \varvec{V}}\delta \varvec{V}_{r}. \end{aligned}$$

(50)

The mean of $\Delta \varvec{V}_{cr}$ is $\Delta \varvec{V}$ and the variance is

$$\begin{aligned} \sigma _{\Vert \Delta \varvec{V}_{cr}\Vert }^{2}&=E\left[ \left( \Vert \Delta \varvec{V}_{cr}\Vert -\Vert \Delta \varvec{V}\Vert \right) \left( \Vert \Delta \varvec{V}_{cr}\Vert -\Vert \Delta \varvec{V}\Vert \right) ^{\top }\right] \end{aligned}$$

(51)

$$\begin{aligned} \sigma _{\Vert \Delta \varvec{V}_{cr}\Vert }^{2}&=E\left[ \left( {\hat{i}}_{\Delta \varvec{V}}^{\top }\delta \varvec{V}_{r}\right) \left( {\hat{i}}_{\Delta \varvec{V}}^{\top }\delta \varvec{V}_{r}\right) ^{\top }\right] \end{aligned}$$

(52)

$$\begin{aligned} \sigma _{\Vert \Delta \varvec{V}_{cr}\Vert }^{2}&={\hat{i}}_{\Delta \varvec{V}}^{\top }\left( P_{TCM}+R_{\Delta V}\right) {\hat{i}}_{\Delta \varvec{V}} \end{aligned}$$

(53)

where ${\hat{i}}_{\Delta \varvec{V}}$ is a unit vector in the direction of the nominal maneuver.

Similarly, the target orbit arrival $\Delta \varvec{V}$ can be combined with a correction to remove remaining velocity dispersion at the target orbit insertion. The statistics of the velocity dispersion cleanup components are represented by the $3\times 3$ velocity submatrix of the state dispersion at target orbit insertion:

$$\begin{aligned} P_{TCM_{v}}=M_{v}P_{n}^{-}M_{v}^{\top }. \end{aligned}$$

(54)

The first-order TSE produces a similar result to Eq. 53:

$$\begin{aligned} \sigma _{\Vert \Delta \varvec{V}_{cv}\Vert }^{2}&={\hat{i}}_{\Delta \varvec{V}}^{\top }\left( P_{TCM_{v}}+R_{\Delta V}\right) {\hat{i}}_{\Delta \varvec{V}}. \end{aligned}$$

(55)

One way to interpret this simplification is vector addition: the only portion of the TCM that adds cost to the combined maneuver is the portion in the direction of the nominal maneuver. This savings is only accurate in cases where the nominal maneuver is much larger than the correction magnitude. When the reverse is true, this model’s perceived savings are unrealistic.

3.6 Random Disturbances/Process Noise

Incorporating process noise is a common technique for estimating the effect of continuous stochastic errors of a process. Spacecraft venting or misaligned reaction control subsystem thrusters result in random impulses that may have a cumulative effect on the trajectory. These random impulses can also be represented by an increase to the dispersion covariance with respect to the nominal trajectory. A simple model for random disturbances is a zero mean white continuous noise process with PSD Q, where $Q=s_{Q}^{2}I_{3\times 3}$, describing the strength of the unmodeled accelerations. The effect of Q accumulates over time via the linear stochastic differential equation, Eq. 56 [26]:

$$\begin{aligned} {\bar{Q}}(t_{f},t_{0})=\int _{t_{i}}^{t_{f}}\Phi (t_{f},\tau )G(\tau )Q(\tau )G(\tau )^{\tau }\Phi ^{\top }(t_{f},\tau )d\tau \end{aligned}$$

(56)

where ${\bar{Q}}$ represents the accumulated state dispersion covariance from process noise and G maps Q to the velocity components of the state dispersion covariance matrix. In the current implementation, Q and G are constant so their time reference $\tau$ is removed, however, this method still applies to time varying Q and G matrices (although the upcoming analytical gradient derivation in Appendix A.2 will likely require additional terms). ${\bar{Q}}$ will be referred to as the Q bar matrix, or QBM.

The TCM optimization method in Sect. 4 references propagated STM histories along a nominal trajectory many times without repropagating between covariance modifying events. Similarly, a new propagation would be required to incorporate ${\bar{Q}}$ between covariance modifying events if Eq. 56 were utilized. Instead, the continuous QBM history is also propagated and saved, from the beginning of each segment, alongside the STM history. Equation 57 [26] is used to numerically integrate the QBM with initial condition ${\bar{Q}}$ $\left( t_{0},t_{0}\right) =0_{6\times 6}$:

$$\begin{aligned} \dot{{\bar{Q}}}(t,t_{0})=F(\varvec{x}){\bar{Q}}(t,t_{0})+{\bar{Q}}(t,t_{0})F(\varvec{x})^{\top }+GQG^{\top } \end{aligned}$$

(57)

where F is the system Jacobian.

With the QBM history along the trajectory, propagated from the beginning of each segment, the appropriate portion of ${\bar{Q}}$ is extracted from the history which contributes to the dispersion covariance at each dispersion covariance modifying event. For example, at the first correction, the dispersion covariance equals the linear covariance growth via the STM plus the accumulated process noise covariance:

$$\begin{aligned} P_{c_{1}}^{-}=\Phi \left( t_{c_{1}},t_{0}\right) P_{0}\Phi \left( t_{c_{1}},t_{0}\right) {}^{\top }+{\bar{Q}}_{t_{c_{1}}}\left( t_{c_{1}},t_{0}\right) \end{aligned}$$

(58)

where the STM ($\Phi$) and the QBM (${\bar{Q}}$) time-histories have been previously saved.

Some manipulation of the QBM history is required as optimizing TCMs along a nominal trajectory allows TCMs to occur independent of segment intersection, and the QBM history is propagated from the beginning to the end of each segment. The first manipulation involves combining two sequential propagated durations of ${\bar{Q}}$. ${\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right)$ represents the effect of process noise covariance at $t_{1}$, accumulated from $t_{0}$ to $t_{1}$. Similarly, ${\bar{Q}}_{t_{2}}\left( t_{2},t_{1}\right)$ represents the effect of process noise covariance at $t_{2}$, accumulated from $t_{1}$ to $t_{2}$. The goal is to combine these two sequential portions of ${\bar{Q}}$ to form the accumulated effect of process noise from $t_{0}$ to $t_{2}$ on the covariance at $t_{2}$, ${\bar{Q}}_{t_{2}}\left( t_{2},t_{0}\right)$. Equation 59 shows the required operation:

$$\begin{aligned} {\bar{Q}}_{t_{2}}\left( t_{2},t_{0}\right) ={\bar{Q}}_{t_{2}}\left( t_{2},t_{1}\right) +\Phi \left( t_{2},t_{1}\right) {\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right) \Phi \left( t_{2},t_{1}\right) ^{\top }. \end{aligned}$$

(59)

The second term can be thought of as linear propagation of ${\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right)$ to $t_{2}$:

$$\begin{aligned} {\bar{Q}}_{t_{2}}\left( t_{1},t_{0}\right) =\Phi \left( t_{2},t_{1}\right) {\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right) \Phi \left( t_{2},t_{1}\right) ^{\top }. \end{aligned}$$

(60)

Another scenario results when the QBM history propagation begins from $t_{0}$ through $t_{2}$ but the desired quantity is ${\bar{Q}}_{t_{2}}\left( t_{2},t_{1}\right)$. Rearranging Eq. 59 produces the desired quantity, shown in Eq. 61.

$$\begin{aligned} {\bar{Q}}_{t_{2}}\left( t_{2},t_{1}\right) ={\bar{Q}}_{t_{2}}\left( t_{2},t_{0}\right) -\Phi \left( t_{2},t_{1}\right) {\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right) \Phi \left( t_{2},t_{1}\right) ^{\top } \end{aligned}$$

(61)

3.7 Stochastic Cost and Constraints

The stochastic cost represents the additional cost of managing the state dispersion along a nominal trajectory to meet mission requirements. The stochastic cost is the sum of the RSS of $n_{\delta V}$ TCMs with execution error plus the additional cost incurred by correcting $n_{\Delta V_{c}}$ nominal maneuvers, multiplied by a scalar that corresponds to the mission’s risk tolerance related to maneuver margin (3$\sigma$ is used in this analysis):

$$\begin{aligned} J_{\sigma }=3\left( \underset{k=1}{\overset{n_{\delta V}}{\sum }}\left( \sigma _{\delta V}\right) +\underset{q=1}{\overset{n_{\Delta V_{c}}}{\sum }}\sigma _{\Vert \Delta \varvec{V}_{c}\Vert }\right) . \end{aligned}$$

(62)

An important parameter at nominal mission events (e.g., nominal maneuvers, target orbit insertion, rendezvous) is spacecraft position relative to the plan. For the analysis in this paper, the nominal trajectory will exactly intersect the planned position. The state dispersion covariance relative to the nominal trajectory represents the statistical deviation from the planned trajectory. TCMs manage the state dispersion within a reasonable level around the nominal trajectory. Said another way, TCMs ensure that the state dispersion constraints are met. The main state dispersion constraint ensures that the RSS of the position dispersion is less than a maximum value, $\sigma _{r,max}$:

$$\begin{aligned} \sqrt{\text {tr}\left( M_{r}PM_{r}^{\top }\right) }\le \sigma _{r,max} \end{aligned}$$

(63)

where $M_{r}=\left[ \begin{array}{cc} I_{3\times 3}&0_{3\times 3}\end{array}\right]$. Pre and post multiplying the state dispersion covariance by the mapping matrix $M_{r}$ extracts the position dispersion (rr) submatrix. In general, Constraint Eq. 63 is applied in this analysis at all nominal maneuvers after the first nominal maneuver.

4 Trajectory Correction Maneuver Optimization

Section 4 explores the optimization of TCMs along a fixed nominal trajectory. Section 4.1 describes a fast method to develop a near-optimal solution to the number and location of multiple TCMs along the deterministic optimal trajectory that also ensures a dispersion constraint is met at a single target. Section 4.1 also introduces a second target event along a nominal trajectory and connects the covariance analysis between two separate TCM target portions of the trajectory. Section 4.2 shows a series of optimal TCM examples along the same nominal trajectory with variations in error sources to highlight the sensitivity of the optimal TCM solution to variations in stochastic problem parameters/error sources. TCM optimization significantly mitigates the total cost of corrections with varying error sources when compared to a default TCM solution (referred to as the “looks about right” solution). The stochastic parameters for the analysis in this section are shown in Fig. 1.

4.1 Optimizing TCM Number and Location Along a Nominal Trajectory

At any time along a dispersed nominal trajectory between $t_{0}$ and $t_{final}$, it is possible to perform a TCM and affect the dispersion covariance at a future time. Figure 1 shows a three impulse LEO to powered lunar flyby (PLF) to NRHO insertion (NRI) trajectory with a fixed initial orbital plane in the CR3BP rotating frame. The stars represent nominal maneuvers. For the TCM optimization example, only the portion of the trajectory between the first and second nominal $\Delta V$s is analyzed (the portion of the trajectory that is plotted with a thicker line and multiple colors in Fig. 1). The targeted position for corrections in this portion is the position at the PLF ($\Delta V_{2}$). $\Delta V_{1}$ is a corrected nominal maneuver. The colors in this trajectory and in subsequent trajectory figures represent the trajectory segments as described in Subsection 2.4.

Fig. 1

Sample nominal trajectory and error parameters

When an error-free correction is performed without random disturbances, the desired position is achieved. In terms of dispersion covariance, the position dispersion at the targeted time along the nominal trajectory is zero. When an initial dispersion, maneuver execution error, and process noise are introduced, the position dispersion at the target becomes a function of these error sources and the TCM execution time along the nominal trajectory. The blue line in Fig. 2a shows the target position dispersion RSS as a function of a single TCM execution time. Figure 2a also shows a horizontal dashed line representing a 1 km target position dispersion RSS constraint. This constraint restricts the feasible TCM execution time options to those below the dashed horizontal line. A vertical dashed red line identifies the earliest TCM option that meets the target position dispersion constraint, with all later TCM options also meeting the target dispersion constraint.

Figure 2b shows the TCM $\delta V$ as a function of execution time for the same TCM options that produce Fig. 2a. The red dot represents the lowest $\delta V$ TCM that meets the target dispersion constraint. Generally, the earliest TCM execution time that meets the target position dispersion constraint is a function of TCM execution error and process noise. With less execution error, the TCM can be performed earlier in the trajectory at a reduced cost. Greater execution error requires a later TCM at greater $\delta V$. This TCM to meet the target dispersion constraint will be referred to as TCM $\alpha$ and is an expensive option in the current example as a sole TCM performed so late in the trajectory.¹ Introducing an additional TCM (TCM $\beta$) has the potential to reduce the total $\delta V$ when compared to the single TCM solution. By fixing the TCM $\alpha$ execution time, TCM $\beta$ can be performed along the trajectory from $t_{0}$ to $t_{c_{\alpha }}$. Figure 3a shows the two TCM total $\delta V$ as a function of TCM $\beta$ execution time and a fixed TCM $\alpha$ execution time (represented by the vertical dashed line). Selecting the TCM $\beta$ execution time that minimizes the total TCM $\delta V$ (the red dot in Fig. 3a) results in the optimal two TCM solution that simultaneously satisfies the target position dispersion constraint.

Fig. 2

Side-by-side comparison of target position dispersion RSS and TCM RSS as a function of TCM execution time along nominal trajectory

Fig. 3

Sequential addition and optimization of TCMs demonstration

The process can be repeated as the first step in finding the optimal three TCM solution. By fixing the TCM $\alpha$ and $\beta$ execution times and introducing a third TCM (TCM $\gamma$), a TCM $\gamma$ execution time exists that again corresponds to a minimum total TCM $\delta V$. An additional step in this case is required however, as the execution time for TCMs $\beta$ and $\gamma$ are variable, affect one another, and affect the total TCM $\delta V$. A gradient-based search, step, and re-search until a minimum value is found is implemented. A test in each direction (one time increment earlier and later) of each TCM execution time identifies if a lower total TCM $\delta V$ solution exists. If so, a gradient vector is created and all TCM execution times are modified one time index in the appropriate direction simultaneously. Figure 3b–d respectively show the sequence of incorporating three, four, and five TCMs from the previous optimal solution identified. Table 1 shows the gradient search steps taken from the initial placement of TCM $\zeta$ (Fig. 3d) to the lowest five TCM total $\delta V$ solution identified.

Table 1 Gradient-based five-TCM optimization steps

After a certain number of TCMs are added to the maneuver plan, the total TCM $\delta V$ will start to increase rather than decreasing. This identifies the optimal number of TCMs and their optimal execution time along a nominal trajectory. The data in Table 2 identifies that the optimal number of TCMs corresponding to the lowest total $\delta V$ is five, as increasing to 6 TCMs results in a total cost increase. However, an improvement threshold may be implemented as savings diminish prior to the cost increase. In this analysis, the improvement threshold chosen is 3 times the RSS of $R_{TCM}$, equating to roughly.05 m/s resulting in four TCMs being chosen despite the marginal additional savings with five TCMs.

Table 2 Optimal total TCM RSS as a function of number of TCMs

The previous analysis only considered TCMs between $\Delta V_{1}$ (departing LEO) and $\Delta V_{2}$ (PLF) to introduce the optimization steps. For scenarios with multiple target dispersion constraints (multiple target portions of the trajectory), the optimization sequence is similar with an additional step. The additional first step is placing TCM(s) at the cheapest option to meet each target’s position dispersion constraint. For example, in Fig. 4, there are two TCM targets, $\Delta V_{2}$ (PLF) and $\Delta V_{3}$ (NRHO insertion). The first TCM is placed to optimally meet the target position dispersion constraint at $\Delta V_{2}$ with a single TCM. Similarly, the second TCM is then placed to optimally meet the target position dispersion constraint at $\Delta V_{3}$ with two total TCMs. The remainder of the process continues as previously described, with eligible options for the new TCMs being across all target portions of the trajectory. TCMs are sequentially added at the cheapest option throughout the entire trajectory and re-optimized via the gradient descent method until the TCM cost increases compared to the previous optimal value. Verification results for this method appear in Sect. 7.2.

4.2 Optimal TCM(s) with Variations in Stochastic Parameters

The objective of this section is to highlight the sensitivity of the optimal TCM set to variations in stochastic parameters through a series of examples. Each example shows the optimal TCM set corresponding to a change in the stochastic parameters in Fig. 4 along the same three impulse nominal trajectory from LEO to NRI via PLF. Points of comparison include the stochastic cost as well as the number and location of TCMs along the trajectory as error sources change. Note that in Figs. 4 through 6, while there is an initial coast in LEO from the green dot to the departure impulsive maneuver (not labeled to avoid congestion) and a final NRHO coast to reach the red square, these only enable flexible departure from the initial orbit and arrival to the target orbit and are not involved in the stochastic analysis. The initial dispersion is applied at $\Delta V_{1}$ and the target dispersion constraint is applied at $\Delta V_{3}$ with all TCMs occurring between these endpoints. The TCMs in the LEO to PLF portion of the trajectory aim to minimize position dispersion at $\Delta V_{2}$ (PLF) and the TCMs in the PLF to NRI portion of the trajectory target $\Delta V_{3}$ (NRI).

Fig. 4

Baseline stochastic parameters, optimal and LAR TCMs along LEO to NRHO Trajectory

The first example in Fig. 4 shows the baseline error parameters, the optimal TCM cost, and a comparison to another TCM selection method that has historically been referred to as the LAR or “looks about right” method [27]. The authors selected a few TCM locations that looked about right to serve as a cost comparison to the optimal TCM set (see LAR $J_{\sigma }$ in subsequent figures as a comparison to optimal $J_{\sigma }$). The LAR TCMs were selected with a few guidelines: (1) a TCM immediately follows nominal maneuvers to “clean up” nominal maneuver execution error; (2) the final TCM in each portion is placed such that it meets the same target position dispersion constraint as the optimal for a fair comparison; (3) the remaining TCMs in each TCM targeted portion of the trajectory roughly visually subdivide the trajectory. The cost increase is minimal for the initial error values.

The LAR TCMs are shown as open circles in Fig. 4, while the optimal TCMs for the baseline error sources occur at the open triangles. The second nominal maneuver at PLF is not a corrected nominal maneuver for this analysis; the magnitude comparison between the nominal maneuver and the TCM, in some cases, is such that the TCM magnitude is too large compared to the size of the nominal maneuver for the savings in Sect. 3.5 to apply.

The next example (Fig. 5) explores the impact of increasing the effect of the process noise by a factor of 10. The final TCM preceding the final target moved closer to the target, which makes sense; additional process noise causes the state dispersion to grow more quickly so the final TCM must be closer to the target to meet the same position dispersion constraint. Additional TCMs along the trajectory serve to reduce the cost of meeting the target position dispersion constraint as well as managing the magnitude of the trajectory dispersion along the trajectory. With increased process noise, the optimal TCM solution proactively manages dispersion growth throughout the trajectory with additional TCMs. The low TCM execution error allows the addition of more TCMs in this case prior to the cost increase. TCMs are grouped near the lowest nominal velocity apogee-like portion of the trajectory. The TCMs prior to the $\Delta V_2$ target minimize the velocity dispersion at PLF, which, when not properly managed, creates a very expensive subsequent TCM (more on this in Sect. 6.1). The total $3\sigma$ correction cost comparison between optimal (44.4 m/s) and LAR (156.1 m/s) in this case is noteworthy. The only LAR TCM change for this example is an update to the final LAR TCM time prior to each target to meet the target position dispersion constraint.

Fig. 5

10$\times$ process noise, optimal and LAR TCMs along LEO to NRHO trajectory

The next example highlights the impact of reducing the initial dispersion. A portion of the total TCM cost is attributed to the corrected initial maneuver. With a small initial dispersion, the correction of the initial dispersion reduces in magnitude.

Increasing the nominal maneuver execution error from 1 m/s to 10 m/s $1\sigma$ increases the total cost of corrections but does not significantly change the optimal TCM set. The increased nominal maneuver execution error is corrected by the first TCM following each nominal $\Delta V$. This results in a large $3\sigma$ TCM cost increase but does not significantly change the optimal TCM solution or result in significantly poor performance of the LAR TCMs when compared to the optimal set.

Figure 6 shows the impact of increasing the TCM execution error to 10 cm/s from 1 cm/s. The main difference in the optimal TCM set is the introduction of additional TCMs to manage the additional error being injected by each TCM into the dispersion covariance. The TCM error is also included in the correction cost, which results in reaching the upper bound on the number of TCMs before the cost begins to increase with fewer TCMs. When comparing the increase of the optimal TCM cost (18.0 m/s initially to 42.1 m/s), the additional TCMs in the optimal set successfully mitigate a significant impact to the overall correction cost. On the contrary, the LAR method performs significantly worse regarding the increased TCM cost from 26.1 to 138.0 m/s. As a result of the additional TCM execution error, the final TCM prior to each target also moves closer to the target to meet the same position dispersion RSS constraint.

Fig. 6

10 cm/s $1\sigma$ TCM error, optimal and LAR TCMs along LEO to NRHO trajectory

The result of reducing the target position dispersion RSS constraint to 100 m from 1 km is a final TCM that is also closer to the target, preceded by an additional TCM to reduce the dispersion magnitude and correction magnitude for the final TCM of each targeting portion. The cost of the optimal TCM solution does not significantly increase as a result of the more stringent constraint. The performance of the LAR method is not terrible but poor by comparison as it does not benefit from additional TCMs preceding each final targeting TCM.

The final two examples show the result of increasing the magnitude of multiple error sources simultaneously, highlighting the importance of an optimized TCM set. Increasing the nominal maneuver execution error and process noise increases the TCM cost to 123.3 m/s for the optimized set, compared to 213.5 m/s for the LAR TCM set. Increasing the TCM execution error in addition to the process noise and nominal maneuver execution error results in only a moderate increase to the TCM cost to 144.4 m/s but an additional significant increase to 407.6 m/s for the LAR TCM set.

Table 3 summarizes the TCM sensitivity to error source magnitude results. There are conclusions related to modifications in each error source. Correcting initial dispersion is expensive whether the optimal TCM set or LAR TCM set is implemented. Similarly, correcting nominal maneuver execution error is also expensive, independent of the TCM set. Optimizing TCMs provides the most benefit for error sources that contribute to the state dispersion along the trajectory, whether continuously in the form of process noise, or discretely through increased TCM execution error. Optimizing TCMs is also beneficial in a scenario that requires a more stringent target position dispersion.

Table 3 TCM sensitivity analysis along deterministic optimal LEO to PLF to NRI trajectory summary

5 Robust Trajectory Design Method

The robust trajectory design method incorporates linear covariance analysis along each nominal trajectory to minimize the sum of the deterministic $\Delta V$ plus an estimate for the upper bound of the optimal TCM set $\delta V$. The resulting cost function represents the statistical upper bound for the total $\Delta V$ requirement, a mission planning factor that directly correlates to on-board spacecraft propellant.

The solution method is nonlinear programming (NLP) with analytical gradients (Matlab’s fmincon and the interior point method). First, an initial guess trajectory is developed using a shooting method. It is not required that the initial guess have complete position continuity or satisfy the constraint equations. The authors will frequently converge to the deterministic optimal trajectory as a refinement step to the initial guess prior to incorporating stochastics to save overall run time and to optimize the initial TCM set.² The state, STM, and QBM history along the initial guess nominal trajectory are numerically integrated. Next, the number and location of TCMs are optimized along the initial guess per the method described in Sect. 4. The TCM locations form the initial segmentation of the initial guess trajectory. Subsequently, corresponding TCMs are fixed to occur at the corresponding node after each iteration, as opposed to performing the approach in Sect. 4 each NLP iteration.

The trajectory segmentation also aids convergence, particularly for nonlinear portions of the trajectory. In some cases, successful NLP convergence requires additional segmentation of particularly long segments between TCMs. Each TCM is tied to a specific segment intersection and additional segments are incorporated for long duration trajectory spans.³ In this manner, the TCM optimization algorithm is only run one time, on the initial guess trajectory.⁴ This places the optimal number of TCMs in the appropriate local minima for the NLP to optimize as the trajectory changes. This also ensures TCMs times are not limited to variable step size STM histories and are instead tied to NLP problem parameters, creating a direct connection to analytical gradients with a smoother solution space.

Section 4 explored the optimization of TCMs along the same nominal trajectory (identified by the trajectory parameter vector $\varvec{S}$). In finding a robust trajectory, each NLP iteration modifies $\varvec{S}$ which corresponds to a new nominal trajectory. At each new nominal trajectory, a new state, STM, STT, QBM (${\bar{Q}}$), and QBT ($\partial {\bar{Q}}$) is propagated in order to calculate a new cost, assess the constraint set, and assemble the analytical gradients to provide back to the NLP to be used in determining the next step. Appendix A describes the steps for building the analytical gradients for each TCM and their total. Iterations continue until the constraints are satisfied within a certain tolerance and a local minimum is found (or the cost ceases to decrease with additional steps with a specified bound). Figure 7 shows a flowchart of the steps of the robust trajectory design method.

Fig. 7

Robust trajectory design method flowchart

The following optimization problem describes the robust trajectory design method; it applies to m nominal maneuver trajectories (indexed by the letter j) along an n segment trajectory (indexed by the letter i).

$$\begin{aligned} \text {optimization parameters}\,&\varvec{S} \end{aligned}$$

(64)

$$\begin{aligned} \text {minimize}\,\,&J=\underset{j=1}{\overset{m}{\Sigma }}\Delta V+3\left( \underset{k=1}{\overset{n_{\delta V}}{\sum }}\left( \sigma _{\delta V}\right) +\underset{q=1}{\overset{n_{\Delta V_{c}}}{\sum }}\sigma _{\Vert \Delta \varvec{V}_{c}\Vert }\right) \end{aligned}$$

(65)

$$\begin{aligned} \text {subject to}\,\,&\varvec{x}_{f,i}=f\left( \varvec{x}_{0,i},\Delta t_{i}\right) \end{aligned}$$

(66)

$$\begin{aligned}&P_{k+1}=\Phi \left( t_{k+1},t_{k}\right) P_{k}\Phi \left( t_{k+1},t_{k}\right) ^{\top }+{\bar{Q}}\left( t_{k+1},t_{k}\right) \end{aligned}$$

(67)

$$\begin{aligned}&P_{k}^{+t_{j}}=P_{k}^{-t_{j}}+GR_{\Delta V}G^{\top }\end{aligned}$$

(68)

$$\begin{aligned}&P_{k}^{+t_{c_{k}}}=\left( I+N\right) P_{k}^{-t_{c_{k}}}\left( I+N\right) ^{\top }+GR_{TCM}G^{\top }\end{aligned}$$

(69)

$$\begin{aligned}&\varvec{x}_{0,i}=\varvec{x}_{f,i-1},i\notin \varvec{d}\end{aligned}$$

(70)

$$\begin{aligned}&\varvec{r}_{0,i}=\varvec{r}_{f,i-1},i\in \varvec{d},i>1\end{aligned}$$

(71)

$$\begin{aligned}&\sqrt{\text {tr}\left( P_{rr,\varvec{d}}\right) }\le \sigma _{r,max},j>1\end{aligned}$$

(72)

$$\begin{aligned}&\Delta t_{i}\ge 0\end{aligned}$$

(73)

$$\begin{aligned} \text {given}\,\,&\varvec{x}_{0,1},\varvec{x}_{f,n},P_{1},\varvec{d},\varvec{e},\varvec{c},R_{\Delta V},R_{TCM},Q,\sigma _{r,max} \end{aligned}$$

(74)

Nominal impulsive maneuvers are allowed at the trajectory nodes identified in the vector $\varvec{d}$; the vector $\varvec{e}$ identifies which of nominal maneuvers in $\varvec{d}$ include a correction (for $n_{\Delta V_{c}}$ total corrected nominal maneuvers indexed by the letter q). The TCM optimization method identifies $n_{\delta V}$ total position-correcting TCMs along the initial guess nominal trajectory; the corresponding TCM execution nodes are stored in the vector $\varvec{c}$ (indexed by the letter k). The cost function (Eq. 65) is the the sum of the nominal maneuvers plus the total $3\sigma$ TCM $\delta V$. Of the constraint equations, Eq. 66 is the system dynamics for each trajectory segment as a function of the initial state and the segment duration. Equation 67 represents the covariance propagation using numerically integrated STM terms along the nominal trajectory and the accumulated process noise covariance between covariance updates. Equations 68 and 69 represent the dispersion covariance update equations for a nominal maneuver with execution error and a TCM with execution error, respectively. Equations 70 and 71 constrain the trajectory segments to be connected by all six state elements (a coast) or allow an impulsive $\Delta V$ between segments, as identified by the nodes in the vector $\varvec{d}$. Equation 72 constrains the RSS of the position dispersion at nominal maneuvers after the first to be less than or equal to $\sigma _{r,max}$. The duration of each trajectory segment must go forward in time (Eq. 73). The total trajectory duration is unconstrained. Upon convergence, the optimal TCM times for the robust trajectory are extracted from the appropriate nodes of $\varvec{S}$.

6 Cislunar Robust Trajectory Results

6.1 Robust LEO to Powered Lunar Flyby to NRHO Trajectory

The initial guess trajectory for this scenario is the same nominal trajectory used for TCM optimization in Sect. 4. The initial constraint set implemented is Eqs. 32, 33, and 34, constraining the initial Earth orbit to be circular with a radius of 450 km. The result effectively frees the initial Earth orbit’s right ascension, inclination, and true anomaly for optimization. The target orbit is the 9:2 synodic resonant member of the L2 Southern Halo family. Figure 8 shows the error parameters for this analysis as well as the converged robust trajectory. In addition to the robust trajectory, for a visual comparison, the deterministic optimal trajectory (without TCMs) is shown as a thinner red line. Table 4 shows a cost comparison of the deterministic optimal trajectory with an optimal set of TCMs to the resulting robust trajectory.

The robust trajectory provides a potential 77.8 m/s in savings compared to the deterministic optimal trajectory. Assuming $\Delta V_{1}$ is performed by a launch vehicle upper stage, the space vehicle maneuver requirement is 509.7 m/s. Appendix C shows the CR3BP state at mission events and coast durations required to recreate this trajectory. This scenario is ideal for pursuing a robust trajectory over the deterministic optimal. The risk of spending additional nominal $\Delta V$ is low (an additional 1.6 m/s) and the potential payoff in terms of correcting errors is meaningful.

The majority of the savings for this trajectory are realized at the TCM following $\Delta V_{2}$. In the deterministic optimal trajectory, the TCM following PLF cost is 125.4 m/s $3\sigma$ compared to 51.1 m/s for the robust trajectory. Correcting accumulated velocity dispersion once attaining the target position at lunar flyby is expensive; with a high velocity magnitude and a relatively low $\Delta V_{2}$ magnitude there are two compounding effects. First, velocity dispersion orthogonal to the velocity vector at flyby effectively requires a plane change-like maneuver to correct, which is more expensive with a large nominal velocity. A major optimization that occurs in the robust trajectory is the minimization of the velocity dispersion at lunar flyby (an RSS of 4.67 m/s) when compared to the deterministic optimal trajectory (RSS of 75.2 m/s). Second, since $\Delta V_{2}$ is a relatively inexpensive maneuver, the corrected nominal savings from Eq. 53 is not applicable because the correction at $\Delta V_{2}$ is comparable in magnitude to the correction, and, in some cases greater. As a result, the first and third nominal maneuvers are the only corrected maneuvers incorporated in this problem. When modeled with the combined maneuver savings for $\Delta V_{2}$, the nonlinear program leverages the savings in an unrealistic way, resulting in an unrealistic combined savings which fails Monte Carlo verification.

In general, robust solutions also result in an earlier arrival to the target orbit. It is difficult to tell in Fig. 8, but the robust NRHO insertion position occurs 1923 km earlier in the NRHO path compared to the deterministic optimal insertion. A shorter duration transfer reduces the total dispersion growth that occurs from dynamics and process noise. More importantly, in this case, the robust trajectory is optimizing the avoidance of a path sensitivity to the error sources present.

Fig. 8

Robust NRI Trajectory with Free Initial Plane

Table 4 Robust NRI trajectory cost comparison

Table 5 shows the result of a study comparing the sensitivity of multiple NRI trajectories with a free initial orbital plane to variations in stochastic parameters. The trajectories compared are: (1) the deterministic optimal trajectory in Table 4; (2) the robust trajectory in Table 4; (3) a new robust trajectory created specifically for the new stochastic parameters. The results shown for Trajectories 1 and 2 are the TCM cost along the nominal trajectory using the algorithm described in Sect. 4.1 and the corresponding total cost upper bound. The nominal $\Delta V$ is not shown again as it does not change for each test for Trajectories 1 and 2. For Trajectory 3, each row represents a new robust trajectory with a new nominal cost and TCM cost, each the converged result from the NLP robust trajectory design method. There are numerous conclusions to be made from this table, related to the sensitivity of each trajectory to various error sources, which error source is driving the large velocity dispersion after PLF, and once a robust trajectory is found for a specific set of error sources (Trajectory 2), whether it continues to perform well to variations in the error sources or is it beneficial to find a new robust trajectory for each change in error sources.

First, observe the change in cost associated with changes to the initial dispersion. Reducing the initial $1\sigma$ position dispersion from 1 km to 100 m results in a large reduction in TCM cost along the deterministic optimal trajectory (200.86–139.99 m/s). This highlights that the deterministic optimal trajectory is sensitive to initial position dispersion. On the other hand, the TCM cost along the robust trajectory is only reduced from 121.49 to 120.29 m/s with the same change in initial position dispersion, which leads to the conclusion that the robust trajectory is robust to initial position dispersion. The TCM after powered lunar flyby continues to be the major cost driver due to large velocity dispersion. The robust trajectory in these cases continues to minimize the velocity dispersion at PLF and the resulting $3\sigma$ RSS of the TCM following PLF.

Second, observe the change in cost associated with changes to the nominal maneuver execution error. A reduction in $1\sigma$ nominal maneuver execution error from 10 to 1 m/s results in a decrease along the deterministic optimal trajectory from 200.86 to 142.39 m/s. The same change to nominal maneuver execution error for the robust trajectories reduces the cost from 121.49 to 41.30 m/s, a larger difference. While the robust trajectory is less sensitive to initial position dispersion it appears to be more sensitive to nominal maneuver execution error. Both trajectories appear to exhibit similar sensitivity to changes in TCM execution error and process noise; decreases to each of these error sources results in a reduction to the cost of corrections. Even in the case with the lowest error source magnitudes, the $3\sigma$ TCM cost is reduced from 19.27 to 11.73 m/s while the nominal $\Delta V$ increases by either 0.5 m/s or 1.6 m/s, further highlighting that the robust trajectory is a worthwhile pursuit with minimal risk of an overall increase in cost.

Third, the performance of optimal TCMs along Trajectory 2 appear to perform quite comparably to a new robust convergence for each reduction in error source values. While this phenomenon has not been extensively tested to verify its universality, in this instance, identifying a robust trajectory to larger error sources appears to also be robust to reductions in smaller magnitude error sources such that there are diminishing savings realized by finding a new robust trajectory.

Table 5 Robust trajectory cost comparison, NRI trajectory with free initial orbital plane

6.2 Robust NRHO Rendezvous Trajectory

The next scenario analyzes an active chaser spacecraft trailing a passive target in the same NRHO⁵ by a specified amount of time (or distance, but the specific distance for a corresponding time delay depends on the true anomaly). Two nominal impulsive maneuvers are allowed by the chaser with the goal of rendezvous with a future target position. The initial and final segments are again flexible in duration resulting in the optimization of the location to perform the two nominal impulsive maneuvers. This method explores long range rendezvous and optimization of impulsive $\Delta V$ rather than terminal guidance. Effectively, two phasing maneuvers are being performed by the chaser, occurring within the same NRHO orbital period.

The deterministic optimal result for any initial and final position within the same orbital period is interesting in this case; with varying chaser trail durations, the location for the two nominal $\Delta V$s remains nearly constant. Figure 9 shows five different initial conditions determined by the duration of time delay between the chaser and the target. All initial chaser positions precede the first $\Delta V$. The nominal $\Delta V$ total varies quite significantly from 0.265 m/s in the 5 min delay case to 38.9 m/s in the 12 h delay case. The transfer durations are likely unrealistic for manned chasers with durations between nominal $\Delta V$s that vary little between cases: 5.29 days for the 12 h delay, 5.76 days for the 5 min delay.

Fig. 9

NRHO Deterministic Optimal Rendezvous Trajectories

As a connection between the NRI trajectory and the subject NRHO rendezvous trajectory, Fig. 10 shows the resulting deterministic optimal trajectory with the initial state equal to the robust NRHO insertion state from Fig. 8. The delay between chaser and target is adjusted to 6 min and 3.77 s such that the target is 100 km in the lead at NRI. The deterministic cost in this scenario is quite minimal, 0.379 m/s, with a transfer duration of 4.90 days.

Fig. 10

Deterministic optimal rendezvous post-NRI with optimal TCMs

Considering the minimal nominal $\Delta V$, the 100 km separation at NRI case with only 0.379 m/s deterministic $\Delta V$ cost could potentially exhibit large variations when comparing the deterministic optimal trajectory to the robust equivalent. Two robust comparisons that apply the initial dispersion covariance at different locations are presented that answer slightly different questions. In Case 1, the initial dispersion covariance is applied at $\Delta V_{1}$. This scenario finds the optimal robust combination without increasing the stochastic cost through additional coast in the first segment. In Case 2, the initial dispersion covariance is applied at the beginning of the trajectory and grows throughout the coast prior to $\Delta V_{1}$. Case 2 finds the optimal robust rendezvous trajectory given the initial conditions at NRI and accounts for the stochastic cost increase of coasting in the first segment.

Figure 10 shows the error sources utilized in both robust trajectory cases. Due to the small nominal $\Delta V$ magnitude, the nominal $\Delta V$ error is reduced to 10 cm/s $1\sigma$; such a small maneuver would likely be performed by a spacecraft RCS subsystem. Process noise is the larger of the values frequently used in this dissertation, simulating disturbances from a manned vehicle. The initial position dispersion matches the NRI target position dispersion constraint as a connection to the NRI trajectory development problem.

Figure 11 shows the robust trajectory result for Case 1 where the initial dispersion covariance is applied at $\Delta V_{1}$. Figure 12 shows the robust trajectory result for Case 2 where the initial dispersion is applied at trajectory node 1 (the initial chaser position). Table 6 shows the cost comparison of the deterministic optimal with optimal TCMs, the Case 1 robust, and Case 2 robust trajectories. Transfer durations decrease from the deterministic optimal’s 4.90 days to 5.20 h for Case 1 and 9.14 h for Case 2.

Fig. 11

Robust NRHO rendezvous trajectory, initial dispersion applied at $\Delta V_{1}$

Fig. 12

Robust NRHO rendezvous trajectory, initial dispersion applied at trajectory node 1

Table 6 Robust NRHO rendezvous trajectory cost comparison

A small study was performed to compare the sensitivity of the robust trajectory to variations in process noise and target dispersion constraint. Figure 10 shows the baseline error sources for Case 1 and Case 2 which appear in the first and fourth rows of Table 7. Less process noise and a larger target position dispersion are tested to observe the sensitivity of the robust results to error sources. The initial dispersion and maneuver execution error remain unchanged from Fig. 10. Rather than replotting each trajectory, the NRHO true anomaly (TA) for $\Delta V_{1}$ (TA1) and $\Delta V_{2}$ (TA2) is shown to define the nominal trajectory. As the stochastic cost increases with more process noise or a more stringent target dispersion constraint, the optimal robust solution slides toward a more expensive (and shorter duration) nominal trajectory. The opposite is true for the case with less process noise and a less stringent target position dispersion constraint.

Table 7 Robust NRHO rendezvous trajectory sensitivity to process noise and target position dispersion constraint

The ratio of nominal $\Delta V$ to TCM $\delta V$ in this scenario is skewed heavily toward the TCM cost. As a result, there is a large opportunity to spend a little more nominal $\Delta V$ in exchange for significant TCM savings resulting in a drastic change to the optimal trajectory. The robust trajectory exhibits similar modifications but on a larger scale for this example: a shorter transfer duration and earlier arrival to the target state minimizes state dispersion growth through problem dynamics and random disturbances. Also, while not explicitly shown through additional figures, optimizing the number and locations of TCMs mitigates a significant increase in TCM $\delta V$ with changes in error source magnitudes when compared to a fixed TCM set.

7 Results Verification

7.1 Stochastic Results Verification via Monte Carlo Analysis

The first comparison verifies that the modeled stochastic TCM estimates are representative of realistic magnitudes when compared to a Monte Carlo analysis. Each Monte Carlo sample represents a full pass through the nominal trajectory with error sources incorporated as samples of random Gaussian error sources of the appropriate variance. In more detail, at the beginning of each trajectory, the initial state serves as the mean position and velocity. The initial state dispersion is incorporated prior to propagating the appropriate $\Delta t$ to the next random trajectory event. Once at the appropriate time along the trajectory, the actual $\Delta V$ magnitude of a correction that achieves the target position is iteratively calculated (using Matlab’s fsolve). The correction error or nominal maneuver error is incorporated in the current dispersed trajectory state and the process is repeated. Each propagation also incorporates random accelerations (process noise) discretely at each time step of a fixed Runge–Kutta 4th-order integration. Following the modeling of 1000 individual dispersed trajectories, the statistics of the magnitude of each correction form the metric by which the modeled results in this dissertation will be compared. The magnitude of a vector is no longer a Gaussian random variable: all values are positive (it is not zero mean) and it is not symmetric about the mean. As such, to produce a $3\sigma$-equivalent value for comparison, a percentile calculation is used to compute a value that contains 99.7% of the sample magnitudes.

Table 8 shows the results of a 1000 run Monte Carlo analysis alongside the stochastic estimates for the robust NRHO insertion trajectory with a free initial orbital plane in Sect. 6.1 (Fig. 8). The linear covariance-based estimates are conservative, however not excessively large. The conservatism of the results is expected; 3 RSS of the TCM covariance matrix bounds the worst case direction of covariance alignment [28]. These results verify that the robust trajectory design method is producing results that are representative stochastic estimates given the error sources present. The magnitude of the correction to $\Delta V_{1}$ appears to be the only outlier in the trend of conservatism with the linear covariance-based estimates.

Table 8 Robust NRI Monte Carlo verification results

7.2 Optimal TCM Set Verification

The purpose of this verification step is to test the optimality of the TCM set chosen using a genetic algorithm. Two sets of results are verified: first, whether the TCM optimization scheme along a nominal trajectory described in Sect. 4.1 finds the optimal TCM set; second, if the nonlinear program converges to the optimal set when finding the robust trajectory. As a reminder, the nonlinear program starts with an initial guess trajectory with the number and location of TCMs identified by the fast optimization algorithm described in Sect. 4.1. The initial trajectory nodes are placed at the TCMs and fixed there. The nonlinear program adjusts the segment durations, which in turn modifieds the location of the TCMs, such that the TCMs continue to be optimized as the NLP iterations occur. The total number of TCMs is not modified in the genetic algorithm search. Each of the following genetic algorithm searches is allowed 500 generations with a population size of 100.

The TCM set verification is along the robust LEO to powered lunar flyby to NRI trajectory with free initial orbital plane (Fig. 8). Table 9 shows the comparison between the fast optimization method along the robust trajectory and the genetic algorithm results as well as the nonlinear program converged TCM set. As another clarification, the fast optimization method was run as a test following NLP convergence of the robust trajectory to produce the results in Table 9, but that is not the normal order of operations. The fast optimization method results in a total $3\sigma$ TCM magnitude of 122.0 m/s while the genetic algorithm produces a TCM set that costs 121.5 m/s. The fast TCM optimization in this case runs in 39 s without parallel processing while the genetic algorithm takes 126 s with parallel processing on 7 cores. All of the results are within 0.5% of each other. This instills confidence in the fast TCM optimization method and the accuracy of previous results presented.

Table 9 Optimal TCM set verification using genetic algorithm

7.3 Robust Trajectory Verification

The purpose of this section is to verify a converged trajectory’s optimality via a different optimization method. The trajectory chosen to verify is the two-burn NRHO rendezvous trajectory from Sect. 6.2, specifically “Robust - Case 2” from Table 6. This trajectory was chosen because it can be simplified to a problem of two independent variables with an associated cost. A mission map displaying the cost on the z-axis enables visual verification of two independent problem variables: coast duration in the first segment prior to nominal $\Delta V_{1}$ and coast duration in the final segment following $\Delta V_{2}$ (the rendezvous maneuver). The target begins 100 km in the lead in each scenario and follows the natural motion trajectory throughout the scenario. By prescribing the first and last segments’ coast times the location of the nominal maneuvers is determined. The result is a fixed rendezvous time for each specific combination, but the transfer time and rendezvous location are variable across combinations. Each individual combination then represents a prescribed $\Delta V_{1}$ and $\Delta V_{2}$ position and fixed transfer duration, which has a single solution (similar to Lambert’s problem). The cost associated with each combination’s singular solution is displayed on the mission map. Single differential correction method is used to adjust the chaser velocity to meet the target position at the specified time.

The first step is verification of the deterministic optimal rendezvous trajectory and comparison to the NLP-converged solution in Fig. 12. Figure 13 shows the contour plot for the deterministic rendezvous cost as a function of the coast time in the first and last segment and the corresponding minimum impulse trajectory. The contour represents an ideal solution space for use by a gradient-based solver with a single minimum value and a monotonic decrease toward the minimum. Validation of the optimal solution is successful as the result matches the NLP-converged deterministic optimal trajectory in Fig. 10.

Fig. 13

Nominal $\Delta V$ optimization via mission map—NRHO Rendezvous

Next, the optimal TCM set cost is computed along each nominal trajectory in the mission map (Fig. 13a). Figure 14 shows the contour of total $3\sigma$ TCM cost. One immediate observation is a nearly opposite cost incentive compared to nominal $\Delta V$; an increase in the duration of coast in segment n increases the nominal $\Delta V$ cost while the opposite is true for $3\sigma$ TCM cost. Another observation is the apparent sub-structure and lack of smoothness in the TCM cost contour. This is an artifact of the optimal TCM set being limited to the set of discretized time increments generated during numerical integration and demonstrates the need for assigning TCMs at segment intersections during optimization. This plot was attempted to be smoothed by increasing the number of nonlinear integration time steps, however, it does not completely rectify the issue. Without the attempted smoothing as shown (which is otherwise costly in terms of additional computation required), the gradient frequently changes sign in an unpredictable way, preventing gradient-based convergence.

Fig. 14

Optimal $3\sigma$ TCM cost mission map

Finally, the robust mission map shows the combination of nominal $\Delta V$ plus $3\sigma$ TCM $\delta V$ for the purpose of verifying the robust trajectory results in Fig. 12 and Table 6. Figure 15a shows the robust mission map contour representing the total cost upper bound for each trajectory. The minimum value is identified on the contour plot and the corresponding robust trajectory is shown in Fig. 15b. The results successfully verify the robust NRHO rendezvous trajectory identified in Sect. 6.2 is the two-impulse local minimum cost solution. The solution space is mostly monotonically decreasing toward the minimum value with the exception of a ridge that forms with long duration coasts in segments 1 and n (representing short duration transfers near apolune).

Fig. 15

Robust optimization via mission map—NRHO rendezvous

8 Conclusion

This paper ultimately presented a robust trajectory design method and two sets of robust trajectory results. As a foundation for the robust trajectory design method, supporting theory for system dynamics, multiple segment trajectory design, and stochastic analysis along a nominal trajectory was presented. Next, a trajectory correction maneuver (TCM) fast optimization method was presented alongside a sensitivity analysis comparing the total TCM cost with changes in error source magnitudes. Error sources included an initial state dispersion, maneuver execution error, and random white disturbances modeled as process noise. The TCM sensitivity analysis also supported building intuition on the correction of error sources, and which error sources benefit the most from an optimized TCM set. Next, the robust trajectory design method was presented where the nominal trajectory and TCMs were then simultaneously optimized using nonlinear programming. Finally, two robust trajectory results were presented: a LEO to powered lunar flyby to NRHO insertion trajectory and a two impulse NRHO rendezvous trajectory. A final section verified results via Monte Carlo analysis, genetic algorithm verification, and manual optimization via mission maps.

The first robust trajectory result was an expensive LEO to PLF to NRHO insertion trajectory that provided a noteworthy amount of savings for a space vehicle. Savings was acquired by avoiding path sensitivities that were amplified by error sources, in addition to minor savings through shortening the overall trajectory duration. A study was performed to determine if the robust trajectory found with the largest error sources is a viable choice for smaller magnitude error sources. In this case, it turned out that there were minimal additional gains to be had by developing a new robust trajectory to new error sources and that the original robust trajectory performed well.

The second robust trajectory result was an NRHO rendezvous scenario where the deterministic optimal trajectory had a very minimal nominal cost. The robust trajectory optimization resulted in a significant change to the trajectory and significant savings percentage-wise managing state dispersion. The majority of the savings in the second case is attributed to shortening a long duration transfer and the corresponding error growth.

Additionally, it was shown that robust trajectories and the corresponding TCM cost of managing state dispersion is dependent on mission-specific error sources. Various sets of error sources were applied to the optimal deterministic LEO to PLF to NRHO insertion trajectory. The TCM cost of the optimal TCM set was compared with another method of selecting TCMs that visually looks about right. Considering the optimal TCM set, there was variation in the total TCM cost with variation in error sources, which in turn affects the robust trajectory. The magnitude of TCM cost increase with increased error sources was mitigated in many cases by optimizing the number and location of TCMs, demonstrated by the comparison with the LAR TCM cost.

The method developed to converge to the robust trajectory was presented using a multisegment approach and nonlinear programming. The most time consuming aspect of the method was implementation of analytical gradients of the problem cost and constraints. A new method to optimize the number and location of TCMs along a nominal trajectory was presented and implemented. Once the optimal TCM set was found along the initial guess trajectory, the trajectory segmentation was performed such that the optimal TCM locations are tied to specific nodes, allowing simultaneous optimization of the nominal trajectory and the TCM locations with NLP iterations. Convergence to the robust trajectory was guided by a cost function which considered the $\Delta V$ upper bound: the sum of the deterministic trajectory cost plus the stochastic cost of an optimal TCM set.

Appendices

Appendix A: Analytical Gradients

The design method in this paper computes, propagates required values, and provides analytical gradients of the cost function and constraints with respect to the problem parameters, $\varvec{S}$, to the NLP. Many stochastic cost terms involve STMs, which require the propagation of second-order STTs to compute the gradient analytically. Similar to propagating second-order STTs, the gradient of QBM terms requires propagating a tensor that characterizes the state sensitivity of the accumulated process noise covariance, $\frac{\partial {\bar{Q}}\left( t_{1},t_{0}\right) }{\partial \varvec{x}_{0,i}}$. This will be referred to as the Q bar tensor, or QBT. This section provides an overview of two gradient formulations: first, a sequential method for assembling the gradient of multiple TCMs and second, the propagation and manipulation of the QBT.

1.1 A.1 Multiple TCM Cost Analytical Gradient

The partial derivative of the deterministic cost, deterministic constraints, a single TCM RSS magnitude, and the target position dispersion covariance constraint are derived in more detail in [20]. This paper incorporates multiple TCMs, maneuver execution error, and process noise. A portion of the derivation for a single TCM is repeated here.

The approach used to calculate the gradient of multiple TCMs starts with the gradient of a single TCM. The partial derivative of the RSS of a single TCM’s covariance, $\sigma _{\delta V_{r}}$, with respect to a segment parameter vector $\varvec{s}_{i}$ is an application of matrix differentiation rules.

$$\begin{aligned} \frac{\partial \sigma _{\delta V_{r,1}}}{\partial \varvec{s}_{i}}=\left[ \begin{array}{cc} \frac{\partial \sigma _{\delta V_{r,1}}}{\partial \varvec{x}_{0,i}}&\frac{\partial \sigma _{\delta V_{r,1}}}{\partial \Delta t_{i}}\end{array}\right] \end{aligned}$$

(75)

Showing the partial derivative of $\sigma _{\delta V_{r}}^{2}$ with respect to a segment initial state makes the following derivation slightly cleaner. Maneuver execution error and process noise are also assumed to be zero for this derivation and will be subsequently included.

$$\begin{aligned} \left[ \frac{\partial \sigma _{\delta V_{r,1}}^{2}}{\partial \varvec{x}_{0,i}}\right] _{y}&=\frac{\left[ \partial \text {tr}\left( T_{1}P_{c_{1}}^{-}T_{1}^{\top }\right) \right] }{\left[ \partial \varvec{x}_{0,i}\right] _{y}} \end{aligned}$$

(76)

$$\begin{aligned}&=\text {tr}_{bg}(\left[ \frac{\partial T_{1}}{\partial \varvec{x}_{0,i}}\right] _{bd,y}\left[ P_{c_{1}}^{-}\right] _{dw}\left[ T_{1}\right] _{gw}+\left[ T_{1}\right] _{bp}\left[ \frac{\partial P_{c_{1}}^{-}}{\partial \varvec{x}_{0,i}}\right] _{pq,y}\left[ T_{1}\right] _{gq}\nonumber \\&\quad +\left[ T_{1}\right] _{bd}\left[ P_{c_{1}}^{-}\right] _{dw}\left[ \frac{\partial T_{1}}{\partial \varvec{x}_{0,i}}\right] _{gw,y}) \end{aligned}$$

(77)

where index notation is used, combined with brackets to avoid confusion when indices are adjacent to other subscripts. The subscripts on the trace operator ($\text {tr}_{bg}$) identify the indices that the trace is performed on, resulting in the corresponding matrix indices collapsing to a scalar. Additionally, when segment i is relevant to the STM terms inside $T_{1}$ or $P_{c_{1}}^{-}$, their partial derivative requires propagated STT terms:

$$\begin{aligned} \frac{\left[ \partial P_{c_{1}}^{-}\right] _{pq}}{\left[ \partial \varvec{x}_{0,i}\right] _{y}}&=\frac{\partial \Phi \left( t_{c_{1}},t_{0}\right) _{pu}\left[ P_{0}\right] _{uv}\Phi \left( t_{c_{1}},t_{0}\right) _{qv}}{\left[ \partial \varvec{x}_{0,i}\right] _{y}} \end{aligned}$$

(78)

$$\begin{aligned}&=\Phi \left( t_{c_{1}},t_{0}\right) _{pu,y}\left[ P_{0}\right] _{uv}\Phi \left( t_{c_{1}},t_{0}\right) _{qv}+\Phi \left( t_{c_{1}},t_{0}\right) _{pu}\left[ P_{0}\right] _{uv}\Phi \left( t_{c_{1}},t_{0}\right) _{qv,y} \end{aligned}$$

(79)

$$\begin{aligned} \frac{\left[ \partial T_{1}\right] _{bd}}{\left[ \partial \varvec{x}_{0,i}\right] _{y}}&=\frac{\left[ \partial \left( \left[ \begin{array}{cc} -\Phi _{rv}^{-1}\left( t_{n_{1}},t_{c_{1}}\right) \Phi _{rr}\left( t_{n_{1}},t_{c_{1}}\right)&\quad -I_{3\times 3}\end{array}\right] \right) \right] _{bd}}{\left[ \partial \varvec{x}_{0,i}\right] _{y}} \end{aligned}$$

(80)

The rr and rv subscripts identify top-left and top-right $3\times 3$ submatrices of the STM terms. When applied to STT terms, the result is a $3\times 3\times 6$ tensor, with no cropping occurring in the third dimension.

$$\begin{aligned} \frac{\partial \left( \Phi _{rv}^{-1}\left( t_{n_{1}},t_{c_{1}}\right) _{bz}\Phi _{rr}\left( t_{n_{1}},t_{c_{1}}\right) _{zd}\right) }{\left[ \partial \varvec{x}_{0,i}\right] _{y}}&=\frac{\partial \Phi _{rv}^{-1}\left( t_{n_{1}},t_{c_{1}}\right) _{bz}}{\left[ \partial \varvec{x}_{0,i}\right] _{y}}\Phi _{rr}\left( t_{n_{1}},t_{c_{1}}\right) _{zd}\nonumber \\&\quad +\Phi _{rv}^{-1}\left( t_{n_{1}},t_{c_{1}}\right) _{bz}\Phi _{rr}\left( t_{n_{1}},t_{c_{1}}\right) _{zd,y} \end{aligned}$$

(81)

An application of the matrix inverse derivative property and STT terms are required to evaluate the partial derivative of $\Phi _{rv}^{-1}\left( t_{n_{1}},t_{c_{1}}\right)$:

$$\begin{aligned} \frac{\partial \Phi _{rv}^{-1}\left( t_{n_{1}},t_{c_{1}}\right) _{bz}}{\left[ \partial \varvec{x}_{0,i}\right] _{y}}=-\Phi _{rv}^{-1}\left( t_{n_{1}},t_{c_{1}}\right) _{bo}\Phi _{rv}\left( t_{n_{1}},t_{c_{1}}\right) _{oe,y}\Phi _{rv}^{-1}\left( t_{n_{1}},t_{c_{1}}\right) _{ez} \end{aligned}$$

(82)

The same fundamental steps apply when evaluating the partial derivative with respect to $\Delta t_{i}$ but the results are simplified by the fact that tensors are not required. Equation 11 is applied for STM time sensitivity rather than utilizing STTs for STM state sensitivity.

Some creative manipulation of STM endpoints is required to obtain the appropriate sensitivity in many cases. As segments are propagated independently of one another each NLP iteration, from the beginning of each segment for the corresponding duration, care must be taken to only incorporate the sensitivity of modifications to the appropriate time indices for the corresponding segment, and not the entire STM sensitivity between endpoints (when the time between corrections and/or a target might span multiple segments).

When multiple TCMs are performed along a nominal trajectory, each at $t_{c_{k}}$ with execution error covariance $R_{TCM}$, the total TCM RSS $\sigma _{\delta V}$ gradient requires gradients of each individual $\sigma _{\delta V_{r,k}}$ plus the gradient of $\sigma _{\delta V_{v}}$. Modifications to TCMs have impacts to the dispersion covariance that affect the gradient of subsequent TCMs. The sequential nature of the following formulation maintains the sensitivity of each TCM to modifications in elements that have an impact on the preceding dispersion covariance. Said differently, each TCM affects the dispersion covariance at all future TCMs. The following sequential covariance sensitivity formulation simplifies this operation.

The first TCM, $k=1$, mirrors the single TCM scenario with the addition of $R_{TCM}$. The RSS of the first TCM, $\sigma _{\delta V_{r,1}}$, is

$$\begin{aligned} \sigma _{\delta V_{r,1}}=\sqrt{\text {tr}\left( T_{1}P_{c_{1}}^{-}T_{1}^{\top }+R_{TCM}\right) } \end{aligned}$$

(83)

The post-TCM covariance is defined by Eq. 47. To simplify notation, the gradient of $\sigma _{\delta V_{r,1}}$ with respect to a segment initial state will be represented by the function ${\mathcal {D}}$, where ${\mathcal {D}}$ and the partials being passed represent the application of the single TCM gradient derivation in Eqs. 75 through 82:

$$\begin{aligned} \frac{\partial \sigma _{\delta V_{r,1}}}{\partial \varvec{x}_{0,i}}={\mathcal {D}}\left( T_{1},P_{c_{1}}^{-},R_{TCM},\frac{\partial T_{1}}{\partial \varvec{x}_{0,i}},\frac{\partial P_{c_{1}}^{-}}{\partial \varvec{x}_{0,i}}\right) \end{aligned}$$

(84)

The second TCM ($k=2$) now incorporates the effects of TCM 1 to the next covariance update $P_{c_{2}}^{-}$; assuming the next covariance update is another TCM:

$$\begin{aligned} \sigma _{\delta V_{r,2}}=\sqrt{\text {tr}\left( T_{2}P_{c_{2}}^{-}T_{2}^{\top }+R_{TCM}\right) } \end{aligned}$$

(85)

$$\begin{aligned} P_{c_{2}}^{-}&=\Phi \left( t_{c_{2}},t_{c_{1}}\right) \left( \left( I+N_{1}\right) P_{c_{1}}^{-}\left( I+N_{1}\right) ^{\top }+GR_{TCM}G^{\top }\right) \Phi \left( t_{c_{2}},t_{c_{1}}\right) {}^{\top } \end{aligned}$$

(86)

The state sensitivity of the dispersion before TCM 2, $\frac{\partial P_{c_{2}}^{-}}{\partial \varvec{x}_{0,i}}$, can be expressed as another function ${\mathcal {J}}$, shortening another lengthy application of matrix differentiation. Evaluating Eq. 87 is similar to Eq. 75 with the addition of the partial derivative of the TCM execution error term, which is nonzero due to being multiplied by STMs.

$$\begin{aligned} \frac{\partial P_{c_{2}}^{-}}{\partial \varvec{x}_{0,i}}={\mathcal {J}}\left( T_{1},\frac{\partial T_{1}}{\partial \varvec{x}_{0,i}},P_{c_{1}}^{-},\frac{\partial P_{c_{1}}^{-}}{\partial \varvec{x}_{0,i}},\Phi \left( t_{c_{2}},t_{c_{1}}\right) ,\frac{\partial \Phi \left( t_{c_{2}},t_{c_{1}}\right) }{\partial \varvec{x}_{0,i}},R_{TCM}\right) \end{aligned}$$

(87)

Now $\frac{\partial P_{c_{2}}^{-}}{\partial \varvec{x}_{0,i}}$ is expressed as a function of gradients at TCM 1 and the dynamics between TCMs 1 and 2. Calculating the dispersion covariance sensitivities sequentially enables subsequent TCMs and their gradients to be expressed as a function of values at the previous dispersion covariance update.

For corrected nominal maneuvers, the gradient of Eqs. 53 and 55 follows a similar process. The only new term is now the partial derivative of the unit vector in the direction of the nominal maneuver, ${\hat{i}}_{\Delta \varvec{V}}$.

$$\begin{aligned} \frac{\partial {\hat{i}}_{\Delta \varvec{V}}}{\partial \varvec{x}_{0,i}}=\frac{\partial {\hat{i}}_{\Delta \varvec{V}}}{\partial \varvec{\Delta V}}\frac{\partial \varvec{\Delta V}}{\partial \varvec{x}_{0,i}} \end{aligned}$$

(88)

where

$$\begin{aligned} \frac{\partial {\hat{i}}_{\Delta V}}{\partial \varvec{\Delta V}}=\frac{I_{3\times 3}}{\Vert \varvec{\Delta V}\Vert }-\frac{\varvec{\Delta V}\varvec{\Delta V}^{\top }}{\Vert \varvec{\Delta V}\Vert ^{3}} \end{aligned}$$

(89)

Suppose the nominal maneuver occurs at the mth trajectory node. The corresponding $\Delta \varvec{V}$ is only sensitive to modifications in segments $m-1$ and m. Therefore, the only nonzero gradients are with respect to $\varvec{x}_{0,m-1}$, which is shown below, and $\varvec{x}_{0,m}$, which is trivial.

$$\begin{aligned} \frac{\partial \varvec{\Delta V}}{\partial \varvec{x}_{0,m-1}}=\frac{\partial \left( \varvec{v}_{0,m}-\varvec{v}_{f,m-1}\right) }{\partial \varvec{x}_{0,m-1}}=\left[ \begin{array}{cc} -\Phi _{m-1,vr}&-\Phi _{m-1,vv}\end{array}\right] \end{aligned}$$

(90)

where $\Phi _{m-1}$ corresponds to the STM from the beginning to the end of segment $m-1$ and subscripts vr and vv are its corresponding bottom-left and bottom-right $3 \times 3$ sub-matrices.

The gradient of the total stochastic cost is the sum of each individual gradient.

1.2 A.2 Accumulated Process Noise Covariance Gradient

When including the effect of process noise and evaluating $\frac{\partial P_{c_{1}}^{-}}{\partial {\bar{x}}_{0,i}}$ in Eq. 58, $\frac{\partial {\bar{Q}}\left( t_{c_{1}},t_{0}\right) }{\partial \varvec{x}_{0,i}}$, the QBT, becomes a required term. These QBM state sensitivities are obtained via numerical integration of Eq. 91, with a brief derivation following. The first step involves taking the partial derivative of $\dot{{\bar{Q}}}$ (Eq. 57) with respect to the initial state. Applying the product rule results in Eq. 91 which is numerically integrated to obtain the QBT, similar to an STT, with initial conditions $\frac{\partial {\bar{Q}}(t_{0},t_{0})}{\partial \varvec{x}(t_{0})}=0_{6\times 6\times 6}$:

$$\begin{aligned} \left[ \frac{\partial \dot{{\bar{Q}}}(t,t_{0})}{\partial \varvec{x}(t_{0})}\right] _{ijk}&=\frac{\partial F(t)_{i,m}}{\partial \varvec{x}(t_{0})_{k}}{\bar{Q}}(t,t_{0})_{mj}+F(t)_{i,m}\frac{\partial {\bar{Q}}(t,t_{0})_{mj}}{\partial \varvec{x}(t_{0})_{k}}\nonumber \\&\quad +\frac{\partial F(t)_{jm}}{\partial \varvec{x}(t_{0})_{k}}{\bar{Q}}(t,t_{0})_{im}+F(t)_{j,m}\frac{\partial {\bar{Q}}(t,t_{0})_{im}}{\partial \varvec{x}(t_{0})_{k}} \end{aligned}$$

(91)

where $F\left( t\right) _{i,j}$ is the system jacobian. A chain rule application utilizes the second derivative of the system dynamics with respect to the state, $F\left( t\right) _{i,jk}$:

$$\begin{aligned} \frac{\partial F(t)_{ij}}{\partial \varvec{x}(t_{0})_{k}}=\frac{\partial F(t)_{ij}}{\partial \varvec{x}(t)_{m}}\frac{\partial \varvec{x}(t)_{m}}{\partial \varvec{x}(t_{0})_{k}}=F(t)_{i,jm}\Phi (t,t_{0})_{m,k} \end{aligned}$$

(92)

Similar to the QBM, some manipulation of the QBT is also required to obtain the appropriate QBT endpoints and its effect at the appropriate time. Finding the equation for sequential QBT combination (i.e., assembling $\frac{\partial {\bar{Q}}_{t_{2}}\left( t_{2},t_{0}\right) }{\partial \varvec{x}(t_{0})}$ from $\frac{\partial {\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right) }{\partial \varvec{x}(t_{0})}$ and $\frac{\partial {\bar{Q}}_{t_{2}}\left( t_{2},t_{1}\right) }{\partial \varvec{x}(t_{1})}$) involves taking the partial derivative of Eq. 59, which equals the following after two chain rule applications and term collection:

$$\begin{aligned} \frac{\partial {\bar{Q}}_{t_{2}}\left( t_{2},t_{0}\right) }{\partial \varvec{x}(t_{0})}&=W_{ij,m}\Phi \left( t_{1},t_{0}\right) _{m,k}+\Phi \left( t_{2},t_{1}\right) _{i,m}\frac{\partial {\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right) _{mn}}{\partial \varvec{x}(t_{0})_{k}}\Phi \left( t_{2},t_{1}\right) _{j,n} \end{aligned}$$

(93)

where

$$\begin{aligned} W_{ij,m}&=\frac{\partial {\bar{Q}}_{t_{2}}\left( t_{2},t_{1}\right) _{ij}}{\partial \varvec{x}(t_{1})_{m}}+\Phi _{II}\left( t_{2},t_{1}\right) _{i,nm}{\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right) _{np}\Phi \left( t_{2},t_{1}\right) _{j,p}\nonumber \\&\quad +\Phi \left( t_{2},t_{1}\right) _{i,n}{\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right) _{np}\Phi _{II}\left( t_{2},t_{1}\right) _{j,pm} \end{aligned}$$

(94)

Subtracting a contribution involves taking the partial derivative of Eq. 61, performing a product rule and two chain rule applications, and collecting terms:

$$\begin{aligned} \frac{\partial {\bar{Q}}_{t_{2}}\left( t_{2},t_{1}\right) _{ij}}{\partial \varvec{x}(t_{1})_{k}}&=\left( \frac{\partial {\bar{Q}}_{t_{2}}\left( t_{2},t_{0}\right) _{ij}}{\partial \varvec{x}(t_{0})_{m}}-\Phi \left( t_{2},t_{1}\right) _{i,n}\frac{\partial {\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right) _{np}}{\partial \varvec{x}(t_{0})_{m}}\Phi \left( t_{2},t_{1}\right) _{j,p}\right) \Phi \left( t_{0},t_{1}\right) _{m,k}\nonumber \\&\quad -\Phi _{II}\left( t_{2},t_{1}\right) _{i,nm}{\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right) _{np}\Phi \left( t_{2},t_{1}\right) _{j,p}\nonumber \\&\quad -\Phi \left( t_{2},t_{1}\right) _{i,n}{\bar{Q}}_{t_{1}}\left( t_{1},t_{0}\right) _{np}\Phi _{II}\left( t_{2},t_{1}\right) _{j,pm} \end{aligned}$$

(95)

Appendix B: Parameter Values Used

• Earth gravitational parameter: $\mu _{E}=398600.4415\text { km}^{3}/\text {s}^{2}$.

• Moon gravitational parameter: $\mu _{M}=4902.8\text { km}^{3}/\text {s}^{2}$.

• Circular lunar orbit radius: 384,400 km.

Appendix C: Robust LEO to PLF to NRHO Insertion Trajectory Parameters

See Table 10.

Table 10 Robust NRI with flexible initial orbital plane trajectory states and durations in the CR3BP