A Low-Complexity Algorithm to Determine Trajectories Within the Circular Restricted Three-Body Problem

Abstract

With the growing volume of traffic within the Cislunar region, there is an increasing need for efficient techniques to propagate trajectories of spacecraft in the circular restricted three-body problem. A low-complexity algorithm utilizing interpolation and incorporating boundary conditions is introduced for generating accurate trajectories and periodic orbits within the Cislunar domain. The proposed approach offers a distinct advantage over existing iterative techniques, as it yields favorable results in terms of arithmetic and time complexities. Once the reliable low-complexity algorithm is developed, it is applied to relevant Cislunar trajectories. Finally, we have compared the time complexity of the proposed algorithm with that of a traditional orbit propagator. The algorithm achieves significant improvements in time complexity for various types of orbital trajectories compared to traditional iterative methods. It demonstrates approximately a 50% enhancement of time efficiency for low-Lunar, Lyapunov, near-rectilinear halo, and distant retrograde orbital trajectories.

1 Introduction

The Cislunar region, shown in Fig. 1, is gaining increased attention throughout the past few years, as 90 missions to the Moon are projected by 2030 [1], with additional missions to Mars. Many upcoming Cislunar missions are focused on the Lunar South pole, as well as periodic orbits about L$_1$ and L$_2$ of the Earth-Moon circular restricted three-body problem (CR3BP) system [2]. Here, L$_1$ and L$_2$ are the equilibrium points of the Earth-Moon system. Russia’s Luna 25 (2022) [3], South Korea’s KPLO (2022) [4], Japan and India’s joint LUPEX (2023) [5], and India’s Chandrayaan-3 (2024) [6] all are missions to observe, or land on, polar regions of the Moon. Additionally, NASA has multiple commercial Lunar payload services (CLPS) missions to the Lunar polar region. NASA’s Artemis program is a multi-stage program to reestablish a presence on the Moon; the first Artemis mission traveled in a distant retrograde orbit (DRO) about the Moon at the end of 2022 [7].

Fig. 1

Cislunar region

The dynamics that govern the motion in the CR3BP are highly non-linear and no closed-form solution has yet been derived. To be able to design trajectories in such a model, different numerical methods are required to analyze spacecraft trajectories that satisfy desired behaviors. Many different formulations of differential corrections algorithms exist within the context of targeting schemes [8, 9]. In recent times, with evolving computational techniques, many are based on free variables and constraints for trajectories that need to meet a certain set of conditions. One example consists of a method for generating long baseline solutions using multiple shooting techniques [10]. Therefore, following ongoing work on trajectory generation [11,12,13,14,15,16,17], the objective is to find an approximated solution to determine trajectories of the CR3BP with a low-complexity algorithm. To propagate orbits and uncertainty within the context of this non-linear realm, typical numerical integration techniques including Gauss–Legendre, Dormand–Prince, Chebyshev–Picard algorithms [18], Gragg–Bulirsch–Stoer [19], and the Adams–Bashforth method [20] are used. Each technique has its own benefits and disadvantages. Using a higher-order Runge–Kutta integrator (ODE45 in this investigation), the solution is usually more accurate. However, these techniques are typically computationally expensive. It is thus important to reduce the complexity of the problem.

Finite element methods (FEM) and finite difference methods (FDM) are conventional techniques in astrodynamics for solving equations by discretizing spatial data [21, 22]. A trade-off exists between resolution and speed when employing these approaches: coarse discretization provides faster results but sacrifices accuracy, whereas fine discretization improves accuracy at the cost of slower computations. When it comes to solving the equations involved in the CR3BP, traditional solvers face significant challenges due to the requirement of very fine discretization in both time and space. This results in a time-consuming process that can be daunting to handle. We propose a technique that utilizes fine discretization in time and space to determine trajectories in the CR3BP. This offers a more efficient alternative to traditional methods that are more challenging and time-consuming.

Efforts to address the need for efficient propagation methods in the CR3BP have extended beyond typical numerical techniques (see [23,24,25] and references therein). Researchers provided detailed explanations of the need for low-complexity algorithms [26], and utilized high-dimensional Poincaré maps for spacecraft orbit design in the CR3BP. Existing propagation methods have been compared in [27], including the polynomial approach and the authors designed a differential algebraic method to guarantee access to any point of a family without any numerical propagation. Additional advancements include the utilization of Gaussian process regression for propagation, efficient algorithms for computing invariant manifolds, orbit classification techniques, and nonlinear stability analysis of periodic orbits. In general, these approaches have enabled more precise predictions and analyses in the CR3BP. However, the existing literature and gap indicate the need for further improvements and low-complexity methods dedicated to efficient CR3BP propagation. This paper aims to bridge this gap by proposing a novel technique that incorporates innovative mathematical strategies to enhance efficiency in orbital propagation within the CR3BP framework.

The primary objective of this investigation is thus to develop a low-complexity algorithm that enables efficient trajectory determination within the Cislunar domain, including periodic orbits. This algorithm utilizes predefined boundary conditions instead of iterative methods based on initial conditions. High-fidelity discrete solutions are extracted at finite time steps, constructing a low-complexity propagation between these boundary conditions. The accuracy of the trajectory generated is demonstrated using analytical evidence within the given set of boundary conditions. A comprehensive description of the algorithm derivation and analysis of the arithmetic and time cost savings are provided. To produce analytical solutions and algorithms that are computationally tractable and inexpensive, particularly in the complex and chaotic three-body dynamics, it is important to address system structures in relevant equations, develop novel theories, and design low-complexity and reliable (in the sense of accuracy and stability) algorithms. For obtaining the position, velocity, and acceleration of the spacecraft within the three-body dynamics at defined finite time steps, ODE45 is utilized. The output data from this integration is then identified as predefined boundary conditions. Subsequently, the low-complexity algorithm in this study is employed to construct the trajectory of the spacecraft within the CR3BP. The study leverages the traditional equations of the CR3BP. Numerical tests are performed for several orbits, including a near-rectilinear halo orbit (NRHO) representing Gateway’s orbit, a direct retrograde orbit (DRO) representing part of the Artemis I trajectory, a low-Lunar orbit (LLO), and a Lyapunov orbit about L$_2$. The numerical results show that the proposed algorithm achieves approximately 50% improvement in time complexity for all these cases. Therefore, a ground-breaking model for orbit determination in the Cislunar region is achieved.

The paper is structured as follows.¹ First, Sect. 2 presents the dynamics of the circular restricted three-body problem, including supplemental information about differential corrections and the state transition matrix in Appendix A. Then, Sect. 3 develops the theory to obtain a low-complexity and reliable algorithm to describe smooth trajectories of the moving body in the presence of multiple gravitational fields. In Sec. 4, a numerical analysis based on the time complexity of the proposed algorithm is developed. Results are compared with a traditional method of orbit integration (i.e., ODE45) for all suggested orbits. Finally, we conclude the paper in Sect. 5.

2 Dynamical Model

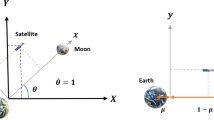
To model the problem, a system of differential equations in the CR3BP is written in dimensionless form [28], in such a way that the characteristic distance is defined as the time-averaged distance between the Earth and the Moon; and the characteristic time is selected to guarantee a dimensionless mean motion of the primaries with a value equal to unity. The mass ratio $\mu =m_{M}/(m_{M}+m_{E})$ is defined for the system, with $m_{M}$ and $m_{E}$ being the masses of the Moon and the Earth, respectively. A barycentric rotating frame is defined with the $\hat{x}$-axis directed from the Earth-Moon barycenter to the Moon, and the $\hat{z}$-axis from the barycenter in the direction of the system angular momentum vector. Figure 2 presents a schematic representation of the model. The Earth and Moon are located at positions $\bar{r}_{p}=[-\mu ,0,0]^T$ and $\bar{r}_{m}=[1-\mu ,0,0]^T$, respectively. The evolution of a spacecraft (s/c) position $\bar{r}_{rot}=[x,y,z]^T$ and velocity $\dot{\bar{r}}_{rot}=[\dot{x},\dot{y},\dot{z}]^T$ is governed by the following equations of motion [29]:

$$\begin{aligned} \displaystyle \ddot{x}-2\dot{y}=\frac{\partial U^{*}}{\partial x}; \ \ddot{y}+2\dot{x}=\frac{\partial U^{*}}{\partial y};\ \ddot{z}&=\frac{\partial U^{*}}{\partial z} \end{aligned}$$

(1)

where dots indicate derivatives with respect to dimensionless time. Then, $U^{*}=\frac{1-\mu }{r_{p-s/c}}+\frac{\mu }{r_{m-s/c}}+\frac{1}{2}(x^2+y^2)$ represents the pseudo-potential function for the system of differential equations; $r_{p-s/c}$ and $r_{m-s/c}$ are the distances of the s/c to the Earth and the Moon, respectively. The Jacobi constant (JC) is the only scalar integral for the given system which gives information of the energy of the s/c, i.e., $JC=2U^{*} -(\dot{x}^{2}+\dot{y}^{2}+\dot{z}^{2})$. Finally, note that motion exists in the vicinity of five equilibrium solutions in the given formulation. Such equilibrium solutions are denoted as $\text {L}_1$ to $\text {L}_5$ in Fig. 2. Such motion can be categorized by families of periodic orbits [30,31,32]. These orbits are usually leveraged for many distinct types of mission scenarios. In this research, different periodic orbits are propagated both using a classical integrator as well as the low-complexity algorithm proposed by the authors in the following section. Appendix A provides more information about the targetting scheme used to compute periodic orbits in this research.

Fig. 2

The CR3BP model represented in the barycentric rotating reference frame with the primaries, the third body and the 5 equilibrium points

3 Low-Complexity Algorithm for Smooth and Continuous Trajectory Determination

Trajectory propagation methods, such as Gauss–Legendre and Dormand–Prince [18], typically generate a trajectory in discrete steps based on a given set of conditions. In contrast, our proposed algorithm generates a trajectory by interpolating a function between a set of boundary conditions. While existing iterative techniques offer accurate solutions, they can be computationally expensive due to the need to compute all predecessors for each different time step. In contrast, the proposed technique generates a trajectory at a given time stamp without the need to compute all previous states from the beginning. This is achieved by using a piecewise continuous function based on polynomial interpolation, which offers a low-complexity solution compared to existing iterative methods. For the dynamics of the spacecraft in the CR3BP, the proposed interpolated polynomial function provides greater accuracy and computational efficiency than linear functions [33]. The differences between the proposed interpolation technique and iterative methods are represented in Table 1. To achieve computationally efficient and time-effective algorithms, particularly for complex and chaotic three-body dynamics, it is essential to consider system structures that result in low-complexity and reliable (in terms of accuracy and stability) algorithms. In this section, novel piecewise-defined functions are proposed to describe smooth trajectories of the spacecraft in CR3BP. While a linear trajectory is often assumed over a given time interval, in reality, trajectories are polynomials in time due to changes in position, velocity, and acceleration at each time stamp. The proposed algorithm can be extended to fully determine trajectories of the n-body problem at each time step, offering a low-complexity solution, but this investigation is limited to the CR3BP. Figure 3 presents a visual flowchart comparing the different trajectory propagation methods.

Table 1 Comparison between interpolation and iterative trajectory propagation methods

Fig. 3

Trajectory propagation using iterative and interpolation techniques

In the context of the CR3BP formulation discussed in the previous section, to obtain the position, velocity, and acceleration of the spacecraft within the three-body dynamics at each defined finite time step, ODE45 is employed, and the resulting data is used as predefined boundary conditions. In the CR3BP, the position, velocity, and acceleration data for the spacecraft are known, providing boundary conditions for each time interval. This would be equivalent to having measured states of spacecraft in regards to orbit determination. Using the Lagrange interpolation theorem with the six data points at the interval’s start and end, a unique degree-five polynomial is obtained that best fits or interpolates the data within the interval. Therefore, each body’s trajectory at any given time interval are uniquely determined as a degree-five polynomial in time, rather than linear in time. The trajectories of the spacecraft in CR3BP are described as piecewise-defined functions in time, ensuring continuity and differentiability for smoothness and curvature at any time domain of interest. To fully describe these functions explicitly and via a low-complexity algorithm, the proposed technique produces smooth, continuous, and differentiable trajectories of the spacecraft in CR3BP for any time domain of interest. Once these trajectories are fully determined, the position, velocity, and acceleration data of any object at any time are retrieved, even in continuous time changes. In this project, two types of complexities are considered: arithmetic and time complexities. The arithmetic complexity is determined by the number of floating-point operations required to execute the algorithm, whereas the time complexity is primarily related to the GPU execution time. These two types of complexities are interdependent, and any reduction in arithmetic complexity leads to a decrease in the GPU execution time. As demonstrated next, the proposed algorithm significantly reduces both complexities.

Let us consider a scenario where the position, velocity, and acceleration vectors, i.e., $\bar{x}(t_i), \dot{\bar{x}}(t_i)$, $\ddot{\bar{x}}(t_i)$ in $\mathbb {R}^3$, of the spacecraft are known at time $t_i$ for $i=0, 1, \ldots , n$ and $t_0<t_1< \cdots <t_n$. Thus, the trajectories of the spacecraft over n time intervals are described via n piecewise-defined functions. Moreover, these functions are defined at each interval $[t_k, t_{k+1}]$, where $k=0, 1, \ldots , n-1$, and from $\mathbb {R}^3$ to $\mathbb {R}$ such that the position functions (i.e. trajectories of the spacecraft) are expressed via

$$\begin{aligned} {G_k({x}(t))}={g}_{0,k}+{g}_{1,k}t+{g}_{2,k}t^2+{g}_{3,k}t^3 + {g}_{4,k}t^4 +{g}_{5,k}t^5, \end{aligned}$$

(2)

and the corresponding velocity and acceleration functions of the spacecraft at each given time interval, respectively, are denoted via,

$$\begin{aligned} {\dot{G_k}({{x}}(t))}= & {} {g}_{1,k}+2{g}_{2,k}t+3{g}_{3,k}t^2 + 4{g}_{4,k}t^3 + 5{g}_{5,k}t^4, \\ {\ddot{G_k}({{x}}(t))}= & {} 2{g}_{2,k}+6{g}_{3,k}t + 12{g}_{4,k}t^2 + 20{g}_{5,k}t^3 \end{aligned}$$

(3)

where $t_k \le t \le t_{k+1}$, x(t) is the dimensionless quantity of the vector $\bar{x}(t)$, and ${g}_{0,k}, {g}_{1,k}, \ldots , {g}_{5,k}$ are dimensionless quantities depend on the position, velocity, and acceleration of the spacecraft at each n time intervals. To accurately describe the trajectories of the spacecraft over n time intervals, it is necessary to explicitly determine the variables ${g}_{0,k}, {g}_{1,k}, \ldots , {g}_{5,k}$ for n time intervals. To do so, one has to solve a system of 6n equations. The brute-force method of calculating these variables in each time interval followed by n intervals yields the explicit equations describing the spacecraft’s trajectories at any time t with $\mathcal {O}(n^3)$ complexity. Therefore, a low-complexity algorithm is proposed that requires only $\mathcal {O}(n^2)$ operations, and hence to obtain these variables and describe the spacecraft’s trajectories at any time.

To achieve this, the following technique for determining the spacecraft’s trajectories is suggested. To begin with, the known vectors at the specific time values $t_{k}$ and $t_{k+1}$ are utilized, which serve as the boundary conditions for the $(k+1)$th time interval. These are expressed as:

$$\begin{aligned} G_k({x}(t_{k}))= & {} x(t_{k}) \nonumber \\ G_k(x(t_{k+1}))= & {} x(t_{k+1}) \nonumber \\ \dot{G_k}({{x}}(t_{k}))= & {} \dot{x}(t_{k}) \nonumber \\ \dot{G_k}({{x}}(t_{k+1}))= & {} \dot{x}(t_{k+1}) \nonumber \\ \ddot{G_k}({{x}}(t_{k}))= & {} \ddot{x}(t_{k}) \nonumber \\ \ddot{G_k}({{x}}(t_{k+1}))= & {} \ddot{x}(t_{k+1}), \end{aligned}$$

(4)

where ${{x}}(t_k), \dot{{x}}(t_k)$, and $\ddot{{x}}(t_k)$ are position, velocity, and acceleration dimensionless quantities of the vectors $\bar{x}(t_k), \dot{\bar{x}}(t_k)$, and $\ddot{\bar{x}}(t_k)$, respectively. Hence, within the time interval $[t_{k}, t_{k+1}]$, the motion of the spacecraft is expressed, as illustrated in Equations (2) and (3) adhering the boundary conditions Eq. (4). This allows to rewrite the set of equations as a matrix equation in the interval $[t_{k}, t_{k+1}]$ (note that there are n time intervals) s.t.

$$\begin{aligned} {\underbrace{\begin{bmatrix} 1 &{} t_{k} &{} t^2_{k} &{} t^3_{k} &{} t^4_{k} &{} t^{5}_{k} \\ 1 &{} t_{k+1} &{} t^2_{k+1} &{} t^{3}_{k+1} &{} t^{4}_{k+1} &{} t^{5}_{k+1} \\ 0 &{} 1 &{} 2t_{k} &{} 3t^{2}_{k} &{} 4t^{3}_{k} &{} 5t^{4}_{k} \\ 0 &{} 1 &{} 2t_{k+1} &{} 3t^{2}_{k+1} &{} 4t^{3}_{k+1} &{} 5t^{4}_{k+1} \\ 0 &{} 0 &{} 2 &{} 6t_{k} &{} 12t^{2}_{k} &{} 20t^{3}_{k} \\ 0 &{} 0 &{} 2 &{} 6t_{k+1} &{} 12t^{2}_{k+1} &{} 20t^{3}_{k+1} \end{bmatrix}}_{A_{k}}}\underbrace{\begin{bmatrix} g_{0,k} \\ g_{1,k} \\ g_{2,k} \\ g_{3,k} \\ g_{4,k} \\ g_{5,k} \end{bmatrix}}_{\underline{x}_{k}} = \underbrace{\begin{bmatrix} { {x}}(t_{k}) \\ { {x}}(t_{k+1}) \\ \dot{{ {x}}}(t_{k}) \\ \dot{{ {x}}}(t_{k+1}) \\ \ddot{{ {x}}}(t_{k}) \\ \ddot{{ {x}}}(t_{k+1}) \end{bmatrix}}_{\underline{b}_{k}}. \end{aligned}$$

(5)

We note here that a brute-force calculation in determining the vectors ${\underline{b}_{k}}$ for all k’s over n time intervals cost $\mathcal {O}(n^3)$ operations. More specifically, the unknown trajectory coefficients for the $(k+1)$th time interval, i.e., $[t_k, t_{k+1}]$ are obtained by taking the explicit inverse of $A_k$ and multiplying it with the boundary conditions vector $\underline{b}_k$. Hence, to fully solve the system this process needs to be repeated for each subsequent time interval, until all n time intervals have been considered, thereby fully determining the satellite’s trajectories at any given time. However, as mentioned earlier this approach is computationally expensive, and more specifically the explicit inverse of dense matrices is rarely computed [34]. To mitigate this and reduce the complexity, LU decomposition is used to factor the coefficient matrix $A_k$ in the system of Eq. (5). Then, the bidiagonal lower triangular matrices $\tilde{L}_r$ are used s.t. $\tilde{L}_r=L^{-1}_r$ to compute the matrix–vector product from $\tilde{L}_1\underline{b}_k$ and multiplying the resultant vector in order $\tilde{L}_2, \ldots , \tilde{L}_5$ followed by the backward substitution to reduce the computational burden. By adopting this approach, the trajectory coefficients are obtained for all n time intervals having $\mathcal {O}(n^2)$ as opposed to $\mathcal {O}(n^3)$ complexity algorithm. Let us, therefore, utilize the LU decomposition of the coefficient matrix $A_k$ in Eq. (5):

$$\begin{aligned} \left( \prod _{r=1}^{5} L_{r}\right) U_k\underline{x}_k=\underline{b}_k,\,\,\,{\textrm{where}}\,\,\,A_k = \left( \prod _{r=1}^{5} L_{r}\right) U_k \end{aligned}$$

(6)

where $L_r \in \mathbb {R}^{6 \times 6}$, $r=1,2,\ldots , 5$ are bidiagonal lower triangular matrices, and $U_k \in \mathbb {R}^{6 \times 6}$ is an upper triangular matrix. Moreover, these bidiagonal and upper triangular matrices are explicitly given via

$$\begin{aligned} L_1= & {} \begin{bmatrix} 1 &{} &{} &{} &{} &{} \\ 1&{} d_k &{} &{} &{} &{} \\ &{} &{} 1 &{} &{} &{} \\ &{} &{} 1&{} d_k &{} &{} \\ &{} &{} &{} &{} 1 &{} \\ &{} &{} &{} &{} 1&{}d_k \end{bmatrix}, \hspace{0cm} \hspace{0.5cm} L_2=\begin{bmatrix} 1 &{} &{} &{} &{} &{} \\ &{} 1 &{} &{} &{} &{} \\ &{} 1&{} -d_k &{} &{} &{} \\ &{} &{} &{} 1 &{} &{} \\ &{} &{} &{} 1&{} -d_k &{} \\ &{} &{} &{} &{} &{}1 \end{bmatrix}, \nonumber \\ L_3= & {} \begin{bmatrix} 1 &{} &{} &{} &{} &{} \\ &{} 1 &{} &{} &{} &{} \\ &{} &{} 1 &{} &{} &{} \\ &{} &{} 2&{} d_k &{} &{} \\ &{} &{} &{} &{} 1 &{} \\ &{} &{} &{} &{} 2 &{}d_k \end{bmatrix},\nonumber \\ \hspace{0.5cm} L_4= & {} \begin{bmatrix} 1 &{} &{} &{} &{} &{} \\ &{} 1 &{} &{} &{} &{} \\ &{} &{} 1 &{} &{} &{} \\ &{} &{} &{} 1 &{} &{} \\ &{} &{} &{} 3 &{} -d_k &{} \\ &{} &{} &{} &{} &{}1 \end{bmatrix}, \nonumber \\ L_5= & {} \begin{bmatrix} 1 &{} &{} &{} &{} &{} \\ &{} 1 &{} &{} &{} &{} \\ &{} &{} 1 &{} &{} &{} \\ &{} &{} &{} 1 &{} &{} \\ &{} &{} &{} &{} 1 &{} \\ &{} &{} &{} &{} 2 &{}d_k \end{bmatrix}, \hspace{0.5cm} U_k=\begin{bmatrix} 1 &{} t_0 &{} t_0^2 &{} t_0^3 &{} t_0^4 &{}t_0^5 \\ &{} 1 &{} c_{1,k} &{} c_{2,k} &{} c_{3,k} &{} c_{4,k}\\ &{} &{} 1 &{} e_{1,k} &{} e_{2,k} &{} e_{3,k}\\ &{} &{} &{} 1 &{} 2c_{1,k} &{} f_{k}\\ &{} &{} &{} &{} 2 &{} 2m_{k}\\ &{} &{} &{} &{} &{}2 \end{bmatrix} \end{aligned}$$

(7)

where the pre-computed entries are given by

$$\begin{aligned} d_k= & {} t_{k+1}-t_{k}, \nonumber \\ c_{1,k}= & {} t_{k+1}+t_{k}, \nonumber \\ c_{2,k}= & {} t^{2}_{k+1}+t_{k+1}t_{k}+t^{2}_{k}, \nonumber \\ c_{3,k}= & {} t^{3}_{k+1}+t^{2}_{k+1}t_{k}+t_{k+1}t^{2}_{k}+t^{3}_{k}, \nonumber \\ c_{4,k}= & {} t^{4}_{k+1}+t^{3}_{k+1}t_{k}+t^{2}_{k+1}t^{2}_{k}+t_{k+1}t^{3}_{k}+t^{4}_{k}, \nonumber \\ e_{1,k}= & {} t_{k+1}+2t_{k}, \nonumber \\ e_{2,k}= & {} t^{2}_{k+1}+2t_{k+1}t_{k}+3t^{2}_{k}, \nonumber \\ e_{3,k}= & {} t^{3}_{k+1}+2t^{2}_{k+1}t_{k}+3t_{k+1}t^{2}_{k}+4t^{3}_{k}, \nonumber \\ f_{k}= & {} 3t^{2}_{k+1}+4t_{k+1}t_{k}+3t^{2}_{k}, \nonumber \\ m_{k}= & {} 2t_{k+1}+3t_{k}. \end{aligned}$$

(8)

The subscript k corresponds to the $(k+1)$th time interval which is $[t_k, t_{k+1}]$, and the empty spaces of the matrices represent zero elements. Even for all n time intervals, the pre-computation cost of the entries in Eq. (8) cost $\mathcal {O}(n)$ operations as it is an update of the consecutive vectors. After obtaining $g_{0,k}, \ldots , g_{5,k}$ for $k=0, 1, \ldots , n-1$, the trajectory of the spacecraft can fully be described via Eq. (3) over n time intervals using $\mathcal {O}(n^2)$ as opposed to a $\mathcal {O}(n^3)$ algorithm. Furthermore, to ensure the reliability of this algorithm, refer to matrix decomposition techniques that have been successfully applied in trajectory determination for a quadcopter [16] and a servicing robotic arm [17]. In conclusion, these trajectories serve as reference trajectories at any given time, and can even be extrapolated to predict the future motion of the spacecraft.

Fig. 4

Propagation of each orbit using respective methods

4 Results

This section shows the accuracy and time complexity of the proposed algorithm while comparing it with the ODE45 which is a well-known, traditional, and accurate orbit propagator. The analysis is performed for a LLO, NRHO, DRO and a Lyapunov orbit. The proposed low-complexity algorithm first requires the position, velocity, and acceleration of the six boundary conditions. Then, the conditions are inputted into the algorithm and the algorithm produces the polynomial that represents the motion of the object. Finally, the process is repeated for the remaining dimensions, and the state at a desired time is found using the generated polynomials. An overview of the process is shown in Fig. 4. The algorithm is tested on a number of important orbit trajectories within the Cislunar region using the CR3BP model. The Artemis I mission traveled in a partial DRO around the Moon at the end of 2022, and the complete DRO will be the first trajectory of interest [7]. Next, low-Lunar orbits are orbits with very low altitudes over the Moon, resulting in motion very similar to two-body motion as the Moon’s gravity dominates the spacecraft’s trajectory. Missions such as KPLO and other Lunar surface surveying missions will fly in low-Lunar orbits, marking the second trajectory of interest [4]. The third trajectory to be tested will be an L$_2$ Lyapunov orbit. Finally, NASA’s Gateway station will be a vital location for missions in the Cislunar region, acting as a staging point for Lunar surface missions [35]. Gateway will orbit the Moon in a southern NRHO, identifying the fourth trajectory of interest. The algorithm is completed using seven boundary conditions, marking six time intervals of a desired trajectory, over one orbit period. The initial conditions of the trajectory are known, and the periodic orbits are originally propagated using ODE45. The boundary conditions are then retrieved from the ODE45 results and used in the low-complexity algorithm (LCA). Finally, the resulting trajectories are represented in the dimensional CR3BP rotating frame.

The DRO orbit is propagated using the LCA and compared to the ODE45 results. Figure 5a shows the DRO orbit constructed using both ODE45 and the LCA. The trajectories are difficult to distinguish because of how close the algorithm’s and ODE45’s trajectories are to one another. Therefore, the difference in position between the LCA and the ODE45 trajectory for the DRO is shown in Fig. 5b. Since the algorithm must meet the boundary conditions outlined by ODE45, the intervals in which the algorithm is broken into are typically distinguished by a difference of 0 between the LCA and ODE45 trajectory. The algorithm matches the ODE45 resolved trajectory extremely closely, deviating up to 27 km. A difference of 27 kms between ODE45 and the LCA is insignificant in reference to the 100,000 kms the DRO stretches across.

Fig. 5

Distant retrograde orbit (DRO) analysis

The analysis between the LCA and ODE45 is completed for LLO next. For the analysis, a sample LLO trajectory is used with a perilune of 100 kms. The resultant trajectories are seen in Fig. 6a and the difference between the LCA and ODE45 trajectories is presented in Fig. 6b. The LLO has a peak difference of 2.3 kms occurring in the fifth time interval of the algorithm. The 2.3 kms difference is also insignificant even though the orbit traverses a smaller distance of around 1000 kms.

Fig. 6

Low-Lunar orbit (LLO) analysis

The L$_2$ Lyapunov orbit constructed by the LCA is presented in Fig. 7a, and the difference from the ODE45 propagation is observed in Fig. 7b. The LCA’s model of the sample Lyapunov orbit has the closest resemblance to the ODE45 trajectory out of all the tested orbits. The peak difference occurs in the third time interval set by the boundary conditions, only reaching right over 2.5 kms.

Fig. 7

L$_2$ Lyapunov analysis

Finally, Fig. 8a shows the LCA’s model of the NRHO orbit and Fig. 8b conveys the difference of the LCA and ODE45 propagated trajectories for the NRHO orbit. Out of the selected sample trajectories, the NRHO is found to be the most challenging to construct accurately using the LCA. The NRHO is the only trajectory in which the ODE45 and LCA models can be distinguished from one another at certain times, as seen in Fig. 8a. The NRHO has the largest difference from the ODE45 path, peaking at about 1800 kms. The large difference is partially a result of how the boundary conditions are spread throughout the trajectory. Points in the trajectory that change rapidly, such as perilune, have tighter spaced boundary conditions to prevent drastic changes in the algorithm. Alternatively, the boundary conditions are more spread out through points in the NRHO where conditions change more slowly, such as apolune, so the algorithm has more of a gradual change over a large period of time. This is shown in Fig. 8a and b, in which the trajectory begins at perilune with low deviations and slowly begins to deviate, reaching the peak difference at apolune, halfway through the orbit.

Fig. 8

Near-recilinear halo orbit (NRHO) analysis

The drive for producing an LCA is to reduce computational time and arithmetic complexity and to address the physical requirements for smooth trajectory determination. Typically, arithmetic complexity is proportional to the time complexity of a given algorithm. Therefore, the computational time (i.e. time complexity) of the algorithm is determined for each of the four trajectories and compared to the computational time of ODE45. The time both methods take to resolve a trajectory can slightly vary based on rounding and computer performance during the propagation. As a result, the computed times shown in Fig. 9 are the average computational time of 100 propagations of each respective trajectory. The reductions in computational time of the algorithm are highlighted in Fig. 9 as it depicts that the algorithm resolves the trajectory significantly faster than ODE45, clocking in at about half of the time for each orbit.

Fig. 9

Propagation time of each orbit using respective methods

The selection of the initial and boundary conditions is paramount when using the low-complexity algorithm. For the sample trajectories above, the conditions are selected to highlight the algorithm’s ability to accurately reconstruct common orbits. This proved challenging for some orbits as changing the initial conditions of sensitive orbits, such as the NRHO, would drastically affect the LCA’s ability to reconstruct the orbit. To demonstrate this effect, take the NRHO example. The NRHO constructed in Fig. 8a used initial conditions near the perilune of the orbit, with frequent boundary conditions near perilune. The reconstruction is slightly inaccurate from ODE45, but generally, the orbit retained its shape. Moving the initial conditions of the problem to around the apolune of the NRHO, with boundary conditions still frequenting perilune, the changes in the trajectory are seen in Fig. 10a. The trajectory generated by the LCA clearly propagates the NRHO incorrectly near apolune, in a more pronounced manner than in Fig. 8a. For a closer examination of the problem, the LCA and ODE45 trajectory is plotted over the x-axis, y-axis, and z-axis (Fig. 10b–d). The algorithm is completed in one-dimension at a time and as a result, the accuracy of the NRHO trajectory varies depending on the axis. In this example, the x-axis and z-axis trajectories have accurate results, but y-axis trajectory deviates more significantly. The clear effect changing the initial conditions of the orbit has on the resultant trajectory highlights the importance of the selecting informative initial conditions for the low-complexity algorithm.

Fig. 10

Apolune NRHO trajectory analysis

Two factors contribute to producing inaccuracy of the LCA, poor selection of the initial conditions and the spacing of the boundary conditions. These factors are presented in the application of the LCA in determining the NRHO (Figs. 8a, 10a). The spacing of boundary conditions resulted in inaccuracy because the algorithm concentrated boundary conditions near intervals of rapid change, allowing for intervals of slow change to slowly deviate. The spacing of the boundary conditions can be resolved by cutting down the length of the trajectory the algorithm must solve for at a time. Previously, the algorithm completed one orbit of the NRHO, now the NRHO will be split into two halves and ran twice to complete the trajectory. Using the apolune initial conditions, Fig. 11a shows the LCA and ODE45 trajectories for the NRHO propagated in two arcs and Fig. 11b shows the difference between the two propagation methods. Breaking the trajectory into two arcs resolves the issue of the LCA being unable to produce the NRHO trajectory. The maximum difference between the LCA and ODE45 propagation drops from 1800 kms (Fig. 8b) to 78 kms (Fig. 11b). Additionally, the initial conditions at the apolune of the NRHO previously generated the less accurate NRHO, but is now able to produce an accurate trajectory. The computational time of the NRHO in two arcs is compared to the propagation time of the NRHO using ODE45 and the LCA in a single arc, shown in Fig. 12. The results show that completing two arcs as opposed to a single arc increases the LCA computation by around 0.005 s. Overall, by breaking the trajectory up, the LCA is able to produce an accurate trajectory for the NRHO orbit with some additional computation time. The method of breaking the trajectory into smaller arcs can be extended further to troubleshooting other trajectories that are inaccurate over a given time interval, as completed for the NRHO.

Fig. 11

Two arc NRHO analysis

Fig. 12

Computation time of NRHO with apolune initial conditions

The selection of boundary conditions used in the algorithm directly impact the results and accuracy of the LCA. Generally, for an orbit to be discretized into different arcs that accurately represent the numerically propagated trajectory, the boundary conditions must be selected to create short intervals during sensitive portions of the trajectory. For the selected orbits, the sensitive portions of the trajectory are points of rapid change, occurring at the locations in space where the orbit is the closest to the Moon. This is seen clearly in the NRHO and LLO examples. Both trajectories start at perilune, with the boundary conditions being needed slightly closer in time at the beginning and end of the orbital periods. In contrast, the DRO is generally the same distance from the Moon and, therefore, the spacing of boundary conditions are uniform. Furthermore, in the instance that the selected discretized arcs do not meet desired accuracy, additional boundary conditions are implemented to further limit the time between boundaries. Once again this is demonstrated in the NRHO case, in which the original process of discretizing the orbit into arcs was unsatisfactory, and thus additional boundary conditions were required to create an accurate representation without significantly impacting computation time.

For efficient use of the LCA in the CR3BP, a relationship between the dynamics of a trajectory and the performance of LCA must be established. The stability of two orbits as well as their associated performance in the LCA are examined. The first selected trajectory is the $L_2$ Lyapunov orbit, a trajectory showing promising performance of the LCA, and the second trajectory is a new $L_2$ Lyapunov orbit. The stability of both orbits is determined using the eigenvalues of the monodromy matrix for each periodic orbit [36]: a saddle mode exists when the eigenvalue has one positive and one negative real part; otherwise, a center mode exists when the eigenvalue has complex conjugates. The original Lyapunov orbit possesses one saddle and two center modes, while the new Lyapunov orbit possesses two saddles and one center mode. The new Lyapunov orbit (Fig. 13a) is initiated for propagation at apolune, similar to the original Lyapunov. The comparison between LCA and ODE45 is represented in Fig. 13b. The first Lyapunov orbit outgrows the performance of the second one. These results possibly indicate that the stability of an orbit is associated to its performance in the LCA. Additionally, the previously analyzed NRHO is found to have one saddle and two center modes, similar to the original Lyapunov orbit. The previous finding has demonstrated that the NRHO yields unsatisfactory outcomes compared to the original Lyapunov orbit, despite possessing similar stability properties, but significantly differing in LCA performance. Consequently, the suggested comparison of two Lyapunov orbits with distinct eigenvalues cannot fully establish that a stability relationship exists between dynamics and the performance of LCA. Therefore, future research will delve into exploring the connection between trajectory properties and LCA performance in greater depth.

Fig. 13

Second $L_2$ Lyapunov for further analysis of LCA performance

5 Conclusions

Analytical solutions to predict trajectories in complex, multi-body dynamic systems, such as the CR3BP, may be computationally expensive to solve iteratively. The expense of iterative methods such as Gauss–Legendre, Dormand–Prince, and Chebyshev–Picard, warrants the need for lower complexity algorithms, specially for on-board navigation purposes. The process stems from the Lagrangian interpolation, fitting curves to given conditions to analytically solve for trajectories. The trajectories are extended from linear fitting to a more accurate polynomial in time solution. Furthermore, interpolation methods can still be computationally expensive when using brute force methods to solve for the polynomial, requiring $\mathcal {O}(n^3)$ operations. The designed low-complexity algorithm takes advantage of the low computational necessities of interpolation and the accuracy of a polynomial fit to create an algorithm that requires $\mathcal {O}(n^2)$ operations.

The low-complexity algorithm is tested by propagating well-known trajectories in the CR3BP and comparing the motion to the results of an ODE45 propagated trajectory. The low-complexity algorithm accurately represented a DRO, LLO, and L$_2$ Lyapunov orbit, with a significantly lower computational time than ODE45. The NRHO initially challenged the algorithm to produce an accurate trajectory due to the diverse motion of the orbit. The selected boundary conditions allowed for accurate motion during intervals of rapid change in the NRHO and slow accumulating deviation in intervals of slow change. Breaking the NRHO into two arcs and running the algorithm twice lowers the time between intervals and allowed for the algorithm to produce accurate motion of the NRHO. Overall, the proposed low-complexity algorithm offers a lower computational (arithmetic and time) method for trajectory propagation. In comparison to ODE45, the algorithm computes accurate trajectories for an array of CR3BP orbits in a significantly lower time. The efficiency and reliability of the proposed algorithm make it for a potential resource for on-board trajectory propagation in the Cislunar region. Throughout this work, the trajectories generated by the LCA are only utilized to interpolate between the provided boundary conditions. Future development entails the testing of the algorithm’s ability to predict trajectories outside of the boundary conditions.

Appendix A: Differential Corrections to Obtain Periodic Orbits in the CR3BP

Spacecraft trajectory design typically relies on numerical strategies such as differential corrections to fulfill mission requirements by targeting specific end conditions while varying a set of initial conditions. Consequently, it is important to find a correlation between the variations in the initial state of a trajectory, $\delta \bar{x}_0$, with the variations of its final states downstream, $\delta \bar{x}_f$:

$$\begin{aligned} \delta \bar{x}_f=\frac{\partial \bar{x}(t_f)}{\partial \bar{x}(t_0)}\delta \bar{x}_{0}, \end{aligned}$$

(9)

where $t_0$ and $t_f$ are the initial and final times along the propagated trajectory, respectively. Note that overbars denote vectors. The vector $\bar{x}$ is a six-dimensional vector that contains position and velocity states of a s/c. Therefore, $\delta \bar{x}(t)=[\delta x,\delta y,\delta z,\delta \dot{x},\delta \dot{y},\delta \dot{z}]^T$ (the subscript “T” denotes the transpose). The term $\frac{\partial \bar{x}(t_f)}{\partial \bar{x}(t_0)}$ in Eq. (9) is a variable sensitivity matrix very useful for targeting schemes and stability analysis. Such a matrix is also denoted as the State Transition Matrix (STM), $\phi (t_f,t_0)$, and it is associated with the variational equations relative to any general reference arc that satisfies any non-linear differential equations:

$$\begin{aligned} \phi (t_f,t_0)=\frac{\partial \bar{x}(t_f)}{\partial \bar{x}(t_0)}. \end{aligned}$$

(10)

Figure 14 illustrates a reference trajectory arc between $\bar{x}_0$ and $\bar{x}_f$, along with a perturbed path $\bar{x}_p$ relative to the reference, requiring modification of the initial state on the reference path to reach the desired position $\bar{x}_p$, considering the first-order form of the non-linear system of differential equations:

Fig. 14

Perturbed path relative to the reference path of a trajectory

$$\begin{aligned} \dot{\bar{x}}=\bar{f}(\bar{x},t), \end{aligned}$$

(11)

where dots indicate the derivative with respect to time, then $\bar{x}_p$ at $t_f$ is represented as a Taylor series expansion relative to the reference. The linear variational equations, derived from the equations of motion, are provided in the form:

$$\begin{aligned} \delta \dot{\bar{x}}(t)={\textbf {A}}(t)\delta \bar{x}(t). \end{aligned}$$

(12)

${\textbf {A}}(t)$ is the Jacobian matrix comprised of the partials of the equations of motion with respect to the states evaluated at time t:

$$\begin{aligned} {\textbf {A}}(t)=\frac{\partial \bar{f}(\bar{x},t)}{\partial \bar{x}(t)}. \end{aligned}$$

(13)

The solution to Eq. (12) is the previously presented Eq. (9). The evolution of $\phi (t,t_0)$ is governed by the following matrix differential equation [36]:

$$\begin{aligned} \dot{\phi }(t,t_0)={\textbf {A}}(t)\phi (t,t_0), \end{aligned}$$

(14)

which represents 36 scalar differential equations, given that $\phi (t,t_0)$ is a 6x6 matrix. In the CR3BP, Eq. (14) holds as:

$$\begin{aligned} \left( \begin{array}{c} \delta \dot{x}\\ \delta \dot{y}\\ \delta \dot{z}\\ \delta \ddot{x}\\ \delta \ddot{y}\\ \delta \ddot{z} \end{array}\right) =\left[ \begin{array}{cccccc} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1\\ U_{xx}^{*} &{} U_{xy}^{*} &{} U_{xz}^{*} &{} 0 &{} 2 &{} 0\\ U_{xy}^{*} &{} U_{yy}^{*} &{} U_{yz}^{*} &{} -2 &{} 0 &{} 0\\ U_{xz}^{*} &{} U_{yz}^{*} &{} U_{zz}^{*} &{} 0 &{} 0 &{} 0 \end{array}\right] \left( \begin{array}{c} \delta x\\ \delta y\\ \delta z\\ \delta \dot{x}\\ \delta \dot{y}\\ \delta \dot{z} \end{array}\right) \end{aligned}$$

(15)

where the $3\times 3$ block at the bottom-left of the matrix corresponds to the second partial derivatives of $U^*$ [37]. The partial derivatives within the STM reflect the impact of changes in initial state elements on the corresponding final state elements:

$$\begin{aligned} \left( \begin{array}{c} \delta x_{f}\\ \delta y_{f}\\ \delta z_{f}\\ \delta \dot{x}_{f}\\ \delta \dot{y}_{f}\\ \delta \dot{z}_{f} \end{array}\right) =\left[ \begin{array}{cccccc} \frac{\partial x}{\partial x_{0}} &{} \frac{\partial x}{\partial y_{0}} &{} \frac{\partial x}{\partial z_{0}} &{} \frac{\partial x}{\partial \dot{x}_{0}} &{} \frac{\partial x}{\partial \dot{y}_{0}} &{} \frac{\partial x}{\partial \dot{z}_{0}}\\ \frac{\partial y}{\partial x_{0}} &{} \frac{\partial y}{\partial y_{0}} &{} \frac{\partial y}{\partial z_{0}} &{} \frac{\partial y}{\partial \dot{x}_{0}} &{} \frac{\partial y}{\partial \dot{y}_{0}} &{} \frac{\partial y}{\partial \dot{z}_{0}}\\ \frac{\partial z}{\partial x_{0}} &{} \frac{\partial z}{\partial y_{0}} &{} \frac{\partial z}{\partial z_{0}} &{} \frac{\partial z}{\partial \dot{x}_{0}} &{} \frac{\partial z}{\partial \dot{y}_{0}} &{} \frac{\partial z}{\partial \dot{z}_{0}}\\ \frac{\partial \dot{x}}{\partial x_{0}} &{} \frac{\partial \dot{x}}{\partial y_{0}} &{} \frac{\partial \dot{x}}{\partial z_{0}} &{} \frac{\partial \dot{x}}{\partial \dot{x}_{0}} &{} \frac{\partial \dot{x}}{\partial \dot{y}_{0}} &{} \frac{\partial \dot{x}}{\partial \dot{z}_{0}}\\ \frac{\partial \dot{y}}{\partial x_{0}} &{} \frac{\partial \dot{y}}{\partial y_{0}} &{} \frac{\partial \dot{y}}{\partial z_{0}} &{} \frac{\partial \dot{y}}{\partial \dot{x}_{0}} &{} \frac{\partial \dot{y}}{\partial \dot{y}_{0}} &{} \frac{\partial \dot{y}}{\partial \dot{z}_{0}}\\ \frac{\partial \dot{z}}{\partial x_{0}} &{} \frac{\partial \dot{z}}{\partial y_{0}} &{} \frac{\partial \dot{z}}{\partial z_{0}} &{} \frac{\partial \dot{z}}{\partial \dot{x}_{0}} &{} \frac{\partial \dot{z}}{\partial \dot{y}_{0}} &{} \frac{\partial \dot{z}}{\partial \dot{z}_{0}} \end{array}\right] \left( \begin{array}{c} \delta x_{0}\\ \delta y_{0}\\ \delta z_{0}\\ \delta \dot{x}_{0}\\ \delta \dot{y}_{0}\\ \delta \dot{z}_{0} \end{array}\right) \end{aligned}$$

(16)

Using the STM is crucial in targeting schemes as it serves as an effective linear predictor of the sensitivity of the final state to variations in the initial state. Iteratively updating initial conditions based on the STM and terminal constraint sensitivities, it is possible to enable the determination of periodic orbits using a multi-variable Newton–Raphson strategy. Consider that $\bar{\mathcal {Y}}$ contains the design variables of the problem (or free variable) and $\bar{\mathcal {F}}(\bar{\mathcal {Y}})$ the terminal constraints:

$$\begin{aligned} \bar{\mathcal {Y}} = (\mathcal {Y}_{1}, \mathcal {Y}_{2}, \dots , \mathcal {Y}_{n}), \;\;\; \bar{\mathcal {F}}(\bar{\mathcal {Y}}) = (\mathcal {F}_{1}(\bar{\mathcal {Y}}), \mathcal {F}_{2}(\bar{\mathcal {Y}}), \dots , \mathcal {F}_{j}(\bar{\mathcal {Y}})). \end{aligned}$$

(17)

The objective is to determine the vector $\bar{\mathcal {Y}}$ that nullifies the constraint vector $\bar{\mathcal {F}}(\bar{\mathcal {Y}})=\bar{0}$, with convergence measured by the norm of $\bar{\mathcal {F}}$ being smaller than a user-defined accuracy $\epsilon$, set to $\epsilon =10^{-12}$, and the update equation for the Newton–Raphson algorithm involving a first-order Taylor series expansion about the initial condition $\bar{\mathcal {Y}}_0$ [38]:

$$\begin{aligned} \bar{\mathcal {F}}(\bar{\mathcal {Y}})\approx \bar{\mathcal {F}}(\bar{\mathcal {Y}}_{0})+D\bar{\mathcal {F}}(\bar{\mathcal {Y}}_{0})(\bar{\mathcal {Y}}-\bar{\mathcal {Y}}_{0})=0, \end{aligned}$$

(18)

where $D\bar{\mathcal {F}}(\bar{\mathcal {Y}}_{0})$ contains the partial derivatives of the constraints with respect to the free variables:

$$\begin{aligned} D\bar{\mathcal {F}}(\bar{\mathcal {Y}}_{0})=\frac{\partial \bar{\mathcal {F}}(\bar{\mathcal {Y}})_{0}}{\partial \bar{\mathcal {Y}}_{0}}=\left[ \begin{array}{cccc} \frac{\partial \mathcal {F}_{1}}{\partial \mathcal {Y}_{1}} &{} \frac{\partial \mathcal {F}_{1}}{\partial \mathcal {Y}_{2}} &{} \cdots &{} \frac{\partial \mathcal {F}_{1}}{\partial \mathcal {Y}_{n}}\\ \frac{\partial \mathcal {F}_{2}}{\partial \mathcal {Y}_{1}} &{} \frac{\partial \mathcal {F}_{2}}{\partial \mathcal {Y}_{2}} &{} \cdots &{} \frac{\partial \mathcal {F}_{2}}{\partial \mathcal {Y}_{n}}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \frac{\partial \mathcal {F}_{j}}{\partial \mathcal {Y}_{1}} &{} \frac{\partial \mathcal {F}_{j}}{\partial \mathcal {Y}_{2}} &{} \cdots &{} \frac{\partial \mathcal {F}_{j}}{\partial \mathcal {Y}_{n}} \end{array}\right] _{0} \end{aligned}$$

(19)

The method to solve the equation depends on the number of constraints relative to the number of free variables. In the case where the number of constraints is equal to the number of free variables and the matrix $D\bar{\mathcal {F}}(\bar{\mathcal {Y}}_{0})$ is invertible, a unique solution is obtained through the iterative process:

$$\begin{aligned} \bar{\mathcal {Y}}=\bar{\mathcal {Y}}_{0}-D\bar{\mathcal {F}}(\bar{\mathcal {Y}}_{0})^{-1}\bar{\mathcal {F}}(\bar{\mathcal {Y}}). \end{aligned}$$

(20)

On the other hand, when the number of constraints is less than the number of free variables, and $D\bar{\mathcal {F}}(\bar{\mathcal {Y}}_{0})$ is not invertible, there are infinitely many solutions, with the solution closest to the final time control variable vector given by the minimum-norm solution:

$$\begin{aligned} \bar{\mathcal {Y}}=\bar{\mathcal {Y}}_{0}-D\bar{\mathcal {F}}(\bar{\mathcal {Y}}_{0})^{T}[D\bar{\mathcal {F}}(\bar{\mathcal {Y}}_{0})D\bar{\mathcal {F}}(\bar{\mathcal {Y}}_{0})^{T}]^{-1}\bar{\mathcal {F}}(\bar{\mathcal {Y}}). \end{aligned}$$

(21)

Each periodic orbit has specific conditions and constraints that need to be satisfied, and the computed $\bar{\mathcal {Y}}$ is assessed to see if the norm of $\bar{\mathcal {F}}$ is within the defined tolerance $\epsilon$, with the process repeated until convergence is achieved.