Introduction

Highly efficient low-thrust propulsion systems enable mission designers to increase the useful spacecraft mass or delivered payload mass above that from high-thrust engine options. This improvement typically comes at the expense of increased times of flight to mission destinations. For low-thrust trajectories about planetary bodies, an orbital period on the order of hours or days provides inadequate time to impart a substantial change to the orbit and results in a large number of revolutions that are traversed before reaching the desired state. Determining the optimal control over hundreds or thousands of revolutions poses a sensitive and often unwieldy, high-dimensional optimization problem.

Historical Approaches to Low-Thrust Many-Revolution Orbit Transfers

Classical approaches employ optimal control theory, named the indirect, Lagrange multiplier, or adjoint method, beginning with Edelbaum’s transfer between circular orbits of different semimajor axis and inclination [1, 2]. Wiesel and Alfano extended Edelbaum’s work to the slow time scale problem, i.e. many-revolution transfers, but the optimal thrust angle must be approximated numerically [3]. Edelbaum [4] and Kéchichian [5,6,7] used orbit averaging techniques for approximate many-revolution rendezvous in classical orbital elements and modified equinoctial elements, respectively.

Under significant assumptions, e.g. the aforementioned examples, analytic expressions for the Lagrange multipliers (adjoints or costates) enable quick trajectory computation. Otherwise, numerical solution requires a non-intuitive initial guess of the Lagrange multipliers and the resulting trajectory is sensitive to those values. That sensitivity is amplified when the trajectory encompasses many revolutions. The indirect approach is further complicated by the need to re-derive the adjoint equations of motion and boundary conditions as different state variables, constraints, and dynamics are considered.

These drawbacks of indirect methods can be avoided by following a control law, or a heuristic policy that the mission designer deems acceptable. Petropolous developed the Q-law, where Q is a candidate Lyapunov function named the proximity quotient [8, 9]. Q captures the proximity to the target orbit, and best-case time-to-go for achieving the desired change in each orbital element. Thrust directions are chosen to maximize the reduction in Q, but the Q-law also includes constraint handling and a mechanism for coasting. Other useful control laws pertinent to the low-thrust many-revolution transfer include Kluever’s approach [10] that blends the optimal thrust directions for changing different orbital elements, and the Lyapunov control law from Chang, Chichka, and Marsden [11] that minimizes the weighted sum of squared errors of the angular momentum and Laplace vectors between the current and target orbit.

While indirect methods solve for the abstract Lagrange multipliers, direct methods seek the physical variables explicitly. A decision vector is formed of control variables, state variables, or other variable parameters that collectively describe an entire trajectory. The decision vector could also be the input parameters for a control law. The direct optimization procedure then updates the decision vector iteratively until convergence criteria are satisfied.

Direct optimization of heliocentric low-thrust trajectories is dominated by direct transcription and nonlinear programming (NLP) techniques. Direct transcription transforms the continuous optimal control problem into a discrete approximation [12]. Nonlinear programming generally involves the assembly and inversion of a Hessian matrix that contains the second derivatives and cross partial derivatives of a scalar objective function with respect to the decision vector. The size of the optimization problem grows quadratically with the number of decision variables and proves to be a computational bottleneck when applying nonlinear programming to planetocentric low-thrust trajectories that require a large decision vector. Nonetheless, Betts solved large-scale NLPs for geocentric trajectories over several hundred revolutions using collocation and sequential quadratic programming in the Sparse Optimization Suite [13,14,15,16,17]. The current state-of-the-art technology for the optimal design of low-thrust planetocentric trajectories is the Mystic Low-Thrust Trajectory Design and Visualization Software [18]. Mystic has best demonstrated its capabilities with the success of NASA’s Dawn mission [19]. Mystic’s optimization engine is built around the Static/Dynamic Optimal Control algorithm, a differential dynamic programming (DDP) approach developed by Whiffen [20]. DDP exhibits a linear scaling of the optimization problem size with number of control variables [21]. Despite the favorability of DDP for large scale optimization, computation time limits Mystic to about 250 revolutions for optimized trajectories before switching to the Q-law [22]. Lantoine and Russell introduced Hybrid Differential Dynamic Programming (HDDP) [23,24,25], a DDP variant that makes the most computationally expensive step suitable for parallelization.

Differential Dynamic Programming

DDP seeks the minimum of a cost functional J(x,u,t), where x(t) = f(x0, u,t) is a state trajectory and u(t) is a control schedule, or policy. A nominal control \(\overline {\boldsymbol {u}}(t)\) is suggested as an initial guess and produces a nominal state trajectory \(\overline {\boldsymbol {x}} = \boldsymbol {f}(\boldsymbol {x}_{0},\overline {\boldsymbol {u}},t)\). The control is iteratively updated by applying δu(t) until optimality conditions are satisfied. It is the δu that are the optimization variables such that the trial control is \(\boldsymbol {u} = \overline {\boldsymbol {u}} + \delta \boldsymbol {u}\). The new state that results from the updated control is similarly described by a deviation from the nominal trajectory, \(\boldsymbol {x} = \overline {\boldsymbol {x}} + \delta \boldsymbol {x}\).

The DDP procedure for updating the nominal control policy is called the backward sweep and is motivated by Bellman’s Principle of Optimality.

An optimal policy has the property that whatever the initial state and initial decision are, the remaining decisions must constitute an optimal policy with regard to the state resulting from the first decision. [26]

Considering the state that results from applying the nominal control up to stage k = N − 1, the sole remaining decision is δuN− 1. Optimization of this final decision is now independent of those preceding it and minimizes the cost-to-go. After performing this optimization and stepping back to stage k = N − 2, the remaining decisions are δuN− 2 and δuN− 1. The latter is known, however, and only the control update at the current stage needs to be determined. An update to the entire control policy is possible by proceeding upstream to the initial state at stage k = 0, while optimizing each stage decision along the way.

DDP solves the stage subproblem for each δu k to optimize a local model of the cost remaining along the trajectory. This is in stark contrast to methods that update the entire control sequence in the computationally expensive matrix inverse of a large Hessian. If the control vector at each stage is of dimension m, then DDP solves N NLP subproblems of size m, rather than a single NLP problem of size Nm.

DDP and a Sundman Transformation

The main contribution of this work is a method for the optimization of low-thrust many-revolution spacecraft trajectories. The method is to apply a Sundman transformation to the spacecraft equations of motion and perform the optimization with DDP. The Sundman transformation [27] is a general change of variables from time to a function of orbital radius, and effectively regulates the step size of numerical integration [28]. Berry and Healy assessed numerical integration accuracy and computational speed to establish an eccentricity threshold at which the transformation proves more effective than time-integration [29]. Pellegrini, Russell, and Vittaldev showed accuracy and efficiency gains for propagation with the Sundman transformation in the Stark and Kepler models [30]. Yam, Izzo, and Biscani previously applied a Sundman transformation to the Sims-Flanagan transcription to optimize interplanetary trajectories [31, 32]. Now the Sundman transformation is applied to HDDP with a focus on geocentric trajectories.

The Sundman Transformation

In regularizing the equations of motion to solve the three-body problem, Karl Sundman introduced a change of independent variable from time t to the new independent variable τ [27].

$$ {dt = c_{n} r^{n} d\tau} $$
(1)

Time and the new independent variable are related by a function of the orbital radius, r. The real number n and coefficient c n may be selected so that τ represents an orbit angle. For n = 0,1,2, the independent variables are the mean anomaly M, eccentric anomaly E and true anomaly f. Those transformations are given by

$$\begin{array}{@{}rcl@{}} dt &= &\sqrt{a^{3}/\mu}dM, \end{array} $$
(2a)
$$\begin{array}{@{}rcl@{}} dt &=& \sqrt{a/\mu} rdE, \end{array} $$
(2b)
$$\begin{array}{@{}rcl@{}} dt &=& r^{2}/h \, df , \end{array} $$
(2c)

where a is the semimajor axis, μ is the gravitational parameter of the central body and h is the angular momentum magnitude.

Transforming time-dependent equations of motion simply requires multiplication by the functional relationship between the two independent variables.

$$ {\boldsymbol{\mathring{X}}}= \frac{d\boldsymbol{X}}{d\tau}=\left( \frac{d\boldsymbol{X}}{dt}\right)\frac{dt}{d\tau} = \dot{\boldsymbol{X}}c_{n} r^{n} $$
(3)

In Eq. 3, X represents a state vector, the overhead dot denotes a time derivative and the overhead ring denotes a derivative with respect to τ. Time-dependent equations of motion \(\dot {\boldsymbol {X}}\) are typically propagated for a prescribed duration of time from the state at an initial epoch. Now, however, propagation is specified for a duration of τ. When τ is an orbit angle, the number of revolutions N r e v may be specified so that the τ duration is 2πN r e v . The elapsed time is unknown a priori but may be tracked by including t in the state vector and numerically integrating dt/dτ.

Sundman-Transformed HDDP

This section summarizes the HDDP algorithm presented by Lantoine and Russell in Reference [23], with necessary changes for the Sundman transformation. Departures from their presentation include expanded use of the augmented state vector and tensor notation. Algorithmic options and differences between the author’s HDDP implementation and Reference [23] are also noted.

Tensor Notation

DDP is a second-order gradient-based method that requires first and second derivatives of the state dynamics, or in this context, Sundman-transformed dynamics. Those second derivatives form a rank three tensor and cause notational difficulties. Tensor notation prevents ambiguities of mathematical operations between tensors, matrices, vectors, and scalars.

The adopted convention uses superscripts as indices. The rank of an object is implied by the number of indices. For example, Xi is the i-th element of state vector X. First and second derivatives of the state dynamics are stated as

$$\begin{array}{@{}rcl@{}} A^{i,a} &=& \frac{\partial\dot{\boldsymbol{X}}^{i}}{\partial\boldsymbol{X}^{a}}, \end{array} $$
(4a)
$$\begin{array}{@{}rcl@{}} A^{i,ab} &=& \frac{\partial^{2}\dot{\boldsymbol{X}}^{i}}{\partial\boldsymbol{X}^{a}\partial\boldsymbol{X}^{b}} . \end{array} $$
(4b)

Ai,a is the (i,a) entry of the dynamics matrix and is the derivative of the i-th element of state dynamics vector \(\dot {\boldsymbol {X}}\) taken with respect to the a-th element of X. Ai,ab is the (i,a,b) entry of the rank three dynamics tensor that is the cross partial derivative, or second derivative if a = b, of the i-th element of \(\dot {\boldsymbol {X}}\) with respect to the a-th and b-th elements of X.

Following Einstein notation, multiplication is performed by summing over repeated γ indices. The familiar differential equation for the state transition matrix, \(\dot {\Phi } = A{\Phi }\), is the product of two matrices and otherwise written as

$$ \dot{\Phi}^{i,a} = A^{i,\gamma_{1}}{\Phi}^{\gamma_{1},a} . $$
(5)

The differential equation for the second-order state transition tensor is

$$ \dot{\Phi}^{i,ab} = A^{i,\gamma_{1}}{\Phi}^{\gamma_{1},ab} + A^{i,\gamma_{1}\gamma_{2}}{\Phi}^{\gamma_{1},a}{\Phi}^{\gamma_{2},b} . $$
(6)

The presence of multiple repeated indices implies multiple summations, e.g. for X with n state variables, \(A^{i,\gamma _{1}\gamma _{2}}{\Phi }^{\gamma _{1},a}{\Phi }^{\gamma _{2},b}\) is a double summation over γ1 = 0,1,...,n, γ2 = 0,1,...,n.

Forward Pass

Evaluating a trial control schedule \(\boldsymbol {x}(t) = \boldsymbol {f}(\boldsymbol {x}_{0},\overline {\boldsymbol {u}}+\delta \boldsymbol {u},t)\) constitutes a forward pass. For the first iteration, \(\overline {\boldsymbol {u}}\) is the initial guess of controls and δu = 0. HDDP is a discrete form of DDP where a trajectory can be described by any number of phases, with each phase described by a number of stages. This work considers single phase trajectories of N stages. The discrete trajectory is [x0, x1,...,x N ] and the control schedule is [u0, u1,...,uN− 1]. A useful construct for both notation and implementation is the augmented state vector XT = [xT, uT]. The forward pass is then the sequence of function evaluations,

$$ \boldsymbol{X}_{k + 1} = \boldsymbol{F}(\boldsymbol{X}_{k}), \ k = 0,1,...,N-1. $$
(7)

The transition function F dictates how the state evolves between stages, and might obey a system of linear, nonlinear or differential equations, and is not necessarily deterministic. DDP is applicable to all of these systems in both continuous and discrete form [21]. Stages in HDDP represent sampling of continuous variables, so that the transition function is the integral of the equations of motion. The relevant transition function for the Sundman-transformed dynamics in Eq. 3 is

$$ \boldsymbol{X}_{k + 1} = \boldsymbol{X}_{k} + \int\limits_{{\tau_{k}}}^{{\tau_{k + 1}}}{\boldsymbol{\mathring{X}}}_{k}(\tau) \, d\tau . $$
(8)

The cost can be determined once the transition functions have been evaluated up to the final state, X N . Nominal states and controls are updated for successful iterations, so that X becomes the new \(\overline {\boldsymbol {X}}\). If optimality conditions are satisfied, then the procedure is finished. Otherwise, a control update is computed in a backward sweep.

Augmented Lagrangian Method

The standard DDP formulation adjoins terminal constraints ψ(x f ) = 0 to the original cost function using a constant vector of Lagrange multipliers. HDDP selects a cost function \(J = \widetilde {\varphi }\) based on the augmented Lagrangian method where a scalar penalty parameter places additional weight on terminal constraint violations. Here a penalty matrix is used so that the additional weight on each constraint may be treated individually.

$$ \widetilde{\varphi} = \phi + \boldsymbol{\lambda}^{T}\boldsymbol{\psi} + \boldsymbol{\psi}^{T}{\Sigma}\boldsymbol{\psi} + \sum\limits_{k = 0}^{N-1}L_{k} $$
(9)

The first term ϕ(X N ) is the original objective to be minimized. Multipliers λ are initialized as the zero vector and updated at every iteration to push the trajectory toward feasibility. The initial guess of zero-valued multipliers is not a requirement but it is nonintuitive how to choose otherwise. Penalty matrix Σ places additional weight on constraint violations and serves to initialize a quadratic cost function space. L k (X k ) is the local cost incurred at stage k. In contrast to previous approaches that continually increase the penalty weight [23, 33], Σ is held constant for all iterations. In practice, the entries of Σ are tuned after observing how the iterates progress toward feasibility. For example, an initial attempt to optimize a trajectory might begin with Σ as a scalar multiple of the identity matrix so that each constraint is weighted equally. If iterates show little progress toward satisfying a particular constraint, its associated Σ entry could be increased and the process restarted. Similarly, if the algorithm appears to prioritize a constraint without working to satisfy the other constraints, the Σ entry for that prioritized constraint could be reduced.

Backward Sweep

Stage Subproblems

The backward sweep solves the sequence of subproblems that minimize the cost-to-go from stage k = N − 1,N − 2,...,0.

$$ J_{k}^{*} = \min_{\delta \boldsymbol{u}_{k}}[J_{k}] $$
(10)

With the addition of the stage subscript, J k is the cost-to-go from stage k. The superscript asterisk denotes an optimal value, so \(J_{k}^{*}\) is the optimal cost-to-go from stage k. The solution to Eq. 10 is the optimal control update \(\delta \boldsymbol {u}^{*}_{k}\). By assuming that the cost function can be approximated by a second-order Taylor series expansion about the nominal states, controls and multipliers, a prediction for \(\delta \boldsymbol {u}^{*}_{k}\) is readily available.

$$\begin{array}{@{}rcl@{}} J_{k}(\overline{\boldsymbol{x}}_{k} &+& \delta\boldsymbol{x}_{k}, \overline{\boldsymbol{u}}_{k} + \delta\boldsymbol{u}_{k}, \overline{\boldsymbol{\lambda}} + \delta\boldsymbol{\lambda}) \approx \ ER_{k + 1} + J_{k}(\overline{\boldsymbol{x}}_{k},\overline{\boldsymbol{u}}_{k}, \overline{\boldsymbol{\lambda}}) + J_{x,k}^{T}\delta\boldsymbol{x}_{k} + J_{u,k}^{T}\delta\boldsymbol{u}_{k} \\&+& J_{\lambda,k}^{T}\delta\boldsymbol{\lambda} + \frac{1}{2}\delta\boldsymbol{x}_{k}^{T}J_{xx,k}\delta\boldsymbol{x}_{k} + \frac{1}{2}\delta\boldsymbol{u}_{k}^{T} J_{uu,k}\delta\boldsymbol{u}_{k}+ \frac{1}{2}\delta\boldsymbol{\lambda}^{T} J_{\lambda\lambda,k}\delta\boldsymbol{\lambda}\\&&+ \delta\boldsymbol{x}_{k}^{T}J_{xu,k}\delta\boldsymbol{u}_{k} +\delta\boldsymbol{x}_{k}^{T}J_{x\lambda,k}\delta\boldsymbol{\lambda} +\delta\boldsymbol{u}_{k}^{T}J_{u\lambda,k}\delta\boldsymbol{\lambda} \end{array} $$
(11)

The expected reduction ERk+ 1 accounts for the predicted change in cost that accumulates with the solution to each subproblem. The left-hand side of Eq. 11 represents the cost-to-go along a neighboring trajectory that differs from the nominal value by δJ k .

$$ \delta J_{k} = J_{k}(\overline{\boldsymbol{x}}_{k} + \delta\boldsymbol{x}_{k}, \overline{\boldsymbol{u}}_{k} + \delta\boldsymbol{u}_{k}, \overline{\boldsymbol{\lambda}} + \delta\boldsymbol{\lambda}) - {J}_{k}(\overline{\boldsymbol{x}}_{k},\overline{\boldsymbol{u}}_{k},\overline{\boldsymbol{\lambda}}) $$
(12)

The quadratic model is then restated as

$$\begin{array}{@{}rcl@{}} \delta J_{k} \approx ER_{k + 1} &+& J_{x,k}^{T}\delta\boldsymbol{x}_{k} + J_{u,k}^{T}\delta\boldsymbol{u}_{k} + J_{\lambda,k}^{T}\delta\boldsymbol{\lambda} + \frac{1}{2}\delta\boldsymbol{x}_{k}^{T}J_{xx,k}\delta\boldsymbol{x}_{k} \\ &+& \frac{1}{2}\delta\boldsymbol{u}_{k}^{T} J_{uu,k}\delta\boldsymbol{u}_{k}+ \frac{1}{2}\delta\boldsymbol{\lambda}^{T} J_{\lambda\lambda,k}\delta\boldsymbol{\lambda} + \delta\boldsymbol{x}_{k}^{T}J_{xu,k}\delta\boldsymbol{u}_{k} + \delta\boldsymbol{x}_{k}^{T}J_{x\lambda,k}\delta\boldsymbol{\lambda}\\ &&+\delta\boldsymbol{u}_{k}^{T}J_{u\lambda,k}\delta\boldsymbol{\lambda} . \end{array} $$
(13)

The minimizing control update is found by taking the derivative of Eq. 13 with respect to δu k and setting it equal to zero. The result is an unconstrained feedback control law,

$$\begin{array}{@{}rcl@{}} \delta \boldsymbol{u}_{k}^{*} &=& A_{k} + B_{k}\delta \boldsymbol{x}_{k} + D_{k}\delta\boldsymbol{\lambda},\\ A_{k} &=& -J_{uu,k}^{-1}J_{u,k} ,\\ B_{k} &=& -J_{uu,k}^{-1}J_{ux,k} , \\ D_{k} &= &-J_{uu,k}^{-1}J_{u\lambda,k} . \end{array} $$
(14)

The feed-forward terms A k and feedback gains B k , and D k are stored to assemble \(\delta \boldsymbol {u}_{k}^{*}\) during the forward pass. For a quadratic cost function and linear system, the model and minimization are exact and DDP exhibits one-step convergence. Algorithmic options from HDDP permit the practical application of Eq. 14, namely the enforcement of control bounds by a null-space method [24]. A trust-region method restricts the size of A k and δλ so that the resulting δx k remains within the valid region of the quadratic model [34]. Furthermore, the trust-region method ensures that Juu,k is positive definite so that \(\delta \boldsymbol {u}_{k}^{*}\) is a descent direction.

Derivatives present in the new control law are obtained by recognizing that the cost-to-go is the sum of the local cost and the optimal cost-to-go from the next stage.

$$ {J_{k} = L_{k} + J_{k + 1}^{*}} $$
(15)

The required derivatives are the Taylor coefficients in Eq. 13, which is the expansion of the left-hand side of Eq. 15. Their counterparts from expanding the right-hand side of Eq. 15 should be equivalent.

$$ \delta L_{k} \approx L_{x,k}^{T}\delta\boldsymbol{x}_{k} + L_{u,k}^{T}\delta\boldsymbol{u}_{k} + \frac{1}{2}\delta\boldsymbol{x}_{k}^{T}L_{xx,k}\delta\boldsymbol{x}_{k} + \frac{1}{2}\delta\boldsymbol{u}_{k}^{T} L_{uu,k}\delta\boldsymbol{u}_{k} + \delta\boldsymbol{x}_{k}^{T}L_{xu,k}\delta\boldsymbol{u}_{k} $$
(16a)
$$\begin{array}{@{}rcl@{}} \delta J_{k + 1}^{*} &\approx& ER_{k + 1} + J_{x,k + 1}^{*T}\delta\boldsymbol{x}_{k + 1} + J_{\lambda,k + 1}^{*T}\delta\boldsymbol{\lambda} + \frac{1}{2}\delta\boldsymbol{x}_{k + 1}^{T}J_{xx,k + 1}^{*}\delta\boldsymbol{x}_{k + 1}\\ &&+ \frac{1}{2}\delta\boldsymbol{\lambda}^{T} J_{\lambda\lambda,k + 1}^{*}\delta\boldsymbol{\lambda} + \delta\boldsymbol{x}_{k + 1}^{T}J_{x\lambda,k + 1}^{*}\delta\boldsymbol{\lambda} \end{array} $$
(16b)

Derivatives in Eq. 16a are obtained directly while those in Eq. 16b are known from the preceding subproblem. Equating Taylor coefficients of like order requires an expression for δxk+ 1 as a function of δx k , δu k and δλ. By definition, that relationship is

$$ \delta\boldsymbol{x}_{k + 1} = \boldsymbol{f}(\overline{\boldsymbol{x}}_{k}+\delta\boldsymbol{x}_{k},\overline{\boldsymbol{u}}_{k}+\delta\boldsymbol{u}_{k},t_{k}) -\boldsymbol{f}(\overline{\boldsymbol{x}}_{k},\overline{\boldsymbol{u}}_{k},t_{k}). $$
(17)

Second-Order Dynamics

Equation 17 suggests the need to compute a neighboring trajectory alongside the new control schedule during the backward sweep. This is avoided by using a quadratic approximation of the dynamics, again obtained by a second-order Taylor series expansion.

$$ \delta\boldsymbol{X}_{k + 1}^{i} \approx \boldsymbol{F}_{X,k}^{i,\gamma_{1}}\delta\boldsymbol{X}_{k}^{\gamma_{1}} + \frac{1}{2}\boldsymbol{F}_{XX,k}^{i,\gamma_{1}\gamma_{2}}\delta\boldsymbol{X}_{k}^{\gamma_{1}}\delta\boldsymbol{X}_{k}^{\gamma_{2}} $$
(18)

Taylor coefficients for the approximate state deviation are the first-order state transition matrix (STM) and second-order state transition tensor (STT).

$$\begin{array}{@{}rcl@{}} {\Phi}^{i,a}(t_{k},t_{k + 1}) = \frac{\partial\boldsymbol{X}_{k + 1}^{i}}{\partial\boldsymbol{X}_{k}^{a}} = \boldsymbol{F}_{X,k}^{i,a} \end{array} $$
(19a)
$$\begin{array}{@{}rcl@{}} {\Phi}^{i,ab}(t_{k},t_{k + 1}) = \frac{\partial^{2}\boldsymbol{X}_{k + 1}^{i}}{\partial\boldsymbol{X}_{k}^{a}\partial\boldsymbol{X}_{k}^{b}} = \boldsymbol{F}_{XX,k}^{i,ab} \end{array} $$
(19b)

The STMs (referring to both the STMs and STTs) between each stage obey the differential equations in Eqs. 5 and 6 with initial conditions Φ(t k , t k )i,a = δi,a, the Kronecker delta or identity matrix, and Φi,ab(t k , t k ) = 0. Equation 18 is now restated in terms of STMs, with arguments are removed so that the implied mapping is from t k to tk+ 1.

$$ \delta\boldsymbol{X}_{k + 1}^{i} = {\Phi}^{i,\gamma_{1}}\delta\boldsymbol{X}_{k}^{\gamma_{1}} + \frac{1}{2}{\Phi}^{i,\gamma_{1}\gamma_{2}}\delta\boldsymbol{X}_{k}^{\gamma_{1}}\delta\boldsymbol{X}_{k}^{\gamma_{2}} $$
(20)

Sundman Transformed Dynamics

As with the state dynamics transformation, the dynamics matrix and tensor need to be transformed to reflect the change of independent variable.

$$\begin{array}{@{}rcl@{}} {\Lambda}^{i,a} &=& \frac{\partial {\boldsymbol{\mathring{X}}}^{i}} {\partial\boldsymbol{X}^{a}} \end{array} $$
(21a)
$$\begin{array}{@{}rcl@{}} {\Lambda}^{i,ab} &=& \frac{\partial^{2} {\boldsymbol{\mathring{X}}}^{i}} {\partial\boldsymbol{X}^{a}\partial\boldsymbol{X}^{b}} \end{array} $$
(21b)

The new dynamics matrix and tensor are obtained first with respect to time then their transformed counterparts in Eqs. 21a and 21b are obtained by extensive application of the chain rule. First, the general Sundman transformation is redefined along with its first and second derivatives with respect to the state vector.

$$\begin{array}{@{}rcl@{}} {\eta = dt/d\tau = c_{n}r^{n}} \end{array} $$
(22)
$$\begin{array}{@{}rcl@{}} {\eta_{X}}^{i} = \frac{\partial \eta}{\partial \boldsymbol{X}^{i}} \end{array} $$
(23)
$$\begin{array}{@{}rcl@{}} {\eta_{{XX}}}^{i,a} = \frac{\partial^{2}\eta}{\partial \boldsymbol{X}^{i}\partial\boldsymbol{X}^{a}} \end{array} $$
(24)

After assembling Eqs. 4a and 4b, the chain rule completes the transformation,

$$\begin{array}{@{}rcl@{}} {\Lambda}^{i,a} &=& A^{i,a}\eta + \dot{\boldsymbol{X}}^{i}{\eta_{X}}^{a} , \end{array} $$
(25a)
$$\begin{array}{@{}rcl@{}} {\Lambda}^{i,ab} &=& A^{i,ab}\eta + A^{i,a}{\eta_{X}}^{b} + A^{i,b}{\eta_{X}}^{a} +\dot{\boldsymbol{X}}^{i}{\eta_{{XX}}}^{a,b} , \end{array} $$
(25b)

and the transformed differential equations for the STMs become

$$\begin{array}{@{}rcl@{}} \mathring{\Phi}^{i,a} &=& {\Lambda}^{i,\gamma_{1}}{\Phi}^{\gamma_{1},a} , \end{array} $$
(26a)
$$\begin{array}{@{}rcl@{}} \mathring{\Phi}^{i,ab} &=& {\Lambda}^{i,\gamma_{1}}{\Phi}^{\gamma_{1},ab} + {\Lambda}^{i,\gamma_{1}\gamma_{2}}{\Phi}^{\gamma_{1},a}{\Phi}^{\gamma_{2},b} . \end{array} $$
(26b)

Stage Cost-To-Go Derivatives

Before making use of the STMs to obtain the stage cost-to-go derivatives, the quadratic expansions of the cost-to-go are restated in terms of the augmented state vector.

$$ \delta J_{k} \approx ER_{k + 1} + J_{X,k}^{T}\delta\boldsymbol{X}_{k} + J_{\lambda,k}^{T}\delta\boldsymbol{\lambda} + \frac{1}{2}\delta\boldsymbol{X}_{k}^{T}J_{XX,k}\delta\boldsymbol{X}_{k} + \frac{1}{2}\delta\boldsymbol{\lambda}^{T} J_{\lambda\lambda,k}\delta\boldsymbol{\lambda} + \delta\boldsymbol{X}_{k}^{T}J_{X\lambda,k}\delta\boldsymbol{\lambda} \ $$
(27a)
$$\begin{array}{@{}rcl@{}} \delta L_{k} &\approx&L_{X,k}^{T}\delta\boldsymbol{X}_{k} + \frac{1}{2}\delta\boldsymbol{X}_{k}^{T}L_{XX,k}\delta\boldsymbol{X}_{k} \end{array} $$
(27b)
$$\begin{array}{@{}rcl@{}} \delta J_{k + 1}^{*} &\approx& \ ER_{k + 1} + J_{X,k + 1}^{*T}{\Phi}\delta\boldsymbol{X}_{k}+ \frac{1}{2}J_{X,k + 1}^{*\gamma_{1}}{\Phi}^{\gamma_{1},\gamma_{2}\gamma_{3}}\delta\boldsymbol{X}_{k}^{\gamma_{2}}\delta\boldsymbol{X}_{k}^{\gamma_{3}} + J_{\lambda,k + 1}^{*T}\delta\boldsymbol{\lambda} \\ && + \frac{1}{2}\delta\boldsymbol{X}_{k}^{T}{\Phi}^{T}J_{XX,k + 1}^{*}{\Phi}\delta\boldsymbol{X}_{k} + \frac{1}{2}\delta\boldsymbol{\lambda}^{T} J_{\lambda\lambda,k + 1}^{*}\delta\boldsymbol{\lambda} + \delta\boldsymbol{X}_{k}^{T}{\Phi}^{T}J_{X\lambda,k + 1}^{*}\delta\boldsymbol{\lambda} \end{array} $$
(27c)

Recall that the control sensitivities of \(J^{*}_{k + 1}\) are zero. Substituting Eq. 20 into Eq. 16b yields third and fourth-order terms in δX k that have been ignored in Eq. 27c. That truncation is inconsequential as Taylor coefficients are only being matched to second-order. Doing so finally yields the stage cost-to-go derivatives with respect to the augmented state and multipliers, from which the submatrices are acquired for Eq. 14.

$$\begin{array}{@{}rcl@{}} J_{X,k} &=& L_{X,k} + {\Phi}^{T}J^{*}_{X,k + 1} \end{array} $$
(28a)
$$\begin{array}{@{}rcl@{}} J_{\lambda,k} &= &J_{\lambda,k + 1}^{*} \end{array} $$
(28b)
$$\begin{array}{@{}rcl@{}} J_{XX,k}^{i,a} &=& L_{XX,k}^{i,a} + J_{XX,k + 1}^{*\gamma_{1},\gamma_{2}}{\Phi}_{\phantom{0}}^{\gamma_{1},i}{\Phi}_{\phantom{0}}^{\gamma_{2},a} + J^{*\gamma_{1}}_{X,k + 1}{\Phi}_{\phantom{0}}^{\gamma_{1},ia} \end{array} $$
(28c)
$$\begin{array}{@{}rcl@{}} J_{\lambda\lambda,k} &=& J_{\lambda\lambda,k + 1}^{*} \end{array} $$
(28d)
$$\begin{array}{@{}rcl@{}} J_{X\lambda,k} &=& {\Phi}^{T}J^{*}_{X\lambda,k + 1} \end{array} $$
(28e)

Stage Update Equations

Before proceeding upstream from stage k to k − 1, the stage update equations predict the effects of the updated control. The expected reduction and derivatives of the optimal cost-to-go are obtained by inserting the optimal control law into Eq. 13.

$$\begin{array}{@{}rcl@{}} ER_{k} &=& ER_{k + 1} + J^{T}_{u,k}A_{k} + \frac{1}{2}A_{k}^{T}J_{uu,k}A_{k} \end{array} $$
(29a)
$$\begin{array}{@{}rcl@{}} J^{*T}_{x,k} &=& J^{T}_{x,k} + J^{T}_{u,k}B_{k}+ A_{k}^{T}J_{uu,k}B_{k} + A_{k}^{T}J_{ux,k} \end{array} $$
(29b)
$$\begin{array}{@{}rcl@{}} J^{*T}_{\lambda,k} &=& J^{T}_{\lambda,k} + J^{T}_{u,k}D_{k} + A_{k}^{T}J_{uu,k}D_{k} + A_{k}^{T}J_{u\lambda,k} \end{array} $$
(29c)
$$\begin{array}{@{}rcl@{}} J^{*}_{xx,k} &=& J_{xx,k} + B_{k}^{T}J_{uu,k}B_{k} + B_{k}^{T}J_{ux,k} + J_{ux,k}^{T}B_{k} \end{array} $$
(29d)
$$\begin{array}{@{}rcl@{}} J^{*}_{\lambda\lambda,k} &= &J_{\lambda\lambda,k} + D_{k}^{T}J_{uu,k}D_{k} + D_{k}^{T}J_{u\lambda,k} + J_{u\lambda,k}^{T}D_{k} \end{array} $$
(29e)
$$\begin{array}{@{}rcl@{}} J^{*}_{x\lambda,k} &=& J_{x\lambda,k} + B_{k}^{T}J_{uu,k}D_{k} + B_{k}^{T}J_{u\lambda,k} + J_{ux,k}^{T}D_{k} \end{array} $$
(29f)

The stage update equations require initial values to solve the first subproblem at stage k = N − 1. These values are straightforward to obtain as there is no subproblem at the final state. The optimal and nominal cost are equivalent, i.e. \(J^{*}_{N} = \widetilde {\varphi }\). Derivatives of the optimal cost-to-go are derivatives of the augmented Lagrangian and there is no expected reduction, ER N = 0.

Multiplier Update

HDDP obtains the optimal multiplier update in the same manner as the optimal control update at each stage, by setting the derivative of the quadratic model with respect to the multiplier update equal to zero.

$$ \delta{\boldsymbol{\lambda}} =-J_{\lambda\lambda}^{-1}J_{\lambda} $$
(30)

In this single-phase formulation, \(J_{\lambda \lambda } = J^{*}_{\lambda \lambda ,0}\) and \(J_{\lambda } = J^{*}_{\lambda ,0}\). The trust-region method is again employed to perform the multiplier update in Eq. 30. Now however, J λ λ is negative-definite, so the update δλ is a maximizer and the expected reduction increases. The expected reduction is updated to reflect the multiplier increment.

$$ ER_{0} = ER_{0} + J^{T}_{\lambda}A_{\lambda} + \frac{1}{2}A_{\lambda}^{T}J_{\lambda\lambda}A_{\lambda} $$
(31)

Trust-Region Quadratic Subproblem

The unconstrained control update in Eq. 14 is likely to step beyond the valid region of the quadratic approximation, as is the multiplier update in Eq. 30. An unconstrained backward sweep and subsequent application of the new control law is likely to lead to divergence or infeasible iterates. The updates also require the Hessians to be invertible, with Juu,k positive definite and J λ λ negative definite. HDDP overcomes these challenges by solving a trust-region quadratic subproblem (TRQP) at each stage subproblem and multiplier update. Now to compute each stage control update, for example, δu k is required to lie within the trust-region radius Δ.

$$\begin{array}{@{}rcl@{}} &&\min_{\delta \boldsymbol{u}_{k}}[ J_{u,k}^{T}\delta \boldsymbol{u}_{k} + \frac{1}{2}\delta \boldsymbol{u}_{k}^{T} J_{uu,k} \delta \boldsymbol{u}_{k} ] \\ &&\text{s.t.} \left\Vert D\delta \boldsymbol{u}_{k}\right\Vert \leqslant {\Delta} \end{array} $$
(32)

The subproblem posed in Eq. 32 is named TRQP(J u , J u u ,Δ) and the multiplier subproblem is TRQP(−J λ ,−J λ λ ,Δ). The methods of Reference [34] have proved robust in solving this subproblem in HDDP. However, the algorithm is sensitive to the selection of a scaling matrix D that determines the shape of the trust-region. In this study, setting D to the identity matrix was sufficient. When components of the gradient and Hessian vary by orders of magnitude, a robust heuristic for selecting D becomes necessary. Reference [24] suggests several scaling methods and provides a performance comparison.

Iteration

A quadratic model of the cost function and dynamics is inexact for higher-order systems and requires iteration to reach a local minimum. The reduction ratio

$$ \rho = \delta J / ER_{0} $$
(33)

serves as an acceptance criterion for new iterates. If ρ ≈ 1, then the quadratic model is good and the reduction in cost is as predicted. The iterate is accepted and a larger trust-region is allowed. Otherwise the model is poor, the iterate is rejected and the trust-region is reduced for the next backward sweep.

$$ {\Delta}_{p + 1} = \left\{\begin{array}{ll} \min((1+\kappa){\Delta}_{p}, {\Delta}_{{\max}}), & \text{if } \rho \in [1-\epsilon_{1},1+\epsilon_{1}]\\ \max((1-\kappa){\Delta}_{p},{\Delta}_{{\min}}), & \text{otherwise} \end{array}\right. $$
(34)

For the trust-region update in Eq. 34, p is the iteration counter, κ and 𝜖1 are an additional set of tuning parameters, as is the allowable trust-region range [Δmin,Δmax].

If ER0 is zero after the backward sweep, or less than some optimality tolerance, the optimization has reached a stationary point of the cost function with respect to controls and multipliers. This point is a minimum if all of the Hessians Juu,k are positive definite and J λ λ is negative definite. The algorithm converges upon reaching a minimum while satisfying terminal constraints to within a feasibility tolerance.

Problem Formulation

Fuel-optimal low-thrust transfers from geostationary transfer orbit (GTO) to geosynchronous orbit (GEO) were computed to demonstrate the efficacy of the Sundman-transformed DDP approach.

Spacecraft State and Dynamics

The spacecraft state is chosen as a Cartesian representation of the spacecraft inertial position and velocity.

$$ \boldsymbol{r} = \left[\begin{array}{lll} x & y & z \end{array}\right]^{T}, \quad \boldsymbol{v} =\left[\begin{array}{lll} \dot{x} & \dot{y} & \dot{z} \end{array}\right]^{T} $$
(35)

The augmented state vector includes time, mass m, and thrust control variables T, α and β.

$$ \boldsymbol{X} = \left[\begin{array}{lllllllllll} t & x & y & z & \dot{x} & \dot{y} & \dot{z} & m & T & \alpha & \beta \end{array}\right]^{T} $$
(36)

Spherical thrust control is defined by magnitude T, yaw angle α and pitch angle β, where the angles are defined relative to the radial-transverse-normal (RSW) frame. RSW basis vectors and the rotation to the inertial frame are defined by

$$ \left[\begin{array}{lll} \hat{\boldsymbol{r}} & \hat{\boldsymbol{s}} & \hat{\boldsymbol{w}} \end{array}\right] = \left[\begin{array}{lll} \frac{\boldsymbol{r}}{r} & \frac{(\boldsymbol{r} \times \boldsymbol{v}) \times \boldsymbol{r}}{\left\|{(\boldsymbol{r} \times \boldsymbol{v}) \times \boldsymbol{r}}\right\|} & \frac{\boldsymbol{r}\times\boldsymbol{v}}{\left\|{\boldsymbol{r}\times\boldsymbol{v}}\right\|} \end{array}\right]. $$
(37)

Thrust vector components are then

$$ \left[\begin{array}{l} T_{r} \\ T_{s} \\ T_{w} \end{array}\right] = \left[\begin{array}{l} T\sin\alpha\cos\beta \\ T\cos\alpha\cos\beta \\ T\sin\beta \end{array}\right], \quad \left[\begin{array}{l} T_{x} \\ T_{y} \\ T_{z} \end{array}\right] = \left[\begin{array}{lll} \hat{\boldsymbol{r}} & \hat{\boldsymbol{s}} & \hat{\boldsymbol{w}} \end{array}\right]\left[\begin{array}{l} T_{r} \\ T_{s} \\ T_{w} \end{array}\right], $$
(38)

so that the pitch angle is measured from the orbit plane about the radial direction and the yaw angle is measured from the transverse direction about the angular momentum. No concern is given for angle wrapping. In fact, computation exhibits favorable performance when the angles are unbounded. Spacecraft dynamics consider geocentric two-body motion perturbed by thrust, J2 and lunar gravity,

(39)

where \(\dot {\boldsymbol {X}}_{\oplus }\) is the two-body motion due to point mass Earth gravity, \(\dot {\boldsymbol {X}}_{T}\) is the thrust acceleration and mass flow rate, \(\dot {\boldsymbol {X}}_{J_{2}}\) is Earth’s J2 perturbation, and is the point mass lunar gravity perturbation. The Sundman transformation is made after assembling the complete equations of motion with respect to time.

(40)

The time derivatives are defined by

$$\begin{array}{@{}rcl@{}} \dot{\boldsymbol{X}}_{\oplus}\! &=&\! \left[\begin{array}{lllllllllll} 1 & \dot{x} & \dot{y} & \dot{z} & -\frac{\mu_{\oplus}}{r^{3}}x &\!\!-\frac{\mu_{\oplus}}{r^{3}}y -\frac{\mu_{\oplus}}{r^{3}}z & 0 & 0 & 0 & 0 \end{array}\right]^{T}, \end{array} $$
(41a)
$$\begin{array}{@{}rcl@{}} \dot{\boldsymbol{X}}_{T}\! &=&\! \left[\begin{array}{lllllllllll} 0 & 0 & 0 & 0 & \frac{T_{x}}{m} & \frac{T_{y}}{m} & \frac{T_{z}}{m} & -\frac{T}{I_{sp}g_{0}} & 0 & 0 &0 \end{array}\right]^{T}, \end{array} $$
(41b)
$$\begin{array}{@{}rcl@{}} \dot{\boldsymbol{X}}_{J_{2}}\! &=&\!-\frac{3J_{2}\mu_{\oplus} R^{2}_{\oplus}}{2r^{5}} \!\left[\begin{array}{lllllllllll}\! 0 & 0 & 0 & 0 & x\!\left( 1-5\frac{z^{2}}{r^{2}}\right) &\! y\!\left( 1-5\frac{z^{2}}{r^{2}}\right) & z\left( 3-5\frac{z^{2}}{r^{2}}\right) & 0 & 0 & 0 & 0 \end{array}\right]^{T}\! , \end{array} $$
(41c)
(41d)

Gravitational parameters for the Earth and the Moon are μ⊕ and , respectively. A constant power model is assumed with T ∈ [0,T m a x ]. Mass flow rate is inversely proportional to the specific impulse I s p , and acceleration due to gravity at sea level g0. The J2 perturbation is owed to the Earth’s oblateness and is a function of the Earth’s equatorial radius R⊕. Table 1 lists these dynamic model constants. Including the lunar perturbation requires the Moon’s inertial position with respect to the Earth,

(42)

that is assumed to evolve according to geocentric two-body motion. The Moon’s state is initialized with the orbital elements listed in Table 2, where i is the inclination, Ω is the right ascension of the ascending node and ω is the argument of periapsis.

Table 1 Dynamic model parameters
Full size table
Table 2 The Moon’s Earth-centered ICRF orbital elements at 01 Jan 2000 00:00:00.0 TDB
Full size table

Augmented Lagrangian cost function

Final conditions for GEO are described in the terminal constraint function ψ, so that ψ(X f ) = 0 for a feasible solution. The cost in Eq. 9 also includes an objective function defined so that the final mass is maximized and does not include local stage costs, i.e. each L k = 0.

$$\begin{array}{@{}rcl@{}} &&\phi = -m_{f} \end{array} $$
(43a)
$$\begin{array}{@{}rcl@{}} &&\boldsymbol{\psi} = \left[\begin{array}{c} \|{\boldsymbol{r}_{f}}\| - r_{target} \\ \|{\boldsymbol{v}_{f}}\| - v_{target} \\ \boldsymbol{r}_{f}\cdot\boldsymbol{v}_{f} \\ z_{f} \\ \dot{z}_{f} \end{array}\right] \end{array} $$
(43b)
$$\begin{array}{@{}rcl@{}} &&{\Sigma}= I_{5\times 5} \end{array} $$
(43c)

The terminal constraint function is satisfied upon arrival at GEO distance with circular orbital velocity, zero flight path angle and zero inclination. The arrival longitude is unconstrained. The penalty matrix is set as the identity matrix so that all constraints are weighted equally. A scaled feasibility tolerance requires ∥ψ∥ < 1 × 10−8 and an optimality tolerance requires ER0 < 1 × 10−9. Scaling improves the numerical behavior of both trajectory computation and optimization but adds to the set of tuning parameters. Here a distance unit DU, time unit TU, force unit FU and mass unit MU are set as

$$\begin{array}{@{}rcl@{}} DU &=& r_{target} ,\\ TU &=& 10\,\sqrt{{DU}^{3}/\mu_{\oplus}} , \\ FU &=& T_{max} ,\\ MU &=& FU\,{TU}^{2}/ \, DU , \end{array} $$
(44)

where the distance unit is approximately GEO radius, the time unit has been scaled by an additional factor of 10, and the force unit is the maximum thrust.

Trajectory Computation

Propagating a trajectory from the initial state requires effective discretization and a numerical method to evaluate the transition function between stages. Trajectories are discretized to 100 stages per revolution and numerically integrated with fixed-step eighth-order Runge-Kutta (RK8) formulae from Dormand and Prince [35]. Stages are equally spaced in the independent variable. Each stage offers an opportunity to update the thrust control variables that are held constant across an integration step. A fixed integration step accumulates Δτ = τk+ 1 − τ k = 2π/100. The initial guess for all stage control variables is zero, so the first iteration considers a ballistic orbit in GTO for a prescribed number of revolutions, N r e v . The fixed transfer duration in orbit angle is 2πN r e v and there are 300N r e v control variables to solve for.

STM Computation

The author’s HDDP implementation is programmed in C+ + and compiled on the RMACC Summit supercomputer [36]. Results were generated on a single node that contains two Intel Xeon E5-2680 v3, 2.50 GHz CPUs with 12 cores each. STM computations were distributed in parallel across all 24 cores with OpenMP [37]. All other steps of the algorithm run serially. To permit parallelization, STMs are obtained separately from attempted trajectories with trial controls. When an iterate is accepted as the new nominal trajectory, Eq. 8 is augmented with the STM differential equations in Eq. 26b. Each X k is known, so integrations from any stage k to k + 1 can be performed separately and in parallel, instead of serially from k = 0 to k = N − 1. The states at integrator substeps are not saved, so the 11 state differential equations are recomputed with the 112 + 113 STM differential equations.

Results

Petropoulos et al. [38] compared direct and indirect methods and the Q-law over several cases of many-revolution transfers, including a GTO to GEO example named Case B. Now HDDP is added to the comparison. Table 3 describes the initial and target orbits, with slight differences between Reference [38] and the HDDP transfer. Eccentricity and inclination targets were set to zero to use of Eq. 41h. The dynamics consider two-body motion and thrust, but not J2 and lunar perturbations, so the equal reduction to initial and target inclination is inconsequential to the comparison. The HDDP transfer requires more effort to completely circularize the final orbit, but the dynamics use a slightly smaller gravitational parameter for the Earth. The effects are small and offsetting with regard to fuel expenditure and time of flight, but have no qualitative implications. The scaled feasibility tolerance corresponds to a 0.42165 m position requirement and 0.003075 mm/s velocity requirement.

Table 3 Case B initial and target orbits
Full size table

Transfers were computed across a range of N r e v and with Sundman transformations to each of the true, mean and eccentric anomalies. Attempts with time as the independent variable were unsuccessful. The result is a Pareto front of propellant mass versus N r e v as shown in Fig. 1a. That is not identically the propellant mass versus time of flight trade-off. The target orbit might be reached before the final revolution is completed, resulting in a terminal coast arc that adds extra flight time. Nonetheless, the Pareto front of propellant mass versus time of flight shown in Fig. 1b is consistent with Petropoulos’ result.

Fig. 1
figure 1

Case B trade-off of propellant mass versus time of flight and number of revolutions

Full size image

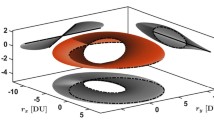
The intuitive limiting cases are continuous thrust for the minimum time of flight transfer that reduces to impulsive apoapsis maneuvers for infinite flight time. The trend is evidenced in Fig. 2, where coast arcs grow in duration and number, while thrust arcs reduce to small maneuvers centered on their optimal locations. Figure 3 shows the thrust magnitude history for the 500 revolution transfer as evidence of the expected bang-bang control structure for the fuel-optimal transfer. It also proves worthwhile for the shorter duration transfers to raise apoapsis beyond GEO radius for more efficient inclination change. The change in maneuver strategy as time of flight increases is shown in Fig. 4, with apsis radii distances and inclination provided through the duration of the 183 and 500 revolution true anomaly transfers. The 183 revolution true anomaly transfer spans 141.95 days and uses 215.64 kg of propellant, but falls short of finding the minimum time solution with a number of perigee centered coast arcs. On the other end, the Sundman-transformed HDDP approach is able to extend the transfer duration out to 2000 revolutions for a 1276.83 days time of flight requiring 146.32 kg of propellant. There are limited returns on extending the flight time, as the 1000 revolution transfer shown only increases the propellant use up to 147.55 kg for 634.35 days time of flight.

Fig. 2
figure 2

Equatorial projections of Case B transfers for a 183, b 210, c 500 and d 1000 revolutions with true anomaly as the independent variable. Thrust arcs are colored orange and coast arcs are colored blue. The x and y coordinates of the first and final revolutions are overlaid in black

Full size image
Fig. 3
figure 3

Thrust magnitude for the 500 revolution true anomaly transfer is shown for a the entire transfer and b zoomed in on the last few revolutions

Full size image
Fig. 4
figure 4

a Apsis radii and b inclination history for the 183 revolution true anomaly transfer, and c apsis radii and d inclination history for the 500 revolution true anomaly transfer

Full size image

The accuracy of each HDDP solution was checked by variable-step RK8(7) integration with a relative error tolerance of 10−11 [35]. The resulting constraint violations are shown in Fig. 5. Solutions with mean anomaly as the independent variable prove unreliable, with actual constraint violations growing six orders of magnitude from what was viewed as a feasible trajectory with fixed-step integration. As with fixed-step time integration, mean anomaly integration incurs errors through large steps around periapsis. Mean anomaly integration, however, automatically adapts the step size as the orbit changes during the transfer, whereas time integration steps remain fixed. An adaptive-mesh technique might enable successful time integration, but that is essentially the point of the Sundman transformation. HDDP attempts with mean anomaly failed when N r e v was increased from 700 to 800. The true anomaly and eccentric anomaly prove more effective in regulating the step size. Most eccentric anomaly trajectories fall just outside of feasibility with constraint violations 10−8 < ∥ψ∥ < 10−7, except for the 1000 and 1500 revolution cases that remain feasible. Every true anomaly trajectory remains feasible. The superiority of true anomaly was first realized for a coarse range of N r e v before proceeding exclusively with true anomaly through a finer resolution of N r e v . Data points are absent for the 200, 220 and 240 revolution true anomaly transfers and 200 and 650 revolution eccentric anomaly transfer. For these cases, the algorithm found a stationary point that was just outside of feasibility, again in the region 10−8 < ∥ψ∥ < 10−7. Given the range of feasible trajectories, this might be resolved by adjusting the many tuning parameters. Optimization of the 2000 revolution eccentric anomaly transfer was cut off after 48 hours of runtime on iteration 1556.

Fig. 5
figure 5

Constraint violations after fixed-step integration solutions were recomputed with variable-step integration and a relative error tolerance of 10−11

Full size image

Computational performance is profiled in Figs. 6 and 7. The quickest solution time was 20 minutes and 40 seconds to compute the 184 revolution true anomaly case in 186 iterations. The lowest number of iterations to convergence was 181 for the 187 revolution true anomaly case and required 21 minutes and 1 second. Generally, both runtime and number of iterations grow with the number of revolutions. The behavior is unpredictable, especially with excessive transfer duration, where the runtime and iterations might jump up or down by a factor of two or more. Runtimes for the forward pass and STM subroutines however, do have a predictable linear growth. The listed times correspond to the first iteration that is ballistic propagation in GTO. Computing the STMs is the most computationally intensive step in the HDDP algorithm. The importance of parallelization is highlighted when comparing the parallel STM elapsed real time to the total CPU time across all cores, and realizing that the STM step would slow by an order of magnitude in the current configuration.

Fig. 6
figure 6

a Elapsed real time and b number of iterations to convergence

Full size image
Fig. 7
figure 7

Elapsed real time for a forward pass and b STM subroutines and c the total CPU time for the STM subroutine

Full size image

GTO to GEO with Perturbations

Next, the robustness of the approach is tested by introducing J2 and lunar gravity perturbations to the 500 revolution Case B transfers with both eccentric and true anomalies as independent variables. Perturbations are introduced one at a time, so that the new cases are J2-perturbed and J2 and Moon-perturbed transfers.

Equatorial projections of the new transfers in Fig. 8 show the pronounced effect of the J2-induced periapsis drift over a long transfer duration. The effect of lunar gravity is less noticeable. Three-dimensional views of the two-body and J2 and Moon-perturbed true anomaly transfers are provided in Fig. 9. Trajectory performance is compared with the two-body case in Table 4, where m p is the propellant mass. Computational performance is summarized in Table 5. The new cases are unable to leverage perturbations to improve upon the two-body result, but propellant mass and time of flight reach similar values. Solution accuracy when checked with RK8(7) integration remains consistent with the two-body results and is summarized in Table 6. These measures collectively add the significant result that Sundman-transformed HDDP can accommodate perturbations to yield a reliable solution without detriment to the computational effort. That is not for free, as seen by the effect on subroutine runtimes in Table 7. Including J2 is an inexpensive addition relative to the cost of computing the lunar perturbation and the necessary derivatives with respect to the spacecraft state. Table 7 adds the comparison to the elapsed real time of a serial STM step, as opposed to the parallel STM step total CPU time in Fig. 7c, and shows an order of magnitude speed improvement owed to parallelization.

Fig. 8
figure 8

Equatorial projections of eccentric anomaly transfers with aJ2 and bJ2 and Moon perturbations and true anomaly transfers with cJ2 and dJ2 and Moon perturbations

Full size image
Fig. 9
figure 9

Three dimensional views of the a two-body and bJ2 and Moon-perturbed true anomaly transfers

Full size image
Table 4 500 revolution transfer results
Full size table
Table 5 Computational performance for 500 revolution transfers
Full size table
Table 6 Constraint violations after variable-step integration of 500 revolution fixed-step solutions
Full size table
Table 7 Subroutine elapsed real time (sec) for 500 revolution transfers
Full size table

Conclusion

The pairing of differential dynamic programming and the Sundman transformation has been presented as a viable approach to the low-thrust many-revolution spacecraft trajectory optimization problem. The utility of this method has been demonstrated by the fuel-optimization of transfers from geostationary transfer orbit to geosynchronous orbit with an implementation of the Hybrid Differential Dynamic Programming algorithm and transformations to the true, mean and eccentric anomalies. The resulting Pareto front of propellant mass versus time of flight is consistent with those of other methods. Beyond just reproducing a past result, the method is demonstrably efficient and amenable to perturbations. Choosing the true anomaly for this study proved most effective and enabled the direct optimization of up to 600,000 variables for the 2000 revolution transfer. The size of the optimization problem and computation time could be significantly reduced by replacing the Cartesian representation of the spacecraft with an orbital element set. Future research should also explore different types of transfers, objectives and constraints, and continue to add fidelity to the dynamic model.