Characterization of Self-Excited, Nearly Axisymmetric, Spinning Rigid-Body Motion as an Oblate Epicycloid

Abstract

A unique formulation of the solution to a spinning, nearly axisymmetric rigid-body is presented. Direct integration of the linearized equations of motion gives accurate results for nearly axisymmetric inertia ellipsoids while avoiding the complexity of more general formulations. The simplicity of the formulation lends itself to a better understanding of the system behavior. Specifically, the motion of the spin axis for this nearly axisymmetric case is described by an oblate epicycloid, providing an extension of the classic epicycloid solution for axisymmetric objects.

Introduction

The solution to Euler’s equations of motion for a spinning rigid-body with a body-fixed torque has been treated by many researchers with varying degree of complexity. At the more general and complex end of the spectrum, Leimanis [1] describes Bödewadt’s solution, which is an exact analytical solution to Euler’s equations for an axisymmetric rigid-body, with any initial angular velocity vector, and subject to constant torques about any axis. Bödewadt’s solution is given in terms of Fresnel integrals, and was found by Longuski [2, 3] to be inaccurate for nearly axisymmetric rigid bodies. Longuski goes on to develop a similar solution for nearly axisymmetric bodies. In later work, Longuski [4–9] and Tsiotras [5–9] develop additional solutions for nearly axisymmetric bodies under a variety of specific conditions, including one that does not utilize the small angle assumption [8] and one for an asymmetric rigid-body subject to large initial angular velocities [9]. All of these solutions [2–9] involve complex equations and Fresnel integrals.

Analyses of the motion of a spinning rigid-body subject to a constant body-fixed torque have also been completed under the assumption that the transverse moments of inertia are nearly equal [10–12]. In References [10, 11], a solution for the nondimensional angular velocity is obtained and the stability properties are developed as a function of the initial conditions. Longuski et al. [12] solve for the attitude of the rigid-body as a function of time by translating the two transverse equations of motion for the Euler angles into a single complex equation. The solution is numerically equivalent to the one presented in this paper and has the merit of being compact, but it does not readily permit the physical interpretation developed herein.

The simplest solution of a self-excited, spinning rigid-body with an axisymmetric inertia ellipsoid has been republished by many, but is described by Wie [11] and Kolk [13] as an epicycloid curve, where the amplitudes and frequencies of precession and nutation are constant functions of the moments of inertia, initial spin rate of the body, and the torque on the body. Due to the assumptions made to derive this solution, it is valid for a narrow range of conditions: the initial spin rate must be entirely about either the major or minor body axis; the two transverse moments of inertia must be equal; the torque must be constant and about a single transverse axis; finally, the torque must be small enough for the deviation of the nominal spin axis to remain small (i.e. small angle assumption).

This paper considers the slightly more general case of a nearly symmetric rigid-body, while maintaining the assumption of small transverse spin rates and Eulerian Angles. It is also assumed that the initial spin rate is primarily about either the major- or minor-axis, and that torques exist only about the transverse axes. The formulation achieves a unique balance between extension of the applicability of the classic case to a nearly symmetric mass distribution and the complexity of the resulting solution, which still retains a physically intuitive description that is deemed herein an “oblate epicycle”.

Theoretical Development

Motion of a Self-Excited, Axisymmetric Rigid-Body as an Epicycloid

Wie [11] gives the solution for the axisymmetric rigid-body with torque about a single transverse axis as:

$$ \theta_{1}\left( t \right)=-A_{p}\left[ 1-\cos \left( \omega_{p}t \right) \right]+A_{n}\left[ 1-\cos \left( \omega_{n}t \right) \right] $$

(1)

$$ \theta_{2}\left( t \right)=A_{p}\sin \left( \omega_{p}t \right)-A_{n}\sin \left( \omega_{n}t \right) $$

(2)

where $\theta _{1}$ and $\theta _{2}$ are part of a set of 1-2-3 Euler Angles describing the attitude of the rigid-body. The precessional and nutational amplitudes and frequencies are given by:

$$ A_{p}=\frac{\mu J}{\lambda nJ_{3}}=precessional\thinspace amplitude $$

(3)

$$ A_{n}=\frac{\mu }{\lambda n}=nutational\thinspace amplitude $$

(4)

$$ \omega_{p}=\frac{J_{3}n}{J}=precessional\thinspace frequency $$

(5)

$$ \omega_{n}=n=nutational\thinspace frequency $$

(6)

where $\mu$ is the disturbance acceleration due to the transverse moment, and $\lambda$ is the relative spin rate. Both of these values are constants given in terms of the torque, moments of inertia, and initial spin rate:

$$ \mu =\frac{M}{J} $$

(7)

$$ \lambda =\frac{\left( J-J_{3} \right)}{J}n $$

(8)

where M is the torque about the transverse axis, J is the transverse moment of inertia, $J_{3}$ is the moment of inertia about the spin axis, and n is the initial spin rate.

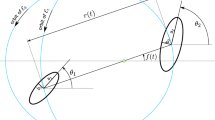
Wie [11] describes the epicycloid as the curve described by a point on a circle of radius $A_{n}$, rolling about the outside of a circle of radius $A_{p}$, as shown in Fig. 1. Kolk [13] describes the epicycloid with two pendulums, the first fixed at one end, and the second attached to the free end of the first. The lengths of the two pendulums are not necessarily equal, nor are their angular rates. The epicycloid is the curve traced out by the free end of the second pendulum, as shown in Fig. 2. Kolk gives the slightly more general form of the equations:

$$ \theta_{1}=L_{1}\left[ 1-\cos \left( \epsilon t \right) \right]+L_{2}\sin \left( \epsilon t \right)+L_{3}\left[ 1-\cos \left( \beta t \right) \right]+L_{4}\sin \left( \beta t \right) $$

(9)

$$ \theta_{2}=L_{1}\sin \left( \epsilon t \right)-L_{2}\left[ 1-\cos \left( \epsilon t \right) \right]+L_{3}\sin \left( \beta t \right)-L_{4}\left[ 1-\cos \left( \beta t \right) \right] $$

(10)

where $L_{1}$, $L_{2}$, $L_{3}$, $L_{4}$, $\epsilon$, and $\beta$ are as shown in Fig. 2, but is quick to assume that $L_{2}$ and $L_{4}$ are negligible and that $L_{1}=A_{p}$; $L_{3}=A_{n}$; $\epsilon =\omega _{p}$; and $\beta =\omega _{n}$ as given in Eq. 3 through Eq. 6. McNair and Tragesser [14] have shown that, due to the relationships between $A_{p}$, $A_{n}$, $\omega _{p}$, and $\omega _{n}$, these two descriptions (i.e. the circles rolling without slip and the double pendulum) are equivalent, with the caveat that the radius of the inner circle in Wie’s qualitative description is equal to the difference between $A_{p}$ and $A_{n}$, rather than simply $A_{p}$.

Fig. 1

Rolling circles description of the epicycloid

Fig. 2

Kolk’s pendulum description of the epicycloid [13]

Inspection will show that an equivalent form of Kolk’s equations, corresponding with the representation shown in Fig. 3, is given by:

$$ \theta_{1}=A_{p}\cos \left( \omega_{p}t+{\Phi} \right)+A_{n}\cos \left( \omega_{n}t+\phi \right)+\theta_{1,c} $$

(11)

$$ \theta_{2}=A_{p}\sin \left( \omega_{p}t+{\Phi} \right)+A_{n}\sin \left( \omega_{n}t+\phi \right)+\theta_{2,c} $$

(12)

where:

$$ A_{p}=\sqrt {{L_{1}^{2}}+{L_{2}^{2}}} $$

(13)

$$ A_{n}=\sqrt {{L_{3}^{2}}+{L_{4}^{2}}} $$

(14)

$$ {\Phi} =\text{atan}\left( \frac{L_{2}}{L_{1}} \right) $$

(15)

$$ \phi =\text{atan}\left( \frac{L_{4}}{L_{3}} \right) $$

(16)

Fig. 3

Pendulum description of the epicycloid

Applying initial conditions to solve for the offset of the inner pendulum, $\theta _{1,c}$ and $\theta _{2,c}$ yields:

$$ \theta_{1,c}=\theta_{1,0}-A_{p}\cos \left( {\Phi} \right)-A_{n}\cos \left( \phi \right) $$

(17)

$$ \theta_{2,c}=\theta_{2,0}-A_{p}\sin \left( {\Phi} \right)-A_{n}\sin \left( \phi \right) $$

(18)

so that the parametric equations become:

$$ \theta_{1}=A_{p}\left[ \cos {\left( \omega_{p}t+{\Phi} \right)-\cos \left( {\Phi} \right)} \right]+A_{n}\left[ \cos \left( \omega_{n}t+\phi \right)-\cos \left( \phi \right) \right]+\theta_{1,0} $$

(19)

$$ \theta_{2}=A_{p}\left[ \sin \left( \omega_{p}t+{\Phi} \right)-\sin \left( {\Phi} \right) \right]+A_{n}\left[ \sin \left( \omega_{n}t+\phi \right)-\sin \left( \phi \right) \right]+\theta_{2,0} $$

(20)

Description of the Oblate Epicycloid

The oblate epicycloid invented in this work can also be described with two rotating pendulums. Instead of having a fixed length, the outer pendulum is allowed to change in length such that if one end were fixed, its free end would trace out the path of an ellipse as shown in Fig. 4 . The parametric equations for an ellipse with semimajor axis a and semiminor axis b are:

$$ x_{e}=a\thinspace \cos(\omega t+\phi ) $$

(21)

$$ y_{e}=b\sin \left( \omega t+\phi \right) $$

(22)

where $a\ne b$, $\omega$ is the angular velocity of the outer pendulum, $\phi$ is the angle of the outer pendulum at the initial time, and the parameters $x_{e}$ and $y_{e}$ are expressed such that $x_{e}$ is in the direction of the semimajor axis of the ellipse and $y_{e}$ is in the direction of the semiminor axis. In order to express the position and length of the outer pendulum in the $\theta _{1}$-$\theta _{2}$ plane, a coordinate transformation must be performed. Since the semimajor axis of the ellipse traced by the outer pendulum is always aligned in the same direction as the inner pendulum, this coordinate transformation is given by:

$$ \theta_{1,p}=x_{e}\cos \left( {\Omega} t+{\Phi} \right)-y_{e}\sin \left( {\Omega} t+{\Phi} \right) $$

(23)

$$ \theta_{2,p}=x_{e}\sin \left( {\Omega} t+{\Phi} \right)+y_{e}\cos \left( {\Omega} t+{\Phi} \right) $$

(24)

Fig. 4

Oblate epicycloid

Substituting in the parametric equations for an ellipse yields expressions for the motion of the outer pendulum:

$$ \theta_{1,p}=a\cos \left( \omega t+\phi \right)\cos \left( {\Omega} t+{\Phi} \right)-b\sin \left( \omega t+\phi \right)\sin \left( {\Omega} t+{\Phi} \right) $$

(25)

$$ \theta_{2,p}=a\cos {(\omega t+\phi )}\sin \left( {\Omega} t+{\Phi} \right)+b\sin \left( \omega t+\phi \right)\cos \left( {\Omega} t+{\Phi} \right) $$

(26)

These expressions are then added to those for the inner pendulum:

$$ \theta_{1}\,=\,R\cos \left( {\Omega} t\,+\,{\Phi} \right)+a\cos \left( \omega t\,+\,\phi \right)\cos \left( {\Omega} t\,+\,{\Phi} \right)-b\sin \left( \omega t+\phi \right)\sin \left( {\Omega} t+{\Phi} \right)+\theta_{1,c} $$

(27)

$$ \theta_{2}\,=\,R\sin \left( {\Omega} t\,+\,{\Phi} \right)+a\cos {(\omega t\,+\,\phi )}\sin \left( {\Omega} t\,+\,{\Phi} \right)+b\sin \left( \omega t+\phi \right)\cos \left( {\Omega} t+{\Phi} \right)+\theta_{2,c} $$

(28)

Applying initial conditions to solve for $\theta _{1,c}$ and $\theta _{2,c}$ results in the parametric equations:

$$\begin{array}{@{}rcl@{}} \theta_{1}&=&R\left[ \cos \left( {\Omega} t\!+{\Phi} \right)-\cos \left( {\Phi} \right) \right]\!+a\left[ \cos \left( \omega t\,+\,\phi \right)\cos \left( {\Omega} t+{\Phi} \right)-\cos \left( \phi \right)\cos \left( {\Phi} \right) \right]\\&&-b\left[ \sin \left( \omega t+\phi \right)\sin \left( {\Omega} t+{\Phi} \right)-\sin \left( \phi \right)\sin \left( {\Phi} \right) \right]+\theta_{1,0} \end{array} $$

(29)

$$\begin{array}{@{}rcl@{}} \theta_{2}&=&R\left[ \sin \left( {\Omega} t+{\Phi} \right)-\sin \left( {\Phi} \right) \right]+a\left[ \cos \left( \omega t+\phi \right)\sin \left( {\Omega} t\!+{\Phi} \right)-\cos \left( \phi \right)\sin \left( {\Phi} \right) \right]\\&&+b\left[ \sin \left( \omega t+\phi \right)\cos \left( {\Omega} t+{\Phi} \right)-\sin \left( \phi \right)\cos \left( {\Phi} \right) \right]+\theta_{2,0} \end{array} $$

(30)

Motion of a Self-Excited, Nearly Axisymmetric Rigid Body as an Oblate Epicycloid

In the axisymmetric case described above, a single moment is chosen without loss of generality, due to the assumption of symmetry; the axes can simply be chosen such that any transverse torque is about a single axis. However, for the asymmetric case, this is not true. Euler’s equations of motion are still used as the starting point, but in this case they are more general, having moments about both transverse axes, and also two different transverse moments of inertia, $J_{1}$ and $J_{2}$:

$$ J_{1}\dot{\omega }_{1}-\left( J_{2}-J_{3} \right)\omega_{3}\omega_{2}=M_{1} $$

(31)

$$ J_{2}\dot{\omega }_{2}+\left( J_{1}-J_{3} \right)\omega_{3}\omega_{1}=M_{2} $$

(32)

$$ J_{3}\dot{\omega }_{3}+\left( J_{2}-J_{1} \right)\omega_{1}\omega_{2}=0 $$

(33)

where a principal axis reference frame is chosen without loss of generality. It is assumed that the spin rate is primarily about the third body axis, such that the transverse angular velocities remain small. Therefore, the nonlinear term in Eq. 33 can be neglected. This is valid, as long as the difference between the two transverse moments of inertia is not significantly larger than the moment of inertia about the spin axis. Thus, Eq. 33 becomes:

$$ J_{3}\dot{\omega }_{3}\approx 0 $$

(34)

The following constant substitutions are made:

$$ n\equiv \omega_{3} $$

(35)

$$ \lambda_{1}\equiv \frac{J_{2}-J_{3}}{J_{1}}n $$

(36)

$$ \lambda_{2}\equiv \frac{J_{1}-J_{3}}{J_{2}}n $$

(37)

$$ \mu_{1}\equiv \frac{M_{1}}{J_{1}} $$

(38)

$$ \mu_{2}\equiv \frac{M_{2}}{J_{2}} $$

(39)

Equations 31 and 32 may then be re-written as:

$$ \dot{\omega }_{1}=\lambda_{1}\omega_{2}+\mu_{1} $$

(40)

$$ \dot{\omega }_{2}=-\lambda_{2}\omega_{1}+\mu_{2} $$

(41)

Solving Eqs. 40 and 41 for $\omega _{1}$ and $\omega _{2}$ yields

$$ \omega_{1}\left( t \right)\,=\,\left( \!\omega_{1}\left( 0 \right)-\frac{\mu_{2}}{\lambda_{2}} \right)\cos \left( \sqrt {\lambda_{1}\lambda_{2}} t \right)+\frac{\sqrt {\lambda_{1}\lambda_{2}} }{\lambda_{2}}\left( \omega_{2}\left( 0 \right)+\frac{\mu_{1}}{\lambda_{1}} \right)\sin \left( \sqrt {\lambda_{1}\lambda_{2}} t \right)+\frac{\mu_{2}}{\lambda_{2}} $$

(42)

$$ \omega_{2}\left( t \right)\,=\,-\frac{\sqrt {\lambda_{1}\lambda_{2}} }{\lambda_{1}}\left( \!\omega_{1}\left( 0 \right)-\frac{\mu_{2}}{\lambda_{2}} \right)\sin\! \left( \! \sqrt {\lambda_{1}\lambda_{2}} t \right)+\left( \!\omega_{2}\left( 0 \right)+\frac{\mu_{1}}{\lambda_{1}} \right)\cos\! \left( \! \sqrt {\lambda_{1}\lambda_{2}} t \right)-\frac{\mu_{1}}{\lambda_{1}} $$

(43)

If the attitude of the rigid-body is described by 1-2-3 Euler angles, the corresponding kinematic equations are:

$$ \dot{\theta }_{1}=\left( \omega_{1}\cos \theta_{3}-\omega_{2}\sin \theta_{3} \right)/\cos \theta_{2} $$

(44)

$$ \dot{\theta }_{2}=\omega_{1}\sin \theta_{3}+\omega_{2}\cos \theta_{3} $$

(45)

$$ \dot{\theta }_{3}=\left( {-\omega }_{1}\cos \theta_{3}+\omega_{2}\sin \theta_{3} \right)\sin \theta_{2}/\cos {\theta_{2}+}\omega_{3} $$

(46)

Applying a small angle assumption to the first two angles yields:

$$ \dot{\theta }_{1}=\omega_{1}\cos \left( nt \right)-\omega_{2}\sin \left( nt \right) $$

(47)

$$ \dot{\theta }_{2}=\omega_{1}\sin \left( nt \right)+\omega_{2}\cos \left( nt \right) $$

(48)

and the solution for the third angle becomes:

$$ \theta_{3}=nt $$

(49)

Substituting the solutions for $\omega _{1}$ and $\omega _{2}$ (from Eqs. 42 and 43) into Eqs. 47 and 48 and integrating yields the following analytical solutions for $\theta _{1}$ and $\theta _{2}$:

$$\begin{array}{@{}rcl@{}} \theta_{1}&=&\frac{\mu_{2}}{\lambda_{2}n}\sin \left( nt \right)-\frac{\mu_{1}}{\lambda_{1}n}\left[ \cos \left( nt \right)-1 \right]\\&&+\left[ \frac{n+\lambda_{2}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{1,0}-\frac{\mu_{2}}{\lambda_{2}} \right)\sin \left( nt \right)\cos \left( \sqrt {\lambda_{1}\lambda_{2}} t \right)\\&&-\left[ \frac{\sqrt {\lambda_{1}\lambda_{2}} +n\frac{\sqrt {\lambda_{1}\lambda_{2}} }{\lambda_{1}}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{1,0}-\frac{\mu_{2}}{\lambda_{2}} \right)\cos \left( nt \right)\sin \left( \sqrt {\lambda_{1}\lambda_{2}} t \right)\\&&+\left[ \frac{n+\lambda_{1}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{2,0}+\frac{\mu_{1}}{\lambda_{1}} \right)\left[ \cos \left( nt \right)\cos \left( \sqrt {\lambda_{1}\lambda_{2}} t \right)-1 \right]\\&&+\left[ \frac{\sqrt {\lambda_{1}\lambda_{2}} +n\frac{\sqrt {\lambda_{1}\lambda_{2}} }{\lambda_{2}}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{2,0}+\frac{\mu_{1}}{\lambda_{1}} \right)\sin \left( nt \right)\sin \left( \sqrt {\lambda_{1}\lambda_{2}} t \right)+\theta_{1,0} \end{array} $$

(50)

$$\begin{array}{@{}rcl@{}} \theta_{2}&=&\frac{\mu_{2}}{\lambda_{2}n}\left[ \cos \left( nt \right)-1 \right]-\frac{\mu_{1}}{\lambda_{1}n}\sin \left( nt \right)\\&&-\left[ \frac{n+\lambda_{2}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{1,0}-\frac{\mu_{2}}{\lambda_{2}} \right)\left[ \cos \left( nt \right)\cos \left( \sqrt {\lambda_{1}\lambda_{2}} t \right)-1 \right]\\&&-\left[ \frac{\sqrt {\lambda_{1}\lambda_{2}} +n\frac{\sqrt {\lambda_{1}\lambda_{2}} }{\lambda_{1}}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{1,0}-\frac{\mu_{2}}{\lambda_{2}} \right)\sin \left( nt \right)\sin \left( \sqrt {\lambda_{1}\lambda_{2}} t \right)\\&&+\left[ \frac{n+\lambda_{1}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{2,0}+\frac{\mu_{1}}{\lambda_{1}} \right)\sin \left( nt \right)\cos \left( \sqrt {\lambda_{1}\lambda_{2}} t \right)\\&&-\left[ \frac{\sqrt {\lambda_{1}\lambda_{2}} +n\frac{\sqrt {\lambda_{1}\lambda_{2}} }{\lambda_{2}}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{2,0}+\frac{\mu_{1}}{\lambda_{1}} \right)\cos \left( nt \right)\sin \left( \sqrt {\lambda_{1}\lambda_{2}} t \right)+\theta_{2,0} \end{array} $$

(51)

This solution can be expressed as the parametric equations of an oblate epicycloid as given in Eqs. 29 and 30, which are repeated here for convenience:

$$\begin{array}{@{}rcl@{}} \theta_{1}&=&R\left[ \cos \left( {\Omega} t\,+\,{\Phi} \right)\!-\cos \left( {\Phi} \right) \right]\!+a\left[ \cos \left( \omega t\!+\phi \right)\cos \left( {\Omega} t+{\Phi} \right)-\cos \left( \phi \right)\cos \left( {\Phi} \right) \right]\\&&-b\left[ \sin \left( \omega t+\phi \right)\sin \left( {\Omega} t+{\Phi} \right)-\sin \left( \phi \right)\sin \left( {\Phi} \right) \right]+\theta_{1,0} \end{array} $$

(52)

$$\begin{array}{@{}rcl@{}} \theta_{2}&=&R\left[ \sin \left( {\Omega} t+{\Phi} \right)-\sin \left( {\Phi} \right) \right]+a\left[ \cos \left( \omega t+\phi \right)\sin \left( {\Omega} t+{\Phi} \right)-\cos \left( \phi \right)\sin \left( {\Phi} \right) \right]\\&&+b\left[ \sin \left( \omega t+\phi \right)\cos \left( {\Omega} t+{\Phi} \right)-\sin \left( \phi \right)\cos \left( {\Phi} \right) \right]+\theta_{2,0} \end{array} $$

(53)

where:

$$ {\Omega} =n $$

(54)

$$ R_{1}=-\frac{\mu_{1}}{\lambda_{1}n} $$

(55)

$$ R_{2}=\frac{\mu_{2}}{\lambda_{2}n} $$

(56)

$$ R=\sqrt {{R_{1}^{2}}+{R_{2}^{2}}} $$

(57)

$$ a_{1}=\left[ \frac{n+\lambda_{1}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{2,0}+\frac{\mu_{1}}{\lambda_{1}} \right) $$

(58)

$$ a_{2}=\left[ \frac{n+\lambda_{2}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{1,0}-\frac{\mu_{2}}{\lambda_{2}} \right) $$

(59)

$$ a=\sqrt {{a_{1}^{2}}+{a_{2}^{2}}} $$

(60)

$$ b_{1}=\left[ \frac{\sqrt {\lambda_{1}\lambda_{2}} +n\frac{\sqrt {\lambda_{1}\lambda_{2}} }{\lambda_{2}}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{2,0}+\frac{\mu_{1}}{\lambda_{1}} \right) $$

(61)

$$ b_{2}=\left[ \frac{\sqrt {\lambda_{1}\lambda_{2}} +n\frac{\sqrt {\lambda_{1}\lambda_{2}} }{\lambda_{1}}}{n^{2}-\lambda_{1}\lambda_{2}} \right]\left( \omega_{1,0}-\frac{\mu_{2}}{\lambda_{2}} \right) $$

(62)

$$ b=\sqrt {{b_{1}^{2}}+{b_{2}^{2}}} $$

(63)

$$ {\Phi} =\text{atan}\left( \frac{R_{2}}{R_{1}} \right)=\text{atan}\left( \frac{a_{2}}{a_{1}} \right)=\text{atan}\left( \frac{b_{2}}{b_{1}} \right) $$

(64)

$$ \omega =\sqrt {\lambda_{1}\lambda_{2}} $$

(65)

$$ \phi =0 $$

(66)

Equivalence to More Specific Cases

The solution presented in Eqs. 49 and 52 through Eq. 66 addresses a general case of a nearly axisymmetric, spinning rigid-body subject to torques about both transverse axes. This can be narrowed down by making certain additional assumptions about the torques, moments of inertia, and initial conditions.

If the transverse moments of inertia of the rigid-body are equal, then

$$ \lambda_{1}=\lambda_{2}=\lambda $$

(67)

and the coefficients defined in Eq. 55 through Eq. 59 become:

$$ a_{1}=b_{1}=\frac{\omega_{2,0}+\frac{\mu_{1}}{\lambda }}{n-\lambda } $$

(68)

$$ a_{2}=b_{2}=\frac{\omega_{1,0}-\frac{\mu_{2}}{\lambda }}{n-\lambda } $$

(69)

If it is additionally assumed that the initial transverse rates are zero, then these simplify further to:

$$ r_{1}=a_{1}=b_{1}=\frac{\mu_{1}}{\lambda \left( n-\lambda \right)}=\frac{J\mu_{1}}{J_{3}\lambda n} $$

(70)

$$ r_{2}=a_{2}=b_{2}=\frac{\mu_{2}}{\lambda \left( n-\lambda \right)}=\frac{J\mu_{2}}{J_{3}\lambda n} $$

(71)

and Eqs. 52 and 53 can be described as:

$$ \theta_{1}\left( t \right)\,=\,R_{1}\left[ \cos \left( nt \right)\,-\,1 \right]-R_{2}\sin \left( nt \right)+r_{1\!}\left[ \cos \left( \left( \lambda \,-\,n \right)\!t \right)\,-\,1 \right]+r_{2}\sin \left( \left( \lambda \,-\,n\! \right)t \right)+\theta_{1,0} $$

(72)

$$ \theta_{2}\left( t \right)\,=\,R_{1}\sin \left( nt \right)+R_{2}\left[ \cos \left( nt \right)\,-\,1 \right]+r_{1\!}\sin \left( \left( \lambda \,-\,n \right)t \right)-r_{2}\left[ \cos \left( \left( \lambda -n \right)t \right)\,-\,1 \right]+\theta_{2,0} $$

(73)

Further assuming a transverse torque only about the first body axis yields the equations presented by Wie [11] and Kolk [13], as $R_{2}$ and $R_{2}$ both become zero.

Repeating Path

When considering the epicycloid approximation as depicted in Fig. 3, inspection will show that the path of the spin axis will repeat itself if either ratio of the two frequencies, $\omega _{n}$ and $\omega _{p}$, is an integer. That is, if either of the following is true:

$$ \frac{\omega_{n}}{\omega_{p}} = \text{integer} $$

(74)

$$ \frac{\omega_{p}}{\omega_{n}} = \text{integer} $$

(75)

By substituting the expressions for the frequencies of nutation and precession from Eqs. 5 and 6, it is possible to arrive at the repeating-path condition in terms of the moments of inertia. This condition is met, for an axisymmetric rigid-body when one of the following terms is an integer, depending on the relative quantities of the transverse and spin-axis moments of inertia:

$$ \frac{J}{J_{3}}= \text{integer} $$

(76)

$$ \frac{J_{3}}{J}= \text{integer} $$

(77)

A similar analysis can also be applied to the oblate epicycloid solution; inspection of Fig. 4 will show that the path of the spin axis will repeat itself if either of the following is true:

$$ \frac{\omega }{\Omega }= \text{integer} $$

(78)

$$ \frac{\Omega }{\omega }= \text{integer} $$

(79)

By substituting the expressions in Eqs. 36, 37, 54 and 59, it is seen that the repeating-path condition for a asymmetric rigid-body is therefore met when one of the following terms is an integer:

$$ \sqrt {1-\frac{J_{3}}{J_{1}J_{2}}\left( J_{1}+J_{2}-J_{3} \right)} = \text{integer} $$

(80)

$$ \left[ \sqrt {1-\frac{J_{3}}{J_{1}J_{2}}\left( J_{1}+J_{2}-J_{3} \right)} \right]^{-1}= \text{integer} $$

(81)

Numerical Examples

Major- and Minor-Axis Spin Examples

Numerical examples for both a major- and minor-axis spin are presented. The basis for comparison is the results obtained by numerically integrating Euler’s Equations and kinematic equations for the Euler Angles. The error is defined as:

$$ \varepsilon \equiv \theta -\hat{\theta } $$

(82)

where $\theta$ is the “exact” solution determined by numerical integration and $\hat {\theta }$ is the analytic approximation of the solution.

Examples with large differences in the transverse moments of inertia are chosen to emphasize the accuracy of the analytic solution for asymmetric (as opposed to nearly axisymmetric) objects.

In developing the oblate epicycloid solution to the asymmetric case, the following term was neglected as being small, due to including the product of two small angular velocities:

$$ \frac{J_{1}-J_{2}}{J_{3}}\omega_{1}\omega_{2} $$

(83)

However, even if both transverse angular rates remain reasonably small, it is possible that this term may become significant if the following quantity is large:

$$ \frac{\left| J_{1}-J_{2} \right|}{J_{3}} $$

(84)

In both numerical examples, the moments of inertia are chosen such that the quantity listed in Eq. 72 is 0.5. For satellites, this value is typically something on the order of 0.1 or less. Due to the inequality law for inertia:

$$ J_{i}\le J_{j}+J_{k} $$

(85)

the largest possible value for Eq. 72 is 1.

The results for the nearly axisymmetric analytic solution are compared to the axisymmetric solutions presented by Wie [11] and Kolk [13] since this is the closest formulation to the current work. The larger of the two transverse moments of inertia was selected for the value of the axisymmetric formulation since it yielded results that were somewhat closer to the numerical integration than those yielded by selecting either the smaller or the average of the two transverse moments of inertia.

Two cases are considered, both with an initial spin rate about the third body axis of 15 rpm and all other initial body rates and angles assumed to be zero. The torque about the first body axis in both examples is 20 Nm. The results are given for a period of 15 seconds. Figures 5 and 6 illustrate the solution for a rigid-body spinning about its major-axis, the following moment of inertia tensor using:

$$ \mathbf{J}=\left[ {\begin{array}{*{20}c} 400 & 0 & 0\\ 0 & 900 & 0\\ 0 & 0 & 1000\\ \end{array} } \right]\thinspace kg\cdot m^{2} $$

(86)

Fig. 5

First and second body angles for a major-axis spin

Fig. 6

Errors in calculated first and second body angles for a major-axis spin

Figures 7 and 8 illustrate the solution for a rigid-body spinning about its minor-axis, using the following moment of inertia tensor:

$$ \mathbf{J}=\left[ {\begin{array}{*{20}c} 233.333 & 0 & 0\\ 0 & 316.667 & 0\\ 0 & 0 & 166.667\\ \end{array} } \right]\thinspace kg\cdot m^{2} $$

(87)

Fig. 7

First and second body angles for a minor-axis spin

Fig. 8

Errors in calculated first and second body angles for a minor-axis spin

The first and second Euler angles, which give the projection of the spin axis onto the transverse plane, are shown in Fig. 5 for the major-axis spin, and Fig. 7 for the minor-axis spin. The difference between these values and the numerical solution are shown in Fig. 6 for the major-axis spin, and Fig. 8 for the minor-axis spin.

In both the major-axis and minor-axis examples, the epicycle solution diverges rapidly, and after the first revolution (at 4 seconds) the error in the epicycloid solution is almost as large as the amplitude of the deviation in the spin-axis from nominal. The errors in the oblate epicycloid representation are more than an order of magnitude lower than those in the epicycloid solution. The errors in the oblate epicycloid solution grow larger with time, but the solution remains representative of the motion for several revolutions (tens of seconds in this case), performing better than the epicycloid solution.

Repeating Path Example

A third numerical example is presented to illustrate the scenario in which the spin axis of the asymmetric body follows a repeating path. The initial spin rate and torque are the same as those in the major- and minor-axis spin examples, and the following moment of inertia tensor is used:

$$ \mathit{J}=\left[ {\begin{array}{*{20}c} 30.619 & 0 & 0\\ 0 & 149.667 & 0\\ 0 & 0 & 238.095\\ \end{array} } \right]\thinspace kg\cdot m^{2} $$

(88)

Using the diagonal terms of this matrix, the expression in Eq. 80 evaluates to a value of 1.9996. The first and second Euler angles for this example are shown in Fig. 9, which shows that the path of the spin axis very nearly repeats itself.

Fig. 9

First and second body angles with a repeating path

Conclusions

In this paper, analytic approximations are derived for the equations of motion for the attitude of a nearly axisymmetric, spinning rigid-body, described by 1-2-3 Euler angles. It is shown that the solution presented in this paper encompasses the solution presented by Wie [11] and Kolk [13] for the specific case where the transverse moments of inertia are equal, and torque is applied about only one transverse axis. It is further shown that the solutions presented in this paper are more accurate than those presented by Wie [11] and Kolk [13] when the transverse moments of inertia are not equal. The solution retains, however, the physically intuitive representation of a relatively simple geometric shape, namely, an oblate epicycloid.