Cyclic zinc capture and zeolite regeneration using a column method, mass transfer analysis of multi regenerated bed

Abstract

Treatment of wastewater and reuse of purified water in an industrial process can provide an alternative source of fresh water as well as reduce pollution load by discharging a lower quantity of wastewater. When adsorption is used for treatment, the regeneration of the used adsorbent may also account for a large portion of the operational cost and cause secondary pollution. This problem may be solved by cyclic repetition of adsorption/regeneration cycles using a column method. In this paper, a total of nine successive cycles of zinc capture and zeolite bed regeneration using a column method have been investigated. The derived form of the breakthrough curve was used for analysing mass transfer in the column. For that purpose, the Dose–response, the Thomas, the Bohart-Adams, the Yoon-Nelson and the Wolborska models were used for modelling the breakthrough curve by nonlinear regression analysis. Simulation results and mathematical similarities between the models were discussed. This is the first study that used derived form of Dose–response model to analyse the inflection points of the breakthrough curve and mass transfer during nine consecutive sorption-regeneration cycles of zinc ions on natural zeolite. Obtained peak shape rate profiles were analysed for all cycles. Optimal operation conditions were evaluated with respect to the inflection point, the model parameters, and the residence time.

Introduction

Industry such as paints, batteries, fabrics, ceramics, wood, drugs, deodorants, sun blocks, etc. uses heavy metal compounds and thus release large quantities of metals effluent solution which can cause a serious human and environmental health threat [1]. Their purification prior to discharge into a natural water system is therefore necessary. However, because of the limitation in water availability and quality at a global scale, the wastewater should not be treated as a waste, but as a source. In this light, there is a need for technological innovation to transform the way that wastewater is treated, distributed, and reused. Water reuse in an industrial process can provide an alternative source of fresh water and reduce pollution load by discharging a lower quantity of wastewater. Thus, water reuse at the industrial scale is encouraged because of the economic savings and its influence in preventing a global water crisis [2]. New trends in purifying of industrial wastewater loaded with heavy metals are based on innovative physico-chemical processes such as adsorption on new adsorbent, membrane filtration, electrodialysis, and photo catalysis [3, 4]. Adsorption on a new adsorbent is recognized as a process which can contribute to increase in the reuse of industrial water. Advantages such as low-cost, easy operation condition, wide pH range for applications and high metal-binding capacities make the application of adsorption attractive. The typical disadvantages of adsorption are connected with low selectivity towards the selected metal compounds and the production of metal-saturated adsorbents as a waste [5, 6]. Metal ions attached to the adsorbent create serious disposal problems and may cause secondary pollution. Thus, regeneration of a saturated adsorbent for additional use or reuse is desirable. Reuse (recycling) of a saturated adsorbent and recovery of the adsorbate from the regenerate solution is the focus of many recent investigations. Proper management of regeneration cycle, saturated adsorbent and recovery of adsorbate are important for the environment and can contribute to financial savings, as well as various possible regenerating agents, such as acids, alkalis, chelating agents and salts, have already been investigated [7-10]. Recovery and reuse of the saturated adsorbent and adsorbate without subsequent solid–liquid separation could easily and efficiently be performed in a fixed bed column [10]. However, only a few of the reported studies focused on regeneration of the used adsorbent and recovery of metals as a valuable source through multiple or repeated adsorption/regeneration cycles in column [11-15]. Osifo et al. (2009) investigated the adsorption of copper in a packed-bed of chitosan beads. In the desorption experiments, 91–99% of the adsorbed copper was regenerated in the first three cycles. They conclude that regeneration with 0.1 M HCl may not be the best option when more than four or five multiple cycles of adsorption and desorption are to be employed due to significant mass loss [11]. Biswas and Mishra (2015) investigated removal of lead ions from the aqueous stream by chemically carbonized rubber wood sawdust (CRSD). Reusability of the adsorbent was done by repeating the adsorption–desorption cycle for four times. They found out that removal efficiency decreases as cycle proceeds because the use of acid solution may destroy the binding sites of the CRSD or insufficient acid solution may allow the lead ion to remain in the binding sites [12]. Negrea et al. (2020) investigated the potential of a new adsorbent material Amberlite XAD 7 to recover Au (III) from real wastewater, in a column with a fixed bed in a dynamic regime. They found out a total of five cycles for adsorption–desorption the new material can be used, until the process was no longer efficient [13]. Satya et al. [14] investigated removal of Cd by dry cyanobacterium Aphanothece sp cultivar in adsorption columns. The regeneration efficiency with 0.1 M HCl through repetitive adsorption–regeneration experiment show that, at the end of the fifth cycle, the desorption efficiency decreased by 21% [14]. Our previous study (Vukojević Medvidović et al., 2006) investigated the removal of lead ions from aqueous solutions by the column method using the fixed bed of natural zeolite clinoptilolite. During alternating exchange and regeneration, the same zeolite mass was used eight times, showing natural zeolite great possibility for successive adsorption-regeneration study of heavy metals removal [15]. Thus, in this study, nine consecutive sorption-regeneration have been performed to evaluate the cyclic zinc capture and natural zeolite regeneration abilities.

For a description of dynamic sorption behaviour, simplified models such as the Bohart-Adams, Thomas, Yoon-Nelson, Clark, Wolborska and Dose–response models are usually used for predicting of breakthrough curves [16-23]. However, several authors have noticed mathematical similarities between the Bohart-Adams, Thomas and Yoon-Nelson models. These models share the identical mathematical forms and their parameters are interconvertible (commutable or interchangeable): k_YN = k_BAc₀ = k_Thc₀ (see Table 1) [22, 24, 25] According to Hui et al. (2019, 2020), the Yoon-Nelson model does not require detailed data with respect to the adsorbate characteristics, the type of adsorbate, and the physical properties of the fixed bed column [22, 23]. The Wolborska model is an exponential function valid for a small exit concentration; thus, it can be successfully applied only for the initial part of the breakthrough curve. The Dose–response model was recognized as a sigmoidal curve only when its parameter satisfies k_DR > 1. In addition, the term inflection point was introduced as an operating time in which the breakthrough curve is converted from concave to convex (see Fig. 1) [22, 23]. On the other side, Hendricks introduced the inflection point as a point of changing the mechanism [26, 27]. By applying the packed bed reactor theory, mass transfer through the packed bed is controlled by particle kinetics or convection/dispersion kinetics. Up to the inflection point, convection/dispersion governs mass transfer, while, particle kinetics governs mass transfer after the inflection point.

Table 1 Breakthrough curves equations of used models

Fig. 1

Typical breakthrough curve with tangent line and inflection point, according to Hui et al. 2019 [22]

In this study, the inflection point was determined from the derivation of the breakthrough curve of the best suitable model. The experimental data were obtained from testing the reusability of the zinc saturated natural zeolite originated from Vranjska Banja deposit through nine successive sorption-regeneration cycles in a fixed bed column. Simulations were performed using nonlinear regression analysis in Mathcad program. The Dose–response model that achieved the best prediction result was chosen for evaluation of the rate profile and position of the inflection point. According to our knowledge, this is first study that used derived form of Dose–response model to analyse the inflection points. In addition, the optimal working condition during nine consecutive sorption-regeneration cycles was analysed with respect to operational and models parameters.

Theoretical background

Mathematical description of breakthrough curve

According to Hu et al. (2019; 2020) the typical breakthrough curve (c/c₀ vs. time) is comprised of three stages (see Fig. 1), lag, exponential, and stationary stage as a microorganism grows [22, 23]. In the lag stage, the adsorbent present in a fixed bed column contains large numbers of vacant adsorption sites and detains the adsorbate ions or molecules consecutively, leading to a reduced effluent concentration. In the exponential stage, as the adsorption advances, the number of vacant adsorption sites decreases and consequently, the effluent concentration increases. In the stationary stage, the vacant adsorbent sites are scarce and the saturation state is approaching gradually. At this point, the effluent concentration becomes more or less constant. Three parameters describe the three stages of the breakthrough curve: λ is the lag time (h), μ_max is the maximum specific breakthrough rate (h⁻¹) and c₀ is the influent concentration, (mmol/L). The parameters μ_max and λ are defined as the slope of the tangent line at the inflection point of the breakthrough curve and the x-axis intercept of this tangent line, respectively. The inflection point is defined as an operating time at which the breakthrough curve is converted from concave to convex. The t₅₀ is referred to as the half-operating time (50% breakthrough c/c₀ = 0.5). The parameters t_I and t₅₀ are proposed to identify the symmetry of the breakthrough curve [22, 23].

The packed bed reactor theory, rate profile and inflection point

According to Hendricks (2006), by feeding adsorbate solution from the top of the column bed filled with adsorbent, the adsorbate concentration varies along the length of the reaction zone at certain times (see Fig. 2a) [26]. Since the adsorbate concentration in the column process is not independent of position, the material balance is applicable only to the infinitesimal volume element, i.e. infinitesimal layer of thickness ∆Z (column slice), which achieves homogeneity as ∆Z approaches zero. Thus, the material balance equation applied to the infinitesimal slice is the differential equation:

$$\left[ {\frac{\partial c}{{\partial t}}} \right] = - v\frac{\partial c}{{\partial Z}} + D_{L} \frac{{\partial^{2} c}}{{\partial Z^{2} }} - \rho \frac{1 - \varepsilon }{\varepsilon }\left[ {\frac{\partial q}{{\partial t}}} \right]$$

(1)

where c is the effluent adsorbent solution concentration (mmol/L), t is the service time (h), v is the linear flow velocity of the adsorbent solution in the adsorbate layer (m/h), Z is the distance along the column from the entrance (m), D_L is the coefficient of axial dispersion (m²/h), ε is the porosity of the adsorbent (-), ρ is the dry density of the adsorbent (g/cm³), q is the quantity of adsorbate retention onto the adsorbent at time t (mmol/g).

Fig. 2

a) The mass transfer zone in a fixed bed column; b) Illustration of the change in the mechanism of adsorbate transfer through a fixed layer of adsorbent according to Hendrickson 2006 [26], c) The derived form of the S-shape breakthrough curve with two characteristic area and inflection point, according to Nuić et al. 2016 [27]

According to Eq. (1), the change in adsorbate concentration with time in the slice Z is equal to the adsorbate transport flux in slice Z (by convection and dispersion) minus the rate of uptake to the adsorbent phase [26].

Particle kinetic controls the rate of sorption if the adsorbate is delivered to the adsorbent particles faster than its uptake rate. But, when the rate of delivery of the adsorbate is less than can be taken up by particle kinetics, then the rate of convection to the adsorbent particles governs the overall rate. These two mechanisms, particle kinetics and convection kinetics, are distinguished symbolically by the term [∂q/∂t]_P and [∂q/∂t]_K, respectively [26]. Figure 2b. illustrates the change in mass transfer mechanism along the bed.

The concentration profile along the slice Z (see Fig. 2b) shows the inflection point. To the left of the inflection point, diffusion through the particles is the slower step of the process, thus, the particle kinetics governs mass transfer (Hendricks 2006):

$$\left[ {\frac{\partial q}{{\partial t}}} \right]_{{\text{P}}} = D_{s} \cdot c \cdot (q^{*} - q)$$

(2)

where D_s is the diffusion coefficient in the solids phase (m³/(s mol)), q^* is the quantity of adsorbate removed per unit of the adsorbent phase in the equilibrium (mmol/g), and q is the quantity of adsorbate remove per unit of the adsorbent phase at time t (mmol/g).

To the right of the inflection point, convection/dispersion governs mass transfer, which can be expressed by Eq. (3):

$$\left[ {\frac{\partial q}{{\partial t}}} \right]_{{\text{K}}} = \frac{\varepsilon }{\rho \cdot (1 - \varepsilon )}\left[ { - v\frac{\partial c}{{\partial Z}} + D_{L} \frac{{\partial^{2} c}}{{\partial Z^{2} }}} \right]$$

(3)

Equation (3) is made with the assumption of steady state at any Z in the advective—dispersion zone [26].

The derivation of the modelled breakthrough curve, d(c/c_o)/dt = f(t), should show the time of the mechanism change [27]. This curve (see Fig. 2c) is comprised of three parts. The first part represents the increase in the process rate, the second represents a constant rate, and the third part represents its decrease. Convection kinetics governs the process from the beginning until around the maximum, i.e., inflection point. At the maximum of the derivation curve, the constant rate part overlaps with the inflection point. At this point, the particle kinetics prevails and controls the overall rate until the exhaustion point [26, 27].

Breakthrough curves model

The nonlinear form of the breakthrough curve kinetic models of the Dose–response, Thomas, Bohart-Adams, Wolborska and Yoon-Nelson are summarized in Table 1.

The nonlinear form of the Dose–response model is given by Eq. (4) [28, 29]:

$$\frac{c}{{c_{0} }}{ = 1 - }\frac{{1}}{{{1 + (}\frac{{c_{{0}} \cdot V}}{{q_{{{\text{DR}}}} \cdot m}}{)}^{{k_{{{\text{DR}}}} }} }}$$

(4)

where c is the adsorbate concentration in the effluent (mmol/L), c₀ is the initial adsorbate concentration (mmol/L), V is the effluent volume (L), m is the mass of the adsorbent bed in column (g), k_DR is the kinetic constant of the Dose–response model (-), and q_DR is the saturation capacity calculated from the Dose Response model (mmol/g).

Equation (4) also can be expressed as a function of time [23, 24, 30]:

$$\frac{c}{{c_{{0}} }}{ = 1 - }\frac{{1}}{{{1 + (}b \cdot t{)}^{{k_{{{\text{DR}}}} }} }}$$

(5)

where $b = (c_{0} \cdot Q)/(q_{DR} \cdot m)$, Q is the flowrate (L/h), and t is the time (h). A reciprocal value of b is defined as the time when the effluent concentration reaches 50% of the influent concentration [11]. The Dose response model achieves a sigmoidal curve only when the parameter k_DR > 1. For k_DR ≤ 1, a parabolic-like curve occurs. For higher values of k_DR, the values of t_I become closer to t₅₀ [23].

The nonlinear form of the Thomas model is given by Eq. (6) [27, 28]:

$$\displaystyle\frac{c}{{c_{{0}}}} = \frac{{1}}{{{\text{1 + exp}}\left[ {\frac{{k_{{\text{T}}} }}{Q} \cdot {(}q_{{\text{T}}} \cdot m{ - }c_{{0}} \cdot V{)}} \right]}}$$

(6)

where k_T is the rate constant of the Thomas model (L/(mmol h)) and q_T is the the saturation capacity calculated from the Thomas model (mmol/g).

Equation (6) can be expressed in terms of time [22, 23, 30, 31]:

$$\displaystyle\frac{c}{{c_{{0}} }} = \frac{{1}}{{{\text{1 + exp}}\left[ {\frac{{k_{{\text{T}}} \cdot q_{{\text{T}}} \cdot m}}{Q} - k_{T} \cdot c_{0} \cdot t} \right]}}$$

(7)

The nonlinear form of the Bohart-Adams model is given by Eq. (8) [24, 25, 32]:

$$\displaystyle\frac{c}{{c_{{0}} }} = \frac{{{\text{exp(}}k_{{{\text{BA}}}} \cdot c_{{0}} \cdot t{)}}}{{{\text{exp(}}k_{{{\text{BA}}}} \cdot q_{{{\text{BA}}}}^{*} \cdot H/\nu{) - 1} + {\text{exp(}}k_{{{\text{BA}}}} \cdot c_{{0}} \cdot t{)}}}$$

(8)

where k_BA is the rate constant of the Bohart-Adams model (L/(mmol h)), q_BA^* is the adsorption capacity calculated from the Bohart-Adams model (mmol/L), H is the fixed bed depth (m), $\nu$ is linear flow velocity (m/h).

Equation (8) can be simplified into Eq. (9) [24, 25, 32]:

$$\displaystyle\frac{c}{{c_{{0}} }} = \frac{1}{{{1} + {\text{exp}}\left[ {{(}k_{{{\text{BA}}}} \cdot c_{0} \cdot {(}\frac{{q_{{{\text{BA}}}}^{*} \cdot H}}{{\nu \cdot c_{{0}} }}{ - }t{)}} \right]}}$$

(9)

It is evident that the Bohart -Adams model given by Eq. (9) displays the characteristic feature of the logistic equation. However, it is important to note that in environmental adsorption literature, the simplified version of the Bohart-Adams model restricted for low effluent concentration (c < 0.15 c₀) is also used very often [24, 25, 32]. The saturation capacity of the Bohart-Adams model, q_BA, can be evaluated as follows:

$$q_{{{\text{BA}}}} = q_{{{\text{BA}}}}^{*} \cdot BV_{{\text{S}}} /m = q_{{{\text{BA}}}}^{*} /\rho$$

(10)

where q_BA is the saturation capacity of the Bohart-Adams model (mmol/g), BV_S is the fixed bed volume (L), and ρ is the apparent density of the adsorbent in the packed bed [35].

The nonlinear form of the Yoon-Nelson model is given by Eq. (11) [23, 29, 30, 33]:

$$\frac{c}{{c_{{0}} }} = \frac{{{\text{exp}}\left[ {k_{{\text{T}}} \cdot {(}t - \tau_{{{\text{YN}}}} {)}} \right]}}{{{1} + {\text{exp}}\left[ {k_{{\text{T}}} \cdot {(}t - \tau_{{{\text{YN}}}} {)}} \right]}}$$

(11)

where τ_YN is the time required for 50% adsorbate breakthrough (h) calculated from the Yoon-Nelson model, and k_YN is the rate constant of the Yoon-Nelson model (h⁻¹).

For a symmetrical breakthrough curve, the value of the saturation capacity of the Yoon Nelson model can be calculated as follows [17, 18, 34]:

$$q_{{{\text{YN}}}} = c_{0} \cdot Q \cdot \tau_{{{\text{YN}}}} /m$$

(12)

where q_YA is the saturation capacity calculated from the Yoon-Nelson model (mmol/g).

The Thomas, Bohart-Adams and Yoon-Nelson models share identical mathematical forms and their parameters are interchangeable (or interconvertible or commutable) [22, 24, 25, 33]:

$$k_{{{\text{YN}}}} = k_{{{\text{BA}}}} \cdot c_{0} = k_{{\text{T}}} \cdot c_{0}$$

(13)

It follows that the Bohart–Adams, Thomas and Yoon-Nelson models are equivalent in mathematical nature. Consequently, the fitting curves provided by the three models are identical and all error values are equal when the curve fitting is carried out.

Wolborska model

The nonlinear form of the Wolborska model is given by Eq. (14) [25, 34]:

$$\frac{c}{{c_{{0}} }} = {\text{exp}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {{(}\frac{{\beta_{a} \cdot c_{{0}} \cdot t}}{{q_{w}^{*} }}{)} - {(}\frac{{\beta_{a} \cdot H}}{\nu}{)}} \right]$$

(14)

and

$$\beta_a=\beta\cdot\varepsilon$$

(15)

where β is the kinetic coefficient of the external mass transfer (h⁻¹), ε is the bed voidage (-), and q_w^* is the sorption capacity of the Wolborska model (mmol/L). By analogy to the BA model, the saturation capacity of the Wolborska model, q_w^*, can be calculated according to Eq. (10).

Materials and methods

Sample and solutions preparation

The natural zeolite sample from the Vranjska Banja (Serbia) deposit of particle size fraction of 0.6–0.8 mm was pre-treated into the Na-form. The chemical composition of the zeolite sample was determined by the chemical analysis of alumosilicates. Expressed in mass percentages the composition was: SiO₂—65.15; Al₂O₃ -11.56; Fe₂O₃—1.35; MgO—1.76; CaO—0.91; K₂O—0.72; Na₂O—4.40; loss of ignition-11.66. X-ray diffraction was used for qualitative mineralogical analysis, using a “Philips-CubiX XRD” type diffractometer (CuKα radiation, 2θ = 0—60, 0.03 2θ/s). The main mineral component of zeolite was clinoptilolite, whose content in the sample was approximately 80% with quart as an impurity [36]. The theoretical exchange capacity equals 1.411 mmol/g [36]. The XRPD (X-ray powder diffraction method), SEM–EDS (scanning electron microscopy and energy dispersive X-ray analysis), a thermal analysis (TG-DTG), and FTIR (Fourier-transform infrared spectroscopy) of raw zeolite sample were published previously [37].

Metal and regeneration solutions were prepared by dissolving Zn(SO₄)₂ and Na₂SO₄ in ultrapure water.

Column studies

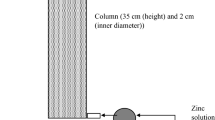
The column studies were performed using glass columns with an inner diameter of 12 mm and a height of 500 mm that were filled with zeolite sample. The zeolite sample was put into the column carefully so that no air remained between the particles, which helped to attain compact layers. Column studies consisted of successively repeating nine service cycles for Zn capture followed by nine regeneration cycles to recover the zeolite bed.

Service cycle for Zn capturing onto the fixed zeolite bed

A total of nine cycles of zinc capturing on the zeolite was performed isothermally (T = 23 °C) at an initial zinc solution concentration, c₀, of 0.770—1.787 mmol Zn/L, a solution flow rates through the column, Q, of 1—3 mL/min, and with decreasing zeolite bed depths (four cycles at H = 120 mm, two cycles at H = 80 mm, and three cycles at H = 40 mm) using the down flow mode. Effluents were collected during the experiment and the zinc concentration was determined by complexometrical titration and checked by ion chromatography [36]. The constant flow rate was maintained by a vacuum pump.

Regeneration cycle for recovery of the zeolite bed

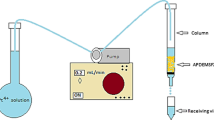
After the service cycle, the regeneration cycle took place with the sodium sulphate solution c₀(Na₂SO₄) = 105.60 mmol/L and the flow rate, Q, of 1 mL/min, also using the down flow mode. The regeneration process was stopped when the zinc concentration in the effluent became less than 0.1 mmol/L. This regenerated bed was employed in the next service cycle to investigate possible reusability of natural zeolite for zinc uptake in multiple operation procedure. Experimental set up of fixed bed column performance are given in Fig. 3 while experimental conditions during the nine cyclic service-regeneration cycles are given in Table 2.

Fig. 3

a) Experimental set up of column fixed bed performance; b) Experimental performance of nine cyclic service-regeneration cycle

Table 2 Experimental conditions during service cycle of Zn capturing onto Na-zeolite and regeneration cycle for recovering of zeolite bed

During the service and regeneration cycle, the changes in pH value were recorded in the influent and the effluent.

Results and discussion

Analysis of the breakthrough curve obtained through successive service cycles

It is well known that the natural zeolites are a good adsorbent for heavy metals, ammonium and radionuclide. Due to their alumosilicate structure, exchangeable cations that compensate for the negative charge of the structure are able to participate as ion-exchanger. However, the mineral heterogeneity, structural imperfection and broken bonds are reason why zeolites behave as ion-exchangers and adsorbents [15]. Thus, the term sorption is generally used to define the surface retention process without specifying the exact retention mechanism. Before starting the experiment, natural zeolite is transformed into the Na-form, thus mostly sodium participates in the ion-exchange process with the zinc from the solution. The experimental results for zinc uptake on a fixed bed of Na-form of natural zeolite are represented by breakthrough curves plotted in Fig. 4. From those curves, the characteristic parameters were calculated by applying the equations published previously [15]. Table 3 shows these parameters.

Fig. 4

The breakthrough curves for removal of Zn ions onto zeolite during: a) 1st, 2nd, 3rd and 4th successive service cycles at at bed depth of 120 mm, b) 5th and 6th cycle for different initial zinc concentration at bed depth of 80 mm, c) 7th, 8th and 9th cycle at different flow rate at bed depth of 40 mm

Table 3 The parameters calculated from breakthrough curves

Saturation of the zeolite bed during the first three successive service cycles (Fig. 4) was carried out under the same conditions of the zeolite bed height of 120 mm, the initial concentration of the zinc ion solution of 1.067 mmol/L and the flow of 1.0 mL/min. It is evident that curves for these three cycles are not overlapping. The breakthrough curves for the second and third cycles are shifted slightly to the right, towards a higher BV (bed volume) value as well as higher value of calculated breakthrough (q_B) and exhaustion capacity (q_E) (Table 3). This indicates that repetition of service and regeneration cycles on the same zeolite bed layer influences the establishment of stable exchange conditions, bed texture, mobility of the participating ions, contact time between zeolite and solution, as well as activation of exchangeable places in the zeolite structure during the regeneration cycles.

Saturation of the zeolite from the fourth to nine service cycles was carried out by varying the initial concentration of the zinc ion solution, zeolite bed depth and the flow through the column. Obtained breakthrough curves show differences in the shape and position of the curve (and thus affecting the values of q_B, q_E, F, hz, see Table 3), which determined the amount of zinc captured by the zeolite bed. The breakthrough curves obtained for the condition of lower zeolite bed, lower initial concentration of the zinc ion solution, and higher flow of solution through the column are flatter (less sharp) and the ratio of c/c₀ has not reached 1, but ranges from 0.810 to 0.957. The reason for this is that, at a lower initial concentration of the zinc solution, the concentration difference (c₀-c), which is the driving force of the process, is smaller, which affects the efficiency of the saturation process. At a lower bed depth and higher flow rate through the bed, the contact time of the zeolite solution is reduced, which is also reflected in a reduced column efficiency. The values of the calculated breakthrough (q_B) and exhaustion capacity (q_E) during nine successive service cycles will be discussed in the following section.

Analysis of successive regeneration cycle and evaluation of the zeolite fixed bed reusability

After each service cycle a regeneration cycle took place with the sodium sulphate solution at a very high concentration. The results are presented by zinc elution curves as Zn concentration in the effluent versus the regeneration solution volume flowed through the bed, expressed by BV. Figure 5 shows the elution curves for nine successive regeneration cycles. All elution curves have a similar unsymmetrical shape; they first show a sharp increase in the Zn effluent concentration, followed by a gradual decrease until the Zn concentration in the effluent reaches under 0.1 mmol/L. Table 4 summarises the characteristic parameters calculated from the elution curves, using equations published previously [8, 14].

Fig. 5

Elution curves of Zn ions obtained during nine successive regeneration cycle of saturated zeolite

Table 4 Characteristic parameters of regeneration curves

During nine regeneration cycles, about 36—71 BV of the regenerate solution is needed for complete regeneration of the zeolite bed. Due to the reduced volume, the Zn concentration is very high and attains the value of 40—98 mmol/L, depending on operational conditions during the service cycles. A very high concentration of Zn ions in the regenerate solution enables their reuse in an industrial process.

In order to evaluate the reusability of the multi-regenerated zeolite fixed bed, the amount of zinc bound onto the zeolite bed up to breakthrough (q_B) and exhaustion (q_E), and eluted (q_R) from the zeolite bed during nine successive cycles is compared in Fig. 6.

Fig. 6

Comparison of q_B, q_E and q_R during nine successive cycles

It is evident that there is no significant reduction in the values of q_B, q_E and q_R compared to its initial sorption capacities, confirming that nine successive service and regeneration cycles were harmless to the binding site. Summing up the exhaustion capacities q_E, the total of 6.208 mmol Zn (or 406 mg Zn) was removed per gram of zeolite. Small changes in the values of q_B and q_E are due to changes in the experimental conditions in the service cycles.

The advantages of column performance can be evaluated by comparing zinc solutions volume treated during the service cycles up to breakthrough (V_B) and exhaustion (V_E), and the volumes of the same solution eluted (V_R) from the zeolite bed during regeneration. This comparison for each of the nine cycles is given in Fig. 7.

Fig. 7

Comparison of volumes of Zn solution treated up to breakthrough and exhaustion, and eluted from the zeolite bed for nine successive service and regeneration cycles

The volumes of solutions eluted during regeneration are about 7—13 times smaller than the volumes of zinc solutions treated up to exhaustion. Due to the reduced volumes, the concentration of Zn is very high (see Table 4), which provides the opportunity for zinc to be reused from such concentrated solutions. Summing up the volume of zinc solution processed up to the breakthrough point, it was found that a total of 27.88 L of zinc solution was treated during nine service cycles on the same layer of zeolite. The effluent solution up to the breakthrough point can be used as an alternative source of fresh water.

The obtained results indicate the advantage of the column method compared to the batch one, especially when large amounts of wastewater need to be purified. Namely, the batch method would require a large capacity reactor, as well as additional separation by sedimentation and/or filtration, which makes the process very expensive and economically unfeasible.

Changes in the pH value during the service and regeneration process

Before starting the experiment, natural zeolite is transformed into the Na-form, to ensure that mostly sodium from zeolite will participate in the replacement process with zinc from the solution during the column study. Thus, it is very interesting to monitor the change in pH values of the effluent solution. The pH profile during the first three successive repetitions of the service and regeneration cycle is shown in Fig. 8. Both graphs give clear indication that pH values have changed, following the opposite shape of the breakthrough and regeneration (elution) curves.

Fig. 8

The pH profile during the service and regeneration cycle

During the service cycles, the pH value achieves almost constant values. After the breakthrough point, the amount of zinc in the effluent increases, and the pH value decreases by one pH unit (from around 6.4 to 5.6). This is due to hydrolysis of the zinc ions in the effluent, according to the reaction:

$$Zn^{2 + } + H_{2} O \Leftrightarrow Zn(OH)^{ + } + H^{ + }$$

(16)

During the regeneration cycle, the amount of zinc in the effluent is significantly higher than during the service cycle, and so the intensity of the pH changes (pH decreases from 6.5 to 4.5).

Such results were obtained for all service and regeneration cycles, which indicate that if the pH value in the effluent is continuously monitored, the completion of the cycle can be determined by simple measurement of the pH value.

Determination of the inflection point of the breakthrough curve

Modelling the experimental breakthrough curve

The breakthrough curves of zinc removal onto Na-zeolite given in Fig. 4 are tested according to the nonlinear form of the kinetic model of the Dose–response, Thomas, Bohart-Adams, Wolborska and Yoon-Nelson. Nonlinear forms of equations of all models are summarized in Table 1.

The testing of the model using the non-linear least square methods was done using the Mathcad program. The parameters were calculated from Eqs. (4), (6), (8), (11) and (14) using Solve block and Minerr as output function. Constraints for models used are:

• for Dose–response model

  $$\frac d{dX}\sum_{i=1}^n\left[({{c/c}_0)}_i-\left(1-\frac1{1+\left(\frac{c_0\cdot V_i}{q_{DR}\cdot m}\right)k_{DR}}\right)\right]^2=0$$

  (17)

• for Thomas model

  $$\frac d{dX}\sum_{i=1}^n\left[({{c/c}_0)}_i-\left(\frac1{1+\exp\left[\frac{k_T}Q\cdot\left(q\cdot m-c_0\cdot V_i\right)\right]}\right)\right]^2=0$$

  (18)

• for Bohart-Adams model

  $$\displaystyle\frac{d}{dX}\sum_{i=1}^n\left[({{c/c}_0)}_i-\left(\frac{\exp\left(k_{\mathrm{BA}}\cdot c_0\cdot t_i\right)}{\exp\left(k_{\mathrm{BA}}\cdot q_{\mathrm{BA}}\cdot H/\nu\right)-1+\exp\left(k_{\mathrm{BA}}\cdot c_0\cdot t_i\right)}\right)\right]^2=0$$

  (19)

• for Yoon-Nelson model

  $$\frac d{dX}\sum_{i=1}^n\left[({{c/c}_0)}_i-\left(\frac{\exp\left[k_{\mathrm T}\cdot\left(t_i-\tau_{\mathrm{YN}}\right)\right]}{1+\exp\left[k_{\mathrm T}\cdot\left(t_i-\tau_{\mathrm{YN}}\right)\right]}\right)\right]^2=0$$

  (20)

• for Wolborska model

  $$\displaystyle\frac{d}{dX}\sum_{i=1}^n\left[({{\frac cc}_0)}_i-\left(\exp\left[\left(\frac{B_a\cdot c_0\cdot t_i}{q_w^\ast}\right)\right]\right)-\left(\frac{B_a\cdot H}\nu\right)\right]^2=0$$

  (21)

where $({{c/c}_{0})}_{i}$ is experimental c/c₀ data, X is a parameter (k_DR and q_DR for the Dose–response model; q_T and k_T for the Thomas model; k_BA and q_BA* for the Bohart-Adams model; τ_YN and k_YN for the Yoon-Nelson model and β_a and q_w^* for the Wolborska model). The number of constraints is equal to the number of parameters.

The correlation coefficient (r²) and the root mean square error (RMSE) were used as indicators of fitting of the experimental results with the results obtained by the model.

$${\text{RMSE}} = \sqrt {\frac{1}{z}\sum\limits_{i = 1}^{z} {\left[ {(c/c_{0} )_{{{\text{model}}}} - (c/c_{0} )_{{{\text{exp}}}} } \right]^{2} } }$$

(22)

The parameters of the model have been evaluated for the 1st, 2nd, 3rd, 4th, 5th, 7th and 8th service cycle and are summarized in Table 5.

Table 5 Parameters of models evaluated for different experimental conditions (1st, 2nd, 3rd, 4th, 5th, 7th, 8^th cycle), and parameters of the model simulated from the curve fitting on Fig. 6 (6th and 9th cycle)

From the results given in Table 5, among the tested models, the Wolborska model achieves the lowest value of r² and highest values of RMSE. As an exponential function, the Wolborska model is applied to the region of low breakthrough concentration, in which the process kinetics is controlled by mass transfer and axial diffusion in the liquid phase [25, 34].

The Dose–response model fitting show quite high values of r², and low values of the RMSE for all cycles. The parameter k_DR is evaluated in the range 7.111—20.167, depending on the operation conditions. For values of the parameter k_DR > 1, the Dose response model achieves a sigmoidal curve, and satisfactory agreement with experimental values was obtained. This is in agreement with previous findings [23].

The Thomas, Bohart-Adams and Yoon-Nelson model parameters show interchangeable properties for almost all cycles, following the rules k_YN = k_BA⋅c₀ = k_T⋅c₀. Small deviations are only observed for the 8th cycle. This indicates that the Bohart-Adams, Thomas and Yoon-Nelson models are equivalent in mathematical nature. Consequently, the fitting curves provided by the three models are identical for all tested cycle and error values are equal when the curve fitting is carried out. This is in agreement with previous findings [22, 24, 25, 33].

All models enabling calculations of saturation capacity (q_DR, q_T, q_BA, q_W, q_YN) and obtained values are comparable with the capacity value of q_E experimentally calculated at the exhausting point. However, the validity of the model is not just a result of good fitting, but also its capability to predict the system behaviour under conditions different from those used to get the model parameters [38]. Thus, based on the parameters evaluated for cycle 2, 7 and 8 (Fig. 9 compares the experimental and model breakthrough curve), the parameters for the experimental condition for the 6th and 9th cycle were predicted using equations given in Table 6.

Fig. 9

Comparison of experimental and model breakthrough curves: a) Dose–response model b) Thomas model c) Bohart-Adams model d) Wolborska model e) Yoon-Nelson model

Table 6 Equation for fitting the parameters

It is evident that the model parameters in the equations are expressed in terms of the residence time or empty bed contact time EBCT, the main parameter which is suggested to keep constant during scale up [17, 19]. The EBCT is calculated by the following equation for different experimental conditions during the cycles:

$${\text{EBCT}} = H/\nu = H/\left( {Q/A} \right)$$

(23)

where A is the cross sectional area of the column which equals A = (d² π)/4 (cm²). The values of EBCT during the cycles are given in Table 7.

Table 7 Evaluation of inflection point

A comparison of experimental and predicted breakthrough curves for the 6th and 9th cycles is given in Fig. 10, while predicted parameters are presented in Table 5.

Fig. 10

Comparison of simulated and experimental breakthrough curves: a) Dose–response model b) Thomas model c) Bohart-Adams model d) Wolborska model e) Yoon-Nelson model

From the graphical comparison of the breakthrough curves (Fig. 9) and calculated parameter and fitting indicators (Table 5, predicted cycles 6th and 9th), among the tested models the Dose–response model shows the best agreement of the predicted values with the experimental points. Other models show satisfactory prediction for the 6th cycle, but fail in predicting the 9th cycle. Therefore, the Dose–response model was chosen to provide a derived form of the breakthrough curve.

Rate profile and inflection point

The term inflection point is defined as an operating time in which the breakthrough curve is converted from concave to convex [23]. By derivation of the breakthrough curve, the rate profile curve achieves the pulse shape. In the first part, the process rate increases, in the second part, d(c/c₀)/dt = 0 and the rate is constant, and the third part shows the decrease in the process rate. Thus, the inflection point of the breakthrough curve coincides with the maximum of its derivation curve [26, 27].

In order to determine the inflection point, define the mass transfer process and characterize the dynamic behaviour of the system, the derivation of the Dose response kinetic model was done:

$$\frac{{d(c/c_{0} )}}{dx} = \frac{{b \cdot k_{DR} \cdot (b \cdot t)^{{k_{DR} - 1}} }}{{\left( {\left( {b \cdot t} \right)^{{k_{DR} }} + 1} \right)^{2} }}$$

(24)

Comparisons of experimental and model breakthrough curves (symbol and dashed lines) with their derived forms (solid lines) during nine successive service cycles are given in Fig. 11.

Fig. 11

Comparison of experimental and Dose–response model breakthrough curves (symbol and dashed lines) with their derived forms (full lines) during nine successive service cycle

It is evident that the derived forms of the breakthrough curves achieve a peak (pulse) shape which change in height and width. The inflection point of the breakthrough curve coincides with the maximum of its derivation curve. This maximum indicates the change in the rate controlling mechanism, explained in Fig. 2. Thus, it can be assumed that from the beginning of the process up to the inflection point the mass transfer rate is governed by the advection kinetics, around the inflection point the particle kinetics becomes more significant, and finally, it controls the overall rate until the exhaustion point.

The time for achieving of the inflection point (t_I) has been evaluated for nine successive service cycles and summarised in Table 7. For comparison, the values for achieving 50% of the breakthrough curve are also listed (t₅₀).

It is evident that at the bed depth of 120 mm, and for a constant initial concentration (1st, 2nd and 3rd cycle), a slight increase in t_I values is due to trained active sites in the zeolite layer during successive repetition of service and regeneration cycles. From the 4th cycle, the t_I values show a decreasing trend. If we are analysing the operating condition during the cycle, it is evident that t_I decreases with increasing initial concentration (comparison of the 3rd with 4th and 5th with 6th cycle), decreasing bed depth/mass of sorbent (comparison of the 3rd, 6th and 7th cycle), and with increasing flow rates (comparison of the 7th, 8th and 9th cycle).

Explanation of this behaviour can be found in the analysis of the quantity of zinc ions bound onto the fixed bed during the service cycle (Fig. 12). It is evident that the quantity of bound zinc increases linearly up to the inflection point, as the higher amount of exchangeable active sites in the zeolite are available. As the process progresses, the numbers of available active sites decrease. At the inflection point, the competition between the zinc from the solution and the sodium from the zeolite structure occurs, resulting in a decrease in the quantity of bonded zinc. Thus, after the inflection, the transfer rate becomes slower, which is probably due to the diffusion and increased mass transfer resistance through the zeolite particles, as well as lower amount of available exchangeable active sites in the zeolite.

Fig. 12

Quantity of zinc ions bound onto the fixed bed as the service cycle progresses (Note: t_I—time for achieving of inflection point in h)

Calculated values of μ_max, h⁻¹ (Table 7) evaluated at the inflection point from Fig. 11 are indicators of maximum specific breakthrough rate. These values significantly increase for the 7th, 8th and 9th cycle; thus, the time for achieving the inflection point at t_I is significantly reduced.

Values of t_I were compared with t₅₀ in Table 7, and differences of t₅₀-t_I were calculated. The results show a positive difference of t₅₀-t_I which indicates that the inflection point occurs below t₅₀ for all cycles, and varies in the range 0.031—0.914 h. It is also evident that the values of c/c_o at which the inflection occurs (see Fig. 11) during nine successive service cycles slightly moved toward lower values of c/c_o. This is comparable with decreasing values of parameter τ (see Table 7.) and k_DR (see Table 5.). This confirmed that the breakthrough curves achieve a sigmoid shape for all cycles, but at the lower bed depth and at increased flowrate (such as for the 9th cycle), it shows a tendency to achieve an asymmetric shape.

Analysis of parameter τ and evaluation of the optimal operating condition during cycle

The term τ is defined as a group of parameters that affects the adsorption performance according to the following equation [23]:

$$\tau = q^{*} \cdot H/\nu \cdot c_{0} = q \cdot m/Q \cdot c_{0}$$

(25)

where τ is the time required for 50% adsorbate breakthrough (h) and c₀, Q, H, m and $\nu$ are dependent on initial operating conditions.

The values of τ were evaluated on the experimental data for zinc capture on natural zeolite through nine successive sorption-regeneration cycles, and compared with values of time for achieving the inflection point t_I.

The good agreement between the values of τ and t_I, with slight deviation for 5th and 9th cycle, is evident (Fig. 13a). This indicates that a simple calculation of τ values based on initial operating conditions can give accurate information on the position of the inflection point as an indicator of the point of change of mechanism.

Fig. 13

Comparison of τ and t_I with q_e during nine cycles; b) Comparison of EBCT and η during nine cycles. Note: Shaded area represents the optimal range of τ and EBCT for different operation conditions

However, according to Eq. (25), the higher values of τ will be achieved at higher saturation/sorption capacity and the bed depth /mass of zeolite in fixed bed depth, while increasing flow rate and initial concentration decreases the τ values.

Our results indicate that τ value is most affected by the flow rate, the bed depth and the initial concentration. Thus, the τ values decrease with decreasing bed depth/mass of zeolite (comparison of the 3rd, 6th and 7th cycle), with increasing flow rates (comparison of the 7th, 8th, and 9th cycle) and initial concentrations (comparison of the 3rd with 4th and the 5th with 6th cycle). But at the same time the values of saturation/sorption capacity slightly increase.

So the question is how to evaluate the optimal range of τ, which is especially important during the process of scaling up. Namely, the main parameter that is suggested to keep constant during scale up is residence time (EBCT), which represents the contact time between the zinc solution and zeolite particles in the fixed bed.

A higher EBCT is desirable, as it results in a higher sorption capacity due to a higher effective diffusion process. At lower EBCT, the zeolite is saturated earlier because the front of the sorption zone quickly reaches the bottom of the column. This usually occurs at a high flow rate and lower bed depth. Thus optimal values of EBCT need to be defined.

As evident from our results (see Table 7), the EBCT value is most affected by the flow rate and the bed depth while change in the initial concentration does not have any impact.

Hence, for design of the column process, the EBCT and τ values should be equally important parameters. In order to identify a suitable range of values for these two variables for the investigated system of Zn capture onto zeolite, they are compared with the removal column efficiency η in Fig. 13b. Namely, higher values of column efficiency is an indicator of sharpness of the breakthrough curve. Thus, the peak sharpness depends on column efficiency.

If we assume that acceptable column efficiency should be η ≥ 75%, from Fig. 13a and b, the optimal (or the most favourable) conditions for the examined system are estimated to be: τ in the range 31.37—97.28 h and EBCT in the range 4.5—13.56 min. The results indicate that although increasing contact time over 4.5 min increases process time, it will ensure satisfying column efficiency. These two parameters, EBCT and τ, ensure more information and easier prediction of breakthrough behaviour during scale up of the process.

Conclusion

This study confirm that natural zeolite is an efficient adsorbent and ion-exchanger for the treatment of zinc-loaded wastewater to obtain high quality effluent, contributing to sustainable water management and water resource conservation. The regeneration of saturated zeolite was carried out sequentially nine times on the same zeolite bed. The typical S-shape of the breakthrough curves of Zn capture on zeolite were obtained for all service cycles, and the typical peak shape of the elution curves of Zn ions were obtained for nine consecutive zeolite regeneration cycles, indicating excellent sorption and regeneration capabilities of the same zeolite bed. A total of 6,208 mmol Zn (or 406 mg Zn) was removed per gram of zeolite which was regenerated during nine successive regeneration cycles. The concentrated regenerated solution allows for the zinc ions recovery and reuse in manufacturing industries, which contribute to the zero waste practice.

Testing of the models on experimental data by nonlinear regressions analysis confirmed that Thomas, Bohart-Adams, and Yoon-Nelson share identical mathematical form and their kinetic parameters are interchangeable: k_YN = k_BA⋅c₀ = k_T⋅c₀. The Wolborska model describes the initial part of the breakthrough curve. The Dose–response model achieves a sigmoidal curve when the parameter k_DR > 1. Additionally, a simulation for a condition different from those used to get model parameters was done, and the Dose–response model was found to be the best for describing the system. Its derived form of the equation is given and used for evaluation of inflection point (t_I). The result shows that the position of the inflection point varies as a function of the operation condition during the cycles. The t_I values decrease with increasing initial concentrations and flow rates of zinc in the solution and with bed depth/mass of zeolite in the fixed bed column. The position of t_I is in agreement with the quantity of zinc ions bound onto the fixed bed during the progress service cycle. Up to the inflection point, the mass transfer through aqueous phase governs the rate, while after the inflection point, the transfer rate becomes slower due to the diffusion and increased mass transfer resistance through the zeolite particles. The adsorption performance was evaluated through the parameters τ, residence time, EBCT, and column efficiency η ≥ 75%. The optimal working conditions for the examined system are estimated to be: τ in the range 31.37—97.28 h and EBCT in the range 4.5—13.56 min.