1 Introduction

Austenite dynamic recrystallization (DRX) is a key physical metallurgy phenomenon in steel industry. During the controlled rolling processing, the austenite grain structure undergoes considerable refinement due to the DRX in the high-temperature region, which remarkably refines the subsequent transformed microstructures of austenite decomposition during the complex cooling on the run-out table [1]. Owing to its importance for the thermo-mechanical processing of steel industry, modeling the DRX microstructures of austenite has received tremendous attention and has been a center piece of the overall microstructure models in variety of steel grades using the concept of microstructure engineering [2] in hot strip rolling. Starting from the concept proposed by Sellars and Whiteman [3] to predict the microstructure evolution during multi-pass hot rolling, a large number of empirical microstructure-based models [4–9] specifically regarding the austenite DRX have been developed. In these models, the DRX microstructure is described with a number of so-called internal state variables such as the recrystallized grain (R-grain) size, volume fraction of recrystallization. They are usually formulated using many experimentally derived parameters to fit the simulation results to the measured values, which are mainly concerned with the quantitative but empirical relationships among the DRX microstructure and the rolling processing parameters. Generally speaking, these models are able to make satisfactory predictions about the overall microstructure properties of the austenite DRX due to the knowledge-based nature. However, they cannot provide a direct view of the microstructure evolutions during DRX.

With the advancement of computer performance, it is now possible to model microstructure on mesoscale, i.e., on the length scale of the microstructure features using various mesoscopic approaches, such as cellular automaton (CA), Monte Carlo (Potts) method and phase field method. [10]. Among the various mesoscopic models, CA can readily be used to simulate the dynamic recrystallization in metallic materials [11]. Goetz and Seetharaman [12] presented the first CA model for the DRX in single-phase alloys. Starting with their pioneering work, a number of sophisticated CA models have been proposed to simulate the microstructures evolution of DRX [13–21]. However, majority of these models appear to be depictive, which mainly present capabilities of the developed tools to model the complex microstructural phenomena taking place during the DRX process. Few of them have to be brought to a stage that reliable quantitative predictions can be made for actual processing.

The object of the study is to develop a physically based CA model to depict the complex microstructural behavior of dynamic recrystallization at the grain scale. Here, both the grain deformation approach and the DRX cycle concept are introduced in order to provide a more accurate description of the DRX grain structures. The use of materials-correlated parameters inputted ensures a realistic model capable of being tested against actual microstructural results. The attention of this paper is placed on model development specified to both topographic and quantitative depictions of the microstructural phenomena for austenite DRX in carbon steels.

2 Model Concept

2.1 Nucleation of DRX

With respect to the nucleation of austenite DRX, two assumptions similar to the model developed by Ding and Guo [13] are utilized: (1) DRX occurs only if the accumulation of the dislocation density reaches the critical value, (2) nucleation of DRX only occurs at the grain boundaries (including the primary grain boundaries and the recrystallized grain boundaries). In other words, only those cells belonging to the grain boundaries can become possible nucleation sites. The nucleation rate, \(\dot{n}\), for DRX as a function of both temperature, T, and strain rate, \(\dot{\varepsilon }\), reads as:

$$\dot{n}(\dot{\varepsilon },T) = C\dot{\varepsilon }^{\eta } \;{ \exp }\left( { - \frac{{Q_{\text{N}} }}{RT}} \right),$$
(1)

where C is a constant, \(Q_{\text{N}}\) is the activation energy for nucleation, and the exponent η is set to 1 in the present simulation. R is the gas constant (8.314 J mol−1 K−1). The critical dislocation density, \(\rho_{\text{c}}\), for nucleation on grain boundaries can be calculated by considering the change of the stored deformation energy, as proposed by Roberts and Ahlblom [22]:

$$\rho_{\text{c}} = \left( {\frac{{20\gamma \dot{\varepsilon }}}{{3blM\tau^{2} }}} \right)^{1/3},$$
(2)

where τ = μb 2/2 is the dislocation line energy. l is the dislocation mean free path. γ is the grain boundary energy. b is the magnitude of the Burger’s vector, and M is the grain boundary mobility.

The dislocation mean free path is taken as the subgrain size and can be expressed as [23]:

$$l = 10.5 \cdot \frac{\mu b}{\sigma },$$
(3)

where μ is the shear modulus of the material and σ is the flow stress.

2.2 DRX Grain Growth

The movement of the recrystallization front is treated as a strain-induced boundary migration process, during which the difference in the stored energy between the deformed matrix and the recrystallized zone provides the driving force [24]. The velocity of the recrystallization front, V, moving into the deformed matrix can be expressed as:

$$V = MP,$$
(4)

where P is the driving pressure for the recrystallization front movement and can be formulated as:

$$P = \frac{1}{2}\mu b^{2} (\rho_{\text{m}} - \rho_{i} ) - \frac{{2\gamma_{i} }}{{r_{i} }},$$
(5)

where \(\rho_{\text{m}}\) is the mean dislocation density of the deformed matrix. ρ i is the dislocation density of the i-th DRX grain, and r i is the equivalent radius of the i-th DRX grain. The grain boundary energy, γ i , as a function of the misorientation is assumed to follow the Read–Shockley equation [25]:

$$\gamma = \gamma_{\text{m}} \frac{\theta }{{\theta_{\text{m}} }}\left[ {1 - { \ln }\left( {\frac{\theta }{{\theta_{\text{m}} }}} \right)} \right],$$
(6)

where θ is the misorientation between two neighboring grains. \(\gamma_{\text{m}}\) and \(\theta_{\text{m}} = 15^{\text{o}}\) are the grain boundary energy and the misorientation when the grain boundary becomes a high-angle boundary. The grain boundary energy is assumed to be a constant if the misorientation is larger than \(15^{{^\circ }}\). The grain boundary mobility, M, is related to the grain boundary self-diffusion coefficient, D 0b, the activation energy for grain boundary motion, \(Q_{\text{b}}\), and the characteristic grain boundary thickness, δ, that can be calculated by [26]

$$M = \frac{{D_{{0{\text{b}}}} b^{2} }}{kT}\;{ \exp }\left( { - \frac{{Q_{\text{b}} }}{RT}} \right),$$
(7)

where b is the magnitude of the Burger’s vector and k is the Boltzmann constant (1.38 × 10−23 J K−1).

2.3 Evolution of Dislocation Density

During hot deformation, part of the deformation energy is stored in the form of dislocations. The stored deformation energy can be calculated according to the dislocation density, ρ

$$E_{\text{def}} = \frac{1}{2}\mu b^{2} \rho .$$
(8)

The evolution of dislocation density with strain during deformation is generally governed by the balance between dislocations generation and storage (hardening) and the removal of dislocations due to annihilation (softening). The mean dislocation density can be expressed as

$$\frac{{{\text{d}}\rho }}{{{\text{d}}\varepsilon }} = \left( {\frac{{{\text{d}}\rho }}{{{\text{d}}\varepsilon }}} \right)_{\text{hard}} - \left( {\frac{{{\text{d}}\rho }}{{{\text{d}}\varepsilon }}} \right)_{\text{soft}} .$$
(9)

Here, a phenomenological model (K–M model) developed by Kocks and Mecking [27] is implemented to describe the variation of the dislocation density with respect to the deformation strain:

$$\frac{{{\text{d}}\rho }}{{{\text{d}}\varepsilon }} = k_{1} \sqrt \rho - k_{2} \rho,$$
(10)

where k 1 = 2θ 0/(aμb) is the constant representing work hardening and \(k_{2} = 2\theta_{0} /\sigma_{\text{s}}\) is the softening parameter that represents recovery of dislocations. θ 0 is the hardening rate which is independent of the strain rate, and only dependent on temperature through the influence of temperature on shear modulus. \(\sigma_{\text{s}}\) is the steady-state stress. Conventionally, θ 0 and \(\sigma_{\text{s}}\) can be determined from the experimental flow stress–strain curves. However, the experimental curves for pure austenite are difficult to be obtained. In the present modeling, the values of θ 0 and \(\sigma_{\text{s}}\) for pure austenite are determined by a predictable stress–strain model developed by Hatta et al. [28]. According to the model, \(\sigma_{\text{s}}\) can be calculated according to the following equation:

$$\dot{\varepsilon } = A_{0} [\sinh (a^{{\prime }} \sigma_{\text{s}} )]^{{n^{{\prime }} }} \;{ \exp }\left( { - \frac{{Q_{\text{A}} }}{RT}} \right),$$
(11)

where A 0, n′, a′ and \(Q_{\text{A}}\) are constants closely correlated with the nominal carbon content of the low-carbon steels and can be formulated in the following forms:

$$\begin{aligned} & { \ln }\;A_{0} = 24.4 - 1.69 \times { \ln }[C] \\ & { \ln }\;n^{{\prime }} = 1.63 - 0.0375 \times { \ln }[C] \\ & { \ln }\;\alpha^{{\prime }} = - 4.822 + 0.0616 \times { \ln }[C] \\ & { \ln }\;Q_{A} = 5.566 - 0.0502 \times { \ln }[C]. \\ \end{aligned}$$
(12)

Here, [C] is the carbon content of the plain carbon steel (mass%). The values of these parameters used in the present simulation are listed in Table 1. Details about their determination can be found in Ref. [28].

Table 1 Values of the fitting parameters for \(\sigma_{\text{s}}\) prediction
Full size table

The macroscopic stress in relation to the average dislocation density \(\bar{\rho }\) can be expressed as [27]:

$$\sigma = \alpha \mu b\sqrt {\bar{\rho }},$$
(13)

where α is a dislocation interaction coefficient which is approximately 0.5 for most metals [13]. The average dislocation density, \(\bar{\rho }\), is associated with the dislocation densities, ρ i of all the lattice sites by the following formula:

$$\bar{\rho } = \frac{1}{n}\sum\limits_{i = 1}^{n} {\rho_{i} }.$$
(14)

Then, changing of the macroscopic stress–strain curve can be determined by combining Eqs. (10, 13 and 14).

3 Cellular Automaton Model with Grain Deformation

3.1 Cellular Automaton Model

In the present study, a deterministic CA model for recrystallization [29] is modified to accomplish this microstructural simulation of austenite DRX. In this CA model, a 2D hexagonal lattice and the von Neumann’s neighbor rule, which considers the nearest six neighbors, are implemented. In order to describe the unique microstructural evaluation during DRX, five state variables are used on each CA lattice site. They are: (1) the grain orientation variable representing the different grains; (2) the dislocation density variable representing the stored energy; (3) the order parameter variable indicating whether it belongs to recrystallized grain, deformed matrix or interface; (4) the DRX cycle variable which is assigned an integer identifier representing the DRX cycles; and (5) the DRX fraction variable representing the volume fraction recrystallized. The values of each state variable on each of the CA nodes are functions of their respective previous states and the previous states of their neighbors. They are determined according to the submodels described in Sect. 2. The kinetics of the automaton is realized by synchronously updating the state variables for all lattice cells in each time step.

A deterministic transformation rule is applied to determine the state changing of each CA cell. For the cell (h, k) in which the order parameter variable belongs to the interface, the moving distance of the interface between the recrystallized grains and the deformed matrix in a single time step, Δt, is calculated as:

$$l_{h,k}^{t} = \int_{t}^{t + \Delta t} {v\text{d}t},$$
(15)

where v is the velocity of the boundary movement. The indices (h, k) denote the coordinate of the selected interface cell. The DRX fraction in (h, k), f t h,k is then calculated by:

$$f_{h,k}^{t} = l_{h,k}^{t} /L_{{\text{CA}}},$$
(16)

where \(L_{{\text{CA}}}\) is the distance between two neighboring cells. If the accumulated value of the DRX fraction variable is greater than 1, the interface cell transfers into the new recrystallized state from the neighboring cells belonging to the corresponding growing grain.

During hot deformation, the grain topology continuously changes concomitant with the deformation and the microstructural evolution of DRX. In present simulation, the grain deformation during DRX is modeled by combination with a topology deformation approach based on a vector operation [30]. In a 2D space, each lattice site can be regarded as a vector based on a certain origin. Each vector can be operated in turn to produce a set of new vectors defining the new grain topology [29]. The grain deformation then can be handled mathematically as a vector operation. For a 2D model, topology deformation can be described by a 2 × 2 deformation matrix. Thus, an original vector u becomes a new vector v as a result of a uniform deformation S

$$\varvec{v} = S\varvec{u}.$$
(17)

The form of matrix can be written as

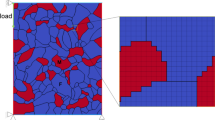
$$\left[ \begin{aligned} {\text{v}}_{x} \hfill \\ {\text{v}}_{y} \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}c} {S_{x} } & 0 \\ 0 & {S_{y} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\text{u}}_{x} } \\ {{\text{u}}_{y} } \\ \end{array} } \right],$$
(18)

where \(u_{i} \left( {i = x, \, y} \right)\) are the components of original vector u and \(v_{i} \left( {i = x, \, y} \right)\) are the components of new vector v after deformation. S i (i = x, y) are the principal nominal deformation at the two directions (the ratios of the final to initial lengths of vectors along two principal axes). Therefore, ɛ i  = ln S i (i = x, y) are the true strains along the two principal axes of deformation. And the determinant of S must be unity so as to remain the volume unchanged, i.e., S x S y  = 1. In a 2D CA model, each regular lattice site can be taken as a discretized point of the space. Then, the geometrical position change of each cell due to the deformation can be determined by this topology deformation approach. Accordingly, the grain deformation during the continuous deformation can be tracked when the deformation step is imposed on the entire lattice. Figure 1 shows an example of the morphology changing of the grain structures due to the uniaxial compression deformation under different strains.

Fig. 1
figure 1

Example of the morphology changing of the grain structures for expressing grain deformation under different strains

Full size image

The flowchart of the overall modeling process of the DRX microstructure evolution is shown in Fig. 2. In essence, the present CA model with grain deformation for DRX simulation is a modification of that developed for a previous study [16], whereas the attention of current work is placed on model development of CA specified to both topographic and quantitative depictions of the microstructures for austenite DRX in carbon steels, including the grain deformation, evolution of the DRX grain structure, the microscopic stress–strain relation and the grain size evolution. When \(\sum {\Delta \varepsilon_{{\text{CA}}} } = \sum {\dot{\varepsilon }\Delta t} \propto \Delta \varepsilon_{\text{d}}\), the grain deformation model is implemented using the microstructures derived from the previous time step as input to produce the deformed grain structures. Then, the deformed grain structure together with the distribution of the stored deformation energy and the stored energy level become the open state for subsequent microstructure modeling of DRX in current time step. In this way, the grain deformation and the concurrent DRX microstructure evolution are then simultaneously simulated.

Fig. 2
figure 2

Flowchart of CA modeling for the dynamic recrystallization simulation

Full size image

Details regarding the numerical implementation of the topology deformation approach in CA are given in Ref. [16]. Here, only the items relevant to the current simulation are outlined in more detail:

  1. (1)

    The initial dislocation density is assumed to be uniformly distribution within all the primary grains and is set to 109 m−2 [31].

  2. (2)

    Evolutions of the dislocation density and the macroscopic stress–strain curve are calculated with a constant strain increment \(\Delta \varepsilon = \dot{\varepsilon } \cdot \Delta t\) according to Eqs. (10) and (13), where Δt is the time step.

  3. (3)

    The DRX cycle number of the primary grains is set to zero. When the new cycle of DRX occurs, the DRX cycle number is set to the number that one is added to the current DRX cycle number.

  4. (4)

    The new cycle DRX grains are assumed to grow up toward either the unrecrystallized primary grains or the DRX grains of former cycles. Thus, the ρ m used in Eq. 5 is taken to be the average dislocation density within the deformed primary grains and all the former DRX cycle grains.

3.2 Simulation Setting

The investigated steel in this study is a plain low-carbon steel with a chemical composition of 0.19C–0.21Si–0.75Mn (mass%). The DRX microstructural behavior which occurs during a uniaxial compression deformation up to ɛ = 0.6 is considered under a strain rate of \(\dot{\varepsilon } = 0.1\;{\text{s}}^{ - 1}\) at a fully austenitic temperature of T = 900 °C. The initial simulation domain is discretized with a 200 × 400 2D regular lattice representing a physical domain of 200 µm × 400 µm. The initial austenitic microstructure is created according to a normal grain growth process, with an average grain size of 63 µm diameter, as shown in Fig. 1. The orientations of each primary grains and recrystallized grains are set by a random integer in the range of 1–180.

In this paper, an equivalent grain diameter D i is used to define the grain size and is calculated as

$$D_{i} = \sqrt {\frac{{4A_{i} }}{\pi }} ,$$
(19)

where A i is the area of the grain i which can be calculated by totalizing the included cells of each ferrite grain. Then, the average diameter of grains \(< \bar{D} >\) is calculated as

$$< \bar{D} > = \frac{{\left( {\sum\limits_{i = 1}^{{N_{\alpha } }} {D_{i} } } \right)}}{{N_{\alpha } }},$$
(20)

where \(N_{\alpha }\) is the total number of grains in the system. The key parameters used in the present modeling are listed in Table 2.

Table 2 Key parameters used in simulations [29]
Full size table

4 Results and Discussion

Figure 3 shows the simulated microstructure at different strains for the low-carbon steel hot-compressed under the given deformation condition (\(\dot{\varepsilon } = 0.1\;{\text{s}}^{ - 1}\), T = 900 °C). The white regions indicate the unrecrystallized deformed matrix. The dark gray regions denote the first-cycle DRX grains, and the light gray regions denote the second-cycle DRX grains. And the gray lines represent the grain boundaries. Different from the static recrystallization, the dislocation density inside the recrystallized grain increases with the progress of DRX. Here, the DRX cycle concept is introduced to depict the microstructural behavior of the austenite DRX. It can be seen that, with the deformation proceeding, the dislocation density (or the strain) increases until the critical dislocation density,\(\rho_{\text{c}}\) for triggering the DRX is reached, when the DRX nuclei appear along the primary grain boundaries. The DRX grains continuously grow up leading to the typical necklace structure around the pre-existing grain boundaries, as seen in Fig. 3c. At the same time, the concurrent work hardening will accumulate new dislocations inside them. When the dislocation density in the new R-grains reaches \(\rho_{\text{c}}\), the next cycle of DRX then occurs, as seen in Fig. 3d.

Fig. 3
figure 3

Simulated microstructural evolution at different strains of a ε = 0.1, b ε = 0.2, c ε = 0.3, d ε = 0.4, e ε = 0.5, f ε = 0.6 during the dynamic recrystallization of austenite under a strain rate of 0.1 s−1 at the temperature of 900 °C

Full size image

The simulation also indicates that, at the given thermo-mechanical conditions, the accumulation of the dislocation density in the R-grains is sufficiently fast so that it has already reached the critical value before the primary deformation matrix is completely consumed. It indicates that a new cycle of DRX can occur before the previous cycle is completed and the cycles of DRX might overlap during the whole hot deformation process. The simulated curve of the DRX kinetics in Fig. 4 shows clearly that the second cycle of DRX has already started before the initial deformation matrix is consumed by the first DRX cycle. And hence, the grain structures of the first, second DRX cycles and the primary grains are mixed at this DRX stage, as seen in Fig. 3d. However, it is rather difficult to distinguish the R-grains from the deformed materials for DRX in experiments [24].

Fig. 4
figure 4

Simulated recrystallization kinetics of different DRX cycles and a comparison with the predictions by the empirical DRX model

Full size image

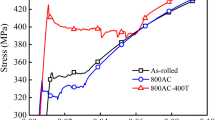
Another phenomenon of relevance is that the aspect ratio of the finite simulation lattice changes with the progress of the compression. The primary grains are observed elongated normal to the compression direction, while the DRX grains remain almost equiaxed gain structures. Figure 5 compares the experimental and simulated microstructures of both the initial grain structures and the recrystallized grain structures. The experimental results are derived from a hot compression testing using the Gleeble 1500 thermo-mechanical simulator by Jin and Cui [17]. The corresponding thermo-mechanical processing schedule is shown schematically in Fig. 6. The specimen is firstly heated up to 1200 °C at a heating rate of 10 °C/s and held for 3 min to obtain a single austenitic microstructure. Then, it is cooled to the deformation temperature at 900 °C and subjected to a uniaxial compression to logarithmic strain of 0.6 at a strain rate of 0.1 s−1. The microstructure of a section in the middle of the specimen is observed under optical microscope. Generally speaking, the simulated results agree well with the experimental findings. The simulated mean R-grain size is 20 µm, compared with the actual mean size of 19.8 µm. Figure 7 shows the comparison of the simulated flow stress curve by CA with the experimental measurement under the given deformation condition. It is seen that the predicted curve also agrees well with the measured one. Therefore, it is confirmed that this CA model with grain deformation presents the great potential to estimate the microstructure evolution for austenite DRX in carbon steels.

Fig. 5
figure 5

Comparison of the initial a, b and resultant c, d microstructures between the micrographs (left) and the CA simulations (right) as a result of the dynamic recrystallization of austenite in the given low-carbon steel

Full size image
Fig. 6
figure 6

Schedule of thermo-mechanical processing used in the DRX experiment

Full size image
Fig. 7
figure 7

Comparison of the simulated flow stress curve with the experimental measurement at a deformation of \(\dot{\varepsilon } = 0.1\;{\text{s}}^{ - 1}\) and T = 900 °C

Full size image

As complementary information, both the overall mean grain size and the recrystallized mean grain size evolutions for the same simulation are displayed in Fig. 8. It can be seen that when the critical strain for DRX is reached, the mean grain size quickly drops from an initial grain size, D 0, toward the steady-state grain size which is 20 µm for the given thermo-mechanical condition. The mean size of the R-grains, however, is found to be increasing gradually approaching its steady state.

Fig. 8
figure 8

Evolutions of the mean grain size and the recrystallized grain size of austenite during the dynamic recrystallization under a strain rate of 0.1 s−1 at 900 °C

Full size image

Further complementary insight into the DRX microstructural characteristics can be referred to Fig. 9, which presents predictions of both the overall grain size distribution (Fig. 9a) and the R-grain size distribution (Fig. 9b) at different strains approaching the steady state. It can be seen that, at the lower strain of ɛ = 0.4, the statistical curve of the overall grain size distribution exhibits a broader distribution stretching to encompass larger values as indicated by the arrow in Fig. 9a. It is easily understood that the grain structure is mixed with the DRX grains and the deformed grains at this DRX stage, leaving several larger primary grains unrecrystallized. This thus leads to the two-peak form in the statistical curve of the grain size distributions, as seen in Fig. 9a. However, further progress of the DRX, especially occurrence of the new DRX cycle, progressively refines the grains. The frequency peak at the larger grain size region is diminishing. The grain size distribution tends to be essentially of log-normal form when the DRX reaches its steady state. During the DRX, as the R-grains grow, the concurrent work hardening builds up the dislocation density inside them. Thus, the driving force for the R-grain boundary migration is reduced till the growth stops. This leads to a limited size range for the R-grains as shown in Fig. 9b. By combination with the grain structures shown in Fig. 5, it can be easily understood that reliable predictions of the grain size distribution have been made by this CA model.

Fig. 9
figure 9

Predicted overall grain size distribution a and the grain size distribution of the DRX grains b at different strains

Full size image

In order to further verify the capability of the present CA model, the simulation results are also compared with the predictions by the macroscopic empirical microstructural models of DRX, as shown in Figs. 4, 8. The macroscopic models are usually formulated concerning the quantitative but empirical relationships among the microstructures and the processing parameters for a given steel grade based on a large amount of experimental data available from laboratory simulations [2]. For this steel grade, evolution of the DRX fraction,\(X_{\text{d}}\), with the progress of strain, ɛ, can be predicted by [32]

$$X_{\text{d}} = 1 - { \exp }\{ - 0.693 \times [(\varepsilon - \varepsilon_{\text{c}} )/(\varepsilon_{0.5} - \varepsilon_{\text{c}} )]^{2} \} ,$$
(21)

where \(\varepsilon_{\text{c}}\) is the critical strain for onset of DRX and \(\varepsilon_{ 0. 5}\) is the strain for 50% recrystallization which is calculated by

$$\varepsilon_{0.5} = 1.144 \times 10^{ - 3} d_{0}^{0.25} \dot{\varepsilon }^{0.05} \;{ \exp }(6420/T),$$
(22)

where d 0 is the initial austenite grain size and \(\dot{\varepsilon }\) is the strain rate. The critical strain of \(\varepsilon_{\text{c}}\) is correlated with the initial grains, d 0, and the strain rate, \(\dot{\varepsilon }\) [2]. In the present modeling, it is taken as 0.16 in accordance with both the experimental and the \(\rho_{\text{c}}\) calculation. The results indicate that the DRX kinetics has typical sigmoidal shape. And the CA simulation results agree very well with the predictions by the macroscopic empirically based models.

The austenite grain size of DRX, \(D_{{\text{RX}}}^{{}}\), for this steel grade can be calculated by [32]:

$$D_{{\text{RX}}} = 5.072 \times 10^{3} \times Z^{ - 0.1555} ,$$
(23)

where Z is the Zener–Hollomon parameter:

$$Z = \dot{\varepsilon } \cdot { \exp }\left( {\frac{363155}{RT}} \right).$$
(24)

The predicted R-grain size is about 22 µm, which is close to the experimental observations as well as the CA predictions as shown in Fig. 8. It should be noted that the macroscopic model can only predict the average microstructure properties, i.e., the overall DRX kinetics, the steady-state mean grain size. However, the physically based CA modeling of the DRX microstructure can offer better insight into how the microstructure evolution occurs. It can not only provide the general average microstructure properties but also describe the actual microstructure evolution. The results presented here confirm the great possibility and effectiveness of the CA model for modeling the austenite DRX during the hot working processing.

5 Conclusions

A modified 2D cellular automaton model that takes into account grain deformation during hot deformation has been developed to quantitatively depict the microstructure and flow stress evolution involving in the austenite DRX of a low-carbon steel. The main conclusions are summarized as follows:

In contrast to the macroscopic empirically based DRX model, the physically based CA modeling of the DRX microstructure can offer better insight into how the microstructure evolution occurs. The growth kinetics of each R-grain, including its dislocation density variation, growth velocity and grain topology, can be tracked through the whole transition process.

As a result of the CA-DRX simulation, it is confirmed that more realistic and accurate predictions of the DRX grain structure and DRX grain size can be made by introducing the multi-cycle concept of DRX as well as the grain deformation approach. The flow stress–strain curve can also be determined directly from the average of the dislocation densities of all the grains in the considered simulation domain. This CA model enables both quantitative and topographic simulations of the microstructural evolution during the austenite DRX.