Microstructural Changes During Static Recrystallization of Austenitic Stainless Steel 304L: Cellular Automata Simulation

Abstract

Static recrystallization and microstructural changes in austenitic stainless steel 304L were studied. The rolling experiments at 200 °C were carried out, and then, annealing treatment was made at temperatures ranging between 500 and 830 °C. A model was also developed to simulate the kinetics of non-isothermal recrystallization within the rolled steel. The distribution of plastic strains during rolling was predicted utilizing an elastic–plastic finite element formulation performed in ABAQUS/Explicit, while the predicted results were used to generate the as-rolled microstructure and to estimate the stored energy. Finally, microstructural–thermal model based on cellular automata was developed to evaluate the rate of static recrystallization within the rolled steel. The comparison between experimental and simulations showed a good consistency. The predictions illustrated that inhomogeneous distribution of plastic strain was produced during multi-pass rolling leading to different rates of recrystallization in the center and the surface regions of the rolled plate. The onset temperature of recrystallization was found about 700 °C, and the activation energies for nucleation and growth for recrystallization were determined as 180 kJ/mol and 240 kJ/mol, respectively. It was found that homogenous nucleation mechanism can be operative in recrystallization of multi-pass rolled steel, i.e., for reduction of 40% or higher.

Introduction

Owing to high corrosion resistance and formability of chromium–nickel austenitic stainless steel, they are widely used in different industries and applications. The main strengthening mechanisms in this type of steels are work hardening and formation of martensite during low-temperature processing, i.e., deformation temperatures less than M_d [1]. However, the formation of strain-induced martensite and/or cold forming could reduce corrosion resistivity [2], and therefore, further partial annealing treatment can be employed to balance between the strength and corrosion resistance [3]. As a result, microstructural events and mechanical properties after rolling processing were studied using experimental techniques and mathematical simulation [4,5,6]. It should be noted that among simulation techniques and approaches, cellular automata can be considered as a powerful tool for modeling phase transformation and microstructural changes during deformation processing of different metal and alloys including stainless steels. For instance, Zheng et al. [7] simulated static recrystallization kinetics in carbon steels utilizing two-dimensional cellular automata modeling coupled with crystal plasticity formulation. Madej et al. [8] developed a coupled cellular automata–finite element algorithm for predicting the rate of dynamic recrystallization during deformation. Lin et al. [9] developed a probabilistic cellular automaton to simulate static recrystallization in Ni-based superalloys, and the rate of recrystallization and grain structure were predicted. In the other work [10], the microstructural events during dynamic recrystallization were predicted employing cellular automata together with a first-order rate equation for estimation of dislocation density during plastic straining. Han et al. [11] proposed a cellular automata simulation based on the unified subgrain growth theory to estimate the kinetics of both continuous and discontinuous recrystallization. Chen et al. [12] used two-dimensional CA model for estimation of dynamic recrystallization kinetics in hot deformation of austenitic stainless steel 316LN. Zhi et al. [13] proposed a CA model to predict microstructural evolution, the rate of recrystallization, and dislocation density during isothermal hot deformation of TRIP steels. In the other work, Zheng et al. [14] employed a simulation based on cellular automata in order for determination of the rate of static and dynamic recrystallization during and after multi-pass hot rolling processes. Salehi and Serajzadeh [15] used a CA-finite element simulation for predicting the microstructures of cold-deformed carbon steel after non-isothermal annealing heat treatment. Contieri et al. [16] proposed a model based on cellular automata for simulation of rate of static recrystallization and grain size distribution within a heavily deformed titanium alloy.

Regarding the published works concentrated on stainless steels, majority of the previous works have been considered homogenous distribution of stored energy and/or isothermal heat treatment conditions; however, annealing treatments of steels are usually made at non-isothermal heating conditions having a non-uniform distribution of plastic strains. This study investigated warm-rolling behavior and subsequent non-isothermal recrystallization of 304L stainless steel. Firstly, multi-pass rolling was conducted at 200 °C and then the static recrystallization was made on the rolled steel in temperatures ranging between 500 and 830 °C. In this regard, a thermo-mechanical model was used to define the distributions of plastic strains and stored energy after multi-pass warm rolling, and then, the results of the model were imported in the other thermal–microstructural simulation as the initial conditions. In the next stage, two-dimensional cellular automata–finite element modeling was developed to determine the progress of static recrystallization and temperature variations during subsequent static recrystallization. Both homogeneous and non-homogeneous nucleation mechanisms were taken into account which can be applicable for heavily deformed conditions. Besides, the effects of heating rate, the recrystallization temperature and prestrain were included in the microstructural simulation. Experimental testing including tensile test, hardness measurement, and optical metallography was carried out on as-rolled and recrystallized samples to define mechanical properties and microstructural evolution as well as to determine the material constants.

Mathematical Modeling

Thermo-Mechanical Modeling

The distributions of effective stress and plastic strain during single- and multi-pass rolling were predicted by an elastic–plastic finite element analysis. The model was performed by ABAQUS/Explicit, while the updated Lagrangian scheme was employed in which the minimization of power functional was done with respect to displacement field as follows [17, 18].

$$ \int\limits_{V} {\rho \, \ddot{u}_{i} \delta u_{i} {\text{d}}V} + \int\limits_{V} {\sigma_{ij} \delta \varepsilon_{ij} {\text{ d}}V} - \int\limits_{S} {q_{i} \delta u_{i} {\text{d}}S} = 0 $$

(1)

here $\sigma_{ij}$ and $\varepsilon_{ij}$ are stress and strain tensors, respectively. $\rho$ is the density, u_i shows the displacement tensor, and q_i is the traction. The model was capable of considering multi-pass forward rolling layouts. For doing so, the distributions of stress and strain after each pass were assigned as the initial state for the subsequent rolling stand. The meshing system was performed by four-node isoparametric elements having 80 elements along length direction and 6 elements along the thickness, i.e., 567 nodes. It should be noted that one-half of the plate was considered in the calculations because of the plane of symmetry, while the material constants and flow stress behavior were determined using the data in Refs. [19, 20]. A coupled thermo-mechanical approach was used to manage the heat conduction problem. At the same time, the following heat transfer equation associated with conduction–convection boundary conditions was coupled with the deformation problem to predict temperature rise during rolling [21]:

$$ \frac{\partial }{\partial x}\left( {k\frac{\partial T}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {k\frac{\partial T}{\partial y}} \right) + \dot{Q} = \rho c\frac{\partial T}{\partial t} $$

(2)

$$ - k\frac{\partial T}{\partial n} = h_{\text{a}} (T - T_{\text{a}} ) $$

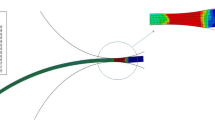
where ρ is density, k is heat conduction coefficient, c is the specific heat, and $\dot{Q}$ denotes the rate of heat generation. T_a and h_a are ambient temperature and corresponding heat convection coefficient, respectively. Figure 1 displays the employed boundary conditions and mesh distortion after single-pass rolling operation. The results of the thermo-mechanical modeling were employed for estimating the stored energy in microstructural model. It is worth noting that because of non-uniform distribution of plastic strains, the stored energy would be varied along the thickness, especially in multi-pass rolled plates.

Fig. 1

Illustration of mesh distortion after single-pass rolling and the imposed boundary conditions

Thermal Modeling and Microstructural Simulation

In the next stage, the recrystallization modeling was made by means of a combined thermal–microstructural analysis. A discretized region using rectangular cells with cell length of 0.5 μm was generated, while periodic boundary conditions were considered. In other words, in the CA domain, the cell condition at each boundary side is considered the same as that one on the opposite side [9, 21]. However, for the case of boundary sides located on symmetry plane, a mirror boundary condition was taken [22]. In order to generate a proper as-deformed microstructure, an initial equiaxed grain structure was first constructed using the random nucleation algorithm and modified Moore neighboring scheme. In the next step, the deformed microstructure was generated regarding the amount of the predicted plastic strain applied at the position of the CA domain by the following transformation [23].

$$ V = LU,{\text{which}}\;L = \left[ {\begin{array}{*{20}l} {\exp (\varepsilon_{xx} )} \hfill & 0 \hfill \\ 0 \hfill & {\exp (\varepsilon_{yy} )} \hfill \\ \end{array} } \right] $$

(3)

here U and V denote the initial and the deformed positions, respectively, and L is transformation matrix that is constructed based on the local strain distribution, i.e., $\varepsilon_{xx}$ and $\varepsilon_{yy}$ are the normal strains along principal axes. After generation the as-deformed structure, the nucleation rate was determined in each CA time step. Driving force for nucleation was calculated in each cell as stored energy plus grain boundary energy. Accordingly, the embryos are placed randomly in different positions, while certain positions were given higher probability for nucleation, e.g., four and three junctions have the highest probability. However, when the stored energy is high, homogenous nucleation mechanism might also be activated and in-grain stable embryos could be formed [24, 25]. In the other words, heterogeneous nucleation would be operative, but for the case of highly deformed samples, homogenous nucleation mechanism could occur simultaneously. The general form of nucleation rate can be expressed as [26].

$$ \dot{N} = c_{0} \left( {\frac{{\sigma_{f}^{2} }}{\alpha G} - \frac{{\sigma_{0}^{2} }}{\alpha G} - \Delta (A\gamma )} \right)V_{\text{CA}} \exp \left( { - \frac{{Q_{\text{N}} }}{RT}} \right) $$

(4)

here R is universal gas constant, T is the absolute temperature, G is the shear modulus, α is a material constant usually taken as 0.5, and V_CA represents the volume of the working domain. $\sigma$ and $\sigma_{\text{f}}$ denote the flow stress of deformed and fully annealed sample, respectively, $\Delta \left( {A\gamma } \right)$ is the change in surface energy of nuclei during recrystallization which is set to be zero for the case of homogenous nucleation, c₀ is a material constant, and $Q_{\text{N}}$ is the activation energy for nucleation. Note that the recrystallized grains grow until they impinge with the other moving grain boundary, or softening fraction reaches 0.95. The growth velocity consists of grain boundary mobility associated with exponential behavior and driving pressure for growth which are calculated as a combination of the curvature and the deformation energy in each cell [27, 28]. So, the velocity of moving boundary can be defined as:

$$ v = M_{0} \exp \left( { - \frac{{Q_{\text{G}} }}{RT}} \right)\left[ {\frac{{(\sigma_{\text{f}}^{2} - \sigma_{0}^{2} )}}{\alpha G} + \kappa \gamma } \right] $$

(5)

where $M_{0}$ is a material constant, $Q_{\text{G}}$ is the activation energy for grain boundary motion, γ is the grain boundary energy, and κ is curvature calculated by the kink template method based on the following equation [9, 29].

$$ \kappa = \frac{A}{{C_{\text{cell}} }}\frac{{{\text{kink}} - N_{i} }}{N + 1} $$

(6)

where $C_{\text{cell}}$ is cell size, A is topological coefficient that was taken as 1.28, N is the number of the first and second nearest neighbor sites for a $5 \times 5$ lattice, $N_{i}$ denotes the number of cells belonging to grain i, and “kink” is the number of cells for a flat interface.

As seen in the kinetics equation, temperature plays an important role; however, during non-isothermal heat treatment, the distribution of temperature is varied, and therefore, this parameter should be computed as function of time and considered in the microstructural simulation. For this purpose, the heat conduction problem with lateral convection was taken into account and then the problem was solved using Galerkin finite element formulation. The governing heat conduction equation can be expressed as below [30]:

$$ \frac{\partial }{\partial x}\left( {k\frac{\partial T}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {k\frac{\partial T}{\partial y}} \right) - 2h_{\text{eff}} (T - T_{\text{f}} ) = \rho cw\frac{\partial T}{\partial t} $$

(7)

$$ \begin{aligned} & - k\frac{\partial T}{\partial n} = h_{\text{eff}} (T - T_{\text{f}} ) \\ & T(x,y,0) = 25\;^\circ {\text{C}} \\ \end{aligned} $$

(8)

Here $T_{\text{f}}$ is the furnace temperature and $h_{\text{eff}}$ is the effective convection heat transfer coefficient and w is the thickness of the plate. To handle this problem, temperature variation on each element was taken as $T^{\text{e}} = Na^{\text{e}}$ [30] in which N is shape-function matrix and a^e is the vector of nodal temperature. Then, the weak form of governing differential equation was derived using Gauss–Green theorem and the above interpolation function together with the natural boundary conditions was considered in the weak formulation as below.

$$ \left( {\int {\left[ {\frac{{\partial N^{\text{T}} }}{\partial x}k\frac{\partial N}{\partial x} + \frac{{\partial N^{\text{T}} }}{\partial y}k\frac{\partial N}{\partial y} + N^{\text{T}} h_{\text{eff}} N} \right]w{\text{d}}A} } \right)a^{\text{e}} + \left( {\int {N^{\text{T}} \rho c_{\text{p}} N} w{\text{d}}A} \right)\dot{a}^{\text{e}} = \int {N^{\text{T}} \left( {k\frac{\partial T}{\partial n}} \right)w{\text{d}}c} + 2\int {N^{\text{T}} h_{\text{eff}} T_{\text{f}} w{\text{d}}A} $$

(9)

Therefore, the assemblage system equation can be determined as first-order system of differential equation as described below:

$$ Ka + C\dot{a} = f $$

(10)

here K is the stiffness matrix, C is the capacitance matrix, and f describes the nodal force. Eventually, the above system of equations was solved using the central difference scheme. Note that in the finite element formulation, four-node isoparametric element was used and also Gauss–Legendre quadrature was utilized for determination of stiffness and capacitance matrices and nodal vector.

According to the above-mentioned solution and the rate equation related to recrystallization, a code in MATLAB R2016a was generated, and accordingly, in each time step the temperature distribution within the steel and the progress of recrystallization were predicted. It is worth mentioning that the following stages were considered in the thermal–microstructural modeling:

• 1. Thermo-mechanical modeling of warm rolling

• 2. The initial microstructure is generated based on the results of step #1, and topological transformation is carried out based on the applied strains during rolling

• 3. Temperature field during subsequent recrystallization is predicted in each time step

• 4. At high temperatures where recrystallization is operative, the nucleation probability is determined and the stable nuclei are formed.

• 5. Normal vector for each grain is calculated

• 6. Time step and growth probability are determined by calculating the highest boundary velocity during the growth process

• 7. Grains growth is made using the modified Moore neighborhood

• 8. Return to step #4 and the calculations are repeated. This continues until the recrystallization is finished as described earlier.

Experimental Procedures

In this work, AISI 304L stainless steel with the chemical composition of 0.02%C, 1.5%Mn, 17.9%Cr, 8.5%Ni, 0.03%Mo, 0.027%Cu, 0.37%Si, and balanced Fe (in wt%) was examined. The as-received plate with the thickness of 4 mm was first cut into samples with the dimensions $115 \times 45 \times 4$ (in mm), and then, they were subjected to high-temperature annealing at 1000 °C for 30 min for eliminating the influence of previous plastic straining.

Rolling and Mechanical Testing

After initial annealing, the rolling experiments were made at different reductions at 200 °C. The samples were first heated up to 200 °C and held at this temperature for 30 min. Then, the rolling was carried out, while for the case of multi-pass rolling the samples in inter-pass sections were heated for 150 (s) at 200 °C to balance the temperature drop in pervious each rolling stand. The details of the experiments are given in Table 1. Also, to determine the flow stress behavior of the rolled steel, tensile testing was carried out according to ASTME8 subsize. The testing was made at room temperature with constant cross-head speed of 2 mm/min. Furthermore, the annealed specimens were examined under different cross-head speeds of 1, 2, 10, and 100 mm/min to evaluate the impact of strain rate on flow stress behavior of 304L stainless steel.

Table 1 The conditions used in the experiments

Static Recrystallization After Rolling

After rolling operations some of the samples were annealed at different temperatures. To do so, non-isothermal recrystallization treatments were carried out on samples B and C according to Table 1. For this purpose, the specimens were cut from the rolled plate with the width of 10 mm and heated in a furnace with temperatures ranging between 500 and 830 °C, while the specimens were held for 3 min to 30 min. After that, Vickers hardness measurements were taken to define the mechanical properties and softening fraction occurred during heat treatment. The fraction of softening was computed as [28, 31].

$$ X_{\text{rex}} = \frac{{H - H_{0} }}{{H_{\text{full}} - H_{0} }} $$

(11)

where Hand H₀ denote hardness of the partially recrystallized and deformed steel, respectively, and H_full is the hardness for the full-annealed condition.

Experimental Measurement of Temperature Variations

In the other set of experiments, the experimental time–temperature diagrams were determined during annealing heat treatments, and then, the effective convection coefficient used in Eq. [8] was defined based on the recorded diagrams. In this regard, a K-type thermocouple was connected to data logger having the recoding capacity of 1 Hz and the thermocouple was embedded in a drilled hole on one side of the plate being heated. Using the experimental time–temperature diagrams and the results of the thermal model, the effective convection coefficients at different temperatures were determined, and by the least-square interpolation technique, the effective convection coefficient was defined as a furnace temperature. The result of interpolation procedure is given below.

$$ h_{\text{eff}} = (4 \times 10^{ - 5} )T^{2} + 0.0493 T + 25.609\;({\text{W/m}}^{2} \;^{ \circ } {\text{C}}) $$

(12)

Additional rolling operations were conducted for determination of temperature variations within the rolling steel. At first, a hole having the diameter of 1.5 mm was made on one side of the examined plate and the thermocouple was embedded. Afterward, the sample was held in the furnace for 30 min and single-pass rolling with the reduction of 20% and rolling speed of 40 rpm was performed during which the temperature variations were recorded with the rate of 1 Hz. In this set of experiments, the initial temperatures of 200 °C and 280 °C were examined, and accordingly, the time–temperature diagrams related to the center of the rolling plate were determined experimentally.

Microstructural Observation

Microstructural evolutions using optical microscopy were also performed utilizing an etchant containing 10 ml of HCl, 15 ml of HCOOH, and 10 ml of HNO3. ImageJ software was used to evaluate average grain size and grain distribution. Also, the martensite fraction was measured with a Ferritescope (Helmut Fischer GmbH). The measurements were taken at different positions on the specimen surface to assess the volume fraction of the produced martensite after tensile testing as well as to assure there is no evidence of martensite in the specimens after warm working.

Results and Discussion

Microstructural and Mechanical Properties

Figure 2 displays the microstructure of the annealed sample. It is observed that the microstructure contains the equiaxed grains with mean diameter of about 41 μm, associated with thermal twinning that has been formed during initial annealing heat treatment as indicated in the figure. Note that similar results were reported in the other work [32]. In addition, stress–strain diagrams show different stages including a low rate hardening followed by a rapid strain-hardening stage regarding Fig. 2b. This phenomenon is attributed to the formation of martensite during plastic straining [3]. However, it should be noted that the regular strain-hardening behavior, i.e., parabolic diagrams instead of sigmoidal-type hardening, is achieved under higher strain rates. This can be reasonably explained based on adiabatic heating producing at higher strain rates which suppresses the formation of strain-induced martensite. The evidence of martensite can also be detected in Ferritescope measurements carried out on the samples after tensile testing. It is seen that the martensite content reached about 50% after deformation under the lowest strain rate. Figure 3a displays the stress–strain diagrams of the single- and multi-pass rolled samples, i.e., samples A, B, C, D, and E, and Fig. 3b shows the variations of hardness and yield stress of the rolled samples as a function of applied strain. As expected, it is seen that the amount elongation is reduced and the yield stress increases at higher reductions. Note that the yield stress reaches over 950 MPa in sample E, while in samples D and E, that failure occurs after considerable deformation after necking. This may be attributed to the occurrence of martensite transformation that allows further deformation in the samples. In other words, the formation of strain-induced martensite retards fracturing due to localization yielding by forming a diffused-necking region.

Fig. 2

a As-annealed microstructure of the examined steel, b stress–strain diagrams of the annealed sample under different tensile speeds

Fig. 3

a Stress–strain diagrams of the as-rolled samples, b hardness and yield stress after different reductions

Figure 4 illustrates the flow stress behavior of double-pass rolled samples annealed at 800 °C for different durations. Similar to as-annealed samples, at the first stage of diagrams, work hardening is the main strengthening mechanism. The high rate of strain-hardening demonstrates the occurrence of strain-induced martensite transformation. Figure 4b depicts the effect of recrystallization time on mechanical properties of the steel. In general, it is found that that hardness and yield stress drop with increasing duration of static recrystallization due to formation and growth of strain-free nuclei which replace the original deformed matrix [31].

Fig. 4

a Stress–strain diagrams of the annealed sample at 800 °C and different durations, b hardness and yield stress in sample B after different annealing times at 800 °C

Calibration and Validation of the Model

To verify the results of the thermo-mechanical model, time–temperature diagrams were utilized. However, a set of data were first employed to assess proper thermo-physical parameter at metal/roll contact region and the other set of results was used for verifying the simulation data. Accordingly, the heat convection coefficient of 16,000 (W/m² °C) was obtained regarding the experimental data achieved for rolling at 200 °C. After that, a comparison was made between the simulated and the measured temperatures for rolling at 280 °C as displayed in Fig. 5. As seen, there is a good consistency between these data indicating the thermo-mechanical models work properly. It should be noted that Md30/50 temperature, i.e., the temperature at which 50% martensite is formed by applying equivalent strain of 0.3, was calculated by means of the equation given in Ref. [33]. The calculation showed that this temperature is about 27 °C that is much lower than the employed rolling temperature. Furthermore, Ferritescope measurements showed no evidence of martensite formation before and after rolling. Thus, the subsequent recrystallization takes place in austenitic state. Also, the stacking fault energy of the examined steel is computed about 19.8 (mJ m⁻²) which is considered as low value [34]. Therefore, cross-slip of dislocations and recovery becomes more difficult and the main softening process during high annealing can be assumed as a result of static recrystallization [35]. Note that in multi-pass rolling shear stress between the work rolls and the rolling strip causes non-uniform equivalent strain distribution as shown in Fig. 1. Hence, the stored energy and the kinetics of static recrystallization would be varied at different positions of the rolled plate. Besides, Fig. 6 shows distribution of equivalent plastic strain along the thickness in different samples. As the rolling reduction increases, the higher gradient of plastic strain is produced. This is attributed to accumulative effect of shear strains at the surface region. The shear strains were generated owing to the geometry of deformation zone together with the friction at contact region. Thus, it is expected that the kinetics of static recrystallization would be faster at the surface regions having higher amount of stored energy.

Fig. 5

Comparing predicted and measured temperature variations for single-pass rolled plate at 280 °C

Fig. 6

Distribution of equivalent plastic strain along the thickness direction predicted by the thermo-mechanical model

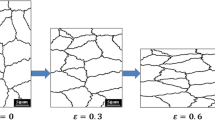
Figure 7a displays the volume fraction of softening achieved after 10 min at different temperatures. Figure 7b shows time–temperature diagrams at different furnace temperatures. As seen, although the material was annealed for 10 min at lower temperatures, i.e., 500 and 600 °C, a trivial fraction of softening can be detected. Therefore, the temperature for start of recrystallization was taken about 700 °C in which the rate of softening became considerable. In the next step, the results of static recrystallization of double-pass rolled sample at 800 °C were considered for definition of material constants. In the first place, a proper microstructure, the as-rolled microstructure, consists of elongated austenite grains and was provided using the results of the thermo-mechanical modeling and Eq. 3, as shown in Fig. 8. In the next step, a calibration process was made to obtain the proper material constants. The experimental recrystallization kinetics and the produced microstructures were used, and based on this procedure, the activation energies for nucleation and growth were defined as listed in Table 2. For instance, Fig. 9 compares the microstructure of sample B at the surface region and the predicted one which shows a good agreement. Afterward, sample C was annealed at 750 °C and 830 °C in order to verify the predictions. Figure 10 compares the real microstructure and the predicted one annealed at 830 °C for 10 min. It can be seen that the microstructure mostly replaced by strain-free equiaxed austenite grains. The surface mean grain size was considerably decreased from 38 μm to 18 μm in sample B after 10 min of heat treatment at 800 °C, while the predicted grain size is of about 16.5 μm. Note that this considerable grain refinement during static recrystallization is attributed to high recrystallization temperature and large stored energy leading to relatively high rate of nucleation as indicated in Eqs. 4 and 5. It should be mentioned that the measured and predicted mean grain sizes were achieved as 12.2 μm and 13.6 μm for the case of recrystallization at 830 °C. Figure 11 displays the experimental and predicted progress of static recrystallization at the surface of samples C and B under non-isothermal circumstances. Regarding the figure and the achieved data, it can be concluded that there is a reasonable agreement between the experimental data and simulated results showing the validity of the utilized models and the developed algorithm.

Fig. 7

a Effect of annealing temperature on softening fraction, b time–temperature diagrams for different furnace temperatures

Fig. 8

Comparing experimental and generated initial microstructure for sample B at the surface region, a real microstructure, b generated grain structure

Table 2 Cellular automata parameters of the examined 304L stainless steel

Fig. 9

Comparing predicted and experimental microstructure at surface region of sample B, annealed for 10 min at 800 °C, a real microstructure, b predicted microstructure

Fig. 10

Comparing predicted and experimental microstructure at surface region of sample C, annealed for 10 min at 830 °C, a real microstructure, b predicted microstructure

Fig. 11

Measured and predicted softening fractions during non-isothermal annealing at surface region of samples B and C

The Impact of Processing Parameters

Given the kinetics rules, it is expected that the recrystallization kinetics increases at higher temperatures. This fact can be detected from Fig. 11 where the incubation time is reduced and at the same time the rate of recrystallization increases dramatically at 830 °C. Figure 12 displays the kinetics of isothermal and non-isothermal recrystallization at 750 °C. As shown, isothermal recrystallization becomes faster and finer grains were produced because of the higher nucleation rate, while under non-isothermal condition, the growth process reduces the possibility of further nucleation during heating stage.

Fig. 12

a Comparing the kinetics of recrystallization under isothermal and non-isothermal conditions at surface region of sample B at 750 °C, b predicted microstructure of sample B under isothermal condition, c predicted microstructure of sample B under non-isothermal condition

Different processing parameters such as initial plastic strain, the heating rate, and recrystallization temperature can affect the rate of nucleation and governing driving force for recrystallization as mentioned in Eqs. 4 and 5. Non-isothermal softening diagrams at the surface region obtained for different reductions and temperatures are presented in Fig. 13. It is observed that at higher reductions, the progress of recrystallization becomes faster due to higher stored energy. The higher recrystallization temperature also leads to much faster rate of recrystallization, and at the same time, the incubation time decreases significantly. This is attributed to the larger heating rate associated with higher recrystallization, affecting both nucleation rate and the velocity of recrystallized boundaries [7, 9]. The impact of heating rate at a given furnace temperature is shown in Fig. 14. In low heating rate, the time required to reach the onset of recrystallization temperature is much longer, while the rate of nucleation is considerably low; thus, the process of growth of stable nuclei would be the rate-control mechanisms as compared to nucleation. On the other hand, the rate of recrystallization increases under high heating rate where the nucleation becomes faster and as a result a fine grain structure is achieved comparing Fig. 14b, c. The grain size distribution at these two heating rates could also be seen in Fig. 15a; the more nuclei number and negligible growth at higher heating rate lead to formation of finer grain sizes. Another point to consider is that the narrower curve at the higher heating rate is attributed to higher nucleation probability that activates homogeneous nucleation process. However, the driving force for nucleation at the lower heating rate is not enough to let embryos become stable inside the grains. The similar results have also been reported in other works [36].

Fig. 13

a Rate of non-isothermal recrystallization after different reductions, b rate of non-isothermal recrystallization for sample B for different furnace temperatures

Fig. 14

a Time–temperature diagrams and recrystallization progress under different heating rates, b predicted fully recrystallized microstructure for h_eff of 120 (W/m² °C), c predicted fully recrystallized microstructure for h_eff of 30 (W/m² °C)

Fig. 15

Grain size distribution fitted by Gaussian function at softening fraction of 0.97, a at two different heating rates, h_eff 120 and 30 (W/m² °C), b at two different prestrains, i.e., samples A and D

Note that by means of Figs. 13 and 14, the time required for start and finish of non-isothermal static recrystallization regarding the heating pattern in the furnace can be defined and also the final microstructure could be produced by imposing a proper heating input. Figure 16 displays microstructural changes at the surface regions of samples A and D during non-isothermal recrystallization at 830 °C. For the case of low strains, i.e., sample A, the nuclei mainly developed on grain boundaries, namely heterogeneous nucleation, occur in this sample; however, in sample D, both homogenous and heterogeneous nucleation mechanisms are operative owing to high amount of stored energy. Figure 15b shows the predicted grain size distribution in these samples. The figure illustrates two main points. Firstly, the higher prestrain, the finer structure produces due to higher stored energy. Secondly, the width of Gaussian curve contracts in sample D displaying more homogeneous structure since stored energy in higher prestrains let recrystallization occur on the grain boundary and grain boundary junctions as well as inside the grains.

Fig. 16

The microstructural changes during non-isothermal recrystallization in samples A and D with furnace temperature of 830 °C, a after 150 s, b after 300 s, c after 400 s, d after 1000 s

Figure 17 illustrates the rate of recrystallization at the surface and center of sample E as well as the produced microstructures in central and surface regions. It is observed that the non-uniform distribution of plastic strain affects the rate of recrystallization and the final microstructures in which higher rate of recrystallization and finer grain size are produced at the surface of the steel being recrystallized. It should be mentioned this non-uniformity is more profound for the case of multi-pass rolled steel owing to the accumulative effect of strain strains as shown in Fig. 6.

Fig. 17

a Comparing the kinetics of recrystallization at the surface and center of sample E, non-isothermally annealed at 750 °C, and h_eff of 90 W/m² °C, b predicted microstructure in surface region, c predicted microstructure in central region

Conclusions

A combined finite element–cellular automata modeling was developed to predict microstructural changes during non-isothermal heat treatment of 304L stainless steels. The samples were first warm rolled at 200 °C under single- and multi-pass rolling programs. Then, the rolled samples were subjected to non-isothermal recrystallization in the range of 500 °C to 830 °C. In order for simulation of these operations, various types of modeling were employed to properly predict the material behavior. In the first place, a thermo-mechanical simulation of multi-pass warm rolling was made to assess the stored energy and its distribution within the rolled plate, while the achieved data were utilized as the initial conditions for the microstructural–thermal model. Regarding the experiments and the results of the model, it was found that:

• 1. A good consistency was found between the real and the predicted data showing that proper assumptions and algorithms were made.

• 2. The recrystallization temperature was defined of about 700 °C, and the activation energies for nucleation and growth for recrystallization were defined as 180 kJ/mol and 240 kJ/mol.

• 3. During multi-pass rolling operation, a gradient of plastic strain was produced between the surface and the central region of the rolled plate leading to different rate of subsequent recrystallization.

• 4. The microstructural model was applicable for low and high levels of plastic straining in which both types of nucleation processes, i.e., heterogeneous and homogeneous nucleation, were considered in the simulation. The results indicated that after the third rolling pass, the homogenous nucleation is possible to occur that resulted in more significant grain refining during subsequent recrystallization.