1 Introduction

With the requirement of fuel efficiency and reduction in CO2 emissions, light weight alloys have attracted more and more attention in recent years. Due to their high strength-to-weight ratio, magnesium and titanium alloys offer a great potential to reduce weight, thus being widely used in electronic devices, aerospace industry, etc. [7–9]. Most of these components were produced by sheet metal forming processes. The ability of sheet metal to deform into desired shape without local necking or fracture is defined as formability. Therefore, understanding and characterizing the formability of metal sheets is of key importance for controlling final product quality and then evaluating the success of the sheet forming operation.

The formability of sheet metals is commonly evaluated using a forming limit curve (FLC), a curve defining maximum allowable strain levels during sheet metal forming, which became a standard tool for assessing and representing the formability of sheet metals. The FLD is experimentally determined by two main kinds of forming methods under different proportional loading paths, like out-of-plane stretching, and in-plane stretching. However, the experimental testing and grid strain measurement procedure is costly, time-consuming and requires both experience and attention in order to determine accurate forming limits. Therefore, analytical/theoretical methods have already attracted more and more attention to predict the forming limit in sheet metal forming. In decades, based on different failure criteria, various theoretical/analytical methods have been developed and employed by different researchers to predict the forming limits of sheet metals, such as the Swift diffuse necking models [10], the Hill [11] localized necking model, the M–K inhomogeneous model [12] and the bifurcation theory [13], perturbation theory [14], modified maximum force criterion (MMFC) [15]. One of the most widely used approaches is the well-known Marciniak–Kuczynski (M–K) model. The M–K model predicts the FLD based on the assumption of an initial defect in perpendicular direction with respect to loading direction. The presence of such defect causes strain localization leading to failure. It was shown that forming limit curves are influenced by material work-hardening exponent and anisotropy coefficient. Within the M–K framework, the influence of various constitutive features on FLDs has been explored using phenomenological plasticity models. Butuc et al. [16] studied the forming limits diagrams for aluminum alloy AA6016-T4 and successfully gave good predictions with Voce hardening law. Bong et al. [17] performed a series of modified Marciniak test and conventional ASTM standard tests to determine the FLD for ferritic stainless steel sheets; after that a conventional M–K model was implemented to predict and compare with the FLD determined experimentally. Results shown that the FLD calculated with this modified model was in good agreement with the measured data for both thin and thick steel sheets. However, most of these researches [2, 3] were used to study the formability of materials with bcc or fcc crystal structure, such as aluminum alloy, steel. However, hexagonal closed packed (HCP) crystallographic structure demonstrates its different mechanical behaviors from other metals with fcc and bcc structures. At room temperature, the activation of twinning plays an important role to accommodate the deformation. The polar nature of deformation twinning promotes a strong asymmetry between yielding in tension and compression, usually known as strength differential effect (SD). Naka et al. [18] adopted Barlat yield criterion to capture the effect of strain rate, temperature and sheet thickness on yield locus of AZ31 magnesium alloy sheets. Cazacu et al. [6] introduced a macroscopic orthotropic yield criterion for HCP materials and described very well the yield asymmetry between tension and compression and anisotropy.

In this study, a generic MATLAB script was developed within the M–K theory framework. The influence of asymmetrical effect on the strain path and formability is discussed. Moreover, the initial imperfection, different hardening laws and yield criteria are also being investigated.

2 Theoretical Modeling and Formability Prediction

2.1 Description of the Marciniak–Kuczinsky (M–K) Model

The Marciniak–Kuczinsky (M–K) analysis in the framework of heterogeneous materials introduced by Marciniak and Kuczynski [12] has become one of the most common theoretical approaches for calculating the FLC of sheet materials.

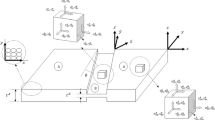
Sheet materials are initially inhomogeneous due to the presence of micro-voids or the roughness at the surface of the sheet. Marciniak and Kuczynski modeled this material inhomogeneity in a sheet as a geometric band with a slightly reduced thickness compared to the rest of the sheet. According to this hypothesis, non-defective zone (region a) and groove zone (region b) are the two regions of the sheet metal should be distinguished, as shown in Fig. 1. The ratio f is used to describe the amplitude of the imperfection. The initial value of the geometrical defect is characterized by the ratio \(f_{0} = t_{0}^{\text{b}} /t_{0}^{\text{a}}\) where \(t_{0}^{\text{a}}\) and \(t_{0}^{\text{b}}\) are the initial thickness in the homogeneous region and in the groove, respectively. This initial inhomogeneity grows continuously with plastic straining to form eventually a localized neck. The x, y and z axes correspond to rolling, transverse and normal directions of the sheet, whereas 1 and 2 represent the principal stress and strain directions in the homogeneous region. The set of axis bound to the groove system is represented by n, t and z axes where ‘t’ is the transverse one. This two-zone material is subjected to constant incremental plastic deformation, the plastic flow occurs in both regions, but the evolution of the strain rates is different in the two zones. The homogeneous region is subjected to proportional strains; meanwhile, the deformation in groove region is close to plane strain. When the flow localization occurs in the groove at a critical strain in homogeneous region, the limiting strain of the sheet is reached.

Fig. 1
figure 1

Schematic diagram of M–K analysis [19]

Full size image

Throughout this section, the sheet metal is considered to behave as an orthotropic membrane under the plane stress conditions; thus, the stress component in the third direction is vanished. The constraints written are valid both for region a and region b. We also assume that the sheet metal is subjected to loads which do not produce tangential stresses and strains in the plastic orthotropic frame:

$$\sigma_{12}^{\text{a}} = 0,\quad \varepsilon_{12}^{\text{a}} = 0.$$
(1)

2.1.1 Computation of Stress and Strain in Homogeneous Region a

The mechanical response of the sheet metal will be described by a rigid-plastic model. Hence total strains and total strain increments are equal to the corresponding plastic strains and plastic strain increments, respectively. Given the strain history from the previous step, the effective strain increment at current step, strain path (stress path), stress, strain, strain increment in region a can be calculated. The main ingredient of the constitutive model is the yield function:

$$\sigma_{\text{eq}}^{\text{a}} \left( {\sigma_{1}^{\text{a}} ,\sigma_{2}^{\text{a}} } \right) - Y\left( {\bar{\varepsilon }^{\text{a}} } \right) = 0,$$
(2)

where Y represents the equivalent stress and is calculated from the hardening law.

The plastic strain increments in the rolling and transverse directions can be computed by the associated flow rule

$$\Delta\varvec{\varepsilon}^{\text{a}} = \Delta\varvec{\gamma} \frac{{\partial \sigma_{\text{eq}}^{\text{a}} }}{{\partial\varvec{\sigma}^{\text{a}} }},$$
(3)

also, by using of the rotation matrix, strain increment tensor is obtained at the groove system of coordinates. Due to the incompressibility constraints, the strain increments though the thickness can be calculated by

$$\Delta \varepsilon_{3}^{\text{a}} = -\Delta \varepsilon_{1}^{\text{a}} -\Delta \varepsilon_{2}^{\text{a}} .$$
(4)

The stress ratio α is defined as

$$\alpha = \frac{{\sigma_{22} }}{{\sigma_{11} }}.$$
(5)

Given the effective strain, it can be coupled with the yield function to calculate the stress tensor under prescribed stress path in the orthotropic referential frame of anisotropy as

$$\left\{ {\begin{array}{*{20}l} {\sigma_{11} = f\left( \alpha \right)Y\left( {\bar{\varepsilon }^{\text{a}} } \right)} \hfill \\ {\sigma_{22} = \alpha \sigma_{11} } \hfill \\ \end{array} } \right..$$
(6)

The strain rate ratio β is given by

$$\beta = \frac{{\dot{\varepsilon }_{22} }}{{\dot{\varepsilon }_{11} }}.$$
(7)

For a given yield function, it is essential to know the correlation between stress ratio α and the strain rate ratio β. Considering that the principal anisotropy axes of orthotropic symmetry are coincident with the principal axes of stress in the homogeneous region a, according to the associated flow rule, the strain ratio can be calculated by

$$\beta = \frac{{\dot{\varepsilon }_{22} }}{{\dot{\varepsilon }_{11} }} = \frac{{{{\partial \sigma_{\text{eq}}^{\text{a}} } \mathord{\left/ {\vphantom {{\partial \sigma_{\text{eq}}^{\text{a}} } {\partial \sigma_{22} }}} \right. \kern-0pt} {\partial \sigma_{22} }}}}{{{{\partial \sigma_{\text{eq}}^{\text{a}} } \mathord{\left/ {\vphantom {{\partial \sigma_{\text{eq}}^{\text{a}} } {\partial \sigma_{11} }}} \right. \kern-0pt} {\partial \sigma_{11} }}}}.$$
(8)

2.1.2 Computation of the Stress and Strain in Groove Region b

After all the stress component, strain components, and strain increment component in homogeneous region a are obtained, all the stress, strain variables in the grooved region b can be calculated according to the requirement of force equilibrium and geometry compatibility between homogeneous region and groove region.

The force equilibrium condition, indicating equivalence of force perpendicular to the necking band in homogeneous region a and groove region b conforms to:

$$\sigma_{\text{nn}}^{\text{a}} t^{\text{a}} = \sigma_{\text{nn}}^{\text{b}} t^{\text{b}} ,$$
(9)
$$\sigma_{\text{nt}}^{\text{a}} t^{\text{a}} = \sigma_{\text{nt}}^{\text{b}} t^{\text{b}} ,$$
(10)

where σ nn and σ nt are components of stress tensor in the groove reference frame, while t a and t b are the sheet thickness outside and the inside the groove, respectively, given by

$$t^{\text{a}} = t_{0}^{\text{a}} \exp \left( {\varepsilon_{3}^{\text{a}} } \right),$$
(11)
$$t^{\text{b}} = t_{0}^{\text{b}} \exp \left( {\varepsilon_{3}^{\text{b}} } \right).$$
(12)

Imperfection factor f is characterized by the ratio t b/t a and is expressed as a function of the initial defect and strain difference through the thickness between these two regions:

$$f = f_{0} \exp \left( {\varepsilon_{3}^{\text{b}} - \varepsilon_{3}^{\text{a}} } \right),$$
(13)

where f 0 is the initial imperfection factor, which has an important influence on the predicted limit strains.

The geometry compatibility requirements assume that the elongation in the direction of the necking band is identical in both regions:

$$\Delta \varepsilon_{\text{tt}}^{\text{a}} =\Delta \varepsilon_{\text{tt}}^{\text{b}} .$$
(14)

Moreover, the deformation in the groove region should also meet the requirement of yield function as follows

$$\sigma_{\text{eq}}^{\text{b}} \left( {\sigma_{11}^{\text{b}} ,\sigma_{22}^{\text{b}} ,\sigma_{12}^{\text{b}} } \right) - Y\left( {\bar{\varepsilon }^{\text{b}} } \right) = 0.$$
(15)

Generally, the imperfection band can be randomly oriented in the sheet metal and this orientation can be specified with the angle θ between the groove axis and the direction of the second principal stress (Fig. 1). The rotation of the groove was considered in this work using the following empirical formula proposed by Sing and Rao [20]:

$$\tan \left( {\theta + \Delta \theta } \right) = \tan \left( \theta \right)\frac{{1 +\Delta \varepsilon_{1}^{\text{a}} }}{{1 +\Delta \varepsilon_{2}^{\text{a}} }},$$
(16)

where \(\Delta \varepsilon_{1}^{\text{a}}\) and \(\Delta \varepsilon_{2}^{\text{a}}\) are the major and minor principal strains in the nominal area of the sheet, respectively.

Equation (16) implies that the orientation of the imperfection band will vary during deformation due to the in-plane plastic strains, and angle θ can be updated at each plastic strain increment.

For any constant value of stress ratio α, by changing angle θ, between 0° and 90°, minimum value of major localization strain is found. This minimum value and its corresponding minor strain are defined as point in the FLD.

2.1.3 Necking Criteria

Due to the initially slightly smaller thickness of the groove compared to the homogeneous region, the strain will become more and more concentrated within the groove. In order to predict the onset of necking, the sheet is subjected to a uniform stress state. As plastic deformation progresses, the difference in strain rate between the two regions will intensify and eventually the strains will localize in the imperfection region. M–K necking criteria in this paper assumes that the plastic flow localization occurs when the equivalent strain increment in imperfect region b becomes more than ten times greater than in homogeneous zone a \(\left( {\Delta \bar{\varepsilon }^{\text{b}} > 10\Delta \bar{\varepsilon }^{\text{a}} } \right)\). When this necking condition is reached, the computation terminates and the corresponding strains \(\left( {\varepsilon_{1}^{\text{a}} ,\varepsilon_{2}^{\text{a}} } \right)\) and stresses \(\left( {\sigma_{1}^{\text{a}} ,\sigma_{2}^{\text{a}} } \right)\) accumulated at that moment in the homogeneous zone represent the limit strains and limit stresses, respectively.

2.2 Yield Function

Plasticity theory deals with yielding of materials under complex stress states. It is used to decide whether or not a material will yield under a stress state and determine the shape change that will occur during yielding. Many phenomenological plastic models for materials have been proposed [21, 22]. The major yield functions used in this paper are the follows.

2.2.1 von Mises Yield Criterion

The von Mises stress is often used in determining whether an isotropic and ductile metal will yield when subjected to a complex loading condition [23]. The von Mises yield criterion is expressed as:

$$\sigma_{\text{eq}} = \sqrt {\frac{{\left( {\sigma_{11} - \sigma_{22} } \right)^{2} + \left( {\sigma_{22} - \sigma_{33} } \right)^{2} + \left( {\sigma_{11} - \sigma_{33} } \right)^{2} + 6\left( {\sigma_{12}^{2} + \sigma_{23}^{2} + \sigma_{13}^{2} } \right)}}{2}} .$$
(17)

2.2.2 Hill Yield Criterion

Because of its simplicity and good accuracy, Hill’s [24] yield criterion has been widely used to predict the behavior of orthotropic steel sheets. This quadratic yield function only requires a limited number of mechanical properties to determine the shape of the yield locus: under plane stress conditions, only three parameters are sufficient, namely the plastic anisotropy coefficients in the rolling (R 0), diagonal (R45) and transverse (R 90) directions.

$$2\sigma_{\text{eq}} = \left[ {F\left( {\sigma_{22} - \sigma_{33} } \right)^{2} + G\left( {\sigma_{33} - \sigma_{11} } \right)^{2} + H\left( {\sigma_{11} - \sigma_{22} } \right)^{2} + 2L\sigma_{23}^{2} + 2M\sigma_{13}^{2} + 2N\sigma_{12}^{2} } \right]^{1/2} ,$$
(18)

where F, G, H, L, M, N are material parameters. In the case of isotropy

$$L = M = N = 3F = 3G = 3H.$$
(19)

This criterion is restricted to materials with orthotropic physical symmetry, i.e., to those with three mutually orthogonal symmetry planes. These can generally be inferred from the symmetry of the strain path employed to produce the anisotropy. The constants can be calculated with three tensile tests.

2.2.3 Barlat Yield Criterion

Barlat and Lian [25] proposed a non-quadratic yield function to model the behavior of orthotropic metallic sheets (typically rolled materials) under plane stress. Unlike the above mentioned yield criteria, this model is restricted to plane stress conditions. The corresponding yield function, written at the outset exclusively in terms of in-plane components of the stress tensor, reads

$$2\sigma_{\text{eq}}^{M} = a\left| {K_{1} + K_{2} } \right|^{M} + a\left| {K_{1} - K_{2} } \right|^{M} + c\left| {2K_{2} } \right|^{M} ,$$
(20)

where K 1, K 2 is described as

$$K_{1} = \frac{{\sigma_{\text{xx}} + h\sigma_{\text{yy}} }}{2};\quad K_{2} = \sqrt {\left( {\frac{{\sigma_{\text{xx}} - h\sigma_{\text{yy}} }}{2}} \right)^{2} + b^{2} \sigma_{\text{xy}}^{2} } .$$
(21)

The formulation is expressed in an x, y, z coordinate system, not necessary coincident with the principal directions. The included constants a, h and b are calculated from relations based on the measured r values at rolling, transverse and 45° orientations.

2.3 Cazacu06 Yield Criterion [6]

To extend isotropic yield function to orthotropic, a 4th order linear transformation is operated on the stress deviator S to obtain the transformed tensor \(\varvec{\Sigma }\), which can be defined as

$$\varvec{\Sigma } = {\mathbf{L}}\varvec{S}\text{,}$$
(22)

where L is a 4th order tensor, which includes nine independent anisotropy coefficients, It is worth noting that although the transformed tensor is not deviatoric, the orthotropic criterion is insensitive to hydrostatic pressure and thus the condition of plastic incompressibility is satisfied. It can be written as 6 × 6 matrix format as

$$\left[ {\begin{array}{*{20}l} {\Sigma_{11} } \hfill \\ {\Sigma_{22} } \hfill \\ {\Sigma_{33} } \hfill \\ {\Sigma_{12} } \hfill \\ {\Sigma_{23} } \hfill \\ {\Sigma_{13} } \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {{\text{L}}_{11} } \hfill & {{\text{L}}_{12} } \hfill & {{\text{L}}_{13} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {{\text{L}}_{12} } \hfill & {{\text{L}}_{22} } \hfill & {{\text{L}}_{23} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {{\text{L}}_{13} } \hfill & {{\text{L}}_{23} } \hfill & {{\text{L}}_{33} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {{\text{L}}_{44} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {{\text{L}}_{55} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {{\text{L}}_{66} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {{\text{S}}_{11} } \hfill \\ {{\text{S}}_{22} } \hfill \\ {{\text{S}}_{33} } \hfill \\ {{\text{S}}_{12} } \hfill \\ {{\text{S}}_{23} } \hfill \\ {{\text{S}}_{13} } \hfill \\ \end{array} } \right].$$
(23)

The orthotropic criterion is of the form

$$\sigma_{\text{eq}} = \left[ {\left( {\left| {\Sigma_{1} } \right| - k\Sigma_{1} } \right)^{\text{a}} + \left( {\left| {\Sigma_{2} } \right| - k\Sigma_{2} } \right)^{\text{a}} + \left( {\left| {\Sigma_{3} } \right| - k\Sigma_{3} } \right)^{\text{a}} } \right]^{{1/{\text{a}}}} ,$$
(24)

where \(\varvec{\Sigma }_1,\,\varvec{\Sigma }_2,\,\varvec{\Sigma }_3\) are the principal values of \(\varvec{\Sigma }\). In order to ensure the convexity of the yield surface, the introduced parameter k should be constrained in the range of k ∈ [−1, 1]. If the transformed matrix L is equal to identity matrix, the proposed formulation can be reduced to the classical von Mises yield criterion.

Since the effective stress σ eq is the first-order homogeneous function in stresses, from the work equivalence principle it follows that the law of evolution for the effective plastic strain (associated with σ eq) reduces to \({\dot{\bar{\varepsilon}}}^{\text{p}} = {\dot{\gamma}}\).

2.4 Hardening Law

During the plastic deformation process, the shape of the material changes and shows increased amount of strength properties, hence called as strain hardening. Each material is completely defined macroscopically by its yield surface and its work-hardening law \(Y\left( {\bar{\varepsilon }} \right)\), which in present work takes two forms:

2.4.1 Swift Law [10]

The strain hardening of the material was defined using a power law function that considers the strain rate sensitivity of the material:

$$Y = K\left( {\bar{\varepsilon } + \varepsilon_{0} } \right)^{n} ,$$
(25)

where ε 0 is the initial uniform strain applied to the sheet, n is the strain hardening coefficient, Y and \(\bar{\varepsilon }\) are the effective stress and strain, respectively.

2.4.2 Você Law [26]

The hardening equation corresponding to Você law takes the form

$$Y = A + B\left( {1 - e^{{ - C\bar{\varepsilon }}} } \right),$$
(26)

where A, B, C are the material parameters identified by the related tensile test; \(\bar{\varepsilon }\) denotes the equivalent plastic strain.

Each material constant in the above hardening law can be calibrated by fitting experimental stress/strain data. A comparison between the two identified hardening laws is plotted in Fig. 2. In this figure, it can be seen that the very good correlation between the two methods and the experimental values for an equivalent strain value is between 0 and 10%. For larger values of the equivalent strain, a clear difference appears between the Swift law and the Você law. In the following section, the influence of the choice of the hardening law on the evaluation of the forming limit curves will be discussed.

Fig. 2
figure 2

Tensile stress–strain response

Full size image

3 Results and Discussion

The aim of this section is to investigate the formability of the rolled magnesium alloy sheets AZ31, to compare the predicted and experimental results and to study several influencing effects on the forming limit curve. The mechanical properties associated with selected magnesium alloys are listed in Table 1, and material constants describing the yield functions are shown in Table 2.

Table 1 Material parameters of AZ31B
Full size table
Table 2 AZ31B coefficients corresponding to the yield surface evolution
Full size table

3.1 Relationship Between Strain Rate Ratio β and Stress Ratio α

Figure 3 shows the strain rate ratio β evolution with stress ratio α under different asymmetrical conditions. When k = 0, the yield locus demonstrates elliptical shape. When increasing the magnitude of absolute k value, the asymmetrical effects increase, the yield surface showing tendency to triangular like shape. From Fig. 3, it can be seen that when the stress ratio increases, the strain ratio also increases; however, they have not a linear relationship, particularly when stress ratio is greater than zero. The asymmetrical effect has a great influence on the correlation between strain ratio and stress ratio.

Fig. 3
figure 3

The function β(α) with different k values

Full size image

In order to further investigate the ratio of first principal stress component with respect to equivalent plastic stress, Fig. 4 plots the evolution of function f(α) (Eq. 6) at different asymmetrical effect condition. When the k value changes, not only the maximum value of function f(α) changes, but also the position of stress ratio, where the function f(α) reach its maximum value, alters.

Fig. 4
figure 4

The function f(α) corresponding to the calculated FLD with different k values

Full size image

Figure 5 shows the function g evolution. The function g is the ratio of first principal strain component with respect to effective strain. According to the principle of work equivalence for proportional straining, the function g can be computed by

$$g = f\left( \alpha \right)\left( {1 + \alpha \beta \left( \alpha \right)} \right).$$
(27)
Fig. 5
figure 5

The function g(α) corresponding to the calculated FLD with different k values

Full size image

From the Fig. 5, it can be seen that when k is negative, there is a minimum g value in the whole range of stress ratio. In contrast, when k is positive, the g value shows influence of stress ratio up to a critical value. After this critical value, the g value has a steeply increase.

3.2 FLC Prediction and Effects of the Main Models’ Parameters

Within the M–K framework, the influence of various constitutive features on FLDs has been explored using phenomenological plasticity models. It is now well known that the FLD is very sensitive to effects of yield surface vertices, anisotropy, and the material rate sensitivity. Research has shown that the calculated forming limit strains using M–K analysis depends sensitively on several factors, such as the material anisotropy, the material hardening, the material texture and microstructure and the strain paths. This subsection presents the M–K model used to predict FLCs and some results for different descriptions of the mechanical behavior of the metallic sheet. We analyze the influences on the limits strain of the asymmetrical effect, the initial imperfection intensity, the yield criterion and the hardening to determine M–K performance.

3.2.1 Influence of Asymmetrical Effect

In the Sect. 3.1, it was already observed that the asymmetrical effect has great influence on the strain ratio evolution, f(α) and g functions with stress ratio. It is essential to study the influence of asymmetrical effect on the FLD and forming limit stress diagram (FLSD).

Figures 6 and 7 show the calculated FLD and FLSD, respectively, at different k values, it can be seen that the FLD under different asymmetrical conditions is remarkably different. Compared with the right side of FLD, the forming limit strain distributes in a narrower zone. For FLSD, as the absolute value of k increases, the first principal stress decreases.

Fig. 6
figure 6

Influence of the asymmetrical effect on FLD

Full size image
Fig. 7
figure 7

Influence of the asymmetrical effect on FLSD

Full size image

3.2.2 Influence of Initial Imperfection Factor

The M–K approach predicts the FLD based on the growth of an initial imperfection. However, the strength of the imperfection cannot be directly measured by physical experiments.

Figures 8 and 9 show the influence of the initial thickness ratio f 0 on FLD and FLSD, respectively. Regular shapes of forming limit curve are found from this figure. They demonstrate that with decreasing groove depth (f 0 approaching 1), the level of FLD and FLSD is shifted to the upper values. This parameter extremely affects the FLD and FLSD, particularly initial imperfection factors f 0 > 0.98. It is also seen that shallow initial grooves are sufficient to cause localization in the M–K model. Generally, the value of the initial imperfection factor f 0 is chosen to make the best fit between the predicted and the experimental results and denotes the level of sheet formability. Hence, to characterize the practical formability of a given sheet, an appropriate value of f 0 should be identified.

Fig. 8
figure 8

Influence of the initial imperfection f 0 on FLD

Full size image
Fig. 9
figure 9

Influence of the initial imperfection f 0 on FLSD

Full size image

3.2.3 Influence of Hardening Law

The prediction of forming limits using the MK analysis is based on the classical continuum plasticity theory in which a yield function describes the onset of plastic deformation in stress space and a strain hardening law defines the evolution of the yield locus as plastic deformation progresses. Since both these elements have a profound influence on the prediction of the plastic behavior of metallic materials, it is essential that the prediction of forming limits be based upon the most representative yield criteria and hardening laws. Isotropic hardening is the simplest and most widely used strain hardening rule, and it is well suited to predict the outcome of metal forming processes involving monotonic loading. Therefore, it has been always been used in the MK analysis.

The influence of hardening law is pointed out in Fig. 10 by using two different hardening laws, namely Swift hardening model and Você equation, whereas the same yield function (Cazacu06) is selected to describe the yield locus. Experimental determined FLD of magnesium alloy at room temperature was extracted from Mariusz Boba research work [27]. The analysis with the Você hardening model shows a less steep curve in the left side of FLD. These results show that the forming limit diagrams obtained using Swift hardening law is always higher that those obtained using Você hardening law. The predicted forming limit strain with Você hardening law is in a good agreement with experimental results.

Fig. 10
figure 10

Influence of hardening law on FLD

Full size image

3.2.4 Influence of Yield Criterion

Sheet metal exhibits a highly anisotropic material behavior due to cold rolling. Thus, the description of the yield criterion is of major importance to the accuracy of forming limit prediction by M–K model where localized necking occurs when the strain path has transformed from biaxial stretching to plane strain.

In order to study the influence of yield criterion, four kinds of yield criteria, von Mises, Hill, Barlat89, Cazacu06(CPB06) were implemented into M–K model to calculate theoretical forming limit strain and forming limit stress. Você hardening law has been used. The initial imperfection f 0 is equal to 0.98. Figures 11 and 12 show the comparison of FLD and FLSD calculated with these four different yield criteria. From these calculated FLCs, it is seen that the shape of the yield locus has not a clear distinct influence on the left side of the forming limit diagram, although for FLSD a great difference of forming limit stress is obtained from different yield criteria. Such higher influence on FLSD when using different yield criteria means that, for magnesium behavior, different yield criteria represent very different yield locus surfaces, which in turn will correspond to very different stresses and very different forming limits for stress. As for the lower influence in FLD, this means that different yield criteria, for magnesium behavior, have not so much difference in strain space behavior and evolution, therefore being strain a variable with less sensitivity to yield criteria in this kind of analysis.

Fig. 11
figure 11

Influence of yield criterion on FLD

Full size image
Fig. 12
figure 12

Influence of yield criterion on FLSD

Full size image

4 Conclusions

In the present study, a generic MATLAB script based on the M–K model has been developed to calculate the limiting strains and forming limit stress in sheet metal forming. The effects of initial imperfection intensity and orientation, the asymmetrical effect, the hardening law and the yield locus on the FLD have been accounted for in the M–K analysis. It can generally be concluded that the calculation of the FLD and FLSD is strongly influenced by the selected hardening law, the initial imperfection and the constitutive description. Asymmetrical effect has also a great influence on the mechanical behavior and formability. The predicted FLDs have been compared with experimental data and the agreements between the predicted and measured FLDs show a very efficient developed tool, in which the characteristic shapes of the experimental FLDs are very well matched.