Introduction

As discussed in Part I of this series, the spherical indentation stress–strain protocols offer novel avenues for interrogating the mechanical responses of individual grains in a polycrystalline sample. Although these measurements provided good insights into the role of grain orientation on the single-crystal mechanical response, especially the grain-level anisotropy, the measurements obtained cannot be used directly to inform the values of the material parameters typically found in crystal elastic–plastic theories. This is because most crystal elastic–plastic theories use specific intrinsic single-crystal properties as material parameters. For example, for the α-Ti hcp crystals studied here, the needed single-crystal properties would include the five elastic stiffness parameters,\(\{{C}_{11},{C}_{12},{C}_{44},{C}_{13},{C}_{33}\}\), as well as the slip resistances of the different potential slip systems, \(\{{s}_{\mathrm{pr}},{s}_{\mathrm{ba}},{s}_{\mathrm{pyr}-a},{s}_{\mathrm{pyr}-\mathrm{ca}}\}\). Currently employed strategies for extracting the values of these intrinsic material properties from indentation tests have generally involved the calibration of physics-based finite element (FE) models of these tests to the corresponding set of experimental indentation measurements [1,2,3,4]. It is pointed out that the estimation of intrinsic material parameters is very robust when this calibration is attempted in the form of the normalized indentation stress–strain curves as opposed to directly matching the load–displacement curve [2, 5, 6]. This is because it is very difficult to discern either the elastic loading segment or the initiation of yield directly from the measured load–displacement curves in indentation. In prior work, indentation stress–strain curves were shown to be valuable in reliably extracting the initial slip resistance in a polycrystalline sample of Fe-3%-Si using indentation measurements performed in multiple grains [2].

In recent work [3], a two-step Bayesian framework was demonstrated for the extraction of intrinsic crystal-level elastic properties from indentation measurements in polycrystalline cubic and hcp metal samples. The first step in this protocol established a high fidelity reduced-order (i.e., surrogate) model that took the crystal orientation and the single-crystal elastic stiffness parameters and predicted the indentation modulus (defined in Eq. 1 in Part I of this series). This low-computational cost reduced-order model was established using Bayesian linear regression (BLR) [3, 7, 8] and a training dataset obtained by establishing a suitable physics-based FE model of the spherical indentation test. The second step then calibrated the intrinsic single-crystal properties of interest by matching a collection of experimentally measured indentation moduli for selected grains in a polycrystalline sample with the reduced-order model established in the first step. This second step of the protocol was accomplished using a Markov Chain Monte Carlo (MCMC) [3, 9,10,11] sampling strategy. One of the salient aspects of the proposed two-step Bayesian framework is that it provides an estimate of the uncertainty (quantified as variance) in the estimated crystal level properties. This novel two-step Bayesian framework has thus far been demonstrated only for the elastic stiffness parameters in one cubic metal and in one hcp metal.

In this work, the two-step Bayesian framework described above will be used on the spherical indentation dataset aggregated in Part I of this series. Our goal is to extract the values of both the single-crystal elastic constants, \(\{{C}_{11},{C}_{12},{C}_{44},{C}_{13},{C}_{33}\}\), and the initial values of the slip resistances for the different potential slip families \(\{{s}_{\mathrm{pr}},{s}_{\mathrm{ba}},{s}_{\mathrm{pyr}-a},{s}_{\mathrm{pyr}-\mathrm{ca}}\}\). Furthermore, we will quantify the uncertainties associated with the estimated values for all these parameters. The availability of the indentation dataset covering the broad range of α-Ti compositions studied in Part I of this series offers an unprecedented opportunity for the critical validation of the two-step Bayesian framework described above. Furthermore, this study represents the first application of these protocols for estimating the slip resistances of the different slip families in a single thermodynamic phase (here, hcp α-Ti). The presence of multiple slip families with a high degree of plastic anisotropy in the slip resistances of the different slip families adds significantly to the challenges involved in the establishment of a reliable surrogate model in the first step of the two-step Bayesian framework. Furthermore, the computational cost of the physics-based simulation of the indentation (needed to establish the training data needed to calibrate the reduced-order model) is several orders of magnitude higher when crystal plasticity theories are implemented [12,13,14]. Success in the tasks undertaken critically depends on the development and implementation of a versatile and highly efficient design strategy that optimally selects the inputs for the execution of the very expensive physics-based crystal plasticity simulation of the spherical indentation experiment. Such a strategy is presented and implemented in this study. It is shown that the protocols presented here produce a comprehensive and reliable dataset of single-crystal elastic–plastic parameter values across a collection of α-Ti compositions.

Two-Step Bayesian Framework for the Estimation of Single-Crystal Properties from Indentation Measurements

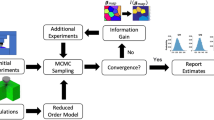
The two-step Bayesian framework utilized in this work is shown schematically in Fig. 1. The first step of the two-step protocol involves the establishment of a reduced-order model that predicts the indentation properties of interest given the grain orientation and the relevant intrinsic single-crystal properties. The crystallographic orientation of a grain relative to the sample frame (associated with the indentation experiment) can be represented by a set of Bunge Euler angles \({\varvec{g}}=\{{\varphi }_{1},\Phi ,{\varphi }_{2}\}\) [15]. Since any rotation about the sample surface normal does not affect the measured spherical indentation properties, it can be seen that the indentation properties are independent of \({\varphi }_{1}\) [15, 16]. Let \({P}_{\mathrm{sim}}^{*}\) denote the simulated indentation property of interest and \({\varvec{p}}\) denote the intrinsic single-crystal properties to be estimated. For the present work, \({\varvec{p}}\) would be set as \(\{{C}_{11},{C}_{12},{C}_{44},{C}_{13},{C}_{33}\}\) for the elastic single-crystal properties and as \(\{{s}_{\mathrm{pr}},{s}_{\mathrm{ba}},{s}_{\mathrm{pyr}-a},{s}_{\mathrm{pyr}-\mathrm{ca}}\}\) for the plastic single-crystal properties, respectively. Likewise, \({P}^{*}\) would be set to the indentation modulus for the elastic properties and to indentation yield strength for the plastic properties, respectively. For both analyses, the reduced-order model to be established in the first step of the two-step framework can then be expressed as:

$${P}_{\mathrm{sim}}^{*}\approx {\widehat{P}}^{*}\left({\varvec{p}},{\varvec{g}}\right)=\sum_{l=0}^{L}\sum_{m=1}^{M(l)}\sum_{{\varvec{q}}}^{{\varvec{Q}}}{A}_{l}^{\mathrm{m}\mathbf{q}}{K}_{m}^{l}\left(\Phi ,{\varphi }_{2}\right)\tilde{P}^{{\varvec{q}}}(\bar{{\varvec{p}}})$$
(1)
$${\stackrel{-}{p}}_{j}=\frac{2{p}_{j}-{p}_{j}^{\mathrm{min}}-{p}_{j}^{\mathrm{max}}}{{p}_{j}^{\mathrm{max}}-{p}_{j}^{\mathrm{min}}}$$
(2)

where \({K}_{m}^{l}\left(\Phi ,{\varphi }_{2}\right)\) denotes the symmetrized surface spherical harmonics (SSH) basis [15] over the relevant orientation space of interest, and \({\stackrel{\sim }{P}}^{{\varvec{q}}}( )\) denotes a multivariate Legendre polynomial product basis. In other words, one can express \({\tilde{ P}}^{{\varvec{q}}}\left(\bar{{\varvec{p}}}\right)={P}^{{q}_{1}}\left({\bar{p}}_{1}\right){P}^{{q}_{2}}\left({\bar{p}}_{2}\right)\dots {P}^{{q}_{R}}\left({\bar{p}}_{R}\right)\), where \({\varvec{q}}={(q}_{1},{q}_{2}\dots {q}_{R})\) forms a multi-index array, each element of which is a nonnegative integer allowed to vary from 0 to the selected maximum degree, \(Q\), i.e., \({q}_{j}\in \left[0,Q\right]\). The use of Legendre polynomials provides an orthonormal basis over the range [-1, 1]. Therefore, each of the single-crystal properties of interest is rescaled in accordance with Eq. 2, where \({p}_{j}^{\mathrm{max}}\) and \({p}_{j}^{\mathrm{min}}\) are the maximum and minimum values of the \(j\)-th property under consideration. In Eq. 1, \(M(l)\) enumerates the spherical harmonics that implicitly reflect the crystal symmetries of interest. Integers Q and L denote the truncation levels adopted in the use of Eq. 1. It should be noted that the model form used in Eq. 1 has been previously shown to produce compact representations for mechanical responses of crystalline solids [2, 3, 17, 18]. The model coefficients, \({\varvec{A}}\), can be trained via BLR using a database of FE simulations of the indentation test [3]. The usage of BLR for building the surrogate model shown in Eq. 1 allows for the estimation of the variance for predictions made for new sets of inputs (i.e., inputs not included in the training set). In fact, the predicted variances can be used to identify specific new inputs for generating additional training points (i.e., additional FE simulations of indentation tests) that maximize the potential for improving the model fidelity and reliability. One of the approaches employed in the literature selects the new training points based on regions of highest predictive variance [3].

Fig. 1
figure 1

Schematic of the Bayesian two-step framework implemented for the extraction of intrinsic material properties via spherical indentation measurements. In the first step, a reduced-order model is established from physics-based finite element models. In the second step, sampling methods are implemented to establish the distributions on the intrinsic material parameters of interest using available experiment indentation measurements

Full size image

This strategy for the optimal design of the training dataset is commonly referred to as a sequential D-optimal design [19,20,21]. During this process, the model coefficients \({\varvec{A}}\) are rigorously tracked as new training data points are added. The systematic convergence of the model coefficients with the addition of the training data points provides objective guidance on when to stop adding new training data points.

The second step of the two-step Bayesian framework used in this work involves the estimation of the intrinsic material properties by calibrating the available measurements on grains of different orientations in a polycrystalline sample to the reduced-order model built in the first step. This task involves the solution to an optimization problem that minimizes the difference between the measurements and the corresponding predictions from the reduced-order model [3]. In this approach, the measured indentation property, \({P}^{*}\), for a specific crystallographic orientation is modeled as differing from the simulated indentation property:

$${P}^{*}={P}_{\mathrm{sim}}^{*}({\varvec{p}},{\varvec{g}})+\epsilon $$
(3)

where \(\epsilon \sim \mathcal{N}(0, {\sigma }^{2})\) denotes a stochastic noise term modeled as a normal distribution with a zero mean and variance \({\sigma }^{2}\). Let {\({{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{G}}}_{\mathrm{exp}}\)} denote the set of experimentally measured indentation properties, \({{\varvec{P}}}_{\mathrm{exp}}^{*}\), at the corresponding crystallographic orientations, \({{\varvec{G}}}_{\mathrm{exp}}\). The likelihood for \(n\) experimental measurements (denoted {\({{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{G}}}_{\mathrm{exp}}\}\)) is expressed as:

$$p\left({{\varvec{P}}}_{\mathrm{exp}}^{*}|{{\varvec{G}}}_{\mathrm{exp}},{\varvec{p}},{\sigma }^{2}\right)={\prod }_{i}^{n}\frac{1}{\sqrt{2\pi {\sigma }^{2}}}\mathrm{exp}\left\{\frac{{-\left({P}_{i}^{*}-{P}_{\mathrm{sim}}^{*}({\varvec{p}},{{\varvec{g}}}_{i})\right)}^{2}}{2{\sigma }^{2}}\right\}$$
(4)

where \({\sigma }^{2}\) is modeled as a homoscedastic variance exhibited by the measured indentation property across the orientation parameter space. In previous studies [3, 22], multiple indentation measurements were available for each grain orientation, and this information was used to provide an estimation of the variance. In the current study, only a single indentation measurement was available for each grain orientation. Thus, the variance, \({\sigma }^{2}\), is treated as a stochastic variable. A Bayesian update of the joint distribution of stochastic variables, {\({\varvec{p}}\), \({\sigma }^{2}\)}, is expressed as:

$$p\left({\varvec{p}},{\sigma }^{2}|{{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{G}}}_{\mathrm{exp}}\right)\propto p\left({{\varvec{P}}}_{\mathrm{exp}}^{*}|{{\varvec{G}}}_{\mathrm{exp}},{\varvec{p}},{\sigma }^{2}\right)p({\varvec{p}},{\sigma }^{2})$$
(5)

Equation (5) presents a generalized formulation for indentation measurements, since direct knowledge of the variance is often unavailable. Prior work [3] has used a single-component Metropolis–Hastings sampler for the posterior updates that accepted/rejected proposed transitions based on an acceptance probability. Since the variance is being treated as unknown in the present generalized implementation, the sampling scheme needs to be suitably modified. The posterior updates in this work were performed by incorporating a Gibbs sampler that generates samples directly from fully determined distributions. The sampled sequences using this approach typically converge to respective distributions much faster than accept/reject-based algorithms [23]. The integration of the two methods described above is referred as a Metropolis-within-Gibbs sampler [11, 21]. Formally, the Metropolis-within-Gibbs sampler generates a Gibbs sequence, \(\{{{\varvec{p}}}_{0},{\sigma }_{0}^{2},{{\varvec{p}}}_{1},{\sigma }_{1}^{2},\dots, {{\varvec{p}}}_{N},{\sigma }_{N}^{2}\}\), where the resulting samples converge to the marginal distributions, \(\left\{{{\varvec{p}}}_{0},{{\varvec{p}}}_{1},\dots ,{{\varvec{p}}}_{N}\right\}\boldsymbol{ }\sim \boldsymbol{ }p\left({\varvec{p}}|{{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{G}}}_{\mathrm{exp}}\right)\) and \(\left\{{\sigma }_{0}^{2},{\sigma }_{1}^{2},\dots ,{\sigma }_{N}^{2}\right\}\boldsymbol{ }\sim \boldsymbol{ }p\left({\sigma }^{2}|{{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{G}}}_{\mathrm{exp}}\right)\), respectively [23, 24]. In practice, the sampler takes the form

$${\sigma }_{N}^{2}\sim p\left({\sigma }^{2}|{{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{p}}}_{N},{{\varvec{G}}}_{\mathrm{exp}}\right)$$
(6)
$${{\varvec{p}}}_{N+1}\sim p\left({\varvec{p}}|{{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{G}}}_{\mathrm{exp}},{\sigma }_{N}^{2}\right)$$
(7)

where samples are drawn from the alternating conditional distributions while fixing the relevant random variables to the sampled value at step \(N\). The main requirement of a Metropolis-within-Gibbs sampler is the ability to sample from the conditional distributions [23]. We will first consider sampling from the conditional distribution of the variance, \({\sigma }^{2}\), for the fixed value, \({{\varvec{p}}}_{N}\). We recognize conditional distribution of variance is pertained to the normally distributed values \({{\varvec{P}}}_{\mathrm{exp}}^{*}\). When considering normally distributed observations, the conditional distribution of homoscedastic variance can be directly described by the scaled inverse Chi-squared distribution [21, 25,26,27]

$${\sigma }_{N}^{2}\sim \mathrm{ inv}{\chi }^{2}({\sigma }^{2}|{\widehat{\sigma }}^{2}\left({{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{p}}}_{N},{{\varvec{G}}}_{\mathrm{exp}}\right),n)$$
(8)

where \({\widehat{\sigma }}^{2}\left({{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{p}}}_{N},{{\varvec{G}}}_{\mathrm{exp}}\right)\) denotes the best estimate of variance for the current parameters, \({{\varvec{p}}}_{N}\), using the available data, i.e., \({\widehat{\sigma }}^{2}=\frac{1}{n}\sum_{i}^{n}{\left({P}_{i}^{*}-{P}_{\mathrm{sim}}^{*}({{\varvec{p}}}_{N},{{\varvec{g}}}_{i})\right)}^{2}\). We note that \(n\) and \({\widehat{\sigma }}^{2}\) control the spread and scaling of the inverse Chi-squared distribution, respectively, and are often augmented using additional hyperparameters to further reflect prior beliefs about the variance. In this work, such augmentations are forgone. Thus, the scaled inverse Chi-squared distribution is fully determined for a given value, \({{\varvec{p}}}_{N}\), and a candidate value for \({\sigma }^{2}\) can be readily sampled using the inverse transform sampling method [21, 25, 28].

Next, we turn our attention to sampling from the conditional distribution of single-crystal properties. The conditional distribution of the intrinsic material properties, \({\varvec{p}}\), for the observed experimental data and a known variance, \({\sigma }_{N}^{2}\), is expressed via Bayes rule as:

$$p\left({\varvec{p}}|{{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{G}}}_{\mathrm{exp}},{\sigma }_{N}^{2}\right)\propto p\left({{\varvec{P}}}_{\mathrm{exp}}^{*}|{\varvec{p}},{{\varvec{G}}}_{\mathrm{exp}},{\sigma }_{N}^{2}\right)p({\varvec{p}})$$
(9)

Considering a uniform prior for \(p({\varvec{p}})\) along with the likelihood function shown in Eq. 4, the conditional distribution of single-crystal properties is known up to a normalizing constant. Consequently, MCMC methods [25] can be implemented in order to sample from the conditional distribution on single-crystal properties. MCMC algorithms sample from a target posterior distribution by accepting/rejecting proposed transitions across a finite parameter space based on an acceptance probability

$$\alpha \left({{\varvec{p}}}_{N+1}^{\boldsymbol{*}}|{{\varvec{p}}}_{N}\right)=\mathrm{min}\left(\frac{p\left({{\varvec{p}}}_{N+1}^{\boldsymbol{*}}|{{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{G}}}_{\mathrm{exp}},{\sigma }_{N}^{2}\right)q({{\varvec{p}}}_{N}|{{\varvec{p}}}_{N+1}^{\boldsymbol{*}})}{p\left({{\varvec{p}}}_{N}|{{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{G}}}_{\mathrm{exp}},{\sigma }_{N}^{2}\right)q({{\varvec{p}}}_{N+1}^{\boldsymbol{*}}|{{\varvec{p}}}_{N})},1\right)$$
(10)

where \(q(\boldsymbol{*}|\boldsymbol{*})\) denotes a proposal distribution from which possible transitions are generated. With the implementation of the acceptance criteria in Eq. (10), Metropolis–Hastings algorithms only necessitate knowledge of the sampled distribution of interest up to a normalizing constant [9]. In this work, the single-component Metropolis–Hastings algorithm is adopted from previous work [3, 10] in order to generate samples from the multivariate parameter space of intrinsic material properties. In summary, the hybrid sampling formulation used in this work consisted of a Gibbs update for Eq. 6, followed by a Metropolis update for Eq. 7. We note that MCMC algorithms can require as many as \(N=5000\) iterations in order to reliably converge. Furthermore, initial samples during a “burn in” phase are typically discarded; during this phase of sampling, the proposal distribution is tuned in order to reach an acceptance rate ~ 23% [29]. Note also that the direct computation of \({P}_{\mathrm{sim}}^{*}\) from the FE simulations is impractical as it requires \(n \times N\) evaluations. Therefore, the availability of a reduced-order model to predict the simulated values is invaluable for the computations described above.

Crystal Plasticity Finite Element Model for Spherical Indentation

The establishment of the reduced-order model needed for the calibration of the slip resistances requires data generated from physics-based models of the indentation experiment that account for the influence of the slip resistances on the indentation measurements. These physics-based models can be developed using the established crystal plasticity theories [12, 30, 31] and their implementations in the finite element code ABAQUS. In these models, the local deformation in a crystalline region is assumed to be accommodated exclusively by crystallographic slip on available slip systems [32]. The imposed plastic velocity gradient tensor, \({{\varvec{L}}}^{P}\), is related to the shearing rates, \({\dot{\gamma }}^{\alpha }\) (\(\alpha \) indexes available slip systems), as:

$${{\varvec{L}}}^{P}=\sum_{\alpha }{\dot{\gamma }}^{\alpha }{{\varvec{S}}}^{\alpha },\;\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }{{\varvec{S}}}^{\alpha }\boldsymbol{ }={{\varvec{m}}}^{\alpha }\otimes{{\varvec{n}}}^{\alpha }$$
(11)

where \({{\varvec{S}}}^{\alpha }\) is the Schmid tensor computed using the slip plane normal, \({{\varvec{n}}}^{\alpha }\), and slip direction \({{\varvec{m}}}^{\alpha }\). The visco-plastic power law commonly used to model the slip activity on slip system \(\alpha \) due to an imposed resolved shear stress \({\tau }^{\alpha }\) is expressed as:

$${\dot{\gamma }}^{\alpha }={\dot{\gamma }}_{0}{\left|\frac{{\tau }^{\alpha }}{{s}^{\alpha }}\right|}^\frac{1}{m}\mathrm{sign}({\tau }^{\alpha })$$
(12)

where \({\dot{\gamma }}_{0}\) is a reference shear rate, \(m\) is the rate sensitivity parameter, and \({s}^{\alpha }\) is the resistance to slip on the \(\alpha \) slip system. Generally, the slip resistances, \({s}^{\alpha },\) are prescribed through hardening laws to capture the overall strain hardening characteristics exhibited by the material. In this work, only the initial values of the slip resistances are of interest; consequently, \({s}^{\alpha }\) are assigned constant values in each of the FE simulations of the indentation experiment performed in this study. Furthermore, the different slip systems in a single class of slip systems are all assigned the same slip resistance value. The different classes of the slip systems considered in the FE simulations along with the variables denoting their slip resistance are summarized in Table 1.

Table 1 Slip systems and the corresponding slip resistances considered in the crystal plasticity finite element simulations of the spherical indentation experiments. In total, 24 slip systems are considered for the primary α grains
Full size table

The FE model developed and utilized in prior work [2] was designed to predict the indentation yield strength using a loading history very similar to the one used in the actual indentation experiment. This FE model consisted of a deformable sample that followed the crystal plasticity material model described in Eqs. (11, 12), and a rigid hemi-spherical indenter in frictionless contact with the deformable sample. Three-dimensional continuum elements (C3D8 solid elements, ABAQUS [33]) were used to mesh the deformable sample. The FE mesh was designed such that the primary indentation zone exhibited the highest mesh density. The FE mesh was made progressively coarser as one moved away from the primary indentation deformed zone toward the free boundaries of the sample. A large deformed sample size was needed to accurately capture the decay of the stress and strain fields in the deformed sample; the resulting FE mesh consisted of 126,560 elements.

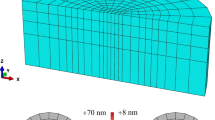
Extension of the prior FE model to the indentation measurements in hcp crystals encountered additional challenges due to (i) the higher levels of plastic anisotropy exhibited by the hcp crystals (e.g., the pyramidal < c + a > slip resistance is significantly larger than the prismatic slip resistance), and (ii) the significantly larger parameter space covering the expected ranges for each of the four slip resistance parameters identified in Table 1. The main consequence of these factors is a substantial increase in the FE model size as well as the number of FE simulations for the present work. In order to address these challenges, an improved FE model with a higher computational efficiency was needed and was developed. This new FE model is shown in Fig. 2a,b. In this new model, instead of coarsening the sample regions further away from the primary zone of indentation, infinite elements designed to simulate the effect of an infinite elastic domain were employed (see Fig. 2b). A similar approach was successfully employed in related prior work [34,35,36], where substantial savings in the computational cost were realized. Infinite elements implement suitable decay functions in the direction toward the free surface allowing the emulation of infinite elastic domains [33]. The size of the primary indentation zone was selected to be larger than the estimated values of the contact diameter in the experiments (see Part I of this series). For the present study, a primary deformation zone of size \(0.76 \times 0.76 \times 1.14 \upmu\mathrm{m}\) directly under the rigid indenter of radius \(15.2 \upmu \mathrm{m}\) was meshed using 13,500 C3D8 elements, while the deformation zones outside the primary indentation zone were meshed using 2700 CIN3D8 elements (eight-noded hexahedral infinite elements; ABAQUS [33]). Surface-to-surface hard frictionless contact was used to simulate the contact between the deformable sample and the rigid indenter. Indentation stress–strain curves were computed by simulating loading and unloading segments producing a loading history similar to the one used in the actual indentation experiment (see Fig. 2c).

Fig. 2
figure 2

a Schematic of the FE model used in this study with a rigid indenter (gray) on top of a deformable sample (this schematic is not drawn to scale). b Cut section of the FE mesh used in this study showing the continuum (C3D8) elements in light yellow, and the infinite (CIN3D8) elements in dark green. c Predicted load–displacement curves in multiple load-unload cycles for an hcp single crystal for three declination angles of \({0}^{o}\), \({45}^{o}\) and \({90}^{o}\). d Indentation stress–strain curve corresponding to the simulations shown in (c)

Full size image

Indentation simulations were performed in various hcp single-crystal orientations using the new FE model described above. As examples, the simulated load–displacement curves and the extracted indentation stress–strain data points from these curves are presented for three selected declination angles of \(0^\circ \), \(45^\circ \), and \(90^\circ \) in Fig. 2c, d , respectively. The slip resistances for these examples are taken from the prior work of Bridier et al. [37] on the primary alpha in Ti-6Al-4 V. As expected, it is clearly seen that both the stiffness and strength are highest for the grains with the c-axis parallel to the indentation direction, which then decrease with an increase in the declination angle. These results match well the trends seen in the measurements (in Part I of this series). As further validation, the results from the new FE model were compared against previously reported results for indentation simulations using both isotropic J2 plasticity theory [6] and for selected bcc single-crystal orientations [2].

Crystal plasticity FE models of spherical indentation can provide important insights into the relative extents of the different slip modes in a given indentation test. For this purpose, the cumulative slip activity in each of the four slip families was computed as a suitably defined equivalent plastic strain:

$${\varepsilon }_{\mathrm{eq}}^{f}=\int \sqrt{\frac{2}{3}{\dot{{\varvec{\varepsilon}}}}_{p}^{f}:{\dot{{\varvec{\varepsilon}}}}_{p}^{f}}\mathrm{d}t$$
(13)

where \(f\) indexes each of the slip families identified in Table 1, \({\dot{{\varvec{\varepsilon}}}}_{p}^{f}\) is the symmetric component of the velocity gradient tensor defined in Eq. 11 while including slip activities on only the slip systems belonging to a single slip family. The FE-predicted equivalent plastic strain contours on a longitudinal section through the sample are plotted in Fig. 3 for each of the four slip families from the simulations discussed above. The plots reveal that the declination angle has a large influence on the slip activities in the primary deformation zone of the spherical indentation. More specifically, it is observed that (i) the indentation parallel to the c-axis is dominated by pyramidal < c + a > slip activity along with a significant contribution from basal slip, and (ii) the basal and prism slip dominated the response at the higher declination angles of \(45^\circ \) and \(90^\circ \). Although it appears from Fig. 3 that the basal slip dominated for the declination angle of \(45^\circ \) and prism slip dominated for the declination angle of \(90^\circ \), one should note that these plots can change significantly in other longitudinal sections in the same simulation, and also are expected to be sensitive to the other Bunge-Euler angle \({\varphi }_{2}\) needed to identify the grain orientation. It is generally seen that the pyramidal slip and basal slip influenced the indentation plastic response at small declination angles, while the prism slip and basal slip almost exclusively influenced the indentation plastic response at the higher declination angles. In addition, the pyramidal < a > slip did not play a major role in the simulations shown in Fig. 3.

Fig. 3
figure 3

FE-predicted cumulative slip activities in the four slip families for an hcp single crystal subjected to indentation at three different declination angles of \({0}^\circ\), \({45}^\circ\), and \({90}^\circ\)

Full size image

The observed slip activities in Fig. 3 do explain the decrease in the indentation yield strength with an increase in the declination angle. The activation of the harder pyramidal < c + a > slip is indeed mainly responsible for the higher indentation yield strengths at the very low declination angles. The activation of the easier prism slip systems is responsible for the lower indentation yield strengths at high declination angles. These observations are consistent with prior reports in the literature [38].

The new FE model developed for this study provided a significant increase in computational efficiency compared to the FE model used in our prior work [2]. The new model required 101 to 136 min using 8 CPU cores on Georgia Tech’s Hive computing cluster to simulate the indentations at the different declination angles, whereas the previous model with 126,560 C3D8 elements took 182–245 min for the same simulations.

Application to Estimation of Single-Crystal Elastic Constants

We now revert back to the primary task of extracting intrinsic single-crystal properties from indentation measurements presented in Part I of this series. More specifically, we focus first on the single-crystal elastic constants, \({\varvec{p}}=\{{C}_{11}\),\({C}_{12},{C}_{44},{C}_{33},{C}_{13}\}\). For this case {\({{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{G}}}_{\mathrm{exp}}\)} (see Sect. 2) would correspond to the experimentally measured combinations of the indentation modulus and the corresponding grain orientations for a selected alloy. We recall that the main requirement for sampling the distribution on the unknown single-crystal elastic constants is the ability to efficiently evaluate the likelihood function in Eq. 4. In other words, we need a high fidelity reduced-order model that captures the dependence of indentation modulus on the orientation of the indented grain and a prescribed set of single-crystal elastic constants. As already mentioned, such a high fidelity reduced-order model applicable to a wide range of hcp metals is already available [3, 22] (expressed in Eq. 1), and is adopted for the present study. We note that this reduced-order model leveraged a database of 2200 finite element elastic indentation simulations performed within the bounds \(80\le {C}_{11}\le 240\)GPa, \(40\le {C}_{12}\le 120\)GPa, \(30\le {C}_{44}\le 90\)GPa, \(70\le {C}_{33}\le 210\)GPa, and \(30\le {C}_{13}\le 90\) GPa. Given the elastic transversely isotropic behavior of hcp materials, only the orientation space defined by \(0^\circ , \le\Phi \le 90^\circ \),needs to be considered in our analyses [3].

For each Ti alloy studied experimentally in Part I of this series, the likelihood function (Eq. 4) for a particular alloy is computed using the reduced-order model mentioned above (Eq. 1), and a posterior distribution of the elastic constants for the selected alloy is sampled using multivariate MCMC chains described in Sect. 2. These resulting distributions are tabulated and summarized in Fig. 4. The computed posteriors are sharpest for \({C}_{44}\), followed by \({C}_{33}\) and \({C}_{11}\). Estimates for \({C}_{12}\) and \({C}_{13}\) show a significant amount of uncertainty relative to the other elastic parameters. The relatively high uncertainty exhibited by \({C}_{12}\) and \({C}_{13}\) is indicative of a smaller influence of these elastic parameters on the indentation modulus (i.e., sensitivity) across the orientation space.

Fig. 4
figure 4

Top: distributions of single-crystal elastic constants extracted for alloys considered in this work. BW denotes the bin width for the distributions in a given column. Bottom: the means and corresponding standard deviations of the extracted single-crystal elastic constants are summarized

Full size image

The elastic constants for selected alloys computed from the sampled MCMC chains are compared to elastic constants previously reported in the literature in Table 2. In general, estimates are found to be in good agreement with those reported in the literature [39,40,41]. In particular, very good agreement is found between the elastic constants computed here and those reported for CP-Ti. Furthermore, all the elastic constants reported for Ti6242 fall within a standard deviation of the values computed in this work.

Table 2 Comparison of estimated elastic constants for selected alloys to elastic constants reported in the literature. The mean and corresponding standard deviation computed using the sampled MCMC chains are shown for the current work
Full size table

It should be recognized that each sampled set of elastic constants from the Markov Chain presents a realization of a possible mean indentation modulus function across the orientation space. One way to understand and visualize the uncertainties expressed in Fig. 4 is to analyze the mean indentation modulus predictions across the orientation space resulting from the sampled MCMC chains. The mean predictions for the indentation modulus are shown in Fig. 5 for the different α-Ti phases studied. The tightest predictions across the orientation space were obtained in the MCMC chains sampled for CP-Ti and Ti64. Indeed, the posteriors for \({C}_{11}\), \({C}_{33}\), and \({C}_{12}\) shown in Fig. 4 were slightly sharper for CP-Ti and Ti64 compared to those for the other alloys. We believe that the sharpness of the posteriors is largely affected by the number of measurements and their distribution in the orientation space. Of course, more measurements generally help sharpen the posteriors. In the present case, Ti64 had the most available number of experimental measurements (67), and Ti811 had the fewest (31). Secondly, the number of measurements close to the zero declination angle also seems to play an important role. This is because this measurement shows some of the highest sensitivities for some of the single-crystal elastic parameters. Furthermore, it is also generally seen that a higher precision in the experimental measurements (reflected by less scatter in the plots of indentation modulus versus the declination angle) leads to sharper extracted posteriors for the single-crystal elastic constants.

Fig. 5
figure 5

Predictions of indentation modulus versus declination angle sampled using MCMC chains and the reduced-order model

Full size image

Application to Estimation of Initial Slip Resistances

Attention is now turned to the extraction of the initial slip resistance values for the different slip families (i.e., \({\varvec{p}}=\{{s}_{\mathrm{pr}},{s}_{\mathrm{ba}},{s}_{\mathrm{pyr}-a},{s}_{\mathrm{pyr}-\mathrm{ca}}\}\)) for all of the alloys studied in Part I of this series. For this application, {\({{\varvec{P}}}_{\mathrm{exp}}^{*},{{\varvec{G}}}_{\mathrm{exp}}\)} would denote the combinations of the experimentally measured indentation yield strengths and the corresponding grain orientations for any selected alloy. Unlike the previous application in Sect. 4, we first need to establish a high-fidelity reduced-order model covering a suitable parameter space as such a model has not yet been established. Such a model was previously established for bcc single crystals using a single slip resistance parameter [2]. Building on this prior experience, it was decided to pursue a reduced-order model to predict the indentation yield normalized by the prismatic slip resistance. In other words, our goal is to establish \({\widehat{P}}^{*}({\varvec{r}},{\varvec{g}})\), defined as \({P}_{\mathrm{sim}}^{*}\left({\varvec{p}},{\varvec{g}}\right)\approx {s}_{\mathrm{pr}}{\widehat{P}}^{*}({\varvec{r}},{\varvec{g}})\), where \({\varvec{r}}=\left\{\frac{{s}_{\mathrm{ba}}}{{s}_{\mathrm{pr}}},\frac{{s}_{\mathrm{pyr}-a}}{{s}_{\mathrm{pr}}},\frac{{s}_{\mathrm{pyr}-\mathrm{ca}}}{{s}_{\mathrm{pr}}}\right\}\). Therefore, the inputs to the desired reduced-order model span a five-dimensional space.

Establishing a Reduced-Order Model for Indentation Yield

Our strategy for establishing the reduced-order model of interest identified above utilizes a Fourier representation similar to Eq. 1. This entails the use of Legendre polynomials as basis for the dependence on the slip ratios,\({\varvec{r}}\) and symmetrized SSH for the dependence on \({\varvec{g}}\).An advantage of this formulation is that by casting the reduced-order model in terms of the slip ratios, a significant range of the initial slip resistance values can be efficiently considered in the establishment of the reduced-order model of interest. In order to establish the desired reduced-order model, a database of finite element simulations populating the relevant parameter space is necessary. The bounds of the parameter space were chosen as \(\{0.75\le \frac{{s}_{\mathrm{ba}}}{{s}_{\mathrm{pr}}}\le 2.0 , 2.0\le \frac{{s}_{\mathrm{pyr}-a}}{{s}_{\mathrm{pr}}}\le 4.5 , 2.5\le \frac{{s}_{\mathrm{pyr}-\mathrm{ca}}}{{s}_{\mathrm{pr}}}\le 6.5\}\), based on values of slip resistances reported in the literature for the alpha phase of Ti alloys [1, 42,43,44], while the bounds of the orientation space were chosen to cover the relevant fundamental zone \(\{0^\circ <\Phi <90^\circ \),\(0^\circ \le {\varphi }_{2}\le 60^\circ \}\) [45]. A database of CPFEM-predicted indentation yield values was generated in two steps: (i) an initial database of 92 simulations was generated to cover the input space identified above in a roughly uniform manner (described in more detail later), and (ii) a sequential design process developed in recent work [3] that selects new inputs for CPFEM simulations based on an assessment of the maximum uncertainty in the predictions made using the available training data.

The truncation levels of the reduced-order model, \(\{Q,L\}\) in Eq. 1, are unknown a priori to observing any simulated data. Following prior studies [3], the truncation levels were treated as hyperparameters and selected in accordance with the model predictive capability judged by multiple error metrics (e.g., mean absolute error over training and test sets) during the sequential model building process. Given the significant anisotropic response of hcp crystals, higher truncation levels for SSH (denoted by L) were anticipated for the present application. Thus, the initial model explored adopted truncation levels of \(Q=1,L=10\) producing a total of 88 Fourier coefficients from Eq. 1. An initial database is needed to start the overall model building effort. Inputs to FE simulations used an arbitrarily chosen value for \({s}_{pr}=200 \mathrm{MPa}\) alongside 92 unique sets of slip ratios and crystallographic orientations, \(\{{\varvec{r}},{\varvec{g}}\}\), chosen from a five-dimensional Max Pro Latin Hypercube Design (LHD) [46]. It is emphasized that the truncation \(Q=1\) corresponds to linear terms expanded about the associated slip ratios. Following the establishment of the initial model, additional inputs to simulations were sequentially selected from a much denser five-dimensional Max Pro LHD of 1000 inputs based on the sequential design strategy outlined in previous work [3]. During this process, various truncation levels were evaluated while systematically increasing the truncation values. Improvement to the model was negligible after truncation levels of \(Q\)=1 and \(L\)=14 (corresponding to a total of 160 Fourier coefficients in Eq. 1). Ultimately, a database of 312 simulations was generated wherein the last 52 simulations were used only to test the predictive capabilities of the model. The predictive performance of the model using the chosen truncation levels in this study (\(Q\)=1, \(L\)=14) is shown in Fig. 6.

Fig. 6
figure 6

Left: predictive performance of the reduced-order model produced in this work for the prediction of the normalized indentation yield. Right: corresponding histograms of test (red) and train (blue) of absolute error for the predictions. Overlapped areas of histograms are shown in magenta

Full size image

MCMC Sampling of Initial Slip Resistance Parameters

With a reduced-order model in place, attention is turned to the extraction of initial slip resistances \({\varvec{p}}=\left\{{s}_{\mathrm{pr}},{s}_{\mathrm{ba}},{s}_{\mathrm{pyr}-a},{s}_{\mathrm{pyr}-\mathrm{ca}}\right\}\) from the experimental measurements presented in Part I of this series. The likelihood shown in Eq. 4 can now be evaluated for an arbitrary set of prescribed slip resistances using the reduced-order model established in the previous section along with the measured indentation yield strengths across the orientation space for a particular alloy. We note that a major advantage to the formulation of the reduced-order model in accordance with normalized indentation yield and slip ratios is that it is unnecessary to directly bound the parameter space of slip resistances during the extraction process. Thus, a broad uniform distribution which only enforces the slip resistances to be strictly positive was used for the prior. With the likelihood(s) and prior(s) established, multivariate MCMC chains of slip resistances were independently sampled for each alloy and the resulting distributions are tabulated and summarized in Fig. 7. The difference between the individual initial slip resistance parameters across the Ti alloys is apparent in Fig. 7. We note the relative uncertainty of the estimates can be ranked; prismatic with the lowest relative uncertainty, basal and pyramidal < c + a > exhibiting slightly more relative uncertainty and pyramidal < a > exhibiting the highest relative uncertainty. This ranking, which is consistent across all alloys, can be seen as reflective of the influence on the indentation yield to changes in the initial slip resistance parameters (i.e., sensitivity). This ranking is also consistent with the slip activity seen from the indentation simulations, as discussed in Sect. 3.

Fig. 7
figure 7

Top: distributions of initial slip resistances for the alloys considered in this work. BW denotes the fixed bin width for the distributions in a given column. Bottom: the means and corresponding standard deviations of the extracted initial slip resistances for the different α -Ti components are summarized

Full size image

The slip ratios for selected alloys computed from the sampled MCMC chains are compared to slip ratios found in the literature and shown in Table 3. In general, a good agreement is found between estimates obtained in this study and those reported in the literature. For example, the pyramidal < c + a > slip ratios fall between the estimates reported in the literature for CP-Ti and Ti64. The basal slip ratio extracted for CP-Ti also falls between the literature estimates. Finally, we note literature values reported for the basal slip ratio of Ti6242 and Ti64 are within a standard deviation of estimates obtained in the current work. It is emphasized that availability of reported estimates for initial slip resistance of slip systems in the literature varies from alloy to alloy (e.g., \({s}_{\mathrm{pyr}-\mathrm{ca}}\) is not reported for Ti6242), and those reported seldom include a rigorous quantification of uncertainty. A major advantage of the approach presented here is the ability to readily compare all the extracted slip resistance parameters between alloys of interest with measures of uncertainty.

Table 3 Comparison of estimated slip resistance ratios for selected alloys to slip resistance ratios reported in the literature. The mean and corresponding standard deviation computed using the sampled MCMC chains are shown for the current work
Full size table

Similar to the extracted distribution of elastic constants, the MCMC predictions for indentation yield strengths across the orientation space can assist in further analyzing the extracted distributions of initial slip resistances. The mean predictions of indentation yield strengths from the MCMC chains across the orientation space for a given alloy are compared to the available experimental data in inverse pole figure plots shown in Fig. 8; the corresponding uncertainties are presented in Fig. 9. The mean predicted indentation yield strength contours are largely consistent with the experimentally reported indentation yield values. We note the largest uncertainties are generally in the [1,0,− 1,0] direction which typically coincides with fewer number of indentation measurements. The high predictive uncertainty is also indicative of a lower sensitivity to any singular dominating slip system, that is, the uncertainty from multiple slip systems is propagated in the prediction for indentation yield. The measure of uncertainty provided by the MCMC prediction can provide guidance to where additional experiments may be performed in order to sharpen the distributions of slip resistances. Additional indents in areas of highest uncertainty are likely to improve the distributions on the estimated slip parameters. We note that recent work has explored a more systematic effort in the improvement of estimated parameter distributions and may be utilized in identifying additional experiments (e.g., for the pyramidal < a > slip resistance whose estimation showed relatively high levels of uncertainty) if desired [22].

Fig. 8
figure 8

IPF contours for indentation yield strength predictions using reduced-order model and sample MCMC chains. The experimental measurements used in the extraction process are shown as distinguished circles colored in accordance with their actual value

Full size image
Fig. 9
figure 9

IPF contours of the standard deviation of predictions from the reduced-order model for indentation yield strength using sampled MCMC chains. Orientations of the available experimental measurements used in the sampling process are displayed by the black dots

Full size image

Conclusions

Protocols for the Bayesian estimation of grain-scale elastic–plastic properties from available experimental spherical indentation stress–strain measurements have been presented. The two-step Bayesian framework presented here enables the quantification and propagation of uncertainty in the observed experimental spherical indentation stress–strain measurements to the extracted grain-scale properties. Although the associated physics-based finite element simulations are computationally expensive, the generation of a suitable database presents a one-time cost in establishing a reduced-order model (Step (1) of the proposed two-step protocol). Once the reduced-order model is established, the calibration of the underlying intrinsic properties to available experimental data (Step (2) of the proposed two-step protocol) can be accomplished with relatively minimal computational resources. The present work highlights the strengths in dividing up the tasks involved in grain-scale properties estimation via spherical indentation into reduced-order model building and calibration steps. This is evidenced by the adoption of a reduced-order model built in a previous work, and used here to extract single-crystal elastic constants. Furthermore, the protocols presented here successfully demonstrate the generation of a consistent dataset of initial slip resistances, with quantified uncertainty, corresponding to multiple titanium alloys with differing chemical compositions. Due to the formulation of normalized indentation yield, the extraction efforts are made much more robust, and additional alloys can be readily considered using the protocols established here. The generation of such a comprehensive dataset of grain-scale properties using spherical indentation measurements is the first of its kind to the authors' knowledge.