An efficient solution of system of generalized Abel integral equations using Bernstein polynomials wavelet bases

Abstract

This work introduces a direct method based on orthonormal Bernstein polynomials wavelet bases, to present a stable algorithm for numerical inversion of a system of generalized Abel integral equations. The application of all the currently existing numerical inversion methods was strictly limited to only one portion of the generalized Abel integral equations. The proposed method is quite accurate, and several numerical illustrations demonstrate the convergence and utilization of the proposed method compared to some of the preexisting numerical solution techniques. The permanence of the numerical result under the effect of small perturbation in input data has been examined, which is depicted with the use of numerical illustrations.

Introduction

In this paper, we propose the method of an approximate numerical inversion for the system of generalized Abel integral equations given by

$$ \left. {\begin{array}{*{20}l} {\mathop \rho \nolimits_{1} (s)\int_{a}^{s} {\frac{{u^{\beta - 1} \varepsilon_{1} (u)\,{\text{d}}u}}{{(s^{\beta } - u^{\beta } )^{\alpha } }}} + \mathop \rho \nolimits_{2} (s)\int_{s}^{b} {\frac{{u^{\beta - 1} \varepsilon_{2} (u)\,{\text{d}}u}}{{(u^{\beta } - s^{\beta } )^{\alpha } }}} = I_{1} (s)} \hfill \\ {\mathop \omega \nolimits_{1} (s)\int_{s}^{b} {\frac{{u^{\beta - 1} \varepsilon_{1} (u)\,{\text{d}}u}}{{(u^{\beta } - s^{\beta } )^{\alpha } }}} + \mathop \omega \nolimits_{2} (s)\int_{a}^{s} {\frac{{u^{\beta - 1} \varepsilon_{2} (u)\,{\text{d}}u}}{{(s^{\beta } - u^{\beta } )^{\alpha } }}} = I_{2} (s)} \hfill \\ \end{array} } \right\};s \in (a,b);\,0 < \alpha < 1,\beta \ge 1, $$

(1)

where the coefficients $\mathop \rho \nolimits_{1} (s),\mathop \rho \nolimits_{2} (s),\omega_{1} (s),\omega_{2} (s)$ must not vanish simultaneously and $I_{1} (s),\,I_{2} (s)$ are the intensity functions.

The system of generalized Abel integral equations in Eq. (1) holds substantial significance in various spheres. It is considered as a mathematical model in the various fields such as water wave scattering [1], plasma spectroscopy [2], elasticity [3], mathematical physics, astrophysics, seismology, solid mechanics [4, 5].

There are various numerical methods to find the solution of different kinds of integral equations, such as Maleknejad et al. proposed Legendre wavelets and rationalized Haar wavelet methods [6, 7], Derili et al. proposed two-dimensional wavelets method [8] and Mandal et al. used the Daubechies scale function [9] method. Several other methods [10,11,12,13,14] have been previously used for the numerical inversion of the system of generalized Abel integral equations. In 1976, Lowengrub [10] showed that certain mixed boundary value problems arising in the classical theory of elasticity converted to the new problem in the form of functions ɛ₁(u) and ɛ₂(u), these functions satisfy the system in Eq. (1). Lowengrub and Waltson [11] provided a method based on converting the system of generalized Abel integral equations into an equivalent boundary value problem of coupled Riemann–Hilbert type. Some particular generalized system of Abel integral equations solved by creating an equivalent system of singular integral equation in [12]. Mandal et al. [13] have solved the system with the implementation of fractional calculus. In [14], Mandal and Pandey gave the numerical solution of the system of generalized Abel integral equations through the Bernstein polynomials bases. Jafarian et al. also used the Bernstein polynomial method [15] and Bernstein collocation method [16] for obtaining the solution of the system of integral equations and Abel integral equations, respectively.

This paper aims to give a new and user friendly algorithm for the numerical inversion of the system of generalized Abel integral equation, based on Bernstein polynomials orthonormal wavelet bases. Numerical examples have been provided to illustrate the convergence and stability of the method.

Bernstein polynomials orthonormal wavelet bases

A class of functions, which is obtained by dilation and translation of a single function known as mother wavelet [17]. The continuous variation of the dilation and translation parameters c and d gives the following continuous wavelet bases [18]

$$ \psi_{c,d} (u) = \left| c \right|^{ - 1/2} \psi \left( {\frac{u - d}{c}} \right),\quad c,d \in R,\quad c \ne 0 . $$

(2)

If the parameters c and d are regulated to $c = 2^{ - k} ;\,\,d = n\,2^{ - k}$, then obtained a family of discrete wavelets from the above equation,

$$ \psi_{k,n} (u) = 2^{k/2} \psi \,(2^{k} u - n);\quad k,n \in Z. $$

The Bernstein polynomials characterized over the interval $[0,\,1]$ are given as;

$$ B_{i,n} (y) = \left( {\begin{array}{*{20}c} n \\ i \\ \end{array} } \right)y^{i} (1 - y)^{n - i} ;\quad \forall \,\,\,i = 0,1,2, \ldots ,n. $$

(3)

Some significant characteristics of Bernstein polynomials are:

• The sum of all Bernstein polynomials of degree n is always one

  $$ \sum\limits_{i = 0}^{n} {B_{i,n} \left( y \right)} = \sum\limits_{i = 0}^{n} {\left( {\begin{array}{*{20}c} n \\ i \\ \end{array} } \right)y^{i} \left( {1 - y} \right)^{n - i} = \left( {1 - y + y} \right)^{n} = 1.} $$

• $B_{i,n} (y) \ge 0$ for all $y \in [0,1]$.

• $B_{n - i,n} (1 - y) = B_{i,n} (y)$.

The recurrence formula to obtain Bernstein polynomial of degree less than n using Bernstein polynomials of degree n is

$$ B_{i,\,n - 1} (y) = \left( {\frac{n - i}{n}} \right)B_{i,\,n} (y) + \left( {\frac{1 + i}{n}} \right)B{}_{i + 1,\,n}(y). $$

The expansion of any polynomial P(y) of degree n can be expressed in terms of a linear combination of B_i,n(y)

$$ P(y) = \sum\limits_{i\, = 0}^{n} {\beta_{i} } B_{i,\,n} (y),\quad n \ge 1. $$

where β_i is called Bernstein polynomials coefficients, these polynomials are not orthonormal, so we used the Gram–Schmidt process [19] to get orthonormal polynomials, which are denoted by b_i(y) given in “Appendix 1”.

We are taking orthonormal Bernstein polynomials for N = 7, which are shown graphically in Fig. 1.

Fig. 1

Eight orthonormal Bernstein polynomials, for N = 7

The four arguments in the Bernstein polynomials orthonormal wavelet bases $\psi_{m,n} (u) = \psi (k,m,n,u)$, where $m = 0,\,1,\, \ldots ,\,2^{k} - 1$ and $k = 0,\,1,\,2,\, \ldots$ are translation and dilation parameters, respectively, $n = 0,\,1,\, \ldots ,\,N$ is the order of Bernstein polynomial and the independent variable u is lying in the closed interval [0, 1]. The orthonormal wavelet bases ψ_m,n(u) are given in [20] on the interval [0, 1), such as

$$ \psi_{m,n} (u) = \left\{ {\begin{array}{*{20}l} {2^{k/2} b_{n} (2^{k} u - m)} \hfill & {\frac{m}{{2^{k} }} \le u < \frac{m + 1}{{2^{k} }}} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right., $$

(4)

where 2 ^k/2 is the orthonormality factor, for the dyadic form of orthonormal Bernstein polynomials wavelet bases of the order n we are setting parameters $c = 2^{ - k}$ and $d = m2^{ - k}$ in Eq. (2).

Now, for $k = 0;\,N = 7,$ there are eight, and for $k = 1;\,N = 7,$ sixteen basis elements of orthonormal wavelet bases are obtained [21].

Function approximation

Let us consider $f \in L^{2} [0,1],$ then may be written as the following expansion of f(u) on the closed interval [0, 1]

$$ f(u) = \sum\limits_{m = 0}^{\infty } {\sum\limits_{n = 0}^{\infty } {c_{mn} \;\psi_{mn} (u)} } , $$

(5)

where $\left\langle {.,.} \right\rangle$ is the inner product on the Hilbert space, and $c_{mn} = \;\left\langle {f(.),\;\psi_{m\,n} \left( . \right)} \right\rangle$ be the wavelet coefficients. We truncate the infinite series in Eq. (5) at the levels m = 2 ^k − 1 and n = N, then obtained an approximate version of these series such as

$$ f\left( u \right) \approx \sum\limits_{m = 0}^{{2^{k} - 1}} {\sum\limits_{n = 0}^{N} {c_{m\,n} \;\psi_{m\,n} \left( u \right)} } = C^{T} \,\varPsi \left( u \right), $$

(6)

where C and Ψ are $2^{k} (N + 1) \times 1$ order matrices given by

$$ C = [c_{00} , \ldots ,c_{0N} ;c_{10} , \ldots ,c_{1N} ; \ldots ;c_{{(2^{k} - 1)0}} , \ldots ,c_{{(2^{k} - 1)N}} ]^{T} , $$

(7)

$$ \varPsi (u) = \left[ {\psi_{00} (u), \ldots ,\psi_{0N} (u);\,\psi_{10} (u), \ldots ,\psi_{1N} (u); \ldots ;\psi_{{(2^{k} - 1)0}} (u), \ldots ,\psi_{{(2^{k} - 1)N}} (u)} \right]^{T} . $$

(8)

The solution of the system of generalized Abel integral equations

In this section, we are discussing the solution of the system of generalized Abel integral equations in Eq. (1) by using Bernstein polynomials orthonormal wavelet bases.

Now, let us take the unknown (emissivity) functions $\varepsilon_{1} (u),\,\varepsilon_{2} (u)$ and the intensity functions $I_{1} (s),I_{2} (s)$ from Eq. (1) and approximates to this by using Eq. (6),

$$ \begin{aligned} & \varepsilon_{1} (u) = C_{1}^{T} \varPsi (u),\,\,\,\varepsilon_{2} (u) = C_{2}^{T} \varPsi (u); \\ & I_{1} (s) = F_{1}^{T} \varPsi (s),\,\,\,I_{2} (s) = F_{2}^{T} \varPsi (s), \\ \end{aligned} $$

(9)

where $C_{1} ,\,C_{2} ;\,F_{1} ,\,F_{2}$ are coefficient matrices. Substituting these approximated values of functions from Eq. (9) and taking $a = 0,\,b = 1$ in Eq. (1), we get

$$ \begin{aligned} & \rho_{1} (s)C_{1}^{T} \int_{0}^{s} {\frac{{u^{\beta - 1} \varPsi (u){\text{d}}u}}{{(s^{\beta } - u^{\beta } )^{\alpha } }}} + \rho_{2} (s)C_{2}^{T} \int_{s}^{1} {\frac{{u^{\beta - 1} \varPsi (u){\text{d}}u}}{{(u^{\beta } - s^{\beta } )^{\alpha } }}} = F_{1}^{T} \varPsi (s) \\ & \omega_{1} (s)C_{1}^{T} \int_{s}^{1} {\frac{{u^{\beta - 1} \varPsi (u){\text{d}}u}}{{(u^{\beta } - s^{\beta } )^{\alpha } }}} + \omega_{2} (s)C_{2}^{T} \int_{0}^{s} {\frac{{u^{\beta - 1} \varPsi (u){\text{d}}u}}{{(s^{\beta } - u^{\beta } )^{\alpha } }}} = F_{2}^{T} \varPsi (s), \\ \end{aligned} $$

(10)

The integrals in Eq. (10) involve evaluating integrals of the types $\int\nolimits_{0}^{s} {\frac{{u^{n} {\text{d}}u}}{{(s^{\beta } - u^{\beta } )^{\alpha } }}}$ and $\int\limits_{s}^{1} {\frac{{u^{n} {\text{d}}u}}{{(u^{\beta } - s^{\beta } )^{\alpha } }}}$.

We calculate these integral using given recursive formulae,

$$ \int\limits_{0}^{s} {\frac{{u^{n} {\text{d}}u}}{{(s^{\beta } - u^{\beta } )^{\alpha } }}} = \frac{{\pi s^{n} \left( {{\beta \mathord{\left/ {\vphantom {\beta s}} \right. \kern-0pt} s}} \right)^{\alpha - 1} (s^{\beta - 1} \beta )^{ - \alpha } \csc (\pi \alpha )\,\varGamma \left( {{{n + 1} \mathord{\left/ {\vphantom {{n + 1} \beta }} \right. \kern-0pt} \beta }} \right)}}{{\varGamma (\alpha )\varGamma \left( {{{n + \beta - \beta \alpha + 1} \mathord{\left/ {\vphantom {{n + \beta - \beta \alpha + 1} \beta }} \right. \kern-0pt} \beta }} \right)}}, $$

(11a)

$$ \int\limits_{s}^{1} {\frac{{u^{n} {\text{d}}u}}{{(u^{\beta } - s^{\beta } )^{\alpha } }}} = \frac{{s^{1 + n - \alpha \beta } }}{\beta }\left[ {\frac{{\varGamma \left[ {1 - \alpha } \right]\varGamma \left[ {\alpha - \left( {\frac{1 + n}{\beta }} \right)} \right]}}{{\varGamma \left[ {\frac{ - n - 1 + \beta }{\beta }} \right]}} - \left( {B_{{s^{\beta } }} \left[ {\alpha - \left( {\frac{1 + n}{\beta }} \right),1 - \alpha } \right]} \right)} \right]. $$

(11b)

where Γ(.) represents the gamma function and B(z, a, b) or B_z(a, b) stands for the incomplete beta function which is defined by

$$ B_{z} \left( {a,b} \right) \equiv \int\limits_{0}^{z} {t^{a - 1} (1 - t)^{b - 1} } {\text{d}}t, $$

Here in Eq. (11b), we have $B_{{s^{\beta } }} (\alpha - n + 1/\beta ,1 - \alpha )$, which is expressed with the help of above function $B_{z} \left( {a,b} \right)$ as

$$ B_{{s^{\beta } }} \left[ {\alpha - \left( {\frac{1 + n}{\beta }} \right),1 - \alpha } \right] \equiv \int\limits_{0}^{{s^{\beta } }} {t^{{\alpha - \left( {\frac{1 + n}{\beta }} \right) - 1}} (1 - t)^{(1 - \alpha ) - 1} } {\text{d}}t. $$

Now, by Eqs. (11a) and (11b) we have

$$ \int\limits_{0}^{s} {\frac{{u^{\beta - 1} \varPsi (u)}}{{(s^{\beta } - u^{\beta } )^{\alpha } }}} {\text{d}}u = W_{1} \varPsi (s),\quad \int\limits_{s}^{1} {\frac{{u^{\beta - 1} \varPsi (u)}}{{(u^{\beta } - s^{\beta } )^{\alpha } }}} {\text{d}}u = W_{2} \varPsi (s) $$

(12)

where $W_{1}$ and W₂ are the almost Bernstein polynomial multiwavelets operational matrix of integration [22, 23] of wavelet bases Ψ(u) of order $2^{k} (N + 1) \times 2^{k} (N + 1)$.

The value of order eight matrices W₁ and W₂ for N = 7 and k = 0 (α = 1/3, β = 1) is:

$$ W_{1} = \left[ {\begin{array}{*{20}c} {0.328623} & {0.421814} & {0.249677} & {0.230090} & {0.174416} & {0.151103} & {0.107665} & {0.064795} \\ { - 0.013906} & {0.307961} & {0.389789} & {0.214733} & {0.204112} & {0.144319} & {0.118830} & {0.062021} \\ {0.001558} & { - 0.027292} & {0.285000} & {0.353173} & {0.177834} & {0.175703} & {0.108464} & {0.071225} \\ { - 0.002993} & {0.004859} & { - 0.039681} & {0.259042} & {0.310580} & {0.139078} & {0.141380} & {0.059758} \\ {0.000082} & { - 0.001308} & {0.009575} & { - 0.050277} & {0.228978} & {0.259821} & {0.098334} & {0.087474} \\ { - 0.000029} & {0.000047} & {0.175703} & {0.139078} & {0.259821} & {0.192848} & { - 0.058880} & {0.023523} \\ {0.000013} & {0.000213} & { - 0.003516} & { - 0.007131} & {0.023177} & { - 0.05888} & {0.146459} & {0.109053} \\ { - 0.000005} & {0.000094} & { - 0.000685} & {0.003100} & { - 0.009843} & {0.023523} & { - 0.044944} & {0.075750} \\ \end{array} } \right] $$

$$ W_{2} = \left[ {\begin{array}{*{20}c} {0.328623} & { - 0.013906} & {0.001558} & { - 0.002993} & {0.000082} & { - 0.000029} & {0.000013} & { - 0.000005} \\ {0.421814} & {0.307961} & { - 0.027292} & {0.004859} & { - 0.001308} & {0.000047} & { - 0.000213} & {0.000094} \\ {0.249677} & {0.389789} & {0.285000} & { - 0.039681} & {0.009957} & { - 0.003516} & {0.001559} & { - 0.000068} \\ {0.230090} & {0.214733} & {0.353173} & {0.259042} & { - 0.050277} & {0.016543} & { - 0.007131} & {0.003100} \\ {0.174416} & {0.204112} & {0.177834} & {0.31058} & {0.228978} & { - 0.057656} & {0.023177} & { - 0.009843} \\ {0.151103} & {0.144319} & {0.175703} & {0.139078} & {0.259821} & {0.192848} & { - 0.058880} & {0.023523} \\ {0.107665} & {0.118830} & {0.108464} & {0.141380} & {0.098334} & {0.196797} & {0.146459} & { - 0.044944} \\ {0.064795} & {0.062021} & {0.071225} & {0.059758} & {0.087474} & {0.052106} & {0.109053} & {0.075750} \\ \end{array} } \right] $$

Similarly, The value of order six matrices W₁ and W₂ for N = 5 and k = 0 (α = 1/2, β = 1) is:

$$ W_{1} = \left[ {\begin{array}{*{20}c} {0.706694} & {0.669669} & {0.282085} & {0.284418} & {0.159798} & {0.111071} \\ { - 0.030444} & {0.669500} & {0.607355} & {0.227492} & {0.239991} & {0.092652} \\ {0.000236} & { - 0.0611950} & {0.622263} & {0.528185} & {0.168287} & {0.158927} \\ {0.000105} & {013697} & { - 0.090295} & {0.558931} & {0.465426} & {0.09712} \\ {0.000380} & { - 0.004750} & {0.028231} & { - 0.112400} & {0.465426} & {0.25556} \\ { - 0.000150} & {0.001866} & { - 0.010731} & {0.039044} & { - 0.10597} & {0.287359} \\ \end{array} } \right], $$

$$ W_{2} = \left[ {\begin{array}{*{20}c} {0.706694} & { - 0.030444} & {0.000236} & {0.000105} & {0.000380} & { - 0.000150} \\ {0.669669} & {0.669500} & { - 0.0611950} & {013697} & { - 0.004750} & {0.001866} \\ {0.282085} & {0.607355} & {0.622263} & { - 0.090295} & {0.028231} & { - 0.010731} \\ {0.284418} & {0.227492} & {0.528185} & {0.558931} & { - 0.112400} & {0.039044} \\ {0.159798} & {0.239991} & {0.168287} & {0.421923} & {0.465426} & { - 0.10597} \\ {0.111071} & {0.092652} & {0.158927} & {0.09712} & {0.25556} & {0.287359} \\ \end{array} } \right]. $$

The matrix W₂ can be calculated directly from W₁, it is the transpose of W₁, so it is easy to calculate them and one matrix can be written in the form of another matrix (W₂ = W ^T₁ , W₁ = W ^T₂ ).

Now on substituting Eq. (12) in Eq. (10), we obtain

$$ \left. {\begin{array}{*{20}l} {\mathop \rho \nolimits_{1} (s)C_{1}^{T} W_{1} \varPsi (s) + \mathop \rho \nolimits_{2} (s)C_{2}^{T} W_{2} \varPsi (s) = F_{1}^{T} \varPsi (s)} \hfill \\ {\mathop \omega \nolimits_{1} (s)C_{1}^{T} W_{2} \varPsi (s) + \mathop \omega \nolimits_{2} (s)C_{2}^{T} W_{1} \varPsi (s) = F_{2}^{T} \varPsi (s)} \hfill \\ \end{array} } \right\} $$

(13)

On simplifying we get

$$ \left. {\begin{array}{*{20}l} {\mathop \rho \nolimits_{1} (s)C_{1}^{T} W_{1} + \mathop \rho \nolimits_{2} (s)C_{2}^{T} W_{2} = F_{1}^{T} } \hfill \\ {\mathop \omega \nolimits_{1} (s)C_{1}^{T} W_{2} + \mathop \omega \nolimits_{2} (s)C_{2}^{T} W_{1} = F_{2}^{T} } \hfill \\ \end{array} } \right\} $$

(13a)

Next, we solve the algebraic system in Eq. (13a), for the vectors C ^T₁ and C ^T₂

$$ \begin{aligned} & C_{1}^{T} = \left[ {F_{1}^{T} \omega_{2} (s)W_{1} - F_{2}^{T} \mathop \rho \nolimits_{2} (s)W_{2} } \right]\,\,\left[ {\mathop \rho \nolimits_{1} (s)W_{1} \omega_{2} (s)W_{1} - \mathop \rho \nolimits_{2} (s)W_{2} \omega_{1} (s)W_{2} } \right]^{ - 1} , \\ & C_{2}^{T} = \left[ {F_{2}^{T} \mathop \rho \nolimits_{1} (s)W_{1} - F_{1}^{T} \omega_{1} (s)W_{2} } \right]\,\,\left[ {\mathop \rho \nolimits_{1} (s)W_{1} \omega_{2} (s)W_{1} - \mathop \rho \nolimits_{2} (s)W_{2} \omega_{1} (s)W_{2} } \right]^{ - 1} \\ \end{aligned} $$

(13b)

We can also calculate the values of C ^T₁ and C ^T₂ for some special cases of the system given in Eq. (1),

(i) When the coefficient $\mathop \rho \nolimits_{1} (s) = \mathop \omega \nolimits_{2} (s)$ and $\mathop \rho \nolimits_{2} (s) = \mathop \omega \nolimits_{1} (s)$, then

On adding and subtracting equations of (13a), we get

$$ \begin{aligned} & \mathop \rho \nolimits_{1} (s)C_{1}^{T} W_{1} + \mathop \rho \nolimits_{2} (s)C_{2}^{T} W_{2} + \mathop \omega \nolimits_{1} (s)C_{1}^{T} W_{2} + \mathop \omega \nolimits_{2} (s)C_{2}^{T} W_{1} = F_{1}^{T} + F_{2}^{T} , \\ & \mathop \rho \nolimits_{1} (s)C_{1}^{T} W_{1} + \mathop \rho \nolimits_{2} (s)C_{2}^{T} W_{2} \mathop { - \omega }\nolimits_{1} (s)C_{1}^{T} W_{2} - \mathop \omega \nolimits_{2} (s)C_{2}^{T} W_{1} = F_{1}^{T} - F_{2}^{T} \\ \end{aligned} $$

(13c)

Using approximations $\mathop \rho \nolimits_{1} (s) = \mathop \omega \nolimits_{2} (s)$ and $\mathop \rho \nolimits_{2} (s) = \mathop \omega \nolimits_{1} (s)$, Eq. (13c) becomes

$$ \begin{aligned} \mathop {\left[ {C_{1}^{T} + C_{2}^{T} } \right]\rho }\nolimits_{1} (s)W_{1} + \left[ {C_{1}^{T} + C_{2}^{T} } \right]\mathop \rho \nolimits_{2} (s)W_{2} = F_{1}^{T} + F_{2}^{T} , \hfill \\ \left[ {C_{1}^{T} - C_{2}^{T} } \right]\mathop \omega \nolimits_{2} (s)W_{1} - \left[ {C_{1}^{T} - C_{2}^{T} } \right]\mathop \omega \nolimits_{1} (s)W_{2} = F_{1}^{T} - F_{2}^{T} \hfill \\ \end{aligned} $$

(13d)

Equation (13d) can be written in the following form

$$ \left. {\begin{array}{*{20}l} {[C_{1} + C_{2} ]^{T} = [F_{1} + F_{2} ]^{T} \left[ {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right]^{ - 1} } \hfill \\ {[C_{1} - C_{2} ]^{T} = [F_{1} - F_{2} ]^{T} \left[ {\mathop \omega \nolimits_{2} (s)W_{1} - \mathop \omega \nolimits_{1} (s)W_{2} } \right]^{ - 1} } \hfill \\ \end{array} } \right\}, $$

(14)

Next, we solve the above algebraic system in Eq. (14) for the vectors C ^T₁ and C ^T₂

$$ \begin{aligned} & C_{1}^{T} = \frac{1}{2}\left[ {[F_{1} + F_{2} ]^{T} \left[ {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right]^{ - 1} + [F_{1} - F_{2} ]^{T} \left[ {\mathop \omega \nolimits_{2} (s)W_{1} - \mathop \omega \nolimits_{1} (s)W_{2} } \right]^{ - 1} } \right], \\ & C_{2}^{T} = \frac{1}{2}\left[ {[F_{1} + F_{2} ]^{T} \left[ {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right]^{ - 1} - [F_{1} - F_{2} ]^{T} \left[ {\mathop \omega \nolimits_{2} (s)W_{1} - \mathop \omega \nolimits_{1} (s)W_{2} } \right]^{ - 1} } \right] \\ \end{aligned} $$

(14a)

(ii) When the values of all coefficients of the system given in Eq. (1) are unity. Then using approximation $\mathop \rho \nolimits_{1} (s) = \mathop \rho \nolimits_{2} (s) = \mathop \omega \nolimits_{1} (s) = \mathop \omega \nolimits_{2} (s) = 1$, in Eq. (13c), we get

$$ \left. {\begin{array}{*{20}l} {[C_{1} + C_{2} ]^{T} = [F_{1} + F_{2} ]^{T} \left[ {W_{1} + W_{2} } \right]^{ - 1} } \hfill \\ {[C_{1} - C_{2} ]^{T} = [F_{1} - F_{2} ]^{T} \left[ {W_{1} - W_{2} } \right]^{ - 1} } \hfill \\ \end{array} } \right\} $$

(14b)

Next, we solve the above algebraic system (14b) for the vectors C ^T₁ and C ^T₂

$$ \begin{aligned} & C_{1}^{T} = \frac{1}{2}\left[ {[F_{1} + F_{2} ]^{T} \left[ {W_{1} + W_{2} } \right]^{ - 1} + [F_{1} - F_{2} ]^{T} \left[ {W_{1} - W_{2} } \right]^{ - 1} } \right], \\ & C_{2}^{T} = \frac{1}{2}\left[ {[F_{1} + F_{2} ]^{T} \left[ {W_{1} + W_{2} } \right]^{ - 1} - [F_{1} - F_{2} ]^{T} \left[ {W_{1} - W_{2} } \right]^{ - 1} } \right] \\ \end{aligned} $$

(14c)

On substituting these values of the vectors C ^T₁ and C ^T₂ [for the general case from Eq. (13b), for the special case (i) from Eq. (14a) and special case (ii) from Eq. (14c)] in Eq. (9), we get the following approximate solutions

$$ \varepsilon_{1} (u) = C_{1}^{T} \varPsi (u);\,\,\varepsilon_{2} (u) = C_{2}^{T} \varPsi (u). $$

(15)

See “Appendix 2”.

Convergence of the wavelet bases

In this section, we discuss a lemma and theorem that supports the absolute error of the proposed method and also presents an error analysis of the proposed method.

Lemma 1

(See [24]) Let the function$\varepsilon (u) \in C^{n} [0,\,\,1]$, be a collection of all real-valued n times continuously differentiable functions. The mean error bound of approximation in Eq. (6) is

$$ \left\| {C^{T} \varPsi (u) - \varepsilon (u)} \right\| \le \frac{2}{{4^{n} 2^{nk} n!}}\mathop {\sup }\limits_{{x \in \left[ {0,1} \right]}} \left| {\varepsilon^{(n)} (u)} \right|. $$

(16)

Proof

Let us divide the existing interval [0, 1] into subintervals $[{m \mathord{\left/ {\vphantom {m {2^{k} ,}}} \right. \kern-0pt} {2^{k} ,}}{{m + 1} \mathord{\left/ {\vphantom {{m + 1} {2^{k} }}} \right. \kern-0pt} {2^{k} }}] = I_{m,k}$(say), on which the restriction of $C^{T} \varPsi (u)$ to one such subinterval I_m,k is the polynomial of order n that interpolates ɛ(u) with the minimum mean error. Following which, we employ the maximum error estimation for the polynomial which interpolates ɛ(u) at Chebyshev nodes, of order n. The interpolation polynomial of $C^{T} \varPsi (u)$ is that unique polynomial that has a value ɛ(u_i) at every point u_i. The interpolation error at u is given by [24],

$$ \varepsilon (u) - C^{T} \varPsi (u) = \frac{{\varepsilon^{(n)} (\xi )}}{n!}\prod\limits_{i = 1}^{n} {(u - u_{i} )} $$

for some ξ (depending on u) in [a, b], so it is obvious to minimize $\mathop {\sup }\limits_{{u \in \left[ {0,\,1} \right]}} \left| {\prod\limits_{i = 1}^{n} {(u - u_{i} )} } \right|$ for better convergence as n → ∞, here product represents in the form of monic polynomials. It can be demonstrated that the maximum norm of such polynomial is bounded below by 2¹⁻ⁿ. This bound is obtained by scaled Bernstein polynomials 2¹⁻ⁿB_n,  which are monic as well. Thus, for an arbitrary interval [a, b] the roots of the given polynomial are the interpolation Chebyshev nodes u_i, and the error satisfies the following equation

$$ \left| {\varepsilon (u) - C^{T} \varPsi (u)} \right| \le \frac{{2^{1 - n} }}{n!}\left( {\frac{b - a}{2}} \right)^{n} \mathop {\sup }\limits_{\xi \in [a,b]} \left| {\varepsilon^{(n)} (\xi )} \right| $$

(17a)

□

The left side of Eq. (16);

$$ \left\| {C^{T} \varPsi (u) - \varepsilon (u)} \right\|^{2} = \int\limits_{0}^{1} {[C^{T} \varPsi (u) - \varepsilon (u)]^{2} } {\text{d}}u $$

$$ \left\| {C^{T} \varPsi - \varepsilon } \right\|^{2} = \sum\limits_{k} {\int\limits_{{I_{m,k} }} {[C^{T} \varPsi (u) - \varepsilon (u)]^{2} {\text{d}}u} } $$

Using Eq. (17a) and $I_{m,k} = [{m \mathord{\left/ {\vphantom {m {2^{k} }}} \right. \kern-0pt} {2^{k} }},{{m + 1} \mathord{\left/ {\vphantom {{m + 1} {2^{k} }}} \right. \kern-0pt} {2^{k} }}]$ we get

$$ \left\| {C^{T} \varPsi - \varepsilon } \right\|^{2} \le \int\limits_{0}^{1} {\left( {\frac{{2^{1 - nk} }}{{4^{n} n!}}\mathop {\sup }\limits_{{u \in \left[ {0,1} \right]}} \left| {\varepsilon^{(n)} (u)} \right|} \right)^{{^{2} }} {\text{d}}u} $$

$$ \left\| {C^{T} \varPsi - \varepsilon } \right\|^{2} \le \left( {\frac{2}{{4^{n} 2^{nk} n!}}\mathop {\sup }\limits_{{u \in \left[ {0,1} \right]}} \left| {\varepsilon^{(n)} (u)} \right|} \right)^{{^{2} }} $$

(17b)

The square root of the Eq. (17b) will give the upper bound of the given approximation in Eq. (6). The approximation error of the function ɛ(u) rapidly decays like 1/2^nk. These bounds of the error obtained are governed by the term $1/(2^{2n + n\,k - 1} n!)$, which varies inversely with values of k and n and minimizes to zero as values of k and n increase significantly. On the contrary, in classical orthogonal bases such as Chebyshev, Legendre and Fourier, it depends on $1/n!$. Here, the two arguments n and k, in the basis are the two degrees of freedom for the B-polynomial wavelet bases, which help in the accuracy of the introduced method. This is the advantage of the proposed method.

Theorem 1

(Ref. [25]) Suppose that the known functions in the system of generalized Abel integral equations are real n + 1 times continuously differentiable functions on the bounded interval [0, 1] and$\sum\nolimits_{i = 0}^{\infty } {c_{i} \;\varPsi (u)}$be the infinite series expansion of exact solution ɛ(u), in the form of Bernstein polynomials orthonormal wavelet bases and ɛ_n(u) denotes its truncation such as$C^{T} \varPsi (u)$ and similarly,$\tilde{\varepsilon }(u)$is the infinite expansion of the approximate solution and$\tilde{\varepsilon }_{n} (u)$is the truncated part of$\tilde{\varepsilon }(u)$, taken as$\tilde{C}^{T} \varPsi (u)$, then there exist the real numbers λ₁and λ₂such that

$$ \Delta \varepsilon (u) = \left\| {\varepsilon (u) - \tilde{\varepsilon }_{n} (u)} \right\|_{2} \le \lambda_{1} S_{n;k} + \,\lambda_{2} \left\| {C - \tilde{C}} \right\|_{2} $$

(18)

where

$$ \begin{aligned} & C = \left[ {c_{00} ,c_{01} , \ldots ,c_{0N} ,c_{10} , \ldots ,c_{1N} , \ldots ,c_{{(2^{k} - 1)0}} , \ldots ,c_{{(2^{k} - 1)N}} } \right]^{T} ; \\ & \tilde{C} = \left[ {\tilde{c}_{00} ,\tilde{c}_{01} , \ldots ,\tilde{c}_{0N} ,\tilde{c}_{10} , \ldots ,\tilde{c}_{1N} , \ldots ,\tilde{c}_{{(2^{k} - 1)0}} , \ldots ,\tilde{c}_{{(2^{k} - 1)N}} } \right]^{T} \\ \end{aligned} $$

and

$$ S_{n;k} = \left( {\frac{1}{{2^{n.k + 2n - 1} n!}}} \right)\mathop {\sup }\limits_{\xi \in [a,b]} \left| {\varepsilon^{(n)} (\xi )} \right|. $$

Proof

Let us take the truncated series ɛ_n(u) and $\tilde{\varepsilon }_{n} (u)$ are in R_n[u] (where R_n[u] is the space of real-valued polynomials of degree less than equal to the space of real-valued polynomials of degree less than equal to n), ɛ_n(u) is the best approximation of ɛ(u) in R_n[u], then

$$ \left\| {\varepsilon (u) - \tilde{\varepsilon }_{n} (u)} \right\|_{2} = \left\| {\varepsilon (u) - \varepsilon_{n} (u) + \varepsilon_{n} (u) - \tilde{\varepsilon }_{n} (u)} \right\|_{2} \le \left\| {\varepsilon (u) - \varepsilon_{n} (u)} \right\|_{2} + \,\left\| {\varepsilon_{n} (u) - \tilde{\varepsilon }_{n} (u)} \right\|_{2} . $$

(19)

Now, the first part of the right-hand side of Eq. (19), yields

$$ \left\| {\varepsilon (u) - \varepsilon_{n} (u)} \right\|_{2} = \int\limits_{0}^{1} {\left[ {\left| {\varepsilon (u) - \varepsilon_{n} (u)} \right|^{2} du} \right]^{{^{1/2} }} } $$

using Lemma 1, we get

$$ \le \left[ {\int\limits_{0}^{1} {(S_{n;k} )^{2} {\text{d}}u} } \right]^{1/2} $$

$$ \left\| {\varepsilon (u) - \varepsilon_{n} (u)} \right\|_{2} \le S_{n;k} ;\,{\text{so}}\quad \lambda_{1} = 1. $$

(20)

Also, the second part of the right-hand side of Eq. (19), yields

$$ \left\| {\varepsilon_{n} (u) - \tilde{\varepsilon }_{n} (u)} \right\|_{2} = \left[ {\int\limits_{0}^{1} {\left| {\sum\limits_{i = 0}^{n} {(C_{i} - \tilde{C}_{i} )\varPsi_{i} (u)} } \right|^{{^{2} }} {\text{d}}u} } \right]^{1/2} $$

i.e.,

$$ \left( {\left\| {\varepsilon_{n} (u) - \tilde{\varepsilon }_{n} (u)} \right\|_{2} } \right)^{2} = \int\limits_{0}^{1} {\left| {\sum\limits_{i = 0}^{n} {(C_{i} - \tilde{C}_{i} )\varPsi_{i} (u)} } \right|^{2} {\text{d}}u} . $$

(21)

□

Now, we use the generalized triangular inequality in the right-hand side of Eq. (21), such as

$$ \begin{aligned} & \int\limits_{0}^{1} {\left| {\sum\limits_{i = 0}^{n} {(C_{i} - \tilde{C}_{i} )\varPsi_{i} (u)} } \right|^{2} {\text{d}}u} \\ & \quad \le \int\limits_{0}^{1} {\left( {\sum\limits_{i = 0}^{n} {\left| {(C_{i} - \tilde{C}_{i} )} \right|\left| {\varPsi_{i} (u)} \right|} } \right)}^{2} {\text{d}}u \\ & \quad = \int\limits_{0}^{1} {\left[ {\sum\limits_{i = j = 0}^{n} {\left| {C_{i} - \tilde{C}_{i} } \right|^{2} \left| {\varPsi_{i} (u)} \right|^{2} + \sum\limits_{i \ne j = 0}^{n} {\left| {C_{i} - \tilde{C}_{i} } \right|\left| {C_{j} - \tilde{C}_{j} } \right|\left| {\varPsi_{i} (u)} \right|\left| {\varPsi_{j} (u)} \right|} } } \right]{\text{d}}u} \\ & \quad = \sum\limits_{i = j = 0}^{n} {\left| {C_{i} - \tilde{C}_{i} } \right|^{2} } \int\limits_{0}^{1} {\left| {\varPsi_{i} (u)} \right|^{2} {\text{d}}u + \sum\limits_{i \ne j = 0}^{n} {\left| {C_{i} - \tilde{C}_{i} } \right|\left| {C_{j} - \tilde{C}_{j} } \right|} \int\limits_{0}^{1} {\left| {\varPsi_{i} (u)} \right|\left| {\varPsi_{j} (u)} \right|} {\text{d}}u} \\ \end{aligned} $$

using orthonormality of Bernstein polynomial multiwavelets

$$ = \sum\limits_{i = 0}^{n} {\left| {C_{i} - \tilde{C}_{i} } \right|^{2} } . $$

(22)

Next, by substituting Eq. (22) in Eq. (21) we get,

$$ \left\| {\varepsilon_{n} (u) - \tilde{\varepsilon }_{n} (u)} \right\|_{2} \le \left\| {C - \tilde{C}} \right\|. $$

(23)

We substituted values from Eq. (20) and Eq. (23) in Eq. (18) and concluded that it holds valid for

$$ \lambda_{1} = 1;\,\,\lambda_{2} = 1. $$

Hence, as illustrated, Δɛ(u) decreases as n → ∞.

Illustrative example

The estimated solution ɛ(u) (emissivity) cannot be calculated exactly if the data function I(s) is given with very small or high-frequency errors. These errors in the data function can occur from experimental errors which results into large errors in emissivity since differentiation of the measured data is required in these formulae, that’s why the stable numerical techniques become vital, but in the proposed method there is no need of the differentiation of data function. Thus, we have suggested a new stable numerical technique for the solution of the system given in Eq. (1). The stability of the proposed method is showing for a system by adding noise μ in I(s) and presented the convergence of the proposed method by calculating the pointwise error. Some suitable illustrative examples with figures are given to show the stability and accuracy of the introduced method for the known system even with particular noise μ.

Next, the exactness of the proposed method is shown by calculating the absolute error $\Delta \varepsilon (u_{i} )$ with the help of Theorem 1, such that

$$ \Delta \varepsilon (u_{i} ) = \left| {\varepsilon (u_{i} ) - \tilde{\varepsilon }_{n} (u_{i} )} \right|, $$

(24)

where $\tilde{\varepsilon }_{n} \,(u_{i} )$ and ɛ(u_i) are the estimated solution and exact solutions calculated at the corresponding point u_i, respectively. Also, I(s) and I^μ(s) represent the exact and noisy profiles, respectively, where I^μ(s) is obtained by adding a noise μ to I(s), i.e., $I^{\mu } (s_{i} ) = I^{\mu } (s_{i} ) + \mu \theta_{i}$ where $\theta_{i}$ stands for the uniform random variable which takes values in [− 1,1], $s_{i} = i\mu ,\,\,i = 1, \ldots ,\tilde{N},\,\,\,\tilde{N}\mu = 1$ and $\mathop {\text{Max}}\limits_{1 \le i \le \,N} \left| {I_{i}^{\mu } (s) - I_{i} (s)} \right| \le \mu$.

Now, using Eqs. (14a) and (15) the reconstructed emissivities ${}^{\mu }\tilde{\varepsilon }_{i}$ are obtained with noise term μ in intensity profile under the condition $\mathop \rho \nolimits_{1} (s) = \mathop \omega \nolimits_{2} (s)$ and $\mathop \rho \nolimits_{2} (s) = \mathop \omega \nolimits_{1} (s)$, are given as

$$ \begin{aligned} & {}^{\mu }\tilde{\varepsilon }_{1} (u) \approx \frac{1}{2}\left[ {\left( {{}^{\mu }F_{1} + {}^{\mu }F_{2} } \right)^{T} \left( {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right)^{ - 1} + \left( {{}^{\mu }F_{1} - {}^{\mu }F_{2} } \right)^{T} \left( {\mathop \omega \nolimits_{2} (s)W_{1} - \mathop \omega \nolimits_{1} (s)W_{2} } \right)^{ - 1} } \right]\varPsi (u), \\ & {}^{\mu }\tilde{\varepsilon }_{2} (u) \approx \frac{1}{2}\left[ {\left( {{}^{\mu }F_{1} + {}^{\mu }F_{2} } \right)^{T} \left( {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right)^{ - 1} + \left( {{}^{\mu }F_{1} - {}^{\mu }F_{2} } \right)^{T} \left( {\mathop \omega \nolimits_{2} (s)W_{1} - \mathop \omega \nolimits_{1} (s)W_{2} } \right)^{ - 1} } \right]\varPsi (u) \\ \end{aligned} $$

(25)

where ${}^{\mu }I_{i} (s)$ and I_i(s) are known functions (i = 1, 2), and they are obtained from the following equations:

$$ {}^{\mu }I_{i} (s) = I_{i} (s) + \mu \theta_{i} \approx {}^{\mu }F_{i}^{T} \varPsi (u) $$

and

$$ I_{i} (s) \approx F_{i}^{T} \varPsi (u). $$

Hence from Eqs. (15) and (25)

$$ \begin{aligned} {}^{\mu }\tilde{\varepsilon }_{1} (u) - \tilde{\varepsilon }_{1} (u) & = \left[ {\frac{1}{2}\left\{ {\left( {{}^{\mu }F_{1} + {}^{\mu }F_{2} } \right)^{T} \left( {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right)^{ - 1} }\right.}\right. \\ & \qquad +\left.{\left.{ \left( {{}^{\mu }F_{1} - {}^{\mu }F_{2} } \right)^{T} \left( {\mathop \omega \nolimits_{2} (s)W_{1} - \mathop \omega \nolimits_{1} (s)W_{2} } \right)^{ - 1} } \right\}\varPsi (u)} \right] \\ & \quad - \left[ {\frac{1}{2}\left\{ {\left( {F_{1} + F_{2} } \right)^{T} \left( {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right)^{ - 1}}\right.}\right.\\ &\qquad \left.{ \left.{+ \left( {F_{1} - F_{2} } \right)^{T} \left( {\mathop \omega \nolimits_{2} (s)W_{1} - \mathop \omega \nolimits_{1} (s)W_{2} } \right)^{ - 1} } \right\}\varPsi (u)} \right] \\ \end{aligned} $$

i.e.,

$$ \begin{aligned} {}^{\mu }\tilde{\varepsilon }_{1} (u) - \tilde{\varepsilon }_{1} (u) & = \frac{1}{2}\left[ {\left( {H_{1}^{T} + H_{2}^{T} } \right)} \right.\left( {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right)^{ - 1} \\ & \quad + \left. {\left( {H_{1}^{T} - H_{2}^{T} } \right)\left( {\mathop \omega \nolimits_{1} (s)W_{1} - \mathop \omega \nolimits_{2} (s)W_{2} } \right)^{ - 1} } \right]\varPsi (u), \\ \end{aligned} $$

where $H_{1}^{T} = {}^{\mu }F_{1}^{T} - F_{1}^{T} ,\,H_{2}^{T} = {}^{\mu }F_{2}^{T} - F_{2}^{T}$ and

$$ \begin{aligned} \left\| {{}^{\mu }\tilde{\varepsilon }_{1} (u) - \tilde{\varepsilon }_{1} (u)} \right\|_{2} & \le \frac{1}{2}\left( {\left\| {H_{1}^{T} + H_{2}^{T} } \right\|\left\| {\left[ {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right]^{ - 1} } \right\|} \right. \\ & \quad \left. { + \left\| {H_{1}^{T} - H_{2}^{T} } \right\|\left\| {\left[ {\mathop \omega \nolimits_{2} (s)W_{1} - \mathop \omega \nolimits_{1} (s)W_{2} } \right]^{ - 1} } \right\|} \right)\left\| {\varPsi (u)} \right\| \\ \end{aligned} $$

Similarly, from Eqs. (15) and (25), we get

$$ \begin{aligned} \left\| {{}^{\mu }\tilde{\varepsilon }_{2} (u) - \tilde{\varepsilon }_{2} (u)} \right\|_{2} & \le \frac{1}{2}\left( {\left\| {H_{1}^{T} + H_{2}^{T} } \right\|\left\| {\left[ {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right]^{ - 1} } \right\|} \right. \\ & \quad \left. { - \left\| {H_{1}^{T} - H_{2}^{T} } \right\|\left\| {\left[ {\mathop \omega \nolimits_{2} (s)W_{1} - \mathop \omega \nolimits_{1} (s)W_{2} } \right]^{ - 1} } \right\|} \right)\left\| {\varPsi (u)} \right\|. \\ \end{aligned} $$

Setting,

$$ h_{1} (u) = {}^{\mu }\tilde{\varepsilon }_{1} (u) - \tilde{\varepsilon }_{1} (u) $$

and

$$ h_{2} (u) = {}^{\mu }\tilde{\varepsilon }_{2} (u) - \tilde{\varepsilon }_{2} (u), $$

then $h_{1} (u)$ and $h_{2} (u)$ reflect the noise reduction capability [23] of the method, which is shown in Figs. 6 and 7, for example, 1. The general behavior of noise reduction is the same irrespective of the value of μ.

Example 1

In the first example, consider Eq. (1) with $\mathop \rho \nolimits_{1} (s),\,\mathop \rho \nolimits_{2} (s)\,;\,\omega_{1} (s)$ and ω₂(s) are unity and β = 1, α = 1/3 for the pairs:

$$ \begin{aligned} I_{1} (s) &= e^{s} \left[ {\varGamma \left( {\frac{2}{3}} \right) - \varGamma \left( {\frac{2}{3},s} \right)} \right] \\ &+ \frac{{ \, e^{2s} \left( {1 - s} \right)^{{\tfrac{2}{3}}} \left[ {\varGamma \left( {\frac{2}{3}} \right) - \varGamma \left( {\frac{2}{3},s - 1} \right)} \right]}}{{2^{{\tfrac{2}{3}}} \left( {s - 1} \right)^{{\tfrac{2}{3}}} }} \\ I_{2} (s) &= \frac{{ \, e^{s} \left( {1 - s} \right)^{{\tfrac{2}{3}}} \left[ {\varGamma \left( {\frac{2}{3}} \right) - \varGamma \left( {\frac{2}{3},s - 1} \right)} \right]}}{{\left( {s - 1} \right)^{{\tfrac{2}{3}}} }} \\ & + \frac{{e^{2s} \left( {1 - s} \right)^{{\tfrac{2}{3}}} \left[ {\varGamma \left( {\frac{2}{3}} \right) - \varGamma \left( {\frac{2}{3},s - 1} \right)} \right]}}{{2^{{\tfrac{2}{3}}} }}, \\ \end{aligned} $$

(26)

where $\varGamma (.)$ represents the gamma functions and

$$ \varepsilon_{1} (u) = e^{u} ,\,\,\,\varepsilon_{2} (u) = e^{2u} , $$

are exact solutions of Eq. (1) for the above values of $I_{1} (s),\,\,I_{2} (s)$ and Eqs. (14c) and (15) provide the desired approximate solutions

$$ \tilde{\varepsilon }_{1} (u) = \tilde{C}_{1}^{T} \varPsi (u),\,\tilde{\varepsilon }_{2} (u) = \tilde{C}_{2}^{T} \varPsi (u). $$

Here, the Bernstein polynomials orthonormal wavelet bases are taking for k = 0, 1; N = 7 and apply the introduced method, to get the approximate solutions of Eq. (26), which are shown in Table 1. Now, the associated absolute errors without noise are depicted by

$$ \begin{aligned} & E_{1} (u) = \left| {\varepsilon_{1} (u) - \tilde{\varepsilon }_{1} (u)} \right| \\ & E_{2} (u) = \left| {\varepsilon_{2} (u) - \tilde{\varepsilon }_{2} (u)} \right|, \\ \end{aligned} $$

which are shown in Figs. 2 and 3, respectively, for dilation parameter k = 0 and k = 1. The comparison of absolute errors E₃(u), E₄(u) for the noise level μ₁ = 0.001 and E₅(u), E₆(u) at the noise level μ₂ = 0.002, respectively, for k = 0 and k = 1 are shown in Figs. 4 and 5.The stability of the proposed method is shown by calculating the noise reducing capability h₁(u) and h₂(u) which are shown in Figs. 6 and 7 for example 1, similarly we can calculate noise reducing capability for other examples.

Table 1 Approximate and exact solution of example 1

Fig. 2

Comparison of the absolute errors with noise μ = 0 in example 1, for k = 0

Fig. 3

Comparison of the absolute errors with noise μ = 0 in example 1, for k = 1

Fig. 4

Comparison of absolute errors with noises $\mu_{1} = 0.001,\,\mu_{2} = 0.002$ in example 1, for k = 0

Fig. 5

Comparison of absolute errors with noises μ₁ = 0.001, μ₂ = 0.002 in example 1, for k = 1

Fig. 6

Noise reduction h₁(u) for the solution function $\tilde{\varepsilon }_{1} (u)$ in example 1

Fig. 7

Noise reduction h₂(u) for the solution function $\tilde{\varepsilon }_{2} (u)$ in example 1

Example 2

Let us consider Eq. (1) with $\rho_{1} (s) = (s^{2} + 1), \, \rho_{2} (s) = \frac{(s + 1)}{4} ; { }\omega_{1} (s) = \frac{{s^{2} }}{2},\,\,\,\omega_{2} (s) = 2 - s$ and $\alpha = 1/2,\beta = 1$ for the pairs [14]:

$$ \begin{aligned} & I_{1} (s) = \frac{16}{15}s^{5/2} (1 + s^{2} ) + \frac{1}{70}\left( {s + 1} \right)\sqrt {1 - s} \left[ {5 + 2s\left( {3 + 4s + 8s^{2} } \right)} \right], \\ & I_{2} (s) = \frac{16}{35}s^{11/2} + (2 - s)\left[ {\frac{2}{15}\sqrt {1 - s} \left( {3 + 4s + 8s^{2} } \right)} \right] \\ \end{aligned} $$

(27)

there exist an analytical solution of Eq. (1) for the above $I_{1} (s),\,\,I_{2} (s)$, like as

$$ \varepsilon_{1} (u) = u^{2} ;\,\,\,\varepsilon_{2} (u) = u^{3} . $$

Here, we applied the proposed method similar to the example 1 for N = 5 and k = 0 to get the desired approximate solution

$$ \tilde{\varepsilon }_{1} (u) = \tilde{C}_{1}^{T} \varPsi (u),\tilde{\varepsilon }_{2} (u) = \tilde{C}_{2}^{T} \varPsi (u). $$

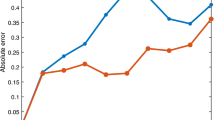
Now, the comparison of the approximated solution for the proposed method and the given method in Ref. [14] is shown in Table 2, even less number of polynomials taken but achieves better results with higher accuracy are obtained in the present method.Next, the absolute errors $E_{1} (u) , { }E_{2} (u)$ for the proposed method are of order 10⁻⁵ as shown in Fig. 8.Whereas, the comparison of absolute errors $E_{3} (u),E_{4} (u)$ for the noise level $\mu_{1} = 0.001$, and $E_{5} (u),\,E_{6} (u)$ at the noise level μ₂ = 0.002, respectively, for k = 0 and k = 1 can be obtained to the similar of example 1.

Table 2 Comparison between the proposed method and Bernstein polynomial method [14]

Fig. 8

Comparison of absolute errors in example 2, for k = 0

Example 3

In this example, we consider Eq. (1) with $\rho_{1} (s) = \rho_{2} (s) = 1;\,\,\,\omega_{1} (s) = \omega_{2} (s) = 1$ and $\alpha = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2},\beta = 2$ for the pairs

$$ \begin{aligned} & I_{1} (s) = \frac{{4s^{3/2} }}{3} + e^{s} \sqrt \pi \,erf(\sqrt s ) + \frac{2}{15}\sqrt {1 - s} \left( {3 + 4s + 8s^{2} } \right), \\ & I_{2} (s) = \frac{{16s^{5/2} }}{15} + \frac{{2(1 + s - 2s^{2} )}}{{3\sqrt {s - 1} }} + \frac{{e^{s} \sqrt {\pi - \pi s} \,erf(\sqrt {s - 1} )}}{{\sqrt {s - 1} }} \\ \end{aligned} $$

(28)

with the exact solution

$$ \varepsilon_{1} (u) = e^{u} + u,\,\varepsilon_{2} (u) = u^{2} , $$

where

$$ erf(s) = \frac{2}{\sqrt \pi }\int\limits_{0}^{s} {e^{{ - t^{2} }} {\text{d}}t.} $$

and its approximate solutions $\tilde{\varepsilon }_{1} (u),\,\tilde{\varepsilon }_{2} (u)$ are free from noise, which is presented in Table 3, for N = 5, k = 0 by the same approach used in the above examples.Now, the absolute errors $E_{1} (u) , { }E_{2} (u)$ associated with example 3 are obtained similar to the first example, and it is shown in Fig. 9.

Table 3 Comparison between the exact and proposed solution

Fig. 9

Comparison of absolute errors in example 3, for k = 0

Next, the comparison to the proposed method for this example is shown in Table 3 from the exact solution.

Conclusions

The system investigated in this paper holds substantial significance in the determination of intensity and emissivity of the plasma spectroscopy model. Our technique demonstrates the comparison between solutions for two different dilation parameters, i.e., k = 0 and k = 1. The stability with relevancy to the data is restored, and a favorable result is obtained, even for small sample intervals with high noise in the data. The selection of a small number of orthonormal polynomials (as shown for n = 5 and n = 7) makes the method easy and straightforward. The error bound obtained demonstrates that a higher degree of convergence is achieved even in the case of an infinite system as compared to the other method in Ref. [25]. This method [25] failed for an infinite system as the series obtained from the difference of truncated functions ɛ_n(u) and $\tilde{\varepsilon }_{n} (u)$

$$ \left\| {\varepsilon_{n} (u) - \tilde{\varepsilon }_{n} (u)} \right\|_{2} \le \left\| {C - \tilde{C}} \right\|_{2} \left( {l\sum\limits_{i = 0}^{n} {\frac{1}{2i + 1}} } \right)^{{\frac{1}{2}}} $$

is a diverging series as $n \to \infty$. Hence, it gives a weaker bound. But in the proposed method, it is less than or equal to $\left\| {C - \tilde{C}} \right\|_{2}$, which holds for every value of n, so it converges slowly even in the case of n → ∞.

Appendices

Appendix 1: Gram–Schmidt process for finding Orthonormal Bernstein Polynomials

The Bernstein polynomial of degree N is $B_{i,\,N} (y)$

• Step 1$b_{0} (y): = \frac{B0,N(y)}{{\left\| {B_{0,N} (y)} \right\|}}$

• Step 2 For i = 1 to N

  $$ C_{i,N} (y): = B_{i,N} (y) - \frac{{\langle Bi,N(y),C_{i - 1,N} (y)\rangle }}{{\left\| {C_{i - 1,N} (y)} \right\|}}*C_{i - 1,N} (y) - \frac{{\langle B_{i,N} (y),C_{i - 2,N} (y)\rangle }}{{\left\| {C_{i - 2,N} (y)} \right\|}}*C_{i - 2,N} (y) \cdots - \frac{{\langle B_{i,N} (y),B_{0,N} (y)\rangle }}{{\left\| {B_{0,N} (y)} \right\|}}*B_{0,N} (y) $$

• Step 3$b_{i} (y): = \frac{{C_{i,N} (y)}}{{\left\| {C_{i,N} (y)} \right\|}}$

  b_i(y) is the required Bernstein polynomial. Here, 〈p(y), q(y)〉represents the inner product of p(y) and q(y) in the Hilbert space L²(R) and ‖ξ(y)‖ is the L² norm of the given function ξ(y).

Appendix 2: Algorithm for the numerical method

• 1. Obtain the orthonormalized version b_n(u) of Bernstein polynomials B_i,n(u).

• 2. Evaluate ψ_mn(u) on the interval [0, 1) using b_n(u).

• 3. Manipulate operational matrices W₁and W₂.

• 4. Find determinant $\left( {W_{1} + W_{2} } \right)$ and determinant $\left( {W_{1} - W_{2} } \right)$, if it is nonzero then we proceed further and go to step 5 otherwise the solution ɛ₁(u) and ɛ₂(u) cannot be computed.

• 5. Manipulate matrices $F_{1}^{T}$ and $F_{2}^{T}$.

• 6. Calculate values of $C_{1}^{T}$ and $C_{2}^{T}$ for different cases accordingly

  In general case

  $$ \begin{aligned} C_{1}^{T} &= \left[ {F_{1}^{T} \omega_{2} (s)W_{1} - F_{2}^{T} \mathop \rho \nolimits_{2} (s)W_{2} } \right] \\ &\quad \times\left[ {\mathop \rho \nolimits_{1} (s)W_{1} \omega_{2} (s)W_{1} - \mathop \rho \nolimits_{2} (s)W_{2} \omega_{1} (s)W_{2} } \right]^{ - 1} , \\ C_{2}^{T} &= \left[ {F_{2}^{T} \mathop \rho \nolimits_{1} (s)W_{1} - F_{1}^{T} \omega_{1} (s)W_{2} } \right]\\ &\quad \times\left[ {\mathop \rho \nolimits_{1} (s)W_{1} \omega_{2} (s)W_{1} - \mathop \rho \nolimits_{2} (s)W_{2} \omega_{1} (s)W_{2} } \right]^{ - 1} \\ \end{aligned} $$

  For particular case (i) when $\mathop \rho \nolimits_{1} (s) = \mathop \omega \nolimits_{2} (s)$ and $\mathop \rho \nolimits_{2} (s) = \mathop \omega \nolimits_{1} (s)$,

  $$ \begin{aligned} C_{1}^{T} =& \frac{1}{2}\left[ {[F_{1} + F_{2} ]^{T} \left[ {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right]^{ - 1} }\right.\\ & \left.{+ [F_{1} - F_{2} ]^{T} \left[ {\mathop \omega \nolimits_{2} (s)W_{1} - \mathop \omega \nolimits_{1} (s)W_{2} } \right]^{ - 1} } \right], \\ C_{2}^{T} =& \frac{1}{2}\left[ {[F_{1} + F_{2} ]^{T} \left[ {\mathop \rho \nolimits_{1} (s)W_{1} + \mathop \rho \nolimits_{2} (s)W_{2} } \right]^{ - 1}}\right.\\ &\left.{ - [F_{1} - F_{2} ]^{T} \left[ {\mathop \omega \nolimits_{2} (s)W_{1} - \mathop \omega \nolimits_{1} (s)W_{2} } \right]^{ - 1} } \right] \\ \end{aligned} $$

  For particular case (ii) when $\mathop \rho \nolimits_{1} (s) = \mathop \rho \nolimits_{2} (s) = \mathop \omega \nolimits_{1} (s) = \mathop \omega \nolimits_{2} (s) = 1$,

  $$ \begin{aligned} & C_{1}^{T} = \frac{1}{2}\left[ {[F_{1} + F_{2} ]^{T} \left[ {W_{1} + W_{2} } \right]^{ - 1} + [F_{1} - F_{2} ]^{T} \left[ {W_{1} - W_{2} } \right]^{ - 1} } \right], \\ & C_{2}^{T} = \frac{1}{2}\left[ {[F_{1} + F_{2} ]^{T} \left[ {W_{1} + W_{2} } \right]^{ - 1} - [F_{1} - F_{2} ]^{T} \left[ {W_{1} - W_{2} } \right]^{ - 1} } \right]. \\ \end{aligned} $$

• 7. Put values of $C_{1}^{T}$ and $C_{2}^{T}$ from step 6 to get the desired solution is $\varepsilon_{1} (u) = C_{1}^{T} \varPsi (u);\,\,\varepsilon_{2} (u) = C_{2}^{T} \varPsi (u).$