Introduction

Fractional-order partial differential equation which is considered as the generalization of the integer-order partial differential equation attracts much attention recently. They provide an excellent instrument for the description of memory and hereditary properties of various materials and processes. The fractional-order partial differential equation was first developed as a pure mathematical theory in the middle of the nineteenth century [25]. Time- and space-nonlinear fractional Schrodinger equation (NFSE) is the fundamental equation of physics for describing nonrelativistic quantum mechanical behavior. This equation was formulated in late 1925, and published in 1926, by the Austrian physicist Erwin Schrodinger. In past years, the time- and space-NFSE has attracted application of various fields such as electromagnetic waves, quantitative finance, quantum evolution of complex systems and dielectric polarization [6, 8, 14, 18, 19, 24, 26].

Let us consider two-dimensional NFSE with fractional derivation in time and space

$$\begin{aligned}&i \partial _{t}^{\alpha }U+\kappa \left( \partial _{x}^{2\beta } U +\partial _{y}^{2\beta } U \right) + G(x,y,t) U+\lambda |U | ^{2}U \nonumber \\&\quad =F(x,y,t),\quad (x,y)\in \varOmega , t \in [0,T], \end{aligned}$$
(1)

with initial condition:

$$\begin{aligned} U(x,y,0) = k_{1}(x,y),\quad (x,y) \in \varOmega , \end{aligned}$$

and boundary conditions:

$$\begin{aligned} U(x_{L},y,t) &= p_{11}(y,t), \quad U(x_{R},y,t) = p_{21}(y,t),\\&\quad t\in [0,1], \quad (x,y)\in \partial \varOmega , \\ U(x,y_{L},t) &= p_{31}(x,t), \quad U(x,y_{R},t)= p_{41}(x,t). \end{aligned}$$

Here, \(\alpha\) and \(\beta\) represent the fractional order of derivatives in time and space, respectively, with values \(0<\alpha \le 1\) and \(1/2<\beta \le 1\). The convex domain \(\varOmega\) is defined as, \(\varOmega =(x,y)\in [x_{L},x_{R}]\times [y_{L},y_{R}]\), \(\kappa\) and \(\lambda\) are constants, G(x, y, t) is a time-dependent potential function, F(x, y, t) is complex source term. The function U(x, y, t) is assumed to be a complex wave function of time and space.

Define U(x, y, t) and F(x, y, t) into their real and imaginary parts

$$\begin{aligned}&U(x,y,t)=V(x,y,t)+{\hbox{i}}W(x,y,t) \quad {\hbox{and}}\nonumber \\&\quad F(x,y,t)=F_{1}(x,y,t)+{\hbox{i}}F_{2}(x,y,t), \end{aligned}$$
(2)

where V(x, y, t), W(x, y, t), \(F_{1}(x,y,t)\) and \(F_{2}(x,y,t)\) are real functions. Using Eq. (2) in Eq. (1), we obtain the following coupled system of equations

$$\begin{aligned}&-\partial _{t}^{\alpha }W+\kappa \left( \partial _{x}^{2\beta }V +\partial _{y}^{2\beta } V \right) + G(x,y,t) V+\lambda \left( W^{1}+W^{2} \right) V \\&\quad =F_{1}(x,y,t),\quad (x,y)\in \varOmega ,\quad t \in [0,T],\\&\partial _{t}^{\alpha }V+\kappa \left( \partial _{x}^{2\beta } W +\partial _{y}^{2\beta }W \right) + G(x,y,t) W+\lambda \left( W^{1}+W^{2} \right) W \\&\quad =F_{2}(x,y,t),\quad (x,y)\in \varOmega ,\quad t \in [0,T]. \end{aligned}$$

In recent years, many authors who have presented numerical solutions for time- and space-NFSE. These numerical methods are very important for understanding physical behavior of the equations. Mohebbi et al. [22] have proposed meshless method based on collocation method for the numerical solutions of NFSE. In this method, the authors have used radial basis function as basis function. Fan and Qi [12] have proposed efficient Galerkin finite element method for the numerical and stability analysis of two-dimensional NFSE on an irregular convex domain. Zhang et al. [33] have proposed Galerkin–Legendre spectral schemes for the numerical solution of space-NFSE. Li et al. [16] have discussed the numerical and stability analysis of multi-dimensional time-NFSE using L1-Galerkin finite element method. Zhao et al. [34] have proposed fourth-order compact ADI method for the numerical solutions and convergence analysis of two-dimensional space-NFSE. In this method, the authors have found fourth order of accuracy. Chang et al. [5] have proposed different numerical method such as Crank–Nicolson method, hopscotch method, split-step Fourier method, pseudospectral method for the numerical solution of generalized NFSE. Chen et al. [7] have introduced symplectic and multi-symplectic methods for the numerical solution of NFSE. Further Eq. (1) was solved by several other numerical methods, such as Riccati expansion method [1], Galerkin finite element method [30], momentum representation method [10], compact boundary value method [23], fractional mapping method [31] and finite difference method [3, 32]. Fan and Liu [11] have proposed finite element method for the numerical and stability analysis of two-dimensional distributed-order time and space-fractional diffusion equation on an irregular convex domain. In this method, the authors have used unstructured mesh adapted to the irregular domain.

Spectral and pseudospectral methods have been developed for numerical simulation of related differential equations in many fields because of its high accuracy, especially sufficiently smooth problems. Lanczos showed the power of Fourier series and Chebyshev polynomials in a number of problems where they had not been used before. Later in the 1970s, Orszag introduced spectral methods again, alongside Kreiss, Oliger and others, for the purpose of solving partial differential equations in fluid mechanics [29]. Many authors have used spectral method to approximate the solution of such equations [2, 17, 20, 21]. In this paper, authors propose a highly accurate pseudospectral method in both space and time to approximate the two-dimensional time- and space- NFSE. For the proposed method, we derive the solution of a nonlinear partial differential equation as a sum of basis functions in both space and time directions. The spectral coefficients of the sum are chosen to satisfy the solution of the nonlinear partial differential equation. The fractional derivatives matrix is considered in the Caputo fractional derivative formula.

The structure of the paper is organized as follows. In “Preliminary” section, we describe some basic definitions and notations. Discretizing and description of the methods are presented in “Pseudospectral method-based discretization” section. In “Numerical results” section, we present numerical solutions and errors by the proposed scheme. In the last section, the conclusion of our work is presented.

Preliminary

In this section, the definition of the Caputo fractional derivative is introduced systematically.

Definition 1

The partial fractional derivatives of order \(n-1<\nu <n\) of a function \({{\L}} _{M}(t)\), with respect to variable t, in the Caputo fractional derivative formula, are defined [9, 15]

$$\begin{aligned} {{\L}} _{M}^{'}(t) &= \partial ^{\nu }_{t} {{\L}} _{M}(t)\nonumber \\ &= \frac{1}{\varGamma (n-\nu )} \int ^{t}_{0}\left( t-s\right) ^{n-\nu -1} \frac{\partial ^{n} {{\L}} _{M}(s)}{\partial s^{n}} {\hbox {d}}s, \end{aligned}$$
(3)

where \(\nu \ge 0\) is the order of derivative, \(\varGamma\) is the gamma function and \(n=\lceil \nu \rceil +1\) with \(\lceil \nu \rceil\) denoting the integral part of \(\nu\). Caputo fractional derivatives have some basic properties which are needed in this paper as follows:

$$\begin{aligned} \partial ^{\nu }_{t} C &= 0,\qquad C\quad {\text {is constant}},\\ \partial ^{\nu }_{t} t^{\upsilon } &= \left\{ \begin{array}{ll} {0}, \quad &{} {\hbox {for}}\quad \upsilon \in N\quad {\hbox {and}} \quad \upsilon <\lceil \nu \rceil ,\\ \frac{\varGamma (\upsilon +1)}{\varGamma (\upsilon +1-\nu )} t^{\upsilon -\nu }, \quad &{} {\hbox {for}} \quad \upsilon \in N \quad {\hbox {and}} \quad \upsilon \ge \lceil \nu \rceil . \end{array}\right. \\ \partial ^{\alpha }_{z} \partial ^{\beta }_{z} z^{\upsilon } &= \partial ^{\beta }_{z} \partial ^{\alpha }_{z} z^{\upsilon }=\partial ^{\alpha +\beta }_{z} z^{\upsilon }. \end{aligned}$$

Construction of Chebyshev fractional differential matrix is given as

$$\begin{aligned} Q^{(\alpha )}= \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \phi _{0}^{'}(z_{0}) &{} \dots &{} \dots &{} \phi _{0}^{'}(z_{M})\\ \ddots &{} \ddots &{} \ddots &{} \ddots \\ \ddots &{} \ddots &{} \ddots &{} \ddots \\ \phi _{M}^{'}(z_{0}) &{} \dots &{} \dots &{} \phi _{M}^{'}(z_{M})\\ \end{array}\right] . \end{aligned}$$

Pseudospectral method-based discretization

We seek a pseudospectral approximation, which can be expressed as a product of Lagrange basis functions in both space and time variable with pseudospectral coefficients.

$$\begin{aligned} I_{M}U &= \sum _{i=0}^{M} \sum _{j=0}^{M}\sum _{k=0}^{M}{{{\L}} _{i}(x)~{{\L}} _{j}(y)}~{{\L}} _{k}(t) {U(x_{i},y_{j},t_{k})}, \end{aligned}$$
(4)

where

$$\begin{aligned} {{\L}} _{j}(z) &= \sum _{i=0}^{M}{ w_{j} \frac{1}{\hat{h_{i}}}\phi _{i}(z_{j})\phi _{i}(z)} {} = \dfrac{S_{M}(z)}{(z-z_{j})\left[ \partial S_{M}(z_{})/ \partial z|_{z=z_{j}} \right] } \end{aligned}$$

here, \(\phi _{i}(z)\) is a Chebyshev polynomial, \(z_{j}\) is a CGL points,

$$\begin{aligned} S_{M}(z) = \prod _{i = 0}^{M} (z - z_{i}), \end{aligned}$$

normalization constant

$$\begin{aligned} \hat{h_{i}}=\left\{ \begin{array}{ll} {\pi }, &\quad i=0\quad {\hbox{and}} \quad M ,\\ \frac{\pi }{2} , &\quad 0<i<M. \end{array}\right. \end{aligned}$$

and Chebyshev–Gauss–Lobbato weight quadrature

$$\begin{aligned} w_{j}=\left\{ \begin{array}{ll} {\frac{\pi }{2M}}, &{}\quad j=0 \quad{\text {and}} \quad M ,\\ \frac{\pi }{M} , &{}\quad 0<j<M. \end{array}\right. \end{aligned}$$

The spectral approximation given in (4) can be expressed in the vector product form using the direct product as

$$\begin{aligned} I_{M} U(x,y,t) &= \left( \varPsi _{[0:M]}(x)\otimes \varPsi _{[0:M]}(y)\otimes \varPsi _{[0:M]}(t)\right) ^{{\mathrm{T}}} {\mathbf{U}}, \end{aligned}$$
(5)

where

$$\begin{aligned} {\mathbf{U}} &= \left[ U_{000},\ldots ,U_{00M}\mid \ldots \mid U_{0M0},\ldots ,U_{0MM}\mid \right. \\&\left.\quad \ldots \mid U_{MM0}, \ldots ,U_{MMM}\right] ^{{\mathrm{T}}},\\ \varPsi _{[0:M]}(z) &= [{{\L}} _{0}(z), \ldots \ldots ,{{\L}} _{M}(z) ] ^{{\mathrm{T}}}. \end{aligned}$$

Here \({\mathbf{U}}\) is the \((M+1) \times (M+1) \times (M+1)\)-vectors, \(\varPsi _{[0:M]}(z)\) is the \((M+1)\)-vectors, and \(\otimes\) denotes Kronecker product of two vectors, which is defined as \([a,b] \otimes [c,d] = [ac,ad,bc,bd]\).

Now, we can define fractional spatial derivative of Eq. (5) with respect to x given by

$$\begin{aligned}&\frac{\partial ^{\beta } I_{M} U(x,y,t)}{\partial x^{\beta }} = \left( \varPsi _{[0:M]}(x)\otimes \varPsi _{[0:M]}(y)\otimes \varPsi _{[0:M]}(t)\right) ^{{\mathrm{T}}}\nonumber \\&\quad \left( Q^{(\beta )}_{[0:M,0:M]} \otimes I_{M+1} \otimes I_{M+1} \right) {\mathbf{U}}. \end{aligned}$$
(6)

Similarly, we can define fractional derivative of Eq. (5) with respect to t given by

$$\begin{aligned}&\frac{\partial ^{\alpha } I_{M} U(x,y,t)}{\partial t^{\alpha }} = \left( \varPsi _{[0:M]}(x)\otimes \varPsi _{[0:M]}(y)\otimes \varPsi _{[0:M]}(t)\right) ^{{\mathrm{T}}}\nonumber \\&\quad \left( I_{M+1}\otimes I_{M+1} \otimes Q^{(\alpha )}_{[0:M,0:M]} \right) {\mathbf{U}}. \end{aligned}$$
(7)

where \(I_{M+1}\) denotes identity matrix of size \(((M+1) \times (M+1))\).

Next, we consider the following transformations which are used to transform the two-dimensional space \([x_{L},x_{R}]\), \([y_{L},y_{R}]\) and time [0, T] in to \([-\,1,1]\).

$$\begin{aligned}&x \longrightarrow \frac{x_{R} -x_{L}}{2} x +\frac{x_{R} + x_{L}}{2},~ \quad y \longrightarrow \frac{y_{R} -y_{L}}{2} y \\&\quad +\frac{y_{R} + y_{L}}{2} \quad \text {and} \quad t \longrightarrow \frac{T}{2} t + \frac{T}{2}. \end{aligned}$$

We obtain the two-dimensional time- and space-NFSE in new space \((x,y)\in [-\,1,1]^{2}\) and time interval \(t \in [-\,1,1]\)

$$\begin{aligned}&- \partial _{t}^{\alpha }W+\kappa \left( \frac{2^{(2\beta -\alpha )}T^{\alpha } }{(x_{R} -x_{L})^{2\beta }} \partial _{x}^{2\beta } V + \frac{2^{(2\beta -\alpha )}T^{\alpha } }{(y_{R} -y_{L})^{2\beta }}\partial _{y}^{2\beta } V \right) \nonumber \\&\quad + \frac{ T^{\alpha } }{2^{\alpha }}\left[ G(x,y,t) V+\lambda \left( W^{2}_{}+W^{2}_{} \right) V\right] \nonumber \\&\quad =\frac{T^{\alpha }}{2^{\alpha }}F_{1}(x,y,t), \end{aligned}$$
(8)
$$\begin{aligned}&\partial _{t}^{\alpha }V+\kappa \left( \frac{2^{(2\beta -\alpha )}T^{\alpha } }{(x_{R} -x_{L})^{2\beta }} \partial _{x}^{2\beta }W + \frac{2^{(2\beta -\alpha )}T^{\alpha } }{(y_{R} -y_{L})^{2\beta }}\partial _{y}^{2\beta } W \right) \nonumber \\&\quad + \,\frac{ T^{\alpha } }{2^{\alpha }}\left[ G(x,y,t) W+\lambda \left( V^{2}_{}+W^{2}_{} \right) U_{2}\right] \nonumber \\&\quad =\frac{T^{\alpha }}{2^{\alpha }}F_{2}(x,y,t), \end{aligned}$$
(9)

with initial condition:

$$\begin{aligned} V(x,y,-1) &= h_{1}(x,y),\quad W(x,y,-1)=h_{2}(x,y),\nonumber \\&\quad x\in [-\,1,1],\qquad y\in [-\,1,1] \end{aligned}$$
(10)

and boundary conditions:

$$\begin{aligned}&V(-1,y,t) = g_{11}(y,t), \quad V(1,y,t) = g_{21}(y,t), \\&\quad t\in [-\,1,1], \quad y\in [-\,1,1], \\&W(-1,y,t) = g_{12}(y,t), \quad W(1,y,t) = g_{22}(y,t),\\&\quad t\in [-\,1,1], \quad y\in [-\,1,1],\\&V(x,-1,t)= g_{31}(x,t), \quad V(x,1,t)= g_{41}(x,t), \\&\quad t\in [-\,1,1], \quad x\in [-\,1,1],\\&W(x,-1,t)= g_{32}(x,t), \quad W(x,1,t)= g_{42}(x,t), \\&\quad t\in [-\,1,1], \quad x\in [-\,1,1]. \end{aligned}$$

Further, we consider a mapping for converting the nonhomogeneous initial and boundary values to homogeneous initial and boundary values [4].

$$\begin{aligned}&\varOmega _{k}(x,y,t) = \frac{1-t}{2} h_{k}(x,y) + \frac{1-x}{4} g_{1k}(y,t) \nonumber \\&\quad +\,\frac{1+x}{4} g_{2k}(y,t) + \frac{1-y}{4} g_{3k}(x,t)\nonumber \\&\quad +\, \frac{1+y}{4} g_{4k}(x,t) - \frac{(1-t)(1-x)}{8} \nonumber \\&\quad g_{1k}(y,-1) - \frac{(1-t)(1+x)}{8} g_{2k}(y,-1)\nonumber \\&\quad - \,\frac{(1-t)(1-y)}{8} g_{3k}(x,-1)\nonumber \\&\quad - \,\frac{(1-t)(1+y)}{8} g_{4k}(x,-1), \end{aligned}$$
(11)

here corner initial and boundary values satisfy,

$$\begin{aligned}&g_{1k}(-1,-1) = g_{3k}(-1,-1) = h_{k}(-1,-1),\\&\quad g_{1k}(-1,1)= g_{3k}(-1,1),\\&g_{1k}(1,-1) = g_{4k}(-1,-1) = h_{k}(-1,1),\\&\quad g_{1k}(1,1)= g_{4k}(-1,1), \\&g_{2k}(-1,-1) = g_{3k}(1,-1) = h_{k}(1,-1),\\&\quad g_{2k}(-1,1)= g_{3k}(1,1),\\&g_{2k}(1,-1) = g_{4k}(1,-1) = h_{k}(1,1),\\&\quad g_{2k}(1,1)= g_{4k}(1,1). \end{aligned}$$

Define new variable \(V_{k}(x,y,t)\).

$$\begin{aligned}&V(x,y,t) = V_{1}(x,y,t) +\varOmega _{1}(x,y,t),\nonumber \\&\qquad W(x,y,t) = V_{2}(x,y,t) +\varOmega _{2}(x,y,t), \end{aligned}$$
(12)

The above equations can be modified with new variable and obtained the new equations residuals,

$$\begin{aligned}&- \partial _{t}^{\alpha }(V_{2}+\varOmega _{2})+\kappa \left( \frac{2^{(2\beta -\alpha )}T^{\alpha } }{(x_{R} -x_{L})^{2\beta }} \partial _{x}^{2\beta } (V_{1}+\varOmega _{1})\right. \\&\qquad \left. + \,\frac{2^{(2\beta -\alpha )}T^{\alpha } }{(y_{R} -y_{L})^{2\beta }}\partial _{y}^{2\beta }(V_{1}+\varOmega _{1}) \right) \\&\qquad +\,\frac{T^{\alpha }}{2^{\alpha }}\left[ G(x,y,t) (V_{1}+\varOmega _{1})\right. \\&\qquad \left. +\,\lambda \left( (V_{1}+\varOmega _{1})^{2}+(V_{2}+\varOmega _{2})^{2} \right) (V_{1}+\varOmega _{1})\right] \\&\quad =\frac{T^{\alpha }}{2^{\alpha }}F_{1}(x,y,t),\\&\partial _{t}^{\alpha }(V_{1}+\varOmega _{1})+\kappa \left( \frac{2^{(2\beta -\alpha )}T^{\alpha } }{(x_{R} -x_{L})^{2\beta }} \partial _{x}^{2\beta } (V_{2}+\varOmega _{2})\right. \\&\qquad \left. + \,\frac{2^{(2\beta -\alpha )}T^{\alpha } }{(y_{R} -y_{L})^{2\beta }}\partial _{y}^{2\beta }(V_{2}+\varOmega _{2}) \right) \\&\qquad +\,\frac{T^{\alpha }}{2^{\alpha }}\left[ G(x,y,t) (V_{2}+\varOmega _{2})\right. \\&\qquad +\,\lambda \left( (V_{1}+\varOmega _{1})^{2}+(V_{2}+\varOmega _{2})^{2} \right) \\&\qquad \left. (V_{2}+\varOmega _{2})\right] =\frac{T^{\alpha }}{2^{\alpha }}F_{2}(x,y,t). \end{aligned}$$

We apply time and space Chebyshev pseudospectral method at CGL points and obtain the system of nonlinear algebraic equation

$$\begin{aligned} H(V_{1}|V_{2}) &= 0. \end{aligned}$$
(13)

The system of nonlinear equation (13) can be solved by using Newton–Raphson method.

Numerical results

In this section, we present numerical results for two-dimensional time- and space-NFSE using the Chebyshev pseudospectral method. We give three examples in this section. To demonstrate the errors in pseudospectral approximation, we consider the errors in the \(L_{2}\) norms, defined by

$$\begin{aligned} L_{2} = \| | U | ^{k} - | U | \| _{2} \end{aligned}$$

where \(| U| ^{k}\) and \(| U |\) are the modulus of pseudospectral approximation and modulus of analytical solution, respectively.

Example 1

In this example, let us consider the time- and space- NFSE on a rectangular region \(\varOmega = [0,1]\times [0,1]\)

$$\begin{aligned}&i\frac{\partial ^{\alpha }U}{ \partial t^{\alpha }}+\kappa \left\{ \frac{\partial ^{2\beta }U}{\partial x^{2\beta }} + \frac{\partial ^{2\beta }U}{\partial y^{2\beta }}\right\} +G(x,y,t) U+\lambda | U| ^{2}U\\&\quad =F(x,y,t),\qquad (x,y)\in \varOmega ,\quad t\in [0,T], \end{aligned}$$

with \(\lambda =\kappa =1\), \(G(x,y,t)=txy(1-x)(1-y)\).

The source term is

$$\begin{aligned}&F(x,y,t)=\left[ i\frac{15t^{1-\alpha }}{\varGamma (2-\alpha )} -\frac{30t^{1-\alpha }}{\varGamma (2-\alpha )} -\frac{30t^{2-\alpha }}{\varGamma (3-\alpha )}\right] \\&\quad x^{2}(1-x)^{2}y^{2}(1-y)^{2}+3375[t^{2}+(1+t)^{4}]\\&\quad [t+i(1+t)^{2}]x^{6}(1-x)^{6}y^{6}(1-y)^{6}+15[t+i(1+t)^{2}]\\&\quad tx^{3}(1-x)^{3}y^{3}(1-y)^{3}\\&\quad -\,\frac{15[t+i(1+t)^{2}]y^{2}(1-y)^{2}}{\cos (\beta \pi )}[h_{1}(x,\beta )+h_{2}(x,\beta )]\\&\quad -\,\frac{15[t+i(1+t)^{2}]x^{2}(1-x)^{2}}{\cos (\beta \pi )}\\&\quad [h_{1}(y,\beta )+h_{2}(y,\beta )]. \end{aligned}$$

where

$$\begin{aligned} h_{1}(x,\beta ) &= \frac{x^{2-2\beta }}{\varGamma (3-2\beta )} \left[ 1-\frac{6x}{3-2\beta }+\dfrac{12x^{2}}{(3-2\beta )(3-4\beta )}\right] ,\\ h_{2}(x,\beta ) &= \frac{(1-x)^{2-2\beta }}{\varGamma (3-2\beta )} \left[ 1-\frac{6(1-x)}{3-2\beta }+\dfrac{12(1-x)^{2}}{(3-2\beta )(3-4\beta )}\right] . \end{aligned}$$

Initial condition is

$$\begin{aligned} U(x,y,0) &= 15ix^{2}(1-x)^{2}y^{2}(1-y)^{2}, \end{aligned}$$

boundary condition is

$$\begin{aligned} U(x,y,t)=0,\quad (x,y) \in \partial \varOmega , \quad t \in [0,T], \end{aligned}$$

and the exact solution is

$$\begin{aligned} U(x,y,t)=15[t+i(1+t)^{2}]x^{2}(1-x)^{2}y^{2}(1-y)^{2}. \end{aligned}$$

For computation purpose we have chosen space interval \(\varOmega =[0,1]^{2}\) with time \(T=1\). Numerical solutions of the proposed method have been computed with different fractional-order derivative \(0<\alpha \le 1\) and \(1/2<\beta \le 1\). Figure 1 shows the numerical solution of the proposed method and contour plot has shown the physical behavior of the proposed method. In Table 1, the tabulated results of the proposed method with different fractional-order derivatives \(\alpha\) and \(\beta\) are presented. The numerical results of the proposed method achieved better accuracy as number of grid points in both space and time directions are increased. Moreover, it is demonstrated that the numerical method is more efficient. Two authors have discussed the numerical solutions of the equation with the different set of data; for comparisons purpose, we refer to [12, 13]. Further, it is found that the results obtained by the proposed method show very good agreement with published results. Moreover, proposed method has obtained 9th order of accuracy.

Fig. 1
figure 1

Numerical solutions of example 1 at time \(T=1.0\) with \(\alpha =0.8\) and \(\beta = 0.85\)

Full size image
Table 1 Numerical solutions of proposed method with different \(\alpha , \beta\) and grid points M for example 1
Full size table

Example 2

Let us consider two-dimensional space-NFSE

$$\begin{aligned}&U_{t}+i \left( \partial _{x}^{\beta } U +\partial _{y}^{\beta } U \right) +i G(x,y,t) U=0,\\&\quad (x,y)\in \varOmega ,\quad t \in [0,T], \end{aligned}$$

where \(G(x,y,t)= \frac{3}{2}-2\frac{\sin (x+y-0.5t)}{\sin (x+y)}\).

Initial condition is

$$\begin{aligned} U(x,y,0)= \sin (x+y),~~t \in [0,T], \end{aligned}$$

boundary condition is

$$\begin{aligned} U(x,y,t)=0,\quad (x,y) \in \partial \varOmega ,\quad t \in [0,T], \end{aligned}$$

and exact solution is [27]

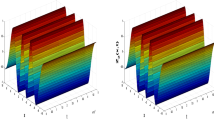
$$\begin{aligned} U(x,y,t)= \exp \left( \frac{-3it}{2}\right) \sin (x+y). \end{aligned}$$

In this example, we obtain the numerical solutions of the proposed method in \(\varOmega =[0,2\pi ]^{2},\,\, t \in [0,1]\) and fractional-order derivative \(1<\beta \le 2\). Error norms for two-dimensional nonlinear space fractional Schrodinger equation have been calculated with different values of grid point and different fractional-order derivative \(\beta\). In Table 2, it can be seen that the accuracy of the numerical results is increased along with the number of grid points and also achieved good order of accuracy. We are also shown the 3D graph of numerical solutions at time \(T= 1\) with fractional derivative order \(\beta = 1.2\) in Fig. 2. Contour plots have clearly shown the physical behavior of the proposed method. Figure 3 shows the graphical results of numerical and exact solutions with fractional derivative order \(\beta =1.2\) at \(T=1\). It is also clear that the 2D plot of the numerical and exact solutions is very close to each other. Authors have discussed the numerical solutions of the equation with the different set of data; for comparisons purpose, we refer to [28]. Further, it is found that the results obtained by the proposed method show very good agreement with published results in [28]. Moreover, proposed method has obtained 7th order of accuracy.

Fig. 2
figure 2

Numerical solutions of example 2 at time \(T=1.0\) with different \(\beta = 1.2\)

Full size image
Fig. 3
figure 3

Numerical and exact solutions of example 2 at time \(T=1.0, y=1\) and \(\beta = 1.2\)

Full size image
Table 2 Numerical solutions of proposed method with different \(\beta\) and grid points M for example 2
Full size table

Conclusion

In this work, we have discussed highly accurate fully discrete time–space Chebyshev pseudospectral method for the two-dimensional time- and space-NFSE, defined on a rectangular domain. The new fractional derivative matrix has been established using a Caputo fractional derivative formula at CGL points for different order of fractional derivatives. To demonstrate the performance, the method has been employed on three different model problems on a convex and rectangular domain and obtained good order of accuracy. Reported numerical results are highly accurate which shows the efficiency of the proposed method.