Low relativistic effects on the modulational instability of rogue waves in electronegative plasmas

Abstract

Relativistic ion-acoustic waves are investigated in an electronegative plasma. The use of the reductive perturbation method summarizes the hydrodynamic model to a nonlinear Schrödinger equation which supports the occurrence of modulational instability (MI). From the MI criterion, we derive a critical value for the relativistic parameter $\alpha _{1}$, below which MI may develop in the system. The MI analysis is then conducted considering the presence and absence of negative ions, coupled to effects of relativistic parameter and the electron-to-negative ion temperature ratio. Under high values of the latter, additional regions of instability are detected, and their spatial expansion is very sensitive to the change in $\alpha _{1}$ and may support the appearance of rogue waves whose behaviors are discussed. The parametric analysis of super-rogue wave amplitude is performed, where its enhancement is debated relatively to changes in $\alpha _{1}$, in the presence and absence of negative ions.

Introduction

Envelope solitons, generic solutions of the nonlinear Schrödinger (NLS) equation, have been extensively studied during the past 30 years, due to their fundamental importance in nonlinear physics. Based on their localization properties, breather solitons have been used as models of rogue waves (RWs) whose behaviors and characteristics are not yet fully unmasked, mainly because they may appear suddenly, propagate within short times, destroy everything on their way and disappear without any trace [1, 2]. For instance, it has been well established that they may appear in physical systems as the consequence of the interplay between nonlinear and dispersive effects, under the activation of the so-called MI phenomenon [3,4,5,6,7,8]. Recently, interest in studying RWs has gone beyond oceanography and hydrodynamics [9, 10] to reach some other areas related to optics and photonics [11,12,13,14], Bose–Einstein condensation [15,16,17], biophysics [18,19,20,21], plasma physics [22, 23], just to name a few. Particularly, ion-acoustic super-RWs were found in an ultra-cold neutral plasma in the presence of ion-fluid and nonextensive electron distribution [24]. In the same direction, magnetosonic RWs, of first and second order, were investigated numerically in a magnetized plasma [25]. The occurrence of fundamental and second-order RWs was also investigated in a relativistically degenerate plasma using the NLS equation [23]. Comparison between experimental and theoretical occurrences of RWs was proposed recently and applied to multicomponent plasmas with negative ions [26]. A comprehensive analysis by El-Tantawy et al. [27] once more brought out the close relationship between the existence of ion-acoustic RWs and MI in electronegative plasmas (ENPs) in the presence of Maxwellian negative ions, where the dynamical behaviors of the Akhmediev breather (AB), Kuznetsov–Ma (KM) breather and super-RWs were compared.

ENPs and their applications have become an active research direction, mainly due to their particular properties related to the simultaneous presence of positive and negative ions, and electrons. Many different processes have been used to experimentally produce ENPs, including plasma processing reactors [28] and low-temperature experiments [29, 30]. Obviously, from recent contributions, when only positive ions are taken into consideration, the nonlinear terms of the Korteweg–de Vries (KdV) equation are positive, and one may obtain only compressive solitary waves [31], whereas in the presence of both positive and negative ions, soliton characteristics considerably change, due to the nonlinear response of the system to the presence of negative ions [32, 33]. This is indubitably related to the charge neutrality condition which changes, leading to a decrease in the number of electrons and a decrease in their subsequent shielding effect. Quite a limited number of works have been devoted to ENPs, including the contributions by Ghim and Hershkowitz [34] and Mamun et al. [35], where the existence of ion-acoustic waves (IAWs) and dust-acoustic waves (DAWs) was addressed in ENPs containing Boltzmann negative ions, Boltzmann electrons and cold mobile positive ions. The response of such waves, solutions of the KdV equation, to external magnetic fields was also studied [32, 33]. Panguetna et al. [36] proposed a comprehensive study of IAWs and their dependence to electronegative parameters such as the negative ion concentration ratio (α) and the electron-to-negative ion temperature ratio ($\sigma _{n}$). In two-space dimensions, beyond the study of MI, dromion solutions and their collision scenario were also studied [37]. More recently, the ENP model was extended to its three-dimensional version, giving Tabi et al. [38] the room to study the effect of the modulation angle on the onset of MI, with application to the three-dimensional Davey–Stewartson equations. Obviously, none of the above-cited works includes relativistic effects which should be considered in the emergence of IAWs when the speed a plasma particle approaches that of light. The nonlinear behaviors of plasma waves may importantly be modified by relativistic effects and lead to fascinating spectra of results, exploitable in the laboratory and in the space. IAWs in weakly relativistic plasmas were studied by Das et al. [39, 40], via the KdV equation, and applied to both nonisothermal and isothermal plasmas. El-Labany [41] reported on the existence of modulated weakly relativistic IAWs in a collisionless, unmagnetized, warm plasma with nonthermal electrons using a NLS equation. The latter was also derived recently by Abdikian [42], in three dimensions, to study the emergence of IAWs, under the activation of MI, in a magnetoplasma with pressure of relativistic electrons. Further confirmation was given on the effect of relativistic parameter to bring about new instability and dynamical regimes in the generation mechanism of modulated IAWs via MI.

The main purpose of the present work is to investigate IAWs properties in an ENP, under weak relativistic effects, in one dimension. One of our main results suggests that there is a critical value, $\alpha _\mathrm{1,cr}$, of the relativistic parameter below which MI and its subsequent nonlinear regime (RWs) may appear in the system.

The layout of the paper goes as follows. In Sect. 2, the relativistic ENP model is presented and a reductive perturbation method (RPM) is employed to derive a NLS equation which describes the evolution of modulated wave packets. In Sect. 3, the criterion for MI is derived, from which we find a critical expression for the relativistic parameter. Importance is then given to the effect of negative ions on such instabilities. The response from RWs solutions to relativistic effects is investigated in the same context, followed by a parametric analysis of the super-RW maximum amplitude when ENP and relativistic parameters are varied. The paper ends with concluding remarks in Sect. 4.

Model and amplitude equation

In its original formulation, the model for ENPs is composed of Maxwellian electron and negative ions in addition to cold mobile positive ions [35,36,37,38, 43]. In the presence of weak relativistic effects, the dynamics of IAWs is governed by the following set of normalized fluid equations:

$$\begin{aligned} \frac{\partial {n_{i}}}{\partial {t}}+\frac{\partial {n_{i}u_{i} }}{\partial {x}}=0, \end{aligned}$$

(1a)

$$\begin{aligned} \frac{\partial {(\gamma u_i) }}{\partial {t}}+u_i \frac{\partial {(\gamma u_i )}}{\partial {x}}+\frac{\partial {\phi }}{\partial {x}}=0, \end{aligned}$$

(1b)

$$\begin{aligned} \frac{\partial ^2{\phi }}{\partial x^2}=\mu _n\exp \sigma _n\phi +\mu _e\exp \phi -n_i. \end{aligned}$$

(1c)

The relativistic character of the studied plasma system relies on the factor

$$\begin{aligned} \gamma =\frac{1}{\sqrt{1-\alpha _1 u_i^2}}\simeq {1+\frac{\alpha _1}{2}}u_i^2, \end{aligned}$$

(2)

which is the result of Lorentz transformations. The parameter $\alpha _1$ incorporates the relativistic effect, here manifested in terms of the plasma density, by the relationship $\alpha _1=c_s^2/c^2$. $n_i$ and $u_i$ are, respectively, the number density positive ions (normalized by the unperturbed value $n_{0}$) and the ion-fluid velocity (normalized by the IA speed $c_s=\sqrt{k_{B}T_{e}/m}$). $\phi$ is the electrostatic wave potential normalized by $m c_s^2/e$, where e is the magnitude of the electron charge. The time and space variables are normalized by the ion Debye length $\lambda _D =\sqrt{k_{B}T_{e}/4 \pi e^2n}$ and the ion plasma period $\omega ^{-1}=1/\sqrt{4\pi e^2n_0/m}$, respectively. Here, $\sigma _n=T_e/T_n$ is the electrons-to-negative ion temperature ratio, $\mu _e=n_{e0}/n_0$ and $\mu _n=n_{n0}/n_0$, where $n_0$ , $n_{n0}$ and $n_{e0}$, are the unperturbed densities of the positive ions, negative ions and electrons, respectively. At equilibrium, the neutrality condition of the plasma reads $\mu _e+\mu _n = 1$, where $\mu _e=n_{e0}/n_0=1/({1+\alpha })$, with $\alpha =n_{n0}/n_{e0}$. Using the power series expansion of the exponential function around zero, Eq. (1c) becomes

$$\begin{aligned} \frac{\partial ^2{\phi }}{\partial {x}^2}=1+a_1\phi +a_2\phi ^2+a_3\phi ^3-n_i, \end{aligned}$$

(3)

where $a_1=\mu _e+\mu _n\sigma _n$, $a_2=\frac{\mu _e+\mu _n\sigma _n^2}{2}$ and $a_3=\frac{\mu _e+\mu _n\sigma _n^3}{6}$. Modulated IAWs appear in physical systems as the consequence of the interplay between nonlinearity and dispersion. Therefore, to explicitly include such effects, the RPM is commonly used [22, 24, 36, 37], which results in equations describing the development of the modulation of the amplitude in the lowest order of an asymptotic expansion. To start, we introduce the stretched variables in space and time as $\xi =\epsilon (x-v_gt)$ and $\tau =\epsilon ^2t$, where the group velocity $v_g$ will be determined later by the solvability condition of Eq. (1). $\epsilon$ is a small real parameter ($\epsilon<<1$) that measures the strength of the perturbation. The dependent physical variables around their equilibrium values are assumed as

$$\begin{aligned} \left( \begin{array}{ccc} n_i(x,t)\\ u_i(x,t)\\ \phi (x,t)\\ \end{array} \right)= & {} \left( \begin{array}{ccc} 1\\ 0\\ 0\\ \end{array} \right) +\sum \limits _{p = 1}^\infty \epsilon ^p \sum \limits _{l = - \infty }^{+\infty } \left( \begin{array}{ccc} n_{l}^{(p)} \left( {\xi ,\tau } \right) \\ u_{l}^{(p)} \left( {\xi ,\tau } \right) \\ \phi _{l}^{(p)} \left( {\xi ,\tau } \right) \\ \end{array}\right) A^l \left( {n,t} \right) . \end{aligned}$$

(4)

We note that the above series includes all overtones $A^{l}(n,t)=\exp [il(kx-\Omega t)]$, up to order p. These are generated by the nonlinear terms, which means that the corresponding coefficients are of maximum order $\epsilon ^{p}$. Then, the relations $n_{l}^{(p)*}= n_{-l}^{(p)}$, $u_{l}^{(p)*}= u_{-l}^{(p)}$ and $\phi _l^{(p)*}= \phi _{-l}^{(p)}$ should be satisfied because of reality condition of physical variables. The asterisk denotes the complex conjugate. Substituting the trial solutions (4) into basic Eqs. (1a), (1b) and (3) and equating the quantities with equal power of $\epsilon$, one obtains several coupled equations in different orders of $\epsilon$.

At $( {\epsilon ^1})$-order, we have the set of equations

$$\begin{aligned}&-i\omega n_{1}^{(1)}+iku_{1}^{(1)}=0,\;\; -i\omega u_{1}^{(1)}+ik\phi _1^{(1)}=0,\nonumber \\&\quad (k^2+a_1)\phi _1^{(1)}-n_{1}^1=0, \end{aligned}$$

(5)

which is solvable under the condition that the dispersion relation $\omega ^2=\frac{k^2}{k^2+a_1}$ be verified, leading to the first harmonic of perturbation

$$\begin{aligned} n_{1}^{(1)}=\frac{k^2}{\omega ^2}\phi _1^{(1)},\;\;\mathrm{and}\;\; v_{1}^{(1)}=\frac{k}{\omega }\phi _1^{(1)}. \end{aligned}$$

(6)

We process the same way to obtain the second-order terms, namely the amplitudes of the second harmonics and constant terms as well as the nonvanishing contribution to the first harmonics. We obtain the following equation for $p =2$ and $l=0$:

$$\begin{aligned} a_1\phi _0^{(2)}-n_{0}^{(2)}+2a_2|\phi _1^{(1)}|^2=0. \end{aligned}$$

(7)

The ($p =2$, $l=1$)-order provides the compatibility condition in terms of group velocity, $v_g=a_1\frac{\omega ^3}{k^3}$. For $l = 2$, the components of the second harmonic mode $n_{2}^{(2)}$, $v_{2}^{(2)}$ and $\phi _2^{(2)}$ are obtained in terms of $\phi _1^{(1)}$ as

$$\begin{aligned} \phi _2^{(2)}= & {} \alpha _{\phi }\left( \phi _1^{(1)}\right) ^2,\;\; n_{2}^{(2)}=\alpha _{n}\left( \phi _1^{(1)}\right) ^2,\nonumber \\ v_{2}^{(2)}= & {} \alpha _{v}\left( \phi _1^{(1)}\right) ^2, \end{aligned}$$

(8)

with

$$\begin{aligned} \alpha _{\phi }= & {} \frac{k^2}{2\omega ^2}-\frac{a_2}{3k^2},\;\; \alpha _{n}=(a_1+4k^2)\alpha _{\phi }+a_2,\\ \alpha _{u}= & {} \frac{\omega }{k}\alpha _{n}-\frac{k^3}{\omega ^3}. \end{aligned}$$

The zeroth harmonic mode also appears due to the self-interaction of the modulated carrier wave. Its expression cannot be completely expressed using the second order. We will have to consider the third-order equations. Therefore, the set of equations given by the ($l=0$)-components of the third-order part are given by

$$\begin{aligned} -v_gn_{0}^{(2)}+v_{0}^{(2)}= & {} -\frac{2k^3}{\omega ^3}|\phi _1^{(1)}|^2,\nonumber \\ -v_gu_{0}^{(2)}+\phi _{0}^{(2)}= & {} -\frac{k^2}{\omega ^2}|\phi _1^{(1)}|^2, \end{aligned}$$

(9)

to which we have added Eq. (7) from ($n=2$, $l=0$). Along the same line, the following second-order quantities in the zeroth harmonic are found:

$$\begin{aligned} \phi _0^{(2)}= & {} \beta _{\phi }|\phi _1^{(1)}|^2,\;\; n_{0}^{(2)}=\beta _{n}|\phi _1^{(1)}|^2,\nonumber \\ v_{0}^{(2)}= & {} \beta _{v}|\phi _1^{(1)}|^2, \end{aligned}$$

(10)

with

$$\begin{aligned} \beta _{\phi }= & {} \frac{-2a_2v_g^2+(k^2-3a_1)}{a_1v_g^2-1},\;\; \beta _{n}=a_1\beta _{\phi }+2a_2,\\ \beta _{v}= & {} \frac{-2\omega }{(k^2+a_1)^2}+v_g\beta _n. \end{aligned}$$

Finally, substituting the above derived expressions into the ($n=3$, $l=1$)-components, we obtain the following nonlinear Schrödinger equation:

$$\begin{aligned} i\frac{\partial \psi }{\partial \tau }+P\frac{\partial ^2\psi }{\partial \xi ^2}+Q|\psi |^2\psi =0, \end{aligned}$$

(11)

for the slow evolution of the first-order amplitude of the plasma perturbation potential $\phi _1^{(1)}=\psi$. P and Q are the dispersion and nonlinearity coefficients, respectively, and their expressions are given by

$$\begin{aligned} P= & {} \frac{\omega ^3}{2k^2}\left[ \frac{3\alpha _1 k^4}{2\omega ^2}-\frac{2k}{\omega }(k^2+a_1)(\alpha _u+\beta _u)\right. \nonumber \\&\quad \left. -(k^2+a_1)(\alpha _n+\beta _n)+2a_2(\alpha _\phi +\beta _\phi )-3a_3\right] ,\nonumber \\ Q= & {} -\frac{3a_1\omega ^5}{2k^4}. \end{aligned}$$

(12)

The nonlinear Schrödinger (NLS) equation provides a canonical description for the envelope dynamics of a quasi-monochromatic plane wave propagating in a weakly nonlinear dispersive medium when dissipative processes are negligible [44]. Later, it was found that NLS equation had applications in different subjects. In quantum mechanics, it is obtained in localizing the potential of the Hartree equation [45]. In chemistry, it appears as a continuous-limit model for mesoscopic molecular structures [46]. In protein folding and bending, in the propagation of Davydov’s solitons, it is responsible for energy transport and storage along α-helix proteins [8, 47, 48], bubble propagation and energy localization for specific molecular processes such as DNA transcription and replication [49, 50]. In laser propagation, the NLS equation describes the propagation of a laser beam in a medium whose index of reflection is sensitive to the wave amplitude [51,52,53]. In hydrodynamics, it describes the interaction between short-wave and long-wave gravitational disturbances in the atmosphere [54,55,56]. Other applications appear in water waves at the free surface of an ideal fluid and in plasma physics (interaction between Langmuir and ion-acoustic waves [22, 23, 27, 36, 42]). Applications of the NLS equation in fiber optics have stimulated further studies in optical communications [57,58,59,60]. NLS equation also appears in the description of the Bose–Einstein condensate (BEC), a context where it is often called the Gross–Pitaevskii equation [61,62,63,64]. Despite the NLS equation support for spatially localized envelope solitons such as the bright- and dark-type solitons, there is a hierarchy of freak (rational) solutions to the self-focusing NLS equation. In the present work, these solutions represent excitations due to the MI of plasma and known as the RWs  [66, 67]. They have been described as waves which appear from nowhere and disappear without a trace. There is also an extensive literature studying various types of solitons on finite background (SFB) consisting of a localized nonlinear structure evolving upon a nonzero background plane wave. In fact, Akhmediev et al. [65, 68, 69], based on the fact the simplest solution of the NLS equation could be a plane wave $\psi \sim e^{i\phi }$, proposed that the emergence of SFB solitons may be a consequence of the instability of the plane wave, through a perturbed solution $\psi \sim \left( 1+\sum _{j=1}^na_j(\xi )\cos j\zeta (\tau -\tau _{0j})\right)$, where $a_j(\xi )$ are Fourier coefficients of the periodic perturbation, $\zeta$ is the external modulation frequency, n is the number of harmonics of the fundamental frequency and $\tau _{0j}$ is the initial phase of the jth harmonic. This, after linearizing around the unperturbed wave, leads to coefficients $a_j$ of the form $a_j(\xi )=A_je^{(i\alpha _j+\delta _i\xi )}+B_je^{(-i\alpha _j-\delta _i\xi )}$, where $\tan \alpha _j=2\delta _j/(j\zeta )^2$, with $\delta _j=j\zeta \sqrt{1-j^2\zeta ^2/4}$ being the growth rate of the jth harmonic of the perturbation which remains positive for frequencies in the range $0<j\zeta <2$. For the first harmonic case, the MI is established and the instability growth rate has a maximum at $\zeta =\sqrt{2}$. However, for arbitrary values of $\zeta$, different cases of RWs were proposed and extensively studied, among which the generalized form  [12, 13, 27, 69,70,71]

$$\begin{aligned} \psi (\xi ,\tau )= & {} \sqrt{\frac{2P}{Q}}\nonumber \\&\times\left\{ \frac{(1-4a)\cosh (2bP\tau )+\sqrt{2a}\cos (c\xi )+i\sinh (2bP\tau )}{\sqrt{2a}\cos (c\xi )-\cosh (2bP\tau )}\right\}\nonumber\\ &\times\exp (2iP\tau ), \end{aligned}$$

(13)

obtained for $\zeta =2/\sqrt{5}$. Here, the single governing parameter a determines the physical behavior of the solution through the function arguments $b=\sqrt{8a(1-2a)}$ and $c=\frac{2\pi }{L}=2\sqrt{1-2a}$, with L being the periodicity length of the solution [69, 70]. We should stress that solution (13) can describe three different kinds of breather solutions, depending on the value of a. The super-RW solutions of the focusing NLS equation (11) are localized in both time and space. There are, in fact, two such solutions, the Peregrine soliton and the second-order rogue wave soliton, which are obtained from the general theory of Akhmediev et al. [68, 69] when $\zeta \rightarrow 0$

$$\begin{aligned} \psi _j(\xi ,\tau )= & {} \sqrt{\frac{2P}{Q}}\nonumber \\ \times &\left\{ (-1)^j+\frac{G_j(\xi ,{\bar{\tau }})+2iP\tau H_j(\xi ,{\bar{\tau }})}{F_j(\xi ,{\bar{\tau }})}\right\} \exp (2iP\tau ), \end{aligned}$$

(14)

where j is the order of the solution and ${\bar{\tau }}=2P\tau$. The functions $G_j(\xi ,{\bar{\tau }})$, $H_j(\xi ,{\bar{\tau }})$ and $F_j(\xi ,{\bar{\tau }})$ are polynomials in variables of ${\bar{\tau }}$ and $\xi$, with $F_j(\xi ,{\bar{\tau }})$ not having no real zero. We should, however, stress that the Peregrine RW can be derived as a limiting case of the KM breather, especially when $a\rightarrow 1/2$ [72]. In order to get the two solutions, we will restrict our study to the cases $j\le 2$.

Modulational instability and rogue waves

The relative sign of P and Q determines the stability of plane-wave solutions to small periodic perturbations. This also implies that any solution whose amplitude is governed by Eq. (11) depends on the sign of PQ, which, in most of plasma systems, depends on system parameters. To this effect, let us assume plane solutions for Eq. (11) to be of the form $\psi (\xi ,\tau )=\psi _{0}(\xi )e^{iQ\psi _0^{2}\tau }$ that is subjected to a small perturbation $\delta \psi (\xi ,\tau )=(U_0+iV_0)e^{i(K\zeta -\Omega \tau )}$, with K and $\Omega$ being, respectively, the wave number and frequency of the perturbation. Following the standard calculations of MI, one obtains the nonlinear dispersion relation

$$\begin{aligned} \Omega ^2=(K^2P)^2\left( 1-\frac{K_\mathrm{cr}^2}{K^2}\right) , \end{aligned}$$

(15)

with the critical wave number of the perturbation being $K_\mathrm{cr}=\psi _0\sqrt{\frac{2Q}{P}}$. For the plane wave to be unstable under modulation, the condition $\Omega ^2<0$ should be satisfied, i.e.,

$$\begin{aligned} K<K_\mathrm{cr}=\psi _0\sqrt{\frac{2Q}{P}}, \end{aligned}$$

(16)

which clearly shows that for $P Q>0$, the amplitude-modulated envelope is unstable. This includes several factors related to the ENP system, including the electron-to-negative ion temperature ratio, the negative ion concentration ratio and the newly introduced relativistic parameter $\alpha _1$.

The relativistic character of the studied plasma system clearly appears in the expression of the dispersion coefficient P, which can be rewritten in the form

$$\begin{aligned} P=P_\mathrm{rel}+P_0, \end{aligned}$$

(17)

$P_0$ being the nonrelativistic expression that was obtained in Ref. [36] in the form

$$\begin{aligned} P_0= & {} \frac{\omega ^3}{2k^2}\left[ -\frac{2k}{\omega }(k^2+a_1)(\alpha _u+\beta _u)\right. \nonumber \\&\left. -(k^2+a_1)(\alpha _n+\beta _n)+2a_2(\alpha _\phi +\beta _\phi )-3a_3\right] . \end{aligned}$$

(18)

The above expression was found to be negative, so that the analysis of MI was found to be controlled by the expression of Q that was positive or negative for some values of the wave number k. We should stress that coefficient of nonlinearity in the present study keeps the same expression and therefore keeps the same features as in Ref. [36]. For its part, the relativistic contribution in the expression of P is such that

$$\begin{aligned} \begin{aligned} P_\mathrm{rel}=\frac{3k^2\omega }{4}\alpha _1, \end{aligned} \end{aligned}$$

(19)

and the MI criterion $P Q>0$ is given by $(P_\mathrm{rel}+P_0)\times Q>0$. Indeed, this criterion can be expanded to get

$$\begin{aligned} \begin{aligned} P_0Q>\frac{9\alpha _1\omega ^6a_1}{8k^2}, \end{aligned} \end{aligned}$$

(20)

where the right-hand side is what was obtained for the nonrelativistic electronegative model. Therefore, the relativistic contribution is a perturbation to the case of Ref. [36], which, to the best of our knowledge, has not been discussed extensively. In the meantime, knowing $P_0Q$, it is possible to find the range of $\alpha _1$ that gives rise to MI through the inequality

$$\begin{aligned} \begin{aligned} \alpha _1<\frac{8k^2}{9\omega ^6a_1}P_0Q=\alpha _\mathrm{1,cr}. \end{aligned} \end{aligned}$$

(21)

Fig. 1

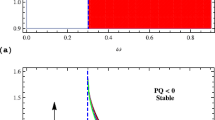
The panels show plots of the critical value of the relativistic parameter $\alpha _1$, versus the wave number k, for different values of the electron-to-negative ion temperature ratio. The blue corresponds to $\alpha =0$ and the red line corresponds to $\alpha =0.1$, with: a$\sigma _n=11.5$ and b$\sigma _n=21$. Regions of modulational instability are denoted by MI, while regions of modulational stability are indicated as MS

Obviously, the critical value of the relativistic parameter depends on the plasma parameter, and its value is sensitive to the change of the negative ion concentration ratio, for example, as shown in Fig. 1. We should stress that in any of the cases, $\alpha _{1}$ should remain positive for MI to occur. Figure 1a is plotted for $\sigma _n=11.5$ and displays the response of $\alpha _1$ to the absence of negative ions ($\alpha =0$) and its comportment when the plasma contains negative ions ($\alpha =0.1$). In the first case, there are two regions where $\alpha _1$ is positive, and such regions, labeled MI, are likely to support the formation of envelope bright solitons, this in the presence of negative ions. However, the absence of negative ions is characterized with only one region where $\alpha _1$ is positive or region of MI. In Fig. 1b, the value of the electron-to-negative ion ratio is increased to 21. One observes that in the absence of negative ions, there is still one region where $\alpha _1$ is positive, but the two regions brought by the presence of negative ions in Fig. 1a merge to form only one large region. Therefore, the electron-to-negative ion temperature ratio enlarges the domain of k and $\alpha _1$ that may lead to the formation of bright, or NLS, envelope solitons as the consequence of MI. One should remember that for intervals of k where $\alpha _1<0$, no MI should be expected. Such regions in Fig. 1 are indicated by the label (MS). Some of the values of $\alpha _1$ appearing in those areas have been chosen to plot the product PQ in Fig. 2. Figure 2a is obtained for the value $\sigma _n=5$ of the electron-to-negative ion temperature ratio. There, the instability domain is very sensitive to the change in $\alpha _1$, and there exists only one region of instability for a value $k>k_\mathrm{cr}$ of the wave number. However, the region of stability expands with increasing $\alpha _1$.

Fig. 2

Panels show how the product PQ responds to the change in $\alpha _1$. a corresponds to $\sigma _n=5$, b to $\sigma _n=11.5$ and c to $\sigma _n=21$. The blue line corresponds to the nonrelativistic case, while the red and color lines picture the correction brought by the relativistic parameter $\alpha _1$, with $\alpha =0.3$

In Fig. 2b, there is only one interval of instability for the nonrelativistic case, while for $\alpha _1=5$, two regions of instability appear. However, when $\sigma _n=10$, the emerging small region of instability disappears. This behavior becomes more obvious in Fig. 2c, where $\sigma _n=21$. For $\alpha _1=0$, the nonrelativistic system presents one large region of instability, which breaks into two regions under relativistic effects.

Fig. 3

Panel shows plots of the critical $K_\mathrm{cr}$ versus the relativistic parameter $\alpha _1$, in the absence ($\alpha =0$) and presence ($\alpha =0.1$) of negative ions, with $\sigma _n=21$

Based on all the above calculations, it is clear that critical wave number of perturbation given by Eq. (16) can also be rewritten in a way we perceive clearly the relativistic contribution in the form

$$\begin{aligned} K_\mathrm{cr}=\frac{K_\mathrm{cr,0}}{\sqrt{1+\frac{P_\mathrm{rel}}{P_0}}}, \end{aligned}$$

(22)

where $K_\mathrm{cr,0}=\psi _0\sqrt{2Q/P}$ is the critical value of K obtained for the nonrelativistic case [36]. Equation (22) suggests that if $P_0\rightarrow \infty$, the nonrelativistic problem will be retried. Otherwise, relativistic effects will be present in the system and influence the features of $K_\mathrm{cr}$ as shown in Fig. 3, where the two curves give information both in the absence and presence of negative ions. In general, $K_\mathrm{cr}$ is an increasing function of $\alpha _1$, but the range for instability to occur is larger when negative ions are absent. In such intervals, one may expect the appearance of RWs.

Fig. 4

The panels show the surface and contour plots of the Akhmediev breather, with their corresponding density plots, for different values of the relativistic parameter: a$\alpha _1=0.1$, b$\alpha _1=0.2$ and c$\alpha _1=0.3$. Values for the rest of parameters are $\alpha$ = 0.1, $\sigma _n$ = 11.5 and $k = 1.8$

Fig. 5

The panels show the evolution and contour plots of the Kuznetsov–Ma breathers, for different values of the relativistic parameter: a$\alpha _1=0.1$, b$\alpha _1=0.2$ and c$\alpha _1=0.3$. Values for the rest of parameters are $\alpha$ = 0.1, $\sigma _n$ = 11.5 and $k = 1$

The growth of periodic perturbations on a plane-wave background arising in many nonlinear dispersive systems is the consequence of the fundamental property of MI, this in the narrow band approximation. Beyond this context, the nonlinear stage of MI is described by the exact breather solution of the NLS equation, which has been considered as prototypes of RWs [73,74,75,76], that can be analytically studied under the conditions that allow MI to emerge in the NLS equation. For example, Figs. 4 and 5 give plots of the Akhmediev breather (AB) [69] and the Kuznetsov–Ma breather (KMB) [74, 77], respectively. The AB from solution (13) is obtained for $0<a <1/2$, and the largest modulation occurs for $\tau =0$, with the maximum of the envelope at $\xi =0$. For its part, the KMB is obtained for $1/2<a <\infty$. Its explicit expression has been proposed in the form [74, 77]

$$\begin{aligned} \psi _{KM}(\xi ,\tau )= & {} \sqrt{\frac{2P}{Q}}\nonumber \\\times&\left\{ 1+\frac{2(1-2a)\cos (2b_1P\tau )-ib_1\sin (2b_1P\tau )}{\sqrt{2a}\cosh (c_1\xi )-\cos (2b_1P\tau )}\right\}\nonumber \\\times& \exp (2iP\tau ), \end{aligned}$$

(23)

where $b_1=-ib=\sqrt{8a(2a-1)}$ and $c_1=-ic=\sqrt{4(2a-1)}$. This waveform is localized in space, but periodic in time. Interestingly, one can recover the Peregrine solution in the limit of infinite temporal period. It was reported recently by Tantawy et al. [27] that these breather solutions are very sensitive to the change in ENP parameters such as $\alpha$ and $\sigma _n$. However, the MI in the improved model has also shown big changes in the features of MI due the presence of the relativistic parameter $\alpha _1$. This is also ostensible in the panels of Fig. 4, where the time and spatial expansion of the breather get modified with increasing $\alpha _1$; this because it appears in the exponential growth rate of the MI through $P=P_0+P_\mathrm{rel}$. For the KMB, the relativistic parameter has the effect of increasing the temporal separation between the adjoining solitonic objects and decreasing their amplitude, which implies reduction in nonlinear effects, causing energy loss and wave amplitude drop. The observed effects, discussed by El-Tanatawy et al.  [27], have also been highlighted by Sun et al. [13], this in the absence of relativistic effects.

Fig. 6

The panels show the evolution and the corresponding contour plots of the fundamental/Peregrine soliton for different values of the relativistic parameter: a$\alpha _1=0.1$, b$\alpha _1=0.2$ and c$\alpha _1=0.3$. Values for the rest of parameters are $\alpha$ = 0.1, $\sigma _n$ = 10 and $k = 1.2$

Fig. 7

The panels show the evolution of the second-order super-rogue waves for different values of the relativistic parameter: a$\alpha _1=0.1$, b$\alpha _1=0.2$ and c$\alpha _1=0.3$. Values for the rest of parameters are $\alpha$ = 0.1, $\sigma _n$ = 10 and $k = 1.2$

From Eq. (14), the Peregrine soliton is obtained for $j=1$, with the polynomials $H_1$, $G_1$ and $F_1$ being such that $H_1(\xi ,{\bar{\tau }})=2G_1(\xi ,{\bar{\tau }})=8$ and $F_1(\xi ,{\bar{\tau }})=1+4\xi ^2+16(P\tau )^2$. The corresponding solution is written in the form [72, 78, 79]

$$\begin{aligned} \psi _P(\xi ,\tau )= & {} \sqrt{\frac{2P}{Q}}\left\{ 1-\frac{4(1+4iP\tau )}{1+4\xi ^2+16(P\tau )^2}\right\} \nonumber \\\times &\exp (2iP\tau ). \end{aligned}$$

(24)

It should be noted that it is also the limiting case of the Akhmediev solution when the spatial period tends to infinity. This solution has the form of a single-peaked structure that decays to a plane-wave asymptotic background at either large $\xi$ or $\tau$, but exhibits non-trivial behaviors over a small region in $(\xi , \tau )$ as shown in Fig. 6, within the MI region. The second-order/super-RW is obtained from Eq. (14) if $j=2$, and the polynomials that build the corresponding solution are given by

$$\begin{aligned} G= & {} \frac{3}{8}-3\xi ^2-2\xi ^4-9{\hat{\tau }}^2-10{\hat{\tau }}^4-12\xi ^2{\hat{\tau }}^2,\nonumber \\ H= & {} \frac{15}{4}+6\xi ^2-4\xi ^4-2{\hat{\tau }}^2-4{\hat{\tau }}^4-8\xi ^2{\hat{\tau }}^2,\nonumber \\ D= & {} \frac{3}{24}+\frac{9}{8}\xi ^2+\frac{1}{2}\xi ^4+\frac{2}{3}\xi ^6+\frac{33}{8}{\hat{\tau }}^2+\frac{9}{2}{\hat{\tau }}^4\nonumber \\&+\frac{2}{3}{\hat{\tau }}^6-3\xi ^2{\hat{\tau }}^2+2\xi ^4{\hat{\tau }}^2+2\xi ^2{\hat{\tau }}^4, \end{aligned}$$

(25)

with ${\hat{\tau }}=2P\tau$. This leads to the simplified expression

$$\begin{aligned} \psi _2(\xi ,\tau )=\sqrt{\frac{2P}{Q}}\left\{ 1+\frac{G+2iP\tau H}{D}\right\} \exp (2i|P|\tau ), \end{aligned}$$

(26)

which is in fact a nonlinear superposition of simple solutions. This implies that two or more Peregrine solitons can be combined into a more complicated doubly localized structures with a higher amplitude. One of the interesting features of such solutions is that the higher-order excitations are of higher amplitudes and more focused ones compared to the principal solution; i.e., their maximum amplitude can reach many times that of the background level. The corresponding solutions are shown in Fig. 7. The two solutions are very sensitive to the change in the relativistic parameter $\alpha _1$. Their amplitude decreases with increasing the latter, as already seen in the previous cases, i.e., for the breather solutions. For example, Abdelwahed et al. [80] studied the effects of superthermal electron on the features of nonlinear acoustic waves in unmagnetized collisionless ion pair plasma with superthermal electrons with application to electronegative plasmas. They found that the relativistic parameter and the wave number have the same effect of causing the amplitude to decrease for ion pairs $\mathrm (H^+,H^-)$, which implies lowering the dispersion, and  nonlinearity with strong impact on the amount of rogue energy.

Experimental observation of second-order RWs has been reported recently by Pathak et al. [23] in a multicomponent plasma containing negative ions, where it was reported that super-RWs were more possible to observe experimentally than ordinary RWs. They considered different cases, including plasmas in the presence and absence of negative ions. As already discussed here, the presence of negative ions can indeed modify the instability features and disturb the appearance of coherent structures in plasma. Coupled with relativistic effects, new behaviors may appear, either in the amplitude or in the width, or in both, of the emerging RWs.

Fig. 8

The panels show the maximum RW amplitude $|\psi _{S,{\max }}|$ versus k and $\sigma _n$, for $\alpha _1=0.1$ and a$\alpha$ = 0, b$\alpha$ = 0.5 and c$\alpha$ = 0.85. The lines delimitate areas of parameters where $P/Q>0$, while the dark-blue region is where $P/Q<0$

Fig. 9

The panels show the maximum RW amplitude $|\psi _{S,{\max }}|$ versus k and $\sigma _n$, for $\alpha _1=0.3$ and a$\alpha$ = 0, b$\alpha$ = 0.5 and c$\alpha$ = 0.85. The lines delimitate areas of parameters where $P/Q>0$, while the dark-blue region is where $P/Q<0$

More interestingly, such waves appear in regions of parameters where modulated IAWs are expected as the result of the interplay between nonlinear and dispersive effects; this because they have in common the term $\sqrt{\frac{2P}{Q}}$ which should be positive. It is for example shown in Fig. 8 that the negative ion concentration ratio $\alpha$ has influence on the RW amplitude, where the different panels correspond, respectively, to $\alpha =0.1$, 0.5 and 0.85. Depending on such values, the regions of instability, related to the RW appearance, display different features. For $\alpha =0$, it is obvious from Fig. 8a that the RW solutions exist in regions of high $\sigma _n$, i.e., $25\le \sigma _n\le 50$, where the highest $|\psi _{S,{\max }}|=|\psi _{S}(0,0)|=4\sqrt{\frac{2P}{Q}}$ belongs to $k=2$, while high-amplitude RWs are expected for $k=1.8$ in the case of $\alpha =0.5$ as depicted in Fig. 8b. Of course, $\alpha =0$ corresponds to the case where there are no negative ions. The result is therefore not surprising because Fig. 1 reveals the appearance of modulated waves even in the absence of negative ions, where $0<\alpha _1<\alpha _\mathrm{1,cr}$. Comparing these two cases, one clearly sees that the wave amplitude in Fig. 8b has decreased and the zone of instability gets delocalized, with the highest MI growth rate appearing in the interval $30\le \sigma _n\le 45$. For $\alpha =0.85$, $|\psi _{S,{\max }}|$ is shown in Fig. 8c. Obviously, $|\psi _{S,{\max }}|$ has increased and regions of instability are expanded, compared to what is observed in Fig. 8b. It should be noted that the calculations of Fig. 8 have been made for a relativistic parameter $\alpha _1=0.1$. The same calculations are repeated in Fig. 9, but for $\alpha _1=0.3$, with $\alpha$ keeping the same values as previously. Although the detected regions of instability display the same behaviors as in Fig. 8, it is nevertheless obvious that the wave amplitude is lower which shows that against $\alpha _1$, $\alpha$ can influence the appearance and formation of RW in the studied weakly relativistic plasma system. The dynamical behaviors of RWs were discussed in the nonrelativistic model of ENPs, and a critical value for $\alpha$ was proposed [25], below which the wave amplitude decreases or increases, depending on the other plasma parameter values. However, in our context, it is highly ostensible that the relativistic character of the studied system contributes to change such behaviors, therefore leading to much richer comportments.

Concluding remarks

In conclusion, a weakly relativistic model of ENP has been proposed in this work, and we have addressed the dynamics of ion-acoustic waves. In fact, after reducing the proposed model to a NLS equation, we have studied the MI, through its growth rate, and its response to plasma parameters such as $\alpha$, $\sigma _n$ and $\alpha _1$. One of the main results was the determination of the critical value of the relativistic parameter $\alpha _1$ under which MI may take place. Based on this, we have characterized the appearance of MI both in the presence ($\alpha \ne 0$) and absence ($\alpha =0$) of negative ions. The influence of the electron-to-negative ion temperature ratio on MI has also been discussed, where additional regions of instability have been detected due to the interplay between $\alpha _1$ and $\sigma _n$. Moreover, the link between instability and the appearance of RWs has been discussed along with their response to both negative ion concentration and relativistic effects. The parametric analysis of the RW amplitude has been performed, showing that it may be enhanced or reduced, depending on the balance between ENP parameters and the introduced relativistic effects.