1 Introduction

Nonlinear waves are one of the most common of all natural phenomena; they possess an extremely rich mathematical structure (Whitham 1974; Ablowitz et al. 2004). Nonlinear rogue waves belong to one of the most difficult problems of fluid dynamics (Osborne 2009). Number of damages due to collisions of rogue waves with ships or platforms has been reported. These waves represent extreme wave events during which a short group of extremely large waves occurs with elevations exceeding the average elevation of the surrounding wave field by a factor two or more (Kharif et al. 2009). Rogue waves have been observed in mid-ocean and coastal waters, the resulting peak may reach the height of 20–30 m and, by some estimates, even 60 m (Kharif and Pelinovsky 2003). The rogue waves has been studied extensively from the several aspects, such as in physical observations in optical systems (Solli et al. 2007), in nonlinear fiber optics (Kibler et al. 2010), in capillary waves (Shats et al. 2010), in Bose-Einstein condensations (Bludov et al. 2009), in optical cavities (Montina et al. 2009), and in plasmas (Moslem 2011; Moslem et al. 2011a; Wang et al. 2013). To obtain extended universality and applicability of the nonlinear rogue waves in real physical systems and the natural phenomena, it is necessary to drive nonlinear Schrödinger equation (NLSE) (Rogister 1971; Yan 2010). Moslem et al. (2011b) showed that the nonlinear coupling between negative group dispersion surface plasma wave and the low-frequency ion acoustic perturbations can lead to propagate the nonlinear surface plasma rogue waves. Abdelwahed and El-Shewy (2013) investigated the improved speed and shape of ion-acoustic waves in a warm plasma and explained the explosive and rouge waves by the rational solutions of KdV and NLSEs. On the other hand, the electrostatic excitations in electron-positron-ion (e-p-i) plasmas observed in many astrophysical and space plasmas (Shatashvili et al. 1997; Sabry et al. 2009). The e-p-i plasmas are found not only in the inner region of accretion discs in vicinity of black holes but also in astrophysical environments such as active galactic cores, magnetosphere of neutron stars and even in the solar flare plasma (Miller and Witta 1987). Clearly, electrons and ions may not follow a Maxwellian distribution due to the formation of phase space holes caused by the trapping in a wave potential (Schamel 1972; Rahman et al. 2008; El-Labany et al. 2012; Zahran et al. 2013). Furthermore, Cairns et al. (1995) used the non-thermality of electrons to investigate the ion acoustic solitary structures observed by the FREJA satellite. The non-thermal distribution attracted significant attention among researchers (Sahu and Roychoudhurya 2006; El-Shewy 2007; Singh and Lakhina 2004; El-Wakil et al. 2007; Alinejad 2010; El-Shewy and Abdelwahed 2013; Asbridge et al. 1968; Feldman et al. 1983; Futaana et al. 2003). Recently, the theory of excess super-thermal particles has undergone substantial development. Furthermore, the particles distribution in velocity space can depart considerably from a Maxwellian, which called a kappa distribution (Vasyliunas 1968). Super-thermal particles arise due to the effect of wave-particle interaction or by an external forces acting on the space environment plasmas. Astrophysical plasmas with an excess of super-thermal non-Maxwellian electrons are generally characterized by a long tail in the high energy region (Mendis and Rosenberg 1994; Leubner and Schupfer 2002; Sabry et al. 2011). In their work, Guo et al. (2013) recently investigated rogue waves in the case of unmagnetized plasma via the nonlinear Schrödinger equation. Depending on the dispersion and nonlinear coefficients that depends mainly on the plasma parameters, the stability (instability) region are also studied and they observed Rogue wave triplets in the unstable region. Moreover, El-Bedwehy and Moslem (2011) studied the properties of nonlinear structures of solitons and shocks in magneto-plasma in the presence of electrons and positrons obeying a kappa distribution. In this paper our aim is to study the dynamics of the modulationally unstable wave packets described by the Kadomstev-Petviashvili equation gives rise to the formation of rogue waves. In another motivation, we aim to explain the dependence of rogue waves on plasma parameters.

This paper is organized as follows: The basic set of fluid equations which governing our system and the derivation of the KP equation are presented in Sect. 2. In Sect. 3, Rogue wave solution of our system is represented. Finally, some results, discussions and conclusions are presented in Sect. 4.

2 Basic equations and KP equation

We consider a plasma system composed of electrons, positrons and ions. The nonlinear dynamics of the ion-acoustic waves (IAWs) are governed by the following normalized ion fluid equations:

$$ \frac{\partial n_{i}}{\partial t} + \frac{\partial}{\partial x}(n_{i}u_{ix}) + \frac{\partial}{\partial y}(n_{i}u_{iy}) = 0, $$
(1a)
$$ \frac{\partial u_{ix}}{\partial t} + u_{ix}\frac{\partial u_{ix}}{\partial x} + u_{iy} \frac{\partial u_{ix}}{\partial y} + 3\sigma_{i}n_{i}\frac{\partial n_{i}}{\partial x} + \frac{\partial \phi}{ \partial x} = 0, $$
(1b)
$$ \frac{\partial u_{iy}}{\partial t} + u_{ix}\frac{\partial u_{iy}}{\partial x} + u_{iy} \frac{\partial u_{iy}}{\partial y} + 3\sigma_{i}n_{i}\frac{\partial n_{i}}{\partial y} + \frac{\partial \phi}{ \partial y} = 0, $$
(1c)
$$ \frac{\partial^{2}\phi}{\partial x^{2}} + \frac{\partial^{2}\phi}{ \partial y^{2}} = n_{i} - n_{e} + n_{p}. $$
(2)

The two densities n e and n p are given by kappa distributions as:

$$ n_{e}(x,y,t) = \mu \bigl[1 + \phi (x,y,t) / \kappa \bigr]^{ - \kappa + \frac{1}{2}}, $$
(3a)
$$ n_{p}(x,y,t) = \nu \bigl[1 + \sigma_{p}\phi (x,y,t) / \kappa \bigr]^{ - \kappa + \frac{1}{2}}. $$
(3b)

Here \(\mu = n_{e}^{(0)} / n_{i}^{(0)}\) and \(\nu = n_{p}^{(0)} / n_{i}^{(0)}\) denote the unperturbed density ratios of electrons- and positrons-to-ions, respectively. σ i =T i /T e and σ p =T p /T e , where T i , T e and T p are the ion, electron and positron temperatures, respectively. The variables appearing in (1a), (1b), (1c), (2), (3a), (3b) have been appropriately normalized. Thus, the ion density n i (x,y,t) is normalized by the unperturbed ion density \(n_{i}^{(0)}\), the ion velocities uix(y)(x,y,t) are normalized by the ion acoustic speed \(C_{si} = \sqrt{k_{B}T_{e} / m_{i}}\), the electrostatic potential ϕ(x,y,t) is normalized by k B T e /e. The space and time variables are in units of the ion Debye radius \(\lambda_{Di} = \sqrt{k_{B}T_{e} / (4\pi e^{2}n_{i}^{(0)})}\) and the ion plasma period \(\omega_{Pi}^{ - 1} = \sqrt{4\pi e^{2}n_{i}^{(0)} / m_{i}}\), respectively. κ is a real parameter measuring deviation from Maxwellian equilibrium (recovered for κ→∞) and k B is the Boltzmann constant. Overall charge neutrality at equilibrium is \(n_{e}^{(0)} = n_{p}^{(0)} + n_{i}^{(0)}\)or μ=ν+1.

To derive the KP equation describing the behavior of the system for longer times and small but finite amplitude IAWs, we introduce the slow stretched co-ordinates:

$$ \xi = \varepsilon (x - \lambda t),\qquad \eta = \varepsilon^{2}y, \qquad \tau = \varepsilon^{3}t, $$
(4)

where ε is a small dimensionless expansion parameter and λ is the speed of IAWs. All physical quantities appearing in (1a), (1b), (1c), (2), (3a), (3b) are expanded as power series in ε about their equilibrium values as:

$$ n_{i}(\xi,\eta,\tau ) = 1 + \varepsilon^{2}n_{i1} + \varepsilon^{4}n_{i2} + \varepsilon^{6}n_{i3} +\cdots , $$
(5a)
$$ u_{ix}(\xi,\eta,\tau ) = \varepsilon^{2}u_{ix1} + \varepsilon^{4}u_{ix2} + \varepsilon^{6}u_{ix3} +\cdots , $$
(5b)
$$ u_{iy}(\xi,\eta,\tau ) = \varepsilon^{2}u_{iy1} + \varepsilon^{4}u_{iy2} + \varepsilon^{6}u_{iy3} +\cdots , $$
(5c)
$$ \phi (\xi,\eta,\tau ) = \varepsilon^{2}\phi_{1} + \varepsilon^{4}\phi_{2} + \varepsilon^{6} \phi_{3} +\cdots . $$
(5d)

The boundary conditions has been taken as |ξ|→∞, n i =1, u ix =u iy =0. Substituting (4) and (5a), (5b), (5c), (5d) into (1a), (1b), (1c), (2), (3a), (3b), and equating coefficients of like powers of ε, then, from the lowest-order equations in ε, the following results are obtained:

$$ n_{i1} = \phi_{1}/(\lambda^2 - 3 \omega_i), \qquad u_{ix1} = \lambda \phi_{1}/(\lambda^2 - 3 \omega_i). $$
(6)

Poisson’s equation gives the linear dispersion relation:

$$ \lambda^{2} = 3\sigma_{i} - 2\kappa /\bigl[(1 - 2\kappa ) ( \mu + \nu \sigma_{p})\bigr]. $$
(7)

The higher order in ε yields the following set of equations:

$$ 3\sigma_{i}\frac{\partial}{\partial \eta} n_{i1} - \lambda \frac{\partial}{ \partial \xi} u_{iy1} + \frac{\partial}{\partial \eta} \phi_{1} = 0, $$
(8a)
$$\begin{aligned} & {\frac{\partial}{\partial \tau} n_{i1} + \frac{\partial}{\partial \eta} u_{iy1} + u_{ix1}\frac{\partial}{\partial \xi} n_{i1} + n_{i1} \frac{\partial}{\partial \xi} u_{ix1} } \\ & {\quad {} - \lambda \frac{\partial}{ \partial \xi} n_{i2} + \frac{\partial}{\partial \xi} u_{ix2} = 0, } \end{aligned}$$
(8b)
$$\begin{aligned} & {\frac{\partial}{\partial \tau} u_{ix1} + 3\sigma_{i}n_{i1} \frac{\partial}{ \partial \xi} n_{i1} + 3\sigma_{i}\frac{\partial}{\partial \xi} n_{i2} + u_{ix1}\frac{\partial}{\partial \xi} u_{ix1} } \\ & {\quad {} - \lambda \frac{\partial}{\partial \xi} u_{ix2} + \frac{\partial}{\partial \xi} \phi_{2} = 0, } \end{aligned}$$
(8c)
$$\begin{aligned} & {\frac{\partial^{2}\phi_{1}}{\partial \xi^{2}} + \bigl[\bigl(\mu - \nu \sigma_{p}^{2} \bigr)/(8\kappa - 2)\bigr]\phi_{1}^{2} } \\ & {\quad {} + (\mu + \nu \sigma_{p})\bigl[(1 - 1/(2\kappa )\bigr]\phi_{2} + n_{i2} = 0. } \end{aligned}$$
(8d)

Eliminating the second order perturbed quantities ni2, uix2, uiy2 and ϕ2, leads to the following KP equation for the first-order perturbed potential ϕ1=φ(ξ,η,τ):

$$ \frac{\partial}{\partial \xi} \biggl[\frac{\partial}{\partial \tau} \varphi + A\varphi \frac{\partial}{\partial \xi} \varphi + B\frac{\partial^{3}}{\partial \xi^{3}}\varphi \biggr] + C\frac{\partial^{2}}{\partial \eta^{2}}\varphi = 0, $$
(9)

where, the nonlinear parameter has the form

$$\begin{aligned} A =& \bigl\{ \bigl(4\kappa^{2} - 1\bigr)\bigl[3\mu \lambda^{4} - 9\mu \bigl(\lambda^{2} - \sigma_{i} \bigr)\sigma_{i} + \nu \bigl(\lambda^{2} - 3 \sigma_{i}\bigr)\sigma_{p}^{2}\bigr] \\ &{} + 4 \kappa^{2}\bigl[1 - \lambda^{2}\bigl(\mu \lambda^{4} - 3\bigr)\bigr] + \mu \lambda^{6} + 3\sigma_{i}\bigr\} \\ &{}\ \big/\bigl[8\lambda \kappa^{2}\bigl(\lambda^{2} - 3 \sigma_{i}\bigr)\bigr], \end{aligned}$$
(10a)

while the dispersion parameters are represented by

$$ B = \bigl(\lambda^{2} - 3\sigma_{i}\bigr)^{2}/(2 \lambda ), $$
(10b)
$$ C = \lambda /2. $$
(10c)

3 Rogue wave solution

Rogue waves are singular, rare, high-energy waves with very high amplitude that carries dramatic impact. It appears in seemingly unconnected systems in the form of oceanic rogue waves, stock market crashes, communication systems, opposing currents flows, Bose-Einstein condensates, propagation of acoustic-gravity waves in the atmosphere, atmospheric and plasma physics. To obtain the possible analytical solutions of Eq. (9), we assume that:

$$ \varphi (\xi,\eta,\tau ) = \varPhi (\zeta,\tau )\quad \mbox{and}\quad \zeta = L\xi + M \eta - v\tau, $$
(11)

where L and M are the directional cosines of the wave vector along the ξ- and η-axes, respectively, so that L2 + M2 = 1 and v is an arbitrary parameter similar to Mach number to be determined later. Putting Eqs. (11) into Eq. (9), we obtain

$$\begin{aligned} & {\frac{\partial}{\partial \tau} \varPhi (\zeta,\tau ) + L A\varPhi (\zeta,\tau ) \frac{\partial}{\partial \zeta} \varPhi (\zeta,\tau ) } \\ & {\quad {} + L^{3}B\frac{\partial^{3}}{\partial \zeta^{3}} \varPhi (\zeta,\tau ) = 0, } \end{aligned}$$
(12)

where v satisfies the condition v=M2 C/L=(1−L2)λ/(2L). We consider the solution of (12) in the form of a weakly modulated sinusoidal wave by expanding Φ(ζ,τ) as (El-Labany et al. 2012):

$$ \varPhi (\zeta,\tau )= \sum_{n=1}^{\infty} \sum_{l=-\infty}^{\infty} \varPhi_l^{(n)}(X,T) \exp \bigl[ il (k \zeta - \omega \tau) \bigr], $$
(13)

where k is the carrier wave number and ω is the frequency of the given wave. The stretched variables X and T are

$$ X = \varepsilon ( \zeta + \varLambda \tau )\quad \mbox{and}\quad \mathrm{T} = \varepsilon^{2}\tau, $$
(14)

where Λ is a parameter that will be derived later.

Assume that all perturbed states depend on the fast scales via the phase (kζ−ωτ) only, while the slow scales (X,T) enter the arguments of the lth harmonic amplitude \(\varPhi_{l}^{(n)}\). Since Φ(ζ,τ) must be real, the coefficients in (13) have to satisfy the condition \(\varPhi_{ - l}^{(n)} = \varPhi_{l}^{(n) *}\), where the asterisk indicates the complex conjugate. The derivative operators appearing in the system of the basic equations become

$$ \frac{\partial}{\partial \tau} \to \frac{\partial}{\partial \tau} + \varepsilon \varLambda \frac{\partial}{\partial X} + \varepsilon^{2}\frac{\partial}{\partial \mathrm{T}}, $$
(15a)
$$ \frac{\partial}{\partial \zeta} \to \frac{\partial}{\partial \zeta} + \varepsilon \frac{\partial}{\partial X}. $$
(15b)

Substituting (13)–(15a), (15b) into (12), we obtain (El-Labany et al. 2012):

$$\begin{aligned} & {\Biggl[ - il\omega \varPhi_{l}^{(n)} + \varLambda \frac{\partial \varPhi_{l}^{(n - 1)}}{\partial X} + \frac{\partial \varPhi_{l}^{(n - 2)}}{\partial \mathrm{T}} } \\ & {\quad {} + LA\sum_{n' = 1}^{\infty} \sum _{l^{ \prime} = - \infty}^{\infty} \biggl(ilk\varPhi_{l}^{(n)} \varPhi_{l - l^{ \prime}}^{ ( n - n' )} + \varPhi_{l - l^{ \prime}}^{ ( n - n' - 1 )} \frac{\partial \varPhi_{l}^{(n)}}{\partial X}\biggr) } \\ & {\quad {} + L^{3}B \biggl( - il^{3}k^{3} \varPhi_{l}^{(n)} - 3l^{2}k^{2} \frac{\partial \varPhi_{l}^{(n - 1)}}{\partial X} } \\ & {\quad {} + 3ilk\frac{\partial^{2}\varPhi_{l}^{(n - 2)}}{\partial X^{2}} + \frac{\partial^{3}\varPhi_{l}^{(n - 3)}}{\partial X^{3}} \biggr)\Biggr] = 0. } \end{aligned}$$
(16)

The first-order approximation (n=1) with (l=1) yields the linear dispersion relation

$$ \omega = - k^{3}L^{3}B. $$
(17)

For the first harmonic (l=1) of the second-order approximation (n=2), we find that

$$ \varLambda = 3k^{2}L^{3}B, $$
(18)

which corresponds to the group velocity. For the second harmonic (l=2), we have

$$ \varPhi_{2}^{(2)} = \bigl[A/\bigl(6k^{2}L^{2}B \bigr) \bigr]\varPhi_{1}^{(1)2}. $$
(19)

Proceeding to the third-order approximation (n=3) and solving for the first harmonic equations (l=1), an explicit compatibility condition will be found, from which we can easily obtain the NLSE:

$$ i \frac{\partial \varPhi}{\partial \mathrm{T}} + R\frac{\partial^{2}\varPhi}{ \partial X^{2}} + S \vert \varPhi \vert ^{2}\varPhi = 0. $$
(20)

For simplicity, we have assumed \(\varPhi_{1}^{(1)} \equiv \varPhi (X,\mathrm{T})\). The dispersion coefficient R and the nonlinear coefficient S are given by:

$$ R = 3kL^{3}B, $$
(21a)
$$ S = A^{2} / (6kLB). $$
(21b)

The NLSE (20) describes the nonlinear evolution of an amplitude modulated wave carrier. The NLSE (20) has a rational solution that is located on a nonzero background and localized both in X and T directions as:

$$\begin{aligned} \varPhi (X,\mathrm{T}) =& \bigl\{ \bigl[4(1 + 2i\mathrm{T}) / \bigl(1 + 4 \mathrm{T}^{2} + 4X^{2}/R\bigr)\bigr] - 1\bigr\} \\ &{}\times e^{i\mathrm{T}}/\sqrt{S}. \end{aligned}$$
(22)

The solution (22) reveals that a significant amount of the wave energy is concentrated into a relatively small area in space. The rogue wave is usually an envelope of a carrier wave with a wavelength smaller than the central region of the envelope. A negative sign for R∗S is required for wave amplitude modulation stability. On the other hand, a positive sign of R∗S allows for a random perturbation of the amplitude to grow and thus the rogue wave could be created.

4 Results and discussion

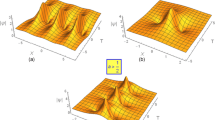
Nonlinear IAWs in unmagnetized collisionless plasma consisting of ions and excess super-thermal electrons and positrons have been investigated. We have derived the KP equation using the reductive perturbation method. The modulation of Kadomstev-Petviashvili equation gives the NLSE. The rational solution of NLSEs produce rogue wave profile. Now, we numerically analyze the envelope rogue wave |Φ(X,T)| and investigate how the spectral index κ change the profile expressed by the wave envelope of the IA rogue wave as in Fig. 1. It is depicts that the amplitudes of the rogue waves decrease with the increase of κ. However, since one of our motivations was to study the effect of directional cosines of the wave vector along the ξ direction L on formation of rogue waves, we have studied the effect of, the carrier wave number K, the unperturbed density ratios of electrons- and positrons-to-ions μ and ν, the ratios of ions- and positrons temperatures-to-electrons temperature σ i and σ p on the properties of rogue waves. Figures 2 and 3 shown that, the amplitude and width of the rogue waves increases by L and K. Finally, the dependence of the rogue wave amplitude on σ i , σ p and μ are depicted in Figs. 4, 5. It is seen that σ i and σ p increasing the ion acoustic rogue wave amplitude while decreasing by μ. In summary, it has been found that the presence of directional cosines of the wave vector along the ξ direction L as well as the spectral index κ would modify the properties of the ion-acoustic rogue waves significantly and the results presented here may be applicable to some plasma environments, such as active galactic cores, magnetosphere of neutron stars.

Fig. 1
figure 1

Variation of Φ for σ i =0.1, σ p =0.3, L=0.45, μ=0.85, K=1 and different values of κ

Full size image
Fig. 2
figure 2

Variation of Φ for σ i =0.1, σ p =0.3, μ=0.85, κ=3, K=1 and different values of L

Full size image
Fig. 3
figure 3

Variation of Φ for σ i =0.1, σ p =0.3, L=0.45, μ=0.85, κ=3 and different values of K

Full size image
Fig. 4
figure 4

Variation of Φ for L=0.45, μ=0.85, κ=3, K=1 and different values of σ i and σ p

Full size image
Fig. 5
figure 5

Variation of Φ for σ i =0.1, σ p =0.3, L=0.45, κ=0.3, K=1 and different values of μ

Full size image

5 Conclusions

We have devoted quite some effort to discuss the proper description of the directional cosines of the wave vector along the ξ direction L as well as the spectral index κ and the carrier wave number K in unmagnetized collisionless plasma consisting of ions and excess super-thermal electrons and positrons. The reductive perturbation technique has been used to reduce the basic set of fluid equations to the well-known KP equation. In the form of a weakly modulated sinusoidal wave, the NLSE has been obtained using similarity transformation. The rational solution of NLSE give rogue wave solution. The scientific discussion of rogue wave explains how a great amount of energy concentrated into a relatively small area in space. It is emphasized that the IA rogue waves have smaller amplitude and narrower width with the increasing of the spectral index and unperturbed density ratios of electrons to ions. It is interesting to point out that the increase of the directional cosines of the wave vector can lead to an enhancement of the nonlinearity, dispersion and then concentrate a significant amount of energy, which makes the pulses wider and taller. On the other hand, it is found that the carrier wave number, the ratios of ions and positrons temperatures to electrons leads to an enhancement of the rogue wave amplitude. Generally speaking, it is seen that both the directional cosines of the wave vector and excess super-thermal electrons and positrons significantly modify the properties of IA rogue waves. The application of our model might be particularly interesting in controlling and maximizing plasma energy along the electron-positron-ion plasma. Investigating the modulation instability is very important task for the existence of rogue waves in the plasma. In the case of magnetized plasma more attention should be paid to study the instability for the existence of rogue waves. This is our future task.