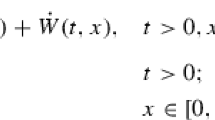Gaussian fluctuations for the stochastic heat equation with colored noise

Abstract

In this paper, we present a quantitative central limit theorem for the d-dimensional stochastic heat equation driven by a Gaussian multiplicative noise, which is white in time and has a spatial covariance given by the Riesz kernel. We show that the spatial average of the solution over an Euclidean ball is close to a Gaussian distribution, when the radius of the ball tends to infinity. Our central limit theorem is described in the total variation distance, using Malliavin calculus and Stein’s method. We also provide a functional central limit theorem.

1 Introduction

We consider the stochastic heat equation

$$\begin{aligned} \frac{\partial u }{\partial t} = \frac{1}{2} \Delta u + \sigma (u) {\dot{W}} , \end{aligned}$$

(1.1)

on ${\mathbb {R}}_+\times {\mathbb {R}}^d$ with initial condition $u(0,x)=1$, where ${\dot{W}}(t,x)$ is a centered Gaussian noise with covariance ${\mathbb {E}}\big [ {\dot{W}}(t,x) {\dot{W}}(s,y)\big ] = \delta _0(t-s) | x-y|^{-\beta }$, $0<\beta < \min (d,2)$. In this paper, $\vert \cdot \vert$ denotes the Euclidean norm and we assume the nonlinear term $\sigma$ is a Lipschitz function with $\sigma (1)\ne 0$; see point (iii) in Remark 3.

Our first result is the following quantitative central limit theorem concerning the spatial average of the solution u(t, x) over $B_R:= \{ x\in {\mathbb {R}}^d: |x| \le R\}$.

Theorem 1.1

For all $t > 0$, there exists a constant $C = C(t,\beta )$, depending on t and $\beta$, such that

$$\begin{aligned} d_{\mathrm{TV}}\left( \frac{1}{\sigma _R} \int _ {B_R} \big [ u(t,x) - 1 \big ]\,dx, ~Z\right) \le C R^{-\beta /2} \,, \end{aligned}$$

where $d_{\mathrm{TV}}$ denotes total variation distance (see (1.2)), $Z\sim N(0,1)$ is a standard normal random variable and $\sigma _R^2 = \mathrm{Var} \big ( \int _ {B_R} [ u(t,x) - 1 ]\,dx \big )$. Moreover, the normalization $\sigma _R$ is of order $R^{d-\frac{\beta }{2}}$, as $R\rightarrow +\infty$ [(see (1.8)].

Remark 1

In the above result we have assumed $u(0,x)=1$ for the sake of simplicity. However, one can easily extend the result to cover more general initial deterministic condition u(0, x). In fact, this is the topic of Corollary 3.3.

We will mainly rely on the methodology of Malliavin-Stein approach to prove the above result. Such an approach was introduced by Nourdin and Peccati in [9] to, among other things, quantify Nualart and Peccati’s fourth moment theorem in [14]. Notably, if F is a Malliavin differentiable (that means, F belongs to the Sobolev space ${\mathbb {D}}^{1,2}$), centered Gaussian functional with unit variance, the well-known Malliavin-Stein bound implies

$$\begin{aligned} d_{\mathrm{TV}}(F, Z) :&= \sup \Big \{ P(F\in A) - P(Z\in A) \,:\, A \subset {\mathbb {R}}\,\,\,\, \text {Borel sets} \Big \} \end{aligned}$$

(1.2)

$$\begin{aligned}&\le 2 \sqrt{ \mathrm{Var}\big ( \langle DF, -DL^{-1}F \rangle _{{\mathfrak {H}}} \big ) } \quad \text {with }Z\sim N(0,1), \end{aligned}$$

(1.3)

where D is the Malliavin derivative, $L^{-1}$ is the pseudo-inverse of the Ornstein-Uhlenbeck operator and $\langle \cdot , \cdot \rangle _{\mathfrak {H}}$ denotes the inner product in the Hilbert space ${\mathfrak {H}}$ associated with the covariance of W; see also the monograph [10].

It was observed in [16] that instead of $\langle DF, -DL^{-1}F \rangle _{\mathfrak {H}}$, one can work with the term $\langle DF, v \rangle _{\mathfrak {H}}$ once F can be represented as a Skorohod integral $\delta (v)$; see the following result from [16, Proposition 3.1] (see also [8, 12]).

Proposition 1.2

If F is a centered random variable in the Sobolev space ${\mathbb {D}}^{1,2}$ with unit variance such that $F = \delta (v)$ for some ${\mathfrak {H}}$-valued random variable v, then, with $Z \sim N (0,1)$,

$$\begin{aligned} d_{\mathrm{TV}}(F, Z) \le 2 \sqrt{\mathrm{Var} \big ( \langle DF, v\rangle _{\mathfrak {H}}\big ) }. \end{aligned}$$

(1.4)

This estimate enables us to bring in tools from stochastic analysis.

Remark 2

Throughout this paper we only work with the total variation distance. However, we point out that we can get the same rate in other frequently used distances. Indeed, if $\texttt {d}$ denotes either the Kolmogorov distance, the Wasserstein distance or the Fortet-Mourier distance, we have as well

$$\begin{aligned} \texttt {d}(F,Z) \le 2 \sqrt{\mathrm{Var} \big ( \langle DF, v\rangle _{\mathfrak {H}}\big ) } , \end{aligned}$$

where F, Z are given as in (1.4); see e.g. [10, Chapter 3] for the properties of Stein’s solution. Thus, proceeding in the exact same lines as in this paper, we will get the same rate in these distances.

It is known (see e.g. [4, 18]) that Eq. (1.1) has a unique mild solution$\{u(t,x): t\ge 0, x \in {\mathbb {R}}^d\}$, in the sense that it is adapted to the filtration generated by W, uniformly bounded in $L^2(\Omega )$ over $[0,T]\times {\mathbb {R}}^d$ (for any finite T) and satisfies the following integral equation in the sense of Dalang-Walsh

$$\begin{aligned} u(t,x) = { \int _{{\mathbb {R}}^d}p_t(x-y)u(0,y)dy}+ \int _0^t \int _{{\mathbb {R}}^d} p_{t-s}(x-y) \sigma (u(s,y))W(ds,dy)\,,\nonumber \\ \end{aligned}$$

(1.5)

where $p_t(x) = (2\pi t)^{-d/2}\exp \big ( - |x|^2/ (2t) \big )$ denotes the heat kernel and is the fundamental solution to the corresponding deterministic heat equation.

Let us introduce some handy notation. For fixed $t > 0$, we define

$$\begin{aligned} \varphi _R(s,y) := \int _{B_R} p_{t-s} (x-y) dx \,\,\,\, \text {and} \,\,\,\, G_R(t): = \int _{B_R} \big [ u(t,x) - 1 \big ] dx \,. \end{aligned}$$

(1.6)

If we put $F_R(t) := G_R(t)/\sigma _R$, then we write, due to the Fubini’s theorem,

$$\begin{aligned} F_R(t) = \frac{1}{\sigma _R}\int _0^t \int _{{\mathbb {R}}^d} \varphi _R(s,y) \sigma (u(s,y)) W(ds,dy) = \delta (v_R )\,, \end{aligned}$$

(1.7)

with $v_R(s,y) = \sigma _R^{-1}{\mathbf {1}} _{[0,t]}(s) \varphi _R(s,y) \sigma (u(s,y) )$ taking into account that the Dalang-Walsh integral (1.5) is a particular case of the Skorohod integral; see [11].

By Proposition 1.2, the proof of Theorem 1.1 reduces to estimating the variance of $\langle DF_R(t), v_R\rangle _{\mathfrak {H}}$. One of the key steps, our Proposition 3.2, provides the exact asymptotic behavior of the normalization $\sigma _R^2$:

$$\begin{aligned} \sigma _R^2 = \mathrm{Var}\big ( G_R(t) \big ) \sim \left( k_\beta \int _0^t \eta ^2(s)\, ds\right) R^{2d-\beta }\,, \quad \text {as } R\rightarrow +\infty ; \end{aligned}$$

(1.8)

and throughout this paper, we will reserve the notation $k_\beta$ and $\eta (\cdot )$ for

$$\begin{aligned} k_\beta := \int _{B_1^2} |x_1-x_2 | ^{-\beta } dx_1dx_2 \quad \mathrm{and}\quad \eta (s) := {\mathbb {E}}\big [ \sigma ( u(s,y) ) \big ] \,. \end{aligned}$$

(1.9)

Remark 3

• (i) The definition of $\eta$ does not depend on the spatial variable, due to the strict stationarity of the solution, meaning that the finite-dimensional distributions of the process $\{u(t, x+y),x\in {\mathbb {R}}^d\}$ do not depend on y; see [4].

• (ii) Another consequence of the strict stationarity is that the quantity

  $$\begin{aligned} K_p(t):={\mathbb {E}}\big [ |u(t,x)| ^p \big ] \end{aligned}$$

  (1.10)

  does not depend on x. Moreover, $K_p(\cdot )$ is uniformly bounded on compact sets.

• (iii) Under our constant initial condition (i.e.$u(0,x)\equiv 1$), the assumption $\sigma (1) \ne 0$ is necessary and sufficient in our paper. It is necessary, in view of the usual Picard iteration, to exclude the situation where $u(t,x)\equiv 1$ is the unique solution, and it is sufficient to guarantee that the integral in (1.8) is nonzero. Moreover, we have the following equivalence

  $$\begin{aligned} \sigma (1)=0 \Leftrightarrow \sigma _R=0,\forall R>0 \Leftrightarrow \sigma _R=0\hbox { for some }R>0 \Leftrightarrow {\displaystyle \lim _{R\rightarrow \infty }\sigma _R^2 R^{\beta -2d}= 0;} \end{aligned}$$

  whose verification can be done in the same way as in [5, Lemma 3.4], so we leave it as an easy exercise for interested readers.

• (iv) Due to the stationarity again, we can see that Theorem 1.1 still holds true when we replace $B_R$ by $\{ x\in {\mathbb {R}}^d: | x - a_R | \le R \}$, with $a_R$ possibly varying as $R\rightarrow +\infty$. Moreover, the normalization $\sigma _R$ in this translated version remains unchanged. To see this translational “invariance”, one can alternatively go through the exactly same arguments as in the proof of Theorem 1.1. Note that this invariance under translation justifies the statement in our abstract.

• (v) By going through the exactly same arguments as in the proof of Theorem 1.1, we can obtain the following result: If we replace the ball $B_R$ by the box $\Lambda _R: = \big \{ (x_1,\ldots , x_d)\in {\mathbb {R}}^d: \vert x_i\vert \le R, i=1,\dots , d \big \}$, Theorem 1.1 still holds true with a slightly different normalization $\sigma '_R$ given by

  $$\begin{aligned} \sigma '_R \sim \left( \int _0^t \eta ^2(s)\int _{\Lambda _1^2} |z- y | ^{-\beta } dzdy \, ds\right) ^{1/2} R^{d-\frac{\beta }{2}}\,, \quad \text {as }R\rightarrow +\infty . \end{aligned}$$

Our second main result is the following functional version of Theorem 1.1.

Theorem 1.3

Fix any finite $T>0$ and recall (1.9). Then, as $R\rightarrow +\infty$, we have

$$\begin{aligned} \left\{ R^{\frac{\beta }{2}-d} \int _{B_R} \big [ u(t,x) -1 \big ] \,dx \right\} _{t\in [0,T]} \Rightarrow \left\{ \sqrt{k_\beta } \int _0^t \eta (s) dY_s\right\} _{t\in [0,T]} \,, \end{aligned}$$

where Y is a standard Brownian motion and the above weak convergence takes place on the space of continuous functions C([0, T]).

A similar problem for the stochastic heat equation on ${\mathbb {R}}$ has been recently considered in [8], but only in the case of a space-time white noise, where $\eta ^2(s)$ appearing in the limiting variance (1.8) is replaced by ${\mathbb {E}}\big [ \sigma ^2(u(s,y)) \big ]$. Such a phenomenon also appeared in the case of the one-dimensional wave equation, see the recent paper [5], whose authors also considered the Riesz kernel for the spatial fractional noise therein, which corresponds to the case $\beta =2-2H$.

Remark 4

When $\sigma (x)=x$, the random variable $G_R(t)$ defined in (1.6) has an explicit Wiener chaos expansion:

$$\begin{aligned} G_R(t) = \int _0^t\int _{{\mathbb {R}}^d} \varphi _R(s,y) \, W(ds, dy) + \text { higher-order chaoses.} \end{aligned}$$

In this linear case, the asymptotic result (1.8) reduces to $\sigma _R^2 \sim t k_\beta R^{2d-\beta }$, while the first chaotic component of $G_R(t)$ is centered Gaussian with variance equal to

$$\begin{aligned} \int _0^t \int _{{\mathbb {R}}^{2d}} \varphi _R(s,y) \varphi _R(s,z) \vert y -z\vert ^{-\beta } \, dydz \sim t k_\beta R^{2d-\beta } \,,\quad \text {as} \,\, R\rightarrow +\infty ; \end{aligned}$$

see (3.9). Therefore, due to the orthogonality of Wiener chaoses with different orders, we can conclude that $F_R(t) = G_R(t)/\sigma _R$ is asymptotically Gaussian. It is worth pointing out that, unlike in our case, for the linear stochastic heat equation driven by space-time white noise as considered in [8], the central limit is chaotic, meaning that each projection on the Wiener chaos contributes to the Gaussian limit. In this case, the proof of asymptotic normality could be based on the chaotic central limit theorem from [7, Theorem 3] (see also [10, Section 6.3]).

The rest of the paper is organized as follows. We present the proofs in Sects. 3 and 4 , after we recall briefly some preliminaries in Sect. 2.

Along the paper, we will denote by C a generic constant that may depend on the fixed time T, the parameter $\beta$ and $\sigma$, and it can vary from line to line. We also denote by $\Vert \cdot \Vert _p$ the $L^p(\Omega )$-norm and by L the Lipschitz constant of $\sigma$.

2 Preliminaries

Let us build an isonormal Gaussian process from the colored noise W as follows. We begin with a centered Gaussian family of random variables $\big \{W(\psi ):\, \psi \in C_c^{\infty }\left( [0,\infty )\times {\mathbb {R}}^{d}\right) \big \}$, defined on some complete probability space, such that

$$\begin{aligned} {\mathbb {E}}\left[ W(\psi )W(\phi )\right] =&\int _0^{\infty } \int _{{\mathbb {R}}^{2d}}\psi (s,x)\phi (s,y)|x-y|^{-\beta } \, d xd yds =: \big \langle \psi , \phi \big \rangle _{\mathfrak {H}}, \end{aligned}$$

where $C_c^{\infty }\left( [0,\infty )\times {\mathbb {R}}^{d}\right)$ is the space of infinitely differentiable functions with compact support on $[0,\infty )\times {\mathbb {R}}^{d}$. Let ${\mathfrak {H}}$ be the Hilbert space defined as the completion of $C_c^{\infty }\left( [0,\infty )\times {\mathbb {R}}^{d}\right)$ with respect to the above inner product. By a density argument, we obtain an isonormal Gaussian process $W:=\big \{W(\psi ):\, \psi \in {\mathfrak {H}}\big \}$ meaning that for any $\psi , \phi \in {\mathfrak {H}}$,

$$\begin{aligned} {\mathbb {E}}\left[ W(\psi )W(\phi )\right] =\big \langle \psi , \phi \big \rangle _{\mathfrak {H}}. \end{aligned}$$

Let ${\mathbb {F}}=({\mathcal {F}}_t,t\ge 0)$ be the natural filtration of W, with ${\mathcal {F}}_t$ generated by $\big \{W(\phi ):\phi$ continuous and with compact support in $[0,t]\times {\mathbb {R}}^d\big \}$. Then for any ${\mathbb {F}}$-adapted, jointly measurable random field X such that

$$\begin{aligned} {\mathbb {E}}( \Vert X \Vert ^2_{{\mathfrak {H}}})= {\mathbb {E}}\left( \int _0^\infty d s\int _{{\mathbb {R}}^{2d}}d x d y\, X(s,y)X(s,x) |x-y|^{-\beta } \right) <\infty , \end{aligned}$$

(2.1)

the stochastic integral

$$\begin{aligned} \int _0^\infty \int _{{\mathbb {R}}^d} X(s,y)W(ds, d y) \end{aligned}$$

is well-defined in the sense of Dalang-Walsh and the following isometry property is satisfied

$$\begin{aligned} {\mathbb {E}}\left( \left| \int _0^\infty \int _{{\mathbb {R}}^d} X(s,y)W(ds, d y) \right| ^2 \right) = {\mathbb {E}}( \Vert X \Vert ^2_{{\mathfrak {H}}}). \end{aligned}$$

In the sequel, we recall some basic facts on Malliavin calculus and we refer readers to the books [11, 12] for any unexplained notation and result.

Denote by $C_p^{\infty }({\mathbb {R}}^n)$ the space of smooth functions with all their partial derivatives having at most polynomial growth at infinity. Let ${\mathcal {S}}$ be the space of simple functionals of the form $F = f(W(h_1), \dots , W(h_n))$ for $f\in C_p^{\infty }({\mathbb {R}}^n)$ and $h_i \in {\mathfrak {H}}$, $1\le i \le n$, $n\in {\mathbb {N}}$. Then, DF is the ${\mathfrak {H}}$-valued random variable defined by

$$\begin{aligned} DF=\sum _{i=1}^n \frac{\partial f}{\partial x_i} (W(h_1), \dots , W(h_n)) h_i\,. \end{aligned}$$

The derivative operator D is closable from $L^p(\Omega )$ into $L^p(\Omega ; {\mathfrak {H}})$ for any $p \ge 1$ and we let ${\mathbb {D}}^{1,p}$ be the completion of ${\mathcal {S}}$ with respect to the norm

$$\begin{aligned} \Vert F\Vert _{1,p} = \Big ({\mathbb {E}}\big [ |F|^p \big ] + {\mathbb {E}}\big [ \Vert D F\Vert ^p_{\mathfrak {H}} \big ] \Big )^{1/p} . \end{aligned}$$

We denote by $\delta$ the adjoint of D characterized by the integration-by-parts formula

$$\begin{aligned} {\mathbb {E}}[\delta (u) F ] = {\mathbb {E}}\big [ \langle u, DF \rangle _{\mathfrak {H}}\big ] \end{aligned}$$

for any $F \in {\mathbb {D}}^{1,2}$ and $u\in \mathrm{Dom} \, \delta \subset L^2(\Omega ; {\mathfrak {H}})$, the domain of $\delta$. The operator $\delta$ is also called the Skorohod integral, because in the case of the Brownian motion, it coincides with Skorohod’s extension of the Itô integral (see e.g. [6, 13]). In our context, any adapted random field X satisfying (2.1) belongs to $\text {Dom}\delta$, and $\delta (X)$ coincides with the Dalang-Walsh stochastic integral. As a consequence, the mild formulation (1.5) can be rewritten as

$$\begin{aligned} u(t,x) = 1 + \delta \Big ( p_{t-\cdot } (x-*) \sigma \big ( u(\cdot , *) \big )\Big ). \end{aligned}$$

It is known that for any $(t,x)\in {\mathbb {R}}_+\times {\mathbb {R}}^d$, $u(t,x)\in {\mathbb {D}}^{1,p}$ for any $p\ge 2$ and the derivative satisfies, for $t\ge s$, the linear equation

$$\begin{aligned} D_{s,y}u(t,x)&= p_{t-s} (x-y) \sigma (u(s,y)) \nonumber \\&\quad + \int _s^t \int _{{\mathbb {R}}^d} p_{t-r} (x-z) \Sigma (r,z) D_{s,y} u(r,z) W(dr,dz), \end{aligned}$$

(2.2)

where $\Sigma (r,z)$ is an adapted process, bounded by L. If in addition $\sigma \in C^1({\mathbb {R}})$, then $\Sigma (r,z)= \sigma '(u(r,z))$. This result is proved in [11, Proposition 2.4.4] in the case of the stochastic heat equation with Dirichlet boundary conditions on [0, 1] driven by a space-time white noise. Its proof can be easily adapted to our case, see also [1, 15].

In the end of this section, we record a technical lemma, whose proof can be found in [3, Lemma 3.11].

Lemma 2.1

For any $p\in [ 2,+\infty )$, $0 \le s \le t \le T$ and $x,y \in {\mathbb {R}}^d$, we have for every $(s,y)\in [0,T]\times {\mathbb {R}}^d$,

$$\begin{aligned} \Vert D_{s,y} u(t,x) \Vert _p \le C p_{t-s} (x-y) \end{aligned}$$

(2.3)

for some constant $C= C_{T,p}$ that may depend on T and p.

Note that in [5], the p-norm of the Malliavin derivative $D_{s,y}u(t, x)$ can be bounded by a multiple of the fundamental solution of the wave equation. So it is natural to expect that a similar estimate like (2.3) may hold for a large family of stochastic partial differential equations.

3 Proof of Theorem 1.1

We first state a lemma, which will be used below.

Lemma 3.1

Let Z be a standard Gaussian vector on ${\mathbb {R}}^d$ and $\beta \in (0,d)$. Then

$$\begin{aligned} \sup _{s>0}\int _{{\mathbb {R}}^d}p_s(x-y)|x|^{-\beta }dx= \sup _{s>0} {\mathbb {E}}\Big [ |y+\sqrt{s}Z|^{-\beta }\Big ]\le C |y|^{-\beta }\,, \end{aligned}$$

(3.1)

for some constant C that only depends on d and $\beta$.

Proof

We want to show that

$$\begin{aligned} \int _{{\mathbb {R}}^d}p_s(x-y)|x|^{-\beta } dx \le C |y|^{-\beta }\,, \end{aligned}$$

where C does not depend on s. We first prove this for $s=1$.

$$\begin{aligned} \int _{{\mathbb {R}}^d} e^{-\frac{|x-y|^2}{2}}|x|^{-\beta } {dx}&=\int _{|x|\le \frac{|y|}{2}}e^{-\frac{|x-y|^2}{2}}|x|^{-\beta } dx + \int _{|x|> \frac{|y|}{2}}e^{-\frac{|x-y|^2}{2}}|x|^{-\beta } dx\\&\le \int _{|x|\le \frac{|y|}{2}} e^{-\frac{|y|^2}{8}} |x|^{-\beta } dx + 2^\beta \int _{|x|\ge \frac{|y|}{2}} e^{-\frac{|x-y|^2}{2}} |y|^{-\beta }dx\\&\le C_1 e^{-\frac{|y|^2}{8}} |y|^{-\beta +d} + C_2 |y|^{-\beta }, \end{aligned}$$

where the constants $C_1$ and $C_2$ only depend on $d,\beta$. So we have proved (3.1) for $s=1$.

Therefore, we have for general $s>0$,

$$\begin{aligned} {\mathbb {E}}\Big [ |y+\sqrt{s}Z|^{-\beta }\Big ] = {\mathbb {E}}\Big [ \Big \vert \big ( ys^{-1/2} + Z\big ) \sqrt{s} \Big \vert ^{-\beta } \Big ] \le C \vert ys^{-1/2} \vert ^{-\beta } (\sqrt{s} )^{-\beta } = C | y |^{-\beta }. \end{aligned}$$

That is, we have proved (3.1) for general $s>0$.

Now we begin with the estimate (1.8) recalled below.

Proposition 3.2

With the notation (1.6) and (1.9), we have

$$\begin{aligned} \lim _{R\rightarrow +\infty } R^{\beta -2d} {\mathbb {E}}[ G^2_R(t)] = k_\beta \int _0^t \eta ^2(s)\, ds. \end{aligned}$$

Proof

We define $\Psi (s, y)={\mathbb {E}}\big [ \sigma (u(s,0))\sigma (u(s,y)) \big ]$. Then

$$\begin{aligned} {\mathbb {E}}[ G_R^2(t)]&= \int _0^t \int _{{\mathbb {R}}^{2d}} \varphi _R(s,y) \varphi _R(s,z) {\mathbb {E}}\big [ \sigma (u(s,y))\sigma (u(s,z)) \big ] | y-z| ^{-\beta } dydzds \\&= \int _0^t \int _{{\mathbb {R}}^{2d}} \varphi _R(s,\xi +z )\varphi _R(s,z) \Psi (s,\xi ) | \xi | ^{-\beta } d\xi dzds \,,\quad \text {by stationarity.} \end{aligned}$$

We claim that

$$\begin{aligned} \lim _{\vert \xi \vert \rightarrow +\infty } \sup _{0\le s\le t } | \Psi (s,\xi ) -\eta ^2(s)|=0. \end{aligned}$$

(3.2)

To see (3.2), we apply a version of the Clark-Ocone formula for square integrable functionals of the noise W and we can write

$$\begin{aligned} \sigma (u(s,y)) = {\mathbb {E}}[ \sigma (u(s,y))] + \int _0^s \int _{{\mathbb {R}}^d} {\mathbb {E}}\Big [ D_{r,\gamma }\big ( \sigma (u(s,y)) \big ) | {\mathcal {F}}_r\Big ] \, W(dr, d\gamma ) \,. \end{aligned}$$

As a consequence, ${\mathbb {E}}\big [ \sigma (u(s,y) )\sigma (u(s,z) ) \big ] = \eta ^2(s)+ T(s, y,z),$ where

$$\begin{aligned} T(s, y,z)&=\int _0^s \int _{{\mathbb {R}}^{2d}} {\mathbb {E}}\Big \{ {\mathbb {E}}\Big [ D_{r,\gamma }\big ( \sigma (u(s,y)) \big ) | {\mathcal {F}}_r\Big ] {\mathbb {E}}\Big [ D_{r,\lambda }\big ( \sigma (u(s,z))\big ) | {\mathcal {F}}_r\Big ] \Big \}\nonumber \\&\quad \times \, | \gamma -\lambda |^{-\beta } d\gamma d\lambda dr. \end{aligned}$$

(3.3)

By the chain-rule (see [11]), $D_{r,\gamma }\big ( \sigma (u(s,y)) \big ) = \Sigma (s,y) D_{r,\gamma } u(s,y)$, with $\Sigma (\cdot ,*)$${\mathbb {F}}$-adapted and bounded by L (in particular, $\Sigma (s,y) = \sigma '(u(s,y))$, when $\sigma$ is differentiable .) This implies, using (2.3),

$$\begin{aligned}&\Big \vert {\mathbb {E}}\Big \{ {\mathbb {E}}\Big [ D_{r,\gamma }\big ( \sigma (u(s,y)) \big ) | {\mathcal {F}}_r\Big ] {\mathbb {E}}\Big [ D_{r,\lambda }\big ( \sigma (u(s,z))\big ) | {\mathcal {F}}_r\Big ] \Big \} \Big \vert \nonumber \\&\quad \le L^2 \Vert D_{r,\gamma } u(s,y)\Vert _2 \Vert D_{r,\lambda } u(s,z)\Vert _2 \le C p_{s-r}(\gamma -y) p_{s-r} (\lambda -z), \end{aligned}$$

(3.4)

for some constant C. Therefore, substituting (3.4) into (3.3) and using the semigroup property in (3.5), we can write

$$\begin{aligned} \vert T(s,y,z) \vert&\le C \int _0^s \int _{{\mathbb {R}}^{2d}} p_{s-r}(\gamma -y) p_{s-r} (\lambda -z) | \gamma -\lambda |^{-\beta } d\gamma d\lambda dr \nonumber \\&= C\int _0^s \int _{{\mathbb {R}}^d} p_{2s-2r}(\gamma +z-y)|\gamma |^{-\beta } d\gamma dr \end{aligned}$$

(3.5)

$$\begin{aligned}&\le C |y-z|^{-\beta } \xrightarrow {\vert y-z\vert \rightarrow +\infty } 0 \,, \end{aligned}$$

(3.6)

by Lemma 3.1. This completes the verification of (3.2).

Let us continue our proof of Proposition 3.2 by proving that

$$\begin{aligned} R^{\beta -2d} \int _0^t \int _{{\mathbb {R}}^{2d}} \varphi _R(s,\xi +z )\varphi _R(s,z) \big [ \Psi (s,\xi ) - \eta ^2(s)\big ] \vert \xi \vert ^{-\beta } d\xi dzds \rightarrow 0 \,, \end{aligned}$$

(3.7)

as $R\rightarrow +\infty$. Notice that

$$\begin{aligned} \int _{{\mathbb {R}}^d} \varphi _R(s,\xi +z )\varphi _R(s,z) dz = \int _{ B_R^2} p_{2(t-s)} (x_1-x_2-\xi ) dx_1dx_2 \le CR^d\,. \end{aligned}$$

(3.8)

From (3.2) we deduce that given any $\varepsilon > 0$, we find $K = K_\varepsilon > 0$ such that $| \Psi (s, \xi ) -\eta ^2(s)| < \varepsilon$ for all $s\in [0,t]$ and $|\xi |\ge K$. Now we divide the integration domain in (3.7) into two parts $\vert \xi \vert \le K$ and $\vert \xi \vert > K$.

Case  (i): On the region $| \xi | \le K$, since $\Psi (s,y-z) - \eta ^2(s) = T(s,y,z )$ is uniformly bounded, using (3.8), we can write

$$\begin{aligned}&R^{\beta -2d} \int _0^t \int _{{\mathbb {R}}^{2d}} \varphi _R(s,\xi +z )\varphi _R(s,z) \big | \Psi (s,\xi ) - \eta ^2(s) \big | {\mathbf {1}}_{\{ \vert \xi \vert \le K\}} \vert \xi \vert ^{-\beta } \, d\xi dzds \\&\quad \le C R^{\beta -2d} \int _0^t \int _{|\xi | \le K} \left( \int _{{\mathbb {R}}^d} \varphi _R(s,\xi +z )\varphi _R(s,z) \, dz \right) \vert \xi \vert ^{-\beta } \, d\xi ds\\&\quad \le C R^{\beta -d} \int _0^t \int _{|\xi | \le K} \vert \xi \vert ^{-\beta } \, d\xi ds \xrightarrow {R\rightarrow +\infty } 0 \,,\quad \text {because of }\beta <d. \end{aligned}$$

Case   (ii): On the region $[0,t]\times B_K^c$, $| \Psi (s, \xi ) -\eta ^2(s)| < \varepsilon$. Thus,

$$\begin{aligned}&R^{\beta -2d} \int _0^t \int _{{\mathbb {R}}^{2d}} \varphi _R(s,\xi +z )\varphi _R(s,z) \big | \Psi (s,\xi ) - \eta ^2(s) \big | {\mathbf {1}}_{\{ \vert \xi \vert > K\}} \vert \xi \vert ^{-\beta } \, d\xi dzds \\&\quad \le \varepsilon R^{\beta -2d} \int _0^t \int _{{\mathbb {R}}^d} \int _{ B_R^2} p_{2(t-s)} (x_1-x_2-\xi ) |\xi |^{-\beta } dx_1dx_2 d\xi ds \\&\quad = \varepsilon R^{\beta -2d} \int _0^t \int _{ B_R^2} {\mathbb {E}}\left[ \left| x_1-x_2 - \sqrt{2s} Z \right| ^{-\beta } \right] dx_1dx_2 ds \\&\quad = \varepsilon \int _0^t \int _{ B_1^2} {\mathbb {E}}\left[ \left| x_1-x_2 -R^{-1} \sqrt{2s} Z \right| ^{-\beta } \right] dx_1dx_2 ds \le C \varepsilon t k_\beta \,, ~\text { by Lemma }3.1, \end{aligned}$$

with Z a standard Gaussian random vector on ${\mathbb {R}}^d$. This establishes the limit (3.7), since $\varepsilon > 0$ is arbitrary.

Now, it suffices to show that

$$\begin{aligned} R^{\beta -2d} \int _0^t \eta ^2(s) \int _{{\mathbb {R}}^2} \varphi _R(s,\xi +z )\varphi _R(s,z) \vert \xi \vert ^{-\beta } d\xi dzds \rightarrow k_\beta \int _0^t \eta ^2(s)ds. \end{aligned}$$

(3.9)

as $R\rightarrow +\infty$. This follows from arguments similar to those used above. In fact, previous computations imply that the left-hand side of (3.9) is equal to

$$\begin{aligned} \int _0^t \eta ^2(s) \left( \int _{ B_1^2} {\mathbb {E}}\Big [ | x_1-x_2 -R^{-1} \sqrt{2s} Z | ^{-\beta } \Big ] dx_1dx_2\right) ds. \end{aligned}$$

In view of Lemma 3.1 and dominated convergence theorem, we obtain the limit in (3.9) and hence the proof of the proposition is completed. $\square$

Remark 5

By using the same argument as in the proof of Proposition 3.2, we obtain an asymptotic formula for ${\mathbb {E}}\big [ G_R(t_i) G_R(t_j) \big ]$ with $t_i, t_j\in {\mathbb {R}}_+$, which is a useful ingredient for our proof of Theorem 1.3. Suppose $t_i , t_j\in {\mathbb {R}}_+$, we write

$$\begin{aligned} {\mathbb {E}}\big [ G_R(t_i) G_R(t_j) \big ] = \int _0^{t_i\wedge t_j} \int _{{\mathbb {R}}^{2d}} \varphi ^{(i)}_R(s,y) \varphi ^{(j)}_R(s,z) \Psi (s,y-z) | y-z| ^{-\beta } dydzds\,, \end{aligned}$$

with $\varphi ^{(i)}_R(s,y) = \int _{B_R} p_{t_i-s}(x-y)\, dx$, and we obtain

$$\begin{aligned}&\lim _{R\rightarrow +\infty } R^{\beta -2d} {\mathbb {E}}\big [ G_R(t_i) G_R(t_j) \big ] \\&\quad = \lim _{R\rightarrow +\infty } R^{\beta -2d} \int _0^{t_i\wedge t_j} ds~ \eta ^2(s) \int _{{\mathbb {R}}^{2d}} \varphi ^{(i)}_R(s,y) \varphi ^{(j)}_R(s,z) | y-z| ^{-\beta } dydz \\&\quad = k_\beta \int _0^{t_i\wedge t_j} \eta ^2(s) \, ds \,. \end{aligned}$$

We are now ready to present the proof of Theorem 1.1.

Proof of Theorem 1.1

Recall from (1.7) that

$$\begin{aligned} F_R:=F_R(t) = \delta (v_R) \,, ~ \text {with }v_R(s,y) = \sigma _R^{-1}{\mathbf {1}} _{[0,t]}(s) \varphi _R(s,y) \sigma (u(s,y)). \end{aligned}$$

Moreover,

$$\begin{aligned} D_{s,y}F_R ={\mathbf {1}} _{[0,t]}(s) \frac{1}{\sigma _R}\int _{B_R} D_{s,y}u(t,x)dx \,, \end{aligned}$$

and by (2.2) and Fubini’s theorem, we can write

$$\begin{aligned}&\int _{B_R} D_{s,y} u(t,x) \, dx = \varphi _R(s,y) \sigma (u(s,y)) \\&\quad + \int _s^t \int _{{\mathbb {R}}^d} \varphi _R(r,z) \Sigma (r,z) D_{s,y} u(r,z) W(dr,dz). \end{aligned}$$

Therefore, we have the following decomposition $\langle DF_R,v_R\rangle _{{\mathfrak {H}}} = B_1 +B_2,$ with

$$\begin{aligned} B_1&= \sigma _R^{-2} \int _0^t \int _{{\mathbb {R}}^{2d}} \varphi _R(s,y)\varphi _R(s, y') \sigma \big (u(s,y)\big ) \sigma \big (u(s,y')\big ) |y-y'| ^{-\beta } \, dydy'ds \end{aligned}$$

and

$$\begin{aligned} B_2&= \sigma _R^{-2}\int _0^t \int _{{\mathbb {R}}^{2d}} \left( \int _s^t \int _{{\mathbb {R}}^d} \varphi _R(r,z) \Sigma (r,z) D_{s,y} u(r,z) \, W(dr,dz) \right) \\&\quad \times \, \varphi _R(s,y') \sigma \big (u(s,y')\big ) | y-y'| ^{-\beta }~ dydy' ds. \end{aligned}$$

By Proposition 1.2, $d_{\mathrm{TV}}(F_R, Z) \le 2 \sqrt{ \mathrm{Var} \big [\langle DF_R,v_R\rangle _{{\mathfrak {H}}} \big ] } \le 2\sqrt{2}(A_1+A_2),$ with

$$\begin{aligned} A_1&= \sigma _R^{-2} \int _0^t ds \Bigg ( \int _{{\mathbb {R}}^{4d}} \varphi _R(s,y)\varphi _R(s,y') \varphi _R(s, {\tilde{y}})\varphi _R(s, {\tilde{y}}') |y-y'| ^{-\beta } \\&\quad \times \, |{\tilde{y}}-{\tilde{y}}'| ^{-\beta } \mathrm{Cov} \Big [ \sigma \big (u(s,y)\big ) \sigma \big (u(s,y')\big ) , \sigma \big (u(s,{\tilde{y}})\big ) \sigma \big (u(s,{\tilde{y}}')\big ) \Big ] ~ dy dy' d{\tilde{y}}d{\tilde{y}}' \Bigg )^{1/2} \end{aligned}$$

and

$$\begin{aligned} A_2&= \sigma _R^{-2} \int _0^t \Bigg ( \int _{{\mathbb {R}}^{6d}} \int _s^t \varphi _R(r,z)\varphi _R(r,{\tilde{z}} ) \varphi _R(s,y') \varphi _R(s,{\tilde{y}}') \\&\quad \times \, {\mathbb {E}}\Big \{ \Sigma (r,z) D_{s,y} u(r,z) \Sigma (r,{\tilde{z}}) D_{s,{\tilde{y}}} u(r,{\tilde{z}}) \sigma \big (u(s,{\tilde{y}}')\big )\sigma \big (u(s,y')\big ) \Big \} \\&\quad \times \, | y-y'| ^{-\beta } | {\tilde{y}}-{\tilde{y}}'| ^{-\beta } |z-{\tilde{z}}| ^{-\beta } dydy' d{\tilde{y}} d{\tilde{y}}' dz d{\tilde{z}} dr \Bigg )^{1/2} ds \,. \end{aligned}$$

The proof will be done in two steps:

Step 1:   Let us first estimate the term $A_2$. By Lemma 2.1,

$$\begin{aligned}&\Big \vert {\mathbb {E}}\Big \{ \Sigma (r,z) D_{s,y} u(r,z) \Sigma (r,{\tilde{z}}) D_{s,{\tilde{y}}} u(r,{\tilde{z}}) \sigma \big (u(s,{\tilde{y}}')\big )\sigma \big (u(s,y')\big ) \Big \} \Big \vert \\&\quad \le \, K_4^2(t) L^2 \Vert D_{s,y} u(r,z) \Vert _4 \Vert D_{s, {\tilde{y}}} u(r,{\tilde{z}}) \Vert _4 \le C p_{r-s} (y-z) p_{r-s}({\tilde{y}} -{\tilde{z}}), \end{aligned}$$

where $K_4(t)$ is introduced in (1.10). By Proposition 3.2, we have

$$\begin{aligned} A_2&\le C R^{\beta -2d} \int _0^t \Bigg ( \int _{{\mathbb {R}}^{6d}} \int _s^t \varphi _R(r,z)\varphi _R(r,{\tilde{z}} ) \varphi _R(s,y') \varphi _R(s,{\tilde{y}}') p_{r-s} (y-z) \\&\quad \times \, p_{r-s}({\tilde{y}} -{\tilde{z}}) | y-y'| ^{-\beta } | {\tilde{y}}-{\tilde{y}}'| ^{-\beta } |z-{\tilde{z}}| ^{-\beta } dydy' d{\tilde{y}} d{\tilde{y}}' dz d{\tilde{z}} dr \Bigg )^{1/2} ds \,, \end{aligned}$$

where the integral in the spatial variables can be rewritten as

$$\begin{aligned} {\mathbf {I}}_R&:= \int _{ B_R^4} \int _{{\mathbb {R}}^{6d} } p_{t-r} (x-z) p_{t-r} ({\tilde{x}}-{\tilde{z}}) p_{t-s} (x'-y') p_{t-s} ({\tilde{x}}'-{\tilde{y}}') p_{r-s} (y-z) \\&\quad \times \, p_{r-s}({\tilde{y}} -{\tilde{z}}) | y-y'| ^{-\beta } | {\tilde{y}}-{\tilde{y}}'| ^{-\beta } |z-{\tilde{z}}| ^{-\beta } ~ dx d{\tilde{x}} dx' d{\tilde{x}}'dydy' d{\tilde{y}} d{\tilde{y}}' dz d{\tilde{z}}\,. \end{aligned}$$

Making the change of variables $\big (\theta = x-z$, ${\tilde{\theta }}= {\tilde{x}} -{\tilde{z}}$, $\eta '= x'-y'$, ${\tilde{\eta }}'= {\tilde{x}}' -{\tilde{y}}'$, $\eta =y-z$ and ${\tilde{\eta }} = {\tilde{y}} -{\tilde{z}}\big )$ yields,

$$\begin{aligned} {\mathbf {I}}_R&= \int _{ B_R^4} \Bigg ( \int _{{\mathbb {R}}^{6d} } p_{t-r} (\theta ) p_{t-r} ({\tilde{\theta }}) p_{t-s} (\eta ') p_{t-s} ({\tilde{\eta }}') p_{r-s} (\eta ) p_{r-s}({\tilde{\eta }}) \\&\quad \times \, | x-x' -\theta +\eta +\eta '| ^{-\beta } | {\tilde{x}}- {\tilde{x}}' - {\tilde{\theta }} + {\tilde{\eta }} + {\tilde{\eta }}'| ^{-\beta }\\&\quad \times \, |x-{\tilde{x}} -\theta +{\tilde{\theta }}| ^{-\beta } ~ d\eta d\eta ' d{\tilde{\eta }} d{\tilde{\eta }}' d\theta d{\tilde{\theta }} \Bigg )dx d{\tilde{x}} dx' d{\tilde{x}}'. \end{aligned}$$

This can be written as

$$\begin{aligned}&{\mathbf {I}}_R = \int _{ B_R^4} dx d{\tilde{x}} dx' d{\tilde{x}}' ~{\mathbb {E}}\Bigg \{ \big \vert x-x' +\sqrt{t-r}Z_1 +\sqrt{r-s}Z_5 + \sqrt{t-s}Z_3\big \vert ^{-\beta } \\&\qquad \times \, \big \vert {\tilde{x}}- {\tilde{x}}' +\sqrt{t-r}Z_2 + \sqrt{r-s}Z_6 + \sqrt{t-s}Z_4 \big \vert ^{-\beta } \big \vert x -{\tilde{x}} +\sqrt{t-r}(Z_1 + Z_2)\big \vert ^{-\beta } \Bigg \}\\&\quad \le C\int _{ B_R^4} dx d{\tilde{x}} dx' d{\tilde{x}}' ~{\mathbb {E}}\Big \{ \big \vert x-x' +\sqrt{t-r}Z_1 \big \vert ^{-\beta } \big \vert {\tilde{x}} - {\tilde{x}}' -\sqrt{t-r}Z_2 \big \vert ^{-\beta } \\&\qquad \qquad \times \big \vert x-{\tilde{x}} +\sqrt{t-r}(Z_1 + Z_2)\big \vert ^{-\beta } \Big \}, \end{aligned}$$

with $Z_1, \ldots , Z_6$ i.i.d. standard Gaussian vectors on ${\mathbb {R}}^d$, here we have used Lemma 3.1 repeatedly for $Z_5, Z_3, Z_6, Z_4$ to obtain the last inequality. Making the change of variables $x\rightarrow Rx$, ${\tilde{x}} \rightarrow R{\tilde{x}}$, $x' \rightarrow Rx'$ and ${\tilde{x}} ' \rightarrow R {\tilde{x}}'$, we can write

$$\begin{aligned} {\mathbf {I}}_R&= CR^{4d-3\beta }~ {\mathbb {E}}\int _{ B_1^4} dx d{\tilde{x}} dx' d{\tilde{x}}' ~ \big \vert x-x' + R^{-1}\sqrt{t-r}Z_1 \big \vert ^{-\beta } \\&\quad \times \, \big \vert {\tilde{x}}- {\tilde{x}}' -R^{-1}\sqrt{t-r}Z_2 \big \vert ^{-\beta } \big \vert x-{\tilde{x}} +R^{-1} \sqrt{t-r} (Z_1 + Z_2)\big \vert ^{-\beta } \\&\le \, CR^{4d-3\beta } {\mathbb {E}}\int _{ B_2^3} dy_1 dy_2 dy_3~ \big \vert y_1 + R^{-1}\sqrt{t-r}Z_1 \big \vert ^{-\beta } \big \vert y_2 -R^{-1}\sqrt{t-r}Z_2 \big \vert ^{-\beta } \\&\quad \times \, \big \vert y_3+R^{-1} \sqrt{t-r} (Z_1 + Z_2)\big \vert ^{-\beta } , \end{aligned}$$

where the second inequality follows from the change of variables $x-x'=y_1$, ${\tilde{x}} -{\tilde{x}} ' =y_2$, $x-{\tilde{x}} =y_3$. Taking into account the fact that

$$\begin{aligned} \sup _{z\in {\mathbb {R}}^d} \int _{ B_2} \big \vert y + z \big \vert ^{-\beta } dy < +\infty , \end{aligned}$$

(3.10)

we obtain

$$\begin{aligned} {\mathbf {I}}_R \le CR^{4d-3\beta } \left( \sup _{z\in {\mathbb {R}}^d} \int _{B_2}\vert y+z \vert ^{-\beta } dy \right) ^3\le CR^{4d-3\beta } \,, \end{aligned}$$

and it follows immediately that $A_2 \le C R^{-\beta /2}$.

Step 2:   We now estimate $A_1$. We begin by estimating the covariance

$$\begin{aligned} \mathrm{Cov} \Big [ \sigma \big (u(s,y)\big ) \sigma \big (u(s,y')\big ) , \sigma \big (u(s,{\tilde{y}})\big ) \sigma \big (u(s,{\tilde{y}}')\big ) \Big ] \,. \end{aligned}$$

(3.11)

Using a version of Clark–Ocone formula for square integrable functionals of the noise W, we can write

$$\begin{aligned} \sigma \big (u(s,y)\big ) \sigma \big (u(s,y')\big )&= {\mathbb {E}}\big [\sigma \big (u(s,y)\big ) \sigma \big (u(s,y')\big )\big ] \\&\quad +\, \int _0^s \int _{{\mathbb {R}}^d} {\mathbb {E}}\Big [ D_{r,z} \Big (\sigma \big (u(s,y)\big ) \sigma \big (u(s,y')\big ) \Big ) | {\mathcal {F}}_r \Big ] W(dr,dz). \end{aligned}$$

Then, we represent the covariance (3.11) as

$$\begin{aligned}&\int _0^s \int _{{\mathbb {R}}^{2d}} {\mathbb {E}}\Big \{ {\mathbb {E}}\Big [ D_{r,z} \Big (\sigma \big (u(s,y)\big ) \sigma \big (u(s,y')\big ) \Big )| {\mathcal {F}}_r \Big ] \\&\quad \times \, {\mathbb {E}}\Big [ D_{r,z'} \Big ( \sigma \big (u(s,{\tilde{y}})\big ) \sigma \big (u(s,{\tilde{y}}')\big )\Big ) | {\mathcal {F}}_r \Big ] \Big \} |z-z'|^{-\beta } ~dz dz'dr . \end{aligned}$$

By the chain rule, $D_{r,z} \big (\sigma (u(s,y) ) \sigma (u(s,y') )\big ) = \sigma \big (u(s,y)\big ) \Sigma (s,y') D_{r,z} u(s,y') + \sigma \big (u(s,y')\big ) \Sigma (s,y) D_{r,z} u(s,y)$. Therefore, $\big \Vert {\mathbb {E}}\big [ D_{r,z} (\sigma (u(s,y) ) \sigma (u(s,y') ) )| {\mathcal {F}}_r \big ] \big \Vert _2$ is bounded by $2K_4(t) L \big \{ \Vert D_{r,z} u(s,y) \Vert _4+ \Vert D_{r,z} u(s,y') \Vert _4\big \}$. Using Lemma 2.1 again, we see that the covariance (3.11) is bounded by

$$\begin{aligned}&4L^2 K_4^2(t) \int _0^s \int _{{\mathbb {R}}^{2d} } \Big ( \left\| D_{r,z} u(s,y)\right\| _4 +\left\| D_{r,z} u(s,y')\right\| _4 \Big ) \\&\qquad \times \, \Big ( \Vert D_{r,z'} u(s,{\tilde{y}}) \Vert _4 + \Vert D_{r,z'} u(s,{\tilde{y}}') \Vert _4 \Big ) |z-z'| ^{-\beta } dz dz'dr \\&\quad \le \, C \int _0^s \int _{{\mathbb {R}}^{2d} } \big ( p_{s-r}(y-z) + p_{s-r}(y'-z) \big ) \\&\qquad \times \big ( p_{s-r}({\tilde{y}}-z') + p_{s-r}({\tilde{y}}'-z') \big ) |z-z'| ^{-\beta } dz dz'dr . \end{aligned}$$

Consequently, the spatial integral in the expression of $A_1$ can be bounded by

$$\begin{aligned} {\mathbf {J}}_R&:=C\int _0^s\int _{{\mathbb {R}}^{6d}} \varphi _R(s,y)\varphi _R(s,y') \varphi _R(s, {\tilde{y}})\varphi _R(s, {\tilde{y}}') \\&\quad \times \, |y-y'| ^{-\beta } |{\tilde{y}}-{\tilde{y}}'| ^{-\beta } |z-z'| ^{-\beta } \Big ( p_{s-r}(y-z) + p_{s-r}(y'-z) \Big ) \\&\quad \times \, \Big ( p_{s-r}({\tilde{y}}-z') + p_{s-r}({\tilde{y}}'-z') \Big ) dy dy' d{\tilde{y}}d{\tilde{y}}' dz dz'dr \\&= 4C\int _0^s dr \int _{{\mathbb {R}}^{6d}} dy dy' d{\tilde{y}}d{\tilde{y}}' dz dz' ~\varphi _R(s,y)\varphi _R(s,y') \varphi _R(s, {\tilde{y}})\varphi _R(s, {\tilde{y}}') \\&\quad \times \, |y-y'| ^{-\beta } |{\tilde{y}}-{\tilde{y}}'| ^{-\beta } |z-z'| ^{-\beta } p_{s-r}(y-z) p_{s-r}({\tilde{y}}-z') , \quad \text {by symmetry. } \end{aligned}$$

Then, it follows from exactly the same argument as in the estimation of ${\mathbf {I}}_R$ in the previous step that ${\mathbf {J}}_R \le C R^{4d-3\beta }$. Indeed, we have

$$\begin{aligned}&\int _0^s \int _{B_R^4} \int _{{\mathbb {R}}^{6d}} p_{t-s} (x-y) p_{t-s} (x'-y')p_{t-s} ({\tilde{x}}-{\tilde{y}})p_{t-s} ({\tilde{x}}'-{\tilde{y}}') \nonumber \\&\qquad \times \, |y-y'| ^{-\beta } |{\tilde{y}}-{\tilde{y}}'| ^{-\beta } |z-z'| ^{-\beta } p_{s-r}(y-z) p_{s-r}({\tilde{y}}-z') \nonumber \\&\qquad \qquad \qquad dx dx' d{\tilde{x}} d{\tilde{x}}' dy dy' d{\tilde{y}}d{\tilde{y}}' dz dz'dr \nonumber \\&\quad = \int _0^s dr \int _{B_R^4} dx dx' d{\tilde{x}} d{\tilde{x}}' \int _{{\mathbb {R}}^{6d}}p_{t-s} (\theta ) p_{t-s} (\theta ')p_{t-s} ({\tilde{\theta }})p_{t-s} ({\tilde{\theta }}' )p_{s-r}(\eta ) \nonumber \\&\qquad \times \, p_{s-r}({\tilde{\eta }}) ~\vert x - x' -\theta + \theta '\vert ^{-\beta } \vert {\tilde{x}} - {\tilde{x}}' -{\tilde{\theta }} + {\tilde{\theta }}'\vert ^{-\beta } \nonumber \\&\qquad \times \, \vert x - {\tilde{x}} -\eta + \theta + {\tilde{\theta }} + {\tilde{\eta }} \vert ^{-\beta } d\theta d\theta ' d{\tilde{\theta }}d{\tilde{\theta }}' d\eta d{\tilde{\eta }} \nonumber \\&\quad = \int _0^s dr \int _{B_R^4} {\mathbb {E}}\Big \{ \big \vert x - x' + \sqrt{t-s}(Z_2-Z_1) \big \vert ^{-\beta } \big \vert {\tilde{x}} - {\tilde{x}}' + \sqrt{t-s}(Z_4-Z_3) \big \vert ^{-\beta } \nonumber \\&\qquad \times \, \big \vert x - {\tilde{x}} + \sqrt{t-s}(Z_1 + Z_3) + \sqrt{2s-2r}Z_5 \big \vert ^{-\beta } \Big \} ~dx dx' d{\tilde{x}} d{\tilde{x}}' \nonumber \\&\quad \le \, C\int _0^s dr \int _{B_R^4} {\mathbb {E}}\Big \{ \big \vert x - x' - \sqrt{t-s}Z_1 \big \vert ^{-\beta } \big \vert {\tilde{x}} - {\tilde{x}}' - \sqrt{t-s}Z_3 \big \vert ^{-\beta } \nonumber \\&\qquad \times \, \big \vert x - {\tilde{x}} + \sqrt{t-s}(Z_1 + Z_3) \big \vert ^{-\beta } \Big \}~dx dx' d{\tilde{x}} d{\tilde{x}}' \end{aligned}$$

(3.12)

$$\begin{aligned}&\quad \le CR^{4d-3\beta }~{\mathbb {E}}\int _{B_1^4} dx dx' d{\tilde{x}} d{\tilde{x}}' \big \vert x - x' -R^{-1} \sqrt{t-s} Z_1 \big \vert ^{-\beta } \nonumber \\&\qquad \times \, \big \vert {\tilde{x}} - {\tilde{x}}' - R^{-1} \sqrt{t-s}Z_3 \big \vert ^{-\beta } \times \big \vert x - {\tilde{x}} +R^{-1} \sqrt{t-s}(Z_1 + Z_3) \big \vert ^{-\beta } \nonumber \\&\quad \le \, CR^{4d-3\beta }~{\mathbb {E}}\int _{B_2^3} \big \vert y_1 -R^{-1} \sqrt{t-s} Z_1 \big \vert ^{-\beta }\nonumber \\&\qquad \times \, \big \vert y_2 - R^{-1} \sqrt{t-s}Z_3 \big \vert ^{-\beta } \times \big \vert y_3 +R^{-1} \sqrt{t-s}(Z_1 + Z_3) \big \vert ^{-\beta } dy_1 dy_2 dy_3 \nonumber \\&\quad \le \, CR^{4d-3\beta } \left( \sup _{z\in {\mathbb {R}}^d}\int _{B_2} \big \vert y + z \big \vert ^{-\beta } \, dy \right) ^3 \le CR^{4d-3\beta } \,,\quad \text { by }(3.10), \end{aligned}$$

(3.13)

where we have used Lemma 3.1 for $Z_5, Z_2, Z_4$ to obtain (3.12). This gives us the desired estimate for $A_1$ and finishes our proof. $\square$

With a slight modification of the above proof, we can extend Theorem 1.1 to more general initial conditions.

Corollary 3.3

Assume that there are two positive constants $c_1,c_2$ such that $c_1\le u(0,x)\le c_2$, and assume one of the following two conditions:

• (1) $\sigma$ is a non-negative, nondecreasing Lipschitz function with $\sigma (c_1) > 0$.

• (2) $-\sigma$ is a non-negative, nondecreasing Lipschitz function with $\sigma (c_1) < 0$.

Define

$$\begin{aligned} {\widetilde{F}}_R(t) = \frac{1}{{\widetilde{\sigma }}_R} \int _{B_R}\Big [u(t,x)- {\mathbb {E}}u(t,x) \Big ]dx\,, \end{aligned}$$

(3.14)

where

$$\begin{aligned} {\widetilde{\sigma }}_R^2 = \mathrm{Var}\left( \int _{B_R}\Big [u(t,x)- {\mathbb {E}}u(t,x) \Big ]dx \right) {\in (0, \infty ) } \end{aligned}$$

for every $R>0$. Then, there exists a constant $C = C(t,\beta )$, depending on t and $\beta$, such that

$$\begin{aligned} d_{\mathrm{TV}}\left( {\widetilde{F}}_R(t), ~N(0,1)\right) \le C R^{-\beta /2} \,. \end{aligned}$$

Proof

We write ${\widetilde{F}}_R(t)$ as ${\widetilde{G}}_R(t) / {\widetilde{\sigma }}_R$. Let $u_1(t,x)$ be the solution to Eq. (1.1) with initial condition $u(0,x)=c_1$. According to the weak comparison principle (see [2, Theorem 1.1]), $u(t,x)\ge u_1(t,x)$ almost surely for every $t\ge 0$ and $x\in {\mathbb {R}}^d$, which immediately implies

$$\begin{aligned} \sigma \big (u(s,y)\big )\sigma \big (u(s,z)\big ) \ge \sigma \big (u_1(s,y)\big )\sigma \big (u_1(s,z)\big ) \ge 0 \quad \text {almost surely,} \end{aligned}$$

so that

$$\begin{aligned} {\mathbb {E}}\big [ {\widetilde{G}}^2_R(t) \big ]&= \int _0^t \int _{{\mathbb {R}}^{2d}} \varphi _R(s,y)\varphi _R(s,z){\mathbb {E}}\Big [ \sigma \big (u(s,y)\big )\sigma \big (u(s,z)\big ) \Big ] |y-z|^{-\beta } dy dz ds \nonumber \\&\ge \, \int _0^t \int _{{\mathbb {R}}^{2d}} \varphi _R(s,y)\varphi _R(s,z){\mathbb {E}}\Big [ \sigma \big (u_1(s,y)\big )\sigma \big (u_1(s,z)\big ) \Big ] |y-z|^{-\beta } dy dz ds. \end{aligned}$$

(3.15)

In view of point (iii) from Remark 3, our assumption $\sigma (c_1)\ne 0$ guarantees that the last integral (3.15) has the exact order $R^{2d-\beta }$: More precisely,

$$\begin{aligned} (3.15) \sim \kappa _\beta \left( \int _0^t \eta _1(s)^2 ds \right) R^{2d-\beta } \quad \text {as }R\rightarrow +\infty , \end{aligned}$$

where $\eta _1(s) := {\mathbb {E}}\big [ \sigma (u_1(s,y))\big ]$ does not depend on y and $\int _0^t \eta _1(s)^2 ds\in (0,\infty )$; see also (1.9).

Now let $u_2(t,x)$ be the solution to the Eq. (1.1) with initial condition $u(0,x)=c_2$. Notice that by our assumption on $\sigma$, we get $\sigma (c_2)\ne 0$. And by applying the same weak comparison principle, we deduce that

$$\begin{aligned} {\mathbb {E}}\big [ {\widetilde{G}}^2_R(t) \big ]&\le \int _0^t \int _{{\mathbb {R}}^{2d}} \varphi _R(s,y)\varphi _R(s,z){\mathbb {E}}\Big [ \sigma \big (u_2(s,y)\big )\sigma \big (u_2(s,z)\big ) \Big ] |y-z|^{-\beta } dy dz ds\\&\sim \, \kappa _\beta \left( \int _0^t \eta _2(s)^2 ds \right) R^{2d-\beta } \quad \text {as }R\rightarrow +\infty , \end{aligned}$$

where $\eta _2(s) := {\mathbb {E}}\big [ \sigma (u_2(s,y))\big ]$ does not depend on y and $\int _0^t \eta _2(s)^2 ds\in (0,\infty )$. This implies that

$$\begin{aligned} 0< \liminf _{R\rightarrow +\infty } {\widetilde{\sigma }}_R^2 R^{\beta -2d} \le \limsup _{R\rightarrow +\infty } {\widetilde{\sigma }}_R^2 R^{\beta -2d} < +\infty \,. \end{aligned}$$

The rest of the proof follows the same lines as the proof of Theorem 1.1. $\square$

4 Proof of Theorem 1.3

In order to prove Theorem 1.3, we need to establish the convergence of the finite-dimensional distributions as well as the tightness.

Convergence of finite-dimensional distributions. Fix $0\le t_1< \cdots <t_m \le T$ and consider

$$\begin{aligned} F_R(t_i) := R^{\frac{\beta }{2} -d} \int _{B_R} \big [ u(t_i,x) - 1 \big ]~dx = \delta \big ( v_R^{(i)}\big ) ~\text {for }i=1, \dots , m, \end{aligned}$$

where

$$\begin{aligned} v_R^{(i)} (s,y) = {\mathbf {1}} _{[0,t_i]}(s) R^{\frac{\beta }{2} -d} \sigma \big (u(s,y)\big )\varphi ^{(i)}_R(s,y) \end{aligned}$$

with $\varphi ^{(i)}_R(s,y) = \int _{B_R} p_{t_i -s} (x-y) dx$. Set ${\mathbf {F}}_R=\big ( F_R(t_1), \dots , F_R(t_m) \big )$ and let Z be a centered Gaussian vector on ${\mathbb {R}}^m$ with covariance $(C_{i,j})_{1\le i,j\le m}$ given by

$$\begin{aligned} C_{i,j} := k_\beta \int _0^{t_i \wedge t_j} \eta ^2(r) ~dr \,,~ \text {with }\eta (r):= {\mathbb {E}}\big [\sigma \big (u(r,y)\big )\big ]. \end{aligned}$$

To proceed, we need the following generalization of [10, Theorem 6.1.2]; see [8, Proposition 2.3] for a proof.

Lemma 4.1

Let $F=( F^{(1)}, \dots , F^{(m)})$ be a random vector such that $F^{(i)} = \delta (v^{(i)})$ for $v^{(i)} \in \mathrm{Dom}\, \delta$ and $F^{(i)} \in {\mathbb {D}}^{1,2}$, $i = 1,\dots , m$. Let Z be an m-dimensional centered Gaussian vector with covariance $(C_{i,j})_{ 1\le i,j\le m}$. For any $C^2$ function $h: {\mathbb {R}}^m \rightarrow {\mathbb {R}}$ with bounded second partial derivatives, we have

$$\begin{aligned} \big | {\mathbb {E}}[ h(F)] -{\mathbb {E}}[ h(Z)] \big | \le \frac{m}{2} \Vert h ''\Vert _\infty \sqrt{ \sum _{i,j=1}^m {\mathbb {E}}\Big [ \big (C_{i,j} - \langle DF^{(i)}, v^{(j)} \rangle _{{\mathfrak {H}}}\big )^2 \Big ] } \,, \end{aligned}$$

where $\Vert h ''\Vert _\infty : = \sup \big \{ \big \vert \frac{\partial ^2}{\partial x_i\partial x_j} h(x) \big \vert \,:\, x\in {\mathbb {R}}^d\, , \, i,j=1, \ldots , m \big \}$.

In view of Lemma 4.1, the proof of ${\mathbf {F}}_R\xrightarrow {\mathrm{law}} Z$ boils down to the $L^2(\Omega )$-convergence of $\langle DF_R(t_i), v_R^{(j)} \rangle _{{\mathfrak {H}}}$ to $C_{i,j}$ for each i, j, as $R\rightarrow +\infty$. The case $i=j$ has been covered in the proof of Theorem 1.1 and for the other cases, we need to show

$$\begin{aligned} {\mathbb {E}}\big [ F_R(t_i) F_R(t_j) \big ] \rightarrow C_{i,j} \end{aligned}$$

(4.1)

and

$$\begin{aligned} \mathrm{Var}\big ( \langle DF_R(t_i), v_R^{(j)} \rangle _{{\mathfrak {H}}} \big )\rightarrow 0, \end{aligned}$$

(4.2)

as $R\rightarrow +\infty$. The point (4.1) has been established in Remark 5. To see point (4.2), we put

$$\begin{aligned} B_1(i,j)&= R^{\beta -2d} \int _0^{t_i\wedge t_j} \int _{{\mathbb {R}}^d} \varphi _R^{(i)}(s,y) \varphi _R^{(j)}(s,y') \sigma (u(s,y)) \sigma (u(s,y'))\\ {}&\quad \times |y-y'|^{-\beta } dy dy' ds \end{aligned}$$

and

$$\begin{aligned} B_2(i,j)&= R^{\beta -2d} \int _0^{t_i\wedge t_j} \int _{{\mathbb {R}}^{2d}} \varphi ^{(j)}_R(s,y') \sigma (u(s,y'))|y-y'|^{-\beta } \\&\quad \times \, \left( \int _s^{t_i}\int _{{\mathbb {R}}^d} \varphi ^{(i)}_R(r,z) \Sigma (r,z) D_{s,y} u(r,z) W(dr,dz) \right) \, dydy'ds, \end{aligned}$$

so that $\langle DF_R(t_i), v_R^{(j)} \rangle _{{\mathfrak {H}}} = B_1(i,j) +B_2(i,j)$. Therefore,

$$\begin{aligned}&{\mathbb {E}}\left[ \Big (C_{ij}-\langle DF_R(t_i), v_R^{(j)}\rangle _{{\mathfrak {H}}} \Big )^2\right] \\&\quad \le \, 3 \big (C_{i,j} - {\mathbb {E}}[ B_1(i,j) ] \big )^2 + 3 \mathrm{Var}\big [ B_1(i,j) \big ] + 3 \mathrm{Var} \big [ B_2(i,j)\big ]\,. \end{aligned}$$

Going through the same lines as for the estimation of $A_1, A_2$, one can verify easily that both $\mathrm{Var}\big [ B_1(i,j) \big ]$ and $\mathrm{Var} \big [ B_2(i,j)\big ]$ vanish asymptotically, as R tends to infinity. By recalling that $C_{ij} = \lim _{R \rightarrow +\infty } {\mathbb {E}}\big [ B_1(i,j)\big ]$, the convergence of finite-dimensional distributions is thus established. $\square$

Tightness The following proposition together with Kolmogorov’s criterion ensures the tightness of the processes $\big \{ R^{\frac{\beta }{2}-d} \int _{B_R} \big [ u(t,x) -1 \big ] \,dx \,, t\in [0,T] \big \}$, $R > 0$.

Proposition 4.2

Recall the notation (1.6). For any $0\le s < t\le T$, for any $p\in [ 2,\infty )$ and any $\alpha \in (0, 1)$, it holds that

$$\begin{aligned} {\mathbb {E}}\big [ \vert G_R(t) - G_R(s) \vert ^p\big ] \le C R^{p(d-\frac{\beta }{2})}(t-s)^{\alpha p/2}~ , \end{aligned}$$

(4.3)

where the constant $C = C_{p,T,\alpha }$ may depend on T, p and $\alpha$.

Notice that the pth moment of an increment of the solution $u(t,x) -u(s,x)$ is bounded by a constant times $|t-s|^ {\frac{\alpha p }{2}(1-\frac{\beta }{2})}$, for any $\alpha \in (0, 1)$, see [17]; and here the spatial averaging has improved the Hölder continuity.

Now we present the proof of Proposition 4.2. Let $0\le s < t\le T$ and set

$$\begin{aligned} \Theta _{x,t,s}(r,y) = p_{t-r}(x-y)\mathbf{1 }_{\{r\le t\}}-p_{s-r}(x-y)\mathbf{1 }_{\{r\le s\}}. \end{aligned}$$

Then,

$$\begin{aligned} G_R(t) - G_R(s)= \int _0^T\int _{{\mathbb {R}}^d}\left( \int _{B_R} \Theta _{x,t,s}(r,y)\, dx\right) \sigma \big (u(r,y)\big ) \,W(dr,dy) \,, \end{aligned}$$

so that

$$\begin{aligned}&{\mathbb {E}}\Big [ | G_R(t) - G_R(s)|^p \Big ]\\&\quad \le C~ \Bigg \Vert ~ \int _0^T dr \int _{{\mathbb {R}}^{2d}} dy dy'~ |y-y'|^{-\beta } \left( \int _{B_R}\Theta _{x,t,s}(r,y)~dx\right) \sigma \big (u(r,y)\big ) \\&\qquad \times \, \left[ \int _{B_R}\Theta _{{\tilde{x}},t,s}(r,y) ~ d{\tilde{x}} \right] \sigma \big (u(r,y')\big ) \Bigg \Vert ^{p/2}_{p/2} \quad \text {by Burkholder's inequality}\\&\quad \le \, C \Bigg \{ \int _0^T dr \int _{{\mathbb {R}}^{2d}} dy dy' |y-y'|^{-\beta } \left| \int _{B_R}\Theta _{x,t,s}(r,y)dx\right| \times \left| \int _{B_R}\Theta _{{\tilde{x}},t,s}(r,y)d{\tilde{x}}\right| \\&\qquad \times \,\big \Vert \sigma (u(r,y))\sigma (u(r,y'))\big \Vert _{p/2} \Bigg \}^{p/2} \quad \text {by Minkowski's inequality}. \end{aligned}$$

Therefore, taking into account that $\Vert \sigma (u(r,y))\sigma (u(r,y'))\Vert _{p/2}$ is uniformly bounded, we obtain

$$\begin{aligned}&{\mathbb {E}}\Big [ | G_R(t) - G_R(s)|^p \Big ]\\&\quad \le \, C \left\{ ~ \int _0^T \int _{{\mathbb {R}}^{2d}} \left| \int _{B_R}\Theta _{x,t,s}(r,y)dx\right| \left| \int _{B_R}\Theta _{{\tilde{x}},t,s}(r,y)d{\tilde{x}}\right| |y-y'|^{-\beta } ~ dy dy'dr\right\} ^{p/2}\\&\quad \le \, C \Bigg \{ \int _0^s \int _{{\mathbb {R}}^{2d}} \left| \int _{B_R}\big (p_{t-r}(x-y) -p_{s-r}(x-y) \big ) dx\right| \\&\qquad \times \,\left| \int _{B_R}\big (p_{t-r}({\tilde{x}}-y') -p_{s-r}({\tilde{x}}-y') \big ) d{\tilde{x}}\right| \big \vert y-y' \big \vert ^{-\beta }~dy dy' dr\Bigg \}^{p/2}\\&\qquad +\, C \Bigg [ \int _s^t \int _{{\mathbb {R}}^{2d}} \left( \int _{B_R^2}p_{t-r}(x-y)p_{t-r}({\tilde{x}}-y')~dxd{\tilde{x}}\right) |y-y'|^{-\beta } dy dy' dr\Bigg ]^{p/2}\\&\quad =:C \big ({\mathbf {T}}_1^{p/2} + {\mathbf {T}}_2^{p/2} \big )\,. \end{aligned}$$

Estimation of the term ${\mathbf {T}}_1$. We need Lemma 3.1 in [2]: For all $\alpha \in (0,1)$, $x,y\in {\mathbb {R}}^d$ and $t'\ge t>0$,

$$\begin{aligned} \left| p_t(x)-p_{t'}(x)\right| \le C t^{-\alpha /2}(t'-t)^{\alpha /2}p_{4t'}(x)\,. \end{aligned}$$

Thus,

$$\begin{aligned}&(t-s)^{-\alpha } {\mathbf {T}}_1\\&\quad \le \int _0^s dr (s-r)^{-\alpha } \int _{B_R^2} dxd{\tilde{x}} \int _{{\mathbb {R}}^{2d}}dy dy' p_{4(t-r)}(x-y) p_{4(t-r)}({\tilde{x}}-y') |y-y'|^{-\beta } \\&\quad = \int _0^s dr (s-r)^{-\alpha } \int _{B_R^2} dxd{\tilde{x}} \int _{{\mathbb {R}}^{2d}}dy dy' p_{4(t-r)}(\theta ) p_{4(t-r)}({\tilde{\theta }}) \big |x- {\tilde{x}} -\theta + {\tilde{\theta }} \big |^{-\beta } \,, \end{aligned}$$

by the change of variable $\theta = x - y$, ${\tilde{\theta }} = {\tilde{x}} - y'$. Consequently, with Z a standard Gaussian random vector on ${\mathbb {R}}^d$, we continue to write

$$\begin{aligned} (t-s)^{-\alpha } {\mathbf {T}}_1&\le \int _0^s dr (s-r)^{-\alpha } \int _{B_R^2} dxd{\tilde{x}} ~{\mathbb {E}}\Big [ \vert x - {\tilde{x}} + \sqrt{8t-8r}Z\vert ^{-\beta } \Big ] \\&= R^{2d-\beta } \int _0^s dr (s-r)^{-\alpha } \int _{B_1^2} dxd{\tilde{x}} ~{\mathbb {E}}\Big [ \vert x - {\tilde{x}} + R^{-1}\sqrt{8t-8r}Z\vert ^{-\beta } \Big ] \\&\le CR^{2d-\beta } \int _0^s dr (s-r)^{-\alpha } \int _{B_1^2} dxd{\tilde{x}} \vert x - {\tilde{x}} \vert ^{-\beta } \quad \text {using Lemma}~3.1 \\&\le CR^{2d-\beta } \,. \end{aligned}$$

Estimation of the term ${\mathbf {T}}_2$. We use a similar change of variable as before:

$$\begin{aligned} {\mathbf {T}}_2&= \int _s^t dr \int _{B_R^2} dx d{\tilde{x}} \int _{{\mathbb {R}}^{2d}} p_{t-r}(\theta )p_{t-r}({\tilde{\theta }} ) \big \vert x - {\tilde{x}} + {\tilde{\theta }} -\theta \big \vert ^{-\beta } d\theta d{\tilde{\theta }} \\&= \int _s^t dr \int _{B_R^2} dx d{\tilde{x}} ~{\mathbb {E}}\Big \{ \big \vert x - {\tilde{x}} + \sqrt{2t-2r} Z \big \vert ^{-\beta } \Big \} \\&\le CR^{2d-\beta } \int _s^t dr \int _{B_1^2} dx d{\tilde{x}} \big \vert x - {\tilde{x}} \big \vert ^{-\beta } \quad \text {using Lemma}~3.1 \\&= CR^{2d-\beta } (t-s) k_\beta \,. \end{aligned}$$

Combining the above two estimates, we obtain (4.3). $\square$