Discrete superior dynamics of a generalized chaotic system

Abstract

In the past few decades, the discrete dynamics of difference maps have attained the remarkable attention of researchers owing to their incredible applications in different domains, like cryptography, secure communications, weather forecasting, traffic flow models, neural network models, and population biology. In this article, a generalized chaotic system is proposed, and superior dynamics is disclosed through fixed point analysis, time-series evolution, cobweb representation, period-doubling, period-3 window, and Lyapunov exponent properties. The comparative bifurcation and Lyapunov plots report the superior stability and chaos performance of the generalized system. It is interesting to notice that the generalized system exhibits superior dynamics due to an additional control parameter $\beta$. Analytical and numerical simulations are used to explore the superior dynamical characteristics of the generalized system for some specific values of parameter $\beta$. Further, it is inferred that the superiority in dynamics of the generalized system may be efficiently used for better future applications.

1 Introduction

In recent times, due to the prominent role of discrete chaos, various discrete chaotic systems are frequently used in different branches of natural and social sciences. In general, chaos theory reports an unpredictable and aperiodic behavior in nonlinear dynamical systems, that displays sensitive dependence upon initial conditions. The chaotic dynamics of nonlinear systems was initially studied by Poincare [38]. However, the recent advancements in chaos theory are primarily based on the research works of Lorenz [32] and May [35]. To know further about discrete chaos, one can also refer to Devaney [17, 18], Diamond [19], Prigogine et al. [39], Wiggins [53], Holmgren [24], Strogatz [49], Robinson [46], Alligood et al. [1], Martelli [34], Elaydi [20], Ausloos and Dirickx [9], Elhadj and Sprott [21], Gleick [22], and Ott [36].

In the 21st century, owing to their simple formations and tremendous chaotic characteristics, the discrete chaotic systems have found significant applications in different domains such as secure communication [48], image encryption [10, 11], particle swarm optimization [50], traffic control model [2, 4], neural network model [14], pseudo-random number generation [27, 31, 52], synchronization control [8, 37], network evolution [33] and physics, population biology, chemistry and engineering [49], etc. Lorenz [32], the founder of modern chaos theory, established the first chaotic system. After that, various other discrete chaotic systems have also been proposed, like, the logistic map [35], Henon map [23], tent map [17], Lorenz-like system [12], coupled map lattices [26], and numerous other chaotic systems [30, 55]. The most celebrated discrete chaotic system model is the standard logistic system, which is a major advancement in the area of nonlinear dynamics and chaos theory. The standard logistic system, given by the discrete difference equation $\rho x (1-x)$, was initially proposed by Verhulst [51] as a prominent model of population growth. Due to its simple structure and complex dynamics, the logistic system has been extensively used to examine different nonlinear phenomena. The logistic system remains in a stable state for $0<\rho \le 3.57$ and chaotic state for $3.57<\rho \le 4$ [17, 24, 51]. Further, for $\rho >4$, the system is undefined as there exists atleast one $x_{n}$ such that $x_{n}\notin [0,1]$.

Distinct iteration processes and feedback algorithms were applied so far to enhance the stability performance and predictability of discrete logistic system for an extensive range of growth-rate parameter $\rho$ and its applications were also studied (see [2,3,4, 16, 25, 41, 42] and various other references therein). Further, different generalized versions of the discrete systems have been studied by various researchers (see [5, 6, 15, 40, 43, 44, 47]). Cao and Ashish[13] explored the different dynamical characteristics of the logistic map along with some scaling methods using Euler’s numerical algorithm. Moreover, the stabilization in fixed and periodic states of discrete chaotic maps via Noor orbit with applications is studied in [7]. Wu and Baleanu [54] also explored the discrete chaos in fractional delayed logistic maps.

Recently, Ashish et al. [5] studied about discrete chaos in a modulated logistic map and reported the superiority in chaos performance of the modulated system via period-doubling, period-3 window, and Lyapunov exponent characteristics. Also, Kumar et al. [28] examined the dynamical characteristics of another one-dimensional chaotic system using different techniques. They showed that the stability and chaotic dynamics of the established system are better than that of the discrete logistic system. Further, Renu et al. [45] examined the discrete chaotic map proposed in [28] using superior orbit and reported its improved stability performance. Motivating by these works and extensive applications of discrete logistic system, in this article, we introduce a generalized chaotic system that exhibits enhanced chaos and stability performance as compared to the existing chaotic systems. The stable and chaotic dynamics of the generalized system are examined through analytical and numerical simulations using different dynamical properties. It is reported that due to the advantage of an ordered parameter $\beta$, the generalized system exhibits stability and chaotic behavior for larger ranges of control parameter $\rho$ in contrast to the traditional chaotic systems. Because of the extensive range of its stability performance, the generalized system may have better applications in various real-life problems where stability is important like population control, traffic control etc. Further, the superiority in chaotic performance makes the system more suitable for chaos-based applications such as image encryption decryption in cryptography, secure communication systems and signal processing.

The complete article is arranged as follows: Sect. 1 provides an introduction and a short literature review while Sect. 2 presents some general definitions, results, and notations that are used in the study. Sect. 3 deals with the formation and dynamical exploration of the generalized system, in which the superior stability and chaotic dynamics of the system is reported via fixed point analysis, time-series plots, cobweb diagrams, periodic evolution, and Lyapunov exponent characteristics. Further, Sect. 4 is devoted to establish the dynamical superiority of the generalized system by comparing the bifurcation and Lyapunov plots and also briefly highlights the possible applications of the generalized system. Finally, the results of the article are concluded in Sect. 5.

2 Basic definitions

This section provides definitions of the specific terminology and concepts that are significant for the study of discrete dynamical systems and chaos theory.

Definition 2.1

(Picard iteration process) [18] Let $f:X\rightarrow X$ be a discrete system, where X is a non-empty set. Then, the iterative sequence $\{x_{n}\}$, for an initial input $x_{0}\in X$, defined as

$$\begin{aligned} x_{n+1}=f(x_{n}), \end{aligned}$$

(1)

where $n=0,1,2,3,...,$ is termed as Picard orbit of iteration and the entire process is called Picard iteration process or one-step feedback algorithm as it takes only one number, say $x_{0}$, as input to provide a new member as output.

Definition 2.2

(Fixed and periodic point) [17] If $f:X\rightarrow X$ denotes a discrete system defined on X, where X is a non-empty set. Then, an arbitrary point $x\in X$ is called fixed for the system f, if it satisfies $f(x)=x$. Further, that point x is known as an order-p periodic point if $f^{p}(x)=x$, where p indicates the smallest positive integer and the iterative sequence $\{x_{1},x_{2},...x_{p}\}$ is called an order-p orbit.

Definition 2.3

(Attracting and repelling fixed point) [18] Let $f:X\rightarrow X$ be a discrete system and X is a non-empty set. Then, a fixed point x for the system f is known as attracting if that satisfies $|f'(x) \vert$ $<1$ and if $|f'(x) \vert$ $>1$, that is known as repelling. If $|f'(x) \vert$ $=1$, the fixed point is termed as weakly attracting or neutral.

Definition 2.4

(Critical point) [17] Suppose $f:X\rightarrow X$ is a discrete system and X denotes a non-empty set. Then, an arbitrary point $x\in X$ is known as a critical point of the system f, if that satisfies $f'(x)=0$. Further, the point is called nondegenerate if $f''(x)\ne 0$ and degenerate for $f''(x)=0$.

Definition 2.5

(Chain rule of differentiation along a cycle) [18] If $f:X\rightarrow X$ denotes a discrete system, where X is a non-empty set. Suppose $\{x_{1},x_{2},\cdots ,x_{n}\}$ is a sequence of iterates lying on period-n cycle of the system f. Then, the differentiation for $n^{th}$ iterate of the system f is given by,

$$\begin{aligned} (f^{n})'(x_{1})=f'(x_{1})\times f'(x_{2})\times \cdots \times f'(x_{n-1})\times f'(x_{n}). \end{aligned}$$

(2)

It gives that the differentiation for $f^{n}$ at point $x_{1}$ is just the multiplication of the derivatives of f at each point of that orbit.

Definition 2.6

(Lyapunov exponent) [1] Let $f:\mathbb {R}\rightarrow \mathbb {R}$ be a discrete system defined on $\mathbb {R}$, where $\mathbb {R}$ denotes the set of real numbers. Then, for an iterative orbit $\{x_{n}\}$ of the system f, the Lyapunov exponent ($\gamma$) is defined by,

$$\begin{aligned} \gamma (x_{1})=\lim _{n\rightarrow \infty }\displaystyle {\frac{1}{n}}\sum _{i=1}^{n}\log |f'(x_{i})\vert , \end{aligned}$$

(3)

provided that the limit exists finitely. The system exhibits stable fixed and periodic states for negative Lyapunov exponent value and chaos or unstable state is reported in the system for positive Lyapunov value. Further, if the Lyapunov exponent value ($\gamma$) is zero, then the system remains in a neutral state. In this way, the Lyapunov exponent value is used to explore the stable and unstable states for the system.

3 Formulation and dynamical exploration of the generalized system $G_{\rho ,\beta }(x)$

Throughout this section, we deal with the formation and detailed analysis of a generalized chaotic system using different dynamical properties. Therefore, let us consider a discrete chaotic map $G: [0,1]\rightarrow [0,1]$ defined as:

$$\begin{aligned} G_{\rho ,\beta }(x)=\frac{\rho x (1-x)^{\beta }}{1+x},\;\;\text {where}\; \rho \in \left( 0,\rho _{max}\right] ,\;\beta >1,\;\text {and}\;x\in [0,1]. \end{aligned}$$

(4)

In particular, through induction, the corresponding discrete dynamical system or difference equation form of the above chaotic map can be given as:

$$\begin{aligned} x_{n+1}=G_{\rho ,\beta }(x_{n})=\frac{\rho x_{n} (1-x_{n})^{\beta }}{1+x_{n}}, \end{aligned}$$

(5)

where $\rho \in \left( 0,\rho _{max}\right]$, $\beta >1$, $n=0,1,2,\cdots ,$ denotes the number of iterations, and $x_{n}\in [0,1]$. The above system $G_{\rho ,\beta }(x)$ (4) is termed as the generalized chaotic system, which at $\beta =1$ reduces to the one-dimensional chaotic system $\frac{\rho x (1-x)}{1+x}$ as suggested by Kumar et al. [28].

The entire dynamics for the generalized chaotic system $G_{\rho ,\beta }(x)$ primarily depends on two control parameters, namely $\rho$ and $\beta$. Now, we explore the discrete dynamics of the generalized system $G_{\rho ,\beta }(x)$ through distinct dynamical features like fixed and periodic points, time-series and cobweb representations, bifurcation analysis, and Lyapunov exponent plots under different subsections.

3.1 Fixed point analysis in the generalized system ${G_{\rho ,\beta }(x)}$

As, we have taken above $G_{\rho ,\beta }(x)=\frac{\rho x (1-x)^{\beta }}{1+x}$ as a generalized chaotic system, where $\rho \in \left( 0,\rho _{max}\right]$, $\beta >1$, and $x\in [0,1]$, so by using Definition 2.1, we obtain the following orbit evolution:

$$\begin{aligned} x_{1}&=G_{\rho ,\beta }(x_{0}),\\ x_{2}&=G_{\rho ,\beta }\left( G_{\rho ,\beta }(x_{0})\right) =G^{2}_{\rho ,\beta }(x_{0}),\\ x_{3}&=G_{\rho ,\beta }\left( G_{\rho ,\beta }\left( G_{\rho ,\beta }(x_{0})\right) \right) =G^{3}_{\rho ,\beta }(x_{0}),\\&\vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots \\ x_{n}&=G_{\rho ,\beta }(G_{\rho ,\beta }(G_{\rho ,\beta }(x_{0})\cdots \text {n-times}))=G^{n}_{\rho ,\beta }(x_{0}), \end{aligned}$$

such that $n\in N$, $G^{n}_{\rho ,\beta }(x_{0})$ denotes the $n^{th}$ iterate of $G_{\rho ,\beta }(x)$ at an initiator $x_{0}\in [0,1]$, and the resulting sequence $\{G^{n}_{\rho ,\beta }(x_{0})\}$ or $\{x_{n}\}$ is called an iterative orbit for the generalized system $G_{\rho ,\beta }(x)$. Further, the sequence $\{x_{0},~~G_{\rho ,\beta }(x_{0})=x_{0},~~G^{2}_{\rho ,\beta }(x_{0})=x_{0},~~G^{3}_{\rho ,\beta }(x_{0})=x_{0},~~....,~~G^{n}_{\rho ,\beta }(x_{0})=x_{0},....\}$ or $\{x_{0}, x_{0},\cdots , x_{0},\cdots \}$ is termed as fixed state iterative orbit of the system $G_{\rho ,\beta }(x)$. Now, we analyze the properties of fixed point of the system $G_{\rho ,\beta }(x)$.

Theorem 3.1

For each $\beta >1$, the generalized chaotic system $G_{\rho ,\beta }(x)$ defined on [0, 1] admits only a trivial fixed point 0 for $0<\rho \le 1$ and two fixed points 0 and $p_{\rho }$ for $\rho >1$ lying in the interval [0, 1].

Proof

Using Definition 2.2 of fixed point for the generalized system $G_{\rho ,\beta }(x)$, we get

$$\begin{aligned}&G_{\rho ,\beta }(x)=\frac{\rho x (1-x)^{\beta }}{1+x}=x,\nonumber \\ \text {that is,}\;\;\;\;&\rho x (1-x)^{\beta }-x(1+x)=0,\nonumber \\&x\left( \rho (1-x)^{\beta }-(1+x)\right) =0,\nonumber \\ \text {either,}\;\;\;\;&x=0\;\;\;\;\text {or}\;\;\;\;\rho (1-x)^{\beta }-(1+x)=0. \end{aligned}$$

(6)

Thus, $x=0$ is one trivial fixed point for the system $G_{\rho ,\beta }(x)$ and the other non-trivial fixed point, say, $p_{\rho }$ (depending on parameter $\rho$) can be evaluated by solving the relation $\rho (1-x)^{\beta }-(1+x)=0$ for some particular value of parameter $\beta$. So, by taking $\beta =2$ in this relation, we find out the value of $p_{\rho }$ of the system $\frac{\rho x (1-x)^{2}}{1+x}$.

In this way, we obtain

$$\begin{aligned} \rho x^{2}+(-2\rho -1)x+(\rho -1)=0. \end{aligned}$$

(7)

Now, by solving (7), we get $x=\frac{(2\rho +1)\pm \sqrt{8\rho +1}}{2\rho }$ for $\rho >0$, out of which $x=\frac{(2\rho +1)-\sqrt{8\rho +1}}{2\rho }$ lies in [0, 1] for each $\rho >1$. Hence, $p_{\rho }=\frac{(2\rho +1)-\sqrt{8\rho +1}}{2\rho }$ for $\rho >1$ is the non-trivial fixed point for the system $G_{\rho ,2}(x)$. Further, putting $\beta =3$ in the relation $\rho (1-x)^{\beta }-(1+x)=0$ to evaluate the value of $p_{\rho }$ for the system $G_{\rho ,3}(x)=\frac{\rho x (1-x)^{3}}{1+x}$, we get

$$\begin{aligned}&\rho (1-x)^{3}-(1+x)=0,\nonumber \\ \text {that is,}\;\;\;\;&-\rho x^{3}+3\rho x^{2}+(-3\rho -1)x+(\rho -1)=0. \end{aligned}$$

(8)

By simplifying (8), we find three values of x out of which two values are not real so we do not consider them. And, the remaining one real value of x lying in the interval [0, 1] for each $\rho >1$ as the non-trivial fixed point $(p_{\rho })$ of the system $G_{\rho ,3}(x)$ is given by:

$$\begin{aligned} p_{\rho }=\frac{-\left( 9\rho ^{2}+\sqrt{3}\sqrt{27\rho ^{4}+\rho ^{3}}\right) ^{2/3}+3^{1/3}\rho }{3^{2/3}\rho \left( 9\rho ^{2}+\sqrt{3}\sqrt{27\rho ^{4}+\rho ^{3}}\right) ^{1/3}}+1. \end{aligned}$$

(9)

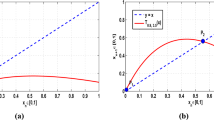
In this way, $p_{\rho }$ given in (9) is the required non-trivial fixed point of the system $G_{\rho ,3}(x)$ for $\rho >1$. Similarly, the fixed point $p_{\rho }$ for other values of parameter $\beta$ can also be obtained. Thus, for each $\beta >1$, the generalized system $G_{\rho ,\beta }(x)$ admits only the trivial fixed point 0 for $0<\rho \le 1$ and the two fixed points 0 and $p_{\rho }$ for $\rho >1$ as shown for $\beta =2$ and 3 respectively in Fig. 1a and b.$\square$

Fig. 1

Fixed points of the system $G_{\rho ,\beta }(x)$ for different values of parameters $\rho$ and $\beta$

Further, for $\beta =2,3,4,5$, the trivial fixed point 0 and the corresponding non-trivial fixed point $p_{\rho }$ of the system $G_{\rho ,\beta }(x)$ lying in [0, 1] as $x_{1}$, $x_{2}$, $x_{3}$ and $x_{4}$ are also shown in Fig. 2, which are the points of intersection of the diagonal $y=x$ and the graph of $G_{\rho ,\beta }(x)$.

Example 3.2

Determine the non-trivial fixed point $p_{\rho }$ of the generalized system $G_{\rho ,\beta }(x)$ for $\beta =2$, $\rho =8.81$ and $\beta =3$, $\rho =11.68$ which lies in the interval [0, 1].

Solution. As proved in Theorem 3.1, the non-trivial fixed point of the system $G_{\rho ,2}(x)$ lying in [0, 1] is given as $p_{\rho }=\frac{(2\rho +1)-\sqrt{8\rho +1}}{2\rho }$ for any $\rho >1$. So, by putting $\rho =8.81$, we get the required fixed point $p_{8.81}\approx 0.58$ as shown by $x_{1}$ in Fig. 2. Also, the non-trivial fixed point $p_{\rho }$ of the system $G_{\rho ,3}(x)$ is given in Eq. (9). Thus, by substituting $\rho =11.68$ in (9), we find $p_{11.68}\approx 0.49$ (see $x_{2}$ in Fig. 2) as the required fixed point at $\beta =3$ and $\rho =11.68$.

Remark 3.3

As the value of control parameter $\beta$ increases from 2, the non-trivial fixed point $(p_\rho )$ value of the generalized system $G_{\rho ,\beta }(x)$ decreases simultaneously (see Figs. 1 and 2).

Fig. 2

Functional plot of $G_{\rho ,\beta }(x)$ fixed points v/s critical points for different values of $\beta$

Theorem 3.4

There exists a nondegenerate (local maxima) critical point lying in the interval [0, 1] of the generalized system $G_{\rho ,\beta }(x)$ for each particular value of parameter $\beta >1$, at which the system $G_{\rho ,\beta }(x)$ admits its peak (maximum) value.

Proof

As, we have from relation (4)

$$\begin{aligned} G_{\rho ,\beta }(x)&=\frac{\rho x (1-x)^{\beta }}{1+x},\nonumber \\ \text {then,}\;\;\;\;G_{\rho ,\beta }'(x)&={-\frac{\rho \left( 1-x\right) ^{\beta -1} \left( \beta x^{2}+\left( \beta +1\right) x-1\right) }{(1+x)^{2}}.} \end{aligned}$$

(10)

Also, we obtain

$$\begin{aligned} G_{\rho ,\beta }''(x)=\frac{\rho \left( 1-x\right) ^{\beta -2} \left[ \beta (\beta -1)x^{3}+2\left( \beta ^{2}-1\right) x^{2}+\left( \beta ^{2}-\beta +4\right) x-2\left( \beta +1\right) \right] }{(1+x)^{3}} \end{aligned}$$

(11)

Now, using Definition 2.4, for critical point of the system $G_{\rho ,\beta }(x)$, we must have

$$\begin{aligned}&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;G_{\rho ,\beta }'(x)=0,\nonumber \\ \text {i.e.,}\;\;\;\;&{-\frac{\rho \left( 1-x\right) ^{\beta -1} \left( \beta x^{2}+\left( \beta +1\right) x-1\right) }{(1+x)^{2}}=0,}\nonumber \\&{\rho \left( 1-x\right) ^{\beta -1} \left( \beta x^{2}+\left( \beta +1\right) x-1\right) =0,}\nonumber \\ \text {either}\;\;\;\;&x=1\;\;\;\;\text {or}\;\;\;\;\beta x^{2}+\left( \beta +1\right) x-1=0.\;\;\;\;(\because \rho >0) \end{aligned}$$

(12)

From (12), first we obtain $x=1$, but $G_{\rho ,\beta }''(1)=0$ for each $\beta >1$. So, $x=1$ is a degenerate critical point and also a point of absolute (global) minima for each $\beta >1$ (see Fig. 2). Thus, the required nondegenerate (local maxima) critical point lying in [0, 1] of the generalized system $G_{\rho ,\beta }(x)$ depending on the parameter $\beta$, at which the system attains its maxima can be determined by solving the relation $\beta x^{2}+\left( \beta +1\right) x-1=0$. In this way, we obtain

$$\begin{aligned}&\;\;\;\;\beta x^{2}+\left( \beta +1\right) x-1=0,\nonumber \\ \text {i.e.},\;\;\;\;&x=\frac{-(\beta +1)\pm \sqrt{\beta ^{2}+6\beta +1}}{2\beta } \end{aligned}$$

(13)

Out of these two values of x obtained in (13), the value $x=\frac{-(\beta +1)+\sqrt{\beta ^{2}+6\beta +1}}{2\beta }$ lies in [0, 1] for each $\beta >1$. Hence, $x=\frac{-(\beta +1)+\sqrt{\beta ^{2}+6\beta +1}}{2\beta }$ is the required critical point of the system $G_{\rho ,\beta }(x)$ lying in [0,1]. Particularly, putting $\beta =2$ and 3 in (13), we get the critical point for $G_{\rho ,2}(x)$ and $G_{\rho ,3}(x)$ as follows:

$$\begin{aligned}&\text {For}\;\;\;\; \beta =2,\;\;x=\frac{-3+\sqrt{17}}{4}\approx 0.28 \nonumber \\&\text {For}\;\;\;\; \beta =3,\;\; x=\frac{-4+\sqrt{28}}{6}=\frac{-2+\sqrt{7}}{3}\approx 0.21 \end{aligned}$$

(14)

Thus, $x\approx 0.28$ and $x\approx 0.21$ are the critical points of the system for $\beta =2$ and 3 respectively as shown by red and blue colors in Fig. 2. Further, we find $G''_{\rho ,2}(0.28)<0$ and $G''_{\rho ,3}(0.21)<0$ for each $\rho >0$. So, by Definition 2.4, these points are nondegenerate critical points and in particular points of local maxima for $G_{\rho ,2}(x)$ and $G_{\rho ,3}(x)$ respectively. Also, the corresponding parameter $\rho _{max}$ values at $\beta =2,3$ are determined as $(\rho _{max})_{\beta =2}\approx 8.81$ and $(\rho _{max})_{\beta =3}\approx 11.68$. Then, by putting $\rho =8.81$, $\beta =2$, and $x=0.28$ in $G_{\rho ,\beta }(x)$, the maximum value is calculated as $(G_{\rho ,2}(x))_{max}\approx 0.9990$. Also, taking $\rho =11.68$, $\beta =3$, and $x=0.21$ in $G_{\rho ,\beta }(x)$, the maximum value is obtained as $(G_{\rho ,3}(x))_{max}\approx 0.9994$.

Likewise, the required critical point for other values of parameter $\beta$ can also be determined. In particular, for $\beta =2,3,4,5$, the corresponding nondegenerate critical points of the system $G_{\rho ,\beta }(x)$ lying in [0, 1], where the system attains its maxima/peak value are also depicted in Fig. 2.$\square$

Remark 3.5

The nondegenerate critical point lying in the interval [0, 1] at which the peak value/maxima of the generalized system $G_{\rho ,\beta }(x)$ is attained decreases simultaneously when the value of parameter $\beta$ increases through 2 (see Fig. 2).

Theorem 3.6

Let $G_{\rho ,\beta }(x)$ be the generalized chaotic system defined on [0, 1] and 0 and $p_{\rho }$ be the fixed points for the system $G_{\rho ,2}(x)$ in [0, 1]. Then, the fixed point 0 is attracting (stable) for $0<\rho \le 1$ and $p_{\rho }$ is attracting (stable) for $1<\rho \le 4.95$.

Proof

As proved in Theorem 3.1 that 0 and $p_{\rho }=\frac{(2\rho +1)-\sqrt{8\rho +1}}{2\rho }$ for $\rho >1$ are the fixed points for the system $G_{\rho ,2}(x)$ lying in [0, 1]. Now, to show that these fixed points are attracting (stable) in their respective ranges of parameter $\rho$, we apply Definition 2.3 of attracting and repelling fixed point for $G_{\rho ,2}(x)$ and show that $|G_{\rho ,2}'(x) \vert$ $<1$.

Now, let us consider

$$\begin{aligned} G_{\rho ,2}(x)&=\frac{\rho x (1-x)^{2}}{1+x},\nonumber \\ \text {then,}\;\;\;\;\left| G_{\rho ,2}'(x)\right|&= \left| {-\frac{\rho \left( 1-x\right) (2 x^{2}+3x-1)}{(1+x)^{2}}}\right| . \end{aligned}$$

(15)

Now, putting $x=0$ in (15), we get $\left| G_{\rho ,2}'(0)\right| =\left| \rho \right| =\rho$, as $\rho >0$, that means, the fixed point $x=0$ is attracting for $\rho <1$, neutral (weakly attracting) for $\rho =1$, and repelling for $\rho >1$. Hence, it shows that the fixed point 0 in the system $G_{\rho ,2}(x)$ is attracting (stable) for each $0<\rho \le 1$. Similarly, to examine the attracting behavior of the fixed point $p_{\rho }$ of the system $G_{\rho ,2}(x)$, by putting $x=p_{\rho }=\frac{(2\rho +1)-\sqrt{8\rho +1}}{2\rho }$, in relation (15), we obtain

$$\begin{aligned} \left| G_{\rho ,2}'(p_\rho )\right|&= \left| -\frac{\rho \left( 1-p_\rho \right) (2 p_{\rho }^{2}+3 p_{\rho }-1)}{(1+p_{\rho })^{2}}\right| ,\nonumber \\ \text {where,}\;\;\;\;p_{\rho }&=\frac{(2\rho +1)-\sqrt{8\rho +1}}{2\rho }. \end{aligned}$$

(16)

which gives that $\left| G_{\rho ,2}'(p_\rho )\right| <1$, that is, the fixed point $p_{\rho }$ of $G_{\rho ,2}(x)$ is attracting for $1<\rho \le 4.95$ and repelling for $\rho >4.95$. Hence, the fixed points 0 and $p_{\rho }$ of the system $G_{\rho ,2}(x)$ are attracting (stable) for $0<\rho \le 1$ and $1<\rho \le 4.95$ respectively.$\square$

3.2 Time-series and cobweb representation in the generalized system ${G_{\rho ,\beta }(x)}$

The dynamical systems are identified by different control parameters around which the entire nonlinear dynamics of the systems revolve. In this section, the discrete dynamics in the generalized system $G_{\rho ,\beta }(x)$ is explored for the specific range of the control parameters $\rho$ and $\beta$. Figures 3, 4, 5, 6, 7, 8 show the time-series and cobweb plots of the system $G_{\rho ,\beta }(x)$ for the parameter values $\beta =2$ and 3 respectively from regular to chaotic dynamics.

(a) For ${\beta =2}$

Figures 3, 4, 5 show that for $\beta =2$, the system $G_{\rho ,2}(x)$ exhibits fixed, periodic, and chaotic dynamics for $0<\rho \le 8.81$. Further, for $0<\rho \le 1$, the iterative orbit of $G_{\rho ,2}(x)$ converges to trivial fixed point $x=0$ and for $1<\rho \le 4.95$, it tends to the non-trivial fixed state solution $p_{\rho }$ as shown in Fig. 3a. This attracting (stable) behavior of fixed points 0 and $p_{\rho }$ of $G_{\rho ,2}(x)$ is also depicted through cobweb plot in Fig. 3b.

Fig. 3

For the generalized system $G_{\rho ,\beta }(x)$, a fixed state time-series plots for $\beta =2$ and $\rho =0.8,2,3.25,4.4$, b fixed state cobweb plots for $\beta =2$ and $\rho =0.8,2,4.4$

Fig. 4

For the generalized system $G_{\rho ,\beta }(x)$, a periodic state time-series plots for $\beta =2$ and $\rho =5.5,6.5$, b periodic state cobweb plots for $\beta =2$ and $\rho =5.5,6.5$

For $\rho >4.95$, a complex situation occurs in the system and it vibrates between the period-2 stable solutions for $4.95<\rho \le 6.42$ as shown by red color in Fig. 4a. Moreover, the blue color in Fig. 4a depicts the stable period-4 oscillations of the system $G_{\rho ,2}(x)$ for $6.42<\rho \le 6.76$. Also, the cobweb plot in Fig. 4b displays the attracting (stable) behavior of period-2 and period-4 fixed points of $G_{\rho ,2}(x)$. Likewise, for $6.76<\rho \le 6.86$, the system fluctuates among $2^{n}$ periodic cycles.

As $\rho _{\infty }\approx 6.86$, the system $G_{\rho ,2}(x)$ enters into an unperiodic state and admits chaos for $6.86<\rho \le 8.81$ as shown in Fig. 5a. In addition, Fig. 5b displays the cobweb plot of unstable or chaotic behavior for the system $G_{\rho ,2}(x)$. And, for $\rho >8.81$, the system $G_{\rho ,2}(x)$ is not defined, as there exists atleast one such $x_{n}$ which does not lie in [0, 1].

Fig. 5

For the generalized system $G_{\rho ,\beta }(x)$, a chaotic state time-series plot for $\beta =2$ and $\rho =7.25$ and b chaotic state cobweb plot for $\beta =2$ and $\rho =7.25$

(b) For ${\beta =3}$

The system $G_{\rho ,3}(x)$ displays its complete dynamics for $0<\rho \le 11.68$ as shown in Figs. 6, 7, 8. In particular, the trajectory of the system admits a convergence to the trivial fixed state $x=0$ for $0<\rho \le 1$ and to the non-trivial state $p_{\rho }$ for $1<\rho \le 5.35$ as shown in Fig. 6a. The cobweb plot in Fig. 6b depicts the attracting (stable) behavior of fixed points 0 and $p_{\rho }$ of $G_{\rho ,3}(x)$.

Fig. 6

For the generalized system $G_{\rho ,\beta }(x)$, a fixed state time-series plots for $\beta =3$ and $\rho =0.75,2.5,3.75,4.9$, b fixed state cobweb plots for $\beta =3$ and $\rho =0.75,4.9$

As shown by blue color in Fig. 7a, the system $G_{\rho ,3}(x)$ alternates between period-2 stable solutions for $5.35<\rho \le 7.32$ and among period-4 stable solutions for $7.32<\rho \le 7.82$. Also, the period-8 vibrations in the system $G_{\rho ,3}(x)$ for $7.82<\rho \le 7.93$ are depicted by red color in Fig. 7a. In addition, the cobweb plot in Fig. 7b displays the attracting (stable) behavior of the period-2 and period-8 fixed points for the system $G_{\rho ,3}(x)$.

Fig. 7

For the generalized system $G_{\rho ,\beta }(x)$, a periodic state time-series plots for $\beta =3$ and $\rho =7,7.85$, b periodic state cobweb plots for $\beta =3$ and $\rho =7,7.85$

In this way, the system $G_{\rho ,3}(x)$ oscillates among $2^{n}$ periodic cycles upto $\rho =7.96$. As $\rho _{\infty }\approx 7.96$, the system admits an irregular or chaotic state for $7.96<\rho \le 11.68$ as displayed in Fig. 8a. Also, a cobweb representation for the irregular or chaotic state of the system $G_{\rho ,3}(x)$ is shown in Fig. 8b. Moreover, for $\rho >11.68$, the system $G_{\rho ,3}(x)$ is undefined, as there exists one such $x_{n}$, which does not lie in the interval [0, 1].

Fig. 8

For the generalized system $G_{\rho ,\beta }(x)$, a chaotic state time-series plot for $\beta =3$ and $\rho =9.25$, b chaotic state cobweb plot for $\beta =3$ and $\rho =9.25$

3.3 Periodic evolution for the generalized system ${G_{\rho ,\beta }(x)}$

Periodic evolution, a tremendous feature of dynamical systems, is generally used to explore the discrete dynamics of nonlinear systems, by analyzing the period-doubling nature of different orbits of the system. So, this section presents the period-doubling bifurcations versus the control parameters $\rho$ and $\beta$ in the generalized system $G_{\rho ,\beta }(x)$. For initiator $x_{0}\in [0,1]$, step size 0.001, and the parameter $\beta =2,3$, the period-doubling representations are shown in Figs. 9a–d and 10a–d respectively.

(a) For ${\beta =2}$

The complete bifurcation plot of the system $G_{\rho ,2}(x)$ is displayed in Fig. 9a. Also, Fig. 9b clearly depicts that as $\rho \approx 4.95$, the fixed point $p_{\rho }$ of the system $G_{\rho ,2}(x)$ turns unstable and the first bifurcation appears in the system where the system starts to vibrate between stable order-2 periodic points $B_{1}$ and $B_{2}$ for $4.95<\rho \le 6.42$. Likewise, the next period-doubling take place for $\rho >6.42$, i.e., for $6.42<\rho \le 6.76$, the period-2 fixed points $B_{1}$ and $B_{2}$ become unstable and the trajectory of the system $G_{\rho ,2}(x)$ starts to alternate among period-4 fixed points $B_{11}$, $B_{12}$, $B_{21}$, and $B_{22}$ as shown in Fig. 9b.

Fig. 9

For the generalized system $G_{\rho ,\beta }(x)$, a bifurcation plot for $\beta =2$ and $1\le \rho \le 8.81$, b periodic regime for $\beta =2$ and $2.5\le \rho \le 6.86$, c magnified chaotic regime for $\beta =2$ and $6.87\le \rho \le 8.81$, d period-3 window for $\beta =2$ and $7.89\le \rho \le 7.95$

Further, the other higher $2^{n}$ order bifurcations can be noticed in the system $G_{\rho ,2}(x)$ for $6.76<\rho \le 6.86$. It is surprising to notice that as $\rho _{\infty }\approx 6.86$, the system displays a shift from the period-doubling state to chaos. The entire beauty of chaos in the magnified form for the parameter values $6.86<\rho \le 8.81$ can be seen in Fig. 9c. Moreover, for $\rho > 8.81$, the system $G_{\rho ,2}(x)$ can not be defined, as $x_{n}\notin [0,1]$ there, i.e., the value of $\rho _{max}$ for the system $G_{\rho ,2}(x)$ is 8.81 (see Fig. 9a). Also, it is evident to observe the existence of order-3 periodic window in the intermittent of chaotic region. So, again magnifying the Fig. 9c, the beauty of period-3 window for the parameter extent $7.89\le \rho \le 7.95$ can easily be seen in Fig. 9d. Thus, from the result of Sarkovaski, the system admits each order periodic windows, which in turn, validates the presence of classical chaos in the discrete system $G_{\rho ,2}(x)$.

Fig. 10

For the generalized system $G_{\rho ,\beta }(x)$, a bifurcation plot for $\beta =3$ and $1\le \rho \le 11.68$, b periodic regime for $\beta =3$ and $3\le \rho \le 7.96$, c magnified chaotic regime for $\beta =3$ and $7.97\le \rho \le 11.68$, d period-3 window for $\beta =3$ and $9.55\le \rho \le 9.7$

(b) For ${\beta =3}$

Figure 10a shows the bifurcation plot of the system $G_{\rho ,3}(x)$ for the parameter range $1\le \rho \le 11.68$, i.e., $\rho _{max}=11.68$ for $G_{\rho ,3}(x)$. Figure 10b clarifies that for $1<\rho \le 5.35$, the trajectory of the system $G_{\rho ,3}(x)$ converges to the non-trivial fixed point $p_{\rho }$ and admits an oscillation between period-2 fixed points $C_{1}$ and $C_{2}$ for $5.35<\rho \le 7.32$. Further, it exhibits vibration among period-4 fixed points $C_{11}$, $C_{12}$, $C_{21}$, and $C_{22}$ for $7.32<\rho \le 7.82$.

Likewise, these $2^{n}$ periodic oscillations of the system $G_{\rho ,3}(x)$ end up at $\rho =7.96$ and for $\rho >7.96$, the system enters into an irregular or chaotic state and thus approaches to $\rho _{max}$, that means, chaos is reported in the system for the parameter range $7.96<\rho \le 11.68$ as depicted in the magnified Fig. 10c. In addition, the magnified Fig. 10d reveals the existence of period-3 window for $9.55\le \rho \le 9.7$, which indirectly implies the presence of all order periodic windows and hence classical chaos in the system $G_{\rho ,3}(x)$ by Sarkovaski’s result.

Remark 3.7

For $\beta =2$, the value of growth-rate parameter $\rho _{max}=8.81$ (Fig. 9a) and for $\beta =3$, it stretches to $\rho _{max}=11.68$ (Fig. 10a). Thus, the value of parameter $\rho _{max}$ increases as the control parameter value $\beta$ increases.

Remark 3.8

The range of growth-rate parameter corresponding to the stability performance of the system for $\beta =2,3$ is given by $0<\rho \le 6.86$ (Figs. 9a, b) and $0<\rho \le 7.96$ (Figs. 10a, b) respectively. Hence, the respective stability range of the system also increases along with the increase in control parameter $\beta$.

Remark 3.9

At $\beta =2$, the system admits chaotic behavior for the parameter range $6.86<\rho \le 8.81$ (Fig. 9a), c and at $\beta =3$, chaos occurs for $7.96<\rho \le 11.68$ (Figs. 10a, c). So, the corresponding chaotic range of the system also increases as we increase the control parameter $\beta$ values through 2.

3.4 Lyapunov exponent analysis in the generalized system ${G_{\rho ,\beta }(x)}$

This section deals with the Lyapunov exponent, a significant characteristic of chaos to ascertain the predictable behavior of nonlinear systems and their sensitivity to the initial conditions for different iterative orbits. Now, for the generalized system $G_{\rho ,\beta }(x)$, the Lyapunov exponent is derived as below:

Let $\Omega$ be the divergence between two iterative orbits starting with two close initial inputs x and $x+\tau$, for $0<\tau <1$, which is estimated in the form of exponential growth $\tau e^{n\gamma }$, where $\gamma$ is the Lyapunov exponent for $G_{\rho ,\beta }(x)$ and n indicates the iteration numbers. Then, we get

$$\begin{aligned}&G^{n}_{\rho ,\beta }(x+\tau )-G^{n}_{\rho ,\beta }(x)=\Omega =\tau e^{n\gamma },\nonumber \\ \text {i.e.},\;\;\;\;&\frac{G^{n}_{\rho ,\beta }(x+\tau )-G^{n}_{\rho ,\beta }(x)}{\tau }=e^{n\gamma }. \end{aligned}$$

(17)

Now, putting limit $\tau \rightarrow 0$ at both sides, we have

$$\begin{aligned}&\lim _{\tau \rightarrow 0}\frac{G^{n}_{\rho ,\beta }(x+\tau )-G^{n}_{\rho ,\beta }(x)}{\tau }=e^{n\gamma },\nonumber \\ \text {i.e.},\;\;\;\;&(G^{n}_{\rho ,\beta })'(x)=e^{n\gamma }. \end{aligned}$$

(18)

By applying logarithm at both sides of (18), we get

$$\begin{aligned} \gamma =\displaystyle {\frac{1}{n}}\log |(G_{\rho ,\beta }^{n})'(x)\vert , \end{aligned}$$

(19)

where $\rho \in \left( 0,\rho _{max}\right]$, $\beta >1$, and $(G_{\rho ,\beta }^{n})'(x)$ signifies the first differentiation of $G^{n}_{\rho ,\beta }(x)$. Further, for the sequence of iterates $\left\{ x_{1}, x_{2}=G_{\rho ,\beta }(x_{1}), x_{3}=G_{\rho ,\beta }(x_{2}), \cdot \cdot \cdot , x_{n+1}=G_{\rho ,\beta }(x_{n}), \cdot \cdot \cdot \right\}$, the derivative for the $n^{th}$ degree polynomial, i.e., $(G^{n}_{\rho ,\beta })'(x_{1})$, by applying chain rule (Definition 2.5), can be determined as below:

$$\begin{aligned} (G^{n}_{\rho ,\beta })'(x_{1})=G'_{\rho ,\beta }(x_{n})\;\cdot \;G'_{\rho ,\beta }(x_{n-1})\cdot \cdot \cdot \cdot G'_{\rho ,\beta }(x_{2})\;\cdot \;G'_{\rho ,\beta }(x_{1}). \end{aligned}$$

(20)

Thus, by (19) and (20), the required Lyapunov exponent is given as:

$$\begin{aligned} \gamma&=\displaystyle {\frac{1}{n}}\log |G'_{\rho ,\beta }(x_{n})\;\cdot \;G'_{\rho ,\beta }(x_{n-1})\cdot \cdot \cdot \cdot G'_{\rho ,\beta }(x_{2})\;\cdot \;G'_{\rho ,\beta }(x_{1})\vert ,\nonumber \\&=\displaystyle {\frac{1}{n}}\left[ \log |G'_{\rho ,\beta }(x_{n})\vert +\log |G'_{\rho ,\beta }(x_{n-1})\vert +\cdot \cdot \cdot \cdot +\log |G'_{\rho ,\beta }(x_{2})\vert +\log |G'_{\rho ,\beta }(x_{1})\vert \right] ,\nonumber \\&=\displaystyle {\frac{1}{n}}\sum _{i=1}^{n}\log |G'_{\rho ,\beta }(x_{i})\vert , \end{aligned}$$

(21)

where $\rho \in \left( 0,\rho _{max}\right]$ and $\beta >1$. Hence, it is explored that the maximum Lyapunov exponent ($\gamma$) is the average value of $\log |G'_{\rho ,\beta }(x)\vert$ for the sequence of iterates $\{x_{n}\}$ in the generalized system $G_{\rho ,\beta }(x)$. Further, the negative Lyapunov exponent value ($\gamma$) corresponds to stable (dissipative) state in the system, while for the positive Lyapunov exponent ($\gamma$), the system displays chaos or irregular behavior and extreme sensitivity to the initial conditions.

Now, for any fixed orbit of $G_{\rho ,\beta }(x)$, Lyapunov exponent ($\gamma$) takes the form:

$$\begin{aligned} \gamma =\log |G'_{\rho ,\beta }(x_{1})\vert . \end{aligned}$$

(22)

Moreover, for any periodic orbit of order p, $\gamma$ changes to the equation:

$$\begin{aligned} \gamma =\displaystyle {\frac{1}{p}}\sum _{i=1}^{p}\log |G'_{\rho ,\beta }(x_{i})\vert . \end{aligned}$$

(23)

However, for the aperiodic orbits, the Lyapunov exponent is estimated by using the entire length of an iterative orbit, which is practically impossible. So, only the finite length of an orbit is used to evaluate the Lyapunov exponent.

Example 3.10

Suppose $G_{\rho ,2}(x)=\displaystyle \frac{\rho x (1-x)^{2}}{1+x}$ is the discrete system, with $\rho \in (0,8.81]$ and $x\in [0,1]$. Then, compute the maximum Lyapunov exponent ($\gamma$) of the system $G_{\rho ,2}(x)$ for $\rho =4$.

Solution. As explained in Sect. 3.2, for the parameter range $1<\rho \le 4.95$, the iterative orbit of the system $G_{\rho ,2}(x)$ tends to the non-trivial fixed point solution $p_{\rho }$ for each $x\in [0,1]$ and the corresponding fixed point for the iterative orbit at $\rho =4$, is given as $p_{4}=\frac{(2\times 4+1)-\sqrt{8\times 4+1}}{2\times 4}=0.41$. Thus, to determine the maximum Lyapunov exponent ($\gamma$) of the fixed state orbit, we must simplify Eq. (22). Now, we have $G'_{\rho ,2}(x)=-\frac{\rho \left( 1-x\right) (2 x^{2}+3x-1)}{(1+x)^{2}}$.

So, by substituting $\rho =4$ and $x=0.41$, we obtain

$$\begin{aligned} G'_{4,2}(0.41)=-\frac{4\times \left( 1-0.41\right) \times (2\times (0.41)^{2}+3\times 0.41-1)}{(1+0.41)^{2}}=-0.67 \end{aligned}$$

(24)

Hence, from (22) and (24), we get

$$\begin{aligned} \gamma =\log |-0.67\vert =-0.1739 \end{aligned}$$

Hence, the estimated Lyapunov exponent ($\gamma$) at $\rho =4$ is $-$0.1739, which is negative so, the fixed point $x=0.41$ is a stable attractor of the system $G_{\rho ,2}(x)$.

Fig. 11

For the generalized system $G_{\rho ,\beta }(x)$, Lyapunov exponent plot, a for $\beta =2$ and $1\le \rho \le 8.81$, b for $\beta =2$ and $6.87\le \rho \le 8.81$, c for $\beta =3$ and $1\le \rho \le 11.68$, d for $\beta =3$ and $7.97\le \rho \le 11.68$

Lyapunov Exponent ($\varvec{\gamma }$) versus parameters $\varvec{\rho }$ and $\varvec{\beta }$ in the generalized system $\varvec{G}_{\varvec{\rho },\varvec{\beta }}(\varvec{x})$

Now, we describe the Lyapunov exponent behavior in the generalized system $G_{\rho ,\beta }(x)$, for parameter $\beta >1$ and via plotting 10,000 points for the system.

(a) For ${\beta =2}$

Figure 11a, b depict the Lyapunov exponent plots of the system $G_{\rho ,2}(x)$. It is clear from Fig. 11a that the maximum Lyapunov exponent tends to a negative value, that is, $\gamma <0$, for the parameter range $0<\rho \le 6.86$, which relates to the fixed stable and periodic states in the system $G_{\rho ,2}(x)$. Also, for $\rho >6.86$, the Lyapunov exponent value $\gamma >0$, that represents the chaotic performance of the system. By magnifying the Lyapunov part for $6.86<\rho \le 8.81$, that interesting behavior of the system can be visualized in Fig. 11b, where the iterative orbit displays extreme sensitivity to the initial conditions and a full-fledged chaos appears in the system.

(b) For ${\beta =3}$

The complete Lyapunov exponent behavior of the system $G_{\rho ,3}(x)$ is displayed in Fig. 11c, d. Figure 11c depicts that the Lyapunov spectrum of the system $G_{\rho ,3}(x)$ tends to a negative maximum Lyapunov exponent value ($\gamma <0$) for $0<\rho \le 7.96$ in the stable fixed and periodic regime whereas it approaches to a positive Lyapunov value for $\rho >7.96$ in the chaotic regime. The beautiful chaos performance of the system $G_{\rho ,3}(x)$ for the parameter range $7.96<\rho \le 11.68$ in the magnified form can be seen in Fig. 11d.

Remark 3.11

It is notable that for $\beta =2$ and 3, the Lyapunov sequence $\{\gamma ^{n}\}$ tends to a negative Lyapunov exponent at the neighbourhood points of the parameter values $\rho =7.9$ and 9.6 respectively, that are the places where the system admits a stable window of period-3 in the chaotic region as displayed in Figs. 11b and d.

Bifurcation-cum-Lyapunov Exponent versus $\varvec{\rho }$ and $\varvec{\beta }$ in the generalized system $\varvec{G}_{\varvec{\rho },\varvec{\beta }}(\varvec{x})$

Further, to validate the different values of growth-rate parameter $\rho$ derived in earlier subsections, for which the generalized system $G_{\rho ,\beta }(x)$ changes its dynamical behavior, combined bifurcation-cum-Lyapunov plots for the system $G_{\rho ,\beta }(x)$ are provided at $\beta =2$ and 3 respectively in Figs. 12a and b.

The system admits two different regions, the stable region and the chaotic region, divided by a brown dotted line at $\rho =6.86$ (Fig. 12a) and 7.96 (Fig. 12b), which are the respective maximum values of the growth-parameter $\rho$ for $\beta =2$ and 3, upto which the system remains in a stable state and after that chaos appears in the system.

Remark 3.12

It is observed that for $\beta =2$ and 3, the Lyapunov exponent ($\gamma$) admits a negative value for $\rho <\rho _{\infty }\approx 6.86$ and 7.96 respectively and tends to zero on the period-doubling bifurcations. The negative spikes of the Lyapunov spectrum relate to $2^{n}$ periodic cycles and an onset of chaos is reported close to $\rho =6.86$ and 7.96, where $\gamma$ initially turns positive. For $\rho >6.86$ and 7.96, the Lyapunov exponent increases in general, excluding the dips due to period-3 windows (see Figs. 12a, b).

4 Dynamical superiority of the generalized chaotic system $G_{\rho ,\beta }(x)$

Now, the question arises how the generalized system is better than the other classical systems? Therefore, to prove the dynamical superiority of the generalized system $G_{\rho ,\beta }(x)$, we comparatively analyze its stability and chaos performance along with the original one-dimensional systems through bifurcation and Lyapunov diagrams.

Fig. 12

For the generalized system $G_{\rho ,\beta }(x)$, bifurcation-cum-Lyapunov plot, a for $\beta =2$ and $3\le \rho \le 8.81$ and b for $\beta =3$ and $3\le \rho \le 11.68$

4.1 Superior stability performance of the generalized system ${G_{\rho ,\beta }(x)}$

First, we examine the stability performance of the generalized system $G_{\rho ,\beta }(x)=\frac{\rho x (1-x)^{\beta }}{1+x}$ for $\rho \in \left( 0,\rho _{max}\right]$, $\beta >1$ in comparison with the existing logistic system $\rho x (1-x)$ and the one-dimensional chaotic system $\frac{\rho x (1-x)}{1+x}$. From the comparative bifurcation plots shown in Fig. 13a, we notice that the logistic system $\rho x (1-x)$ remains stable for the parameter range $0<\rho \le 3.57$ and the chaotic system $\frac{\rho x (1-x)}{1+x}$ is stable for $0<\rho \le 5.21$. On the other hand, the generalized system $G_{\rho ,\beta }(x)$ exhibits stable behavior in the parameter extent $0<\rho \le 6.86$ and $0<\rho \le 7.96$ for $\beta =2$ and 3 respectively.

Further, the negative Lyapunov spikes, corresponding to stable fixed and periodic behavior, in the respective ranges of growth-rate parameter $\rho$, for different systems, also confirm the superiority of the generalized system $G_{\rho ,\beta }(x)$ in terms of stability performance (see Fig. 13b). Thus, the generalized system $G_{\rho ,\beta }(x)$ has enhanced stability range than the existing chaotic systems and that stability range also increases as the control parameter value $\beta$ increases.

4.2 Superior chaos performance of the generalized system ${G_{\rho ,\beta }(x)}$

The chaos performance of a discrete system is a significant characteristic for chaos-based cryptography. The distinct features of chaotic systems like aperiodicity, unpredictabilty, and extreme sensitivity to the initial conditions are very much effective for image encryption-decryption applications. Here, we comparatively examine the chaos performance of the generalized system $G_{\rho ,\beta }(x)$ with existing chaotic systems in terms of bifurcation plots.

Fig. 13

For the generalized chaotic system $G_{\rho ,\beta }(x)$, a comparative bifurcation plots for $1\le \rho \le 11.68$ and $\beta =2,3$ and b comparative Lyapunov plots for $1\le \rho \le 11.68$ and $\beta =2,3$ versus the traditional chaotic systems $\rho x (1-x)$ and $\frac{\rho x (1-x)}{1+x}$

Fig. 14

Comparative chaos performance of the generalized chaotic system $G_{\rho ,\beta }(x)$ for $\beta =2,3$ versus parameter $\rho$ and the traditional chaotic systems $\rho x (1-x)$ and $\frac{\rho x (1-x)}{1+x}$

So, from the comparative bifurcation plots shown in Fig. 14, we observe that there exists chaos in the logistic system $\rho x (1-x)$ for $3.58\le \rho \le 4$ and in the one-dimensional chaotic system $\frac{\rho x (1-x)}{1+x}$ for $5.22\le \rho \le 5.83$. Whereas the generalized system $G_{\rho ,\beta }(x)$ exhibits chaos performance in the parameter range $6.87\le \rho \le 8.81$ and $7.97\le \rho \le 11.68$ for $\beta =2$ and 3 respectively.

Hence, the generalized system $G_{\rho ,\beta }(x)$ admits more complex chaotic behavior and a wider chaotic range as compared to the existing chaotic systems. Also, the respective chaotic range of $G_{\rho ,\beta }(x)$ increases rapidly when the value of control parameter $\beta$ increases through 2. Table 1 provides a comparative analysis of the main dynamical aspects for the generalized system $G_{\rho ,\beta }(x)$ versus the logistic system $\rho x (1-x)$ and the one-dimensional chaotic system $\frac{\rho x (1-x)}{1+x}$.

Table 1 Comparative table of generalized system ${ G_{\rho ,\beta }( x)}$ v/s the existing chaotic systems

Table 2 Comparative analysis versus key space region, key space length, and Lyapunov exponent (LE) of the generalized system ${ G_{\rho ,\beta }(x)}$ in terms of control parameters $\beta$ and $\rho$

4.3 Applications of the generalized system ${G_{\rho ,\beta }(x)}$

From the above discussion, we observe that the generalized system $G_{\rho ,\beta }(x)$ admits a wider range of stability and chaos performance in contrast to the existing chaotic systems. Further, the respective stability and chaotic ranges in the system $G_{\rho ,\beta }(x)$ also increase rapidly when the value of ordered parameter $\beta$ increases from 2. The extensive range of stability performance makes the generalized system $G_{\rho ,\beta }(x)$ more suitable for distinct real-life nonlinear phenomena in which stability is important, such as, traffic control [2, 4].

Also, due to the enhanced chaotic range, the generalized system $G_{\rho ,\beta }(x)$ may have credible applications in chaos-based cryptography, image encryption, end-to-end encryption, and random number generation, etc. (see [29, 30, 37, 52] and various other references therein). So, for possible applications in cryptography, a comparative analysis versus key space length, key space region, and Lyapunov exponent in the generalized system $G_{\rho ,\beta }(x)$ for distinct values of control parameters $\rho$ and $\beta$ is also given in Table 2.

5 Conclusions

In this article, we examine the discrete dynamics of a generalized chaotic system $G_{\rho ,\beta }(x)=\frac{\rho x (1-x)^{\beta }}{1+x}, \rho \in \left( 0,\rho _{max}\right] , \beta >1$, and $x\in [0,1]$. Distinct dynamical characteristics such as fixed points, time-series evolution, cobweb representation, period-doubling bifurcation, period-3 window, and Lyapunov exponent for the system are explored in detail. The superiority in stability and chaos performance of the generalized system is reported via comparative bifurcation and Lyapunov plots. The following conclusions are drawn from the study:

• The experimental analysis is performed for $\beta =2$, $0<\rho \le 8.81$ and $\beta =3$, $0<\rho \le 11.68$ and it is shown that the stability and chaotic characteristics of the system increase rapidly along with the value of parameter $\beta$.

• The trivial fixed point $x=0$ of the system is stable (attracting) for $0<\rho \le 1$ and the non-trivial fixed point $p_{\rho }$(depending on $\rho$) is stable in the range $1<\rho \le 4.95$ and $1<\rho \le 5.35$ respectively for $\beta =2$ and 3.

• The generalized system displays periodicity for $4.95<\rho \le 6.86$ and $5.35<\rho \le 7.96$ in case of $\beta =2$ and 3 respectively.

• The existence of period-3 window, an evidence of classical chaos for the generalized system is also reported in the parameter range $7.89\le \rho \le 7.95$ and $9.55\le \rho \le 9.7$ for $\beta =2$ and 3 respectively.

• Further, for $\beta =2$ and 3, the generalized system exhibits chaotic behavior in the parameter range $6.86<\rho \le 8.81$ and $7.96<\rho \le 11.68$ respectively.

Hence, it is strongly believed that the extensive range of stability as well as chaos performance of the generalized system $G_{\rho ,\beta }(x)$ in contrast to the traditional chaotic systems makes it more fit to different potential real-life applications like traffic control and chaos-based cryptography in the future.