1 Introduction

In recent years, there have been remarkable developments in the context of the Nearly \(\hbox {AdS}_{2}\)/Nearly \(\hbox {CFT}_{1}\) (\(\hbox {NAdS}_{2}\)/\(\hbox {NCFT}_{1}\)) correspondence. \(\hbox {NAdS}_{2}\) arises from an appropriate dimensional reduction of a near extremal black hole geometry while \(\hbox {NCFT}_{1}\) may appear as a low energy approximation of a one-dimensional quantum system like the SYK model. (See [1] for a review and also references therein.) The Jackiw–Teitelboim (JT) model (coupled with a matter field) [2,3,4] is a specific 2d dilaton gravity for the \(\hbox {NAdS}_2\) geometry, which may be reduced to the Schwarzian dynamics along the boundary cutoff trajectories [5]. Combined with various information-theoretic techniques, this model provides a computable test bed for various ideas about the resolution of the black hole information loss problem [6].

A two-sided AdS black hole geometry is well known to be dual to the so-called thermofield double state in the boundary side [7]. The (undeformed) thermofield initial state may be prepared by the Euclidean time evolution in the context of Hartle–Hawking construction [7]. In this note, we are mainly interested in rather general deformations of the two-sided black hole geometry by turning on a bulk matter field that is dual to the corresponding boundary operator. In the so-called standard quantization,Footnote 1 the normalizable modes of the bulk matter field correspond to the vev’s of the boundary operator while the non-normalizable modes are dual to the source deformations of the boundary theory by the same boundary operator.

Thus any excitation of a black hole geometry by the normalizable modes will lead to the corresponding deformations of the thermofield double state. In this note, specialized to the case of the massless scalar field, we would like to clarify the structure of deformations in the 2d bulk as well as in the dual boundary theory side. Especially, we shall show that the initial state, to the leading order of vev deformations, may be prepared with an operator insertion at the mid-point of the Euclidean time evolution [10, 11].

In general, deformations would affect the dynamics of the cutoff trajectories. One may then try to obtain the information of the deformations by probing the cutoff trajectories at the boundary. This would, in principle, be possible if the trajectories contain all the information of the bulk deformations. There are, however, nontrivial behind-horizon degrees of freedom in the bulk such as Python’s degrees of freedom [12,13,14]. It is not clear at all whether this hidden information can be fully recovered by collecting boundary data. In fact, by explicitly solving the equations of motion, we will see that the cutoff trajectories do not have enough information for the full recovery.

Since \(\hbox {AdS}_{2}\) is rigid even under the bulk matter deformation, the SL\((2,\textbf{R})\) symmetries of the background geometry provide useful information for understanding the relevant dynamics [16]. In this paper, we explore the SL\((2,\textbf{R})\) symmetry realization of the inserted operators corresponding to the vev deformations of the thermofield double state. To simplify the discussion, we consider these vev deformations only up to their leading order. We show that these inserted operators form a specific SL\((2,\textbf{R})\) representation. See [15,16,17] for some related discussions.

This paper is organized as follows. In the next section, we review the Jackiw–Teitelboim model focusing on the 2d two-sided black hole geometries and the induced Schwarzian dynamics along their cutoff trajectories. In Sect. 3, we investigate the structure of generic bulk deformations by turning on a massless scalar field. We argue that the bulk information may not be fully recovered from the boundary data collected along the cutoff trajectories. Sections 4 and 5 are devoted to the realization of SL\((2,\textbf{R})\) symmetries of the inserted operators. To the leading order, we explicitly identify the operators inserted at the mid-point which reproduce the most general vev deformations and show that they form a unitary SL(2,R) representation. In the final section, we summarize our results and comment on some future directions.

2 Two-dimensional dilaton gravity

The JT model of our interest is a 2d dilaton gravity with a matter field described by action

$$\begin{aligned} I= & {} I_\mathrm{{top}}+\frac{1}{16\pi G}\int _M d^2 x \sqrt{-g}\, \phi \left( R+\frac{2}{\ell ^2}\right) \nonumber \\{} & {} + I_\mathrm{{surf}} + I_M(g, \chi ) , \end{aligned}$$
(1)

where \(\phi\) is a dilaton field, \(\chi\) a matter field and

$$\begin{aligned} I_\mathrm{{top}}&= \frac{\phi _0}{ 16\pi G}\int _M d^2 x \sqrt{-g} R\,, \nonumber \\ I_\mathrm{{surf}}&= \frac{1}{ 8\pi G}\int _{\partial M} \sqrt{\gamma }\, (\phi _0 + \phi ) \, K \,, \nonumber \\ I_M&= -\frac{1}{2}\int _M d^2 x \sqrt{-g} \left( \nabla \chi \cdot \nabla \chi + m^2 \chi ^2 \right) \,. \end{aligned}$$
(2)

In this action, \(\ell\) is the AdS radius, and \(\gamma _{ij}\) and K denote the induced metric and the extrinsic curvature on the boundary \(\partial M\), respectively.

The variation of the dilaton field \(\phi\) leads to

$$\begin{aligned} R+\frac{2}{\ell ^2}=0, \end{aligned}$$
(3)

which sets the metric to be \(\hbox {AdS}_2\). The other equations of motion are obtained from the variation of the metric g and the scalar field \(\chi\),

$$\begin{aligned} \nabla _a \nabla _b \phi -g_{ab} \nabla ^2 \phi + \frac{1}{\ell ^{2}}g_{ab} \phi&= - 8 \pi G T_{ab}\,, \end{aligned}$$
(4)
$$\begin{aligned} \nabla ^2 \chi -m^2 \chi&=0\,, \end{aligned}$$
(5)

where \(T_{ab}\) is the stress tensor of the matter field,

$$\begin{aligned} T_{ab} = \nabla _a \chi \nabla _b \chi -\frac{1}{2} g_{ab} \left( \nabla \chi \cdot \nabla \chi + m^2 \chi ^2 \right) . \end{aligned}$$
(6)

In the global coordinates, the metric of the \(\hbox {AdS}_2\) space is written as

$$\begin{aligned} \mathrm{{d}}s^2 =\frac{\ell ^2}{\cos ^2 \mu } \left( -\mathrm{{d}}\tau ^2 + \mathrm{{d}}\mu ^2 \right) , \end{aligned}$$
(7)

where \(\mu \in [-\frac{\pi }{2},\frac{\pi }{2}]\). The most general vacuum solution to the dilaton equation of motion (4) with \(T_{ab}=0\) is given by

$$\begin{aligned} \phi= & {} \phi _{BH}(L,b,\tau _{B})\nonumber \\{} & {} \equiv {\bar{\phi }} \, L\,\,\frac{(b+b^{-1}) \cos (\tau -\tau _B) -(b-b^{-1}) \sin \mu }{2 \cos \mu } , \end{aligned}$$
(8)

By the coordinate transformation

$$\begin{aligned} \frac{r}{L}&= \frac{(b+b^{-1}) \cos (\tau -\tau _B) -(b-b^{-1}) \sin \mu }{2\cos \mu }\,, \nonumber \\ \tanh \frac{t L }{\ell ^2}&=\frac{2\sin (\tau -\tau _B)}{(b+b^{-1}) \sin \mu -(b-b^{-1}) \cos (\tau -\tau _B)}\,, \end{aligned}$$
(9)

we obtain the AdS black hole metric

$$\begin{aligned} \mathrm{{d}}s^2= - \frac{r^2-L^2}{\ell ^2} \mathrm{{d}}t^2+ \frac{\ell ^2}{r^2-L^2} \mathrm{{d}}r^2, \end{aligned}$$
(10)

with \(\phi = {\bar{\phi }} \, r\). Utilizing the SL(2, R) isometry of \(\hbox {AdS}_2\), we can set \(b=1\) and \(\tau _B=0\) [18]. This metric describes the Rindler wedge of two-sided AdS black holes with the radius of black hole horizon L. The location of singularity is defined by the curve \(\Phi ^2\equiv \phi _0 +\phi =0\) in the above dilaton field, and \(\Phi ^2\) might be viewed as characterizing the size of “transverse space" [4]. In this left/right symmetric two-sided black hole case, one can see that the Gibbons-Hawking temperature, the entropy and energy are given by

$$\begin{aligned} T= \frac{1}{2\pi } \frac{L}{\ell ^2}, \qquad S= S_0 +\mathcal{C} T, \qquad E = \frac{1}{2} \mathcal{C}T^2, \end{aligned}$$
(11)

where \(S_0\) is the ground state entropy given by \(S_{0}= \frac{\phi _0}{4\,G}\) and \(\mathcal{C} =\frac{\pi {\bar{\phi }} \ell ^2}{2\,G}\). In general, these physical quantities could be different for left/right Rindler wedges in the two-sided black hole case. In the next sections we consider some deformation of black hole configuration through the dilaton field and show that these quantities are indeed different for the left/right Rindler wedges.

The boundary time u may be introduced in \(\epsilon \rightarrow 0\) limit through the prescription

$$\begin{aligned} \mathrm{{d}}s^2|_{\text {cutoff}} = -\frac{1}{\epsilon ^2} \mathrm{{d}}u^2, \qquad \phi |_{\text {cutoff}} = {\bar{\phi }} \frac{\ell }{\epsilon }. \end{aligned}$$
(12)

We will adopt the convention that the right boundary time \(t_r\) runs upwards whereas the left boundary time \(t_l\) runs downward. In other words, we identify

$$\begin{aligned} u=t_r = -t_l. \end{aligned}$$
(13)

See Sect. 4 for the details.

The boundary dynamics is equivalently described by a Schwarzian theory [19,20,21],

$$\begin{aligned} S=\int \mathrm{{d}}u \left[ -\phi _l \left\{ \tan \frac{\tau _l(u)}{2},u \right\} -\phi _r \left\{ \tan \frac{\tau _r (u)}{2},u \right\} \right] , \end{aligned}$$
(14)

where \(\phi _l=\phi _r\) can be identified with \({\bar{\phi }}\) in the bulk and \(\tau _{l/r}(u)\) corresponds to the left/right global time coordinate, respectively, at each cutoff trajectory. If the matter is turned on, the Schwarzian action would get corrections which, in general, can be asymmetric at the left and the right boundaries. To the leading order in the deformation, however, the correction vanishes, as seen in the next section.

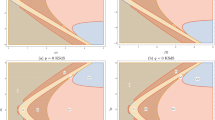
We depict the Penrose diagram of a deformed space in Fig. 1. In the figure, the curves near the boundaries represent typical cutoff trajectories of the boundary dynamics. Given dilaton configurations that are deformed away from (8), one can obtain the cutoff trajectories by using the prescription (12) or from the boundary action with deformed terms.

Fig. 1
figure 1

The left and the right cutoff trajectories are illustrated as curves near the boundaries in the Penrose diagram of a typical deformed space

Full size image

Now we briefly review the general deformation by the matter field. As a simple left-right asymmetric case, let us recall the eternal Janus deformation [18] which makes the Hamiltonians of left-right boundaries differ from each other by turning on exact marginal operators. It is given by

$$\begin{aligned} \chi =\gamma (\mu -\kappa _{0}), \qquad \phi = \bar{\phi }L \frac{\cos \tau }{\cos \mu } -4\pi G\gamma ^{2}(1+\mu \tan \mu ). \end{aligned}$$
(15)

In this case, though the matter field \(\chi\) is asymmetric, the dilaton field \(\phi\) and the black hole temperature are left-right symmetric under the exchange of \(\mu \leftrightarrow -\mu\).

Since the metric is fixed to be \(\hbox {AdS}_2\), the matter field equation (5) can be solved. In the global coordinates, the general solution is given by [22]

$$\begin{aligned} \chi = \sum ^\infty _{n=0} c^\mathcal{D} _n \, \mathcal{N}_n \cos ^\mathcal{D} \mu \, C_n^\mathcal{D} (\sin \mu ) \, e^{-i(n+\mathcal{D})\tau } + \mathrm{c.c.}\, \end{aligned}$$
(16)

where

$$\begin{aligned} \mathcal{N}_n =2^{\mathcal{D} -1} \Gamma (\mathcal{D}) {\textstyle \sqrt{\frac{\Gamma (n+1)}{\pi \Gamma (n+2\mathcal{D})}}}, \end{aligned}$$
(17)

and \(C^\mathcal{D}_n(x)\) denotes the Gegenbauer polynomial. Here, the parameter \(\mathcal{D}\) is defined in terms of the mass of the scalar field \(\chi\) as

$$\begin{aligned} \mathcal{D}=\Delta _\pm = \frac{1}{2} \left( 1 \pm \sqrt{1+4m^2}\right) . \end{aligned}$$
(18)

According to the AdS/CFT correspondence, the bulk matter \(\chi\) is dual to a scalar primary operator \(O_\Delta (t)\) of a certain dimension \(\Delta\). If \(m^2 \ge 0\), it is identified as \(\Delta _+\), i.e.,

$$\begin{aligned} \Delta = \Delta _{+} =\frac{1}{2} \left( 1 + \sqrt{1+4m^2}\right) . \end{aligned}$$
(19)

In this case, the deformation by the matter \(\chi\) with \(\mathcal{D}=\Delta _{+}\) in (16) corresponds to a vev deformation of the dual field theory, while the other deformation with identifying \(\mathcal{D}=\Delta _{-}\) describes a source deformation. In \(\hbox {AdS}_2\), there is another possibility that \(m^2\) is negative as long as the Breitenlohner-Freedman bound [8] holds, namely \(-1/4 \le m^2 < 0\) in our case. Then, we have two possible values as the operator dimension \(\Delta\),

$$\begin{aligned} \Delta =\Delta _\pm = \frac{1}{2} \left( 1 \pm \sqrt{1+4m^2}\right) . \end{aligned}$$
(20)

3 Structure of bulk deformations

From this section, we shall consider turning on a massless scalar field dual to a scalar operator of dimension \(\Delta =1\). In this case, the bulk scalar equation (4) can be solved explicitly by [14]

$$\begin{aligned} \chi = \chi _s +\chi _v, \end{aligned}$$
(21)

where

$$\begin{aligned} \chi _v=\sum ^\infty _{n=1}a_{n}\sin n\bigg (\mu +{\frac{\pi }{2}}\bigg ) \cos n(\tau -\tau ^v_n) \end{aligned}$$
(22)

and

$$\begin{aligned} \chi _s=b_0 +\sum ^\infty _{n=1}b_{n}\cos n\bigg (\mu +{\frac{\pi }{2}}\bigg ) \cos n(\tau -\tau ^s_n) . \end{aligned}$$
(23)

This describes a fully general set of classical solutions to the scalar equation in the ambient \(\hbox {AdS}_2\) space where \(\chi _{v/s}\) satisfies the Dirichlet/Neumann boundary condition at \(\mu =\pm \pi /2\). In our JT model, the metric remains always to be \(\hbox {AdS}_2\) and won’t be corrected by any matter perturbations. For the dilaton field, we shall start from the vacuum solution

$$\begin{aligned} \phi _{bg} =\, {\bar{\phi }} L \, \frac{\cos \tau }{\cos \mu } \end{aligned}$$
(24)

without loss of any generality. As was mentioned previously, this background describes a two-sided black hole with temperature \(T=\frac{1}{2\pi }\negthinspace \frac{L}{\,\,\ell ^2}\). With the scalar deformation (21), the dilaton solution becomes

$$\begin{aligned} \phi= & {} \phi _{bg} + 8\pi G \sum ^\infty _{m=1}\sum ^\infty _{n=1}\nonumber \\{} & {} \quad \left( \, a_{m}a_{n} \phi ^v_{m,n} +b_{m}b_{n} \phi ^s_{m,n} + 2a_{m}b_{n} \phi ^c_{m,n} \, \right) , \end{aligned}$$
(25)

where the full detailed functional forms of \(\phi ^{v,s,c}_{\, m,n}\) are given explicitly in [14].

We now turn to the standard AdS/CFT interpretation of the above bulk deformation. To this end, note that the scalar solution in any asymptotic region of Lorentzian \(\hbox {AdS}_2\) spacetime may be expanded asFootnote 2 (see [23] for instance)

$$\begin{aligned} \chi _\Delta =s(\tau ) \left( \frac{\ell ^2}{r}\right) ^{1-\Delta } (1+ \cdots ) +u(\tau ) \left( \frac{\ell ^2}{r}\right) ^\Delta (1+ \cdots )~, \end{aligned}$$
(26)

where the radial coordinate r is defined by \(\phi /{\bar{\phi }}\) and \(\cdots\) denotes higher order contributions of each power series expansion in \(\left( \ell ^2 /r\right) ^2\). In this note, we are dealing with deformations of the two-sided black hole which involves two (left and right) asymptotic regions in general. In the left/right asymptotic region, the presence of nonvanishing \(s_{l/r}(\tau _{l/r}(u))\) represents a source deformation of the left/right boundary theory by

$$\begin{aligned} \mathcal{L}_{l/r}(u) = \mathcal{L}_0 (u)+ s_{l/r}(\tau _{l/r}(u)) O_\Delta (u), \end{aligned}$$
(27)

where \(\tau _{l/r}(u)\) describes the reparameterization along the left/right cutoff trajectory respectively. Below for the simplicity of our presentation, we shall write \(\tau _{l/r}(u)\) simply as \(\tau\) once it is not confusing. With our normalization in (1), the vev of operator with \(s=0\) may be identified as [23]

$$\begin{aligned} \langle O^{l/r}_{\Delta }(u)\rangle _{s=0}= (2\Delta -1) u_{l/r}(\tau ). \end{aligned}$$
(28)

In our case of \(\Delta =1\), we shall also introduce normalized vev functions \(w_{l,r}(u)\) by

$$\begin{aligned} \langle O_{l/r}(u) \rangle _{s=0}=u_{l/r}(\tau ) \equiv \frac{2\pi }{\beta } w_{l/r}(u). \end{aligned}$$
(29)

From the above solution in (21), the source term for our \(\Delta =1\) case may be identified as

$$\begin{aligned} s_{l/r}=b_0 +\sum ^\infty _{n=1}(\pm 1)^n b_{n} \cos n(\tau -\tau ^s_n) . \end{aligned}$$
(30)

Here and below, the upper/lower sign is for the left/right system respectively. Similarly the vev function can also be identified as

$$\begin{aligned} w_{l/r} =Q_{l/r}(\tau )\sum ^\infty _{n=1}(\pm 1)^{n+1} n \, a_{n} \cos n(\tau -\tau ^v_n) , \end{aligned}$$
(31)

where \(Q_{{{\ell }}/r}\) is defined by

$$\begin{aligned} Q_{l/r} (\tau ) =\lim _{\mu \rightarrow \mp \pi /2} \frac{\phi \cos \mu }{ {\bar{\phi }} \, L}. \end{aligned}$$
(32)

Without the source deformation, the \(Q_{l,r}\) functions may be computed as [14]

$$\begin{aligned} Q_{l/r} (\tau ) =\sqrt{A^2_{l/r}+B^2_{l/r}} \,\,\Bigl (\, \cos (\tau -\tau _{l/r}^B) -q_{l/r}\Bigr ), \end{aligned}$$
(33)

where

$$\begin{aligned} A_{l/r}= & {} 1+\mathcal{O}(a^2), \ \ B_{l/r}=\mathcal{O}(a^2), \ \ q_{l/r}=\mathcal{O}(a^2),\nonumber \\ \tan \tau _{l/r}^B= & {} \frac{B_{l/r}}{A_{l/r}}=\mathcal{O}(a^2), \end{aligned}$$
(34)

whose precise functional forms are also given in [14]. Once this function \(Q_{l/r}\) is given, the left/right reparameterization dynamics may be solved explicitly by [14]

$$\begin{aligned} \cos (\tau -\tau _{l/r}^B) -q_{l/r} =\frac{1-q^2_{l/r}}{ \cosh \frac{2\pi u}{\beta _{l/r}} +q_{l/r}} \end{aligned}$$
(35)

with the temperature

$$\begin{aligned} T_{l/r} =T \sqrt{A^2_{l/r}+B^2_{l/r}}\sqrt{1-q^2_{l/r}}=T \, \big (1+\mathcal{O}(a^2)\big ). \end{aligned}$$
(36)

One is then led to

$$\begin{aligned} Q_{l/r}=\frac{\sqrt{1-q^2_{l/r}}}{ \cosh \frac{2\pi u}{\beta _{l/r}} +q_{l/r}} \frac{{\beta } }{{\beta _{l/r}} }. \end{aligned}$$
(37)

Thus from these overall factors in the vevs, one may see that the vevs decay exponentially in the boundary time u, whose decay rate is precisely the expected one with our dimension one operator. With these vev deformations, the boundary Schwarzian dynamics are basically those of asymptotically black hole spacetimes.

By turning on source deformations only, the boundary reparameterization dynamics may be solved in a similar manner. The resulting 2d spacetime describes again left-right asymmetric black holes in general. If one turns on both the source and the vev deformations at the same time, the left and right black holes are further excited, which will be reflected in the boundary Schwarzian dynamics by the excitation of the corresponding reparameterization modes. In any of the deformations mentioned in the above, one may show that \(\tau _{l/r}(u=\infty )-\tau _{r/l}(u=-\infty ) \le \pi\), which implies that one cannot send a signal from one side to the other [14]. Namely the two boundaries are causally disconnected from each other. From the view point of boundary systems, the left and right systems are completely decoupled from each other without any direct interactions to permit any information transfer between them. Note further that in general the left and right black holes become different from each other as a result of deformation. Especially their temperatures become different from each other in general.

From now on, let us focus on the above deformations only to the leading order, ignoring any higher order corrections. In this limit, the left-right black holes remain unperturbed with \(T_{l}=T_r=T\). On the left/right cutoff trajectory, \(\tau _{l/r}(u)\) is ranged over \((-\pi /2, \pi /2)\) and the reparameterization is solved by \(\sin \tau _{l/r} = \tanh \frac{2\pi }{\beta }u\), respectively. The left and right source terms \(s_{l,r}\) take the same forms as (30) and the vev functions \(w_{l,r}\) become

$$\begin{aligned} w_{l/r} =\cos \tau \,\sum ^\infty _{n=1}(\pm 1)^{n+1} n \, a_{n} \cos n(\tau -\tau ^v_n) . \end{aligned}$$
(38)

Let us first show the independence of the left and right perturbations. By defining

$$\begin{aligned} s(\tau ) =\left[ \begin{array}{lll} s_r(\tau ) &{} \ \ \ \textrm{for} &{} -\frac{\pi }{2}< \tau< \frac{\pi }{2} \\ s_l(\tau -\pi ) &{} \ \ \ \textrm{for} &{} \frac{\pi }{2}< \tau < \frac{3\pi }{2} \end{array} \right. \end{aligned}$$
(39)

one then finds

$$\begin{aligned} s(\tau )=b_0 +\sum ^\infty _{n=1}(-1)^n b_{n} \cos n(\tau -\tau ^s_n) \end{aligned}$$
(40)

which describes a general \(2\pi\)-periodic real function defined over the range \((-\pi /2, 3\pi /2)\). This implies that the source functions \(s_{l,r}\) defined over the range \((-\pi /2, \pi /2)\) become totally independent from each other. This of course agrees with the fact that the source terms in the left and right boundary actions can be turned on independently from each other. By a similar argument, one may show that the vev functions \(w_{l,r}\) may also be turned on independently from each other.

One straightforward consequence of the above consideration is that one may in principle recover the full set of source mode-coefficients \(\{ b_n e^{-i n\tau ^s_n} \}\) from the left and right boundary data specified by \(s_{l,r}(\tau )\) with \(\tau \in (-\pi /2,\pi /2)\). (Of course a similar statement can also be made for the vev deformations.) Therefore, in the small deformation limit (i.e. working in the leading order of the above deformations), probing the left and right boundary perturbations all together, one may recover the corresponding mode-coefficients completely. However, including the higher order correction in bulk geometries, the situation changes completely. Due to the shifts in \(\tau _{l/r}(\pm \infty )\), the total interval size \(\Delta \tau _l + \Delta \tau _r\) of the left right cutoff trajectories in \(\tau\) space becomes in general less than \(2\pi\) where \(\Delta \tau _{l/r}\) denotes \(\tau _{l/r}(\infty )-\tau _{l/r}(-\infty )\), respectively. This implies that the mode-coefficients cannot be fully recovered from the left and right boundary data collected along the full trajectories. On the other hand, one may try to investigate the corresponding bulk profiles of the scalar field. For instance consider the two-independent bulk functions \(\chi _{s/v} (\mu ,\tau _1)\) and \(\chi _{s/v} (\mu ,\tau _2)\) with an appropriate choice of \(\tau _1\) and \(\tau _2\) (\(\tau _1 \ne \tau _2\)), for which the Neumann/Dirichlet boundary condition is imposed at \(\mu =\pm \pi /2\) for the source/vev deformation, respectively. From these two independent functions, one may verify that the mode-coefficients can be recovered completely.Footnote 3 Thus it seems that the bulk in this case contains more information than the ones that may be probed from the boundaries. One may speculate that this hidden information in the bulk is responsible for those nontrivial behind-horizon degrees of freedom such as Python’s lunch degrees of freedom discussed in [14].

In the next section, we shall identify the deformed boundary states from which the above leading-order bulk gravity results follow precisely.

4 Deformation of thermofield double state

In this section, we shall introduce the thermofield double state [24] in the boundary theory and its deformations that reproduce the above mentioned bulk results to the leading order. Especially, we would like to focus on the state deformations which lead to the vev functions in (29) and (38). Below we shall also discuss their relation to the bulk gravity description. In these vev deformations, we expect that the SL(2,R) symmetries of the boundary system will be realized with a certain Hilbert space representation [15, 16]. In the next section we shall present a specific form of orthonormal basis that is directly related to the operator basis of the vev deformations.

We shall begin with the thermofield double initial state in the boundary theory defined by

$$\begin{aligned} |\Psi \rangle = \frac{1}{\sqrt{Z}}\sum _{m,n} \langle n| \, U \,|m\rangle ~ |\bar{m}\rangle _{l} |n\rangle _{r}, \qquad Z=\textrm{tr}\, U^\dagger U, \end{aligned}$$
(41)

where U is a Euclidean evolution operator that will be further specified below and \(|\bar{m}\rangle\) denotes the CTP conjugated state of a basis state \(|m\rangle\). In our convention, any operators labeled by l/r will act on the left/right Hilbert space respectively with an extra transpose operation in the case of left side operators. The Lorentz time evolution of this initial state \(|\Psi \rangle\) is given by

$$\begin{aligned} |\Psi (t_{l},\, t_{r})\rangle = \mathcal{T}_l\,e^{ i\int ^{t_{l}}_{0} \mathrm{{d}}t_{l}\, H^T_l(-t_{l})} \otimes \mathcal{T}_{r\,} e^{- i\int ^{t_{r}}_{0} \mathrm{{d}}t_{r}\, H_r(t_{r})}~ |\Psi \rangle , \end{aligned}$$
(42)

where the left/right time parameters denoted as \(t_{l,r}\) may run independently in general but our boundary time u is related to them by \(t_r=-t_l =u\). Here, \(H_{l/r}(u)\) is the Hamiltonian obtained from (27) and \(\mathcal{T}_{l}/\mathcal{T}_{r}\) represents the time ordering in the direction where \(-t_{l}/t_r\) increases, respectively.

For the undeformed case, the Euclidean evolution operator is given by

$$\begin{aligned} U_0=e^{-\frac{\beta }{2} H_0} , \end{aligned}$$
(43)

and the thermofield double state becomes [7]

$$\begin{aligned} |\Psi \rangle _0 = \frac{1}{\sqrt{Z_0}}\sum _{n} e^{-\frac{\beta }{2} E_n} |\bar{n}\rangle _{l} |n\rangle _{r}, \qquad Z_0=\sum _{n} e^{-{\beta } E_n}, \end{aligned}$$
(44)

with an energy eigen-basis of \(H_0\), from which usual thermal correlation functions may be obtained as their expectation values.

Now let us deal with the leading order of perturbation. In this case the Euclidean evolution U consists of the left, the right Euclidean evolution and a mid-point insertion of the operator for the vev deformation. Namely, it has a form of

$$\begin{aligned} U= U_r\, e^\mathcal{{V}}\, U_l . \end{aligned}$$
(45)

The left and right evolution operators are basically obtained by an appropriate Euclidean continuation of the Lorentzian counterparts in (42). For the right side, we use the usual analytic continuation rule with \(t_r= -i t_E\); The right Lorentzian time ranged over \((-\infty ,0)/(0,\infty )\) is mapped to the Euclidean time \(t_E\) ranged over \((-\beta /4,0)/(0,\beta /4)\), respectively. On the right side of Fig. 2, we depict the Euclidean version of the (undeformed) bulk geometry where the blue/red colored semicircle is for the left/right boundary, respectively. The red-colored (right-side) semicircle is covered by the Euclidean time range \(t_E \in (-\beta /4, \beta /4)\) where the full circle has a circumference \(\beta\). The continuation of the left side is more subtle; We use an analytic continuation rule \(t_l \rightarrow i t^l_E\) but with a further shift by \(\pm \frac{\beta }{2}i\) leading to \(t_l= i t_E=i(t^l_E \pm \beta /2)\). Then the Lorentzian time \(t_l\) ranged over \((-\infty ,0)/(0,\infty )\) is first mapped to \(t^l_E\) ranged, respectively, over \((-\beta /4,0)/(0,\beta /4)\) but, including the shift, to the Euclidean time \(t_E\) ranged over \((\,\beta /4,\,\beta /2)/(-\beta /2,-\beta /4)\), respectively. This range of the Euclidean time is depicted by the blue-colored semicircle on the right panel of Fig. 2. Combining the left and right semicircles, the full boundary circle is covered by the range \((-\beta /2,\beta /2)\). With this preparation, it is proposed in [25] that the left and right Euclidean evolutions are given, respectively, by

$$\begin{aligned} U_{l}=\mathcal{T}_E \, e^{-\int _{\negthinspace -\negthinspace \frac{\beta }{2}}^{\negthinspace -\negthinspace \frac{\beta }{4}} \mathrm{{d}}t_E \, H_{l}(-i t_E)}, \ \ \ U_{r}=\mathcal{T}_E\, e^{-\int _{\negthinspace -\negthinspace \frac{\beta }{4}}^{\,\, 0} \mathrm{{d}}t_E \, H_{r}(-i t_E)}. \end{aligned}$$
(46)

This proposal with \(\mathcal{V}=0\) is tested for the two-sided Janus black holes [25, 26] and shown to reproduce the expected vev function to the leading order precisely [25]; indeed, one can also show that the vev for the 2d two-sided Janus black hole in (15) is reproduced by a similar computation, whose details will be omitted in this note. We shall not test this part of the proposal any further and, instead, focus on the vev deformation in the following.

On the left side of Fig. 2, we depict the lower half of Euclidean geometry combined with the subsequent Lorentzian evolution where the former is used to generate the deformed thermofield initial state. To prepare a thermofield initial state by the Hartle-Hawking construction, we need to patch the Euclidean part to the Lorentzian one along an appropriate hypersurface. To the leading order of deformation, the bulk geometry will not be deformed and one may patch the geometries along the time-reversal symmetric slice at \(\tau =0\).

Fig. 2
figure 2

On the left, we depict the lower half of the Euclidean geometry combined with the subsequent Lorentzian evolution. The former is used to generate the deformed thermofield initial state. The right figure illustrates the full Euclidean evolution which may be used to compute the normalization factor Z or the thermal expectation value (vev) of operators with an appropriate insertion of operator O(t)

Full size image

Let us now include the vev deformation and construct the corresponding mid-point inserted operator given by

$$\begin{aligned} \mathcal{{V}}=\frac{\beta }{2}\sum ^\infty _{n=1} a_n \, e^{i n\tau ^v_n} \, O_n \bigg ( \frac{\beta }{4} i \bigg ) \end{aligned}$$
(47)

with

$$\begin{aligned} O_n (-it_E) = \mathcal{P}_{n-1} \, O (-it_E) , \end{aligned}$$
(48)

where a differential operator \(\mathcal{P}_{n-1} \, (n=1,2,\ldots )\) will be further specified below. The operator \(e^\mathcal{V}\) may also be realized as a Euclidean evolution operator

$$\begin{aligned} e^\mathcal{{V}}= \mathcal{T}_E\, e^{+\int ^{\,\, \epsilon -\frac{\beta }{4}}_{-\epsilon -\frac{\beta }{4}} \mathrm{{d}}t_E g(t_E) O(-it_E)} \end{aligned}$$
(49)

with

$$\begin{aligned} g(t_E)= \frac{\beta }{2}\,\delta \bigg (t_E+ \frac{\beta }{4}\bigg ) \sum ^\infty _{n=1} a_n e^{ i n \tau ^v_n} \, \mathcal{{P}}_{n-1} , \end{aligned}$$
(50)

where we take the \(\epsilon \rightarrow 0\) limit in the end. In Fig. 2, these insertions are represented by the black dots in the lower or the upper half of the Euclidean evolution.

One may also introduce a Hamiltonian along the lower half of the Euclidean evolution by

$$\begin{aligned} H(-it_E) =\left[ \begin{array}{lll} \ H_l (-it_E), &{} &{} \ \, \,-\frac{\beta }{2}\,\,< \, t_E< \negthinspace \negthinspace - \epsilon \negthinspace -\negthinspace \frac{\beta }{4} \\ -g(t_E) O(-it_E), &{} &{} - \epsilon \negthinspace -\negthinspace \frac{\beta }{4}\negthinspace<\, t_E<\, \, \epsilon \negthinspace -\negthinspace \frac{\beta }{4}\\ \ H_r (-it_E), &{} &{} \ \ \epsilon \negthinspace -\negthinspace \frac{\beta }{4}<\, t_E \,< \, \, \, 0 \end{array}\right. . \end{aligned}$$
(51)

Then U will be given by

$$\begin{aligned} U= \mathcal{T}_E\, e^{-\int ^{\, 0}_{{\negthinspace }-{\negthinspace }\frac{\beta }{2}} \mathrm{{d}}t_E H(-it_E)} \end{aligned}$$
(52)

including the contribution from the mid-point insertion. In the Euclidean space, the counterpart of the Lorentzian unitarity requires the reflection positivity

$$\begin{aligned} H^\dagger (-it_E) = H( i t_E), \end{aligned}$$
(53)

by which one may also introduce the Euclidean Hamiltonian \(H(-i t_E)\) for the upper half of the full thermal circle ranged over \((0, \beta /2)\). Based on this, it is straightforward to show that

$$\begin{aligned} U^\dagger = \mathcal{T}_E\, e^{-\int _{\, 0}^{\frac{\beta }{2}} \mathrm{{d}}t_E H(-it_E)} \end{aligned}$$
(54)

and the Euclidean evolution along the full-circle is then given by \(U^\dagger U\).

We shall now come to the purely vev deformation without any source terms introduced. The Euclidean evolution operator U in this case reads

$$\begin{aligned} U=e^{-\frac{\beta }{4} H_0}\, e^\mathcal{V} e^{-\frac{\beta }{4} H_0} , \end{aligned}$$
(55)

from which we would like to reproduce (29) with (38). Below we shall focus on \(\langle O_r(t)\rangle\); Of course \(\langle O_l(t)\rangle\) may be treated in the same way, but we shall not repeat the latter computation in this note. Let us first note thatFootnote 4

$$\begin{aligned} \langle {O_r}(t) \rangle =\langle \Psi | \textbf{1}\otimes { O}(t) |\Psi \rangle \end{aligned}$$
(56)

which may be evaluated perturbatively. With the fact that the undeformed vev of O vanishes, it is straightforward to show that

$$\begin{aligned} \langle {O_r}(t) \rangle =\mathcal{A}_-(t) +\mathcal{A}_+(t) + \mathcal{O}(a_n^2) , \end{aligned}$$
(57)

where

$$\begin{aligned} \mathcal{A}_\pm (t)=\lim _{\epsilon \rightarrow 0} \int ^{\,\, \epsilon \pm \frac{\beta }{4}}_{-\epsilon \pm \frac{\beta }{4}} \mathrm{{d}}t_E\, g(t_E) \, \frac{1}{Z_{0}}\text {tr} \Big [ e^{-\beta H_{0}}\, { O}(t)\,{ O}(-it_E) \Big ] . \end{aligned}$$
(58)

For the boundary CFT, the thermal two-point correlation is well known as

$$\begin{aligned} \frac{1}{Z_{0}} \text {tr} \Big [ e^{-\beta H_{0}}\, {O}(t)\,{ O}(-i t_E) \Big ] =\frac{2\pi /\beta ^{2}}{1-\cosh \frac{2\pi }{\beta }({t}+i{t_E})}, \end{aligned}$$
(59)

where its normalization is worked out in [27] (see also [11]). In order to reproduce (38) from the above perturbative computation with only \(a_1\) turned on, we need to take \(g(t_E)\) in (58) as

$$\begin{aligned} g_{1}(t_E) = \frac{\beta }{2}\Big [e^{i\tau ^v_{1}}\, \delta (t_E + \beta /4 ) + e^{-i\tau ^v_{1}}\, \delta (t_E - \beta /4 ) \Big ] , \end{aligned}$$
(60)

where we have introduced a notation \(g(t_E)=\sum ^\infty _{n=1} a_n g_n(t_E)\) and used the identity (Recall that \(\cosh \frac{2\pi }{\beta } t =1/\cos \tau\))

$$\begin{aligned} \frac{1}{1-\cosh \frac{2\pi }{\beta }\big (t- \frac{\beta }{4}i \big ) }=e^{-i\tau }\cos \tau . \end{aligned}$$
(61)

From this, we conclude that \(\mathcal{{P}}_0 =1\). One may also check that no choice other than the above insertion point works in reproducing (38).

For \(g_n\) with \(n > 1\), one could adopt the following recursive strategy. The integration in (58) together with the expression in (59) can be used to find the differential operator \(\mathcal{{P}}_{n}\) acting on a function of \(t_E\) as

$$\begin{aligned}{} & {} \mathcal{{P}}_{n}(x) \frac{1}{1-\cosh \frac{2\pi }{\beta }(t+i t_E) } \bigg |_{t_E=-\beta /4} \nonumber \\{} & {} \quad = (-1)^{n}(n+1)~ e^{-i(n+1)\tau }\cos \tau , \end{aligned}$$
(62)

where x denotes the differential operator \(-\frac{\beta }{2\pi } \frac{\mathrm{{d}}}{\mathrm{{d}} t_E}\). By a change of variables \(\cosh \frac{2\pi }{\beta } t =1/\cos \tau\), the above expression becomes

$$\begin{aligned} \mathcal{{P}}_{n}(x) e^{-i\tau }\cos \tau = (-1)^{n}(n+1)~ e^{-i(n+1)\tau }\cos \tau . \end{aligned}$$
(63)

with \(x= -i\cos \tau \frac{\mathrm{{d}}}{\mathrm{{d}}\tau }\). Acting with the differential operator \(-i\cos \tau \frac{\mathrm{{d}}}{\mathrm{{d}}\tau }\) on this defining equation once more, one may obtain the following recursion relation

$$\begin{aligned} 2x\,\mathcal{{P}}_{n}(x) = (n+1)\mathcal{{P}}_{n+1}(x) + (n-1)\mathcal{{P}}_{n-1}(x) \end{aligned}$$
(64)

with initial conditions

$$\begin{aligned} \mathcal{{P}}_{0}(x)=1, \quad \mathcal{{P}}_{1}(x) =2x. \end{aligned}$$
(65)

One may notice that the solutions to this recursion relation are given by a special type of the Meixner-Pollaczek polynomials [28] ,

$$\begin{aligned} \mathcal{{P}}_{n}(x) = \mathcal{{P}}^{\lambda =1}_{n}(x;\, {\textstyle \phi =\frac{\pi }{2} }), \end{aligned}$$
(66)

which can be defined through a hypergeometric function as

$$\begin{aligned} \mathcal{{P}}^{\lambda }_{n}(x;\, \phi ) = \frac{(2\lambda )_{n}}{ n!} e^{in\phi } F(-n,\lambda + ix;\, 2\lambda \,|\, 1-e^{-2i\phi }). \end{aligned}$$
(67)

This completes the identification of the inserted operator \(\mathcal{{V}}\) that reproduces the vev in (38). In the above construction of the thermofield double state, we have not included higher order corrections as we mentioned repeatedly. For instance, consider the left-right asymmetric black hole spacetime, which arises in quadratic order of the above deformations generically. In this case, the above mid-point insertion will not be working anymore and, then, one needs another prescription which, unfortunately, we do not know how to arrange. We leave this issue to the future study.

5 SL(2,R) representation in the operator space

In the previous section, we have constructed the mid-point inserted operator \(\mathcal V\) which is realized as a linear combination of the operators \(\{ O_1, O_2, \ldots \}\). By each of this insertion, one may obtain the corresponding initial state \(|\psi \rangle _{\mathcal{V}}\). This amounts to a variation of operator-state maps in general CFTs. This realization of states is highly nonlinear in terms of the coefficients \(\{a_1e^{i\tau _1^v}, a_2e^{2i\tau _2^v},\ldots \}\) especially including the gravity correction via the deformation of the dilaton field which is quadratic in \(a_n\) as shown in (25).

Since our \(\hbox {AdS}_2\) dynamics involves SL(2,R) symmetries in general, it is expected that the inserted operators also transform under the symmetries. In this section, we would like to clarify how these operators \(O_n\) form a representation of the SL(2,R) algebra

$$\begin{aligned}{}[B, E]=iP, \ \ \ [E, P]=iB, \ \ \ [B,P]=iE , \end{aligned}$$
(68)

where B, P and E denote the three SL(2,R) generators. For later purpose, let us also introduce a Casimir operator \(\mathcal{C}=B^2+P^2-E^2=K_+ K_- -E(E-1)\) where the raising and lowering operators \(K_\pm\) are defined by \(K_\pm =B\mp i P\). We note that this realization of the symmetries is already explored in Section 4.2 of Ref. [16], where the generators of SL(2,R) are identified asFootnote 5

$$\begin{aligned} B= & {} - i\cos \tau \partial _{\tau } , \qquad P =- i\Bigg (\sin \tau \partial _{\tau } + \frac{1}{\cos \tau }\Bigg ), \nonumber \\ E= & {} i\Bigg (\partial _{\tau } + \tan \tau \Bigg ). \end{aligned}$$
(69)

Below, we shall show how these generators are acting upon the space of \(\mathcal{{P}}_n\) explicitly.

First, using the orthogonality property of Meixner-Pollaczek polynomials given by [28]

$$\begin{aligned}&\int ^{\infty }_{-\infty }\mathrm{{d}}x\, P^{\lambda }_{n}(x)P^{\lambda }_{m}(x)w(x\,;\lambda ,\phi ) \\&\quad = \frac{2\pi \, \Gamma (n+2\lambda )}{\,\,n!\,(2\sin \phi )^{2\lambda }}\, \delta _{nm}\,, \quad \lambda >0\,, \ 0<\phi <\pi \,, \end{aligned}$$

with \(w(x\,;\lambda ,\phi )=|\Gamma (\lambda \negthinspace +\negthinspace ix)|^{2}e^{(2\phi -\pi )x}\), one may introduce a new set of orthonormal polynomials \(e_{m}(x)\) defined by

$$\begin{aligned} e_{m}(x) \equiv \sqrt{\frac{2}{m\pi }} \, \mathcal{{P}}_{m-1}(x), \quad m=1,2,\ldots \end{aligned}$$
(70)

These normalized polynomials \(e_{m}(x)\) satisfy then the following recursion relation

$$\begin{aligned} x\, e_{m}(x) = {\textstyle \frac{\sqrt{m(m+1)}}{2}\, e_{m+1}(x) + \frac{\sqrt{m(m-1)}}{2}\, e_{m-1}(x) }. \end{aligned}$$
(71)

This also implies that

$$\begin{aligned}&B\cdot e_{m}\cdot e^{-i\tau }\cos \tau \nonumber \\&\quad = \left[ {\textstyle \frac{\sqrt{m(m+1)}}{2}\, e_{m+1} + \frac{\sqrt{m(m-1)}}{2}\, e_{m-1} }\right] \cdot e^{-i\tau }\cos \tau \,, \nonumber \\&P\cdot e_{m}\cdot e^{-i\tau }\cos \tau \nonumber \\&\quad = i\Bigg [ {\textstyle \frac{\sqrt{m(m+1)}}{2}\, e_{m+1} - \frac{\sqrt{m(m-1)}}{2}\, e_{m-1} }\Bigg ]\cdot e^{-i\tau }\cos \tau \,, \nonumber \\&E\cdot e_{m}\cdot e^{-i\tau }\cos \tau = m\, e_{m} \cdot e^{-i\tau }\cos \tau \,, \end{aligned}$$
(72)

where the actions of P and E are computed using (63) followed by the \(\tau\)-space operations given by (69). Thus these latter two computations require an auxiliary function \(e^{-i\tau }\cos \tau\) on which \(e_m\) is acting upon.

In fact, one may construct the SL(2,R) generators that are acting on \(e_{m}(x)\) directly. This may be achieved by additionally including a finite translation operation given by (see [29, 30] for mathematical precedents)

$$\begin{aligned} e^{\pm i\frac{\mathrm{{d}}}{\mathrm{{d}}x}}f(x) = f(x \pm i). \end{aligned}$$
(73)

Then the three generators may be realized as

$$\begin{aligned} B= x, \ \ \ P = i\cos \bigg ({\textstyle \frac{\mathrm{{d}}}{\mathrm{{d}}x}}\bigg )\, x, \ \ \ E = \sin \bigg ({\textstyle \frac{\mathrm{{d}}}{\mathrm{{d}}x}}\bigg )\, x, \end{aligned}$$
(74)

which act on an arbitrary square-integrable complex function f(x). To verify these expressions, we first note that \(\{e_1(x), e_2(x), \ldots \}\) forms an orthonormal basis for any square-integrable function f(x). The identification of \(B=x\) is already introduced in the above construction. The expression for E can be found as follows; One starts from the generating function of \(\mathcal{{P}}_{n}(x)\) given by

$$\begin{aligned} G(t,x) \equiv \sum _{n=0}^{\infty }t^{n}\mathcal{{P}}_{n}(x) = \frac{1}{1+t^{2}}\, e^{2x\arctan t}. \end{aligned}$$
(75)

By integration of the both sides with respect to t followed by a multiplication of x, one obtains

$$\begin{aligned} \sum _{m=1}^{\infty }\frac{1}{m}t^{m}\, x \, \mathcal{{P}}_{m-1}(x) = \frac{1}{2}\, \left( e^{2x\arctan t}-1\right) \end{aligned}$$
(76)

and, by a further action of \(\sin ({\textstyle \frac{d}{dx}})\) on both sides, is led to

$$\begin{aligned}{} & {} \sum _{m=1}^{\infty }\frac{1}{m}t^{m}\,\sin \bigg ({\textstyle \frac{\mathrm{{d}}}{\mathrm{{d}}x}}\bigg ) \bigg [\, x \, \mathcal{{P}}_{m-1}(x)\bigg ] = \frac{1}{2} e^{2x\arctan t} \sin 2\arctan t \nonumber \\{} & {} =\frac{t}{1+t^2} e^{2x\arctan t} =\sum _{m=1}^{\infty }t^{m}\mathcal{{P}}_{m-1}(x). \end{aligned}$$
(77)

Thus, with \(E=\sin ({\textstyle \frac{\mathrm{{d}}}{\mathrm{{d}}x}})x\), \(E \, e_m(x)= m \, e_m(x)\) which is the desired result reproducing the third line of (72). This demonstrates our expression for E in (74). Finally, the expression for P in (74) can be found from \(-i[B,E]\), which is acting on \(e_m\) by

$$\begin{aligned} P\, e_{m} = i\Big [ {\textstyle \frac{\sqrt{m(m+1)}}{2}\, e_{m+1} - \frac{\sqrt{m(m-1)}}{2}\, e_{m-1} }\Big ]. \end{aligned}$$
(78)

It is also straightforward to check the generators constructed in this way satisfy the SL(2,R) algebra in (68) with \(\mathcal{C}=0\). Among unitary representations of SL(2,R), there is the so called discrete representation \(\mathcal{D}^+_j\) (See for example [31]), which is realized in the Hilbert space

$$\begin{aligned} \mathcal{D}^+_j = \{ |jm\rangle ; m=j, j+1,j+2,\ldots \} \end{aligned}$$
(79)

with j real and positive, \(K_- |jj\rangle =0\), and \(\mathcal{C}=-j(j-1)\). Now one may straightforwardly confirm that the above representation belongs to \(\mathcal{D}^+_{j=1}\) with \(\mathcal{C}=0\).

It is natural to anticipate that the dimension \(\Delta\) operator dual to the massive scalar field is represented by \(\mathcal{D}^{+}_{j=\Delta }\) with \(\mathcal{C}= - \Delta (\Delta -1)= -m^2\). It may be interesting to construct all the representations of operators dual to the massive scalar fields by our method. For a more group-theoretic approach to this topic, one may refer to the reference [15].

6 Conclusions

In this work, we have considered the most general normalizable and nonnormalizable bulk deformations in Jackiw–Teitelboim gravity with a massless field which corresponds to either vev deformations or source deformations of the thermofield double state in the dual boundary theory. Such deformations are, in general, left-right asymmetric, resulting in different black hole temperatures. Moreover, we have argued that, classically, the bulk profiles may not be fully recovered from the data collected along the boundary cutoff trajectories. Then the bulk seems to contain more information than the cutoff boundaries and this might be responsible for the behind-horizon degrees of freedom such as those of Python’s lunches.

The deformed state can be prepared by inserting operators on the boundary of Euclidean \(\hbox {AdS}_2\) in the context of Hartle–Hawking construction. In the limit of small vev deformations, we have explicitly identified the operators for the bulk deformations which are all inserted at the mid-point during the Euclidean time evolution along the lower half of the boundary of the thermal disk. We have found that inserted operators form a discrete SL(2,R) representation \({\mathcal {D}}_{j=1}^+\) with vanishing Casimir. Since the boundary system has SL(2,R) symmetries, it is natural to anticipate such a realization in the operator space. If the matter is massive with mass m instead of massless, the corresponding SL(2,R) representation would be \({\mathcal {D}}_{j=\Delta }^+\) with \({\mathcal {C}} = -m^2\). See [15] for this conclusion from a slightly different perspective.

In constructing the operators corresponding to vev functions, we have ignored higher order corrections. The approximation allows us to work in left-right symmetric undeformed geometries, since the asymmetry arises starting from the second order in deformations. Inclusion of higher order terms would involve asymmetric black hole spacetime, and the mid-point insertion of operators would no longer be a valid prescription. We leave this issue to the future study. Finally, it would be interesting to generalize the results of this paper by turning on both the vev and the source deformations at the same time, for which black holes are further excited as discussed in [14].