Experimental and Numerical Evaluation of In-plane Tensile Mode Stress Intensity Factor for Edge Crack Using Empirical Formulation of Displacement Extrapolation Method

Abstract

This paper presents a comprehensive study on fracture mechanics, with a focus on stress intensity factor (SIF) determination, using a combination of experimental, numerical, and empirical methods. The investigation focuses on the creation of an improved finite element model using the AL2014 alloy, which is commonly used in aerospace and structural engineering. Compact tension (CT) specimens of AL2014 were subjected to fatigue pre-cracking in accordance with ASTM E399 guidelines. The study proposes an empirically modified displacement extrapolation technique for accurate SIF calculation that takes pre-crack conditions into account. The experimental results were used to validate ANSYS numerical simulations. The proposed empirical displacement extrapolation method outperformed traditional finite element analysis and displacement extrapolation in terms of accuracy. For example, the stress intensity factor (K_Q) for Sample 1 was determined experimentally as 28.873 MPam0.5, numerically as 30.44 MPam0.5, and empirically as 29.01 MPam0.5, demonstrating the precision of the new approach. The results demonstrate the empirical equation's ability to predict stress intensity factors with high precision when both initial crack length and pre-crack conditions are taken into account. In terms of accuracy and applicability, the proposed method outperforms traditional approaches, with promising implications for fracture mechanics analysis.

Introduction

It is essential in the field of contemporary structural engineering to design structures that are resistant to at least some degree of damage. As a consequence of this, there is an increasing demand for the development of improved methodologies for predicting the breakdown of defective components. The linear elastic fracture mechanics' principles, which include methods such as T-stress, higher-order, and factor of stress intensity terms, have being frequently utilized in evaluating damage tolerance process. The SIF is particularly important in terms of defining fractures among these. It is helpful for describing the distribution of stress close to a crack's tip, which in turn helps in the prognosis of fracture conditions and the estimation of the remaining lifespan of mechanical components with cracks [1].

When calculating the SIF, the two primary estimation methods that are used are those which rely on field extrapolation close to the tip of the fracture [2, 3] and that are based on the energy released while the crack is propagating. Examples of methods that fall into the second category include the extension of elemental crack, integration of J-contour integration, the approach of stiffness derivative, and the integral formulation of energy domain that was developed relatively recently [4,5,6]. In order to achieve an accurate crack-tip fields' numerical representation during field fitting procedures carried out in close proximity to a crack tip, finer meshes are required. The results that are produced by methods that are as per the nodal displacements, they are the main outcomes of finite element programmes, are the most accurate.

As a result of the significant potential that FEM possesses in the fracture mechanics' applications, in this study, this approach was chosen for its numeric way of calculating fracture toughness. In earlier research, Zare et al. [7] employed FEM to effectively compute the stress intensity factor for a finite plate featuring an edge crack and exposed to the loading of uniaxial stress with a favourable outcome. In addition, the relationship between the edge crack position and SIF throughout the plate's length was correctly predicted by the neural network approach. This correlation was found to be highly significant. Other studies [8, 9] focused on calculating SIF utilizing FEM and contrasting the outcomes of the simulation with potential solutions. The purpose of this was to verify the method's accuracy. Extensive research has revealed that specialized crack-tip elements that are responsible for SIF generation (K_IC) hold promise as a potential solution. In general-purpose FEM systems, you will not frequently come across elements such as enhanced, stress hybrid, and displacement hybrid elements. In order to solve this problem, a commercial finite element analysis programme has incorporated a modified version of the iso-parametric element that was proposed by Barsoum [10]. This element contributes to an improvement in the finite element modelling of cracked components and structures as it provides an adequate description field near the single strain's fracture tip.

For the purposes of this investigation, the AL2014 alloy was selected. This alloy is second only to the 2024 alloy in terms of popularity among the aluminium alloys that are part of the 2000-series. Typically, it is extruded and forged. 2014, due to the metal's exceptional strength, it is frequently used in a variety of structural projects that involve the aerospace industry. In addition, it is essential in the production of military vehicles and weaponry, as well as truck frames, bridges, and other essential structural projects.

This study's foremost aim is to convey the progression of an enhanced finite element model's development as well as to cultivate an empirically modified displacement extrapolation technique. Another objective of this study is to develop an empirically modified displacement extrapolation technique. This methodology aim is to diligently ascertain the stress intensity factor with precision, also known as K_I, for surface and corner cracks that can be located and oriented in any way. After that, the empirically modified displacement extrapolation technique and the numerical results were validated by comparing them to the values that were determined through experimentation. The precision and reliability of fracture mechanics analysis stands to benefit significantly from the application of this method.

Methodology of Experimental Research

The NANO TEST SYSTEM BI-7000, manufactured by BISS in Bangalore, India, was employed to conduct fracture toughness testing. For the experimental investigation, compact tension (CT) specimens fabricated from AL2014 (as shown in Table 1) were chosen due to its high strength and good machinability. Because of its widespread use in aerospace and structural engineering, the AL2014 study promised insights that would be directly applicable to these industries. The conducted experiments adhered to the standards delineated in the ASTM E399 [11] guideline.

Table 1 AL2014 material properties

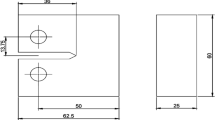
It is beneficial to conduct a triplicate testing (using 3 specimens) for each material condition. The specimens' dimensions must adhere to the specifications outlined in the drawings. In order to calculate the fracture toughness (K_IC) value, it is necessary to have information regarding the specimen thickness, width (W), and crack size (a). The pre-cracking process is a crucial step in the determination of K_IC. It is necessary because even the tiniest machined notch, which is commonly used in practical applications, cannot accurately replicate the characteristics of a natural crack. Consequently, relying on such notches would yield measurements of K_IC that are not representative or reliable. An artifice is employed wherein a narrow notch is utilized, from which a relatively short fatigue crack, known as the pre-crack, extends. A fatigue pre-crack is generated through the application of cyclic loading to a notched specimen, with a stress ratio ranging from a minimum of 1 to a maximum of + 0.1. This loading is repeated for a specific number of cycles, typically falling within the range of 104–106. A test record documenting the relationship between the force-sensing transducer's output and the displacement gauge's output is necessary. The experiment will be conducted iteratively until the specimen reaches its maximum threshold for withstanding any additional applied force. The maximum force, denoted as P_max, shall be duly observed and documented. The empirical examinations' results have been explicated within the confines of Sect. 6.1. Figure 1 depicts a CT specimen utilized for the purpose of conducting fracture toughness testing.

Fig. 1

Dimensions and drawing of CT specimen (mm) [11]

To calculate fracture toughness $K_{{{\text{IC}}}}$, first determine the conditional stress intensity factor value $K_{Q}$. Then, in the event that all the requisites and conditions stipulated in the ASTM E399 standard are duly satisfied, it becomes admissible to assert that $K_{Q}$ =  $K_{{{\text{IC}}}}$. To get K_Q, a load versus CMOD (crack mouth opening displacement) calculation must be performed first. A shoulder extensometer is used to measure CMOD experimentally by positioned on a machined V-shaped notch on the specimen's end in Fig. 2.

Fig. 2

Types of force–displacement (CMOD) records

Tracking the notch edge displacement yields the CMOD. A generated curve is used to compute the loads $P_{Q}$ and $P_{{{\text{max}}}}$. $P_{{{\text{max}}}}$ is the load value at the curve’s highest load point. $P_{Q}$ stands for the load that exists when the SIF reaches $K_{Q}$. It is necessary to draw additional lines to accomplish this. As seen in Fig. 2, when the O point is situated at curve origin, the OA line indicates a tangent to the curve linear portion. (P/v)₅ = 0.95(P/v)O gives rise to the secant line OP₅, which has a slope of 5%. $P_{Q}$ is located at the place where the curve of Type I intersects the secant line in this scenario. The load $P_{Q}$ is situated at the inaugural vertex of both Type II as well as Type III curves. Knowing the $P_{Q}$ load, $K_{Q}$ can be derived analytically for a standard CT specimen using the following equation [11]:

$$ K_{Q} = \left( {P_{Q} /BW^{1/2} } \right) f\left( \frac{a}{W} \right) $$

(1)

$$ f\left( \frac{a}{W} \right) = \frac{{\left( {2 + \frac{a}{W}} \right)}}{{\left( {1 - \frac{a}{W}} \right)^{3/2} }} . \left[ {0.886 + 4.64\frac{a}{W} - 13.32\left( \frac{a}{W} \right)^{2} + 14.72\left( \frac{a}{W} \right)^{3} - 5.6\left( \frac{a}{W} \right)^{4} } \right]. $$

(2)

where the load $P_{Q}$ at which $K_{Q}$ is found, the specimen's thickness denoted as B, specimen's width as 'W', and a represents the crack's length.

The calculation of $K_{{{\text{max}}}}$ is performed employing identical Equations (i) as well as (ii) as those used for the determination of $K_{Q}$, with the sole substitution being the exchange of load $P_{Q}$ with load $P_{{{\text{max}}}}$.

Finite Element Model Development

Finite element modelling refers to the process by which an analyst chooses the material properties, type of elements, order of elements, method of discretization, type of boundary condition, governing matrix equations, and processing options and furthermore, the methods associated with these equations are implemented within a commercial finite element analysis application to facilitate the desired analysis' execution.

The conceptual finite element model encapsulates a highly intricate mesh, replete with SINGULAR iso-parametric pentahedral solid elements (commonly referred to as SPENTA15), distinguished by a myriad of user-defined parameters, including NS, signifying the quantity of segments between crack faces, and the length 'a' spanning one crack face to the other. Additionally, it encompasses the parameter NSEG, which signifies the subdivision of the surface crack front [12]. In consonance with this, a mesh that is harmoniously congruous is deployed, incorporating conventional elements, specifically iso-parametric SPENTA15 solid elements denoted as PENTA15 and iso-parametric hexahedral solid elements referred to as HEXA20. These elements serve the purpose of discretizing the residual domain under scrutiny. A succinct explication of the derivation of these elements is proffered within the confines of Fig. 3. Eight nodes are spatially situated at the vertex positions of every individual element, each of which collectively possesses a grand total of 20 nodes. The residual nodes find their placement at the intermediary points along the sides of the progenitor element, a structural representation portrayed as a cube with a dual-unit configuration. The parent element domain is utilized for approximating various variables using an incomplete quadratic order polynomial. This entails the derivation of explicit shape functions Ni (ξ, η, ζ) for this polynomial basis, where i ranges from 1 to 20, and these functions are readily accessible. By harnessing an iso-parametric methodology, the progenitor element can be pliably contorted to accommodate either linear or curvilinear boundaries or planar or curved surfaces, as delineated within the graphical representation provided in Fig. 3. It is advisable to utilize a trivariate Gauss quadrature scheme in each of the coordinate dimensions' that is ξ, η, and ζ for the purpose of calculating the element matrices and vectors. The necessary coordinates Gauss point and their corresponding weight coefficients are readily available and accessible. In practical applications, the HEXA20 element is frequently favoured and is an integral component of virtually all commercial finite element analysis systems, serving as a standard element.

Fig. 3

Hexahedral solid element (Quadratic order)

Figure 4 illustrates a SPENTA15 solid element belonging to the serendipity family of quadratic order, featuring 15 nodes. This element is constructed by adapting the HEXA20 element, as demonstrated in Fig. 4. The modification entails the collapsing of a face and enforcing that the nodes collocated in this region possess identical degrees of freedom. This particular element is denoted as PENTA15 and functions as a conventional element within the model. Another PENTA15 element distortion produces a singular element named SPENTA15 for computational fracture mechanics [13]. In particular, the edge defined by nodes 3–19-7 aligns with a curved crack front. The mid-side nodes, numbered 10, 12, 14, and 16, are repositioned to quarter-point locations nearer to the crack front. To attain convergence in the computed stress intensity factors, it is possible to incrementally increase the count of SPENTA15 elements (NS) between each crack face and adjust the number of segments (NSEG) along the crack front, while concurrently reducing the size of the singular elements (Δa). For the remaining domain under consideration, a compatible mesh of regular elements (NREG) is employed. Numerical experimentation is an imperative undertaking aimed at ascertaining the most favourable values for NREG, NS, Δa, and NSEG finely tuned to the specific nature of each problem, thereby guaranteeing the convergence of the computed stress intensity factors.

Fig. 4

Singular SPENTA15 element

Numerical Simulation

For the purpose of numerical simulation of fracture toughness, a finite element (FE) model of a CT specimen was developed using finite element code ANSYS. Because the specimen is symmetrical, just half of it has been fabricated in order to cut down on the amount of time spent modelling and computing. A numerical model of the experiment has the same dimensions as the experiment's specimen (refer to Fig. 1 for further explanation). The fatigue pre-crack length was utilized for each and every condition that was simulated using numerical methods. For the purpose of determining the boundary conditions, reference points were positioned in the exact middle of the pin hole on the specimen model. The response force, factor of stress intensity, and crack mouth opening displacement were discovered by the use of the numerical model. The configuration of the components that are located close to crack tip is depicted in Fig. 5.

Fig. 5

Element arrangement near crack tip

As illustrated in Fig. 6, the CT model's opening mode was guaranteed by the loading requirements as well as boundary conditions. The requirements for the elements' compatibility were guaranteed.

Fig. 6

Boundary conditions and loading conditions used in ANSYS

The preconditioned conjugate gradient (PCG) solver was utilized in order to conduct the analysis on the SIF. The creation of an element matrix is the first step in this solver's process. PCG solvers construct the complete global stiffness matrix instead of factoring the global matrix, and they iterate until they reach convergence before calculating the DOF solution. Following the establishment of the suitable system of local coordinate for crack’s vicinity, both the plane strain condition and local coordinate system were used to obtain the stress intensity component [14].

Empirical Displacement Extrapolation Equation

The method of displacement extrapolation is based on field extrapolation, which calculates the factor of stress intensity by utilizing nodal displacements near the fracture tip. This method is referred to as "field extrapolation". To ensure a precise depiction of the crack-tip field, quarter-point iso-parametric elements are employed, in accordance with the recommendations presented in references [10, 15]. Figure 7 illustrates the advancement of the crack along the x-axis.

Fig. 7

SINGULAR elements and crack extension coordinates of the crack tip

For a bi-dimensional crack subjected to mode I stress, the asymptotic equation for the displacement perpendicular to the crack plane, v, is expressed as [16]

$$ v = K_{I} \frac{1 + v}{{4E}}\sqrt {\frac{2r}{\pi }} \left\{ {\left( {2\kappa + 1} \right)\sin \frac{\theta }{2} - \sin \frac{3\theta }{3}} \right\} + A_{1} \frac{{\left( {1 + v} \right)r}}{E}\left( {\kappa - 3} \right)\sin \theta + A_{2} \frac{{\left( {1 + v} \right)r^{\frac{3}{2}} }}{E}\left\{ {\frac{{\left( {2\kappa - 1} \right)}}{3}\sin \frac{3\theta }{2} - \sin \frac{\theta }{2}} \right\} + \cdots $$

(3)

Here, modulus of elasticity as ‘E’, Poisson's ratio as $v$, $\kappa$ for plain strain $\left( {3 - 4v} \right)$ and for plane stress $\left( {3 - v} \right)$/$\left( {1 + v} \right)$, The specimen's load as well as geometry affect the parameters A_i, while the polar coordinates are r and y, as shown in Fig. 7. As prescribed to the symmetry of mode I, at the fracture tip the normal displacement, v(r = 0), is zero.

When assessing the displacement $v$ along the crack faces (θ =  ± π), Eq. (3) exclusively encompasses terms with r^1/2, r^3/2, r^5/2, and so on, enhancing the precision of the extrapolation, as discussed by Chen in 1992. Customizing Eq. (3) for nodes A and B located on the singular element at the upper face of the crack, we obtain: (θ =  ± π).

$$ V_{A} = K_{I} \sqrt {\frac{2}{\pi }} \frac{{\left( {1 + v} \right)\left( {\kappa + 1} \right)}}{4E}\sqrt l - \frac{{A_{2 } \left( {1 + v} \right)\left( {\kappa + 1} \right)}}{12E}l^{\frac{3}{2}} + O(l)^{\frac{5}{2}} $$

(4)

$$ V_{B} = K_{I} \sqrt {\frac{2}{\pi }} \frac{{\left( {1 + v} \right)\left( {\kappa + 1} \right)}}{4E}\sqrt l - \frac{{2A_{2 } \left( {1 + v} \right)\left( {\kappa + 1} \right)}}{3E}l^{\frac{3}{2}} + O(l)^{\frac{5}{2}} $$

(5)

where $l$ is the element side TB's length. Equations (4) and (5) can be solved or $K_{I}$ and $A_{1}$ by ignoring higher order terms. Thus, the value of the stress intensity factor is:

$$ K_{I} = \frac{E}{{3\left( {1 + v} \right)\left( {\kappa + 1} \right)}}\sqrt {\frac{2\pi }{l}} \left( {8v_{A} - v_{B} } \right) $$

(6)

or

$$ K_{I} = \frac{{E^{\prime}}}{12}\sqrt {\frac{2\pi }{l}} \left( {8v_{A} - v_{B} } \right) $$

(7)

The definition of the efficient elastic modulus (E′) referred to as E/(1 − v 2) for plane strain and E for planar stress. The quarter-node displacement allows for a more simple calculation of $K_{I}$, $v_{A}$, if terms in $l^{\frac{3}{2}}$ and Eq. (4) ignores higher:

$$ K_{I} = \frac{2E}{{\left( {1 + v} \right)\left( {\kappa + 1} \right)}}\sqrt {\frac{2\pi }{l}} v_{A } = \frac{E^{\prime}}{2}\sqrt {\frac{2\pi }{l}} \left( {v_{A} } \right) $$

(8)

Finally, In the event that the coefficient containing the r^(1/2) term in the displacement expansion along the upper crack face aligns with the analogous coefficient in the element's interpolation function for $v\left( r \right)$, a different estimation of $K_{I}$ can be obtained.

For a single eight-node or six-node iso-parametric element, the displacement field along the crack edge θ = π is a function of the nodal displacements $v_{A}$ and $v_{B}$ and is given by:

$$ V\left( r \right) = \left( {4v_{A} - v_{B} } \right)\sqrt{\frac{r}{l}} - \left( {4v - 2v_{B} } \right)\frac{r}{l} $$

(9)

By setting θ = π in Eq. (2) and identifying terms with $\sqrt r$ in Eqs. (3) and (9), we obtain:

$$K_{I} = \sqrt {\frac{2}{\pi }} \frac{{\left( {1 + v} \right)\left( {\kappa + 1} \right)}}{2E}\sqrt {r } = \left( {4v_{A} - v_{B} } \right)\sqrt{\frac{r}{l}} $$

(10)

And the stress intensity factor now is

$$K_{I} = \frac{E}{{\left( {1 + v} \right)\left( {\kappa + 1} \right)}}\sqrt {\frac{2\pi }{l}} \left( {4v_{A} - v_{B} } \right) = \frac{E^{\prime}}{4}\sqrt {\frac{2\pi }{l}} \left( {4v_{A} - v_{B} } \right)$$

(11)

The quarter-point element's nodal displacements on the crack's upper face are used in Eqs. (7), (8), and (11) to calculate $K_{I}$. The lower face element could accomplish the same outcome due to symmetry.

Formulation of Empirical Displacement Extrapolation Method.

The suggested empirical equation is obtained from a thorough examination of crack propagation mechanics, taking into account the effects of both pre-crack and initial crack lengths. The factor of stress intensity must be precisely predicted, consider initial crack length a_o and the pre-crack length a_pc in Eq. 11. Formulating empirical displacement extrapolation equation:

$$ K_{I} = \left( {\frac{E^{\prime}}{4}\sqrt {\frac{2\pi }{l}} \left( {4v_{A} - v_{B} } \right)} \right) \cdot \left( {\frac{{a_{0} }}{{a_{0} + a_{{{\text{pc}}}} }} + 0.15 } \right) $$

(12)

where $a_{0}$ =  initial crack length; $a_{pc}$ =  pre-crack length.

To demonstrate the reliability and adaptability of the suggested empirical equation, a comprehensive set of experiments and numerical simulations on a variety of materials and fracture geometries were carried out. These experiments and simulations were performed on a variety of different fracture surfaces. The findings demonstrate an astonishing concordance between the predicted parameters of stress intensity and the actual data, outperforming earlier approaches in terms of accuracy and applicability. Furthermore, the capability of the equation to account for various combinations of pre-crack lengths and initial crack lengths highlights its potential to increase our understanding of crack growth behaviour in a variety of different scenarios [16,17,18].

Results and Discussion

Experimental Research Outcomes

The factor of stress intensity had been assessed for the crack propagation’s opening mode using the experimental method, FEM, and empirical displacement extrapolation methods. Table 2 gives the results of fatigue pre-cracking, and Fig. 8 shows fatigue crack propagation. Experimentally determined load vs. COD curves for samples 1, 2, and 3 depicted in Figs. 9, 10, and 11, respectively. The numerical model for fracture toughness simulation used these curves to describe material behaviour. The experimentally determined stress intensity factor is shown in Table 3 for three samples, and the results are evaluated against P_Q and P_max.

Table 2 Fatigue pre-crack length

Fig. 8

Fatigue pre-cracking

Fig. 9

Load Vs COD curve for specimen 1

Fig. 10

Load Vs COD curve for specimen 2

Fig. 11

Load Vs COD curve for specimen 3

Table 3 Experimental fracture toughness results

Results of Numerical Fracture Toughness Simulation

In accordance with ASTM E398, we have conducted finite element analysis, and the CT specimen was subjected to a variety of loading conditions. In the CT specimen, Fig. 12 portrays the plastic zone and stress state located in immediate proximity to the crack tip. The fracture toughness' numerical outcomes are presented in Table 4. ANSYS was used to derive the u, v, and w displacement components along coordinates x, y, and z, respectively. As a result of the fact that they are derived from converged solutions of finite element, the factor of stress intensity that is presented here is thought to be accurate. The stressed model and the plastic region are depicted in Fig. 1. Figure 13 presents the findings of an analysis that compares the results of numerical and experimental calculations of the stress intensity factor.

Fig. 12

Photograph of stressed model

Table 4 Fracture toughness (Numerical results)

Fig. 13

Stress intensity factor (K_Q, experimental and numerical)

Results of Empirical Displacement Extrapolation Method

The finite element analysis at the nodes that were flagged allowed for the nodal displacements' extraction. We determined the factor of stress intensity by applying Eqs. 7, 8, and 11 to the situation. Table 5 demonstrates the SIF when DEM is used by making use of the empirically modified displacement extrapolation method (Eq. 12). Figure 14 displays a findings comparison that were derived from empirically modified approach of displacement extrapolation, the numerical method, the method of displacement extrapolation, and the experimental method. It was discovered through examination of Fig. 14 that the SIF derived from the empirically modified DEM equation produces the most precise outcomes. Table 6 displays all of the obtained mode I SIF results alongside their corresponding deviation values. ASTM's solution is compared to these results. Material properties can significantly affect stress intensity factor (SIF) values. Disparities can result from material inhomogeneities or simulation property differences. Due to small variations in experimental set-up or execution, loading rates, environmental factors, and crack length precision can also affect SIF values. Variations can result from FEM and DEM model assumptions like boundary conditions, mesh size, and element types. These method simplifications or approximations may not fully capture the physical scenario. The empirically modified DEM (E-DEM) may be more accurate due to refined material behaviour, crack geometry, and loading conditions assumptions.

Table 5 Stress intensity factor in MPa m^0.5

Fig. 14

Comparison of results (ASTM, FEM, DEM, E-DEM)

Table 6 Mode I stress intensity factor for compact tension specimen with deviation values

Conclusion and Future scope

The primary focus of a comprehensive investigation into fracture mechanics was to determine stress intensity variables using ASTM E399 standards. The outcomes of the factor of stress intensity were experimentally validated to ensure their accuracy and reliability. The serendipity family's iso-parametric solid elements, SPENTA15 and hexahedral in shape, and ANSYS' quadratic order were then used in finite element analysis. P_Q was used to calculate K_Q, and nodal displacements in the y-axis were calculated at flagged nodes. The stress intensity factors were also computed using displacement extrapolation while accounting for nodal displacement, providing an in-depth assessment of stress intensity factors.

The study discovered an empirically derived equation for stress intensity factor calculation that outperformed both FEM analysis and the displacement extrapolation method in terms of accuracy. This proposed equation extracted the pre-crack condition for evaluating SIF, which had previously been overlooked in previous studies. Based on empirical data, the proposed equation demonstrated a high level of agreement with experimental results. Its ability to predict stress intensity factors with high accuracy holds great promise for fracture mechanics practitioners and researchers. This empirical formulation can be further investigated for in-plane shear mode and out-of-plane shear mode crack propagation by taking the u and w displacements for the flagged nodes into account, and it can be effectively used for extracting the FCG condition using the respective Paris–Erdogan equation. The mixed mode crack propagation can be evaluated using an efficient virtual fixture conditions for a compact tensile test specimen. As a result, the derived results and the experimental findings are in good agreement.