Introduction

In general, the soft landing mission from an initial parking orbit (say, 100 km circular) consists of the following flight phases. (1) Orbit transfer phase that transfers the spacecraft from an initial orbit to an intermediate elliptical parking orbit. The apolune altitude of the intermediate orbit is the initial circular orbit altitude and a perilune altitude is selected to meet the mission requirements. (2) A powered braking descent phase starting from perilune altitude to reduce both the horizontal and vertical velocities to zero at touchdown. The powered braking phase may be divided into subphases to meet some specific mission requirements. In this paper, powered braking phase is considered as a single phase till touchdown. For a lunar soft landing mission, the powered braking phase is very critical and must be executed as precisely as possible by maximizing the landing mass.

Many numerical solution schemes have been explored in the literature to generate an optimal powered braking trajectory since the first Apollo mission. The researcher [1] discusses the Apollo lunar landing mission design, and the gravity turn trajectory was adapted for powered descent phase therein. Earlier, the scientist [2] analyzes various soft landing mission strategies using POST software. Many of the other landing trajectory design schemes are based on optimal control theory. It is well known that an optimal control problem can be solved mainly by two approaches: (i) direct approach and (ii) indirect approach. In direct approach, the optimal control problem is converted into a parameter optimization problem by discretizing the state and control variables (sometimes, state variables are obtained by numerical integration) and is solved by nonlinear programming (NLP) approach. Many authors [3,4,5,6,7] have solved the lunar landing problem by using direct approach. They mainly use pseudo spectral methods to discretize the states and control variables at the selected nodal points along the trajectory. It is well known that the solution accuracy of direct approach depends on the number of nodes and their distribution. When numbers of nodes increase, the number of unknowns also increases making the problem computationally expensive. Further, a good initial guess is essential for rapid convergence. In indirect approach, the problem is transformed into a two-point boundary value problem involving the state and co-state variables and the related equations representing their variations. The control law is obtained as a function of time-variant co-state variables. The variation of co-states is governed by co-state dynamics which is derived using Pontryagin’s principle. But the initial co-states (corresponding to the components of the state vector) are unknown and are obtained using, in general, some optimization technique. The researcher [7] solves the lunar soft landing optimal trajectory in planar form using indirect approach. The unknown initial co-states are obtained using controlled random search method. Some of the researchers [8] use both direct and indirect approaches to solve the problem and present the merits and demerits of the approaches. They use both heuristic and a gradient-based methods for solving the problem. The sensitivity of gradient-based method to the initial guess on the unknowns is highlighted therein. The performance of indirect approach is found to be better in terms of convergence and accuracy in that study [8]. The major advantage of indirect approach is that the number of unknowns is very less compared to direct approach.

However, the unknown co-states do not represent any physical phenomena, and so, determining them becomes a challenging problem. This is the major reason for the non-convergence encountered while using gradient-based methods through indirect approach. Many researchers attempted to find the initial co-states by introducing assumptions. The researchers [9, 10] presented a Legendre pseudospectral method and the scientists [10] presented a Gauss pseudospectral method to find the co-state history. These studies solved the optimal control problem using direct approach by representing the problem as a nonlinear programming problem through pseudospectral methods. As pointed out earlier, the number of unknowns depends on the number of nodes. Further, in these formulations, when the final time is unknown, the number and distribution of nodes pose additional complexities. Some of the researchers [11] obtained the co-states using shape-based method for trajectory construction. The trajectory construction is carried out using constant thrust. The formulations reported in the literature are specific to some performance measure, and many of them are valid for minimum time problems only in which the final time is free.

In the current research, a method to determine the initial co-states which is uniformly valid for all performance measures, viz. minimum time, minimum fuel and minimum control effort, is developed. Note that minimizing fuel is equivalent to maximizing the landing mass. The differential transformation (DT) technique [12] is employed to determine the initial co-states using the information about the target site. The DT scheme is used by some authors [13, 14] to solve a two-point boundary value problem in single step with final time which is known.

But for landing at a target site problem, in general, the final state that represents the target landing site is known and the final time (flight time) is unknown. With the unknown initial co-states determined using DT technique, the number of unknowns reduces to one, viz. the flight time. The unknown flight time is selected using differential evolution (DE) technique [15].

In the proposed computational scheme, the computation of initial co-states is carried out in a multi-step DT technique using the pre-specified target state vector and the randomly selected flight time. The process of selection of flight time and the computation of initial co-states is continued till the touchdown boundary conditions are met. This novel scheme is named as DT–DE scheme. The technique DE needs only bounds for the unknown parameter. So, guidelines to arrive at narrow bounds even for the only unknown the flight time are discussed herein. With the co-states determined using multi-step DT technique and the guidelines, for selecting bounds for the unknown final time available, the soft landing trajectory problem becomes easily solvable. The robustness and validity of the proposed scheme are demonstrated for three popular performance measures: (i) minimum control effort, (ii) minimum fuel and (iii) minimum time. For all three problems, the thrust is assumed to be limited and throttling is available.

Problem Formulation

The lunar lander module must be transferred from an initial orbit to a target site such that the touchdown velocity is zero. The state vector of target site is given by

$${x}_{t}={r}_{t} \mathrm{cos}({\phi }_{t})\mathrm{cos}({\lambda }_{t})$$
(1a)
$${y}_{t}={r}_{t} \mathrm{cos}({\phi }_{t})\mathrm{sin}({\lambda }_{t})$$
(1b)
$${z}_{t}={r}_{t} \mathrm{sin}({\phi }_{t})$$
(1c)

where \({r}_{t}, {\phi }_{t}\mathrm{ and} {\lambda }_{t}\) are radial distance, selenocentric latitude and selenocentric longitude, respectively. To achieve precise and soft landing, the thrust direction along the trajectory must be chosen satisfying the performance measure.

The problem is formulated using Pontryagin’s principle for different performance measures. First, the system dynamics is given, and in subsequent sections, different formulations are described.

The assumptions used in the formulations are: (i) Lander is a point mass with three degrees of freedom; (ii) specific impulse of engine is constant; (iii) moon is spherical; and (iv) rotational effect of moon on landing trajectory is negligible.

System Dynamics

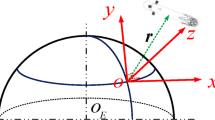
To represent the dynamics of motion, moon-centered inertial (MCI) coordinate frame (XYZ) is used with origin at moon’s center. The schematic of coordinate system and landing trajectory is shown in Fig. 1. In this frame, X-axis is toward the 0-deg longitude (prime meridian of moon) and XY plane coincides with equatorial plane of moon and Z-axis is toward north pole of moon. This coordinate system is not inertial because of the rotation of moon about its axis. However, this effect is very small during the landing phase (landing duration is very small compared to rotation period), and so, it is neglected.

Fig. 1
figure 1

Soft landing coordinate system and thrust vector schematic

Full size image

The equations of motion are:

$$\dot{\overrightarrow{r}}=\overrightarrow{v}$$
(2a)
$$\dot{\overrightarrow{v}}=\frac{-\mu }{{r}^{3}}\overrightarrow{r}+k*{\overrightarrow{a}}_{T}$$
(2b)
$$\dot{m}=\frac{-k*{T}_{max}}{g*Isp}=\frac{-k*m*\sqrt{{{a}_{Tx}}^{2}+{{{{a}_{Ty}}^{2}+a}_{Tz}}^{2}}}{g*Isp}$$
(2c)

where \(\overrightarrow{r}=[x,y, z ]\),\(\overrightarrow{v}=[{v}_{x}, {v}_{y}, {v}_{z}]\), \({\overrightarrow{a}}_{T}=[{a}_{Tx}, {a}_{Ty}, {a}_{Tz}]\), \(x,y,z\) are positions, \({v}_{x },{v}_{y },{v}_{z}\) are velocity components, and \(r\) is the radial distance from moon’s centre. All these quantities are in SI units, i.e., position in meter and velocity in meter per second. The quantities \({a}_{Tx},{a}_{Ty},{a}_{Tz}\) are acceleration components of thrust (T), and k is the throttling parameter. The parameters \(m,{T}_{max,} Isp, g,\mu\) are the mass of the lander module, maximum thrust, specific impulse, acceleration due to gravity of Earth (9.80665 ms−2) and gravitational parameter of moon (4.902800476E12 m3s−2), respectively. Note that for propulsion system in which the thrust is restricted (referred to as limit thrust), the throttling parameter \(k\) varies between 0 and 1. For a propulsion system with unlimit thrust, actual required thrust will be computed.

Formulation for Landing Problem (Indirect Approach)

Introduce co-state variables \({( \overrightarrow{\lambda }=[ p}_{x}{, p}_{y }, {p}_{z}, {p}_{{v}_{x}}, { p}_{{v}_{y}}, { p}_{{v}_{z}}, {p}_{m}] )\) corresponding to the state variables \((\overrightarrow{X}=[x,y, z, {v}_{x}, {v}_{y}, {v}_{z}, m])\). The control variables of the problem are given by \(\overline{u }={(k, a}_{Tx},{a}_{Ty},{a}_{Tz})\).

Let the performance measure be

$$\mathrm{min} J={\int }_{{t}_{0}}^{{t}_{f}}\Gamma (t)dt$$
(3)

Following Pontryagin’s principle, the Hamiltonian \(H\) is written as

$${H=\Gamma +\overrightarrow{\lambda }*\dot{\overrightarrow{X}}}^{T}$$
(4)

The co-state dynamics is derived using

$$\dot{\overrightarrow{\lambda }}=-\left[\frac{\partial H}{\partial x} \frac{\partial H}{\partial y} \frac{\partial H}{\partial z} \frac{\partial H}{\partial {v}_{x}} \frac{\partial H}{\partial {v}_{y}} \frac{\partial H}{\partial {v}_{z}}\frac{\partial H}{\partial m}\right]$$
(5)

The control law by the optimality condition

$$\frac{\partial H}{\partial \overline{u} }=0 \forall t \epsilon [{t}_{o}, {t}_{f}]$$
(6)

Formulation for Minimum Control Effort

The performance measure of minimum control effort problem with variable thrust is given by

$$\mathrm{min} J={\int }_{{t}_{0}}^{{t}_{f}}\frac{1}{2}{k}^{2}({{a}_{Tx}}^{2}+{{a}_{Ty}}^{2}+{{a}_{Tz}}^{2})dt$$
(7)

The co-state equations of motion (cf. Equation (5)) are

$${\dot{p}}_{x}=\frac{\mu }{{r}^{5}}\left[{p}_{{v}_{x }}\left({y}^{2}+{z}^{2}-2{x}^{2}\right)-3x({p}_{{v}_{y }}y+{p}_{{v}_{z }}z)\right]$$
(8a)
$${\dot{p}}_{y}=\frac{\mu }{{r}^{5}}\left[{p}_{{v}_{y }}\left({x}^{2}+{z}^{2}-2{y}^{2}\right)-3y({p}_{{v}_{x }}x+{p}_{{v}_{z }}z)\right]$$
(8b)
$${\dot{p}}_{z}=\frac{\mu }{{r}^{5}}\left[{p}_{{v}_{z }}\left({x}^{2}+{y}^{2}-2{z}^{2}\right)-3z({p}_{{v}_{x }}x+{p}_{{v}_{y }}y)\right]$$
(8c)
$${\dot{p}}_{{v}_{x}}=-{p}_{x}$$
(8d)
$${\dot{p}}_{{v}_{y}}=-{p}_{y}$$
(8e)
$${\dot{p}}_{{v}_{z}}=-{p}_{z}$$
(8f)
$${\dot{p}}_{m}=\frac{{p}_{m}*k*\sqrt{{{a}_{Tx}}^{2}+{{{{a}_{Ty}}^{2}+a}_{Tz}}^{2}}}{Isp*g}$$
(8g)

Unlimit Thrust

For minimum control effort, ideally, the thrust available must be unbounded. So, for unlimit thrust, the control variables are considered as\(\overline{u }=(k{a}_{Tx},{ka}_{Ty},k{a}_{Tz} )\). That means the product of the acceleration component and the throttling parameter is considered as a single parameter. So, there are only three control parameters for this formulation and they are given by the control laws [cf. Equation (6)] for \(\forall t \in [{t}_{0 },{t}_{f }]\)

$$k*{\overrightarrow{a}}_{T}=-{\overrightarrow{p}}_{v}$$
(9)

where \({\overrightarrow{p}}_{v}=[{p}_{{v}_{x}}, { p}_{{v}_{y}}, { p}_{{v}_{z}}]\).

Limit Thrust

To suit realistic conditions wherein the thrust level is limited, the formulation [cf. Equation (9)] is modified and the thrust acceleration vector given by,

$$k*{\overrightarrow{a}}_{T}=-\frac{{\overrightarrow{p}}_{v}}{p}*\frac{{T}_{max}}{m}$$
(10)

where \(p=\sqrt{{{p}_{{v}_{x}}}^{2}+{{p}_{{v}_{y}}}^{2}+{{p}_{{v}_{z}}}^{2}}\). Note that the control laws are independent of the co-state of the mass (\({p}_{m}\)).

Formulation for Minimum Fuel

For minimum fuel problem, the thrust is limited to a maximum value and the thrust variation is handled using the throttling parameter (\(k\)). The flight time of the minimum fuel problem can be either free or fixed. Note that the minimizing the fuel consumption leads to maximum landing mass. The performance measure of minimum fuel problem with limit thrust is given by

$$\mathrm{min} J={\int }_{{\mathrm{t}}_{0}}^{{t}_{f}}-\frac{dm}{dt}dt={\int }_{{\mathrm{t}}_{0}}^{{t}_{f}}\frac{k*m*\sqrt{{{a}_{{T}_{x}}}^{2}+{{a}_{{T}_{y}}}^{2}+{{a}_{{T}_{z}}}^{2}}}{Isp*g}dt$$
(11)

The co-state equations of motion (cf. Equation (5)) except for mass are as given in Eqs. (8a)–(8f). The co-state equation for mass is

$${\dot{p}}_{m}=\frac{\left({p}_{m}-1\right)*k*{T}_{max}}{m*Isp*g}$$
(12)

Note that Eq. (12) and Eq. (8 g) are not same. The optimal thrust acceleration components and magnitude are found using the optimality condition (Eq. (6)), and they are given as follows:

$${\overrightarrow{a}}_{T}=-\frac{g*Isp*{T}_{max}*{\overrightarrow{p}}_{v}}{{m}^{2}*(1-{p}_{m})}$$
(13)

To solve for the throttling parameter \(k\), group the terms containing \(k\) in Hamiltonian (cf. Equation (4))

$${H}_{k}=k*\frac{{T}_{max}}{m}*\left(\frac{m*(1-{p}_{m})}{g*Isp}-\frac{g*Isp}{m*\left(1-{p}_{m}\right)}({{p}_{{v}_{x}}}^{2}+{{p}_{{v}_{y}}}^{2}+{{p}_{{v}_{z}}}^{2})\right)$$
(14a)

Let

$${H}_{k}=k*\frac{{T}_{max}}{m}*S$$
(14b)

where

$$S=\left(\frac{m*(1-{p}_{m})}{g*Isp}-\frac{g*Isp}{m*\left(1-{p}_{m}\right)}({{p}_{{v}_{x}}}^{2}+{{p}_{{v}_{y}}}^{2}+{{p}_{{v}_{z}}}^{2})\right)$$
(14c)

It can also be easily verified that the quantity \([m(1-{p}_{m})]\) is invariant along the trajectory. Clearly, the minimum of \({H}_{k}\) is controlled by the function (\(S\)), known as switching function. The function \({H}_{k}\) is minimum, when

$$k = \left\{ \begin{gathered} 0\quad for\quad S > 0\quad \hfill \\ 1\quad for\quad S < 0 \hfill \\ \end{gathered} \right\}$$
(15)

When \(S=0\), the value of \(k\) is set to zero or one based on the previous value of \(S\). This, clearly, is a bang-bang type of control. That means, for minimum fuel problem, the thrust level is set either to maximum or to zero, along the trajectory. Note that the initial value of co-state of mass (\({p}_{m}\)) cannot be equal to one. When set to one, \({\dot{p}}_{m}=0\) and the co-state of m is frozen to one always and Eq. (14) becomes indeterminant. This observation will be used in the formulation for differential transformation technique.

Formulation for Minimum Time

The performance measure of minimum time problem is given by

$$\mathrm{min }J={\int }_{{\mathrm{t}}_{0}}^{{t}_{f}}dt$$
(16)

The co-state equations of motion (cf. Equation (5)) except for mass are as given in Eqs. (8a)–(8f). The co-state equation for mass is

$${\dot{p}}_{m}=\frac{{p}_{m}*k*{T}_{max}}{m*Isp*g}$$
(17)

The optimal thrust acceleration components obtained using the optimality condition (Eq. (6)) is:

$${\overrightarrow{a}}_{T}=-\frac{g*Isp*{T}_{max}*{\overrightarrow{p}}_{v}}{{m}^{2}*{p}_{m}}$$
(18)

As in the case of minimum fuel, to find the throttling parameter \(k\), group the terms containing \(k\) in Hamiltonian (cf. Equation (4)) and the resulting switching function is

$$S=\left(-\frac{m*{p}_{m}}{g*Isp}-\frac{g*Isp}{m*{p}_{m}}({{p}_{{v}_{x}}}^{2}+{{p}_{{v}_{y}}}^{2}+{{p}_{{v}_{z}}}^{2})\right)$$
(19)

It can also be easily verified that the quantity \((m {p}_{m})\) is constant along the trajectory. The minimum of \({H}_{k}\) is controlled by the function \(S\). For \({H}_{k}\) to be minimum, the choice of \(k\) is as follows:

$$k = \left\{ \begin{gathered} 0\quad for\quad S > 0\quad \hfill \\ 1\quad for\quad S < 0 \hfill \\ \end{gathered} \right\}$$

When \(S=0\), the value of \(k\) is set to zero or one, based on the previous value of\(S\). The sign of the switching function (\(S\)) (refer Eq. (19)) depends on the sign of the co-state \({p}_{m}\). If \({p}_{m}({t}_{0})<0,\) then \(S({t}_{0})>0\) and hence \(k \left({t}_{0}\right)=0\), which implies that \({\dot{p}}_{m} \left({t}_{0}\right)=0.\) So, \({p}_{m}\) remains negative in the time interval \([{t}_{0}\),\({t}_{f}\)], which, in turn, leads to no thrust throughout which means the probe is not descending. Therefore, the initial co-state \({p}_{m}\) cannot have negative value or zero. It must remain always positive which makes the throttling parameter \(k\) as one always.

Solution Scheme

In all the above formulations, the control variables are expressed as functions of co-state variables (cf. Equations (9), (10), (13), (18)). As pointed out earlier, in the indirect approach, if the initial co-states are known, the time history of control can be computed. The determination of co-states is attempted, in general, using optimization techniques. The objective function for optimization (different from the one for optimal control) represents the achievement of the target site with zero velocity.

$$F=\sqrt{{(x-{x}_{t})}^{2}+{(y-{y}_{t})}^{2}+{(z-{z}_{t})}^{2}+{{v}_{x}}^{2}+{{v}_{y}}^{2}+{{v}_{z}}^{2}}$$
(21)

It is well known that the gradient-based technique fails in the absence of good initial guess. In this problem, there is no prior knowledge of initial co-states and so gradient techniques are not suitable for solving an optimal control problem using indirect approach. In an earlier study [8], differential evolution (DE) technique has been used to determine the co-states that minimize the objection function \(F\). The advantage of DE technique is that it does not need an initial guess for the unknown and needs only bounds within which the unknown varies. When very wide bounds for the unknowns are used, the process requires large computational time. To overcome the complexity in determining the co-states and reduce the computational time, a novel computation scheme is proposed in this paper. The unknown initial co-states are determined using differential transformation (DT) technique. However, in addition to target state the time of flight must be known for the use of DT technique. Although for landing problem the target site is known, the flight time is an unknown quantity. So, in this computation scheme, the unknown flight time is randomly using DE technique and DT determines the initial co-states using the selected flight time. Both DE and DT operate concurrently to minimize the function ‘F.’ In the following sections, first a brief account of DE is given. Then, the procedure to determine the co-states using DT is explained. Finally, the computation scheme is presented.

Differential Evolution (DE)

In the first step of differential evolution technique, an initial population of a fixed size (NP) is built. If there are ‘N’ unknown variables, the population matrix is of the size NP x (N + 1). Of the N + 1 elements of each row, first ‘N’ of them are unknown variables selected randomly from their respective bounds according to uniform distribution and the (N + 1)th element is the objective function value. The set of randomly selected unknowns are used to evaluate the objective function at touchdown after numerical propagation. In the second step, each row (say \({z}_{i}\)) of the population undergoes three operations: mutation, crossover and selection and a new set of elements is constructed. These two steps are repeated until the value of objective function is less than a prefixed small tolerance value. The DE parameters are fixed as follows after few trial simulations: the mutation factor = 0.8, CR = 0.9 and the population size = 30 for the present problem.

Initial Co-States using Differential Transformation

DT is a technique that is used for solving a two-point boundary value problem when the final state and the time are known. DT transforms the equations from time domain into a set of nonlinear algebraic equations in a transformed domain. In DT, unlike Fourier and Laplace transforms, the transformed function is expressed in terms of differential operators. That is, if \({f(t}_{e}\)) is a function where \({t}_{e }\epsilon [{t}_{0}, {t}_{f}]\), the image of this function (F(\({t}_{e}\))) for \({t}_{e }\in [{t}_{0}, {t}_{f}]\) in the transformed domain is given by

$$F\left({t}_{e },j\right)= \frac{1}{j!}{\left[\frac{{d}^{j}f(t)}{{dt}^{j}}\right]}_{t={t}_{e}}, j=\mathrm{0,1}, 2\dots .$$
(22)

and \(F\left({t}_{e },j\right)\) is the jth-order differential spectra of f(t) at the time instant\({t}_{e}\). Now the solution to the function \(f\left(t\right)\) in the original domain is obtained using inverse transformation given as follows:

$$f\left(t\right)= \sum_{j=0}^{\infty }F\left({t}_{e },j\right){(t-{t}_{e })}^{j}$$
(23)

The solution is obtained as a Taylor-series expansion about the step size of the independent variable. For various types of functions, the expressions for images are available in the literature (Pukhov, 1981; Hwang et al., 2008). Some examples are: When the function is a differential function (\(f\left(t\right)= \dot{x})\), the jth-order transformed function is given by \(\left(j+1\right) X\left({t}_{e },j+1\right) \mathrm{and}\) when the function is an algebraic expression (\(f\left(t\right)= b x)\), the jth-order transformed function is given by\(b X\left({t}_{e },j\right)\).

In the current problem, the unknown initial co-states are obtained using DT technique. The details of the procedure are given below. For use in DT, it is convenient to express the state and co-state equations [Eqs. (2) and (8)] in state space matrix form.

Let \(\overline{x }\),\(\overline{p }\), \(\overline{u }\) be the state, co-state and the control vectors of the system, respectively, where

$$\overline{x}={[x y z {v}_{x} {v}_{y} {v}_{z}]}^{T}$$
$${\overline{p}=[ p}_{x}{ p}_{y } {p}_{z} {p}_{{v}_{x}} {p}_{{v}_{y}} {{p}_{{v}_{z} }]}^{T}$$
$$\overline{u}={[0 0 0 {ka}_{{T}_{x}} k{a}_{{T}_{y}} k{a}_{{T}_{z}} ]}^{T}$$

The mass state (m) is not considered in the DT process because of the following reasons: (i) the co-state equation of m does not explicitly depend on either \(\overline{x}\) or \(\overline{p};\) (ii) the control law does not depend on the co-state of ‘m’ for minimum control effort case; and (iii) there are invariant quantities \((m {p}_{m })\) and \([m {(1-p}_{m})]\) for minimum time and minimum fuel cases. For these reasons, the co-state of m need not be determined through differential transformation technique.

For all performance measures, the co-state equations are same except for co-state equation of mass. So, the state and co-state equations [Eqs. (2) and (8)] are rewritten as

$$\dot{\overline{x}}={A}_{1} \overline{x}\left(t\right)+{C}_{1}\overline{u}\left(t\right)$$
(24a)
$$\dot{\overline{p}}={A}_{2} \overline{p}(t)$$
(24b)

where

$${A}_{1=}\left[\begin{array}{cccccc}0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ \frac{-\mu }{{r}^{3}}& 0& 0& 0& 0& 0\\ 0& \frac{-\mu }{{r}^{3}}& 0& 0& 0& 0\\ 0& 0& \frac{-\mu }{{r}^{3}}& 0& 0& 0\end{array}\right]$$
(24c)
$${C}_{1}=(0 0 0 1 1 1)$$
(24d)
$${A}_{2=}\left[\begin{array}{cccccc}0& 0& 0& \frac{\mu ({y}^{2}+{z}^{2}-2{x}^{2})}{{r}^{5}}& \frac{-3\mu xy}{{r}^{5}}& \frac{-3\mu xz}{{r}^{5}}\\ 0& 0& 0& \frac{-3\mu xy}{{r}^{5}}& \frac{\mu ({x}^{2}+{z}^{2}-2{y}^{2})}{{r}^{5}}& \frac{-3\mu zy}{{r}^{5}}\\ 0& 0& 0& \frac{-3\mu xz}{{r}^{5}}& \frac{-3\mu zy}{{r}^{5}}& \frac{\mu ({y}^{2}+{x}^{2}-2{z}^{2})}{{r}^{5}}\\ -1& 0& 0& 0& 0& 0\\ 0& -1& 0& 0& 0& 0\\ 0& 0& -1& 0& 0& 0\end{array}\right]$$
(24e)

Equations (24a) and (24b) can be written in the matrix form by substituting optimal control law [Equation (9)] of minimum control effort.

$$\left[\begin{array}{c}\dot{\overline{x}}\\ \dot{\overline{p}}\end{array}\right]=\left[\begin{array}{cc}{A}_{1}& {B}_{1}\\ 0& {A}_{2}\end{array}\right]\left[\begin{array}{c}\overline{x}\\ \overline{p}\end{array}\right]$$
(25a)

where

$${B}_{1}=\left[\begin{array}{cccccc}0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& -1& 0& 0\\ 0& 0& 0& 0& -1& 0\\ 0& 0& 0& 0& 0& -1\end{array}\right]$$
(25b)

The matrix \({B}_{1}\) will have to be set according to the performance measure.

Let \({B}_{T}={B}_{1}\)

Then, for minimum time case, matrix \({B}_{1}\) becomes

$${B}_{1}=\left(\frac{g*Isp*{T}_{max}}{{m}^{2}*{p}_{m}}\right)*{B}_{T}$$
(25c)

For minimum fuel case, matrix \({B}_{1}\) becomes

$${B}_{1}=\left(\frac{g*Isp*{T}_{max}}{{m}^{2}*{(1-p}_{m})}\right)*{B}_{T}$$
(25d)

Let the matrix \(A\) be

$$A={\left[\begin{array}{cc}{A}_{1}& {B}_{1}\\ 0& {A}_{2}\end{array}\right]}_{12 x 12}$$
(25e)

The initial and final conditions are given by

$$\overline{x}\left({t}_{0}\right)={\overline{x} }_{0} \mathrm{and} \overline{x}\left({t}_{f}\right)={\overline{x} }_{f}$$
(26)

Now, define a single vector to represent state and co-state variables together as follows:

$$\overline{y}={\left[\begin{array}{cc}\overline{x}& \overline{p}\end{array}\right]}_{12 x 1}^{T}$$
(27)

and Eq.  (25a) becomes

$$\dot{\overline{y}}=A \overline{y}$$
(28)

Let the variables \(\overline{y}\left(t\right),\overline{x}\left(t\right),\overline{p}\left(t\right)\) be represented by \(\overline{Y}, \overline{X},\overline{P},\) respectively, in the transformed domain. Applying the DT concept for Eq. (28), we get

$$\left(\text{j+1}\right)\overline{Y}(j+1)=A\overline{Y}(j)$$
(29)

for \(j=0, 1,\dots ,n\) (the infinite series is restricted to ‘n’ terms). The value for ‘n’ depends on the problem sensitivity. Using the above recursive relation (cf. Equation (29)), we get

$$\overline{Y}(j)=\frac{1}{j!}{A}^{j}\left[\begin{array}{c}\overline{X}(0)\\ \overline{P}(0)\end{array}\right]$$
(30a)

where \({{[A}^{j}]}_{12 x 12}=A \times A\times A\dots \times A, j times\). It is represented as

$${{[A}^{j}]}_{12 x 12}={\left[\begin{array}{cc}{{[A}_{j1}]}_{6 x 6}& {{[A}_{j2}]}_{6 x 6}\\ {{[A}_{j3}]}_{6 x 6}& {{[A}_{j4}]}_{6 x 6}\end{array}\right]}$$
(30b)

Applying inverse transformation, we get

$$\overline{x }\left(t\right)= \sum_{j=0}^{n}{(t-{t}_{0})}^{j} \overline{X }(j)$$
(31)
$$\overline{p }\left(t\right)= \sum_{j=0}^{n}{(t-{t}_{0})}^{j} \overline{P }(j)$$
(32)

When \(={t}_{0}\), and on expansion of Eqs. (31) and (32), we have

$$\overline{x }\left({t}_{0}\right)=\overline{X }\left(0\right) \mathrm{and} \overline{p }\left({t}_{0}\right)=\overline{P }\left(0\right)$$
(33)

The state vector at the final time is given by,

$$\overline{x }\left({t}_{f}\right)= \sum_{j=0}^{n}{({t}_{f}-{t}_{0})}^{j} \overline{X }(j)$$
(34)
$$\overline{x }\left({t}_{f}\right)= \sum_{j=0}^{n}\frac{{({t}_{f}-{t}_{0})}^{j}}{j!}\left[\begin{array}{cc}{A}_{j1}& {A}_{j2}\end{array}\right] \left[\begin{array}{c}\overline{X }\left(0\right)\\ \overline{P }\left(0\right)\end{array}\right]$$
(35)
$$\overline{x }\left({t}_{f}\right)= \sum_{j=0}^{n}\frac{{({t}_{f}-{t}_{0})}^{j}}{j!}{A}_{j1}\overline{X }\left(0\right)+\sum_{j=0}^{n}\frac{{({t}_{f}-{t}_{0})}^{j}}{j!}{A}_{j2}\overline{P }\left(0\right)$$
(36)
$$\overline{x }\left({t}_{f}\right)= \overline{Q}+ R*\overline{p }\left({t}_{0}\right) (\mathrm{using Eq}. (33))$$
(37a)

where

$$\overline{Q}= \sum_{j=0}^{n}\frac{{({t}_{f}-{t}_{0})}^{j}}{j!}{A}_{j1}\overline{x }\left(0\right) \mathrm{and} R=\sum_{j=0}^{n}\frac{{({t}_{f}-{t}_{0})}^{j}}{j!}{A}_{j2}$$
(37b)

Rearranging Eq. (37a),

$$\overline{p }\left({t}_{0}\right)={R}^{-1} \left[\begin{array}{c}\overline{x }\left({t}_{f}\right)\end{array}-\overline{Q}\right]$$
(38)

Using Eq. (38), the initial co-state can be computed if the final state is known. The step size (\({t}_{f}-{t}_{0}\)) used in the determination of initial co-states is referred to as DT step size.

DT–DE Scheme—Algorithm

Combining differential evolution and differential transformation techniques, a novel computational scheme is presented. In the landing problem on hand, there are eight unknowns in all, namely flight time and the seven initial co-states. As earlier pointed out, the co-state \({p}_{m}\) need not be determined in the DT scheme and it can be assigned an arbitrary value. The remaining six co-states are determined using DT scheme as described in the previous section. For DT process, the final flight time must be a known parameter. But in the landing problem, as pointed out earlier, the flight time is an unknown parameter. In the proposed scheme, the unknown flight time is selected using differential evolution (DE) technique. The DE technique explores over a range of values to obtain the optimal flight time. With each randomly selected value of flight time from DE, the co-states are computed using DT. Using these co-states, the state equations are propagated to find the objective function (cf. Equation (21) of the optimization process.

The performance of DT process with step size as the whole flight time (chosen using DE) is found to result in large target deviations. So, the chosen flight time is split into several intervals resulting in discrete time instants (\({t}_{0}, {t}_{1}\dots \dots {t}_{f})\) and at each time instant DT is applied to determine the co-states at that instant. So, there are two step sizes in this scheme: (i) propagation step size (e.g., (\({t}_{1}-{t}_{0}) , {(t}_{2}-{t}_{1}),\) etc.), used for the numerical propagation of system dynamics and (ii) DT step size (initially (\({t}_{f}-{t}_{0})\), then reduces to (\({t}_{f}-{t}_{1}) ,{(t}_{f}-{t}_{2})\dots\) and so on), used for the determination of co-states at different time instants of numerical propagation. The multi-step DT process along with DE is named as DT–DE scheme.

The steps of DT–DE algorithm are the following:

I. By fixing ‘NP’ as the size of the population, a population matrix (NP × 2) each row of which consists of the unknown flight time and the objective function is constructed. The objective function is evaluated after propagating system dynamics. The steps involved in constructing initial population are given as follows:

1. Choose \({t}_{f}\) randomly from its bounds.

2. Compute the co-states at \({t}_{0}\) using the specified terminal states and \({(t}_{f }-{t}_{0})\) as the DT step size.

3. Compute the thrust accelerations at \({t}_{0}\) as in Eq. (9) or (10) or (13) or (18) (depending on the performance measure) using the determined co-states.

4. Propagate the state equations to next time step (\({t}_{1}\)) using DT/numerical integration.

5. Update the DT step size as \(t_{go} = (t_{f } {-}t_{1} )\). Compute the co-state at \({t}_{1}\) using \({t}_{go}\) and the states at \({t}_{f}\). During propagation, at different time instants (\({t}_{i}\)), \(t_{go} = (t_{f } {-}t_{i} )\).

6. Repeat steps 3 to 5 till \({t}_{f}\) is reached and evaluate the final objective function given by Eq. (21)

At the end of step (6), one row of the population is generated.

7. Repeat steps (1) to (6) for different randomly selected flight times till the population is built.

II. Find the minimum of the objective function values of the population matrix. If objective function < \(\epsilon\)( a small prefixed tolerance value), the solution is obtained.

III. Otherwise, update the population. In the update process, each row is subjected to three operations (mutation, crossover and selection) as mentioned in Sect. 3.1. For each trial parameter (flight time, \({t}_{f}\)), steps I-(2) to I-(6) are executed to evaluate the objective function.

IV. Steps (II) and (III) are repeated till convergence.

In DT–DE scheme, the major advantage is that the co-state equations need not be numerically integrated to find the control variables at each computational step. Furthermore, the number of unknowns reduces to one.

Guidelines for Bounds for Flight Time

For DT–DE scheme, the flight time is selected using differential evolution. The DE technique needs bounds for the unknown flight time. The bounds for the flight time are fixed by using the ideal rocket equation and the burn duration.

$$\Delta v=g*Isp*ln\frac{{m}_{0}}{{m}_{f}}$$
(39)
$${t}_{burn}={m}_{0}\frac{\left(1- \frac{1}{{\mathrm{e}}^{\left[\frac{\Delta v}{g*Isp}\right]}}\right)}{\dot{m}}$$
(40)

where \({m}_{0 }\mathrm{and} {m}_{f}\) are initial and final masses, respectively. For this computation, it is assumed that the thrust is continuous and constant throughout the descent. The constant mass flow rate is given by,

$$\dot{m}=\frac{T}{g*Isp}$$
(41)

In general, the thrust level (\(T\)), \(Isp\), and initial mass are the known quantities. To derive the guidelines, the orbital velocity is treated as the minimum velocity impulse the propulsion system needs to produce. The burn time required for the reduction in orbital velocity provides the minimum limiting value for the actual flight time. For example, if the lunar soft landing phase starts from perilune of 15 × 100 km orbit, then the orbital velocity to be reduced to zero is 1.692 km/s. For a propulsion system with \(Isp\) of 315 s and with thrust of 2200 N and a mass of 874.4 kg (mass in 100 × 100 km orbit is 880 kg), the burn time is 518 s. So, the lower bound for flight time is set as 518 s. The upper bound is set as (lower bound + 100 s). Table 1 provides the lower and upper bounds of time for different thrust levels. However, these guidelines are not applicable, for the performance measure of minimum control effort with unlimited variable thrust case which is practically improbable scenario.

Table 1 Bounds for flight time required for velocity braking
Full size table

Results and Discussion

For the case studies presented in this paper, the parking orbit size and shape correspond to 100 × 15 km lunar orbit. The braking maneuver starts from the perilune, i.e., when true anomaly is zero. The values of physical constants are: equatorial radius of moon (\({\mathrm{r}}_{\mathrm{t}}\)) = 1,738,000 m and gravitational constant of moon (\(\mu\)) = 4.902800476E12 m3/s2. The initial location is chosen on the equator (0 deg latitude and 0 deg longitude). The initial state at which the landing starts corresponds to the orbital elements given in Table 2. To demonstrate the performance of the DT–DE scheme, a target landing site is required. For this purpose, the minimum time formulation is solved using differential evolution scheme and the resulting landing site is used as the target site. To have confidence in the optimal solution of DT–DE scheme, all problems have been solved using DE scheme (Remesh et al., 2016) also for which all the initial co-states are the unknowns. In all simulations, the switching function \(S\) is considered to be negative if \(S\) < 1.0E-15.

Table 2 Input parameters
Full size table

Minimum Time Trajectory using Differential Evolution

To generate a target site for use in DT–DE algorithm, the minimum time problem is solved using DE scheme. As pointed out earlier, there are eight unknowns: seven co-states and the flight time for this scheme. Considering the conditions that the co-state of mass cannot be negative, the initial co-state of mass is arbitrarily fixed at + 3. For all other initial co-states, [-2, 2] is used as bounds. Because the final time is unknown, the objective function given in Eq. (21) is computed by terminating the numerical integration at touchdown. By this choice of termination, determination of one of the unknowns, flight time is eliminated. The threshold value for convergence is kept as 1.0E-02. This value ensures an accuracy of < 1 cm/s in velocity and < 1 mm in position. Table 3 presents the initial co-states obtained for the minimum time landing trajectory. The values of the ratio (\(\frac{{p}_{{v}_{z}}}{{p}_{i}})\) are given for comparison with the result of DT–DE algorithm. The optimal flight time and the related landing mass are given in Table 4. The landing site of the optimal trajectory is given in Table 5 and is used as the target site in the studies with DT_DE algorithm.

Table 3 Unknown initial co-states for minimum time trajectory using DE
Full size table
Table 4 Optimal minimum time trajectory
Full size table
Table 5 Landing site of the optimal minimum time trajectory
Full size table

Minimum time Trajectory Using DT–DE Scheme

Performance of DT Scheme

To assess the performance of the DT scheme, the optimal flight time obtained in the previous section is used as the flight time (cf. Table 4) with other input parameters remaining same as given in Table 2 and Table 5. The critical parameter in the DT scheme is the size of the time step used, referred to as DT step size. To demonstrate the criticality of the time step, first the whole flight time is used as the step size which means that determination of co-states is attempted in a single step. The co-states determined using single step are given in Table 6. To assess the accuracy of these initial co-states, the equations of motion of state (Eqs. (2a and b)) and co-states (Eqs. (8a–f) and Eq. (17)) are numerically integrated till the final flight time. The deviations in the position and velocity from the target site are found to be large. So, in order to reduce the deviations, a multi-step DT scheme is proposed and used. The deviations in the target state are given in Table 7 for different DT step sizes. It was noted that with the decrease in the DT step size, the deviations in the target state decrease. The error stabilizes after the DT step size of 0.5 s, and so, for all further studies a step size of 0.5 s is used.

Table 6 Determined initial co-states with single step using DT
Full size table
Table 7 Influence of DT step size on DT scheme
Full size table

Another parameter that influences the performances of DT is the number of terms to be considered in the series expansion. With few simulation trials, it was observed that when the number of term is \(\ge 15\), the deviations remain same (cf. Table 8). So, for further studies, the number of terms is fixed at 20.

Table 8 Influence of number of terms of series expansion (n) on DT scheme
Full size table

Minimum Time Trajectory Using Multi-step DT Scheme (DT–DE Scheme)

As discussed earlier, in the DT–DE scheme, the flight time is an unknown parameter. The unknown flight time is selected using DE and the multi-step DT scheme is employed to find the deviation at the selected final time. The objective function for the optimization process is the deviation in the position and velocity components of corresponding to the target site (cf. Equation (21)). The target site given in Table 5, as mentioned earlier, is used. The optimal flight time and the landing mass obtained using DT–DE scheme are given in Table 9. Note that the optimal trajectory with DE scheme is reproduced and the target site is achieved using the DT–DE scheme. The initial co-states determined using DT are given in Table 10. The values of initial co-states given in Table 6 and 10 are slightly different because of the small difference in flight time (544.0836 s against 544.06 s).

Table 9 Optimal trajectory using multi-step DT–DE scheme
Full size table
Table 10 Determined initial co-states using multi-step DT–DE scheme
Full size table

The profiles of altitude, velocity and thrust acceleration components are given in Fig. 2 (a–c) for both DE and multi-step DT–DE schemes. Also the differences between the altitudes and velocities of the two schemes are given in Fig. 2 (a and b). A perfect match of the profiles for the two schemes can be seen. The computational time for DT–DE scheme is very less compared to DE scheme (cf. Table 11). The computational time for DE scheme will be even larger than 170 s if wider bounds are used for the unknowns. All computations have been carried out in a desktop computer with Intel Core i5 (3570 CPU @3.4 GHz) processor and 4 GB RAM.

Fig. 2
figure 2

a Altitude profile comparison—minimum time problem. b Velocity profile comparison—minimum time problem. c Thrust acceleration components—minimum time

Full size image
Table 11 Comparison of computational time
Full size table

Minimum Control Effort Trajectory Using DE and DT–DE Schemes (with Thrust Limit)

For demonstration, the thrust limit is kept as 2200 N. Table 12 provides the optimal trajectory parameters. The final landing mass is close to the landing mass obtained in minimum time solution (cf. Table 4), i.e., total impulse required for velocity braking is same. The initial co-states obtained using both schemes are given in Table 13. Although the initial values are different as in the earlier case studies, the optimal trajectory parameters and the control parameters are same. To derive more confidence, the ratios are also provided in Table 13. Figure 3 depicts the thrust acceleration profiles.

Table 12 Optimal trajectory parameters—minimum control effort with thrust limit
Full size table
Table 13 Unknown initial co-states comparison—minimum control effort with thrust limit
Full size table
Fig. 3
figure 3

Thrust acceleration profile comparison—minimum control effort with thrust limit

Full size image

Minimum Fuel Trajectory using DE and DT–DE Schemes

The minimum fuel trajectory is generated using DE scheme and DT–DE scheme and is provided in Table 14. The trajectory corresponds to the input conditions provided in Table 2 and targets the site given in Table 5. As in other cases, the initial co-states obtained using the two schemes are given in Table 15. Clearly, there are several combinations of the initial co-states that lead to the same optimal solution. However, the optimal trajectory is uniquely generated by both the schemes. The profiles of thrust acceleration components are given in Fig. 4 for both DE and multi-step DT–DE scheme. A perfect match of the profiles from the two schemes can be seen.

Table 14 Optimal trajectory—minimum fuel
Full size table
Table 15 Unknown initial co-states—minimum fuel
Full size table
Fig. 4
figure 4

Thrust acceleration components—minimum fuel

Full size image

Comparison of Optimal Solution with Different Performance Measures

The optimal solution with DT–DE scheme as discussed for minimum time, minimum fuel and minimum control effort with thrust limit is summarized in Table 16. It is to be noted that results for all three cases are nearly same. These results are nearly the same because of the following reasons: (i) the target landing site of minimum time solution used as the target in all cases; (ii) variable thrust but limited to a maximum value; and (iii) time-free problem. For minimum time case, the thrust settles at maximum throughout the descent phase. For minimum fuel case, for a time-free problem the thrust settles to the maximum throughout the descent. For minimum control effort also, for a time-free problem, the thrust settles to maximum value in the limit thrust case. So in all cases the optimal solution is nearly same.

Table 16 Comparison optimal solutions
Full size table

Performance of Gradient-Based Method with DT

In this section, the efficiency of gradient-based scheme in selecting the single unknown parameter of flight time is explored. In this study, MATLAB function ‘fmincon’ is used to find the flight time and used in DT scheme. This scheme is named as DT-SQP scheme, and its performance is compared with DT–DE scheme. The performance measure chosen for this assessment is minimum control effort with variable unlimit thrust. For this case, the guidelines for getting the bounds for flight time are not applicable. Both DE and the function fmincon need a range of values (bounds) for the unknown, and additionally, fmincon needs an initial guess for the unknown parameter. For the flight time bounds [400 s—600 s], fmincon converges in less computational time compared to DE (cf. Table 17). In the absence of DT, fmincon using direct scheme takes about 50 s with close initial guess. So, the use of DT brings down the computational time for a direct scheme also. However, when the range is wider, fmincon converges to a local minimum with the initial guess as 400 s. Therefore, the DT–DE scheme which avoids non-convergence is preferred over DT-SQP.

Table 17 Comparison of computational time
Full size table

Summary of Merits and Demerits of Different Solution Schemes

The merits and demerits of different solution schemes are compared in Table 18. In DT–DE scheme, the major advantage is that the co-state equations need not be numerically integrated to find the control variables at each computational step. Furthermore, the number of unknowns reduces to one. In a conventional indirect approach without DT, the numbers of unknowns are eight and numbers of equations are 14 including the co-state equations. In direct scheme, the number of unknowns depends on the number of nodes selected.

Table 18 Comparison of solution schemes
Full size table

Conclusion

The challenge in determining the initial co-states is dealt through a new computational indirect scheme. The efficiency of multi-step differential transformation technique in achieving the target site precisely is demonstrated. With a step size of 0.5 s, the deviation in the target site is brought down to 35 cm in position and to 3.6 cm/s in touchdown velocity. The number of unknowns of the two-point boundary value problem is reduced to just one which removes the complexity in the solution process to a large extent. The differential evolution technique obtains the solution very quickly using the initial co-states determined by DT technique and the guidelines on the flight time. The optimal landing trajectory is generated quickly without losing the advantages of the indirect scheme. The computational time to generate the optimal solution using DT–DE scheme is about 35 to 40 s, whereas using DE scheme which uses bounds for initial co-states also, it is about 170 s. The computational time for DT–DE scheme is comparable with a gradient-based optimizer that uses the initial co-states determined by DT technique. Further, the use of DE technique along with DT technique avoids non-convergence and local convergence scenarios which occur when gradient-based optimizer is used. The robustness of the scheme is demonstrated through the performance of proposed DT–DE scheme for different performance measures. The ability of the proposed scheme to introduce coasting during descent is demonstrated.