Introduction

Laminates integrated with piezoelectric layers are known as ‘smart structures.’ Piezoelectric material layers are used to regulate the static and dynamic behavior of the structures through actuation and sensing and also used to control the vibration generated during operation which increases safety, usability and durability of structures [1]. Thus, the application of piezoelectric composite laminates in structural components has increased extensively in the field of civil engineering, automobile, aeronautics and medical fields. In engineering and medical fields, we use load cells, pressure sensors, accelerometers, gyroscopes and ultrasonic transducers in which piezoelectric beams or disks act as sensing and actuating mechanism. Piezoelectric beams are also used in small-scale energy harvesting devices, which convert vibrational energy into an electrical voltage or DC power with the help of an electronic circuit. Therefore, for proper functioning and designing of these components, it is very important to know the dynamic behavior of piezoelectric beams under various boundary conditions.

Bailey and Hubbard [2] employed distributed parameter control theory to design and analyze the active vibration damper for a thin cantilever beam. Using Euler–Bernoulli beam theory, Crawley and De Luis [3, 4] developed static and dynamic computational models for beams with highly distributed actuators and sensors which were either bonded on their top surface or embedded in between the elastic layers. Yang and Lee [5] presented an analytical model to obtain mode shapes and the fundamental frequencies of a stepped piezoelectric cantilever beam having surface-bonded piezoelectric layers. By developing the constituent equations for piezoelectric bimorph beam, Low and Guo [6] presented a dynamic model with hysteresis for three-layered piezoelectric bimorph beam. Sunar [7] documented the application of piezoelectric materials in the field of sensing and active control of flexible structures in his review article. Saravanos and Heyliger [8] and Gopinathan et al. [9] presented a detailed review of several theories and analytical model for the analysis of smart piezoelectric structures.

Kapuria et al. [10] developed a new efficient one-dimensional coupled model, on the basis of third-order zigzag approximation, for the dynamic analysis of simply supported piezoelectric composite beams. Further, Kapuria et al. [11] presented a new coupled consistent third-order theory (CTOT) to obtain an analytical solution for dynamic and static analysis of simply supported hybrid piezoelectric beams. Using the pseudospectral method, Kekana [12] presented the free vibration solution for composite beams mounted with piezopatch acting as sensors and actuators. Based on the Euler–Bernoulli beam theory and Rayleigh–Ritz approximation, Della and Shu [13] developed a micromechanics technique to obtain the free vibration solution for beams embedded with piezoelectric material actuators and sensors. Further, Della and Shu [14] extended this approach to develop a dynamic solution for beams with piezoelectric inclusions. Using the transfer matrix, Wang [15] obtained fundamental frequencies and corresponding mode shapes of a beam with surface-bonded pair of piezoelectric segments. Khdeir et al. [16] presented analytical solutions for the free vibration analysis of cross-ply piezolaminated beams embedded with piezoelectric actuators. The state-space approach is applied to obtain fundamental frequencies and corresponding mode shapes for different combinations of support conditions. Further, Khdeir and Aldraihem [17] presented a novel zigzag theory for free vibration analysis of sandwich beams with softcore. Muthalif and Nordin [18] developed an approach to find an optimum shape for cantilever-type energy harvester to improve its performance. Fu et al. [19] and Li et al. [20] presented free vibration analysis of functionally graded (FG) beams with piezoelectric sensors and actuators. Nilanjan Chattaraj and Ranjan Ganguli [21,22,23] presented Euler–Bernoulli-based 1D nonlinear analytical model to analyze the detailed electromechanical behavior of piezoelectric bimorph actuators at the high electric field. Most of the above works on piezoelectric beam are based on one-dimensional theories. Kapuria et al. [24] presented the exact 2D piezoelasticity solution for simply supported beams with damping under harmonic electromechanical loads. A review of the literature on the free vibration analysis of elastic and piezoelectric beams can be found in the recent review articles [25,26,27,28]. An extensive literature survey has revealed that analytical 2D piezoelasticity free vibration solution for arbitrary supported beams is not available in the literature [27].

Due to the coupled constitutive relation between elastic and electric field, the behavior of these types of hybrid beam structures is very complex. Hence, an efficient solution method is needful to predict the complex behavior of arbitrarily supported piezoelectric laminated beams which will also act as a benchmark for assessing other approximate or numerical method. Analytical techniques are preferred because of its simplicity and high accuracy. Moreover, the closed-form 2D piezoelasticity solution helps to understand the electromechanical behavior of hybrid beams and helps to make a suitable assumption for the kinematic and the kinetic field for 1D theories of the beam.

The EKM, proposed by Kerr [29, 30], is a very powerful and elegant analytical method for solving partial differential equations (PDEs). Recently, extended Kantorovich method becomes popular to analyze the dynamic and static behavior of structures. The detailed literature on extended Kantorovich method can be found in a recent review article presented by Wu et al. [31] and Singhatanadgid and Singhanart [32]. Recently, Kapuria and Kumari [33] presented an extended Kantorovich approach for the three-dimensional (3D) piezoelasticity solution of the piezoelectric plate under cylindrical bending and subjected to arbitrary support condition. Kumari et al. [34] also used this approach to obtain three-dimensional piezoelasticity solution for static analysis of piezoelectric laminated plates subjected to Levy-type supports. Further, Kumari and Behera [35] extended this approach to develop 3D free vibration solution for a rectangular composite plate under Levy-type support conditions. Recently, Kumari et al. [36,37,38] extended this approach to obtain an analytical solution for the in-plane functionally graded flat panels and rectangular plates. Recently, Moeenfard and Maleki [39] applied extended Kantorovich method to obtain the static response of microplates under electrostatic actuation.

In this paper, analytical 2D piezoelasticity free vibration solution is presented for the beams under different combinations of support conditions, using the multi-term multi-field extended Kantorovich method (MMEKM). Piezoelasticity-based extended Hamilton principle with the mixed variational field is applied to derive the governing equations in terms of stresses, displacements along with electric displacements and electric potential. Therefore, boundary conditions, both natural and essential, are satisfied in an exact manner at all points. By employing MMEKM, the first-order differential–algebraic system of 8n equations is obtained along the z-direction (thickness) for each layer and another set along the x-direction (in-plane). The final solution for these first-order ODEs is obtained in closed form. The numerical results are verified by comparing against the exact 2D solution, available in the literature, for the simply supported boundary condition case and with 2D finite element (FE) results for other support conditions. New benchmark results for free vibration are presented for piezoelectric beams subjected to arbitrary boundary conditions.

Mathematical Modeling

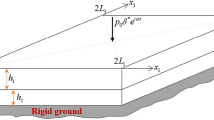
A hybrid cross–ply laminated beam having total thickness ‘h’ along the z-axis and length ‘a’ along the x-axis, as shown in Fig. 1, is considered for modeling. The hybrid laminated beam has ‘L’ number of perfectly bonded laminas which is generally orthotropic, and a few of them can be orthotropic piezoelectric/PFRC material which could be utilized as distributed sensors and actuators, and these piezoelectric/PFRC laminas are poled along the thickness direction z. The governing equations hold for each layer (kth layer) having thickness t(k), and its bottom surface is denoted by zk−1, where the interface of kth and (k + 1)th ply symbolized as the kth interface.

Fig. 1
figure 1

Geometry of a hybrid beam

Full size image

For the plane stress condition, electric field–potential and strain–displacement relations are as follows [10]:

$$\varepsilon_{x} = u_{,x} ;\quad \gamma_{zx} = w_{,x} + u_{,z} ;\quad \varepsilon_{z} = w_{,z} ;\quad E_{z} = - \phi_{,z} ;\quad E_{x} = - \phi_{,x}$$
(1)

where a subscript comma represents differentiation.

\(\varepsilon_{x} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varepsilon_{z} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma_{zx} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} E_{x}\) and \(E_{z}\) can be represented in terms of \(\sigma_{x}\), \(\sigma_{z}\), \(\tau_{xy}\), \(D_{x}\) and \(D_{z}\) as [33]:

$$\begin{aligned} \varepsilon_{x} = \bar{s}_{11} \sigma_{x} + \bar{s}_{13} \sigma_{z} + \bar{d}_{31} D_{z} \,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\varepsilon_{z} = \bar{s}_{13} \sigma_{x} + \bar{s}_{33} \sigma_{z} + \bar{d}_{33} D_{z} \,\,, \hfill \\ E_{z} = - {\kern 1pt} \,(\bar{d}_{31} \sigma_{x} + \bar{d}_{33} \sigma_{z} - \bar{\varepsilon }_{33} D_{z} )\,,\,\,\,\,\,\,\,\gamma_{zx} = \bar{s}_{55} \tau_{zx} + \bar{d}_{15} D_{x} \,,\,\,\,\,\,\,\,\,\,\,\,E_{x} = \bar{\varepsilon }_{11} D_{x} - \bar{d}_{15} \tau_{zx} \hfill \\ \end{aligned}$$
(2)

where \(\bar{s}_{ij} = {s}_{ij} - d_{3i} \bar{d}_{3j} ,\)\(\bar{d}_{3i} = d_{3i} /\varepsilon_{33} ,\)\(\bar{\varepsilon }_{ii} = 1/\varepsilon_{ii}\) for \(i,j\) = 1,3. The displacement elements \(u\) and \(w\) are taken along \(x\) and \(z\) axes, respectively. \(\sigma_{i}\) and \(\varepsilon_{i}\) denote the normal stress and normal strains components, respectively. \(\tau_{ij}\) and \(\gamma_{ij}\) denote shear stress and shear strains, and \(E_{i}\) denotes electric field. \(D_{i}\) and \(\phi\) denote the electric displacements and electric potential, and \(\rho\) is the density of the material.\(\bar{s}_{ij}\) represents the transformed elastic compliances, where \(\bar{d}_{ij}\) and \(\bar{\varepsilon }_{ii}\) represent piezoelectric strain constants and dielectric permittivity’s constants at constant stress field, respectively.

Piezoelasticity-based extended Hamilton principle in a mixed form, without any internal charge and body force source, for the bending case can be written as:

$$\begin{aligned} & \int\limits_{t} {\int\limits_{a} {\int\limits_{h} {[\delta u\,(} } } \sigma_{x,x} + \tau_{xz,z} - \rho \ddot{u}) + \delta w(\tau_{zx,x} + \sigma_{z,z} - \rho \ddot{w}){\kern 1pt} + \delta \sigma_{x} (\bar{s}_{11} \sigma_{x} + \bar{s}_{13} \sigma_{z} + \bar{d}_{31} D_{z} - u_{,x} ) \\ {\kern 1pt} & \quad + \delta \sigma_{z} (\bar{s}_{31} \sigma_{x} + \bar{s}_{33} \sigma_{z} + \bar{d}_{33} D_{z} - w_{,z} ) + \delta \tau_{zx} (\bar{s}_{55} \tau_{zx} + \bar{d}_{15} D_{x} - u_{,z} - w_{,x} ) \\ & \quad {\kern 1pt}+ \delta \phi (D_{x,x} +D_{z,z})+ \delta D_{x} (\bar{d}_{15} \tau_{zx} - \bar{\varepsilon }_{11} D_{x} - \phi_{,x} ) + \delta D_{z} (\bar{d}_{31} \sigma_{x} + \bar{d}_{33} \sigma_{z} - \bar{\varepsilon }_{33} D_{z} - \phi_{,z} )]{\text{d}}z\,{\text{d}}x\,{\text{d}}t = 0 \\ \end{aligned}$$
(3)

Here, \(t\) is the time variable. The bottom and top surfaces of the beam are shear traction free (\(\tau_{zx} = 0\)). Dimensionless in-plane coordinates considered are \(\xi = x/a\) along the \(x\)-direction, respectively. A thickness coordinate \(\zeta\) for a layer along the \(z\)-direction is defined which varies from 0 to 1. The boundary conditions considered at the top and bottom surfaces are at \(z = \pm h/2\), \(\tau_{zx} = 0,\,\,\,\,\sigma_{z} = 0,{\kern 1pt} \,{\text{for open circuit}}\,D_{z} = 0\,{\text{and for close circuit}}\,\phi = 0\). Along the x-axis, beam can have any type of support such as simply supported (S): \(w = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma_{x} = 0\); free (F): \(\tau_{zx} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma_{x} = 0\); clamped (C): \(w = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} u = 0\).

The Generalized EKM

These are eight primary field variables \(X = [u\,\,\,\,w\,\,\,\,\sigma_{x} \,\,\,\,\sigma_{z} \,\,\,\,\tau_{zx} \,\,\,\,\phi \,\,\,\,D_{x} \,\,\,\,D_{z} ]\) which are to be solved. Using multi-term EKM, the field variable for the kth lamina is expressed as:

$$X_{l} (\xi ,\zeta ) = \sum\limits_{i = 1}^{n} {f_{l}^{i} (\xi )g_{l}^{i} } (\zeta )\quad {\text{for}}\;l = 1,2, \ldots \ldots .8$$
(4)

where \(f_{l}^{i} (\xi )\) and \(g_{l}^{i} (\zeta )\) are the unknown functions of \(\xi\) and \(\zeta\), respectively. The functions \(g_{l}^{i} (\zeta )\) are dependent on the kth layer, while functions \(f_{l}^{i} (\xi )\) are valid for all layers. These unknown functions of \(\zeta\) and \(\xi\) are to be solved in two iterative steps by satisfying all homogenous support conditions.

First Iteration Step Along the Thickness Direction

Functions \(f_{l}^{i} (\xi )\), along \(\xi\)-direction, are considered for the variation \(\delta X_{l}\)

$$\delta X_{l} = \sum\limits_{i = 1}^{n} {f_{l}^{i} } (\xi )\;\delta g_{l}^{i} \quad l = 1,2, \ldots \ldots \ldots 8$$
(5)

Functions \(g_{l}^{i} (\zeta )\) are segregated into two column vectors \(\bar{G}\) and \(\hat{G}\), where \(\bar{G}\) contains these particular six variables which come in the support and interface conditions along \(\zeta\)-direction, and \(\hat{G}\) contains the remaining variables:

$$\begin{aligned} \bar{G} & = \left[ {g_{1}^{1} \ldots g_{1}^{n} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} g_{2}^{1} \ldots g_{2}^{n} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} g_{4}^{1} \ldots g_{4}^{n} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} g_{5}^{1} \ldots g_{5}^{n} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} g_{6}^{1} \ldots g_{6}^{n} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} g_{8}^{1} \ldots g_{8}^{n} } \right] \\ \hat{G} & = \left[ {g_{3}^{1} \ldots g_{3}^{n} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} g_{7}^{1} \ldots g_{7}^{n} } \right] \\ \end{aligned}$$

Substitute Eqs. (4) and (5) in Eq. (3) and perform the integrations along \(\xi\)-direction. Since variations for \(\delta g_{l}^{i}\) are arbitrary, the coefficients of \(\delta g_{l}^{i}\) must vanish (equal to zero) which generates the following set of 8n governing differential–algebraic equations for each layer:

$$M\bar{G}_{,\zeta } = \bar{A}\bar{G} + \hat{A}\hat{G}$$
(6)
$$K\hat{G} = \tilde{A}\bar{G}$$
(7)

where \(M_{6n \times 6n} ,{\kern 1pt} \,\,\bar{A}_{6n \times 6n} ,{\kern 1pt} \,\,\hat{A}_{6n \times 2n} ,{\kern 1pt} \,\,K_{2n \times 2n}\) and \(\tilde{A}_{2n \times 6n}\) are known matrices. Nonzero elements of the matrices are given below:

$$\begin{array}{*{20}c} {M_{{i_{1} j_{1} }} = M_{{i_{4} j_{4} }} = \left\langle {f_{5}^{i} f_{1}^{j} } \right\rangle_{a} ,} & {M_{{i_{2} j_{2} }} = M_{{i_{3} j_{3} }} = \left\langle {f_{4}^{i} f_{2}^{j} } \right\rangle_{a} } & {M_{{i_{5} j_{5} }} = M_{{i_{6} j_{6} }} = \left\langle {f_{8}^{i} f_{6}^{j} } \right\rangle_{a} ,} \\ {\bar{A}^{{}}_{{i_{1} j_{2} }} = \frac{ - t}{a}\left\langle {f_{5}^{i} f_{2,\xi }^{j} } \right\rangle_{a} ,} & {\bar{A}^{{}}_{{i_{1} j_{4} }} = t\,\bar{s}_{55} \left\langle {f_{5}^{i} f_{5}^{j} } \right\rangle_{a} ,} & {\hat{A}^{{}}_{{i_{1} j_{2} }} = t\,\bar{d}_{15} \left\langle {f_{5}^{i} f_{7}^{j} } \right\rangle_{a} ,} \\ {\hat{A}^{{}}_{{i_{2} j_{1} }} = t\,\bar{s}_{13} \left\langle {f_{4}^{i} f_{3}^{j} } \right\rangle_{a} ,} & {\bar{A}^{{}}_{{i_{2} j_{3} }} = t\,\bar{s}_{33} \left\langle {f_{4}^{i} f_{4}^{j} } \right\rangle_{a} ,} & {\bar{A}^{{}}_{{i_{2} j_{6} }} = t\,\bar{d}_{33} \left\langle {f_{4}^{i} f_{8}^{j} } \right\rangle_{a} ,} \\ {\bar{A}^{{}}_{{i_{3} j_{4} }} = \frac{ - t}{a}\left\langle {f_{2}^{i} f_{5,\xi }^{j} } \right\rangle_{a} ,} & {\hat{A}^{{}}_{{i_{4} j_{1} }} = \frac{ - t}{a}\left\langle {f_{1}^{i} f_{3,\xi }^{j} } \right\rangle_{a} ,} & {\bar{A}^{{}}_{{i_{5} j_{3} }} = t\,\bar{d}_{33} \left\langle {f_{8}^{i} f_{4}^{j} } \right\rangle_{a} ,} \\ {\hat{A}^{{}}_{{i_{5} j_{1} }} = t\,\bar{d}_{31} \left\langle {f_{8}^{i} f_{3}^{j} } \right\rangle_{a} ,} & {\bar{A}^{{}}_{{i_{5} j_{6} }} = - t\,\bar{\varepsilon }_{33} \left\langle {f_{8}^{i} f_{8}^{j} } \right\rangle_{a} ,} & {\hat{A}^{{}}_{{i_{6} j_{2} }} = \frac{ - t}{a}\left\langle {f_{6}^{i} f_{7,\xi }^{j} } \right\rangle_{a} ,} \\ {K_{{i_{1} j_{1} }}^{{}} = \bar{s}_{11} \left\langle {f_{3}^{i} f_{3}^{j} } \right\rangle_{a} ,} & {\tilde{A}^{{}}_{{i_{1} j_{1} }} = \frac{1}{a}\left\langle {f_{3}^{i} f_{1,\xi }^{j} } \right\rangle_{a} ,} & {\tilde{A}^{{}}_{{i_{1} j_{3} }} = - \,\bar{s}_{13} \left\langle {f_{3}^{i} f_{4}^{j} } \right\rangle_{a} ,} \\ {K_{{i_{2} j_{2} }}^{{}} = \bar{\varepsilon }_{11} \left\langle {f_{7}^{i} f_{7}^{j} } \right\rangle_{a} ,} & {\tilde{A}^{{}}_{{i_{1} j_{6} }} = - \,\bar{d}_{13} \left\langle {f_{3}^{i} f_{4}^{j} } \right\rangle_{a} ,} & {\tilde{A}^{{}}_{{i_{2} j_{5} }} = - \frac{1}{a}\left\langle {f_{7}^{i} f_{6,\xi }^{j} } \right\rangle_{a} ,} \\ {\tilde{A}^{{}}_{{i_{2} j_{4} }} = - \,\bar{d}_{15} \left\langle {f_{7}^{i} f_{5}^{j} } \right\rangle_{a} ,} & {\bar{A}^{{}}_{{i_{4} j_{1} }} = - \rho \omega^{2} t\left\langle {f_{1}^{i} f_{1}^{j} } \right\rangle_{a} ,} & {\bar{A}^{{}}_{{i_{3} j_{2} }} = - \rho \omega^{2} t\left\langle {f_{2}^{i} f_{2}^{j} } \right\rangle_{a} } \\ \end{array}$$

The algebraic Eq. (7) is solved to obtain \(\hat{G}\) and put into Eq. (6) which yields a set of 6n first-order homogeneous ODEs as:

$$\bar{G}_{,\zeta } = A\bar{G}$$
(8)

where \(A = M^{ - 1} [\bar{A} + \hat{A}K^{ - 1} \tilde{A}]\). Equation (8) represents a set of 6n homogeneous first-order ODEs with constant coefficient. The general solution of Eq. (8) is obtained by applying the approach given in Ref. [35], and the final solution is:

$$\bar{G}(\zeta ) = \sum\limits_{i = 1}^{6n} {F_{i} (\zeta )C_{i} }$$
(9)

where \(F_{i} (\zeta )\) are column vector which depend upon eigenvector and eigenvalue and \(C_{i}\) unknown constant. After applying top and bottom boundary conditions and interface conditions, Eq. (9) yields,

$$\sum\limits_{i = 1}^{6n} {K_{di} (\zeta )C_{i} } = 0$$
(10)

where the coefficient matrix \(K_{d}\) is a function of \(\omega\). For nontrivial solutions, its determinant should be zero and \(\omega\) can be obtained by root finding of the equation \(|\det (K_{d} )| = 0\) using bisection method. The un-damped natural frequencies \(\omega_{01} = \omega_{n}\) are determined by using the approach of Kapuria and Acharya [40].

Second Iteration Step Along the x-axis

Now \(g_{l}^{i} (\zeta )\) is known from the first step, and arbitrary variation is considered along the x-direction. Therefore, the variation for this case is written as:

$$\delta X_{l} = \sum\limits_{i = 1}^{n} {g_{l}^{i} } (\xi )\;\delta f_{l}^{i} \quad l = 1,2, \ldots \ldots ..8$$
(11)

Similarly, like the first step, \(f_{l}^{i} (\xi )\) are segregated into two column vectors \(\bar{F}\) and \(\hat{F}\), where \(\bar{F}\) carries these particular six variables which come in the support conditions at edges \(\xi\) = 0, 1 and \(\hat{F}\) contains the remaining two variables.

$$\begin{aligned} \bar{F} & = \left[ {f_{1}^{1} \ldots f_{1}^{n} \;f_{2}^{1} \ldots f_{2}^{n} \;f_{3}^{1} \ldots f_{3}^{n} \;f_{5}^{1} \ldots f_{5}^{n} \;f_{6}^{1} \ldots f_{6}^{n} \;f_{7}^{1} \ldots f_{7}^{n} } \right] \\ \hat{F} & = \left[ {f_{4}^{1} \ldots f_{4}^{n} \;f_{8}^{1} \ldots f_{8}^{n} } \right] \\ \end{aligned}$$

Substitute Eqs. (4) and (11) into Eq. (3) and perform integration along the z-axis on the known functions \(g_{l}^{i} (\zeta )\). Since variations for \(\delta f_{l}^{i}\) are arbitrary, the coefficients of \(\delta f_{l}^{i}\) must vanish (equal to zero) which generates the following set of 8n governing differential–algebraic equations:

$$\begin{aligned} N\bar{F}_{,\xi } = \bar{B}\bar{F} + \hat{B}\hat{F} \hfill \\ L\hat{F} = \tilde{B}\bar{F} \hfill \\ \end{aligned}$$
(12)

where \(N_{6n \times 6n} ,{\kern 1pt} \,\,\bar{B}_{6n \times 6n} ,{\kern 1pt} \,\,\hat{B}_{6n \times 2n} ,{\kern 1pt} \,\,L_{2n \times 2n}\) and \(\tilde{B}_{2n \times 6n}\) are known matrices. The nonzero terms of these matrices are given as:

$$\begin{array}{*{20}c} {N_{{i_{1} j_{1} }} = N_{{i_{3} j_{3} }} = \left\langle {g_{3}^{i} g_{1}^{j} } \right\rangle_{h} ,} & {N_{{i_{2} j_{2} }} = N_{{i_{4} j_{4} }} = \left\langle {g_{5}^{i} g_{2}^{j} } \right\rangle_{h} ,} & {N_{{i_{5} j_{5} }} = N_{{i_{6} j_{6} }} = \left\langle {g_{7}^{i} g_{6}^{j} } \right\rangle_{h} ,} \\ {\bar{B}^{{}}_{{i_{1} j_{3} }} = \,\left\langle {\bar{s}_{11} g_{3}^{i} g_{3}^{j} } \right\rangle_{h} ,} & {\hat{B}^{{}}_{{i_{1} j_{1} }} = \,\left\langle {\bar{s}_{13} g_{3}^{i} g_{4}^{j} } \right\rangle_{h} ,} & {\hat{B}^{{}}_{{i_{1} j_{2} }} = \,\left\langle {\bar{d}_{31} g_{3}^{i} g_{8}^{j} } \right\rangle_{h} ,} \\ {\bar{B}^{{}}_{{i_{2} j_{1} }} = \, - \frac{1}{t}\left\langle {g_{5}^{i} g_{1,\zeta }^{j} } \right\rangle_{h} ,} & {\bar{B}^{{}}_{{i_{2} j_{4} }} = \,\left\langle {\bar{s}_{55} g_{5}^{i} g_{5}^{j} } \right\rangle_{h} ,} & {\bar{B}^{{}}_{{i_{2} j_{6} }} = \,\left\langle {\bar{d}_{15} g_{5}^{i} g_{7}^{j} } \right\rangle_{h} ,} \\ {\bar{B}^{{}}_{{i_{3} j_{4} }} = \,\frac{1}{t}\left\langle {g_{5,\zeta }^{i} g_{1}^{j} } \right\rangle_{h} ,} & {\hat{B}^{{}}_{{i_{4} j_{1} }} = \, - \frac{1}{t}\left\langle {g_{2}^{i} g_{4,\zeta }^{j} } \right\rangle_{h} ,} & {\bar{B}^{{}}_{{i_{5} j_{6} }} = - \,\left\langle {\bar{\varepsilon }_{11} g_{5}^{i} g_{5}^{j} } \right\rangle_{h} ,} \\ {\bar{B}^{{}}_{{i_{5} j_{4} }} = \,\left\langle {\bar{d}_{15} g_{7}^{i} g_{5}^{j} } \right\rangle_{h} ,} & {\hat{B}^{{}}_{{i_{6} j_{2} }} = \, - \frac{1}{t}\left\langle {g_{1}^{i} g_{8,\zeta }^{j} } \right\rangle_{h} ,} & {L_{{i_{1} j_{1} }} = \left\langle {\bar{s}_{33} g_{4}^{i} g_{4}^{j} } \right\rangle_{h} ,} \\ {\tilde{B}^{{}}_{{i_{1} j_{3} }} = \, - \left\langle {\bar{s}_{13} g_{4}^{i} g_{3}^{j} } \right\rangle_{h} ,} & {\tilde{B}^{{}}_{{i_{1} j_{2} }} = \,\frac{1}{t}\left\langle {g_{4}^{i} g_{2,\zeta }^{j} } \right\rangle_{h} ,} & {L_{{i_{1} j_{2} }} = \left\langle {\bar{d}_{33} g_{8}^{i} g_{4}^{j} } \right\rangle_{h} ,} \\ {L_{{i_{2} j_{2} }} = - \left\langle {\bar{\varepsilon }_{33} g_{8}^{i} g_{8}^{j} } \right\rangle_{h} ,} & {L_{{i_{2} j_{1} }} = L_{{i_{1} j_{2} }} } & {\tilde{B}^{{}}_{{i_{2} j_{3} }} = \, - \left\langle {\bar{d}_{31} g_{8}^{i} g_{3}^{j} } \right\rangle_{h} ,} \\ {\tilde{B}^{{}}_{{i_{2} j_{5} }} = \,\frac{1}{t}\left\langle {g_{8}^{i} g_{6,\zeta }^{j} } \right\rangle_{h} ,} & {\bar{B}^{{}}_{{i_{3} j_{1} }} = - a\rho \omega^{2} \left\langle {g_{1}^{i} g_{1}^{j} } \right\rangle_{h} ,} & {\bar{B}^{{}}_{{i_{4} j_{2} }} = - a\rho \omega^{2} \left\langle {g_{2}^{i} g_{2}^{j} } \right\rangle_{h} ,} \\ \end{array}$$

The same procedure is followed as in the first step, and a set of 6n first-order homogeneous ODEs are obtained for \(f_{l}^{i}\), which are solved in a similar fashion as mentioned in the previous step.

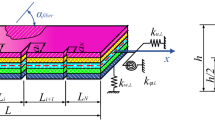
The flowchart of iterative procedure for multi-term extended Kantorovich method is shown in Fig. 2.

Fig. 2
figure 2

Flowchart of applied multi-term EKM approach

Full size image

Numerical Results

In this section, various numerical results are presented and discussed for a hybrid beam (a) consisting of a laminate substrate having a piezoelectric (PZT-5A) layer of thickness 0.1 h (a = 1) bonded at the top of the beam. The piezoelectric substrate is grounded at the bottom and top surfaces. The composite substrate of the beam has symmetric 4-ply laminate [0°/90°/90°/0°] of graphite–epoxy (Material 1) with layers of equal thickness 0.225 h, as shown in Fig. 3. Beam (b) is an elastic composite beam with symmetric 4-ply laminate [0°/90°/90°/0°] of Material 1 and each lamina of equal thickness 0.25 h, as shown in Fig. 3.

Fig. 3
figure 3

Configuration of piezoelectric beam and elastic beam

Full size image

The material properties like Young’s moduli (\(Y_{i}\)), shear moduli (\(G_{ij}\)), Poisson’s ratios (\(\nu_{ij}\)), constant strain electric permittivities (\(\eta_{ij}\)), and piezoelectric strain constants (\(d_{ij}\)) are taken from Ref. [10] as:

[Y1, Y2, Y3, G12, G23, G31, \(\nu_{12}\), \(\nu_{13}\), \(\nu_{23}\)]: Material 1: [(181, 10.3, 10.3, 7.17, 2.87, 7.17) GPa, 0.28, 0.28, 0.33], PZT-5A: [(61, 61, 53.2, 22.6, 21.1, 21.1) GPa, 0.35, 0.38, 0.38], [(\(\eta_{11}\), \(\eta_{22}\), \(\eta_{33}\)); (d31, d32, d33, d15, d24)] = [(1.53, 1.53, 1.5) × 10−8 F/m; (−171, −171, 374, 584, 584) × 10−12 m/V]. The densities of materials 1 and PZT-5A are 1578 and 7600 kg/m3, respectively. The natural frequency \(\omega_{n}\), the modal displacements, stresses and electrical state variables are non-dimensionalized as:

$$\bar{\omega } = \omega_{n} aS\sqrt {{{\rho_{0} } \mathord{\left/ {\vphantom {{\rho_{0} } {Y_{0} }}} \right. \kern-0pt} {Y_{0} }}} ;\quad (\bar{u},\,\,\bar{w}) = (u,\,\,w)/\hbox{max} (u,\,\,w)$$
$$(\bar{\sigma }_{x} ,\,\,\bar{\tau }_{zx} ) = (\sigma_{x} ,\,\,\tau_{zx} ){{Sh} \mathord{\left/ {\vphantom {{Sh} {Y_{0} \hbox{max} (u,\,\,w)}}} \right. \kern-0pt} {Y_{0} \hbox{max} (u,\,\,w)}};\quad \bar{\phi } = \phi \,d_{0} /\hbox{max} (u,\,\,w);\;\bar{D}_{x} = D_{x} {{Sh} \mathord{\left/ {\vphantom {{Sh} {d_{0} }}} \right. \kern-0pt} {d_{0} }}Y_{0} \hbox{max} (u,\,\,w)$$

where S (a/h) denotes span-to-thickness ratio. Max (u, w) denotes the largest value of (u, w) through the thickness for a particular mode. \(Y_{0}\) = 10.3 GPa, \(\rho_{0}\) = 1578 kg/m3 and \(d_{0} = d_{33}\) pm/V. The length of piezoelectric beam is assumed equal to unity for all cases, and thickness of beam is taken according to span-to-thickness ratio (S = a/h). For S = 5, 10, 20, the values of ‘h’ are 0.2, 0.1, 0.05, respectively.

Dimensionless natural frequencies for the first three bending modes of the hybrid beam are given in Table 1 for the simply supported boundary conditions. Presented results are compared with exact 2D results of Kapuria et al. [11]. It is noticed that the presented results match excellently with Ref. [11]. Since there is no 2D analytical free vibration solution for a beam with other combination of support conditions, present numerical results are compared with 2D FE (Abaqus) for other combination of boundary conditions.

Table 1 Lowest five natural frequencies of piezoelectric simply supported composite beam (a)
Full size table

The 2D FE solution is obtained using the Abaqus software. In the 2D FE analysis, eight-node brick elements of type CPS8RE for piezoelectric layers and CPS8R for elastic layers with reduced integration are used. Converged results are obtained with a mesh size of 50 (length) × 18 (thickness), as shown in Figs. 4 and 5.

Fig. 4
figure 4

Two-dimensional FE model with mesh discretization 50 (length) × 18 (thickness)

Full size image
Fig. 5
figure 5

Two-dimensional FE model of hybrid beam (S = 10) under S–S boundary conditions

Full size image

The lowest three natural frequencies are presented in Tables 2, 3, and 4 for different combinations of support conditions: clamped–simply supported (C–S), clamped–free (C–F) and clamped–clamped (C–C)) for three span-to-thickness ratios (S = 5, 10 and 20). The present results are compared with 2D FE solution. It is observed that the present EKM results match excellently with 2D FE results. It is observed that for the thick beam, S = 5, the difference between the present and 2D FE results is more than moderately thick to thin beams for all modes and all boundary conditions.

Table 2 Lowest three natural frequencies of the piezoelectric composite beam (a) under clamped–simply supported boundary conditions
Full size table
Table 3 Lowest three natural frequencies of the piezoelectric composite beam (a) under clamped–free boundary conditions
Full size table
Table 4 Lowest three natural frequencies of the piezoelectric composite beam (b) under clamped–clamped boundary conditions
Full size table

Boundary conditions have a significant effect on fundamental frequencies. One can easily observe from Tables 2, 3 and 4 that first fundamental frequency is the highest for C–C case for all three values of S (a/h) and lowest for C–F case. For higher modes, such as 2 and 3, the frequencies are near to S–S case for C–C and C–S conditions, whereas, for C–F boundary condition, the frequencies for all modes and all S (5, 10, 20) are the lowest. It is observed that as the thickness-to-span ratio (S) increases, the non-dimensionalized natural frequency parameters increase for all types of boundary conditions and the increment is more pronounced at higher modes as compared to the first mode which can also be observed from Fig. 6 where the non-dimensionalized frequency parameters are plotted against thickness-to-span ratio (S) numbers for S–S, C–C, C–S and C–F cases.

Fig. 6
figure 6

Effect of span-to-thickness ratio (S) on frequency parameter of beam (a) for different boundary conditions

Full size image

In Fig. 7, the longitudinal variation of field variables (\(\bar{u},\)\(\bar{w}\), \(\bar{\sigma }_{x}\), \(\bar{\tau }_{zx}\), \(\bar{D}_{x}\), \(\bar{\phi }\)) is presented for the first mode of beam (a) (S = 10) under S–S boundary conditions. Similarly, the longitudinal variation of field variables (\(\bar{u},\)\(\bar{w}\), \(\bar{\sigma }_{x}\), \(\bar{\tau }_{zx}\), \(\bar{D}_{x}\), \(\bar{\phi }\)) for the third mode of beam (a) (S = 10) under S–S boundary conditions is plotted in Fig. 8. Converged results of single-term EKM are presented for both cases which are in excellent agreement with 2D FE results for both mode shapes. Similarly, the longitudinal variation of displacements (\(\bar{u}\)), normal stress (\(\bar{\sigma }_{x}\)) and shear stress (\(\bar{\tau }_{zx}\)) is presented in Fig. 9 for piezoelectric beam (a) (S = 10) under C–F and C–C cases, respectively. For these cases also, present EKM results match excellently with the 2D FE results.

Fig. 7
figure 7

Longitudinal variation of displacements, stresses and electrical variables for the first modes of beam (a) under S–S boundary conditions

Full size image
Fig. 8
figure 8

Longitudinal variation of displacements, stresses and electrical variables for the third modes of beam (a) under S–S boundary conditions

Full size image
Fig. 9
figure 9

Longitudinal variation of displacements and stresses for the first modes of beam (a) under C–F and C–C boundary conditions

Full size image

The through-thickness distributions of in-plane displacement (\(\bar{u}\)) and stresses (\(\bar{\sigma }_{x}\) and \(\bar{\tau }_{zx}\)) are compared in Fig. 10 for beam (a) and beam (b) (S = 10) subjected to C–C and C–F boundary conditions. It is observed that the piezoelectric layer (PZT-5A), on the top of the elastic beam, significantly affects the behavior and natural frequency of the beam. The first-mode non-dimensionalized natural frequency parameter for beam (b) (elastic beam, S = 10) is \(\bar{\omega }_{CC}\) = 14.3008 and \(\bar{\omega }_{CF}\) = 3.62942 for C–C and C–F conditions, respectively. Then the inclusion of piezoelectric (PZT-5A) layer, of thickness 0.1h, on the top of beam decreases the natural frequency parameter to \(\bar{\omega }_{\text{CC}}\) = 11.2637 and \(\bar{\omega }_{\text{CF}}\) = 2.8586 for C–C and C–F conditions, respectively.

Fig. 10
figure 10

Effect of piezoelectric layer on through-thickness distributions of in-plane displacements and stresses and electrical variables for C–C and C–F boundary conditions

Full size image

Conclusion

A coupled 2D piezoelasticity solution is presented for the free vibration analysis of a piezoelectric beam. The fundamental frequencies and corresponding mode shapes are presented for the laminated piezoelectric beams under different combinations of support conditions. The present numerical results are compared with the 2D exact solution for simply supported support conditions and with 2D FE results for other combination of boundary conditions. It is noticed that the present EKM results match excellently with 2D FE results. It is also determined that as the span-to-thickness ratio increases, the non-dimensionalized natural frequency parameters increase and the increment is more pronounced for clamped–clamped boundary condition. It is observed that the piezoelectric layer (PZT-5A), on the top of the elastic beam, significantly affects the behavior and natural frequency of the beam. The presented results can be utilized for assessing 1D theories.