Fig. 1
figure 1

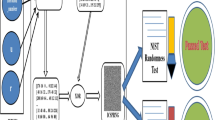
Block diagram of the proposed pseudo-random binary sequence (PRBS) generator using a B-exponential map. The user-defined inputs X, Z, B, K1, K2, K3, and \(\mu\) are fed to the B-exponential map (A) controlled by X. For a feedback purpose a secondary B-exponential map (D). The output of the closed-loop map is fed to a multiplying block K3. Another B-exponential map (Z) controlled by X, G, K3 is added to the output of a multiplier K3 producing the overall output (O = A x K3 + Z). A modulo operation is carried on O with modulo 1 operator to achieve the floored value producing a decimal point stream which can then be further compared. Based on the value of G, X and Z decimal places were compared as per the user-specified precision to produce the final randomly generated bit. If the initial value X is higher than Z then the random bit generated is 1 and 0 otherwise

Full size image
Fig. 2
figure 2

A plot of Lyapunov exponent for different values of B. The output chaotic nature is confirmed when the Lyapunov exponent is positive. For the proposed algorithm for any value of B up to 10,000 Lyapunov exponents was found to be positive (approx. 3.8) showing that the system is chaotic

Full size image
Fig. 3
figure 3

A graph showing the proportion of all proposed 40 tests suggested by the NIST SP800-22 test suite. It was found that almost all test results were above 95% success and hence we can conclude that the proposed chaotic system passes the bitstream randomization process as mentioned by NIST tests. The overall success rate was 98.45%

Full size image
Fig. 4
figure 4

The histogram of p-values for the linear complexity test of the NIST suite. It can be seen that out all experiments, the p-value is almost 50% of all times was found out to be higher than 0.6. Maximum frequency occurred at a p-value of 1 and 0.9 with a frequency of 14. The overall distribution of the p-value is peaking around 0.6 but has non-Gaussian distribution showing its chaotic behavior

Full size image

Introduction

Chaotic systems are dynamic systems whose output appears to be random but is actually generated using underlying patterns and highly sensitive initial conditions. An essential element in developing a chaotic system is a pseudo-random binary sequence generator. The randomness of a chaotic system can be improved, if the system parameters, on which the chaotic map depends, are also generated using a chaotic system.

Random number generation is one of the most important processes in the security domain. These deterministic and yet chaotic bits are useful for secured data transfer, e-commerce encrypted messaging, and even in some of the apps. The software that generates the random number is a system for creating deterministic chaotic numbers with high-quality random sequences. The chaos was first determined in semi-conductor super-lattices with the temperature being a variable that controlled the nature of chaos. Later on, this chaos was mathematically modeled and became the characteristic equation for chaotic oscillation models. Chaos is defined as a complete disorder or deterministic confusion. Many of the graphic designing and animation industries use this chaos to produce effects such as ocean waves and clouds in the background.

A B-exponential map has a dynamic behavior and is well-known for producing chaotic values for certain range of B parameter. The current technologies use a generator polynomial to produce a pseudo-random sequence of numbers. However, the B-exponential map can be very useful because of its chaotic hoping and still act as a deterministic random number generator. The name map is given to the B-exponential map because it has a function that produces value in the given range space and is determined by a nonlinear discrete iterative equation. Chaos is characterized by dynamic nature with deterministic nonlinearity. Chaotic maps are typically non-periodic and show high sensitivity towards the initial seed values. Before the B-exponential map, the most popular chaotic map used was the logistic map which has 1D iterative nature. The logistic map was proposed for population and is very useful in determining the twin effect of reproduction and starvation. The B-exponential map was derived from this logistic map.

Precision is a refinement in the measurement represented by the number of digits that are exact or accurate. Precision-controlled chaotic maps were typically used with space experimental circuits along with switch and skip chaotic maps. The finite precision chaotic map allows computational accuracy and control over a logistic map. The combination of precision control and B-exponential map gives rise to new horizons in the field of random number generators. In this manuscript, it was proposed a B-exponential map that generates pseudo-random numbers in a chaotic manner. The proposed system generates a large number of pseudo-random bit sequences and its randomness is tested using NIST SP800-22 tests.

Literature Review

Many literature reports used precision-controlled chaotic pseudo-random number generators and there were also a few reports with a B-exponential map. The following section covers a summary of the existing studies on pseudo-random number generation. Previous studies performed on pseudo-random number generators like the one done by Kocarev et al. [6] have summarized different chaos-based cryptography techniques. They found that, the term Random is linked to compressibility and has deterministic dynamical parameters that are dependent on system trajectory. Most of the random number generators try to use the shortest program. Also, there are entropy-based random generators that use probability distributions. According to Kocarev et al., the number of iterations for encryption is usually less than 32, but the number can also be as high as 65536 and the discrete probability distribution, positive exponents result in a higher entropy and large value of complexities. They also mention that although chaos is a significant property in encryption algorithms, it is not sufficient.

Pareek et al. [11] have built a system using external keys to generate discrete chaotic cryptography. They proposed a symmetric key block cipher algorithm that creates an initial condition due to the 128-bits long secret key. Their algorithm was secured but deterministic. They have produced different ciphertexts and found that the number of alphabets appearing in this ciphertext is uniformly distributed. They suggested this cryptography can be used over the Internet and other public networks. They have used only 3000 characters for their testing and it took almost 17 seconds for execution and their file size can be as big as 1.4Mb. The main drawback of their proposed system was is the attacker gets the information about symmetric block key cipher their entire chaotic map can be easily decoded and hence the system cannot be considered safe enough to use for internet banking. Also, their ciphering algorithm was using a common 128-bit secret key ’wh91-qa9g-k*xd/.’, which was static. Hence, it is necessary to develop an algorithm that does not use such static keys.

Shastry et al. [14] proposed a method to generate pseudo-random numbers using a generalized 1D B—exponential map. They found that the B-exponential map exhibits the most random behavior for all real values of B where B is greater than or equal to e\(^-4\). They then built an algorithm using B-exponential maps to generate pseudo-random numbers using a method that randomly hopped from different values of B. For testing, the system was compressed using the ENT Pseudo-random Number Sequence Test Program which gave an entropy of 1 per bit indicating the system is random. The sequences generated by their proposed method fell in the range of 25 to 75% for the chi-square test. The mean was seen to be 0.5 for one-bit sequences and 127.5 for 8-bit sequences. They also achieved a correlation coefficient of 0.000035 for a sequence length of 1 Gb. They also tested their system of the NIST and DIEHARD statistical test suites and showed that the sequences passed all tests with great results. But they discovered that the randomness of the system ended at B = 2.618.

Patidar et al. [12] used chaotic logistic maps to build a pseudo-random bit generator and they also performed statistical tests on it. They have used two chaotic standard maps to produce the random initial seeds. The outputs from both the chaotic maps were compared to produce a bit. They generated 2000 random binary sequences with 10\(^6\) bits each and tested them with DIEHARD and NIST suite for randomness checking with a passing rate in the range of 98 to 99.5%. Although their system shows great results when tested on the NIST tests, the use of two chaotic maps and their comparison makes the bit generation process more time-consuming.

Zhang et al. [17] broke a chaotic image encryption algorithm built using perceptron model. They also proposed a chaotic picture encryption technique that uses perceptron for security reasons to test the security of the method. They found that the complex encryption scheme was equivalent to stream cipher and could easily be broken using known plain text (ciphertext). They also showed how this technique was insensitive to plain images and images with no randomness. They tested 100 random sequences generated by the algorithm and found that only 4 to 5 tests were able to be passed by the sequences whereas the other tests were passed by 0 sequences making it a bad PRBS.

Mansingka et al. [8] have developed a fully digital jerk-based chaotic oscillator to achieve high throughputs of up to 8.77 Gbps for PRNGs. They have used Xilinx Virtex 4 FPGA to implement the PRNG and the maximum throughput was 15.59 Gbps for the chaotic oscillator. They could achieve logic utilization up to 1.73%. Although the throughput achieved are very high the Virtex 4 FPGA is costly hardware resulting in an overall high cost for manufacturing the device. Hence, a low-cost solution was required to be developed that are trying to solve using B-exponential chaotic map-based PRNG.

Franccois et al. [4] proposed a method to generate pseudo-random bits using three logistic maps that are chaotic in nature. In their proposed algorithm, at the end of each iteration of the chaotic maps, a 32-bit sequence is generated where the initial seed of the sequence is chosen randomly. Their generator algorithm also relied on the use of the IEEE 754-2008 floating-point representation. Their system had a keyspace of 10\(^173\) bits, and even with little similarities in the seed, it gave completely random outputs. Their system achieved a fast throughput with 44.112 Mbps. But their system is very sensitive to the initial seed making it susceptible to attack in cases where the initial key is guessed.

Chaudhary et al. [2] proposed an encryption method built using chaotic logistic map. They have used chaotic encryption techniques to generate the initial values and applied these seeds to a modified logistic map for making images more secure. Their system has similar complexity as two 1-Dimensional (1D) chaotic maps.

Pak et al. [9] used a combination of 1D chaotic maps to encrypt color images. They have used a basic chaotic system that performs encryption of a picture. They used linear-nonlinear-linear encryption for total shuffling in picture encryption. They proved 1D chaotic systems are better performers at large ranges. They have used 5 security keys u, x0, k, N0, lp to create a keyspace of 2\(^138\) to make their system less susceptible to brute force attacks. The initial values of u, k, and N0 were taken as 5.4321, 14, and 1000, respectively. They tested their method by attacking the encrypted image with a 64 X 64 data-cut and 3% salt and pepper noise. Although most of the attacked images were very close to the original images there was still some data loss.

Recently Krishnamoorthi et al. [7] have published a similar work where they have used a turbulence-padded chaotic map instead of a B-exponential chaotic map. Their method achieved chaotic behavior, 3.6 times more space with a 5% improvement in computing performance. They tested their proposed method with the NIST SP 800-22 statistical test suite. The disadvantage of the system was that although they had improved computational capacity, the system was taking a lot of time and their system was also periodic.

Saber et al. [13] have designed a PRNG using a Lemniscate Chaotic Map. In their system, fractal behavior is seen up to r = 1. They have also used a Spartan-6 FPGA board for hardware implementation. They achieved a 48% resource consumption reduction and a 34.6% power reduction. They achieved an entropy of 7.9980, a correlation coefficient of 0.0014, and the number of changing pixel rate was 99.661%. But the FPGA implementation is very expensive.

Akhshani et al. [1] proposed a pseudo-random number generator based on the quantum chaotic map. They used different values of the controlling parameter r to the quantum map. Their proposed method was able to achieve an entropy of 7.999995 with a \(\chi ^2\) value of 255.19 and a correlation coefficient of 0.0001. They tested their system on the NIST SP 800-22 test suite, DIEHARD test suite, ENT and TestU-01 to validate the randomness of the system.

Methodology

In the proposed system uses the basic idea of the B-exponential map by Shastry et al. [14] and modified their proposed method with positive feedback which is used due to which the chaos in the system should increases. The proposed system generates sequences of random bits (i.e., ones and zeros) based on the concept of positive feedback of the control system with a B-exponential map.

Figure 1 shows the block diagram of the proposed Pseudo-Random Binary Sequence (PRBS) generator built using a B-exponential map. Here X, Z, B, K1, K2, K3, and \(\mu\) are user-defined inputs that are fed into the B-exponential map (A) controlled by X. These inputs act as a seed point and control the output. A secondary B-exponential map (D) is used for feedback. This secondary map (D) is identical to the forward map (A). The closed-loop map’s output is fed into a multiplying block (K3). Another B-exponential map (Z), controlled by X, G, and K3, is added to the output of the multiplier (K3), yielding the overall output (O = A x K3 + Z). A modulo operation is performed on O with the modulo 1 operator to obtain the floored value, resulting in a decimal point stream that can then be compared. Here, the precision is controlled by defining the type of the input going to the modulo one operation. It can vary between uint8 to long 128 bit. The user-specified precision was used to compare the decimal places of G, X, and Z to produce the final randomly generated bit. If the initial value X is greater than Z, the random bit generated is 1, otherwise, it is 0. This is the modified precision-based approach different than the ones reported in the literature.

As shown in Fig 1, the B-exponential map (A) is the forward path and the B-exponential map (D) is the feedback path. The Positive sign at the mixer indicates the feedback is positive. Considering equation of B-exponential map as a transfer function of block 1 (A) is controlled by x, denoted by Eq. 1.

$$\begin{aligned} GL(B,x)=A=\frac{B-x \times B^{x}-(1-x)\times B^{1-x}}{B-\sqrt{B}} \end{aligned}$$
(1)

Equation 1 shows output 1 at the block diagram (Fig. 1). In the proposed system, positive feedback ensures that the current output is greater than the past and output will be generated without any input. Considering a random value of x at the start of the iteration, set K1, K2, and K3 as \(K1> 33.5, K2>37.9, K3> 35.7\) as mentioned by Franccois et al. [4] and B = 100 for the proposed system after seeing Lyapunov exponent value is positive (with B can be any value up to 10,000).

$$\begin{aligned} Transfer function = A/(1- A\times A) \end{aligned}$$
(2)

equation 2 shows output 2 at the block diagram (Fig. 1).

As shown in the block diagram the block K1 is considered in series with the oscillator part (i.e., transfer function of the oscillator) hence, output at point 2 represented by Eq. 3 is obtained.

$$\begin{aligned} Output 2 = \frac{K1\times A}{1- A\times A} \end{aligned}$$
(3)

This output is added with z (where z is initially a random value produced with a B-exponential map) to produce output at point 3 as O and denoted by Eq. 4.

$$\begin{aligned} Output 3 = \frac{K1\times A}{1- A\times A} + Z \end{aligned}$$
(4)

Equation 4 shows output 3 at the block diagram (Fig. 1).

The remainder is calculated by dividing O by number 1 (modulo 1 operation) which is shown by G and denoted by Eq. 5.

$$\begin{aligned} G = mod ((\frac{K1\times A}{1- A\times A} + Z),1) \end{aligned}$$
(5)

Equation 5 shows output 4 at the block diagram (Fig. 1).

Let,

$$\begin{aligned} Q1= & {} (\mu \times sin(Z))\times K2) \end{aligned}$$
(6)
$$\begin{aligned} Q2= & {} \mu \times Z \end{aligned}$$
(7)
$$\begin{aligned} Q3= & {} X \times K3 \end{aligned}$$
(8)

The value of x is used when the next value of A is generated using Eq. 9. Where \(0<\mu <=3.999\) is used to increase chaotic behaviour [17]. Hence,

$$\begin{aligned} X = mod ((Q1 + G),1) \end{aligned}$$
(9)

Extraction of values after decimal points is done for G and z. The value of x is found out using Eq. 10.

$$\begin{aligned} Z = mod ((Q2 + Q3 +G),1) \end{aligned}$$
(10)

Let, P = Rounded value of X

T = Rounded value of Z

These Values of P and T are compared.

If P > T then set bit as 1

Else set bit as 0

In this way, random bit sequence is generated as per user’s requirement.

B-Exponential Map

The B-exponential map is as explained in Eq. 11, which is the function of variables B and x. The x lies between 0 and 1 and B can be any value in positive real numbers. Due to the positive loop, the B has an iterative function i.e., Xn+1 = GL (B, Xn).

$$\begin{aligned} GL(B,x)=A=\frac{B-x \times B^{x}-(1-x)\times B^{1-x}}{B-\sqrt{B}} \end{aligned}$$
(11)

where, \(0<= x < 1\) and B belongs to R+

The fixed-point analysis [6] defines GL(B,0) = 0 and GL(B,0.5) = 1. Hence, B-exponential function has at least 5 critical points, due to symmetry around 0.5 and unimodal nature of GL(B,x).

Lyapunov Exponent

The Lyapunov exponent is given by Eq. 12.

$$\begin{aligned} \lambda (x)= \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=0}^{n-1}ln \left| f'{(x_{i})} \right| \end{aligned}$$
(12)

A Lyapunov exponent quantifies the rate at which extremely small trajectories in a non-static system separate from each other. A positive value of Lyapunov exponent denotes the potential chaotic behaviour of a system.

NIST Test Suite Details

There are 15 tests of the National Institution of Standard and Technology (NIST) Suite, that can be used to check the randomness of a binary sequence created by the Pseudo-Random Number Generator. These sequences being tested on this suite could be implemented at the hardware level or on software. These tests focus on the several types of non-randomness that can be found in a pseudo-random sequence. It’s one of the most widely used tests for determining how efficient random number generators are. The 15 tests in the NIST Statistical Test Suite (STS) tests and evaluate a given sequence’s attributes against those of a perfectly random sequence. This NIST STS has been used, for the Puesdo-random sequence generator for validating with files with 10\(^6\) bits and a bitstream/iteration of 200 files. Individual tests are considered passed if the p-value was between 0.01 and 0.99. The likelihood of a perfect random number generator delivering the same or a worse test result was represented by the p-value. The 15 tests were classified into the nonparameterized tests and the parameterized tests.

Results

Figure 2 shows a plot of the Lyapunov exponent for various values of B. By the definition of Lyapunov exponent, if the value of Lyapunov exponent is positive, then the chaotic nature of the system output can be confirmed. To verify this it has been varied the value of B from 5 to 10k in steps of 100. For all the values of B up to 10,000, we found that the Lyapunov exponents for the proposed algorithm were found to be positive (approx. 3.8), indicating that the system is chaotic.

Figure 3 shows the graph of the proportion of passing of the bitstreams for the NIST SP800-22 test suite’s proposed 40 tests. It has been found that for all 40 tests the test results values were greater than 95%. This allowed us to conclude that the proposed chaotic system passes the bitstream randomization process, as specified by the NIST test rules. The overall average success rate was 98.45%. The cases like DFT, Block frequency test, and Binary matrix rank test were successful with 99% accuracy. On the other hand, cumulative sum and the cumulative sum was around 97%.

Figure 4 shows the histogram of p-values for the NIST test suite’s linear-complexity test. As can be seen, the p-value is nearly 50% or more times greater than 0.6 with maximum frequency occurring at the p-value of 0.9 and 1, each with a frequency of 14. The overall distribution of the p-value is peaking at around 0.6. But, the overall distribution is non-Gaussian distribution, indicating the chaotic behavior of the proposed system.

Table 1 Result obtained with different precision values using NIST SP 800-22 test suite for the proposed pseudo-random sequence generator using B-exponential map
Full size table

Table 1 shows how the precision digit consideration can still pass the NIST tests even if digits are greater than 10. For only 8 or 9 precision digits 2 or 3 tests such as non-overlapping or serial test were slightly producing non-randomness and hence the proposed system should always run with precisions greater than 10 digitals to ensure sufficient randomness.

Table 2 Result of NIST SP800-22 test suite for proposed pseudo-random sequence generator using B-exponential map
Full size table

Table 2 shows the results obtained by performing various statistical tests using the NIST SP800-22 test parameters on our proposed B-exponential map-based pseudo-random sequence generator. The input sequence, which consisted of 0’s and 1’s, was provided in the form of an ASCII file. The PRBS generated by the proposed B-exponential map generator passed all 15 NIST tests successfully. The NIST test parameters examined the consistency of p-values in 200 streams of 10\(^6\) bits each and returned the p-value of the p values obtained for each test. The spectral Discrete Fourier Transform (DFT) achieved a p-value of 0.3 with a 99% passing rate i.e., 198 out of 200 tests were successful. In this test, the DFT of each sequence is calculated and the variance in peak height is measured. The overlapping template matching test achieved a 98% accuracy with 196 successful attempts out of 200 and a p-value of 0.19. Here, an M-bit window slides over the bit sequence searching for a specific pattern. If the pattern is found, it restarts the process, or else it moves slide by 1 bit. The mono bit frequency test achieved a p-value of 0.03 with a 98% proportion of passing i.e., 196 out of 200 tests were successful. This test determines and compares the sequence’s one-to-zero ratio to that of a random sequence. For the universal statistical test, which determines the level of compressibility of the sequence without any error formation, the p-value obtained was 0.38 with a 97% passing rate i.e., 194 out of 200 tests were successful. The system achieved a 0.15 p-value and 99% proportion of passing for the block frequency test, 198 out of 200 tests were successful here. This test finds out the equality of 1’s and 0’s in a sequence. For the binary matrix rank test, the system achieved a p-value of 0.67 with 198 successful tries out of 200 i.e., 99% accuracy. In this test, the reliability of a specific substring on the input is checked. For the linear complexity test, which determines the randomness of a sequence based on its length in terms of the linear-feedback shift registers, the system obtained a p-value of 0.98 with 196 successful attempts out of 200 i.e., 98% passing rate. The run test showed a p-value of 0.4 and 98% passing rate with 196 successful tries out of 200. This test checks for the variation from 0 to 1 and vice versa in the consecutive bits. The serial test gave a p-value of 0.28 with 196 out of 200 successful tries with a 98% passing rate. This test checks if specific N-bit patterns repeat in the sequence. The non-overlapping template matching test gave a 0.57 p-value with a 98 % passing rate i.e., 196 successful tries. This test is similar to overlapping template matching except that the window slides with 1-bit increments. The run test showed a p-value of 0.27 with a 98% passing proportion with 196 successful attempts out of 200. In this test, a comparison between the number of consecutive 1’s in a sequence and a random sequence is done. For the approximate entropy test, the system gave a 0.43 p-value with a 98% pass rate i.e., 196 successful tries. This test gives an estimate of entropy using the frequency of consecutive blocks having a length difference of one. The forward cumulative sums test gave a 97% passing proportion i.e., 194 out of 200 tests were successful with a p-value of 0.69 and the backward cumulative sums test gave a p-value of 0.59 with a 98 % passing rate. These tests check whether the sum of bits, in a forward and backward direction, in a sequence is as close to 0 as possible. The random excursion test was tried using different values of X ranging from − 4 to + 4. The average p-value obtained was 0.43 with a 98.62% passing proportion. This test checks the divergence of the number of trips to a certain state in one cycle of a sequence to that of a random sequence. The random excursion variant test was performed for different values of X from − 9 to + 9. The system achieved an average p-value of 0.64 with a passing rate of 98.67%. In this test, the 18 different tests are performed to determine the number of times a specific state repeats and then comparing this to a random sequence.

For the verification of the randomness,  it has been performed the DIEHARD test and ENT test and have passed all the tests with successful results. The ENT test resulted in entropy of 7.9999 bits per byte where the optimum value is achieved. The chi-square distribution came out to be 0.54 which randomly would exceed this value by 47% of the time. The arithmetic means value achieved with data bits is 0.49 and the Monte-Carlo value of pi came out to be 3.141725651. The correlation coefficient in our case was 0.00076.

For the DIEHARD statistical tool, the birthday spacing p-value came out to be 0.910523. The overlapping permutations were 0.284522. The rank of 31 X 31 matrices, 32 X 32 matrices, and 6 X 8 matrices were 0.3313, 0.4827, and 0.7415, respectively. Monkey test on 20-bit word, Overlapping-Pairs-Sparse-Occupancy (OPSO), Overlapping-Quadruples-Sparse-Occupancy (OQSO), and DNA were 0.019, 0.071, 0.723, and 0.298, respectively. The count of 1’s in a stream of a byte, and in a specific byte were 0.24 and 0.062, respectively. The parking lot test was successful with a p-value of 0.805. The minimum distance test was successful with 0.326. The random sphere test achieved a p-value of 0.901. The sequence test was successful with 0.812 and the overlapping sum test was successful with a p-value of 0.802. The run test Up and Down values were 0.81 and 0.80, respectively. The crab test for the number of wins and throws per game were 0.501 and 0.404, respectively. The overall bit generation speed was 21 Mbps.

Many methods have reported B-Exponential chaotic map for various purposes, such as, generation of mathematically random patterns (Nagraj et al. [14]), But none of the reported work combined methods of precision-based pseudo-random binary sequence generator. The main novelty of this work lies with the precision-based method in combination with the unique construction of the generator as shown in Fig. 1. Here a total of 3 B-exponential Random number generators are connected in series-parallel combination making the chaotic nature more complex and possible periodicity is further extended with such feedback and series approach. The precision digit matching with modulo 1 operation is implemented first time with any chaotic map pseudo-random number generator. The uniqueness of the proposed method also lies in how we are generating the final bit. Instead of directly outputting bits, the decision has been taken based on the comparison of two bits from two pseudo-random binary sequence generators. The matching mechanism doubles the periodicity. It is expected that this kind of approach helps future researchers in developing more complex maps using simple mathematical functions.

Table 3 Comparison between the proposed method and existing studies in the literature
Full size table

Table 3 shows a comparison between the proposed method and existing methods reported in the literature. It has been found that most of the methods could reach a very good entropy value Pan et al. [10] being the least at 7.98 and Shastry et al. [14] being the best at 8. The proposed method could reach 7.9999 which is one of the best among the reported literature. The correlation coefficient should ideally be 0 but most of the reported literature could reach up to 2 digits precision. Shastry et al. [14] had the best correlation coefficient of 0.000024 and Tang et al. [15] could just reach up to 7.99. The proposed method could reach up to 0.00076.

Although Shastry et al. [14] provided better results when using the B-exponential map, their system did not use precision tuning. Due to the absence of precision tuning in their algorithm, the complexity of their method is more. This complex nature in turn leads to a slower execution time. Whereas our system provides precision-based tuning thus reducing the complexity and hence, the random bits are generated at a faster speed. So while the method proposed by Shastry et al. [14] is good to use in systems that want to acquire high entropy and low correlation coefficient, our approach is more reliable for real-time applications that require a fast generation of bits. Although the result of the NIST SP800-22 test suite obtained by Shastry et al. [14] was 99%, which was 0.55% better than ours, our approach was able to outperform or perform equally well in most tests. But, it was only due to the Universal Statistical test and Cumulative sums (Forward) test that the results of our system reduced slightly.

Conclusion

The proposed precision-based PRBS generator using a B-exponential chaotic map can generate random bits. This map could pass all the NIST tests with an overall success rate of 98.45%. It has been checked the randomness of our bit generator’s various precisions ranging from 8 bits to 128 bits and found the average correlation coefficient to be 0.00076. Randomly generated bit sequences have a wide range of applications such as online transactions, image encryption, etc. Because of the CPU processing limitation, it could only reach up to 1.09 Mbps but, when implemented on a standalone FPGA hardware platform, even higher bit rates are possible. The produced random bit file can be used to create one-time passwords (OTPs) that can be used in a variety of security activities. Researchers can explore more applications of these PRBS generators in this online era.