Introduction

Power transmission system, being one of the most expanded overhead networks, is often subjected to various transient or permanent faults. Identification and hence earliest removal of the fault is indispensible to restore system stability. Relays and circuit breakers need to respond immediately on occurrence of fault, to restrict possible hazards, and more importantly, for the safety of the living world. Environmental effects and frequent environmental instability often cause minor to severe power system faults, often posing threats. Hence, prompt identification, as well as isolation of the faulty line, is most important.

Electrical faults disrupt the power flow in long overhead transmission line, affecting the electrical parameters like voltage, current, etc. These parameters are examined to extract key features for fault analysis. The proposed work attempts to apply multivariate statistical tool like principal component analysis (PCA) in power system fault classification [1,2,3,4]. PCA is very useful in reducing the dimension of a large data set, retaining the principal directions of variation in the descending order of importance [5, 6]. Hence, PCA has a vast application in power system analysis. Electrical power system is a large multivariate system with several parameters like voltage, current, frequency, power, etc. This multidimensionality of system increases computational burden. PCA helps in reducing the dimension of such a large data set, retaining the most vital fault information in the form of key features [7]. These features are processed directly by several mathematical analyses or with the help of other analysis tools like wavelet transform, fuzzy inference, artificial neural network (ANN), etc., to develop fault classifier. ANN, on the other hand, is also very useful in developing fault analysis algorithms [8,9,10,11,12]. ANN, as well as its major variant PNN, has immense application in power system research. PNN is a special structure of ANN which uses probability density function (PDF) to identify the highest probability of the test case with any one of the pattern classes using a neural network structure. Thus, PNN is immensely useful in fault classification, especially due to its well-established capability of accurate pattern recognition [13,14,15].

In this work, attempts have been made to develop two robust fault classifier models. One of the models is developed using the PCA features, simple numerical ratio analysis and nearest neighbor approach. Another model is designed to analyze the fault features obtained from a statistical method like PCA, with the help of supervised learning tool like PNN. A 150-km three-phase single-end-fed, single-circuit, overhead long transmission line has been modeled in Electromagnetic Transient Programming (EMTP) simulation software [16]. Among the various electrical power system faults, unsymmetrical type of faults includes single line to ground (SLG) faults: SLG-A, SLG-B and SLG-C; double line (DL) faults: DL-AB, DL-BC and DL-CA; and double line to ground (DLG) faults: DLG-A, DLG-B and DLG-C. Symmetrical faults include triple line fault (LLL). All these ten different types of faults mentioned above are conducted at different locations along the line. Fault resistances (Rf) are also varied. Sending-end three-phase line currents are used as working data here. Three intermediate equidistant locations have been selected as the training points, and the rest are used for testing.

The proposed work is distributed into two segments. The first part of the work is concerned with extracting key fault features from the working data using PCA. These features are further analyzed with a different method of ratio-based analysis [3] to obtain modified PCA fault indices, which are assigned as the fault signatures. The test data are processed similarly to obtain test point on the same fault signature plot. Nearest neighborhood analysis using least geometric distance is applied between the test point and the 11 classes to identify the fault pattern. The second part of the work is intended to design an algorithm for the fault classification using combined approaches of PCA and PNN [17]. PNN is used here with for its pattern recognition features. The fault features in terms of training PCA scores (PCS) are fed to a PNN-based classifier for training the network. The test data are fed to the trained model to find out the fault pattern. Finally, both the proposed schemes are validated using test data taken at different locations along the line with Rf other than training to authenticate the algorithm. Finally, a comparative analysis has been carried out between the two methods of classification.

Transmission Line Modeling

A 150-km 400 kV, 500 MVA three-phase, single-end-fed, overhead, long transmission line has been modeled combining 15 individual LCC blocks of 10 km each in EMTP. EMTP-ATP software has been used to simulate ten different types of faults in the said transmission line at 15 intermediate locations, each 10 km apart at the junction of two consecutive blocks, as is done in [3]. The corresponding three-phase voltage and current waveforms are collected. The faults are further modeled with variable Rf and power system noise to impose more practicality of modeling. The data so collected are further analyzed using PCA and PNN classifier algorithms in MATLAB. White Gaussian noise has been impregnated in the voltage and current signals using MATLAB. The noise level is adjusted to approximately 20 dB SNR [12]. This develops a more practical transmission line signal with close resemblance to practical signals. The single-line diagram of the simulated model is shown in Fig. 1a, and Fig. 1b shows the line model simulated in EMTP.

Fig. 1
figure 1

Simulated transmission line: (a) single-line diagram, (b) simulation model in EMTP

Full size image

Principal Component Analysis

Principal component analysis, as mentioned earlier, is a linear dimensionality reduction technique which broadly highlights the similarities and differences between a set of data and finds out the primary uncorrelated directions of variation of data, called principal components (PCs), in the chronological descending order of importance [1,2,3,4,5]. A graphical representation is shown in Fig. 2 which represents a two-dimensional data set which are distributed in the X–Y plane as pointed by the triangles. It is observed that the data are distributed along a principal direction as given by the U-axis and the second most important direction is given by V-axis, which is orthogonal to U. If the U–V axis system is now placed at the mean of the data, it gives a bidirectional representation. Now, on transforming the X–Y coordinate into U–V coordinate system, the data become de-correlated. These directions as given by U, V, etc., are called the principal components. For any given system, PCA finds the set of axes along the principal directions of variance.

Fig. 2
figure 2

Distributed data set and direction of variation of data

Full size image

Development of PCA Algorithm

PCA uses the mean and standard deviation to form covariance matrix of a multidirectional data set and, from there, finds out eigenvalues and eigenvectors of the covariance matrix. These eigenvalues along with eigenvalues are arranged in the decreasing order of importance to form Feature Vector. The eigenvector with the highest eigenvalues is assigned as the first Principal Component (PC). Further, a new set of data is constructed using the new feature vector and data adjust matrix. This new set of data is the Principal Component Scores (PCS) which is the most useful outcome of the PCA. It is needful to mention here that if the original data are of n dimensions, n eigenvectors are obtained on PCA. Depending on the significance of the eigenvalues, first m eigenvectors are normally retained, and the rest are discarded. The proposed method is illustrated here in the form of pseudocode in the following section.

PCA Algorithm

//A distributed data set is obtained with m variables and n observations: [X]n×m;

//Find the mean (µ) and variance (σ) of X;

//Form data adjust matrix XA by normalizing (autoscaling) X matrix; scaling XA to zero mean and unit variance:

$$\left[ {X_{\text{A}} } \right]_{n \times m } = \left[ {\left( {X_{i} {-}\mu_{i} } \right)/\sigma_{i} } \right];$$

//Calculate covariance matrix [A]m×m;

$$A = \frac{1}{{\left( {n - 1} \right)}}X^{\text{T}} X$$

Calculate Eigenvectors and Eigenvalues of the covariance matrix:

Method 1: Using singular value decomposition (SVD)

//A being symmetrical, it can be computed via the singular value decomposition (SVD):

$$A = E^{\text{T}} \lambda E$$

with ET E = E ET = I

where I is the identity matrix, λ = diag (λ1, λ 2, … λ m) is the eigenvalue matrix with elements in decreasing order of magnitude, and E = (e1, e2, … em) is the eigenvector matrix corresponding to eigenvalues λ.

Method 2: using direct analysis

Eigenvalues: By finding the roots of the characteristic equation (CE)

$${\text{Determinant}}\;{\text{of}}\;\left( {A{-}\lambda I} \right) = 0$$

where I = m × m identity matrix and this CE has m roots,

Eigenvector: If λ is an eigenvalue, there exists a vector e such that:

$$Ae = \lambda e$$

where e is called an eigenvector associated with the eigenvalue λ

Formation of Feature Vector:

Arrange eigenvectors in the descending order of eigenvalues

$$\begin{aligned} {\text{Feature}}\;{\text{Vector}} = \left( {{\text{eig}}v_{1} ,{\text{eig}}v_{2} , \ldots ,{\text{ eig}}v_{m} } \right) \hfill \\ {\text{i}} . {\text{e}} . ,\;{\text{Feature}}\;{\text{Vector}} = \left( {e_{1} , \, e_{2} , \ldots , \, e_{m} } \right) \hfill \\ \end{aligned}$$

The principal components (PCs) are constructed as a linear transformation of X by combining E as:

$$T = E^{\text{T}} X$$

where T = [t1, t2, …, tm]T and t1, t2, …, tm are the PCs of X in the descending order of variance.

//Row Feature Vector: Matrix with the eigenvectors in the columns transposed

//Row Data Adjust: Mean-adjusted data transposed

//Final data or principal component scores (PCS)

$${\text{PCS}} = {\text{Row}}\;{\text{Feature}}\;{\text{Vector}} \times {\text{Row}}\;{\text{Data}}\;{\text{Adjust}}$$

Artificial Neural Network

Artificial neural network (ANN) is one of the most important tools of the artificial intelligence (AI) family which bear tremendous capabilities of classification, and hence has a huge application in power system studies. ANN is intended for computation of a large number of data sets, especially for pattern recognition and prediction purpose. The ANN model is required to be trained extensively with prototype fault signatures, based on which it can predict the most similarity of the unknown type with one of the target classes, thus classifying fault.

Probabilistic Neural Network (PNN)

PNN is a special variant of ANN, extensively used for classification and pattern recognition. PNN is a feedforward neural network. PNN is as much as five orders of magnitude faster than backpropagation [18]. PNN converges to a Bayesian classifier with sufficient training data. This multilayered feedforward network has four layers: input layer, hidden layer, summation layer and output or decision layer. The probability density functions or PDFs are used to statistically estimate the activation function of the neurons based on the training pattern [14]. Figure 3 describes a prototype PNN model used here for the proposed work, and Fig. 4 shows an empirical two-class PNN Gaussian PDF distribution approximated by a Parzen window.

Fig. 3
figure 3

PNN classifier mode

Full size image
Fig. 4
figure 4

A typical two-class PNN Gaussian PDF approximated by a Parzen window

Full size image

The first layer computes an error vector by computing the distances between the input vector and the training vector. This error vector is basically a measure of closeness of the input vector and the training vector. The next layer adds up these errors for each of the classes of the inputs to produce its output as a vector of probabilities, obtained as a continuous probability density function (PDF). In PNN, a Gaussian PDF is approximated by a Parzen window PDF estimator for each class i as:

$$Fa \left( X \right) = 1/\left( {2\pi } \right)^{p/2} \sigma^{p} = \frac{1}{Na}\mathop \sum \limits_{i = 1}^{Na} \frac{1}{{\sqrt {2\pi } }}\exp \left( { - \left( {X - Yai} \right)^{t} \left( {X - Yai} \right)/ 2\sigma^{2} } \right) ^{ }$$

where Fa(X) is the value of class A at point X, i is the training vector number, p is the number of components in the training vector, σ is the smoothing variable, Na is the number of training vectors in class A, X is the test vector to be classified, Yai is the ith training vectors from class A and t is the vector response [18].

This is done to obtain the class-conditional densities or the ‘likelihoods’ of a class. These PDFs of each class are used to compute the class probability of input data for each of the classes. The class with the highest probability for the new input is then decided employing Bayes’ rule. This is done using a transfer function on the output of the second layer which identifies the maximum probability among all the class probabilities. In hidden layer, each weight has the value of a component of that vector. Neurons of this layer are grouped by the known classification of its associated training vector. Each of these neurons sums the weighted inputs from each of the input layer neurons. Next, it applies the nonlinear PDF to that sum to estimate the output Zci from this layer. The subscript c signifies the class, and i indicates the hidden layer neuron computing the class [18].

The specific number of neurons in each layer is decided by the number of samples representing a class or type in a training set. The number of input neurons is equal to the number of separable parameters required for describing the classifier objects. The hidden layer contains one neuron for each training class [13]. Each neuron of the summation layer receives all the previous layer outputs of each given class and is summed by a single summation layer neuron. It produces 1 for the class with the highest probability and 0 for others.

PNN Adopted for the Proposed Work

In the present work, the input layer takes the feature vector, i.e., principal component scores (PCS) as input. This layer receives modified feature inputs of PCS from the input layer. This layer is very important as it receives the examples or the training patterns as input. In this work, classification of ten different types of power transmission line electrical faults is executed. These include three single-line-to-ground faults (SLG-A, SLG-B and SLG-C), three double-line faults (DL-AB, DL-BC and DL-CA), three double-line-to-ground faults (DLG-AB, DLG-BC and DLG-CA) and finally the three-phase fault (LLL). Along with these ten fault classes, healthy or no-fault is added as another class for initial identification, thus making the total number of input classes as 11.

The input data set contains 1000 elements each for A, B and C phase fault features for the proposed PNN fault classifier model. The model consists of two hidden layers denoted as hidden layer and summation layer. The number of neurons in the hidden layer is 3 × 11, where 3 represents the three-phase input features (i.e., PCSA, PCSB and PCSC of the three phases) and 11 represent the number of classes. The activation function of this hidden layer is governed by the PDF of each of the fault classes. The Gaussian probability distribution function (PDF) of each of the 11 classes is calculated from the Parzen window PDF estimator [13, 15, 18]. The output layer contains a total of 11 decision-making nodes, each signifying one class. Hence, the size of the summation or output layer is 1 × 11. The features obtained from the PCA in terms of PCS of ten fault signals of each and the no-fault condition has been used for training. As each of the training set contains 1000 elements, the modeled PNN network is designed with features for fault conducted at three intermediate distances [12, 14].

Thus, the overall function of the proposed PNN network is summarized as below:

figure a

Preparation of Data

Half cycle post-fault, three-phase sending-end noise-contaminated line current is used here as working data, followed by normalization and scaling. Ten different types of faults with variable Rf are conducted at intermediate locations of a 150-km-long transmission line. The Rf is varied in discrete steps of 1 Ω, 5 Ω, 10 Ω, 20 Ω, 40 Ω, 60 Ω, 80 Ω, 100 Ω and 120 Ω for testing. The sampling frequency is 100 kHz, i.e., 2000 samples/cycle. Hence, the working data vector for each phase corresponds to 1000 samples.

Training Data Matrix

Three equidistant points at 30 km, 70 km and 110 km from the sending end are chosen to collect the training data. Hence, three-phase working data of each training location for any particular fault class are 1000 × 3 matrix. PCA algorithm compares each of the three-phase line current vectors to that of the same under healthy condition, thus finding out the extent of disturbance of each phase under fault. Only one Rf of 10 Ω is used here for the purpose of training for all the three locations. Hence, the phase-separated training current matrix becomes as:

$$\begin{aligned} {\text{Xa}}_{{{\text{TR}}\_i}} & = \left[ {\begin{array}{*{20}c} {{\text{Xa}}_{H} } & {{\text{Xa}}_{30\_i} } & {{\text{Xa}}_{70\_i} } & {{\text{Xa}}_{110\_i} } \\ \end{array} } \right]_{1000 \times 4} ; \\ {\text{Xb}}_{{{\text{TR}}\_i}} & = \left[ {\begin{array}{*{20}c} {{\text{Xb}}_{H} } & {{\text{Xb}}_{30\_i} } & {{\text{Xb}}_{70\_i} } & {{\text{Xb}}_{110\_i} } \\ \end{array} } \right]_{1000 \times 4} ; \\ {\text{Xc}}_{{{\text{TR}}\_i}} & = \left[ {\begin{array}{*{20}c} {{\text{Xc}}_{H} } & {{\text{Xc}}_{30\_i} } & {{\text{Xc}}_{70\_i} } & {{\text{Xc}}_{110\_i} } \\ \end{array} } \right]_{1000 \times 4} ; \\ \end{aligned}$$

where Xa30_i signifies the sending-end line A current vector at 30 km from sending end for Rf of 10 Ω for ith type of fault.

Test Data Matrix

The test data set is constructed in an identical way, corresponding to a fault conducted at any intermediate geometric location with Rf other than that used for training. Hence, the test data matrix, for any unknown location and unknown Rf, is formed as:

$$X_{\text{TEST}} = \left[ {\begin{array}{*{20}c} {{\text{Xa}}_{\text{TEST }} } & {{\text{Xb}}_{\text{TEST }} } & {{\text{Xc}}_{\text{TEST}} } \\ \end{array} } \right]_{1000 \times 3}$$

Data Matrix for PCA Algorithm

PCA is carried out on per phase basis, i.e., each phase current data are analyzed separately. Hence, the three phases are analyzed independently to find out PCA scores separately. The data are arranged accordingly to form working data matrices (P):

$$\begin{aligned} & {\text{Pa}}_{i} ={\text{PCA of }} \left[ {\begin{array}{*{20}l} {{\text{Xa}}_{H} } & {{\text{Xa}}_{30\_i } } & {{\text{Xa}}_{70\_i} } & {{\text{Xa}}_{110\_i} } & {{\text{Xa}}_{\text{TEST }} } \\ \end{array} } \right]_{1000 \times 5} ; \\ & {\text{Pb}}_{i} ={\text{PCA of }} \left[ {\begin{array}{*{20}l} {{\text{Xb}}_{H} } & {{\text{Xb}}_{30\_i } } & {{\text{Xb}}_{70\_i} } & {{\text{Xb}}_{110\_i} } & {{\text{Xb}}_{\text{TEST }} } \\ \end{array} } \right]_{1000 \times 5} ; \\ & {\text{Pc}}_{i} ={\text{PCA of }} \left[ {\begin{array}{*{20}l} {{\text{Xc}}_{H} } & {{\text{Xc}}_{30\_i } } & {{\text{Xc}}_{70\_i} } & {{\text{Xc}}_{110\_i} } & {{\text{Xc}}_{\text{TEST }} } \\ \end{array} } \right]_{1000 \times 5} ; \\ \end{aligned}$$

Hence, [PCSi] = [Pai Pbi Pai]1000×15;

Data Matrix for PNN Algorithm

The proposed PNN model is trained and tested using the principal component scores (PCS), which are the re-oriented form of the working data along the directions of highest importance and are obtained from the PCA analysis. These data are rearranged to form the training set for PNN model. The target class is the ten different fault prototypes and the healthy condition. Hence, the target class has been designed with numerical values from 1 to 11 in sequential order; each index defines each fault class separately. The relationship between the target vector and the target vector index takes the form:

Class name

Healthy

SLG-A

SLG-B

SLG-C

DL-AB

DL-BC

DL-CA

DLG-AB

DLG-BC

DLG-CA

LLL

Class no (i).

1

2

3

4

5

6

7

8

9

10

11

So in the case of healthy condition, i.e., for fault index 1, the [PCS] training matrix is written as:

$${\text{Ph}} = \left[ {\begin{array}{*{20}c} {{\text{Pa}}_{h} } & {{\text{Pb}}_{h} } & {{\text{Pc}}_{h} } \\ \end{array} } \right]_{1000 \times 3} ;$$

The target class corresponding to this healthy set is:

$${\text{Tg}} = \left[ {1\;0\;0\;0\;0\;0\;0\;0\;0\;0\;0} \right]_{1 \times 11} ;$$

The input training matrix to the PNN model for other faults is designed similarly. Training of the fault classes has been carried out with data corresponding to three locations, viz. 30 km, 70 km and 110 km, with fixed Rf of 10 Ω. The PCS obtained for one class of fault are arranged sequentially in the same order. For example, the training set for SLG-A, which is fault class 2, is formed using the three-phase PCS of three training locations as:

$$\begin{aligned} P_{2\_30} & = \left[ {\left( {{\text{Pa}}_{2\_30 } \;{\text{Pb}}_{2\_30 } \;{\text{Pc}}_{2\_30} } \right)} \right]_{1000 \times 3} ; \\ P_{2\_70} & = \left[ {\left( {{\text{Pa}}_{2\_70 } \;{\text{Pb}}_{2\_70 } \;{\text{Pc}}_{2\_70} } \right)} \right]_{1000 \times 3} ; \\ P_{2\_110} & = \left[ { \left( {{\text{Pa}}_{2\_110 } \;{\text{Pb}}_{2\_110 } \;{\text{Pc}}_{2\_110} } \right)} \right]_{1000 \times 3} ; \\ \end{aligned}$$

where 2 signifies fault class and 30, 70 or 110 define the three training locations. These matrices are fed sequentially to the PNN model for training. The target class vector corresponding to this SLG-A for each training set of this class remains constant as:

$${\text{Tg}} = \left[ {0\;1\;0\;0\;0\;0\;0\;0\;0\;0\;0} \right]_{1 \times 11} ;$$

which shows that the index of Tg will be 1 for the corresponding fault, and all other indices will remain 0. Thus, the generalized training matrix for ith fault class is:

$$\begin{aligned} P_{i\_30} & = \left[ {\left( {{\text{Pa}}_{i\_30 } \;{\text{Pb}}_{i\_30 } \;{\text{Pc}}_{i\_30} } \right)} \right]_{1000 \times 3} ; \\ P_{i\_70} & = \left[ {\left( {{\text{Pa}}_{i\_70 } \;{\text{Pb}}_{i\_70 } \;{\text{Pc}}_{i\_70} } \right)} \right]_{1000 \times 3} ; \\ P_{i\_110} & = \left[ { \left( {{\text{Pa}}_{i\_110 } \;{\text{Pb}}_{i\_110 } \;{\text{Pc}}_{i\_110} } \right)} \right]_{1000 \times 3} ; \\ \end{aligned}$$

where i is the target vector index mentioned above and i = 1,2, …, 11. Hence, the target vector corresponding to each such set is

$${\text{Tg}}\left[ i \right] = 1;$$
$${\text{Tg}}\left[ j \right] = 0;\quad {\text{ for}}\;j \ne \, i;\;{\text{where}}\;j = 1,2, \ldots ,11.$$

So the output from the PNN classifier will be a number among 1–11 showing fault class according to the target vector index.

Algorithm Development: Two Methods of Feature Extraction

For ground faults like SLG and DLG, the directly affected phase(s) is disturbed maximum and the other line(s) remains less disturbed, primarily due to the flow of zero sequence currents through the faulted ground line and the grounded neutral. This measure of disturbance of the un-faulted line of ground faults is higher than the unaffected line disturbance in the case of DL faults, but it is much lesser than the disturbances of the directly affected line(s) of ground faults. This is one of the key features for distinguishing between DL and DLG faults, and hence the classifier algorithm. The extent of disturbances measured using PCA are used to develop fault features in both methods of classification. In one scheme, the three-phase PCS are found which are actually the re-oriented working data along the directions of maximum variability, i.e., the principal components (PCs). These are fed to the proposed PNN structure to predict fault class. In the other method, three-phase principal component indices (PCI) are found for each fault class. These PCS are the measures of disturbance of any fault data from the healthy condition. The three PCs are arranged in descending order of importance. The Euclidian distance between the three-dimensional (3D) PCI of 11 training and test cases is arranged to form [P], thus forming PCI. These PCI denote the vector distance of each class from that of the healthy condition. These are further processed using a modified ratio analysis algorithm. The proposed classifier is tested with different faults conducted at varying geometric locations along the 150-km-long transmission line with Rf varying between 1 and 120 Ω. The proposed algorithm is represented schematically in the form of a flowchart as shown in Fig. 5.

Fig. 5
figure 5

Flowchart of the proposed two methods of fault classification

Full size image

Results and Discussion

Case Study and Analysis

The proposed work is done using noise-corrupted current signals to incorporate practicality of system. Figure 6 shows a noisy waveform line A current under healthy condition. The same is filtered, normalized and scaled to obtain final working signal. A DL-AC fault is considered here as a test case for analysis of the schemes. The three-phase line currents for faults carried out at the intermediate training locations are shown in Fig. 7. It is observed from Fig. 7 that A and C lines are disturbed most and B is least affected for DL-AC fault. The variation of sending-end line currents with the variation in fault location for line A and C is prominent. It is evident that as the fault point moves away from source, the magnitude of fault current reduces. Line B current does not produce any significant conclusion due to the non-involvement of line B and the power line noise. Other fault classes too show similar observations. Variation in Rf causes further complications to the signals.

Fig. 6
figure 6

Noise-contaminated sending-end line A current under healthy condition

Full size image
Fig. 7
figure 7

Sending-end three-phase line currents for healthy condition and DL-AC fault carried out at three training locations at 30 km, 70 km and 110 km distance from the sending end with Rf 10 Ω, waveforms are shown for a A line, b B line and c C line

Full size image

Figure 8 shows that decreasing Rf causes increased fault current nonlinearly. Fault signal at certain location with a particular Rf sometimes becomes largely identical with the same fault conducted at a different location, with a different Rf. Here lies the complexity of our work. The proposed algorithms are designed to classify faults with variation in both of these two factors. Figure 8 represents the current signals for variation of Rf for fixed location.

Fig. 8
figure 8

Sending-end three-phase line currents for healthy condition and DL-AC fault carried out at 30 km distance from sending end with variable fault resistances; waveforms are shown for a A line, b B line and c C line

Full size image

PCI Ratio (PCIM)-Based Classifier

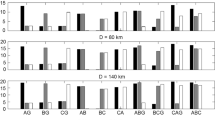
In the first phase of the experiment, the PCI are formed by the proposed PCA-based feature extractor algorithm. Figure 9 shows a graphical representation of the training set of three-phase PCI values for SLG, DL, DLG and LLL faults and healthy condition at three distinct training locations.

Fig. 9
figure 9

Three-phase principal component indices (PCI) for faults conducted at three training locations of 30 km, 70 km and 110 km for a SLG faults, b DL faults, c DLG faults, d LLL faults and e healthy condition

Full size image

It is observed in common for all that the three-phase PCI follow a particular pattern for each fault type. To further emphasize these features, the PCI are further processed and scaled with respect to the PCI column with any of the near minimum magnitude. Hence, the modified PC indices (PCIM) are formed as represented in Table 1 as well as represented in Fig. 10. This modified ratio analysis scheme emphasized the interrelationship of the three-phase PCI more 7effectively than [3].

Table 1 Three-phase modified principal component indices (PCIM) for all fault classes carried out at three training locations of 30 km, 70 km and 110 km with fault resistance of 10 Ω
Full size table
Fig. 10
figure 10

Three-phase modified PCI (PCIM) at three training locations of 30 km, 70 km and 110 km values for a SLG faults, b DL faults, c DLG faults and d LLL faults

Full size image

It is observed from Fig. 9b that for DL faults, the third and unaffected line are disturbed the least, even in comparison with the DLG faults as shown in Fig. 9c. The only disturbance caused in the unaffected line is due to the power system noise. Hence, for DL faults, classification is initially done by observing the three PCI directly. For example, for DL-AB fault, PCI-A and PCI-B have higher values, but PCI-C has values less than unity. It is further observed from Fig. 10b that the affected line PCIM, for the same DL faults, are much larger in comparison with the unaffected lines. These are even much larger compared to the closest DLG faults, which are shown in Fig. 10c. Hence, DL faults are detected by observing both PCI and PCIM simultaneously in connection with Figs. 9b and 10b.

Healthy condition is also identified directly in a similar way by observing the PCI values directly governed by Fig. 9e, where all three PCI are very low due to the presence of only power system noise.

Other fault classes like SLG, DLG and LLL are done using the PCIM. It is noted from Fig. 10a, c and d that three PCIM follow uniformity irrespective of the fault location. Similar trend is also observed for variation of Rf. This feature is investigated and is key for developing the classifier model. The three training PCIM for three training locations are shown in a clustered form in a three-dimensional plot in Fig. 11.

Fig. 11
figure 11

Three-dimensional cluster plot of the three-phase modified PCI (PCIM) values for SLG, DLG and LLL faults at three training locations

Full size image

It is observed from Fig. 11 that the three PCIM in each cluster are close to each other. Hence, the centroid of each cluster is found mathematically from the 3D fault signature. These centroids for the three classes are plotted in PCIM centroid map of Fig. 12 in the form of a bar diagram and in a three-dimensional plot in Fig. 13a. Figure 13a is treated as the fault signature map for the PCIM-based classifier. This is used to estimate the distance proximity of the test case and the three fault categories.

Fig. 12
figure 12

Fault signatures, formed as the centroid of three training location modified PCI (PCIM) values for SLG, DLG and LLL faults

Full size image
Fig. 13
figure 13

a Three-dimensional plot of the fault signatures for SLG, DLG and LLL faults. b Three-dimensional distance between the test fault PCIM and the fault signature PCIM

Full size image

The unknown fault is first tested for healthy and the DL fault classes from the combined analysis using three PCI and PCIM. If the fault class does not match with these two categories, the PCIM of the unknown fault are analyzed using fault signature map of Fig. 13a with the other fault classes. The minimum vector distance between the test data PCIM and each of the fault class centroids of Fig. 13a are computed. This is shown in Fig. 13b. It is observed that the vector distance between the test PCIM, shown as a triangle in Fig. 13b, and fault class PCIM is least for DLG-CA fault. Hence, for this test case, the classifier assigns the fault as DLG-CA.

Analysis of the PCS-PNN-Based Classifier

The PCS-PNN-based classifier uses the three PCS. The designed PNN network is trained using PCS of ten faults classes and healthy condition. The model is further trained using several PCS corresponding to faults conducted at three different locations at 30 km, 70 km and 110 km from the sending end with Rf as 10Ω. Testing of the algorithm is carried out using PCS of faults conducted at intermediate locations.

Classifier Results

Both the fault classifiers are tested with 12 noise-contaminated test data of each fault class. These faults are carried out at different geometric distances from the sending end along the 150-km line. Rf is also varied simultaneously. Both the algorithms produce same and 100% accurate result as shown in Tables 2, 3 and 4. Totally, 120 different test faults and 10 healthy condition data are used for testing the proposed algorithms. These test faults are carried out with different combinations of Rf and fault locations, other than those which are used for training the algorithms.

Table 2 Results of fault class prediction of both fault classifiers
Full size table
Table 3 Results of fault class prediction of both fault classifiers with varying fault location
Full size table
Table 4 Results of fault class prediction of both fault classifiers with varying fault resistance
Full size table

Comparative Analysis of Two Classifiers

It is found from Tables 2, 3 and 4 that both the classifiers are 100% accurate in classifying power system faults in overhead transmission lines within half cycle of the occurrence of fault. The PCIM-based classifier is modeled based on a single fault signature generated from fault data taken at three equidistant points. The PCA–PNN model is trained using all the three training location fault data sequentially. Rf is kept as 10 Ω in all the training cases. Rf and fault location are varied largely to validate the robustness of the system. Both the algorithms produce 100% correct results as seen from these tables.

Conclusion

The proposed work discusses the development and analysis of two power system fault classifier models for a 150-km-long single-end-fed overhead transmission line. The first method discusses about a modified principal component indices (PCIM) and ratio analysis-based fault classifier model, and the second scheme analyzes a combined approach of principal component analysis (PCA) and probabilistic neural network (PNN). Both the classifiers use sending-end three-phase currents as the working data. Fault data of three intermediate locations are fed to PCA model to extract essential features. The PCIM ratio-based classifier scheme uses the PCA features corresponding to these three locations to develop a single training fault signature. The PCA–PNN model uses these features directly to train the fault classifier structure. Both the schemes are 100% accurate in fault classification, even considering practical uncertainties like power system noise and variable fault resistance. Training time of the PNN-based scheme is marginally higher than the ratio-based classifier since PNN is required to be trained using a large number of data. The proposed classifiers are validated using diverse test data containing variable Rf, different locations and noise. The success rate in all the cases is found 100% using either of the methods.