Introduction

Aircrafts are subjected to severe structural and aerodynamics loads during their service life, which may result from repeated landing and take-off, manoeuvring, ground handling, bird strike and environmental degradation such as stress corrosion. Load carrying capacity. Hence, repair or reinforcement of damaged or weakened part of structures has become an important issue for restoring the structural efficiency and assuring the durability of aircraft in recent years [1]. One of the ways of repairing cracked structural component is providing an adhesive bonded composite patch. Composite patch provides higher structural efficiency and it increases the life of cracked component. Several studies have been conducted to investigate the mechanics of bonded composite patches used for repairing cracked metallic structures, especially to analyse the stress redistribution in the repaired structure and to compute the Stress Intensity Factor, which is an influential fracture parameter. Damage tolerant design is based on the information about the effect of cracks on the residual strength/remaining life of the structure or a component.

Stress Intensity Factor plays a crucial role for service life assessment of structures containing cracks. It is very difficult to calculate SIF for most of the practical problems. Using stress intensity factor handbooks [2], SIF can be calculated for simple problems. For complex crack geometry calculation of SIF is a difficult task. Hence a stable numerical method is required for the accurate computation of SIF for panels with complex crack geometry and loading. Finite element method is one of most widely used numerical technique for solving complex mechanics problems. The limitations of FEM are meshing should be done along the crack, remeshing has to be done as the crack propagates and it is difficult to track the entire propagating crack history. In order to avoid these difficulties associated with the Finite Element Method (FEM), XFEM was proposed by Belytschko’s group for fracture analysis of cracked structural components [3,4,5]. In XFEM, crack is modeled independent of the mesh and crack need not be conforming to the mesh and same initial mesh can be used throughout the crack growth. Ratwani [6] performed a finite element analysis to study the behaviour of composite patches where plane stress two dimensional elements were considered for modelling the cracked plate and the composite patch and also an elastic singular element was employed at the crack tip to calculate the stress intensity factor directly. Sun and Klug [7] presented a simple analytical method to analyse cracked aluminium plates repaired with composite patch based on Mindlin panel theory and comparison was made between SIF estimated from analytical method and ABAQUS. Rose [8] and Callinan et al. [9] used the finite element method to analyze performance of the bonded composite repair and they concluded that the presence of the patch highly reduces the stress intensity factor at the crack tip. Bouiadjra et al. [10] and Belhouari et al. [11] used a finite element method to analyze the behaviour of repaired cracks with bonded composite patches in mode I and mixed mode by computing the stress intensity factors at the crack tip and they investigated the effects of patch size and adhesive properties on the stress intensity factor variation. They carried out study for both single and double patch and they concluded double symmetric patches improves the fatigue life of the repaired structures significantly as compared to single patch. Madani et al. [12] examined the behaviour of centrally cracked aluminium panels repaired with single and double-sided graphite/epoxy composite patches subjected to uni-axial loading and it was concluded that double sided patch performed better as compared to single sided patch. Kaddouri et al. [13] and Ouinas et al. [14] examined the performance of the octagonal, circular and elliptical shapes of patches using numerical method and showed that the patch shape has a significant effect on the reduction in value of the stress intensity factor. Gu et al. [15] studied the mechanical behaviour of a single edge V-notch aluminium plate repaired with 1-ply and 4-ply composite patches through the finite element method and examined the effect of the adhesive epoxy film, patch material, thickness and ply orientation on stress intensity factor. Omidi et al. [16] performed the fracture analysis of centrally cracked aluminium plates repaired with single and double sided composite patches using XFEM framework in ABAQUS. They examined the effect of crack lengths, patch materials, orientation of plies, adhesive and patch thickness on SIF of the repaired plate and the repair performance and concluded that double sided composite are much effective as compared to single sided in reducing SIF. Shouyan et al. [17] implemented the XFEM program to investigate the effects of voids, inclusions and minor cracks on the path of major crack propagation. Omidi et al. [16] applied XFEM methodologies to examine the fracture behaviour of centrally cracked aluminium plates with single and double sided composite patches.

Based on the literature review, it is observed that very limited work has been carried out on repaired cracked panel using XFEM. Thus, the aim of this paper is to implement XFEM methodologies to investigate the performance of single boron/epoxy patch used for repairing cracked 2024-T3 aluminium panel. The influence of different shapes of patch such as rectangular, square, circular and elliptical on stress intensity factor is investigated. Stress Intensity Factor estimated using XFEM framework is incorporated in Paris crack growth model to predict the remaining life of repaired cracked panels. Residual strength of repaired cracked panels is determined by using the method proposed by authors earlier.

XFEM Formulation

In XFEM, the following approximation is used to compute the displacement for the point x located within the domain [18]

$${\mathbf{u}}^{h} ({\mathbf{x}}) = {\mathbf{u}}^{FE} + {\mathbf{u}}^{enr} = \sum\limits_{i = 1}^{n} {N_{i} ({\mathbf{x}}){\mathbf{u}}_{{\mathbf{i}}} + \sum\limits_{k = 1}^{m} {N_{k} ({\mathbf{x}})\psi ({\mathbf{x}}){\mathbf{a}}_{{\mathbf{k}}} } }$$
(1)

where ui is the vector of regular degrees of nodal freedom in the finite element method, n is the total number of nodes in finite element model, Ni shape function associated with node i, ak is the added set of degrees of freedom to the standard finite element model, m is the number of enriched nodes and ψ(x) is the discontinuous enrichment function defined for the set of nodes that the discontinuity has in its influence (support) domain. The enrichment function ψ(x) can be chosen by applying appropriate analytical solutions according to the type of discontinuity. The first termon the right hand side of Eq. (1) is the classical finite element approximation to determine the displacement field, while the second term is the enrichment approximation which takes into account the existence of any discontinuities. The second term utilises additional degrees of freedom to facilitate modelling the existence of any discontinuous field, such as a crack, without modelling it explicitly in the finite element mesh.

Displacement Field Formulation

When XFEM is applied to fracture analysis of cracked panels, the displacement field is taken as,

$${\mathbf{u}}^{h} ({\mathbf{x}}) = \sum\limits_{i = 1}^{n} {N_{i} ({\mathbf{x}}){\mathbf{u}}_{{\mathbf{i}}} + \sum\limits_{j \in J} {N_{j} ({\mathbf{x}})H({\mathbf{x}}){\mathbf{a}}_{{\mathbf{j}}} + \sum\limits_{{k \in K_{1} }} {N_{k} \left( {\sum\limits_{l = 1}^{4} {F_{l}^{1} ({\mathbf{x}}){\mathbf{b}}_{{{\mathbf{kl}}}}^{{\mathbf{1}}} } } \right) + \sum\limits_{{k \in K_{2} }} {N_{k} \left( {\sum\limits_{l = 1}^{4} {F_{l}^{2} ({\mathbf{x}}){\mathbf{b}}_{{{\mathbf{kl}}}}^{{\mathbf{2}}} } } \right)} } } }$$
(2)

where, H(x) is the heaviside enrichment function defined such that it equals 1 for all x above the crack and − 1 for all x below the crack as shown in the Fig. 1 and a j is the heaviside enriched node. J is the set of nodes, enriched with heaviside enrichment function, whose nodal shape function support contain crack but not crack tip.

Fig. 1
figure 1

Heaviside enrichment function definition

Full size image

Here k1 and k2 are the set of nodes, associated with crack tips 1 and 2, whose element contain crack tips respectively, \({\mathbf{b}}_{\text{kl}}^{1} ,{\mathbf{b}}_{\text{kl}}^{2}\), are vectors of additional degrees of nodal freedom for modelling crack faces and the two crack tips. The crack tip enrichment function with respect to crack tip coordinates is given by Fl(x) which is given as

$$F_{l} (r,\theta )_{l = 1}^{4} = \left[ {\sqrt r \sin \frac{\theta }{2},\sqrt r \cos \frac{\theta }{2},\sqrt r \sin \theta \sin \frac{\theta }{2},\sqrt r \sin \theta \cos \frac{\theta }{2}} \right]$$
(3)

where (r,θ) are crack tip polar coordinate system. The graphical representation of Eq. (3) is shown in Fig. 2. From Fig. 2, it is clear that F1 is discontinuous function and rest of the functions are continuous. Thus F1 models the discontinuity from the tip of the crack to the edge of the crack tip enriched element. Nodal enrichment strategy is shown in Fig. 3.

Fig. 2
figure 2

Crack tip enrichment functions Fl l = 1, 2, 3, 4. a F1, b F2, c F3, d F4

Full size image
Fig. 3
figure 3

Nodal enrichment strategy in XFEM

Full size image

Element Stiffness Matrix Formulation

A two dimensional cracked panel with four node bi-linear element has been considered for element stiffness formulation. Hence the generalized element stiffness matrix formulation in XFEM for four node bilinear element is given as follows. The displacement field within the four node bi-linear element in the context of XFEM is given as

$${\mathbf{u}}^{{\mathbf{h}}} {\mathbf{(x)}} = \left[ {\begin{array}{*{20}c} {{\mathbf{N}}^{{{\mathbf{fem}}}} } & {{\mathbf{N}}^{{\mathbf{a}}} } & {{\mathbf{N}}^{{\mathbf{b}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\mathbf{u}} \\ {\mathbf{a}} \\ {\mathbf{b}} \\ \end{array} } \right\}$$
(4)

where, Nfem finite element shape functions, Na and Nb shape functions modified due to enrichment with heaviside enrichment functions and crack tip enrichment function respectively

$${\mathbf{u}}^{{\mathbf{h}}} {\mathbf{(x)}} = \left\{ {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right\},\quad {\mathbf{N}}^{{{\mathbf{fem}}}} = \left[ {\begin{array}{*{20}c} {{\text{N}}_{1} } & 0 & {{\text{N}}_{2} } & 0 & {{\text{N}}_{3} } & 0 & {{\text{N}}_{4} } & 0 \\ 0 & {{\text{N}}_{1} } & 0 & {{\text{N}}_{2} } & 0 & {{\text{N}}_{3} } & 0 & {{\text{N}}_{4} } \\ \end{array} } \right]$$
(5)
$${\mathbf{N}}^{{\mathbf{a}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{N}}_{{\mathbf{1}}}^{{\mathbf{a}}} } & {{\mathbf{N}}_{{\mathbf{2}}}^{{\mathbf{a}}} \ldots {\mathbf{N}}_{{\mathbf{P}}}^{{\mathbf{a}}} } \\ \end{array} } \right] \, such \, that \, {\mathbf{N}}_{{\mathbf{P}}}^{{\mathbf{a}}} = \left[ {\begin{array}{*{20}c} {N_{P} H} & 0 \\ 0 & {N_{P} H} \\ \end{array} } \right]$$
(6)
$${\mathbf{N}}^{b} = \left[ {\begin{array}{*{20}c} {{\mathbf{N}}_{{\mathbf{1}}}^{b} } & {{\mathbf{N}}_{{\mathbf{2}}}^{b} \ldots {\mathbf{N}}_{Q}^{b} } \\ \end{array} } \right] , { }{\mathbf{N}}_{Q}^{b} = \left[ {\begin{array}{*{20}c} {N_{Q} F_{1} } & 0 & {N_{Q} F_{2} } & 0 & {N_{Q} F_{3} } & 0 & {N_{Q} F_{4} } & 0 \\ 0 & {N_{Q} F_{1} } & 0 & {N_{Q} F_{2} } & 0 & {N_{Q} F_{3} } & 0 & {N_{Q} F_{4} } \\ \end{array} } \right]$$
(7)
$${\mathbf{u}} = \left\{ {u_{1} ,v_{1} ,u_{2} ,v_{2} ,u_{3} ,v_{3} ,u_{4} ,v_{4} } \right\}^{T} {\text{ and }}{\mathbf{a }} = \left\{ {{\mathbf{a}}_{{\mathbf{1}}} {\mathbf{,a}}_{{\mathbf{2}}} {\mathbf{,}} \ldots {\mathbf{,a}}_{{\mathbf{p}}} } \right\}^{{\mathbf{T}}} {\text{ where }}{\mathbf{a}}_{{\mathbf{P}}} = \left\{ {a_{P} ,b_{P} } \right\}$$
(8)
$${\mathbf{b}} = \left\{ {{\mathbf{b}}_{{\mathbf{1}}} {\mathbf{,b}}_{{\mathbf{2}}} {\mathbf{,}} \ldots {\mathbf{,b}}_{{\mathbf{Q}}} } \right\}{\text{where }}{\mathbf{b}}_{{\mathbf{Q}}} = \left\{ {b_{Q}^{1} ,c_{Q}^{1} ,b_{Q}^{2} ,c_{Q}^{2} ,b_{Q}^{3} ,c_{Q}^{3} ,b_{Q}^{4} ,c_{Q}^{4} } \right\}$$
(9)

Here P, Q represents the number of nodes in bi-linear elements enriched with heaviside enrichment function and crack tip enrichment functions respectively such that, depending on the position of the crack, 1 ≤ P, Q ≤ 4. Now, the strain displacement relation is obtained as,

$${\mathbf{B}}_{{\mathbf{u}}} = \left[ {\begin{array}{*{20}c} {{\text{N}}_{{ 1 , {\text{x}}}} } & 0& {{\text{N}}_{{ 2 , {\text{x}}}} } & 0& {{\text{N}}_{{ 3 , {\text{x}}}} } & 0& {{\text{N}}_{{ 4 , {\text{x}}}} } & 0\\ 0& {{\text{N}}_{{ 1 , {\text{y}}}} } & 0& {{\text{N}}_{{ 2 , {\text{y}}}} } & 0& {{\text{N}}_{{ 3 , {\text{y}}}} } & 0& {{\text{N}}_{{ 4 , {\text{y}}}} } \\ {{\text{N}}_{{ 1 , {\text{y}}}} } & {{\text{N}}_{{ 1 , {\text{x}}}} } & {{\text{N}}_{{ 2 , {\text{y}}}} } & {{\text{N}}_{{ 2 , {\text{x}}}} } & {{\text{N}}_{{ 3 , {\text{y}}}} } & {{\text{N}}_{{ 3 , {\text{x}}}} } & {{\text{N}}_{{ 4 , {\text{y}}}} } & {{\text{N}}_{{ 4 , {\text{x}}}} } \\ \end{array} } \right]$$
(10)
$${\mathbf{B}}_{{\mathbf{a}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{B}}_{{\mathbf{1}}}^{{\mathbf{a}}} } & {{\mathbf{B}}_{{\mathbf{2}}}^{{\mathbf{a}}} \ldots {\mathbf{B}}_{{\mathbf{P}}}^{{\mathbf{a}}} } \\ \end{array} } \right]{\text{where }}{\mathbf{B}}_{{\mathbf{P}}}^{{\mathbf{a}}} = \left[ {\begin{array}{*{20}c} {\left( {N_{P} H} \right)_{,x} } & 0 \\ 0 & {\left( {N_{P} H} \right)_{,y} } \\ {\left( {N_{P} H} \right)_{,y} } & {\left( {N_{P} H} \right)_{,y} } \\ \end{array} } \right]$$
(11)
$${\mathbf{B}}_{{\mathbf{b}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{B}}_{{\mathbf{1}}}^{{\mathbf{b}}} } & {{\mathbf{B}}_{{\mathbf{2}}}^{{\mathbf{b}}} \ldots {\mathbf{B}}_{{\mathbf{Q}}}^{{\mathbf{b}}} } \\ \end{array} } \right]$$
(12)
$${\mathbf{B}}_{{\mathbf{Q}}}^{{\mathbf{b}}} = \left[ {\begin{array}{*{20}c} {\left( {N_{Q} F_{1} } \right)_{,x} } & 0 & {\left( {N_{Q} F_{1} } \right)_{,x} } & 0 & {\left( {N_{Q} F_{1} } \right)_{,x} } & 0 & {\left( {N_{Q} F_{1} } \right)_{,x} } & 0 \\ 0 & {\left( {N_{Q} F_{1} } \right)_{,x} } & 0 & {\left( {N_{Q} F_{1} } \right)_{,x} } & 0 & {\left( {N_{Q} F_{1} } \right)_{,x} } & 0 & {\left( {N_{Q} F_{1} } \right)_{,x} } \\ {\left( {N_{Q} F_{1} } \right)_{,x} } & {\left( {N_{Q} F_{1} } \right)_{,x} } & {\left( {N_{Q} F_{1} } \right)_{,x} } & {\left( {N_{Q} F_{1} } \right)_{,x} } & {\left( {N_{Q} F_{1} } \right)_{,x} } & {\left( {N_{Q} F_{1} } \right)_{,x} } & {\left( {N_{Q} F_{1} } \right)_{,x} } & {\left( {N_{Q} F_{1} } \right)_{,x} } \\ \end{array} } \right]$$
(13)

Therefore element stiffness matrix is given by

$${\mathbf{K}} = \int\limits_{\varOmega } {{\mathbf{B}}^{{\mathbf{T}}} {\mathbf{DB}}d\varOmega }$$
(14)
$${\mathbf{B}} = \left[ {\begin{array}{*{20}c} {{\mathbf{B}}_{{\mathbf{u}}} } & {{\mathbf{B}}_{{\mathbf{a}}} } & {{\mathbf{B}}_{{\mathbf{b}}} } \\ \end{array} } \right]$$
(15)

Substituting Eq. (15) in (14), element stiffness matrix in XFEM is obtained as

$${\mathbf{K}} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{{{\mathbf{uu}}}} } & {{\mathbf{K}}_{{{\mathbf{ua}}}} } & {{\mathbf{K}}_{{{\mathbf{ub}}}} } \\ {{\mathbf{K}}_{{{\mathbf{au}}}} } & {{\mathbf{K}}_{{{\mathbf{aa}}}} } & {{\mathbf{K}}_{{{\mathbf{ab}}}} } \\ {{\mathbf{K}}_{{{\mathbf{bu}}}} } & {{\mathbf{K}}_{{{\mathbf{ba}}}} } & {{\mathbf{K}}_{{{\mathbf{bb}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\int\limits_{{\varvec{\Omega}}} {{\mathbf{B}}_{{\mathbf{u}}}^{{\mathbf{T}}} {\mathbf{DB}}_{{\mathbf{u}}} {\mathbf{d\varOmega }}} } & {\int\limits_{{\varvec{\Omega}}} {{\mathbf{B}}_{{\mathbf{u}}}^{{\mathbf{T}}} {\mathbf{DB}}_{{\mathbf{a}}} {\mathbf{d\varOmega }}} } & {\int\limits_{{\varvec{\Omega}}} {{\mathbf{B}}_{{\mathbf{u}}}^{{\mathbf{T}}} {\mathbf{DB}}_{{\mathbf{b}}} {\mathbf{d\varOmega }}} } \\ {\int\limits_{{\varvec{\Omega}}} {{\mathbf{B}}_{{\mathbf{a}}}^{{\mathbf{T}}} {\mathbf{DB}}_{{\mathbf{u}}} {\mathbf{d\varOmega }}} } & {\int\limits_{{\varvec{\Omega}}} {{\mathbf{B}}_{{\mathbf{a}}}^{{\mathbf{T}}} {\mathbf{DB}}_{{\mathbf{a}}} {\mathbf{d\varOmega }}} } & {\int\limits_{{\varvec{\Omega}}} {{\mathbf{B}}_{{\mathbf{a}}}^{{\mathbf{T}}} {\mathbf{DB}}_{{\mathbf{b}}} {\mathbf{d\varOmega }}} } \\ {\int\limits_{{\varvec{\Omega}}} {{\mathbf{B}}_{{\mathbf{b}}}^{{\mathbf{T}}} {\mathbf{DB}}_{{\mathbf{u}}} {\mathbf{d\varOmega }}} } & {\int\limits_{{\varvec{\Omega}}} {{\mathbf{B}}_{{\mathbf{b}}}^{{\mathbf{T}}} {\mathbf{DB}}_{{\mathbf{a}}} {\mathbf{d\varOmega }}} } & {\int\limits_{{\varvec{\Omega}}} {{\mathbf{B}}_{{\mathbf{b}}}^{{\mathbf{T}}} {\mathbf{DB}}_{{\mathbf{b}}} {\mathbf{d\varOmega }}} } \\ \end{array} } \right]$$
(16)

The material matrix D under plane stress and plane strain conditions are given in Eqs. (17) and (18) respectively

$${\mathbf{D}} = \frac{E}{{\left( {1 - \nu^{2} } \right)}}\left[ {\begin{array}{*{20}c} 1 & \nu & 0 \\ {\nu (} & 1 & 0 \\ 0 & 0 & {\frac{1 - \nu }{2}} \\ \end{array} } \right]$$
(17)
$${\mathbf{D}} = \frac{E}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left[ {\begin{array}{*{20}c} {1 - \nu } & \nu & 0 \\ \nu & {1 - \nu } & 0 \\ 0 & 0 & {\frac{1 - 2\nu }{2}} \\ \end{array} } \right]$$
(18)

Computation of Stress Intensity Factor

For structures having complex geometry, the evaluation of stress intensity factor is very difficult. Accurate estimation of SIF is required for proper prediction of the crack growth and remaining life. In this work, the domain form of interaction integral which is available in finite element software ABAQUS has been used to evaluate SIF for repaired cracked panels and which is given as,

$${\text{I}}^{ ( 1 , 2 )} = \int\limits_{\text{A}} {\left( {\upsigma_{\text{ij}}^{ ( 1 )} \frac{{\partial {\text{u}}_{\text{i}}^{ ( 2 )} }}{{\partial {\text{x}}_{ 1} }} +\upsigma_{\text{ij}}^{ ( 2 )} \frac{{\partial {\text{u}}_{\text{i}}^{ ( 1 )} }}{{\partial {\text{x}}_{ 1} }} - {\text{W}}^{ ( 1 , 2 )}\updelta_{\text{ij}} } \right)\frac{{\partial {\text{q}}}}{{\partial {\text{x}}_{\text{j}} }}{\text{dA}}}$$
(19)

where superscript (1) represents the equilibrium state corresponding to the XFEM analysis and superscript (2) represents the auxiliary equilibrium state corresponding to Westergaard’s stress analysis. W(1,2) is the interaction strain energy density given as,

$$W^{{\left( {1,2} \right)}} = \sigma_{ij}^{\left( 1 \right)} \varepsilon_{ij}^{\left( 2 \right)} = \sigma_{ij}^{\left( 2 \right)} \varepsilon_{ij}^{\left( 1 \right)}$$
(20)

For the numerical evaluation of the above integral, the domain A is set from the collection of elements about the crack tip. We first determine the characteristic length of an element touched by the crack tip and designate this quantity as hlocal. For two-dimensional analysis, this quantity is calculated as the square root of the element area. The domain A is then set to be all elements which have a node within a ball of radius rd about the crack tip as shown in Fig. 4. The q function is taken to have a value of unity for all nodes within the ball of radius rd and zero on the outer contour. The function is then easily interpolated within the elements using the nodal shape functions.

Fig. 4
figure 4

Domain for the computation of interaction integral

Full size image

Once the domain form of interaction integral is computed, computation of mixed mode stress intensity factor is carried out using Eqs. (21) and (22). The mode I stress intensity factor is obtained using Eq. (21) and similarly for mode II stress intensity factor is obtained using Eq. (22)

$$K_{I}^{(1)} = \frac{{I^{(1,2)} }}{2\alpha }{\text{ With K}}_{\text{I}}^{\text{aux}} = 1{\text{ and K}}_{\text{II}}^{\text{aux}} = 0$$
(21)
$$K^{(2)}_{II} = \frac{{I^{(1,2)} }}{2\alpha }{\text{ With K}}_{\text{I}}^{\text{aux}} = 0{\text{ and K}}_{\text{II}}^{\text{aux}} = 1$$
(22)

where, α = 1/E for plane stress and α = (1 − ν2)/E for plane strain with E and ν are modulus of elasticity and Poisson’s ratio respectively evaluated at the crack tip.

Remaining Life Prediction of Cracked Panels

Analysis of fatigue crack growth and remaining life prediction involves obtaining several data in relation to the loading condition, type of material and crack geometry. A suitable crack growth law is given below,

$$\frac{da}{dN} = f(\Delta K,R, \ldots )$$
(23)

where, da is increment in crack length, dN is number of fatigue cycles, ΔK = Kmax − Kmin. Kmax is stress intensity factor evaluated for cracked component at max stress (\(\sigma_{\hbox{max} }\)) and similarly Kmin is stress intensity factor evaluated for cracked component at min stress (\(\sigma_{\hbox{min} }\)).

$${\text{R}}\;{\text{is}}\;{\text{the}}\;{\text{stress}}\;{\text{ratio}} = \frac{{\sigma_{\hbox{min} } }}{{\sigma_{\hbox{max} } }}$$

The number of loading cycles required to extend the crack from an initial length a0 to the final critical crack length af is given by,

$${\text{N}} = \int\limits_{{{\text{a}}_{0} }}^{{{\text{a}}_{\text{f}} }} {\frac{\text{da}}{{{\text{f}}(\Delta {\text{K}},{\text{R}}, \ldots )}}}$$
(24)

Many crack growth model are available to predict the fatigue crack growth and remaining life. In the present study, Paris crack growth model is used to estimate the remaining life of cracked panels. Paris crack growth model is given as follows:

$$\frac{da}{dN} = C(\Delta K)^{m}$$
(25)

where, C and m are Paris crack growth constants which are obtained experimentally.

Residual Strength Estimation

Popularly, there are two methods to estimate the residual strength of structural components. The methods include (i) Plastic collapse condition and (ii) fracture toughness criterion. Both the methods will not account the crack growth parameters such as C and m in estimation of residual strength. Authors proposed a method Murthy et al. [19]. To estimate the residual strength by considering the crack growth parameters and it was found that the estimated residual strength using the proposed method is lower compared to those estimated by using other two approaches and will govern the design. In the present study, the method proposed by Murthy et al. [19] was employed to estimate the residual strength. Brief details of the method are given below.

Irwin proposed the SIF, Ks to quantify the intensity of the stress field surrounding the crack tip in a finite width plate with a remote stress, \(\sigma\):

$${\text{K}}_{\text{s}} = \beta \sigma \sqrt {\pi a}$$
(26)

where a, half-length of the crack; β, geometry factor

Fracture will occur when the applied stress \(\sigma_{x}\) satisfies the equation

$${\text{K}}_{\text{c}} = \beta \sigma_{x} \sqrt {\pi a_{x} }$$
(27)

where, K c , critical SIF, which is a material property.

The general crack growth equation is

$$da/dN = C(\Delta K)^{m}$$
(28)

Using the above equation, the following equation can be deduced to find the number of cycles to failure

$$N_{f} = \int_{{2a_{i} }}^{{2a_{x} }} {\frac{da}{{C(\Delta K)^{m} }}}$$
(29)

where C and m are Crack growth constants and \(\Delta K\) = range of SIF by the cyclic load \(\Delta \sigma\).

The SIF range (ΔK) can be written as,

$$\Delta {\text{K}} = \beta \Delta \sigma \sqrt {\pi a}$$
(30)

From Eq. (27),

$${\text{a}}_{\text{x}} = K_{c}^{2} /\beta^{2} \sigma_{x}^{2} \pi$$
(31)

Substituting (30) and (31) into (28) and after integration, the following equations can be derived.

$$N_{c} = D_{1} - S_{1} (1/\sigma_{c}^{2} )^{(1 - (m/2))}$$
(32)
$${\text{Where}}\quad D_{1} = (2a_{i} )^{1 - (m/2)} /\left[ {C\beta^{m} (\Delta \sigma )^{m} \pi^{{\frac{m}{2}}} \left( {\frac{m}{2} - 1} \right)} \right]$$
(33)
$${\text{and}}\quad S_{1} = \left( {\frac{{2K_{c}^{2} }}{{\beta^{2} \pi }}} \right)^{1 - (m/2)} /\left[ {C\beta^{m} (\Delta \sigma )^{m} \pi^{{\frac{m}{2}}} \left( {\frac{m}{2} - 1} \right)} \right]$$
(34)

where, \(\sigma {}_{c}\) is the residual strength after Nc cycles of load and fora fixed initial crack size ai the parameters D1 and S1 are constant.

Numerical Studies

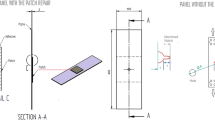
In this section, XFEM technique which is inbuilt in finite element software ABAQUS is used to model the un-patched and repaired aluminium cracked panels (Abaqus 6.10) [20]. Fatigue and fracture analysis of un-patched and patched cracked aluminium panels are carried out. The cracked aluminium panel with different crack length configuration and having various shapes of patch are modelled to study the behaviour and performance of repaired panels. The basic geometry of the cracked panel with single patch considered in the present study is shown in Fig. 5. The following properties are assumed for analysis

Fig. 5
figure 5

Geometrical model of the centre cracked panel with single patch subjected to tensile loading (pure mode I)

Full size image

  • Panel is homogenous, isotropic, linear and elastic.

  • Dimension of the panel: height h = 120 mm, width w = 120 mm, thickness t = 3 mm.

  • Dimension of the rectangular patch and adhesive: height hp = ha = 90 mm, width wp = wa = 180 mm, thicknesstp = 1.15 mm and ta = 0.2 mm.

  • Dimension of the square patch and adhesive: side sp = sa = 127.28 mm, thickness tp = 1.15 mm and ta = 0.2 mm.

  • Dimension of the circular patch and adhesive: radius rp = ra = 71.81 mm, thickness tp = 1.15 mm and ta = 0.2 mm.

  • Dimension of the elliptical patch and adhesive: major axis ap = aa = 90 mm, minor axis bp = ba = 57.29 mm, thickness tp = 1.15 mm and ta = 0.2 mm.

  • Fracture Toughness: 50.54 MPa√m.

  • Yield Strength: 365.42 MPa.

  • Paris crack growth constants C = 0.829 × 10−11 and m = 3.284.

  • Initial Crack length (2a): 24, 48, 72, 96 and 120 mm.

  • An eight node linear brick element (C3D8) has been used for meshing cracked panel and Boron/Epoxy patch.

  • An eight node three dimensional cohesive element (COH3D8) is used for simulation of adhesive film.

  • The material properties for the aluminium panel,FM73 adhesive, boron/epoxy patch are summarized in Table 1. E and G are in GPa. Directions: 1-normal to crack, 2-along crack and 3-thickness.

    Table 1 Material property of the cracked panel, boron/epoxy patch and adhesive
    Full size table

Fracture Analysis of Un-patched Cracked Aluminium Panel

The un-patched aluminium panel with centre crack whose properties are given in “Numerical Studies” section is modelled and analysed using the commercially available finite element software ABAQUS and it is shown in Fig. 6a. Mesh view of unrepaired cracked panel is given in Fig. 6b. The numerical solutions which are obtained by implementing XFEM in ABAQUS for mode-I un-patched centre cracked aluminium panel with different crack length to panel width ratio (a/w) are validated with the analytical solution given in the handbook [13].

Fig. 6
figure 6

a Cracked aluminium panel subjected to tensile load, b Mesh of unrepaired cracked panel

Full size image

For a crack length to panel width ratio (a/w) equal to 0.1, KI obtained from handbook [13] is 13.67 MPa√m and from finite element software using XFEM framework is 13.77 MPa√m, having error of 0.7611%. Stress intensity factor increases from 13.67 to 36.14 MPa√m as crack length to panel width ratio increases from 0.1 to 0.5. The values of stress intensity factor obtained from handbook [2] and XFEM-ABAQUS are presented in Table 2. Figure 7 shows the plot of stress intensity factor for different crack length to panel width ratio.

Table 2 Comparison of the SIF for un-patched centre cracked panel
Full size table
Fig. 7
figure 7

Comparison of the SIF for un-patched centre cracked panel

Full size image

It can be observed from Table 2 and Fig. 7 that stress intensity factors obtained by numerical solution (KXFEM-ABAQUS) are in good agreement with the corresponding analytical values obtained from the handbook [2].

Fracture Analysis of Repaired Cracked Aluminium Panels

Various shapes of patch such as rectangular, square, circular and elliptical are modelled using ABAQUS according to properties given in “Numerical Studies” section and models are shown in Fig. 8. Fracture analysis is carried out to investigate the effects of single boron/epoxy patch on cracked aluminium panel subjected to tensile load of 70 MPa. Different shapes of patch are taken in consideration to study the influence of shape of patch on stress intensity factor (KI) which is one of the important fracture mechanics parameters. XFEM analysis is carried out in for repaired cracked aluminium panel with different shapes of patch keeping the volume of patch material same and the corresponding mode-I Stress intensity factors (KXFEM) are obtained.

Fig. 8
figure 8

ABAQUS model of Repaired cracked aluminium panel with various shapes of patch. a Rectangular, b circular, c square, d elliptical

Full size image

Table 3 shows the comparison of SIF for rectangular, square, circular and elliptical single boron/epoxy patch cracked aluminium panel and compared to un-patched cracked aluminium panel for different crack lengths to panel width ratio. It can be seen that as a/w increases, stress intensity factor increases. For a/w equal to 0.1, the stress intensity factor for unpatch, rectangular, square, circular and elliptical patch repaired panel are 13.78 MPa√m, 12.38, 12.76, 12.65 and 12.96 MPa√m respectively. As crack length to panel width ratio increases to 0.5, stress intensity factor for unpatch, rectangular, square, circular and elliptical patch repaired panel are 36.40, 29.96, 31.61, 33.35 and 32.26 MPa√m respectively. Figure 9 shows the variation of stress intensity factor for different shapes of patch for varying crack length to panel width ratio.

Table 3 Stress intensity factor for various shapes of patch
Full size table
Fig. 9
figure 9

Variation of SIF for un-patched and patched centre cracked panel

Full size image

It can be seen from the Table 3 and Fig. 9 that single boron/epoxy patch is effective in reducing the stress intensity factor of cracked aluminium panel and also rectangular single boron/epoxy patch is the most effective in reducing the stress intensity factor when compared to other shapes of patch.

Fatigue Analysis of Repaired Cracked Aluminium Panels

Fatigue analysis is carried out to predict the remaining life and residual strength of un-patched and repaired cracked panels whose properties given in “Numerical Studies” section. Unpatched and patched panels are subjected to constant amplitude fatigue tensile loading of σmax = 70 MPa and σmin = 0 MPa. Stress intensity factor (KI), one of the most important fracture mechanics parameters, is evaluated for un-patched and repaired aluminium cracked panels using XFEM framework available in ABAQUS. Stress intensity factor is an important parameter to evaluate the remaining life and residual strength of cracked panels. Using curve fitting technique in MATLAB; equations of stress intensity factor are obtained for unpatched and repaired cracked panels. SIF equation is then incorporated in Paris crack growth model to evaluate the remaining life of un-patched and repaired cracked aluminium panels. Paris crack growth law has been used to predict the magnitude of crack growth for given number of cycles. Fatigue life criteria used in Paris crack growth model is defined as number of cycles required for crack to reach 50% of panel width. Residual strength is determined using fracture toughness criterion for un-patched and repaired cracked aluminium panels.

Fatigue crack growth and remaining life studies of repaired cracked panel is carried out using Paris crack growth model given by Eq. (25) and it is compared with un-patched cracked panel. Table 4 presents the comparison of remaining life of un-patched and repaired cracked panels obtained using Paris crack growth law. Un-patched cracked aluminium panel having initial crack length of 24 mm, the remaining life obtained is 230,900 cycles. Figure 10 shows the plot of half crack length versus number of cycles for repaired cracked panel having various shapes of patch. It can be observed from the Table 4 and Fig. 9 that the predicted remaining life of repaired cracked panel under fatigue loading increases compared to un-patched cracked panel. Remaining life obtained is 382,500, 282,000, 345,800 and 279,700 cycles for rectangular, square, circular and elliptical respectively. Thus, it can be seen that there is maximum enhancement in remaining fatigue life of 65.66% for rectangular single boron/epoxy patch compared to un-patched cracked panel.

Table 4 Remaining life prediction of repaired cracked aluminium panels
Full size table
Fig. 10
figure 10

Variation in remaining life of repaired cracked panel as compared to un-patched cracked panel

Full size image

Residual strength of the repaired cracked panel is determined as per the procedure described above and is compared with the un-patched cracked panel. Table 5 and Fig. 11 presents the variation in residual strength for un-patched and repaired cracked panels for different crack lengths. It can be seen that as crack length increases, the residual strength decreases. It can be observed that repaired panels are having higher residual strength as compared to un-patched cracked panel for a given crack length.

Table 5 Comparison of residual strength of un-patched and repaired cracked panel
Full size table
Fig. 11
figure 11

Variation in residual strength for single patch repaired panel with respect to un-patched cracked panel

Full size image

Fatigue analysis of cracked aluminium panels repaired with single Boron/Epoxy patch with various shapes of patch is performed using XFEM. It can be observed that repaired panels have more remaining life and residual strength as compared to un-patched cracked panel. It can be seen that rectangular single patch is effective in improving the remaining life and residual strength compared to all other patch shapes.

Conclusion

In this paper an attempt has been made to implement Extended Finite Element Method (XFEM) for fatigue and fracture analysis of cracked aluminium panel repaired with single boron/epoxy patch. The main focus of this paper is to accurately compute the Stress Intensity Factor (SIF) for repaired cracked panels having various shapes of patch. XFEM formulations such as displacement field, element stiffness matrix formulation are presented in detail. Numerical studies on repaired cracked panels are carried out using XFEM framework in ABAQUS and SIF obtained from XFEM analysis is incorporated in Paris crack growth model to predict the remaining life and also it is used to estimate residual strength of repaired panels which are the objectives of damage tolerant analysis.

From the Numerical studies following observations can be made

  • Stress intensity factor evaluated for un-patched cracked panel using XFEM are in good agreement with the analytical solution available in the handbook.

  • For a given crack length, among all various shapes of patch which are taken into consideration, rectangular patch has maximum reduction in stress intensity factor when compared to un-patched cracked panels.

  • For a given crack length, cracked panel repaired with rectangular patch gives more residual strength as well as remaining life compared to other shapes of patch.

The predicted remaining life and residual strength will be useful for design of structures/components subjected to fatigue loading.