1 Introduction

Most conventional heat transfer fluids, such as water, ethylene glycol and engine oil, have limited capabilities in terms of thermal properties, which, in turn, may impose serve restrictions in many thermal applications. Hence, one can then expect that fluid-containing solid particles may significantly increase its conductivity. Recent research on nanofluid showed that nanoparticles changed the fluid characteristics because thermal conductivity of these particles is higher than the convectional fluids.

The first paper on stretching sheet in nanofluid was discussed by Khan and Pop [1]. They investigated the problem of laminar fluid flow which results from the stretching of a flat surface in a nanofluid. The natural convective boundary layer flow of a nanofluid past a vertical plate is studied analytically by Kuznetsov and Nield [2]. The model used for the nanofluid incorporated the effects of Brownian motion and thermophoresis. Mustafa et al. [3] developed an analytic solution of the flow of a nanofluid near a stagnation point toward a stretching surface by homotopy analysis method. Bachok et al. [4] studied the steady two-dimensional stagnation-point flow of a nanofluid over a linearly stretching/shrinking sheet in its own plane. Makinde and Aziz [5] studied the boundary layer flow induced in a nanofluid due to a linearly stretching sheet numerically. They used a convective heating boundary condition. Nanoparticle research is currently an area of intense scientific interest due to a wide variety of potential applications in biomedical, optical and electronic field. Sivashanmugam [6] investigated the drawbacks in suspensions of solid particles with sizes on the order of 2 mm or micrometers. The emergence of modern materials technology provided the opportunity to produce nanometer-sized particles. He observed that nanofluids having properly dispersed nanoparticles possess the significant advantages which will play an important role in developing the next generation of cooling technology. Das [7] discussed the effects of partial slip on mixed convection stagnation-point flow and heat transfer of nanofluid impinging normally toward a shrinking sheet numerically. Ferdows et al. [8] studied numerically the boundary layer flow past unsteady stretching surface in nanofluid under the effects of suction and viscous dissipation.

Nadeem and Hussain [9] examined the two-dimensional flow of Williamson fluid over a stretching sheet under the effects of nano-sized particle also described as nano-Williamson fluid. The results were found that the velocity increases with an increase in the curvature parameter and decreases with an increase in Williamson parameter and Hartman number. Makinde et al. [10] analyzed the combined effects of buoyancy force, convective heating, Brownian motion, thermophoresis and magnetic field on stagnation-point flow and heat transfer due to nanofluid flow toward a stretching sheet. They found that the dual solutions exist for shrinking parameter. Haq et al. [11] examined the two-dimensional boundary layer flow of a natural convective micropolar nanofluid along a vertically stretching sheet. He also analyzed the influences of nanoparticles for both assisting and opposing flow. Kuznetsov and Nield [12] revisited the problem of natural convective boundary layer flow of a nanofluid past a vertical plate. Zaimi et al. [13] investigated the steady two-dimensional flow and heat transfer over a stretching/shrinking sheet in a nanofluid. Kuznetsov and Nield [12] and Zaimi et al. [13] have considered the case when the nanofluid particle fraction on the boundary is passively rather than actively controlled. Nield and Kuznetsov [14] revised linear stability analysis for the onset of natural convection in a horizontal nanofluid layer. They assumed that the value of the temperature can be imposed on the boundaries, but the nanoparticle fraction adjusts so that the nanoparticle flux is zero on the boundaries. They have shown that, with the new boundary conditions, oscillatory convection can no longer occur.

Bachok et al. [15] studied the unsteady boundary layer flow of a nanofluid over a permeable stretching/shrinking sheet theoretically. Mahdy [16] has presented numerical analysis to investigate the unsteady mixed convection boundary layer flow and heat transfer due to uncertainties of thermal conductivity and dynamic viscosity of nanofluid over a stretching vertical surface. Mukhopadhyay et al. [17] investigated the unsteady two-dimensional flow of a non-Newtonian fluid over a stretching surface having a prescribed surface temperature. They used the Casson fluid model to characterize the non-Newtonian fluid behavior. Malvandi et al. [18] considered the unsteady two-dimensional stagnation-point flow of a nanofluid over a stretching sheet numerically. Navier’s slip condition has been applied. The behavior of the nanofluid was investigated for three different nanoparticles in the water-base fluid. Mustafa et al. [19] considered the unsteady laminar boundary layer flow of nanofluid caused by a linearly stretching sheet.

Subhashini et al. [20] discussed the development of mixed convection flow near the stagnation-point region over an exponentially stretching/shrinking sheet in nanofluids. The external flow, stretching velocity and wall temperature were assumed to vary as prescribed exponential functions. Avramenko and Kuznetsov [21] investigated the stability of a suspension of motile gyrotactic micro-organisms in a system that consists of superimposed fluid and porous layer. This is relevant to many biological applications, such as growing motile micro-organisms in Petri dishes. Nield and Kuznetsov [22] discussed a linear stability analysis to investigate the onset of bioconvection in a horizontal layer of fluid containing a suspension of motile micro-organisms with heating or cooling from below. Kuznetsov [23] developed a theory of bio-thermal convection in a suspension that contains two species of micro-organisms exhibiting different taxes, gyrotactic and oxytactic micro-organisms. Khan et al. [24] investigated the combined effects of Navier slip and magnetic field on boundary layer flow with heat and mass transfer of a water-based nanofluid containing gyrotactic micro-organisms over a vertical plate. Mehryan et al. [25] studied the behavior of a water-based nanofluid containing motile gyrotactic micro-organisms passing an isothermal nonlinear stretching sheet in the presence of a non-uniform magnetic field. Halim et al. [26, 27] discussed the stagnation-point flow on a stretching/shrinking surface in the presence of active and passive control. Recent advances in the field of the active and passive flow separation control, particularly blowing and suction flow control techniques, applied on the common airfoils are briefly reviewed by Moghaddam et al. [28]. The effectiveness of active and passive control strategies for suppressing spar vortex-induced motion is assessed by Korpus et al. [29].

In the present work we consider the stagnation-point flow of a Williamson nanofluid containing gyrotactic micro-organisms that included both active and passive controls of mass fluxes on the flow characteristics. Similarity transformations are applied to reduce the governing nonlinear partial differential equations into nonlinear ordinary differential equations with suitable guess of initial condition, and they are solved numerically. The behavior of the velocity, temperature, nanoparticle volume fraction, micro-organisms, skin friction and heat transfer rate has been discussed graphically for a various range of physical parameters.

2 Problem Formulation

2.1 Governing Equations and Boundary Conditions

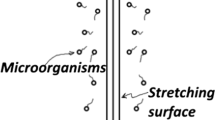
Consider a two-dimensional unsteady stagnation-point flow of an incompressible Williamson nanofluid containing gyrotactic micro-organisms toward a horizontal linearly stretching/shrinking sheet. Sheet coincides with the plane y = 0 as described in Fig. 1. The flow is assumed to be confined to y > 0 with stretching/shrinking velocity \(u_{w}\)(x,t) = \(\frac{ax}{{1 - ct}}\) where a and c are positive constants. It is also assumed that the stretching/shrinking surface has constant value of temperature defined as \(T_{w}\). The density of motile micro-organisms Nw at the stretching surface is assumed to be constant. Nanoparticle volume fraction takes the value \(N_{w}\) at the surface for actively controlled mass flux, while the ambient temperature, concentration and the density of motile micro-organisms are denoted by \(T_{\infty }\), \(C_{\infty }\) and \(N_{\infty }\). The nanoparticle volume fraction for passively controlled mass flux is defined separately by the temperature gradient resulting with zero nanoparticles normal flux. The classification of boundary layer control methods into active and passive categories is one of the most common schemes. Vortex generator, distributed roughness, streamlining, and uniform blowing and suction are among various devices that are employing for the passive flow control technique. On the other hand, some of the active flow control methods are heating wall, movement of surface elements, oscillatory blowing and suction, and synthetic jets.

Fig. 1
figure 1

Geometry of the flow in two dimensions

Full size image

With the assumptions mentioned above, the governing equations are written as [30, 31]:

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0 $$
(1)
$$ \frac{\partial u}{{\partial t}} + u\frac{\partial u}{{\partial x}} + \nu \frac{\partial u}{{\partial y}} = \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} + \sqrt {2\nu } \Gamma_{0} \frac{\partial u}{{\partial y}}\frac{{\partial^{2} u}}{{\partial y^{2} }} + g\left( {\beta_{T} \left( {T - T_{\infty } } \right) + \beta_{c} \left( {C - C_{\infty } } \right) - \gamma \left( {N - N_{\infty } } \right)} \right) $$
(2)
$$ \frac{\partial T}{{\partial t}} + u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\rho_{p} c_{p} }}{\rho c}D_{B} \left( {\frac{\partial C}{{\partial y}}\frac{\partial T}{{\partial y}}} \right) + \frac{{\rho_{p} c_{p} }}{\rho c}\frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial y}}} \right)^{2} $$
(3)
$$ \frac{\partial C}{{\partial t}} + u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} = D_{B} \left( {\frac{{\partial^{2} C}}{{\partial y^{2} }}} \right) + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) $$
(4)
$$ \frac{\partial N}{{\partial t}} + u\frac{\partial N}{{\partial x}} + v\frac{\partial N}{{\partial y}} = D_{m} \left( {\frac{{\partial^{2} N}}{{\partial y^{2} }}} \right) - \frac{{bW_{c} }}{{\left( {C_{w} - C_{\infty } } \right)}}\left( {\frac{\partial }{\partial y}\left( {N\frac{\partial C}{{\partial y}}} \right)} \right) $$
(5)

where \(u\) and v are the velocity components in the x, y directions, respectively, \(\nu\) is the kinematic viscosity, \(\Gamma_{0}\) = \(\Gamma\)/x > 0(x ≠ 0) is a time constant, α is the thermal diffusivity, ρc and \(\rho_{p} c_{p} \) are heat capacities of nanofluid and nanoparticles, respectively, \(D_{B}\) is the Brownian diffusion coefficient, \(D_{T}\) is the thermophoretic diffusion coefficient, and \(D_{m}\) is the diffusivity of micro-organisms. b is the chemotaxis constant, \(W_{c}\) is maximum cell swimming speed, and bWc is assumed to be constant. Details of the derivation of Eqs. (1)–(4) are given in the papers by Buongiorno [32], Tzou [33, 34]. The nanoparticle volume fraction at the surface is controlled passively by the temperature gradient resulting with zero nanoparticles normal flux. The new boundary conditions for the flow are given as:

$$ u = Su_{w} \left( {x,t} \right) = S\frac{ax}{{1 - ct}}, v = 0,T = T_{w} , N = N_{w} , \;{\text{at}}\;y = 0, $$
(6)
$$ \left\{ {\begin{array}{*{20}l} {D_{B} \frac{\partial C}{{\partial y}} + \frac{{D_{T} }}{{T_{\infty } }}\frac{\partial T}{{\partial y}} = 0,} \hfill & {{\text{for}}\;{\text{passive}}\;{\text{control}}\;{\text{of}}\;\phi } \hfill \\ {C = C_{w} , } \hfill & {{\text{for}}\;{\text{active}}\;{\text{control}}\;{\text{of}}\;\phi } \hfill \\ \end{array} } \right.{\text{at}} y = 0. $$
(7)
$$ u = u_{e} \left( {x,t} \right) = 0, T = T_{\infty , } C = C_{\infty } , N = N_{\infty } as y \to \infty . $$
(8)

where \(S\) is the stretching/shrinking parameter that can take a positive value for stretching sheet or a negative value for shrinking sheet.

2.2 Similarity Transformations

Governing Eqs. (2)–(5) can be transformed to a set of nonlinear ordinary equations by introducing the following non-dimensional variables:

$$ \begin{aligned} & \eta = y\sqrt {\frac{a}{{\nu \left( {1 - ct} \right)}}} ,\psi = \sqrt {\frac{\nu a}{{1 - ct}}xf\left( \eta \right),} \\ & \theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}, \chi \left( \eta \right) = \frac{{N - N_{\infty } }}{{N_{w} - N_{\infty } }} \\ & \phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{\infty } }} {\text{for}}\;{\text{passive}}\;{\text{control}}\;{\text{of}}\;\phi , \\ & \phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C - C_{\infty } }} {\text{for}}\;{\text{active}}\;{\text{control}}\;{\text{of}}\;\phi \\ \end{aligned} $$
(9)

where \(\psi\) is the stream function which satisfies (1) and

$$ u = \frac{\partial \psi }{{\partial y}} = cxf^{\prime } \left( \eta \right) \;{\text{and}}\; v = - \frac{\partial \psi }{{\partial x}} = - \sqrt {c\nu } f\left( \eta \right) $$
(10)

Using expressions (9) and (10), the nonlinear ordinary differential equations are obtained as

$$ f^{\prime \prime \prime } + ff^{\prime \prime } - f^{\prime 2} + \lambda f^{\prime \prime } f^{\prime \prime \prime } - A\left( {f^{\prime } + \frac{1}{2}\eta f^{\prime \prime } } \right) + \lambda_{1} \left( {\theta + R\phi - Rb\chi } \right) = 0 $$
(11)
$$ \theta^{\prime \prime } - \Pr \left( {\frac{1}{2}A\eta \theta^{\prime } - f\theta^{\prime } } \right) + \frac{{N_{c} }}{Le}\theta^{\prime } \phi^{\prime } + \frac{{N_{c} }}{{LeN_{bt} }}\theta^{\prime 2} = 0 $$
(12)
$$ \phi^{\prime \prime } - Sc\left( {\frac{1}{2}A\eta \phi^{\prime } - f\phi^{\prime } } \right) + \frac{1}{{N_{bt} }}\theta^{\prime \prime } = 0 $$
(13)
$$ \chi^{\prime \prime } - Lb\left( {\frac{1}{2}A\eta \chi^{\prime } \left( \eta \right) - f\chi^{\prime } } \right) - Pe\left( {\phi^{\prime \prime } \left( {\Omega + \chi } \right) + \phi^{\prime } \chi^{\prime } } \right) = 0 $$
(14)

subject to the corresponding boundary conditions

$$ f\left( 0 \right) = 0, f^{\prime } \left( 0 \right) = S, \theta \left( 0 \right) = 1, \chi \left( 0 \right) = 1, $$
(15)
$$ \left\{ {\begin{array}{*{20}l} {N_{c} \phi^{\prime } \left( 0 \right) + \frac{{N_{c} }}{{N_{bt} }}\theta^{\prime } \left( 0 \right) = 0,} \hfill & {{\text{for}}\;{\text{passive}}\;{\text{control}}\;{\text{of}}\;\phi ,} \hfill \\ {\phi \left( 0 \right) = 1,} \hfill & {{\text{for}}\;{\text{active}}\;{\text{control}}\;{\text{of}}\;\phi ,} \hfill \\ \end{array} } \right. $$
(16)
$$ f^{\prime}\left( \infty \right) = 0, \theta \left( \infty \right) = 0, \phi \left( \infty \right) = 0, \chi \left( \infty \right) = 0 $$
(17)

where primes denote differentiation with respect to the similarity variable η. Here, \(A = c{/}a\) is the unsteadiness parameter. The ratio of the buoyancy force R = \(\lambda_{1}^{*}\)/\(\lambda_{1}\) appearing in Eq. (11) is the non-dimensional parameter representing the ratio between the buoyancy force due to concentration difference (\(\lambda_{1}^{*}\) = \(Gr_{C}\)/\(\left( {{\text{Re}}_{x} } \right)^{2}\)) and the buoyancy force due to temperature difference (\(\lambda_{1} = Gr_{T}\)/\(\left( {Re_{x} } \right)^{2}\)).

Here \(Gr_{T} = \frac{{g\beta_{T} \left( {T_{w} - T_{\infty } } \right)x^{3} }}{{\nu^{2} }} \), here \(Gr_{C} = \frac{{g\beta_{C} \left( {C_{w} - C_{\infty } } \right)x^{3} }}{{\nu^{2} }} \) and \({\text{Re}}_{x} = \frac{{u_{w} \left( {x,t} \right)x}}{\nu } \) are the thermal Grashof number, the solutal Grashof number and the local Reynolds number, respectively. \(Rb = \gamma \Delta N\Delta \rho {/}\beta_{T} \left( {T_{w} - T_{\infty } } \right)\) where \(\Delta N = N_{w} - N_{f}\), \(\Delta \rho = \rho_{m} - \rho_{f}\) with \(\rho_{m}\)—cell density, \(\rho_{f}\)—fluid density, \(Rb\)is bioconvection Rayleigh number. \(\gamma\) is the average volume of a micro-organism. Moreover, \(R = 0 \) is for non-buoyancy effect due to mass diffusion, \(R = 1\) is for non-buoyancy effect due to thermal diffusion, and \(R = 1\) is for thermal and mass buoyancy forces of the same strength. Also, \(\lambda_{1}\) is called the mixed convection parameter denoting the buoyancy force effects on the flow field.\( Pr = \gamma /\alpha\) is the Prandtl number, \( Le = \alpha /D_{B}\) is the Lewis number, \(Sc = \gamma /D_{B}\) is the Schmidt number, \(Lb = \gamma /D_{m}\) is the bioconvection Lewis number,\( Pe = bWc/D_{m}\) is the bioconvection Peclet number, and Ω is the micro-organisms concentration difference parameter. The following non-dimensional parameters are given by:

$$ \lambda = \Gamma \sqrt {\frac{2}{\nu }\left( {\frac{a}{1 - ct}} \right)^{3} } $$
$$ N_{c} = \frac{{\rho_{p} c_{p} }}{\rho c}\left( {C_{w} - C_{\infty } } \right),\;\left( { = \frac{{{\text{nanoparticles}}\;{\text{heat}}\;{\text{capacity}}}}{{{\text{nanofluid}}\;{\text{heat}}\;{\text{capacity}}}}} \right), $$
$$ N_{bt} = \frac{{D_{B} T_{\infty } \left( {C_{w} - C_{\infty } } \right)}}{{D_{T} \left( {T_{w} - T_{\infty } } \right)}}\quad \left( { = \frac{{{\text{Brownian}}\; {\text{diffusivity}}}}{{{\text{Thermophoretic}}\;{\text{diffusivity}}}}} \right). $$

where λ is the non-Newtonian Williamson parameter, \(N_{c}\) the heat capacity ratio and \(N_{bt}\) the diffusivity ratio. It is important to note that we redefined the Williamson parameter \(\lambda\) by introducing the term \(\Gamma_{0} = \frac{\Gamma }{x} > 0\) to eliminate \( x\). The physical quantities of interest are the local skin friction coefficient, the wall heat transfer coefficient′ (or the local Nusselt number), the wall deposition flux (or the local Sherwood number) and the local density number of the motile micro-organisms. These expressions are defined as

$$ \begin{aligned} & Cf_{x} = \frac{{\tau_{w} }}{{\rho u_{w}^{2} \left( x \right)}}, Nu_{x} = \frac{{q_{w} x}}{{\alpha \left( {T_{w} - T_{\infty } } \right)}}, \\ & Sh_{x} = \frac{{q_{m} x}}{{D_{B} \left( {C_{w} - C_{\infty } } \right)}}, Nn_{x} = \frac{{q_{n} x}}{{D_{m} \left( {N_{w} - N_{\infty } } \right)}} \\ \end{aligned} $$
(18)

where the wall shear stress \(\tau_{w}\), wall heat flux, \(q_{w}\), the mass flux from wall, \(q_{m}\), and the motile micro-organisms flux on the wall, \(q_{n}\), are given by

$$ \tau_{w} = \mu \left[ {\frac{\partial u}{{\partial y}} + \frac{{\Gamma_{0} }}{\sqrt 2 }\left( {\frac{\partial u}{{\partial y}}} \right)^{2} } \right]_{y = 0} ,\;q_{w} = - \alpha \left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0} , $$
$$ q_{m} = D_{B} \left( {\frac{\partial C}{{\partial y}}} \right)_{y = 0, } q_{n} = - D_{m} \left( {\frac{\partial N}{{\partial y}}} \right)_{y = 0} $$

Equation (18) then can be reduced into the dimensionless form below:

$$ Cf_{x} {\text{Re}}_{x}^{\frac{1}{2}} = f^{\prime \prime } \left( 0 \right) + \frac{\lambda }{2}f^{\prime \prime } \left( 0 \right)^{2} , Nu_{x} {\text{Re}}_{x}^{\frac{1}{2}} = - \theta^{\prime } \left( 0 \right), $$
$$ Sh_{x} Re_{x}^{1/2} = - \phi^{\prime } \left( 0 \right), Nn_{x} Re_{x}^{{ - \frac{1}{2}}} = - \chi^{\prime } \left( 0 \right). $$

With boundary condition (16) for passive control, the Sherwood number which represents the mass flux will follow the Nusselt number accordingly.

3 Method of solution

Nonlinear ordinary differential Eqs. (11)–(14) together with boundary conditions (15)–(17) are solved using bvp4c package in MATLAB software. Finite difference method is used to develop the code and is used to solve boundary value problems for ordinary differential equations by collocation method. The computation time is found to be less than 1 s in all the cases. The system of differential Eqs. (11)–(14) is first converted into a first-order system as below:

$$ x_{3}^{\prime } = \frac{1}{{\left( {1 + \lambda x_{3} } \right)}}\left( {x_{2}^{2} - x_{1} x_{2} + A\left( {x_{2} + \frac{1}{2}\eta x_{3} } \right) - \lambda_{1} \left( {x_{4} + \frac{{\lambda^{*}_{1} }}{{\lambda_{1} }}x_{6} - Rbx_{8} } \right)} \right) $$
(19)
$$ x_{5}^{\prime } = \Pr \left( {\frac{1}{2} A\eta x_{5} {-} x_{1} x_{5} } \right) - \frac{{N_{C} }}{Le} \left( {x_{5} x_{7} + \frac{1}{{N_{bt} }}x_{5}^{2} } \right) $$
(20)
$$ x_{7}^{\prime } = Sc\left( {\frac{1}{2}A\eta x_{7} {-}x_{1} x_{7} } \right) - \frac{1}{{N_{bt} }}x_{5}^{\prime } $$
(21)
$$ x_{9}^{\prime } = Lb \left( {\frac{1}{2} A\eta x_{9} {-} x_{1} x_{9} } \right) + Pe\left( { x_{7}^{\prime } \left( {\Omega + x_{8} } \right) + x_{7} x_{9} } \right) $$
(22)

Subject to boundary conditions:

$$ x_{1} \left( 0 \right) = 0, x_{2} \left( 0 \right) = S, x_{4} \left( 0 \right) = 1, x_{8} \left( 0 \right) = 1 $$
$$ \left\{ {\begin{array}{*{20}l} {N_{c} x_{7 } \left( 0 \right) + \frac{{N_{c} }}{{N_{bt} }}x_{5} \left( 0 \right) = 0,} \hfill & {{\text{for}}\;{\text{passive}}\;{\text{control}}\;{\text{of}}\;\phi } \hfill \\ {x_{6} \left( 0 \right) = 1,} \hfill & {{\text{for}}\;{\text{active}}\;{\text{control}}\;{\text{of}}\;\phi } \hfill \\ \end{array} } \right. $$
(23)
$$ x_{2} \left( \infty \right) = 0, x_{4} \left( \infty \right) = 0, x_{6} \left( \infty \right) = 0, x_{8} \left( \infty \right) = 0, $$
(24)

where

$$ \begin{aligned} & x_{1} = f,\,x_{2} = x_{1}^{\prime } = f^{\prime } ,\; x_{3} = x_{2}^{\prime } = f^{\prime \prime } , \\ & x_{4} = \theta ,\;x_{5} = x_{4}^{\prime } = \theta^{\prime } , \\ & x_{6} = \varphi ,\;x_{7} = x_{6}^{\prime } = \phi^{\prime } , \\ & x_{8} = \chi ,\; x_{9} = x_{8}^{\prime } = \chi^{\prime } , \\ \end{aligned} $$
(25)

The desired solution for ordinary differential Eqs. (19)–(22) requires an initial guess that should satisfy boundary conditions (23) and (24). The mesh selection and error control are based on the residual of the continuous solution. The relative error tolerance has been set to \(10^{ - 10}\), and a suitable finite value of η \(\to \infty\) is chosen as η = \(\eta_{\infty } = 10.\) Unless otherwise specified, the parameter values used throughout the paper are as follows: \(A = 0.1, Pr = 10, N_{bt} = 2, Nc = 0.5, Le = 4,\lambda = 0.2,\lambda_{1} = 5,Rb = 0.1, Sc = 2, Lb = 1, Pe = 1, \Omega = 0.1, R = 0.5, {\text{and }} S = 1.\)

4 Results and Discussion

To ensure the accuracy of our results, comparisons between present and available published results are made in Tables 1 and 2. In Tables 1 and 2, values for skin friction coefficient \(f^{\prime \prime } \left( 0 \right)\), reduced Nusselt number, \(- ^{\prime } \left( 0 \right)\), and reduced Sherwood number, \(- \phi^{\prime } \left( 0 \right)\), for different parameters are compared with the results of Ref. [26].

Table 1 Comparison of results for the physical quantities of interest when S = 1, A = 0, λ = 0.2, \(\lambda_{1}\) = 0, R = 0, \(N_{bt}\) = 2, \(N_{c}\) = 0.5, Le = 4, Pr = 0.5, Sc = 2, Pe = 0, Lb = 0, Ω = 0
Full size table
Table 2 Comparison of results for the physical quantities of interest when Le = 1, Pr = 1, \( N_{bt}\) = 1, Sc = 1, Nc = 0.2, λ = 0, S = 1, Pe = 0, Lb = 0, Ω = 0, \(\lambda_{1}\) = 0, R = 0, A = 0
Full size table

Computations have been made to see the influence of various emerging parameters such as shrinking/stretching parameter \(S\), the Lewis number \(Le\), the Prandtl number \(Pr\), the Schmidt number \(Sc\), the diffusivity ratio \(N_{bt}\) and the heat capacity ratio \(N_{c} \) under both active and passive control environments. The comparison of temperature and nanoparticle volume fraction is given in Figs. 2, 3, 5, 6, 7 and 8. The results for velocity profile are presented in Figs. 4, 9 and 10. The variations in physical quantities for various parameters are shown in Figs. 11, 12, 13, 14, 15. Numerical values of reduced skin friction coefficient \(Re_{x}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Cf_{x}\), reduced Nusselt number \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x}\), reduced Sherwood number \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Sh_{x}\) and reduced density number of motile micro-organisms \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nn_{x}\) for various parameters are tabulated for both active and passive controls of mass transfer.

Fig. 2
figure 2

Temperature and nanoparticle volume fraction profiles for both active and passive controls for different Prandtl number, Pr

Full size image
Fig. 3
figure 3

Temperature and nanoparticle volume fraction profiles for both active and passive controls for different stretching/shrinking parameters, S

Full size image
Fig. 4
figure 4

Velocity and motile micro-organisms density profiles for both active and passive controls for different stretching/shrinking parameters, S

Full size image
Fig. 5
figure 5

Temperature and nanoparticle volume fraction profiles for both active and passive controls for different Schmidt number, Sc

Full size image
Fig. 6
figure 6

Temperature and nanoparticle volume fraction profiles for both active and passive controls for different diffusivity ratios, \(N_{bt}\)

Full size image
Fig. 7
figure 7

Temperature and nanoparticle volume fraction profiles for both active and passive controls for different Lewis number, Le

Full size image
Fig. 8
figure 8

Temperature and nanoparticle volume fraction profiles for both active and passive controls for different heat capacity ratios, \(N_{c} .\)

Full size image
Fig. 9
figure 9

Velocity and nanoparticle volume fraction profiles for both active and passive controls for different values of \(\lambda_{1}\)

Full size image
Fig. 10
figure 10

Velocity profile for both active and passive controls for different values of \(R\)

Full size image
Fig. 11
figure 11

Variation of reduced skin friction for different values of Williamson parameter \(\lambda\) at different stretching/shrinking rates, \(S\)

Full size image
Fig. 12
figure 12

Variation of reduced skin friction for different values of Rb at different stretching/shrinking rates, \(S\)

Full size image
Fig. 13
figure 13

Variation of reduced Nusselt number for both active and passive controls for different capacity ratios, \(Nc\), at different stretching/shrinking rates, \(S.\)

Full size image
Fig. 14
figure 14

Variation of reduced Nusselt number for both active and passive controls for different heat capacity ratios, \(Nc\), and diffusivity ratio, \(N_{bt}\)

Full size image
Fig. 15
figure 15

Variation of reduced density number of motile micro-organisms for both active and passive controls for different capacity ratios, \(N_{c}\), at different stretching/shrinking rates, \(S.\)

Full size image

Figure 2 shows the effects of Prandtl number \(\left( {Pr} \right)\) toward temperature and nanoparticle volume fraction profiles. Temperature is a decreasing function of \(\left( {Pr} \right)\) in both active and passive control environments. Nanoparticle volume fraction seems to be quite sensitive with Prandtl number. It appears that for each \(\left( {Pr} \right)\) value the trend for \(\phi\) flips to opposite direction at different critical points, from increasing to decreasing manner in active control and vice versa in passive control, respectively.

Figures 3 and 4 display the effects of the stretching/shrinking parameter \(S\). The negative value of \(S \) represents shrinking surfaces, while the positive value of \(S\) represents a stretching surface. The behavior of temperature in active control slightly differs from the passive one where in Ref. [26] negligible differences were found. Although temperature is a decreasing function of \(S\) in both active and passive control, the nanoparticle volume fractions react in the opposite manner. In active control, \(\phi\) decreases as \(S\) increases, but in passive control, \(\phi\) increases with \(S\). Velocity flips to opposite direction at different critical points, from increasing to decreasing manner in both active and passive control. Originally, density of motile micro-organisms decreases with an increase of \(S\) and continues only in the case of passive control, but in the case of active control χ flips to increase at a critical point.

The temperature and nanoparticle volume fraction profiles for both active and passive controls are displayed in Fig. 5, and Fig. 6 shows the velocity and motile micro-organisms. These figures indicate that \(Sc\) has almost negligible effects on temperature in active and passive controls. Nanoparticle volume fraction \(\phi\) is a decreasing function in active control, and it overshoots when \(Sc\) is \(< 0.8\). When the Brownian diffusivity is stronger \((Sc < 1),\) the nanoparticles are spread out more due to frequent collisions between the particles, hence increasing the nanoparticles volume fraction. In passive control \(\phi\) increases before flips to decrease with increasing value of \(Sc\). Figures 5 and 6 show the effects \(Sc\) and \(N_{bt}\), respectively, which is almost the same toward temperature and nanoparticle volume fraction. Similar to \(Sc\), \(N_{bt}\) also has negligible effects on temperature in active and passive controls. Nanoparticle volume fraction \(\phi\) is a decreasing function in active control, and it overshoots when \(N_{bt} < 1\). Thermophoresis controls the migration of nanoparticles that arise due to temperature difference. With higher temperature gradient, the nanoparticles are dispersed more while increasing the volume fraction. In passive control \(\phi\) increases before flips to decrease with increasing value of \(N_{bt}\).

Figure 7 shows that \(Le\) has little effect on temperature in active control and almost insignificant effect in passive control. Temperature decreases with an increase of \(Le\) in active control, and nanoparticle volume fraction increases with \(Le\) in the region near the surface before converging as the flow moves away from the surface. Temperature and nanoparticle volume fraction have no changes in passive control.

Figure 8 reveals that \(N_{c}\) and \(Le\) have similar but opposite effects toward temperature and nanoparticle volume fraction in active control. The temperature increases and nanoparticle volume fraction decreases with an increase of \(N_{c}\) in active control, but both have slight changes only. Both temperature and nanoparticle volume fraction have no effect in passive control.

Figure 9 shows that the velocity increases with an increase of the buoyancy force due to temperature difference,\( \lambda_{1}\) in both active and passive controls. Nanoparticle volume fraction is a decreasing function of \( \lambda_{1}\) in active control. It has insignificant effect toward \( \lambda_{1}\) in passive control. Figure 10 establishes that the velocity increases with R in both active and passive control. When R is negative, the velocity decreases in active control as the flow moves from the surface before starts increasing. When \(R\) is positive, the velocity overshoots in active control.

Figures 11 and 12 show the effect of increasing value of the non-Newtonian Williamson parameter \(\lambda\) and bioconvection Rayleigh number \(Rb\) toward skin friction at different rates of stretching and shrinking parameter \(S\). The active and passive boundary conditions do not affect the reduced skin friction in Ref. [26], but in the present work, active and passive boundary conditions affect the reduced skin friction. Here, \(\lambda = 0\) represents the special case of Newtonian fluid. It is observed that the reduced skin friction \(Re_{x}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Cf_{x}\) increases when \(\lambda\) increases in both active and passive controls, whereas it decreases as \(Rb\) increases in both the controls. The results agree with Eq. (21). It can also be seen that skin friction is larger on shrinking surface than on the stretching surface in both the controls. Also it meets the same value for different \(\lambda\) in the stretching region.

In Figs. 13 and 14, the effects of heat capacity ratio \(N_{c}\) toward the reduced Nusselt number \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x} \) are presented. The rate of heat transfer is decreasing as \(N_{c}\) increases in active control. The effect in passive control is very minimum compared to its effect in active control. This is due to the disappearance of \(N_{c}\) in the boundary condition for passive control of \(\phi \left( \eta \right)\) and also observed that the heat transfer on shrinking surface is less compared to that on stretching surface. On the other hand \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x}\) tends to a constant value as \(N_{bt}\) increases in both active and passive controls.

Figures 15 and 16 show the effects of \(N_{c}\) toward the reduced density number of motile micro-organisms \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nn_{x}\) in active and passive control. \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x}\) is a decreasing function of \(N_{c}\) in active control for different values of \(S\), and the effect is negligible in passive control. Similarly, \(N_{c}\) has an insignificant effect toward \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x}\) in passive control. \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x}\) is a decreasing function of \(N_{c}\) for different values of \(N_{bt}\) in passive control.

Fig. 16
figure 16

Variation of reduced density number of motile micro-organisms for both active and passive controls for different heat capacity ratios, Nc, and diffusivity ratio, \(N_{bt}\)

Full size image

From Figs. 2, 3, 5, 6, 7, 8 and 9, it can be seen that the variable \(\phi \left( \eta \right)\) in passive control overshoots and attains negative values in the immediate vicinity of the surface. This behavior illustrates that the nanoparticle flux at the surface is being suppressed due to zero nanoparticle flux condition at the surface.

Tables 3 and 4 display the values of reduced skin friction, reduced Nusselt number, reduced Sherwood number and reduced density number of motile micro-organisms for different parameters. It is observed that the values of \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Sh_{x}\) in passive controls are all negative. The mass is being transferred to surroundings due to the zero mass flux condition at the surface that prevents nanoparticle deposition. Shrinking/stretching parameter \(S\) has mixed effects on skin friction, heat flux, mass flux and motile micro-organisms flux. Values of \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Cf_{x}\) in passive control seem to be fluctuated with the increase of \(S\). Critical point of \(S\) for skin friction is at \(S_{cf} = - 0.64\). Increasing value of skin friction starts decreasing at the critical point. Values of \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Sh_{x}\) and \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nn_{x}\) in active control fluctuate with increasing \(S\). Critical points of \(S\) for \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Sh_{x}\) and \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nn_{x}\) are at \(S_{sh} = - 0.496\) and \(S_{Nn} = - 0.46\), respectively. The reduced Sherwood number is increasing before it turns to decrease at the critical point and the reduced density of motile micro-organisms behaves in a opposite manner. \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Sh_{x}\) increases with \(Sc\) in both active and passive controls, \(Sc\) has opposite effects in \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nn_{x}\) for active and passive controls, and \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x}\) is a decreasing function of \(Sc\) and is fluctuating in passive control. It is increasing before turning to decrease at the critical point \(Sc_{Nu} = 0.76\). \(Le\) and \(N_{c}\) have similar effects toward \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x}\) and \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nn_{x}\) but opposite effects toward \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Sh_{x}\). \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x}\) and \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nn_{x}\) are increasing functions of \(Le\); \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Sh_{x}\) is a decreasing function in both active and passive control. \(N_{c}\) effects in opposite manner that is \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x}\) and \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nn_{x}\) are decreasing functions of \(N_{c}\), and \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Sh_{x}\) is an increasing function in both active and passive controls. \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Sh_{x}\) increases and \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x}\) decreases with \(N_{bt}\) in both active and passive controls. \(Re_{x}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} Nu_{x}\) increases in active control and decreases in passive control with increasing \(N_{bt}\).

Table 3 Values of \(Re_{x}^{1/2} Cf_{x} ,\) \(Re_{x}^{ - 1/2} Nu_{x} ,\) \(Re_{x}^{ - 1/2} Sh_{x} ,\) \(Re_{x}^{ - 1/2} Nn_{x} ,\) for both active and passive control when S varies
Full size table
Table 4 Values of \(Re_{x}^{ - 1/2} Nu_{x} ,\) \(Re_{x}^{ - 1/2} Sh_{x} ,\) \(Re_{x}^{ - 1/2} Nn_{x}\), for both active and passive control with various parameters
Full size table

5 Conclusion

The present work solves the problem of a two-dimensional unsteady flow of an incompressible Williamson nanofluid containing micro-organisms numerically over a shrinking/stretching surface. Both conditions of zero and nonzero normal fluxes are introduced at the surface while taking into account the effects of both Brownian motion and thermophoresis. The numerical results are found by converting the partial differential equations into ordinary differential equations. The main results of the present analysis are listed below:

  • Both temperature and nanoparticle volume fraction result in identical behaviors for Schmidt number \(\left( {Sc} \right)\) and diffusivity ratio \(\left( {N_{bt} } \right)\) effects.

  • Temperature distribution in passive control model is always greater or equal to the temperature distribution in active control model.

  • Reduced Nusselt number and reduced density of motile micro-organisms are decreasing functions of \(N_{c}\).

  • \(Sc\), \(N_{c}\), \(N_{bt} \) and \(Le\) have negligible effects on temperature in passive control.

  • In the vicinity of surface, velocity increases in both active and passive control as stretching/shrinking parameter increases, but density of micro-organisms decreases.

  • Velocity increases as buoyancy force due to temperature difference and \(R\) increases.

  • Reduced skin friction is an increasing function of λ.