Improving the genetic bee colony optimization algorithm for efficient gene selection in microarray data

Abstract

Feature selection is a very critical component in the workflow of biomedical data mining applications. In particular, there is a need for feature selection methods that can find complex relationships among genes, yet computationally efficient. Within the scope of microarray data analysis, the genetic bee colony (Gbc) algorithm is one of the best feature selection algorithms, which leverages the combination between genetic and ant colony optimization algorithms to search for the optimal solution. In this paper, we analyse in depth the fundamentals lying behind the Gbc and propose some improvements in both efficiency and accuracy, so that researchers can even take more advantage of this excellent method. By (i) replacing the filtering phase of Gbc with a more efficient technique, (ii) improving the population generation in the artificial colony algorithm used in Gbc, and (iii) improving the exploitation method in Gbc, our experiments in microarray data sets reveal that our new method Gbc+ is not only significantly more accurate, but also around ten times faster on average than the original

1 Introduction

A fundamental issue in microarray data analysis is to learn the functional relationship $\ell ( )$ between different expression levels of m sequence of genes $X=\{x_1,x_2,\ldots ,x_m\}$ and a discrete class output $C=\{c_1,c_2,\ldots ,c_t\}$. $x_j$ is a vector of real numbers, where $x_j^i\in g_i$ is the expression level of the i-th gene in the j-th sequence. C represents a finite set of possible results associated with a given sequence. As an instance, $x_j$ might be a vector of values (or sequence) associated with the cells of a tumour biopsy or the cells of the tissue of a healthy patient, whereas C represents whether the patient has cancer or not. In high-dimensional microarray data, the output C is not necessarily determined by the complete set of genes $\{g_1,g_2,g_n\}$; instead, it may be determined by a relatively small number of genes $\{\bar{g}_1,\bar{g}_2,\dots ,\bar{g}_{n'}\}$, where $n'\ll n$. In fact, finding a set of genes that approximately determine C brings three key benefits to the knowledge discovery process:

• Simplification of models, so that researchers can interpret them more easily. This allows a better understanding of the relationship between the input and the output [1].

• Shorter training time, which leads to a faster and more cost-effective microarray data classification.

• Improvement of the prediction performance of classification due to the removal of noisy genes.

Gene selection methods are able to identify and remove unneeded, irrelevant, and redundant genes from data that do not contribute to the improvement of the accuracy of a predictive model [2]. A gene selection algorithm can be seen as the combination of a search method that generates candidate gene subsets, along with an evaluation function, which assigns a score to the candidate gene subset according to its ability to uniquely determine class labels with high likelihood [1].

The simplest algorithm is to test each of the $2^n$ possible subset of genes finding the one which minimizes the error prediction rate. However, this is an exhaustive search of the space, and its computational cost is prohibitively high. Therefore, alternative search-based techniques have been constantly proposed by the machine learning community. In a broad sense, gene selection algorithms take either the filter approach, the wrapper approach, or the hybrid approach. The filter approach takes advantage of statistical properties intrinsic to data sets and aims to extract relevant genes that are effective to arbitrary classifier algorithms. By contrast, the wrapper approach aims to select relevant genes so as to improve performance of particular focused classifier algorithms, by involving the classifier algorithms in the selection process. The filters are fast while the wrappers guarantee good results. The hybrid approach takes advantage of both the filter and the wrapper: as a general rule, they are faster than wrappers and more accurate than filters. The genetic bee colony (Gbc) algorithm is a good example within the hybrid approach [3].

Gbc is a twofold algorithm, which leverage genetics and ant colony operators to guarantee not to be trapped by local optima. In the first step, Gbc uses the filter-based Mrmr algorithm to remove irrelevant and redundant genes. Only a few tens or hundreds out of hundred thousands genes are selected in this step. The main goal of feature selection is to identify features (1) that have high correlation with the target class (relevance) but (2) low mutual relevance among them (redundancy). Peng et al. [4] have proposed the algorithm named the Max-Relevance and Min-Redundancy algorithm (Mrmr), which finds approximate solutions to the aforementioned problem efficiently. Mrmr evaluates each subset of genes by the Mutual Information Difference measure $\mathrm {MID}_\alpha (\cdot , \cdot )$ defined as shown below:

$$\begin{aligned} \mathrm {MID}_\alpha (f, \emptyset )&=I(f,C); \end{aligned}$$

(1)

$$\begin{aligned} \mathrm {MID}_\alpha (f, S)&=I(f,C) - \frac{2\alpha }{k}\sum _{f'\in {}S}I(f,f'), \end{aligned}$$

(2)

where $I(f,f')$ represents the mutual information between the two genes f and $f'$. Mrmr takes the forward search approach, and hence, the variable S that holds the features selected at each iteration of the for loop (line 2–5) is initialized to the empty set (line 1). Then, for each iteration of the for loop, a single feature f that maximizes $\mathrm {MID}_\alpha (f, S)$ is added to S.

In the second step of the Gbc algorithm, the genes selected by Mrmr are combined to search for the best subset in a narrower search space. The generation of new candidate subsets is accomplished through some bio-inspired operators in the following order: (1) generation of random solutions of a population, (2) update of the solutions with more promising neighbour solutions, (3) crossover between the best solution found so far and the candidate solutions, and (4) mutation. Every candidate subset is assessed by training and testing the Support Vector Machine (Svm) in the reduced data set.

Despite Gbc is fast, very accurate, and difficult to be trapped by local optima; we found through empirical experiments that Gbc has three main gaps in its design that are still subject to improvements:

• In very high-dimensional data sets, Mrmr is relatively slow, taking around fifty percentage of the running time of the entire algorithm.

• Gbc does not use the information provided by Mrmr (i.e. the correlation of each gene with the class variable or the correlation between genes) to create an initial population of solutions closer to the global optima. The initial solutions are created at random, instead.

• During the search, no useful information that can give insight on the quality of the features is stored or analysed. Taking advantage of such information may lead to a significantly faster convergence.

We address these issues as follows.

• 1. We propose changing the Mrmr method by the Mrmr+ [6], which finds the same solution of Mrmr, but is significantly faster.

• 2. To generate subsets in the initial population of Gbc, we propose a new function that leverages the correlation scores given by Mrmr to efficiently create diverse solutions while being closer to the optimal solution.

• 3. During the entire search, we constantly predict the goodness of a gene, by observing the effect of adding such features to the candidate solutions in the population. Later on, the goodness of a gene is used to discover the level of interaction among genes. Genes with high interaction score are then likely to be grouped in the same subset, while the creation of subsets with genes with low interaction score is avoided. This method tends to make Gbc converging faster and escaping from local optima.

Section 2 gives a brief explanation of Gbc algorithm. In Sect. 3, we formally present our contribution as an improvement of Gbc algorithm and propose a new algorithm called Gbc+. In Sect. 4, we make an extensive evaluation by comparing the proposed algorithm Gbc+ with other four feature selection benchmark algorithms in 16 microarray data sets.

2 Genetic bee colony for gene selection

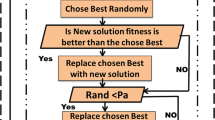
Gbc is a novel hybrid meta-heuristic algorithm that takes advantage of two bio-inspired methods: genetic algorithms (Ga) and artificial bee colony (Abc) optimization algorithm. As Fig. 1 shows, Gbc is composed of five phases. In the Preprocessing phase, the grand majority of features are removed by the filter-based Mrmr algorithm. Afterwards, the first SN candidate solutions are randomly generated in the initialization phase similarly to the initialization phase in the Abc meta-heuristic algorithms [7].

Fig. 1

Main phases of the Gbc algorithm

In the Employee Bee phase, the genetic crossover operation is performed between the Queen Bee, which is the best solution found so far and solutions randomly chosen from the population, to generate new diverse solutions closer to the optima. Subsequently, the Scout Bee phase is accomplished by resetting the solutions trapped by local optima. Also, in this phase, the genetic mutation operation is performed over the Queen Bee to intensify the search. The search stops when a number of generations are accomplished. Usually, the number of generations is equal to 100 [3]. The candidate solutions are evaluated by testing the Svm classifier using the leave-one-out cross-validation procedure. In addition to represent a candidate solution, a binary representation is used (0 for a gene not selected and 1 otherwise) as suggested in [3]. In the remainder of this section, we briefly explain the different phases aforementioned.

2.1 Phase 1: the preprocessing phase

In high-dimensional microarray data sets, with hundred of thousands of genes, it is infeasible to apply evolutionary algorithms such as Ga and Abc. Therefore, Gbc takes advantage of the filter-based algorithm Mrmr to remove irrelevant and redundant genes at the very beginning of the search to narrow down the space of solution from $2^n$ to $2^{qt}$ subsets, with $qt\ll n$.

Fig. 2

Preprocessing phase in the Gbc algorithm. t is usually fixed to 50 genes

As shown in Fig. 2, Mrmr is run several times until the stopping criteria are met. In each run, Mrmr returns the subset selected in the previous run plus t additional genes. The preprocessing phase stops when the returned subset can uniquely determine the class variable. That is $\mathrm{SVM}(G)=1.0$, being $\mathrm{SVM}(G)$ the accuracy reached by the classifier Svm in the reduced data set composed of the current qt genes in G.

2.2 Phase 2: the initialization phase

In the second phase, Gbc generates the initial population composed of SN solutions. Each solution is represented as a group of genes indices that are selected from the subset G, returned by the Mrmr algorithm. To build a solution, a linear forward selection search is performed. That is, a gene is randomly selected from G and then is tested in the current solution. If the current solution improves by adding the gene, then we continue adding genes while the current solution improves. The solution is built when a gene does not improve it. The i-th gene in a solution is randomly selected according to the following equation:

$$\begin{aligned} x_j^i=\mathrm{rand}(0,1)\times qt, \end{aligned}$$

(3)

where $\mathrm{rand}(0,1)$ represents a random number generator in the range of [0,1) with a normal distribution.

2.3 Phase 3: the employee bee phase

In the artificial bee colony (Abc) population-based algorithm, the colony consists of three group of bees: employee bees, onlooker bees, and scout bees [8]. The position of a food source represents a potential solution while the amount of nectar in a food source corresponds to the accuracy of the associated solution. The Abc optimization problem consists in finding the food source with higher amount of nectar through the social cooperation of bees.

Gbc algorithm uses this analogy to improve the current population of solutions. Gbc sends the employee bees to search in the neighbour of the current SN solutions (food sources) to find solutions that may be closer to the global optima. A neighbour solution is determined by changing the index genes of a current solution by the following equation:

$$\begin{aligned} v_j^i= {\left\{ \begin{array}{ll} x_j^i + K &{} \text {if }|S|-K > x_j^i \\ x_j^i - K &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(4)

with $K=\mathrm{rand}(-1,1)\times (x_j^i-x_j^k)$, where $\mathrm{rand}(-1,1)$ denotes a random real number in the range of $[-1,1]$ and k is a random integer number in $[0,SN-1]$.

2.4 Phase 4: the onlooker bee phase

In Gbc, the crossover operation is used to share information between employee and onlooker bees in the optimization search space (hive). The employee bees indicate their location of the food sources to the onlooker bees, by a waggling movement.

Fig. 3

Crossover operation between the Queen Bee and a solution randomly selected from the population. The crossover parameter was fixed to 0.6 as recommended in [3]

As Fig. 3 depicts, the crossover operation is accomplished by the Queen Bee, which is the best solution found so far, and a solution randomly selected from the current population of bees. The probability a solution has to be selected depends only on its accuracy and can be computed as follows:

$$\begin{aligned} P(x_j)=\frac{\mathrm{SVM}(x_j)}{\sum _{k=1}^{SN}\mathrm{SVM}(x_k)}. \end{aligned}$$

(5)

Uniform crossover works by treating each gene independently and making a random choice as to which parent it should inherit, as shown in Fig. 3.

2.5 Phase 5: the scout bee phase

In the Gbc algorithm, the scout bee phase is twofold. First, we check all the employee bees in the population and reset all those that have been trapped by local optima. This is achieved by counting the number of times c that we perform an operation in a solution with no improvements. At this point, if $c>\delta$, then we replace the solution with a new subset randomly generated. $\delta$ represents the consecutive number of times we allow a solution to fail on its attempt to be improved. Usually, $\delta =5$ is used.

Fig. 4

Percentage of time required by Mrmr (the lighter area) in the Gbc algorithm

Second, a mutation operator is applied to the Queen Bee to intensify the search in the neighbourhood of the best solution found so far. Consequently, for each gene in the Queen Bee, we generate a random number r in [0, 1] and if $r<\alpha$ then the i-th gene mutates according to the following equation:

$$\begin{aligned} v_j^i= {\left\{ \begin{array}{ll} \mathrm{Queen}B^i + K &{} \text {if }|S|-K > \mathrm{Queen}B^i\\ x_j^i - K &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(6)

with $K=\mathrm{rand}(-1,1)\times (\mathrm{Queen}B^i-x_j^k)$, where $\mathrm{rand}(-1,1)$ denotes a random number generator in the range of $[-1,1]$, k is an integer random number in $[0,SN-1]$, and $\mathrm{Queen}B$ is the best solution found so far. Usually, $\alpha =0.01$ is used.

3 Our proposal

Since we are especially interested in high-dimensional data, we made some modifications to the Gbc algorithm, so that Gbc could be effectively used in high-dimensional domains. In this section, we present some improvements made to the Gbc algorithm in terms of efficiency and accuracy.

3.1 First phase of Gbc: the Mrmr algorithm

Mrmr is used in Gbc as a filter to remove redundant and irrelevant genes prior to the population-based search. Although Mrmr drastically reduces the search space, we have found that the time taken by Mrmr is extremely large in relation to the total running time of Gbc. Figure 4 depicts the percentage of the running time of Mrmr in Gbc (lighter area), and the percentage of the running time of the rest of the algorithm (darker area). The data sets used are six microarray data sets from the Rough Sets and Current Trends in Computing conference (RSCTC’2010) discovery challenge [9]. The data sets in Fig. 4 are sorted according to their number of genes. The number of genes and number of instances of these data sets can be found in Table 2. As can be seen, for the first three data sets, which have fewer genes, the running time of Mrmr is nearly to the fifty percentage of the entire running time of the Gbc algorithm, while for the remaining of the data sets, the running time of Mrmr represents more than the sixty percentage of the total running time.

In fact, at each iteration, Mrmr computes $\mathrm {MID}_\alpha (f, S)$ for $(n - k + 1)$ features, and $\mathrm {MID}_\alpha (f, S)$ includes k values of mutual information. Hence, the algorithm computes $(n - k + 1)k$ mutual information values at each iteration, and the total number of computing mutual information is

$$\begin{aligned} \sum _{k=1}^q (n - k +1)k = \frac{(3n - 2q + 2)q(q+1)}{6}, \end{aligned}$$

(7)

where $n = \vert \mathbb {F}\vert$. This number is not small enough to perform gene selection on large microarray data sets [5].

In [6], we present a solution to this problem by proposing the algorithm Mrmr+, which finds the same set as Mrmr, but in a significantly shorter time. Our experiments in very high-dimensional data reveal that Mrmr+ is 13 times faster than Mrmr on average [6]. Therefore, we may expect a significant improvement in terms of efficiency when we replace Mrmr with Mrmr+ in the Gbc algorithm. To test the effect of replacing Mrmr with Mrmr+ over Gbc, we run experiments in the RSCTC’2010 challenge data sets and collect the running time of both versions as shown in Fig. 5.

Fig. 5

Comparison of running time (in seconds) in the Gbc algorithm when using the original Mrmr and the faster Mrmr+ in the filter phase. The area with the + symbol represents the Mrmr+ while the darker area is the running time of the rest of the Gbc algorithm. Results of the original Gbc are on the right of the Mrmr+

In all cases, Mrmr+ is more than two times faster than the original Mrmr, which significantly improves the running time of Gbc.

3.2 Initialization phase

Most population-based techniques for solving optimization problems in artificial intelligence generate the first solutions of the population randomly. While this is essential to ensure diversity at the early stage of the search, it also may affect the convergence speed of the algorithm. Gbc, in the initialization phase, does not make use of neither the relevance nor the redundancy scores of each gene, computed by Mrmr, to build the SN initial solutions. Instead, Gbc selects features at random. Since we work with high-dimensional microarray data, we are very interested in making Gbc to converge faster towards the most promising solutions. Therefore, in the initialization phase, we propose to make use of the relevance and redundancy score of each gene, which are computed by Mrmr in the previous phase, to efficiently create an initial population composed of diverse, but accurate solutions.

We define our proposal as follows. Given a set of all genes sorted according to the order they were selected by Mrmr, we randomly select a feature and test it in the current solution (initially the empty solution), if the accuracy of the current solution is increased, then we add the gene; otherwise, we stop the search and start creating a new solution by the same procedure. This is, in fact, the same procedure Gbc uses to create the initial population. However, additionally we assign to each gene $g_i$ a probability $P_{\gamma _j}(i)$ to be selected when creating the j-th solution as follows:

$$\begin{aligned} P_{\gamma _j}(i) = \frac{1-\gamma _j}{1-\gamma _{j}^n}\times \gamma _j^{i-1}, \end{aligned}$$

(8)

where n is the number of features in the data and $\gamma _j$ is a decreasing function in the range of (0, 1) as follows:

$$\begin{aligned} \gamma _j=1-\frac{1}{j+1} \end{aligned}$$

(9)

Figure 6 represents the shape of the probability function $P_{\gamma _j}(i)$. As can be inferred from Fig. 6, $P_{\gamma _j}(i)$ has several properties:

• First, as a probability function, $P_{\gamma _j}(i)$ is exhaustive, that is: $\sum _{i=1}^n P_{\gamma _j}(i)=1$.

• Second, $P_{\gamma _j}(i)$ is a decreasing function. Therefore,

  $$\begin{aligned} P_{\gamma _j}(1)>P_{\gamma _j}(2)>\dots > P_{\gamma _j}(n), \end{aligned}$$

  (10)

  always holds. This means that first genes in the ranking are likely to be selected. Genes will be ranked in the same order they were selected by the Mrmr algorithm. Therefore, the first genes in the ranking are highly correlated with the class variable and are not highly correlated with other features in the ranking.

• Third, the larger the number of solutions already built, the more equal are the probabilities to be chosen for all genes. That is,

  $$\begin{aligned} P_{\gamma _t}(i)>P_{\gamma _{t+1}}(i)>\dots > P_{\gamma _{SN}}(i). \end{aligned}$$

  (11)

  However, for a sufficiently large value of j, for example, with $SN/2\le k\le SN$,

  $$\begin{aligned} P_{\gamma _{k}}(1)\approx P_{\gamma _{k}}(2)\approx \dots \approx P_{\gamma _{k}}(n), \end{aligned}$$

  (12)

  holds.

Fig. 6

Chart representing the probability of choosing feature $f_i$ to be tested in the j-th solution

$P_{\gamma _{j}}(i)$ guarantees that the first solutions are likely to contain genes with high correlation with the class and low correlation with the other genes. Therefore, these solutions may have high accuracy. For the rest of the solutions, the probability of selecting any gene tends to 1 / SN. Consequently, we can expect that the initial population will be composed of two types of solutions: solutions with high accuracy and random solutions. This creates a good synergy in the search since now we have a diverse population with some accurate solutions that may make the algorithm converge faster. To evaluate our proposed method, we run experiments in several data sets and measure the accuracy of the solutions in the population of the original method (grey curve) and the proposed (black curve). Figure 7 depicts the results. To build the chart, we sorted the solutions according to their accuracy for both methods.

Fig. 7

Accuracy of the solutions in the population of the original method (grey) and the proposed method (black curve). A number of selected genes are located over each solution. a DA1, b DA2, c DA3, d DA4, e DA5, f DA6

Fig. 8

Comparison between the original Gbc (grey points) and Gbc with the proposed method of intensification (black points). The line between two black points quantifies an improvement in the Queen Bee by the proposed method. a DA1, b DA2, c DA3, d DA4, e DA5, f DA6

3.3 Intensification

Meta-heuristic optimization algorithms often perform well approximating solutions because they first diversify the search looking for candidate solutions without making any assumption about the underlying fitness landscape. Second, they intensify the search looking for more promising solutions once they explore diverse regions in the solution space. In Gbc, the intensification process is accomplished by means of the genetic crossover and mutation operations in the onlooker bee and scout bee phases, respectively. However, through experiments, we realized that in the scout bee phase the mutation operation, described in Sect. 2.5, does not make any effect in the intensification process due to the extremely low mutation probability of genes. To carry out a richer intensification process, we adopt the following method.

• First, we determine the goodness of a gene according to its occurrence in the solutions of the population. A gene $f_i\in {}S$ that is in solutions S, with $\mathrm{SVM}(S)>\mu$, and is not in solutions R, with $\mathrm{SVM}(R)\le \mu$, must have high goodness. We define the goodness $\ell (f_i)$ of feature $f_i$ as follows.

  $$\begin{aligned} \ell (f_i)=\frac{\sum \nolimits _{S\in P}\delta ^+_{f_i,\mu }\times \mathrm{SVM}(S)}{\theta ^+}- \frac{\sum \nolimits _{S\in P}\delta ^-_{f_i,\mu }\times \mathrm{SVM}(S)}{\theta ^-}, \end{aligned}$$

  (13)

  where $\delta ^+=1$ if $\delta ^+>\mu$ and $\delta ^+=0$ if $\delta ^+\le \mu$, being $\mu$ the average of the fitness of all solutions in the population, $\delta ^-$ has opposite value to $\delta ^+$, and $\theta ^+$ and $\theta ^-$ are the sum of the fitness of all solutions S in the population such that $\mathrm{SVM}(S)>\mu$ and $\mathrm{SVM}(S)\le \mu$,respectively. $\ell (f_i)$ is a normalized coefficient in the range of $[-1,1]$. A value of 1 means gene $f_i$ is in all solutions where $\delta ^+_{f_i,\mu }=1$ and is not in any solution where $\delta ^-_{f_i,\mu }=1$. A value of $-1$ means $f_i$ is present in all solutions where $\delta ^-_{f_i,\mu }=1$ and not in any solutions with $\delta ^+_{f_i,\mu }=1$.

• Second, we sort the genes according to their goodness $\ell$ and store them in two different sets. Genes with $\ell (f_i)>0$ are sorted in increasing order and stored in $S^+$ while genes with $\ell (f_i)\le 0$ are sorted in decreasing order and stored in $S^-$. Afterwards, we run a greedy forward selection search starting with the Queen Bee solution and using genes in $S^+$. That is, we test adding to Queen Bee, all genes in $S+$, one by one, and the gene that maximize $\mathrm{SVM}(\mathrm{Queen}B\cup \{f_i\})$ is added to QueenB. We stop searching when neither of the genes improves the current QueenB. Subsequently, a greedy backward search is performed using the genes in $S^-$. That is, we start with the current Queen bee and test eliminating genes in $S^-$ from QueenB, if present. The gene that maximizes $\mathrm{SVM}(\mathrm{Queen}B\setminus \{f_i\})$ is removed from QueenB. The search stops when no feature improves QueenB.

To test our method, we run Gbc twice for each data set: first, we run the original Gbc and second we replace the mutation operation with our proposed intensification method. Figure 8 depicts the results. The line between two black points quantifies an improvement in the Queen Bee by the proposed method.

3.4 Minor improvements

In addition to the improvements we have proposed in the previous sections, we have detected some small gaps on the design of the original Gbc that could lead to undesirable results. Our final proposals are as follows.

• First, we consider two more stopping criteria in the Gbc algorithm: (i) stopping the search when $\mathrm{SVM} ($QueenB$)\ge \lambda$ and (ii) stopping the search when the current QueenB remains the same after t consecutive cycles.

• Second, we implement a lookup table that stores the solutions already evaluated and their respective accuracy. Every time a candidate solution is going to be evaluated, we inspect the lookup table to avoid duplicated evaluations.

These modifications may look naive. However, we run experiments to determine the evaluations saved by implementing these modifications in the original Gbc algorithm and results were very impressive. Table 1 shows the results. We report that in neither of the data sets the accuracy varies with respect to the original Gbc.

Table 1 Percentage of time saved by the minor improvements respect to the original Gbc algorithm

Table 1 represents how efficient the minor improvements are. The results are expressed as % of number of evaluation saved/percentage of running time saved. For example, for the Da1 data set, the 79 and 41% were saved with respect to the number of evaluations and running time of the original Gbc algorithm, respectively.

4 Experimental evaluation

4.1 Experimental set-up

To validate our proposed algorithm Gbc+, we run experiments and collect the running time, the accuracy of each algorithm, and the number of genes selected. We compare our proposed algorithm with four feature selection algorithms, including Gbc.

For each data set, we generate m pairs of training and test data subset, where m is the number of instances in the data. Each test data subset represents an instance in the data set, and the training data subset is composed of the rest of the instances. First, we run the feature selection algorithms in the training data and then we reduce the test data according to the features eliminated by the algorithms. Second, we train the C-SVM-with-RBF-Kernel classifier with the reduced training data and then test them on the reduced test data to determine the Area Under the Receiver Operating Characteristic curve (AUC-ROC) score. In addition, the average of the running time taken by each algorithms and the number of genes selected, when is applied to the training data, is collected. In the comparison, we use four feature selection algorithms: Gbc, Mrmr-Ga [10], Mrmr-Ba [11], and Pso [12], which are population-based algorithms. Mrmr-Ga is very similar to Gbc, but after running Mrmr, uses a genetic algorithm to search for the optimal solution. Mrmr-Ba is also a meta-heuristic algorithm that also uses Mrmr as a filter in the first phase to narrow down the search space. In the second phase, Mrmr-Ba uses the Bat algorithm, which is a bio-inspired technique that emulates the echolocation behaviour of bats. The Pso algorithm is the Particle Swarm Optimization algorithm implemented in weka [13]. However, we have added a first phase by running Mrmr to reduce the search space as in the Gbc algorithm. All the algorithms use as evaluation function the accuracy of the Svm when tested in the given subset to evaluate.

Table 2 shows the characteristics of the data sets used in the experiments, which were collected from two machine learning data repositories: Open Machine Learning [14] and Machine Learning Data; and the feature selection challenge RSCTC’2010 [9].

Table 2 Characteristics of the data sets used in the experiments

4.2 Accuracy

Table 3 shows the Auc values of the support vector machine classifier over the reduced sets output by every algorithm. Surprisingly, Gbc+ wins in 11 data sets while in the other data sets gets the best results with ties. The other algorithms got good results in a general sense. However, the results of Gbc+ are outstanding .

Table 3 Accuracy of SVM in the reduced sets outputted by different feature selection algorithms in several data sets

To detect significant differences among algorithms, we compute averaged ranking and the critical distance as stated in the Nemenyi test. Figure 9 shows the critical distance chart, where the group of algorithms that has no significant differences are connected by a thick line. From Fig. 9, we state that Gbc+ is significantly more accurate than the rest of the algorithms, in these data sets with a confidence of 90%. However, results of the rest of the algorithms are not significantly different.

Fig. 9

Nemenyi post hoc chart. Group of algorithms with no significance difference are connected by the thick lines with a confidence of 90%

Table 4 Running time of the feature selection algorithms in several data sets

Table 5 Number of genes selected by the feature selection algorithms in several data sets

4.3 Running time and number of features selected

Speaking about the running time, Gbc+ is the fastest in all data sets. In fact, Gbc+ is ten times faster than Gbc on average. Moreover, through a deep analysis of Gbc+ behaviour, we discover that although the intensification procedure proposed in Sect. 3.3 may increase the accuracy of Gbc+, it also may have a negative impact on its efficiency. We discovered that the intensification process tends to increase the number of features in the QueenBee. Therefore, in the crossover operation, all the solutions in the population grows in number of features, which makes the rest of the procedures in the algorithm very heavy and high costly. Although we do not have a solution to this problem at the moment, Gbc+ is still fast. Speaking about the number of features selected, we realize that all the algorithms get good results. However, algorithm Gbc gets the best results in general (Tables 4, 5).

5 Conclusions

In this paper, we deeply analyse the Gbc algorithm and point out some drawbacks on its design. We improve the Gbc algorithm by improving the filter phase, where we speed up the Mrmr algorithm. In addition, we create a new mechanism to generate initial solutions that are closer to the local and global optima. In this sense, we expect the new algorithm to converge faster. Finally, we propose the implementation of a new intensification procedure that leads to a substantial improvement in the accuracy of Gbc. Experiments reveal that the new version of Gbc is significantly faster and more accurate than its original version and other three state-of-the-art algorithms.