Introduction

Polyethylene terephthalate (PET) is the most important commercial member of thermoplastic polyesters produced globally. The final properties of PET parts are related to its microstructure, which is formed during the production process or its cycle life. Amorphous and semi-crystalline are the two main types of microstructures that are constructed based on thermomechanical history. Differential scanning calorimetry (DSC) is the most widely used in crystallization studies. In the cooling and heating curves, amorphous polymers show the glass transition temperature (Tg), which is the change from the glassy state to the melt phase. Apart from Tg, semi-crystalline polymers also exhibit additional transitions, such as crystallization and melting [1]. Reorganization of polymer morphology, structure and chain conformation can affect the crystallization kinetics and final properties [2]. Recently, a three-phase model for thermoplastic polyesters, especially PET, has been presented. It was concluded that PET consists of a large fraction of rigid amorphous region [3]. Manipulating crystallization variables makes it possible to reach a great variety of microstructures. PET morphology and its effect on properties have been studied by many researchers. Jog [4] presented an outstanding review on the crystallization of PET. Controlling the crystallization process can affect the orientation and crystallite perfection. Therefore, properties of the final products could be found by acquiring deeper insight into the crystallization process [4]. Pressure, molecular weight, catalyst and production conditions affect the crystallization behavior of PET in either isothermal or non-isothermal processes [5,6,7,8]. Crystallization rate, morphology, and other characteristics could be manipulated by adding a nucleating agent. Up to the present various nucleating agents, such as talc, sodium benzoate, ionomer Na+, calcium carbonate and cassava starch have been reported [9,10,11]. Even sodium salts, such as –CO2Na, –ONa, SO3Na and –PO3Na, as nucleating agent, have been added to PET through the in situ polymerization and crystallization of PET [12]. Chemical structure manipulation, such as copolymerization, branching and compounding, are among interesting methods to change crystallization behavior [13,14,15]. The crystallization behavior and mechanical properties of PET and polylactic acid (PLA) blends were investigated during an in-depth study [16]. Different techniques have been employed to study the crystallization kinetics, in which measurement of density is applicable [17]; X-ray diffraction has been applied to determine the degree of crystallinity of PET-oriented films and fibers [18,19,20]; terahertz time-domain spectroscopy (THz-TDS) has been harnessed to monitor the isothermal crystallization kinetics of amorphous PET [21]; Raman spectroscopy has been utilized to study the kinetics of an initially quasi-amorphous PET [1]. DSC is among the most effective thermal analysis methods for studying the structure and properties of polymers [2, 22]. Moreover, knowledge of crystallization could have a variety of industrial applications, such as preparing PET granules upon solid-state polymerization (SSP) to reach higher molecular weights [23]. Moreover, polymers have been used as a nucleating agent in crystallization processes [24]. It is well known that PET has a secondary crystallization phenomenon [25]; hence, the overall crystallization consists of primary and secondary ones [26]. Primary and secondary crystallization processes occur simultaneously, affecting kinetics parameters [27]. Crystallization kinetics of isothermal and non-isothermal mathematical modeling are under investigation. Providing mathematical models for crystallization kinetics, isothermal or non-isothermal, is a valuable tool for applying the required microstructure of semi-crystalline polymers. Many Models have been introduced, such as Avrami, Ozawa, Ziabicki, Tobin, Hay, Nakamura, etc. [28, 29]. The Avrami model has been the most reported model for various polymers [30,31,32]. A review of the literature shows that the crystallization kinetics of polymers, such as PET, has been under intensive investigation. However, ongoing research and recent achievements in this field make it necessary to apply these results to PET. The use of new models, such as the Hay model, has not been reported. Moreover, most of the reported data are within a small range of cooling rates. The crystallization behavior of commercially available PET can be affected by the additives present. Studies on neat PET can help to estimate additive effects. In this work, PET was synthesized through two-step esterification and polycondensation method, and PET samples with no additives and fillers were obtained. Upon characterization of the PET samples, using FTIR and NMR, non-isothermal crystallization was studied using DSC under a wide range of cooling rates, namely, 5, 10, 15, 20, 30 and 40 K/min from a melt state. Different kinetics models were applied by evaluating their related parameters. Due to the convergence problem in model fitting, an algorithm was depicted to reach the regression coefficient as close as possible to 1.0000. Such results can be used in processing of polymers to have final products with various applications. Moreover, this is the first time that Tobin, Hat and Nakamura's models are applied to PET over such a wide range of cooling rates.

Experimental

Materials

The primary reactants used are ethylene glycol (EG) and terephthalic acid (TPA), which were supplied by Shahid Tondgooyan Petrochemical Company (STPC). Antimony oxide, as the polycondensation catalyst, was prepared by Polychem Industrial Co., Ltd., China. Dichloroacetic acid as a solvent in measuring intrinsic viscosity, ortho-cresol and chloroform as solvents in measuring the acid end group, and potassium hydroxide as a potentiometry agent were bought from Merck Co., Germany.

Synthesis of polyethylene terephthalate

All samples were prepared in a home-made laboratory-scale reactor. This setup consists of a one-liter stainless steel reactor, EG condenser, water separator, heating system, and vacuum pump as the main constituents of the system. Some preliminary runs were performed to determine the suitable synthesis condition to obtain a polymer with adequate intrinsic viscosity and molecular weight. In each run, 248.70 g of EG and 475.5 g of TPA were agitated for 20 min in laboratory conditions before pouring into the reactor. Next, the reactor was completely sealed. During the esterification step, the EG condenser temperature was 433 K. The inner reactor temperature was controlled above 468 K, around 2 bar pressure and agitated for 15 min. Next, the mixture temperature and pressure were elevated to 528 K and 5 bar, respectively. Water production is an indication of esterification reaction. The condensed water was collected every 15 min to determine the reaction progress. The esterification step terminates whenever that water production stops. In the next step, the amount of 0.19 g Sb2O3 was added to the system and the temperature was increased to 548 K, and a vacuum was applied to help EG removal and polycondensation progress. The synthesized PET was removed from the reactor after 2 h. The mixing rate was constant at 100 rpm over the whole process. Polymer weight in each batch was about 550 g.

Characterization of polymer

The intrinsic viscosity (IV) of samples was measured using solution viscometry based on ISO-1628-5 standard using a Lauda-Konigshofen viscometer at 298 ± 0.1 K. To do so, the solution of polymer in the dichloroacetic acid with 10 mg/mL concentration was prepared through agitating at 373 K. The acid end groups of samples were determined by gravimetric methodology. A solution containing 1 g of PET in a 70:30 mixture of ortho-cresol/chloroform was prepared under heating and reflux. The mixture was titrated with 0.5 M KOH solution in ethanol using a model 798 MPT Titrino Metrohm titrator with a Solvotrode model electrode. The potentiometry and Tiamo 2.4 software were used to determine the titration end. Acid number (AN) is the concentration of acidic group at the end of esterification.

The DEG content of samples was determined using a GC3800 model of Varian Co., gas chromatography. Hence, 1–1.5 g of sample in 30 mL methanol was prepared at 493 K for 2 h. Consequently, the mixture was cooled down, and dimethyl terephthalate crystals were separated using filtration. A BYK spectrophotometer was applied to measure L and b parameters as color indices. The amount of 5–10 mg PET with KBr was mixed to form a pellet for FTIR spectroscopy. FTIR spectra were produced using a Bruker FTIR spectrometer. Sample solution in trifluoroacetic acid, including CDCl3, the detector locking, was prepared to obtain an 1H NMR spectrum using a Bruker 400 MHz Ultra Shield branded instrument. A Swiss-made Mettler Toledo, 822e model instrument was applied to plot DSC curves. First, samples were heated and kept at 573 K for 3–5 min to eliminate their history. Accordingly, the samples were cooled as quickly as possible to obtain an amorphous polymer. Next, the sample was heated with a heating rate of 10 K/min to determine Tm. For non-isothermal tests, the sample was heated to 573 K, kept for 3–5 min and cooled at a cooling rate of \(\Phi\). After cooling down to the ambient temperature, the samples were heated again with a heating rate of 10 K/min to evaluate Tg, Tm, recrystallization and melting.

Results and discussion

PET samples were prepared based on the procedure that was explained in the experimental section. Also, the repeatability of the synthesis method was studied. The characterization of samples revealed that PET samples with the following features were produced: IV = 0.5, \(\overline{M}_{n}\) = 9650 Da, AN = 30 mg/KOHg at the end of the esterification step; AN = 30 mg/KOHg of the final sample; DEG = 1.54% (by weight), L = 89.8, b = 6.8, and melting point = 524.6 K. Number-average molecular weight was estimated based on the following equation [33]:

$$\left[ \eta \right] = K\,\overline{M}_{n}^{a} = 67 \times 10^{ - 4} \,\overline{M}_{n}^{0.47} .$$
(1)

Hence, polymer with suitable IV, molecular weight, and melting point was produced. The samples showed AN less than 35 mg KOH/g, DEG less than 3% (by weight), and COOH less than 25, indicating acceptable PET samples produced from a commercial point of view.

FTIR spectra

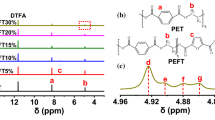
Figure 1 represents the FTIR spectra of the synthesized PET sample. All related peaks are presented, and their assignment is consistent with the literature [34]. Table 1 presents a list of observed peaks in the spectra [34]. fingerprint peaks are as follows: the peak at 1250 cm−1 for c–o–c asymmetric stretching/CCH asymmetric bending, the peak at 1720 cm−1 for C–C ring stretching/C=O stretching, the peak at 720 cm−1 for OCH symmetric bending and the peak at 3070 cm−1 for C–H aromatic stretching. Therefore, the presence of such bonds approved the production of PET.

Fig. 1
figure 1

FTIR spectra of prepared PET

Full size image
Table 1 FTIR characteristic peaks of PET sample
Full size table

1H NMR analysis

Figure 2 depicts the 1H NMR spectrum of the PET sample. The corresponding protons shifts are also illustrated in Fig. 2, which are in agreement with the literature [35, 36]. Hence, PET was successfully synthesized, as it is consistent with the FTIR result.

Fig. 2
figure 2

H NMR spectrum of PET sample

Full size image

Thermal behavior

Figure 3 illustrates the DSC plots of cooling curves with \(\Phi =\) 5, 10, 15, 20, 30 and 40 K/min cooling rates. These cooling rates were chosen according to the opinion of researchers reported in published articles. The data were plotted in three-dimensional coordinates to compare the crystallization trends. It is observed that the crystallization trend changes with changes in \(\Phi\). There is a bimodal trend for \(\Phi = 15\) and 20 K/min. It is well known that PET presents primary and secondary crystallization. Dominance of primary or secondary crystallization depends on many parameters such as cooling rate. A bimodal peak is observed whenever both the primary and secondary regimes are comparably present [2, 3]. Hence, there is a change in the nature of crystallization form \(\Phi = 5\) to 40 K/min. The overall degree of crystallinity during cooling is calculated by:

$$\chi_{{\text{C}}} = \frac{{\Delta H_{{\text{C}}} }}{{\Delta H_{{{\text{C}}\;\infty }} }},$$
(2)
Fig. 3
figure 3

DSC curves of sample cooling at different cooling rates

Full size image

where\(\Delta H_{{\text{C}}}\) and \(\Delta H_{{{\text{C}}\;\infty }} = 84.52\;\;{{\text{J}} \mathord{\left/ {\vphantom {{\text{J}} {\text{g}}}} \right. \kern-\nulldelimiterspace} {\text{g}}}\) are the measured heat of crystallization and complete crystallized PET, respectively [7]. The same calculation could be performed using melting enthalpy. The heat of fusion for crystallite PET is found to be \(\Delta H_{m}^{0} = 117.4\;{{\text{J}} \mathord{\left/ {\vphantom {{\text{J}} {\text{g}}}} \right. \kern-\nulldelimiterspace} {\text{g}}}\) [37]. Table 2 presents the numerical values of different parameters. Figure 4 shows the DSC curves of the heating step. In Fig. 4, the peaks related to Tg, recrystallization and melting are detectable. Corresponding data are also presented in Table 2.

Table 2 DSC data results at various cooling rates*
Full size table
Fig. 4
figure 4

DSC heating curve of PET samples

Full size image

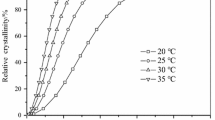
Analysis of data in Table 2 reveals valuable results. In Fig. 4 and Table 2, it can be found that there is a slight change in Tg. Therefore, the cooling rate and variation in the overall degree of crystallinity and quality of crystallites have no meaningful impact on the glass transition temperature. A typical DSC heating curve of partially crystallized PET shows the glass transition and melting temperatures as well as a recrystallization peak, at times called cold crystallization [4]. DSC heating curves for \(\Phi = 5\) and 10 K/min show no recrystallization. It is deduced that at slow cooling rates such as \(\Phi = 5\) and 10 K/min, crystallization is complete. However, at higher cooling rates, partial crystallization happens. A higher cooling rate gives less crystallization. Therefore, in heating curves, a larger recrystallization peak is observed. Nevertheless, the location of recrystallization peaks remains unchanged. The same is valid for melting temperature. For samples without recrystallization, the melting point is around 522 K, while it is around 519 K for samples with recrystallization. Although the difference is not much, it can be attributed to the quality and quantity of crystals. Small dependency of Tm was also reported previously [1]. DSC curves of \(\Phi = 5\) and 10 K/min present a small shoulder in the beginning of melting peaks. Such a shoulder was reported previously and contributed to the existence of microcrystallite that is formed in the boundary layer between the larger crystallites [11]. Even the presence of three melting points was also reported [38]. Thermal history is one of the most important reasons for such observation. It is observed that TC and \(\chi_{C}\) are strongly a function of \(\Phi\). Figure 5 presents TC and \(\chi_{C}\) versus \(\Phi\). It is interesting that both TC and \(\chi_{C}\) change linearly. Also, in the literature, it was reported that crystallization exotherms shift to lower temperatures with increase in \(\Phi\) [2, 7], which can be explained by the dynamic nature of crystallization. Crystallization consists of nucleation and growth steps. At higher cooling rates, longer time is required for sufficient nucleation, which means lower temperatures. A linear function was fitted on each data with an acceptable regression coefficient.

Fig. 5
figure 5

Crystallinity temperature and percent versus cooling rate

Full size image

Crystallization kinetics modeling

To study the crystallization kinetics, it is necessary to obtain a degree of crystallinity. DSC data were used to calculate the degree of crystallinity,\(\chi_{t}\), with respect to time, by integrating the areas under exothermic peaks:

$$\chi_{t} = {{\int\limits_{0}^{t} {\frac{{{\text{d}}H_{t} }}{{{\text{d}}t}}{\text{d}}t} } \mathord{\left/ {\vphantom {{\int\limits_{0}^{t} {\frac{{{\text{d}}H_{t} }}{{{\text{d}}t}}{\text{d}}t} } {\int\limits_{0}^{\infty } {\frac{{{\text{d}}H_{t} }}{{{\text{d}}t}}{\text{d}}t} }}} \right. \kern-\nulldelimiterspace} {\int\limits_{0}^{\infty } {\frac{{{\text{d}}H_{t} }}{{{\text{d}}t}}{\text{d}}t} }},$$
(3)

where\({{{\text{d}}H_{t} } \mathord{\left/ {\vphantom {{{\text{d}}H_{t} } {{\text{d}}t}}} \right. \kern-\nulldelimiterspace} {{\text{d}}t}}\), \(t\) and \(\chi_{t}\) are heat flow, time, and degree of crystallinity, respectively. In the following, various models are introduced to calculate the degree of crystallinity:

Modified Avrami model

The modified Avrami model is the basis for the most presented models. The Avrami model has been the most discussed model, giving the degree of crystallinity with respect to time:

$$\chi_{t} = 1 - \exp \left( { - k \cdot t^{n} } \right),$$
(4)

where\(k\) is the kinetic constant (a function of nucleation and growth rate), and \(n\) is the Avrami exponent (indicating nucleation mechanism). The main assumptions in this model are as follows: complete crystallization of samples, no change in volume throughout the process, constant growth rate and no secondary crystallization [28]. Initially, Avrami suggested this model for isothermal crystallization; then, it was modified and extended to non-isothermal models. In the latter case, the parameters concept would not be the same. It is well known that there is an incomplete crystallization, as given in Table 2 and shown in Fig. 5; Wunderlich introduced the final degree of crystallinity, \(\chi_{\infty }\), into the model to calculate relative crystallinity, \(\chi_{t}\)[39]:

$$\chi = \frac{{\chi_{t} }}{{\chi_{\infty } }} = 1 - \exp \left( { - k \cdot t^{n} } \right).$$
(5)

To acquire the model parameters, experimental data were fitted on the double logarithmic form:

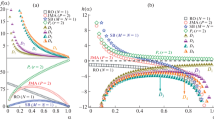
$$\log \left( { - \ln \left( {1 - \chi } \right)} \right) = \log k + n \cdot \log t\quad \quad k = \frac{0.69}{{t_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{n} }}.$$
(6)

In this linear form, regression is a trivial task. Figure 6 depicts the comparison of the Avrami model and experimental data in the double logarithmic form.

Fig. 6
figure 6

Avrami model fitting results for relative crystallinity

Full size image

The calculated model parameters, including regression coefficient (R2), are given in Table 3. The Avrami exponent, n, value has a wide range. The range of 2.5–6.5 suggests that thermal nucleation occurs in the primary crystallization step, producing a three-dimensional spherical structure growth. Most of the crystallization happens in this step. A higher value of n means more three-dimensional structures than two-dimensional structures [2]. The extensive change in n is a sign of the asymmetry in crystallization behavior; therefore, different rate parameters would be calculated that are not comparable directly. The term k as the rate parameter indicates the overall crystallinity and its dependency on the process conditions. For example, k could be applied to determine the temperature of the maximum crystallization rate and the amount of crystal produced. A higher value of k demonstrates a higher nucleation density and growth rate. There is an immense variation in the \(k\) values; and in such a case, the normalized cooling rate,\(k^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}}}\), may be calculated with a unit of inverse time, namely the Avrami reduced rate constant. In the course of non-isothermal DSC, there are variations in nucleation and rate with respect to temperature. These variations could be taken into account by calculation of \(k^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}}}\) [40]. \(k^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}}}\) values are presented in Table 3. The variations in \(k^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}}}\) and \(n\) indicate a heterogeneous nucleation, leading to three-dimensional crystal growth. The R2 values of models reveal an acceptable fitness for the relative crystallinity in the range of 10–90%. However, the inspection of the curves shows that there is a roll-off of around 60% relative crystallinity. This roll-off is contributed to the secondary crystallization that causes the deviation from the Avrami plots, as seen in Fig. 6. Therefore, the Avrami model is not a good predictor for crystallization kinetics. It is obvious that there is a change in the slope of the curve, indicating the existence of a secondary crystallization in PET.

Table 3 Calculated model parameters
Full size table

Ozawa model

Ozawa introduced an equation for non-isothermal kinetics based on the kinetic analysis of thermo-analytical data of the process [41]. The primary assumption in this theory is that non-isothermal crystallization is an outcome of many small isothermal crystallization steps. This equation relates the cooling rate with time and temperature:

$$\chi = 1 - \exp \left( {\frac{ - K\left( T \right)}{{\Phi^{m} }}} \right)\quad \Rightarrow \quad \log \left( { - \ln \left( {1 - \chi } \right)} \right) = \log \left( {K\left( T \right)} \right) - m\log \Phi ,$$
(7)

where\(m\) is the Ozawa exponent, and \(K\left( T \right)\) is a cooling function at temperature T. For PET, in a small temperature range, parameter m, the Ozawa’s exponent, is more or less constant [41]. However, in an extensive range, it varies with temperature. The Ozawa’s exponent depends on the nucleation and crystalline growth geometry. Figure 7 illustrates the result of curve-fitting on Ozawa model and the resulting model parameters. It was expected that \(\log \left( { - \ln \left( {1 - \chi } \right)} \right)\) would be linear versus \(\log \Phi\); however, two distinct regimes are recognized, due to the primary and secondary crystallizations. These regions are determined in Fig. 7a; at a low relative crystallinity, when the primary process is dominant, while the secondary process is dominant at a high relative crystallinity. Moreover, the relative crystallinity corresponding to the change in crystallization regime decreases with the temperature increase. Due to these variations, the Ozawa analysis is limited, and this deviation is related to the primary and secondary crystallizations [42]. The calculated parameters of the Ozawa model at various cooling rates are given in Table 3. These parameters are presented in the primary as well as secondary crystallization stages. For the sake of comparison, the relative crystallinity at various cooling rates was calculated and plotted in Fig. 8. Based on the obtained data, the Ozawa model is not suitable for calculating the experimental relative crystallinity. The parameters evaluated in the secondary stage were applied in plotting Fig. 8. The results with the primary stage parameters are worse. Such a plot has not been observed in the literature, and the Ozawa model is not successful in modeling of non-isothermal crystallinity over a wide range of temperatures and cooling rates. It should be mentioned that in such a wide range of cooling rates, \(\Phi \in \left[ {5,\;40} \right]\), the model error is very high, but the result is acceptable in a small range [34]. Nevertheless, the Ozawa's exponent, m, increases with temperature, and m is higher in the primary crystallization.

Fig. 7
figure 7

Ozawa model fitting results: a double logarithmic of the Ozawa model plot and fitted lines, and b Ozawa model parameters versus temperature at the secondary stage

Full size image
Fig. 8
figure 8

Double logarithmic degree of crystallinity based on the Ozawa model

Full size image

Tobin model

Taking into consideration secondary crystallization and impingement of spherulites, Tobin suggested the following model [43,44,45]:

$$\chi \left( t \right) = \frac{{\left( {K_{{\text{T}}} \cdot t} \right)^{{n_{{\text{T}}} }} }}{{1 + \left( {K_{{\text{T}}} \cdot t} \right)^{{n_{{\text{T}}} }} }}\quad \Rightarrow \quad \log \left( {\frac{\chi \left( t \right)}{{1 - \chi \left( t \right)}}} \right) = n_{{\text{T}}} \log K_{{\text{T}}} + n_{{\text{T}}} \log t,$$
(8)

where\(n_{{\text{T}}}\) is the Tobin's exponent and \(K_{{\text{T}}}\) is the Tobin's kinetic parameter. These parameters could be determined by plotting the logarithmic form, as given in Eq. 8. Table 3 reports the calculated parameters of the Tobin model at various cooling rates. The reduced rate constants for this model are also given. The Tobin's exponent is normally greater than the Avrami's exponent [46]. With simple mechanism for nucleation and growth, \(n_{{\text{T}}}\) is 2 and 3 for two- and three-dimensional networks [45]. Higher \(n_{{\text{T}}}\) could be contributed to the secondary crystallization of samples. Figure 9 shows the double logarithmic form of relative crystallinity obtained from the Tobin model. The model has the ability to show curvature in the plots.

Fig. 9
figure 9

Double logarithmic degree of crystallinity based on the Tobin model

Full size image

So far, the main models that could be converted to linear form (double logarithmic equations) have been discussed. Hence, calculation of the model parameters would be an easy task. However, some models, which involve nonlinear regression, are introduced in the following, among which the Hay model is quite new.

Hay model

Recently, Hay et al. [27] have performed detailed studies on the primary and secondary crystallization of PET. They used DSC and FTIR methods to analyze the mechanism of crystallization. They observed a narrowing of the melting peak with heating after the primary crystallization and concluded that lamellae thickening happens in the secondary crystallization [47]. Furthermore, they studied the crystallization of PET using FTIR spectroscopy [48]. In general, they made a conclusion that in the course of the secondary crystallization, the local diffusion of chain segments increases the thickness of lamellae. They proposed that the secondary relative crystallinity rises proportionally to the square root of the crystallization time. In other words, secondary crystallization happens around the boundaries of the spherulites. Consequently, the total relative crystallization is the addition of primary and secondary processes. Hence, they suggested the following equation:

$$\chi = x_{{\text{p}}} \left( {1 - \exp \left( { - kt^{n} } \right)} \right) \cdot \left( {1 + k_{{\text{s}}} \sqrt t } \right),$$
(9)

where \(x_{{\text{p}}}\) is the degree of primary crystallinity, \(n\) is the Avrami's exponent for primary crystallization, \(k\) is the rate constant for nucleation and growth, and \(k_{{\text{s}}}\) is the rate constant for growth of the secondary crystallization. The comparison of Eqs. 5 and 9 demonstrates that the overall relative crystallization is a sum of two terms; the first one is described by the Avrami type equation related to the primary crystallization; the second term describes the secondary crystallization, which is a square root of time-weight of the first term. Assuming the same justification for the modified Avrami model, the Hay model was fitted to the non-isothermal data. Parameter calculation for the Hay model needs the use of nonlinear regression algorithms. The simplex method of Lagarias et al. [49] was used by applying the least-square criterion that was employed as an objective function to calculate the model parameters:

$${\text{Objective}}\;{\text{function}} = \sum\limits_{i = 1}^{n} {\left( {\chi_{\exp } - \chi_\mathrm{{model}} } \right)^{2} } .$$
(10)

Due to the nonlinear nature of optimization, convergence problems are encountered. The convergence rate is very slow. Therefore, various objective functions were examined; the following is the best one:

$${\text{Objective}}\;{\text{function}} = 1 - R^{2} ,$$
(11)

where R2 is the regression coefficient. Unfortunately, this objective function leads to another optimum point that is the normal nature of nonlinear problems; thus, a new algorithm was introduced. Calculation loop starts with Eq. 10 as an objective function, and whenever the regression coefficient reaches over 0.96, the objective function switches to Eq. 11. This approach suggested that the algorithm was successful in all calculations. Figure 10 presents the comparison of the experimental and the Hay model data. As can be observed, the Hay model has an excellent ability to predict the relative crystallinity compared to the Avrami model. The only slight deviations observed at cooling rates \(\Phi = 15\) and 20 K/min could be attributed to the bimodal nature of the degree of crystallization, as seen in the Fig. 3. Despite the variation in parameters, the reduced rate constant gives a smooth trend in model interpretation.

Fig. 10
figure 10

Double logarithmic degree of crystallinity based on the Hay model

Full size image

Nakamura model

Nakamura model was suggested and applied for non-isothermal crystallization [50,51,52]. This model assumes that non-isothermal crystallization is a series of many small isothermal steps. Consequently, each step could be described by the Avrami model. Nakamura et al. presented the following equation:

$$\chi \left( t \right) = 1 - \exp \left( { - \left[ {\int\limits_{0}^{t} {k\left( T \right){\text{d}}t} } \right]^{n} } \right).$$
(12)

Typically, to acquire the Nakamura model parameters, the differential form of Eq. 12 was applied:

$$\frac{{{\text{d}}\chi }}{{{\text{d}}t}} = n \cdot k\left( T \right)\left( {1 - \chi } \right)\left[ { - \ln \left( {1 - \chi } \right)} \right]^{{\frac{n - 1}{n}}} .$$
(13)

However, the differentiation of experimental data intensifies random errors during real time data gathering. Therefore, in this work, it is suggested to use the original integral form of Equation 13:

$$\chi = \int\limits_{0}^{\chi } {{\text{d}}\chi } = \int\limits_{0}^{t} {n \cdot k\left( T \right)\left( {1 - \chi } \right)\left[ { - \ln \left( {1 - \chi } \right)} \right]^{{\frac{n - 1}{n}}} {\text{d}}t} .$$
(14)

To do so, nonlinear regression was applied. The expression \(k\left( T \right)\) was needed to be able to continue calculations. Hoffman-Lauritzen suggested the following equation for the secondary nucleation theory [53]:

$$k\left( T \right) = \frac{{\left( {\ln 2} \right)^{\frac{1}{n}} }}{{\left( {t_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \right)_{0} }}\exp \left( {\frac{{ - {U \mathord{\left/ {\vphantom {U R}} \right. \kern-\nulldelimiterspace} R}}}{{T - T_{\infty } }}} \right)\exp \left( {\frac{{ - K_{g} }}{T\Delta Tf}} \right)\;{\text{where}}\;\Delta T = T_{m}^{0} - T\quad \& \quad f = \frac{2T}{{T_{m}^{0} + T}},$$
(15)

where: \(U\) is the crystalline molecular transport activation energy between crystal and melt; \(\left( {t_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}^{ - 1} } \right)_{0}\) is a factor including all temperature-independent terms; \(K_{g}\) is the secondary nucleation constant; \(T_{\infty }\) is a hypothetical temperature that molecular transport starts; \(T_{m}^{0}\) is the equilibrium melting temperature, \(\Delta T\) is the under-cooling degree; \(f\) is a correction factor to take into account the bulk enthalpy of fusion variation; and \(R\) is the universal gas constant. The crystallization time can be converted to crystallization temperature:

$$t = \frac{{T_{0} - T}}{\Phi }\quad \Rightarrow \quad {\text{d}}t = - \frac{{{\text{d}}T}}{\Phi }.$$
(16)

The final equation is:

$$\chi = \int\limits_{0}^{t} {n \cdot \frac{{\left( {\ln 2} \right)^{\frac{1}{n}} }}{{\left( {t_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} } \right)_{0} }}\exp \left( {\frac{{ - {U \mathord{\left/ {\vphantom {U R}} \right. \kern-\nulldelimiterspace} R}}}{{T - T_{\infty } }}} \right)\exp \left( {\frac{{ - \left( {T_{m}^{0} + T} \right)K_{g} }}{{2T^{2} \left( {T_{m}^{0} - T} \right)}}} \right)\left( {1 - \chi } \right)\left[ { - \ln \left( {1 - \chi } \right)} \right]^{{\frac{n - 1}{n}}} \frac{{ - {\text{d}}T}}{\Phi }} .$$
(17)

Due to its highly nonlinear nature, initial postulates for parameters are very important in the fitting calculation. Hence, 3 for the Avrami's exponent and Tg-30 for T∞ were selected. The optimization of fitting parameters was performed using the simplex method of Lagarias et al. [49]. Hoffman and Weeks theory was applied to assess the correct equilibrium temperature [54]:

$$T_{m} = T_{m}^{0} \left( {1 - \frac{1}{\beta }} \right) + \frac{{T_{C} }}{\beta },$$
(18)

where factor \(\beta\) depends on the final thickness of lamellar. Using the data in Table 3, \(T_{m}^{0}\) and \(\beta\) were estimated to be 504.28 K and 11.31, respectively. The experimental estimation of \(U\) is a difficult task. However, using DSC data, it is possible to predict such parameters. Similar to the calculation algorithm for the Hay model, the objective function was changed during the calculation to obtain the appropriate regression coefficient. Table 3 gives the calculated Hoffman-Lauritzen parameters. Figure 11 shows the comparison of the experimental and Nakamura model results.

Fig. 11
figure 11

Nakamura model results

Full size image

In Fig. 11, it can be seen that the Lauritzen-Hoffman model clearly could point out the presence of secondary crystallization. However, at the beginning of crystallization, in which the primary process is dominant, this model is less successful than the end of the process with the dominant secondary crystallization.

Conclusion

Due to dependency of the final properties of polymeric parts, it is vital to have information about non-isothermal crystallization from melt state. Although, many research results have been published in the crystallization behavior of PET, still there are more information to be studied. Hence, additive free polyethylene terephthalate was synthesized through direct esterification of TPA and EG, and then polycondensation at 513 and 548 K, respectively. Fingerprint peaks of PET were recognized in the FTIR spectrum. 1H NMR spectrum of PET was consistent with its chemical structure. Therefore, suitable PET samples were prepared. Moreover, their determined properties showed that very fine PET samples were at hand. Consequently, the non-isothermal crystallization behavior of samples was studied. Non-isothermal crystallization studies were performed in a wide range of cooling rates, namely 5, 10, 15, 20, 30 and 40 K/min. This range is comparable to the cooling rate during the production of PET products. Although, the modified Avrami is one of the most widely used models, it is seen that it cannot take into account the secondary crystallization. A change in slope and deviation from linear behavior in the double logarithmic plot is an indication of a secondary crystallization. Tobin's model has the ability to fit experimental data. However, Hay and Nakamura models have better physical background.

The newly introduced Hay model has an excellent ability to describe the crystallization kinetics. Nakamura model associated with Hoffman-Lauritzen expression, with a theoretical background, fitted the data well. The results demonstrated that the Hay model is the most suitable model for the non-isothermal crystallization kinetics of polyethylene terephthalate from the melt state.