Introduction

Blade coating is a procedure of fluid layer coating on a moving substrate amid the wedge created between the blade and substrate. The coating technique is significant in terms of its practical applications in the field of paint and electronics industries. The coating offers a protective layer in paints; however, it stores information in electronics industries. A common lab process is blade coating, with practical applications in the production of newspapers, magnetic storage devices, and photographic films. A plane coater is widely used for practical purposes as well as the exponential coater that is also considered in some cases. First, Ruschak [1] in his research article and Middleman [2] in his book, provided a comprehensive study on the blade coating process. Greener and Middleman [3] theoretically inspected the viscoelastic fluids in blade coating by applying the perturbation technique to analyze the viscoelastic impact on the flow and engineering parameters. Hwang [4] analyzed the laminar flow of the power-law model in the blade coating phenomena. Ross et al. [5] have studied the generalized Newtonian fluid considering the power-law model in both plane and exponential blade coaters. Penterman et al. [6] presented the analysis of liquid crystal coating after passing inside the blade and plastic substrate. The coating process of nematic liquid crystal and optical layers has been analyzed by Quintans et al. [7] via blade coating theory and Ericksen–Leslie expressions were employed to devise the mathematical model for this process of a nematic liquid crystal. Giacomin et al. [8] studied the flexible blade coating process of a Newtonian fluid. Willinger and Delgado [9] reported an analytical investigation of roll coating process for the case of counter-rotating deformable rolls and negative gaps. Williamson fluid model for blade coating analysis was evaluated by Siddique et al. [10]. Rana et al. [11] scrutinized the blade coating process by adopting a Powell–Eyring fluid flow in a theoretical study. Ali et al. [12] inspected the roll-over web coating analysis by employing the couple stress model. The roll coating technique was also employed by Atif et al. [13] in the case of micropolar fluid to explore the rheology of non-Newtonian fluid. Under Lubrication approximation theory (LAT), they simplified the governing system and later numerically solved by employing the Runge–Kutta method. Sajid et al. [14] utilized the third-grade model in fixed blade coating and simplified equations were solved by both numerical and perturbation techniques. Again, Sajid et al. [15] discussed the magnetic field impact along with slip condition in the blade coating process on a Newtonian model. The shooting technique was utilized to numerically solve the simplified differential equations. Both the magnetic field and slip parameters at the surface provide the controlling parameters for the sheet velocity and coating thickness.

Ershad-Langroudi and Rahimi [16] studied the corrosion protection by hybrid coatings of zirconia nanoparticles. Sugumaran et al. [17] applied the dip coating method and Mirmohseni et al. [18] employed the antistatic coating technique in their experimental studies. Nal et al. [19] applied epoxy coating using bio-based materials (eugenol and vanillin) for the synthesis of a novel crosslinking agent. Zheng et al. [20] analysed the reverse roll coating procedure to calculate the coating windows of liquid films. Recently, Oldroyd 4-constant fluid was adopted in the blade coating technique by Shahzad et al. [21] to study both plane and exponential coaters. Wang et al. [22] applied a viscous fluid model to analyze the blade coating procedure to observe the effects of the magnetic field (MHD) in case of the flexible coater. Khaliq and Abbas [23] presented the Cu–water nanoparticles suspended in a Newtonian fluid to observe the roll coating process on a porous web. Then, flexible blade coater was investigated by Kanwal et al. [24] using the same nanofluid model to debate the blade coating analysis. Viscous nanofluid was discussed by Abbas and Khaliq [25] in their investigation of the calendering process to analyze the influence of Cu-nanoparticles. Recently, Khaliq and Abbas [26] examined the viscoelastic effects during blade coating analysis by employing the simplified Phan–Thien–Tanner (SPTT) model. Zahid et al. [27] studied the calendering process by employing the upper convected Jeffery’s fluid. Khaliq and Abbas [28] investigated the effect of temperature dependent viscosity on the blade coating process of non-isothermal viscous fluid. Mughees et al. [29] applied a second grade fluid coating on a porous substrate in blade coating analysis. Numerical technique was employed to verify the results in this study. Azam et al. [30] applied a numerical technique to study the cross-nanofluid model with heat source/sink. In addition, Azam et al. [31] in their study, adopted the radiative cross nanofluid model to study the impacts of Arrhenius activation energy and binary chemical reaction on a radially stretching surface.

Oldroyd-B fluid model is among the simplest non-linear models to study the viscoelastic effects in modeling and simulation. In this non-linear model, when the frame invariance is considered, becomes equivalent to Jeffery’s fluid model. In addition, swapping the time partial derivatives in Jeffery’s model with the Upper-Convected time derivative leads to the Oldroyd-B model, with extra stress tensor \(\left( {\tau + \lambda_{1} \dot{\tau } = \mu \left( {{\varvec{A}}_{1} + \lambda_{2} \dot{\user2{A}}_{1} } \right)} \right)\). The upper-convected Maxwell model can be achieved by taking \(\lambda_{2} = 0\), and finally a Newtonian model is attained by keeping \(\lambda_{1} = \lambda_{2} = 0\). The infinite extensional rate offered by this model is naturally unrealistic and a major limitation of Oldroyd-B is that it does not facilitate second normal stress difference as well as strain dependency. Inquiry on this fluid material over the past few years was reviewed as follows. First, analytical solutions of Oldroyld-B liquid were attained by Rajangopal and Bhatnagar [32] for numerous modest streams. Five distinct problems were studied by Hayat et al. [33] by obtaining closed form solutions of the Oldroyd-B model. Brandi et al. [34] investigated this model’s stability of the problem between two parallel plates. Chemical reaction effect on the Jeffery fluid with Lorentz force was recently studied by Abbas et al. [35] in peristaltic channel flow. Hayat et al. [36] in their study used Oldroyd-B nanofluid flow with impacts of double stratified radiation and nonlinear convection.

The present work involves the theoretical analysis of Jeffery’s fluid material to report the viscoelastic effects in the blade coating process by taking both the plane and exponential coaters. The section of experimental gives details of the flow problem and geometry description. Next section gives the governing Oldroyd-B expressions. Then, simplification of the equations and the asymptotic solution of the dimensionless system is given. The results and discussion section explains the analysis outcome in detail. Finally, main conclusions derived from the acquired outcomes are given in the last section.

Experimental

Problem description

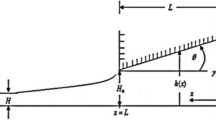
Schematic of a blade coater along with moving substrate is represented in Fig. 1. For this investigation, an incompressible, unsteady, upper convected Jeffery’s material is passed with velocity \(u\) (\(x -\)axis) through a thin gap between the blade and substrate to produce a uniform layer of coating with thickness H. Blade with length \(L\) is fixed at \(y = h\left( x \right)\) and having height \(H_{1}\) at \(x = 0\), \(H_{0}\) at \(x = L\).

Fig. 1
figure 1

Schematic of a blade coater along a moving substrate

Full size image

Governing equations and mathematical formulation

The basic expressions for incompressible, steady, and isothermal flow of upper-convected Jeffery’s fluid material minus the body forces are given as follows:

$${\text{div }}{\varvec{V}} = 0$$
(1)
$$\rho \left( {{\varvec{V}} \cdot \nabla } \right){\varvec{V}} = - \nabla p + \nabla \cdot \tau$$
(2)

where \(\Im\) as an extra stress tensor, satisfying this equation [32, 33] as follows:

$$\tau + \lambda_{1} \dot{\tau } = \mu \left( {{\varvec{A}}_{1} + \lambda_{2} \dot{\user2{A}}_{1} } \right)$$
(3)

and

$${\varvec{A}}_{1} = \nabla {\varvec{V}} + \left( {\nabla {\varvec{V}}} \right)^{t}$$
(4)
$$\dot{\tau } = \left( {{\varvec{V}} \cdot \nabla } \right)\tau + \frac{1}{2}\left( {{\varvec{w}}\tau - \tau {\varvec{w}}} \right)$$
(5)

where t represents the transpose and

$${\varvec{w}} = \nabla {\varvec{V}} - \left( {\nabla {\varvec{V}}} \right)^{ \it{t}}$$
(6)

the velocity field for this flow under consideration is given as follows:

$${\varvec{V}} = [u(x,y),v(x,y),0]$$
(7)

applying Eq. (7) in Eq. (4), we get

$$\begin{gathered} {\tau } = \left[ {\begin{array}{*{20}c} {\tau_{xx} \left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)} & {\tau_{xy} \left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)} \\ {\tau_{xy} \left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)} & {\tau_{yy} \left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)} \\ \end{array} } \right] \hfill \\ + \frac{1}{2}\left\{ {\left[ {\begin{array}{*{20}c} {\tau_{xy} \left( { - \frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}} \right)} & {\tau_{yy} \left( { - \frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}} \right)} \\ {\tau_{xx} \left( {\frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}} \right)} & {\tau_{xy} \left( {\frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}} \right)} \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {\tau_{xy} \left( {\frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}} \right)} & {\tau_{xx} \left( { - \frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}} \right)} \\ {\tau_{yy} \left( {\frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}} \right)} & {\tau_{xy} \left( {\frac{\partial u}{{\partial y}} - \frac{\partial v}{{\partial x}}} \right)} \\ \end{array} } \right]} \right\}. \hfill \\ \end{gathered}$$
(8)

Likewise, \({A}_{1}\) is equal to

$$\begin{gathered} {A}_{1} = \left[ {\begin{array}{*{20}c} {\left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)2\left( {\frac{\partial u}{{\partial x}}} \right)} & {\left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)\left( {\frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}} \right)} \\ {\left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)\left( {\frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}} \right)} & {\left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)2\left( {\frac{\partial v}{{\partial y}}} \right)} \\ \end{array} } \right] \hfill \\ + \frac{1}{2}\left\{ \begin{gathered} \left[ {\begin{array}{*{20}c} {\left( {\frac{\partial u}{{\partial y}} - \frac{\partial v}{{\partial x}}} \right)\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)} & {2\frac{\partial v}{{\partial y}}\left( {\frac{\partial u}{{\partial y}} - \frac{\partial v}{{\partial x}}} \right)} \\ {2\frac{\partial u}{{\partial x}}\left( {\frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}} \right)} & {\left( {\frac{\partial u}{{\partial y}} - \frac{\partial v}{{\partial x}}} \right)\left( { - \frac{\partial u}{{\partial y}} - \frac{\partial v}{{\partial x}}} \right)} \\ \end{array} } \right] \hfill \\ - \left[ {\begin{array}{*{20}c} {\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right)\left( {\frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}} \right)} & {2\frac{\partial u}{{\partial x}}\left( {\frac{\partial u}{{\partial y}} - \frac{\partial v}{{\partial x}}} \right)} \\ {2\frac{\partial v}{{\partial y}}\left( {\frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}} \right)} & {\left( { - \frac{\partial u}{{\partial y}} - \frac{\partial v}{{\partial x}}} \right)\left( {\frac{\partial v}{{\partial x}} - \frac{\partial u}{{\partial y}}} \right)} \\ \end{array} } \right] \hfill \\ \end{gathered} \right\} \hfill \\ \end{gathered}$$
(9)

Taking Eqs. (8) and (9) into consideration, Eqs. (1, 2, 3) were expanded as follows:

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0$$
(10)
$$\rho \left( {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right) = - \frac{\partial p}{{\partial x}} + \frac{{\partial \tau_{xx} }}{\partial x} + \frac{{\partial \tau_{xy} }}{\partial y}$$
(11)
$$\rho \left( {u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}}} \right) = - \frac{\partial p}{{\partial y}} + \frac{{\partial \tau_{xy} }}{\partial x} + \frac{{\partial \tau_{yy} }}{\partial y}$$
(12)
$$\begin{gathered} \tau_{xx} + \lambda_{1} \left\{ {u\frac{{\partial \tau_{xx} }}{\partial x} + v\frac{{\partial \tau_{xx} }}{\partial y} + \tau_{xy} \left( {\frac{\partial u}{{\partial y}} - \frac{\partial v}{{\partial x}}} \right)} \right\} = \hfill \\ \mu \left\{ {2\frac{\partial u}{{\partial x}} + \lambda_{2} \left( {\left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)2\frac{\partial u}{{\partial x}} + \left( {\frac{\partial u}{{\partial y}}} \right)^{2} - \left( {\frac{\partial v}{{\partial x}}} \right)^{2} } \right)} \right\} \hfill \\ \end{gathered}$$
(13)
$$\begin{gathered} \tau_{xy} + \lambda_{1} \left\{ {u\frac{{\partial \tau_{xy} }}{\partial x} + v\frac{{\partial \tau_{xy} }}{\partial y} + \frac{1}{2}\left( {\frac{\partial u}{{\partial y}} - \frac{\partial v}{{\partial x}}} \right)\left( {\tau_{yy} - \tau_{xx} } \right)} \right\} = \hfill \\ \mu \left\{ {\left( {\frac{\partial u}{{\partial y}} + \frac{\partial v}{{\partial x}}} \right) + \lambda_{2} \left( {\left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)\left( {\frac{\partial v}{{\partial x}} + \frac{\partial u}{{\partial y}}} \right) + \left( {\frac{\partial v}{{\partial y}} - \frac{\partial u}{{\partial x}}} \right)\left( {\frac{\partial u}{{\partial y}} - \frac{\partial v}{{\partial x}}} \right)} \right)} \right\} \hfill \\ \end{gathered}$$
(14)
$$\begin{gathered} \tau_{yy} + \lambda_{1} \left\{ {u\frac{{\partial \tau_{yy} }}{\partial x} + v\frac{{\partial \tau_{yy} }}{\partial y} + \tau_{xy} \left( {\frac{\partial u}{{\partial y}} - \frac{\partial v}{{\partial x}}} \right)} \right\} = \hfill \\ \mu \left\{ {2\frac{\partial v}{{\partial y}} + \lambda_{2} \left( {2\left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)\frac{\partial v}{{\partial y}} + \left( {\frac{\partial v}{{\partial x}}} \right)^{2} - \left( {\frac{\partial u}{{\partial y}}} \right)^{2} } \right)} \right\} \hfill \\ \end{gathered}$$
(15)

with physical conditions:

$$\left. {\begin{array}{*{20}l} {u = U} \hfill & {{\text{at }}{\mkern 1mu} y = 0,} \hfill \\ {u = 0} \hfill & {{\text{at }}{\mkern 1mu} y = h(x).} \hfill \\ \end{array} } \right\}$$
(16)

assuming the coating thickness H is considerably small as compared with the blade length L, i.e.,\(H/L\ll 1\), considering the lubrication approximation theory (LAT). Moreover, a parallel flow was assumed in the gap between the substrate and blade for convenience. These assumptions lead to \(v < < u\) and \(\frac{\partial }{\partial x} < < \frac{\partial }{\partial y}\). Therefore, Eqs. (10, 11, 12, 13, 14, 15) were simplified as follows:

$$0 = - \frac{\partial p}{{\partial x}} + \frac{{\partial \tau_{xy} }}{\partial y}$$
(17)
$$0 = - \frac{\partial p}{{\partial y}} + \frac{{\partial \tau_{yy} }}{\partial y}$$
(18)
$$\tau_{xx} + \lambda_{1} \left( {\tau_{xy} \frac{\partial u}{{\partial y}}} \right) = \lambda_{2} \mu \left( {\frac{\partial u}{{\partial y}}} \right)^{2}$$
(19)
$$\tau_{xy} + \frac{{\lambda_{1} }}{2}\left( {\frac{\partial u}{{\partial y}}\left( {\tau_{yy} - \tau_{xx} } \right)} \right) = \mu \frac{\partial u}{{\partial y}}$$
(20)
$$\tau_{yy} - \lambda_{1} \left( {\tau_{xy} \frac{\partial u}{{\partial y}}} \right) = - \left( {\frac{\partial u}{{\partial y}}} \right)^{2} \mu \lambda_{2}$$
(21)

amending Eq. (18), we get

$$\frac{\partial }{\partial y}\left( {p - \tau_{yy} } \right) = 0$$
(22)

assuming \(P^{ * } = p - \tau_{yy}\), leads to \(\frac{{\partial P^{ * } }}{\partial y} = 0\), which further illustrated that \(P^{ * } = P^{ * } \left( x \right)\), thus we can write as

$$\frac{{dP^{ * } }}{dx} = \frac{\partial p}{{\partial x}} - \frac{{\partial \tau_{yy} }}{\partial x}$$
(23)

applying LAT, Eq. (23) was converted into

$$\frac{{dP^{ * } }}{dx} = \frac{\partial p}{{\partial x}}$$
(24)

by solving Eqs. (19, 20, 21) and Eq. (17) the following equation was obtained:

$$\frac{\partial }{\partial y}\left( {\frac{{\left( {\frac{\partial u}{{\partial y}}} \right) + \lambda_{2} \lambda_{1} \left( {\frac{\partial u}{{\partial y}}} \right)^{3} }}{{\left[ {1 + \lambda^{2}_{1} \left( {\frac{\partial u}{{\partial y}}} \right)^{2} } \right]}}} \right) = \frac{1}{\mu }\frac{{dP^{ * } }}{dx}$$
(25)

then, Eq. (25) was integrated with respect to ‘y’:

$$\frac{{\left( {\frac{\partial u}{{\partial y}}} \right) + \lambda_{2} \lambda_{1} \left( {\frac{\partial u}{{\partial y}}} \right)^{3} }}{{\left[ {1 + \lambda^{2}_{1} \left( {\frac{\partial u}{{\partial y}}} \right)^{2} } \right]}} = \frac{y}{\mu }\frac{{dP^{ * } }}{dx} + c.$$
(26)

The above system was non-linear and its exact solution was not possible. Hence, an asymptotic solution was obtained and verified with the numerical solution for this above-modelled expression.

Dimensionless analysis

The following dimensionless parameters were invoked to study the current problem [27]:

$$\left( {\overline{u} = \frac{u}{U},\overline{x} = \frac{x}{L},p = \frac{{P^{ * } H_{0} }}{\mu UL},\overline{y} = \frac{y}{{H_{0} }},\overline{h} = \frac{h}{{H_{0} }},Ws = \frac{{U\lambda_{1} }}{{H_{0} }},\frac{{\mu_{s} }}{{\mu_{0} }}Ws = \frac{{\lambda_{2} U}}{{H_{0} }}.} \right)$$
(27)

Equations (25) and (26) were modified into the following equations (ignoring the bar (-) sign for simplicity):

$$\frac{\partial }{\partial y}\left( {\frac{{\left( {\frac{\partial u}{{\partial y}}} \right) + \alpha \varepsilon \left( {\frac{\partial u}{{\partial y}}} \right)^{3} }}{{\left[ {1 + \varepsilon \left( {\frac{\partial u}{{\partial y}}} \right)^{2} } \right]}}} \right) = \frac{dp}{{dx}}$$
(28)
$$\frac{{\left( {\frac{\partial u}{{\partial y}}} \right) + \alpha \varepsilon \left( {\frac{\partial u}{{\partial y}}} \right)^{3} }}{{\left[ {1 + \varepsilon \left( {\frac{\partial u}{{\partial y}}} \right)^{2} } \right]}} = \frac{dp}{{dx}}y + C$$
(29)

where \(\left( {Ws} \right)^{2} = \varepsilon\), with Ws as the Weissenberg number (ratio of elastic forces to viscous forces) and \({{\mu_{s} } \mathord{\left/ {\vphantom {{\mu_{s} } {\mu_{0} }}} \right. \kern-\nulldelimiterspace} {\mu_{0} }} = \alpha\) with \(\mu_{0} = \mu_{s} + \mu\) signified the total shear viscosity and \(\mu_{s}\) represented the Newtonian solvent viscosity. In addition, \({{H_{0} c} \mathord{\left/ {\vphantom {{H_{0} c} {\mu U}}} \right. \kern-\nulldelimiterspace} {\mu U}} = C\) was described as the modified integration constant.

Now, the dimensionless velocity conditions were as follows:

$$\left. {\begin{array}{*{20}l} {u = 1} \hfill & {{\text{at }}y = 0} \hfill \\ {u = 0} \hfill & {{\text{at }}y = h(x)} \hfill \\ \end{array} } \right\}.$$
(30)

In addition, the pressure at both the detachment and entrance points approached to zero, which directed to pressure boundary conditions as follows:

$$\left. {\begin{array}{*{20}l} {p = 0{\text{ at }}x = 0} \hfill \\ {p = 0{\text{ at }}x = 1} \hfill \\ \end{array} } \right\}$$
(31)

and variable height h(x) was given by

$$\left. {\begin{array}{*{20}l} {{\text{plane}}\hfill \;{\text{coater:}}} \hfill & {h\left( x \right) = \gamma - \left( {\gamma - 1} \right)x} \hfill \\ {{\text{exponential}} \hfill \;{\text{coater:}}} \hfill & {h\left( x \right) = \gamma^{1 - x} } \hfill \\ \end{array} } \right\}.$$
(32)

The flow rate was defined as

$$\frac{\it{{\text{Q}}}}{\it{{\text{W}}}}\it{{\text{ = UH = }}}\int\limits_{{0}}^{{\text{h}}} {{\text{udy}}} ,$$
(33)

where the substrate speed was U having width W and \({H \mathord{\left/ {\vphantom {H {H_{0} }}} \right. \kern-\nulldelimiterspace} {H_{0} }} = \eta\) was the dimensionless coating thickness. In addition, Load \(\left( \Pi \right)\) was given by the following relation:

$$\Pi = \int\limits_{0}^{1} {p\left( x \right)dx} .$$
(34)

Solution of the problem

The solution of dimensionless velocity (u), pressure, constant (C), blade load \(\left( \Pi \right)\), and sheet thickness \(\left( \eta \right)\) was found by employing the asymptotic perturbative technique with \(\varepsilon < < 1\) (as perturbation parameter) as follows:

$$\left. \begin{gathered} u = u_{0} + \varepsilon \, u_{1} + ... \hfill \\ p = p_{0} + \varepsilon \, p_{1} + ... \hfill \\ C = C_{0} + \varepsilon \, C_{1} + ... \hfill \\ \eta = \eta_{0} + \varepsilon \, \eta_{1} + ... \hfill \\ \Pi = \Pi_{0} + \varepsilon \Pi_{1} + ... \hfill \\ \end{gathered} \right\}.$$
(35)

Putting Eq. (35) in Eq. (29), we got

$$\begin{gathered} \left( {\frac{\partial }{\partial y}\left( {u_{0} + \varepsilon u_{1} + ...} \right)} \right) + \alpha \varepsilon \left( {\frac{\partial }{\partial y}\left( {u_{0} + \varepsilon u_{1} + ...} \right)} \right)^{3} \hfill \\ = \left( {y \cdot \frac{d}{dx}\left( {p_{0} + \varepsilon p_{1} + ...} \right) + C_{0} + \varepsilon C_{1} + ...} \right)\left( {1 + \varepsilon \left( {\frac{\partial }{\partial y}\left( {u_{0} + \varepsilon u_{1} + ...} \right)} \right)^{2} } \right) \hfill \\ \end{gathered}$$
(36)
$$\left. {\begin{array}{*{20}c} {u_{0} + \varepsilon u_{1} + ... = 1} & {{\text{at}}\,y = 0} \\ {u_{0} + \varepsilon u_{1} + ... = 0} & {{\text{at}}\,y = h(x)} \\ {p_{0} + \varepsilon p_{1} + ... = 0} & {{\text{at}}\,x = 0} \\ {p_{0} + \varepsilon p_{1} + ... = 0} & {{\text{at}}\,x = 1} \\ \end{array} } \right\}$$
(37)
$$\eta_{0} + \varepsilon \,\eta_{1} + ... = \int\limits_{0}^{h} {\left( {u_{0} + \varepsilon u_{1} + ...} \right)dy}$$
(38)
$$\Pi_{0} + \varepsilon \,\Pi_{1} + ... = \int\limits_{0}^{1} {\left( {p_{0} + \varepsilon p_{1} + ...} \right)dx} .$$
(39)

In system Eqs. (36, 37, 38, 39), the like powers of \(\varepsilon\) were compared, led to zeroth and first-order sub-problems solved as follows.

Solution of zeroth-order problem

The sub-problem of \(\varepsilon_{0}\) was

$$\frac{{\partial u_{0} }}{\partial y} = y\frac{{dp_{0} }}{dx} + C_{0}$$
(40)
$$\left. {\begin{array}{*{20}l} {u_{0} = 1} \hfill & {{\text{at}}{\mkern 1mu} y = 0} \hfill \\ {u_{0} = 0} \hfill & {{\text{at}}{\mkern 1mu} y = h(x)} \hfill \\ {p_{0} = 0} \hfill & {{\text{at}}{\mkern 1mu} x = 0} \hfill \\ {p_{0} = 0} \hfill & {{\text{at}}{\mkern 1mu} x = 1} \hfill \\ \end{array} } \right\}$$
(41)
$$\eta_{0} = \int\limits_{0}^{h} {u_{0} dy}$$
(42)
$$\Pi_{0} = \int\limits_{0}^{1} {p_{0} dx}$$
(43)

solving Eq. (40) with respect to Eq. (41), the expression of velocity profile was obtained as follows:

$$u_{0} = 1 + \frac{{dp_{0} }}{dx}\left( {\frac{y - h}{2}} \right)y - \frac{y}{h}$$
(44)

which was the same as Middleman’s [2]. Zeroth-order pressure gradient was found by substituting Eq. (44) in Eq. (42) as follows:

$$\frac{{dp_{0} }}{dx} = \frac{6}{{h^{3} }}\left( {h - 2\eta_{0} } \right).$$
(45)

Integrating Eq. (45) using pressure conditions in Eq. (41), we get the values of film thickness and pressure and then load was calculated using Eq. (43). We get the following equations for both plane and exponential coaters:

For plane coater

$$\eta_{0} = \frac{\gamma }{1 + \gamma }$$
(46)
$$p_{0} \left( x \right) = \frac{{6\left( {1 - \gamma } \right)\left( {x - 1} \right)x}}{{\left( {1 + \gamma } \right)\left( {\gamma + x - \gamma x} \right)^{2} }}$$
(47)

and

$$\Pi_{0} = \frac{{6\left( {2 - 2\gamma + \left( {\gamma + 1} \right){\text{Log}} [\gamma ]} \right)}}{{\left( {\gamma + 1} \right)\left( {\gamma - 1} \right)^{2} }}.$$
(48)

For exponential coater

$$\eta_{0} = \frac{{3\gamma \left( {\gamma + 1} \right)}}{{4\left( {\gamma^{2} + \gamma + 1} \right)}}$$
(49)
$$p_{0} \left( x \right) = \frac{1}{{{\text{Log}} \left[ \gamma \right]}}\frac{{3\left( {\gamma^{x} \left( {\gamma + 1} \right) + \gamma } \right)\left( {\gamma - \gamma^{x} } \right)\left( {\gamma^{x} - 1} \right)}}{{\left( {1 + \gamma + \gamma^{2} } \right)\gamma^{2} }}$$
(50)

and

$$\Pi_{0} = \frac{{1 - \frac{1}{{\gamma^{2} }} - \frac{{6{\text{Log}} \left[ \gamma \right]}}{{\left( {\gamma^{2} + \gamma + 1} \right)}}}}{{2{\text{Log}} \left[ \gamma \right]^{2} }}$$
(51)

Solution of the first-order problem

The system of \(\varepsilon_{1}\) is

$$\frac{{\partial u_{1} }}{\partial y} + \alpha \left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{3} = y\frac{{dP_{1} }}{dx} + C_{1} + \left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{2} \left( {y\frac{{dP_{0} }}{dx} + C_{0} } \right)$$
(52)
$$\left. {\begin{array}{*{20}l} {u_{1} = 0} \hfill & {{\text{at}}{\mkern 1mu} y = 0} \hfill \\ {u_{1} = 0} \hfill & {{\text{at}}{\mkern 1mu} y = h(x)} \hfill \\ {p_{1} = 0} \hfill & {{\text{at}}{\mkern 1mu} x = 0} \hfill \\ {p_{1} = 0} \hfill & {{\text{at}}{\mkern 1mu} x = 1} \hfill \\ \end{array} } \right\}$$
(53)
$$\eta_{1} = \int\limits_{0}^{h} {u_{1} dy}$$
(54)
$$\Pi_{1} = \int\limits_{0}^{1} {p_{1} dx}$$
(55)

putting Eqs. (44) and (45) in Eq. (52) and solving the resulting equation using Eq. (53), we got the velocity profile as follows:

$$u_{1} = \frac{{\left( {h - y} \right)y}}{{2h^{9} }}\left[ \begin{gathered} - \frac{{dp_{1} }}{dx}h^{9} - 108h^{5} \left( {1 - \alpha } \right) + 864\left( {1 - \alpha } \right)y^{2} \eta_{0}^{3} - 432\left( {3y + 2\eta_{0} } \right)\left( {1 - \alpha } \right)hy\eta_{0}^{2} \hfill \\ + 36\left( {5y + 14\eta_{0} } \right)\left( {1 - \alpha } \right)h^{4} + 72\left( {1 - \alpha - 1} \right)\left( {6\eta_{0}^{2} + 22y\eta_{0} + 9y^{2} } \right)h^{2} \eta_{0} \hfill \\ - 36\left( {22\eta_{0}^{2} + 26y\eta_{0} + 3y^{2} } \right)\left( {1 - \alpha } \right)h^{3} \hfill \\ \end{gathered} \right]$$
(56)

Equation (56) was substituted in Eq. (54), to attain the first-order pressure gradient as follows:

$$\frac{{dp_{1} }}{dx} = \frac{{36\left( {h - 2\eta_{0} } \right)\left( {\alpha - 1} \right)\left( {7h^{2} - 18h\eta_{0} + 18\eta_{0}^{2} } \right)}}{{5h^{7} }} - \frac{{12\eta_{1} }}{{h^{3} }}$$
(57)

integrating Eq. (57) using pressure conditions in Eq. (53), we acquired the value of the film thickness and pressure, while load was calculated using Eq. (55). We got the following equations concerning both plane and exponential coaters:

For plane coater

$$\eta_{1} = \frac{{2\left( {1 - \alpha } \right)\left( {\gamma - 1} \right)^{2} \left( {13 - \gamma + 13\gamma^{2} } \right)}}{{25\gamma \left( {\gamma + 1} \right)^{3} }}$$
(58)
$$\begin{gathered} p_{1} \left( x \right) = \frac{{12\left( {\alpha - 1} \right)}}{{25\left( {1 + \gamma } \right)^{3} }}\left[ \begin{gathered} \frac{{13 + 8\gamma + 13\gamma^{2} }}{{\gamma - \gamma^{2} }} + \frac{{\left( {1 - \gamma } \right)\left( {13 - \gamma + 13\gamma^{2} } \right)}}{{\left( {x - \gamma x + \gamma } \right)^{2} \gamma }} - \frac{{35\left( {1 + \gamma } \right)^{3} }}{{\left( {x + \gamma - \gamma x} \right)^{3} \left( {1 - \gamma } \right)}} \hfill \\ + \frac{{90\gamma^{3} - 120\left( { - x - \gamma + \gamma x} \right)\left( {\gamma + 1} \right)^{2} \gamma + 162\left( { - x - \gamma + \gamma x} \right)\left( {\gamma + 1} \right)\gamma^{2} }}{{\left( {1 - \gamma } \right)\left( {x + \gamma - \gamma x} \right)^{6} }} \hfill \\ \end{gathered} \right] \hfill \\ \,\, \hfill \\ \end{gathered}$$
(59)

and

$$\Pi_{1} = \frac{{12\left( {\alpha - 1} \right)\left( {\gamma - 1} \right)\left( {13 - \gamma + 3\gamma^{2} } \right)}}{{25\gamma^{2} \left( {1 + \gamma } \right)^{3} }}.$$
(60)

For exponential coater

$$\eta_{1} = \frac{{9\left( {1 - \alpha } \right)\left( {\gamma - 1} \right)^{2} \left( {\gamma + 1} \right)\left( {88 + 440\gamma + 745\gamma^{2} + 604\gamma^{3} + 745\gamma^{4} + 88\gamma^{5} \left( {5 + \gamma } \right)} \right)}}{{2800\gamma \left( {1 + \gamma + \gamma^{2} } \right)^{4} }}$$
(61)
$$\begin{gathered} p_{1} \left( x \right) = \frac{{9\left( {1 - \alpha } \right)}}{{700{\text{Log}} \left[ \gamma \right]\left( {1 + \gamma + \gamma^{2} } \right)^{4} \gamma^{4} }}\left[ {\gamma^{3} \left( {88 + 1332\gamma + 1449\gamma^{2} + 1390\gamma^{3} + 1449\gamma^{4} + 1332\gamma^{5} + 88\gamma^{6} } \right)} \right. \hfill \\ \,\,\, - \gamma^{3x} \left( { - 1215\gamma^{4x} \left( {1 + \gamma } \right)^{3} \left( {1 + \gamma + \gamma^{2} } \right) + 2835\gamma^{3x} \left( {1 + \gamma + \gamma^{2} } \right)^{2} \left( {1 + \gamma } \right)^{2} - 2688\gamma^{2x} \left( {1 + \gamma + \gamma^{2} } \right)^{3} \left( {1 + \gamma } \right)} \right. \hfill \\ \,\,\,\left. {\left. { + 980\left( {1 + \gamma + \gamma^{2} } \right)^{4} \gamma^{x} + \left( {88 + 440\gamma + 745\gamma^{2} + 604\gamma^{3} + 745\gamma^{4} + 88\gamma^{5} \left( {5 + \gamma } \right)} \right)\left( {\gamma - 1} \right)^{2} \left( {1 + \gamma } \right)^{2} } \right)} \right] \hfill \\ \end{gathered}$$
(62)

and

$$\begin{gathered} \Pi_{1} = \frac{{3\left( {\alpha - 1} \right)}}{{49000{\text{Log}} \left[ \gamma \right]^{2} \left( {1 + \gamma + \gamma^{2} } \right)^{4} \gamma^{4} }} \times \left[ {\left( {1 + \gamma } \right)\left( {\gamma - 1} \right)\left( {1 + \gamma + \gamma^{2} } \right)\left( {7489 + 22467\gamma + 29809\gamma^{2} } \right.} \right. \hfill \\ \,\,\,\left. { + 29662\gamma^{3} + 70626\gamma^{4} + \left( {14831 + 7489\gamma \left( {1 + \gamma } \right)} \right)\left( {2 + \gamma } \right)\gamma^{5} } \right) - 210\gamma^{3} \left( {88 + 1332\gamma + 1449\gamma^{2} } \right. \hfill \\ \left. {\,\,\,\,\left. { + 1390\gamma^{3} + 1449\gamma^{4} + 1332\gamma^{5} + 88\gamma^{6} } \right){\text{Log}} \left[ \gamma \right]} \right]. \hfill \\ \end{gathered}$$
(63)

Numerical solution

The numerical solution of differential Eq. (28) was found by employing shooting technique. First, the stream functions were introduced as follows:

$$u = \frac{\partial \Phi }{{\partial y}},v = - \frac{\partial \Phi }{{\partial x}}$$
(64)

applying Eq. (64) in Eq. (28), we got

$$\frac{\partial }{\partial y}\left( {\frac{{\left( {\frac{{\partial^{2} \Phi }}{{\partial y^{2} }}} \right) + \varepsilon \alpha \left( {\frac{{\partial^{2} \Phi }}{{\partial y^{2} }}} \right)^{3} }}{{\left[ {1 + \varepsilon \left( {\frac{{\partial^{2} \Phi }}{{\partial y^{2} }}} \right)^{2} } \right]}}} \right) = \frac{dp}{{dx}}$$
(65)

pressure gradient (\({{dp} \mathord{\left/ {\vphantom {{dp} {dx}}} \right. \kern-\nulldelimiterspace} {dx}}\)) was eliminated when Eq. (65) was differentiated for y, as follows:

$$\frac{{\partial^{2} }}{{\partial y^{2} }}\left( {\frac{{\left( {\frac{{\partial^{2} \Phi }}{{\partial y^{2} }}} \right) + \alpha \varepsilon \left( {\frac{{\partial^{2} \Phi }}{{\partial y^{2} }}} \right)^{3} }}{{\left[ {1 + \varepsilon \left( {\frac{{\partial^{2} \Phi }}{{\partial y^{2} }}} \right)^{2} } \right]}}} \right) = 0.$$
(66)

Equation (33) was modified in terms of \(\Phi\) and used to find the coating thickness (dimensionless) as follows:

$$\eta = \int\limits_{0}^{h} {\frac{\partial \Phi }{{\partial y}}dy} .$$
(67)

Equation (66) required two additional conditions on \(\Phi\) given as follows:

$$\Phi \left( {x,h} \right) = \eta ,\Phi \left( {x,0} \right) = 0$$
(68)

along with, Eq. (30) was converted as follows:

$$\frac{\partial \Phi }{{\partial y}}\left( {x,0} \right) = 1,\frac{\partial \Phi }{{\partial y}}\left( {x,h} \right) = 0$$
(69)

to start the numerical procedure, Eq. (66) was solved for \(\Phi\) with boundary conditions in Eqs. (68) and (69) for the particular value of \(\eta\). In the second step, Eq. (65) was solved after substituting the value of \(\Phi\) to acquire pressure gradient. Next, pressure was found by integrating the last result. Finally, Eq. (34) was employed to find blade load. In this whole procedure, a root finding algorithm was used to adjust the value of \(\eta\) to satisfy the condition \(p\left( 1 \right) = 0\).

Results and discussion

Blade coating process was reported in this study of both plane and exponential coaters by passing an upper-convected Jeffery’s material through moving substrate and blade. Both perturbation and numerical solutions were found and discussed through graphs and tables for distinct values of perturbation parameter \(\left( \varepsilon \right)\), viscosities ratio \(\left( \alpha \right)\) and normalized coating thickness \(\left( \gamma \right)\). Perturbation and numerical techniques were compared on the pressure profile by varying \(\varepsilon\), as presented in Fig. 2. The perturbation solution is indicated by a solid line, whereas the numerical solution is in dashed line. Both solutions in Fig. 2 were overlapped by taking small values of \(\varepsilon\); however, solution difference was slightly increased as noted for enhanced values of \(\varepsilon\). As this study was assumed for small perturbation parameter, hence the perturbation solution showed good agreement with the numerical technique.

Fig. 2
figure 2

Comparison of perturbation and numerical solutions on pressure profile at a ε = 0.1 and b ε = 1 (for α = 3 and γ = 2)

Full size image

In Figs. 3, 4, 5, 6, 7, 8, 9, 10, plane coater results are presented and exponential coater results are given in Figs. S1–S8 in Supplementary file. Figures 3, 4, 5 represent the pressure gradient curves by taking distinct values for \(\alpha\), \(\varepsilon\) and \(\gamma\), respectively. One can notice that pressure gradient was maximum at the start of the blading, then, it decreased and reached to its minimum value at the blade tip. This minimum pressure gradient increased the coating material velocity near the blade, helps in coating of fluid on the substrate. In these figures, the magnitude of pressure gradient was enhanced by increasing \(\varepsilon\) (Fig. 3) and \(\alpha\) (Fig. 4), and by reducing \(\gamma\) (Fig. 5). In Fig. 3, as Weissenberg number (perturbation parameter) is the ratio of elastic forces to viscous forces; hence by enhancing the Weissenberg number, it was led to dominant elastic forces, which further led to enhance the magnitude of pressure gradient. Moreover, it is worth mentioning that, fluid is more elastic as it reached the point after blade tip, hence fluid coating on the substrate occurs due to these dominant elastic forces over viscous forces. In addition, at \(\varepsilon = 0\) it presents the Newtonian case already discussed by Middleman [2]. The effects for the exponential coater cases in Figs. S1–S3 are similar to the plane coater cases.

Fig. 3
figure 3

Pressure gradient versus \(x\) for plane coater by changing \(\varepsilon\) values (for α = 3 and γ = 2)

Full size image
Fig. 4
figure 4

Pressure gradient versus \(x\) for plane coater by changing \(\alpha\) values (for ε = 0.1 and γ = 2)

Full size image
Fig. 5
figure 5

Pressure gradient versus \(x\) for plane coater by changing \(\gamma\) values (for ε = 0.1 and α = 3)

Full size image
Fig. 6
figure 6

Plots of pressure versus \(x\) for plane coater by changing \(\varepsilon\) values (for α = 3 and γ = 2)

Full size image
Fig. 7
figure 7

Plots of pressure versus \(x\) for plane coater by changing \(\alpha\) values (for ε = 0.1 and γ = 2)

Full size image
Fig. 8
figure 8

Plots of pressure versus \(x\) for plane coater by changing \(\gamma\) values (for ε = 0.1 and α = 3)

Full size image
Fig. 9
figure 9

Plots of maximum pressure versus \(\gamma\) for plane coater by changing \(\varepsilon\) values (for α = 3 and γ = 2)

Full size image
Fig. 10
figure 10

Plots of maximum pressure versus \(\gamma\) for plane coater by changing \(\alpha\) values (for ε = 0.1 and γ = 2)

Full size image

In Figs. 6, 7, 8, pressure profiles were portrayed by taking distinct values for \(\varepsilon\), \(\alpha\) and \(\gamma\), respectively. One observes that, pressure was zero at the start of the blade, then, it increased to its maximum value and then dropped to zero at the blade tip. Pressure is positive under the blade. From these figures, we noticed a rise in the pressure curve by increasing \(\varepsilon\) (Fig. 6 and Fig. S4 in Supplementary file) and \(\alpha\) (Fig. 7 and Fig. S5 in Supplementary file) due to dominant elastic forces. In addition, pressure decreased by increasing \(\gamma\) as shown in Fig. 8 and Fig. S6 in Supplementary file. Moreover, increasing \(\gamma\) resulted in maximum pressure shifting toward the blade tip as is represented in Fig. 8. Physically, increasing \(\gamma\) increased the blade height ratio, enhancing the film thickness and, therefore, less pressure was needed to maintain the flow. The exponential coater results in Figs. S4–S6 in Supplementary file are the same as plane coater results. In addition, at \(\varepsilon = 0\) it presents the Newtonian case already discussed by Middleman [2].

Variations of maximum pressure influenced by normalized coating thickness \(\gamma\) are portrayed in Figs. 9 and 10 for plane coater samples by taking distinct values for \(\varepsilon\) and \(\alpha\), respectively. We noted that for initial values of \(\gamma\), maximum pressure showed an abrupt increase at first, then reduced smoothly leading to a constant value at higher \(\gamma\). As \(\gamma\) was related to blade height ratio, hence increasing \(\gamma\) indicated less maximum pressure value. Moreover, maximum pressure was enhanced by increasing \(\varepsilon\) (Fig. 9) and \(\alpha\) (Fig. 10). By comparison of results of the plane coater with those of the exponential coater (Figs. S7 and S8 in Supplementary file), the decrease in \(p_{max}\) was more prominent in plane coater than in the exponential coater at higher values of \(\gamma\).

Table 1 presents the calculated values of coating thickness \(\eta\) and load \(\Pi\) by taking distinct values of \(\varepsilon\), \(\alpha\) and \(\gamma\). Table 1 indicates that coating thickness was reduced as a result of increases in \(\varepsilon\) and \(\alpha\), but with the same outcome in plane and exponential coater cases by decreasing \(\gamma\). Moreover, blade load \(\Pi\) was enhanced as we increased \(\varepsilon\) and \(\alpha\) values, and was enhanced as we decreased \(\gamma\) value. As increase of Weissenberg number led to dominant elastic forces, hence coating thickness was decreased. Physically, this decrease in coating thickness by these rheological parameters resulted in more efficient coating process as compared with the Newtonian case (Middleman [2]), hence improving the life of the substrate. On the other hand, increasing \(\gamma\) resulted in increased blade angle, hence coating thickness was increased.

Table 1 Coating thickness and load variations in (plane coater) and [exponential coater] cases
Full size table

The perturbation and numerical results are compared in terms of coating thickness displayed in Table 2 and for numerous values of perturbation parameter, \(\varepsilon\), both methods were observed to be in good agreement with each other.

Table 2 Comparison of perturbation and numerical values of coating thickness in (plane coater) and [exponential coater] cases
Full size table

Conclusion

In this work, an upper-convected Jeffery’s model was adopted to examine the blade coating analysis. The basic equations were stated and simplified using LAT, then transformed into dimensionless equations. Asymptotic perturbation and shooting technique were employed to find the problem solution. The effect of material parameters on various flow and engineering quantities were debated through graphs and in a tabular manner. The main findings are given as: both pressure distribution and pressure gradient were enhanced for increased values of \(\varepsilon\) and \(\alpha\). Enhancing \(\gamma\) resulted in decreased values of pressure distribution and pressure gradient. Maximum pressure was directly proportional to \(\varepsilon\) and \(\alpha\). Parameters \(\varepsilon\) and \(\alpha\) were the controlling parameters for both the load and final coating thickness, hence may help in increasing the efficiency of coating process. Increasing \(\varepsilon\) and \(\alpha\) resulted in reduced coating thickness and increased blade load. Perturbation results were validated by comparing with the numerical outcomes and found good agreement.